中国高等级公路设计中,水泥稳定碎石基层的设计厚度一般超过30 cm。传统施工方法采用分层不连续摊铺工艺,存在层间粘结效果差、基层易产生早期损伤等问题。基于此,大厚度水稳基层连续摊铺技术逐渐被运用于实际工程中。达姆施塔特大学[1-2]研究认为双层连续摊铺技术可节省施工成本;李晋鹏[3]以鹤大高速大厚度基层半幅摊铺段为依托,得到大厚度基层连续摊铺技术减轻分层铺筑形成的层间不连续变化规律;王选仓[4-5]等人通过大量的室内试验与理论研究,根据不同级配、不同厚度的路面结构组合,对双层摊铺层间黏结状况、温度散失规律、施工机械配置等进行了系统研究。综合研究可知,双层连续摊铺技术是传统施工工艺的一次革新,虽然国内外专家进行了深入的研究,但并未有规范对双层连续摊铺技术的施工控制与质量检验进行规定,新工艺施工过程中的基层塑性变形关键技术仍待进一步研究。
为研究大厚度连续摊铺下基层的塑性变形[6-9],笔者从材料的屈服条件入手,分析了水稳碎石材料弹、塑性变形的分界点,采用改进的Duncan-Chang模型计算大厚度基层的塑性变形;根据不同荷载作用下塑性变形规律,给出双层摊铺模式下下承层施工位移预估模型,通过平整度传递规律和现场检测数据,最终提出了基层双层连续摊铺平整度控制标准。
1 基于改进DUNCAN-CHANG的塑性变形邓肯-张(Duncan-Chang)模型[10-12]可以反映土体变形的主要规律,因其参数测试简单、实际应用方便而被广泛用于土层计算中。Duncan-Chang模型是根据双曲线应力应变关系提出的增量弹性模型,因此在计算大厚度基层连续摊铺导致的塑性变形前,应先确定水稳碎石材料弹、塑性变形的分界点,从而给出模型的适用范围。
1.1 水稳碎石屈服条件研究屈服条件是判断材料处于弹性阶段还是塑性阶段的准则,即物体内某一点开始产生塑性应变时,应力或应变所必须满足的条件[13]。Drucker-Prager准则(下文简称D-P准则)考虑了静水压力对于屈服强度的影响和屈服时的体积膨胀,相较Mohr-Coulomb准则更加合理的模拟岩土类材料,因此研究选用D-P准则作为屈服准则,屈服条件为
| $ \alpha {I_1} + \sqrt {{J_2}} - k = 0, $ | (1) |
式中:α,k为正的材料参数;I1为应力张量第一不变量;J2为应力偏张量第二不变量。
引入工程界常用的材料参数内摩擦角φ和黏结力c,将上式变换为如下
| $ \frac{{2\sin \;\varphi }}{{\sqrt 3 (3 - \sin \;\varphi )}}{I_1} + \sqrt {{J_2}} - \frac{{6c\;\cos \;\varphi }}{{\sqrt 3 (3 - \sin \;\varphi )}} = 0。$ | (2) |
采用JTG E40-2007静三轴试验测定混合料抗剪强度,材料组成如表 1所示,不考虑水泥的影响,级配为水泥:集料1(0~4.75 mm):集料2(4.75~9.5 mm):集料3(9.5~19 mm):集料4(19~37.5 mm)=4.5: 39: 21: 20: 20。
| 表 1 集料的基本性能 Table 1 basic properties of aggregates |
混合料加水密封18 h后制备φ 30 cm×60 cm的试件,将其固定在三轴仪上。控制围压为50 kPa、100 kPa、150 kPa 3种。试验结果如表 2所示。
| 表 2 剪切试验结果 Table 2 Shear test results |
将实验得到的c,φ值代入D-P屈服条件,并取σ3=100 kPa,得到未养生水稳混合料的屈服极限为220 kPa,即当偏应力≤220 kPa时,水稳混合料基层处于弹性阶段,当偏应力>220 kPa时,塑性变形开始累积。
1.2 基于改进DUNCAN-CHANG理论的塑性变形1963年,Kondner通过大量的三轴试验发现,(σ1-σ3)~ε1曲线可用双曲线来拟合,对于给定的σ3,(σ1-σ3)~ε1关系可以表示如下
| $ {\sigma _1} - {\sigma _3} = \frac{{{\varepsilon _1}}}{{a + b\;{\varepsilon _1}}}, $ | (3) |
Duncan等人根据这一双曲线应力应变关系提出了一种目前被广泛的增量弹性模型,一般被称为Duncan-Chang模型。
根据摩尔库伦准则,初始切线模量与固结压力的关系,可将公式变化得到塑性变形公式
| $ \begin{array}{l} {\varepsilon _1} = \frac{{{\sigma _1} - {\sigma _3}}}{{K\;{P_{\rm{a}}}{{\left( {\frac{{{\sigma _3}}}{{{P_a}}}} \right)}^n}}}/\left[ {1 - \frac{{\left( {{\sigma _1} - {\sigma _3}} \right)(1 - \sin \varphi ){R_{\rm{f}}}}}{{2c\;\cos \varphi + 2{\sigma _3}\sin \varphi }}} \right], \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{R_{\rm{f}}} = \frac{{{{\left( {{\sigma _1} - {\sigma _3}} \right)}_{\rm{f}}}}}{{{{\left( {{\sigma _1} - {\sigma _3}} \right)}_{{\rm{ult}}}}}}, \end{array} $ | (4) |
式中:Pa为大气压力;K,n为实验常数;一般情况下0.2<n<1,这里引入Pa,是为了将坐标化为无因次量。
Duncan-Chang模型公式简单,试验参数较少,而且物理、几何意义比较明确,在一定程度上反应了岩土材料的非线性应力应变关系,但是,Duncan-Chang模型是依据粘土提出来的,并没有考虑粗集料的剪胀性和压硬性。
因此,郑春婷[14-15]为克服传统模型所存在的数学缺陷,提出引入试验常数θ,将切线模量表达式改进为下式
| $ {E_i} = K\;{P_{\rm{a}}}{\left( {\frac{{{\sigma _3}}}{{{P_{\rm{a}}}}}} \right)^n}{\left[ {1 - \frac{{\left( {{\sigma _1} - {\sigma _3}} \right)(1 - \sin \varphi ){R_{\rm{f}}}}}{{2c\;\cos \varphi + 2{\sigma _3}\sin \varphi }}} \right]^\theta }, $ | (5) |
通过研究上述改进模型,发现并不能很好的适用于未养生的水稳碎石塑性变形。为克服Duncan-Chang模型的不足,使其能够适用于未养生的水泥稳定碎石材料,根据实测应力应变曲线,比较分析了Duncan-Chang及改进了切线模量后的公式,提出在公式4中引入调节因子θ如下式
| $ {\varepsilon _1} = \frac{{{\sigma _1} - {\sigma _3}}}{{K\;{P_{\rm{a}}}{{\left( {\frac{{{\sigma _3}}}{{{P_{\rm{a}}}}}} \right)}^n}}}/{\left[ {1 - \frac{{\left( {{\sigma _1} - {\sigma _3}} \right)(1 - \sin \varphi ){R_{\rm{f}}}}}{{2c\;\cos \varphi + 2{\sigma _3}\sin \varphi }}} \right]^\theta }。$ | (6) |
由研究可知,对于围压为100 kPa的未养生水泥稳定碎石,当偏应力小于220 kPa时,基层处于弹性阶段,此时材料的初始切线模量在数值上等于回弹模量,因此,对试件进行三轴试验。
试验方案:根据AASHTO试验规定,采用FHWA试验设备,制备φ102 mm×203 mm的试件,设置侧限压力为103.5 kPa,并依次施加6.9、14、35、69、104和138 kPa的偏应力,并记录各偏应力重复作用200次的结果。根据试验结果,取初始切线模量为500 kPa。试验结果表 3所示。
| 表 3 回弹模量的计算 Table 3 Calculation of Resilient Modulus |
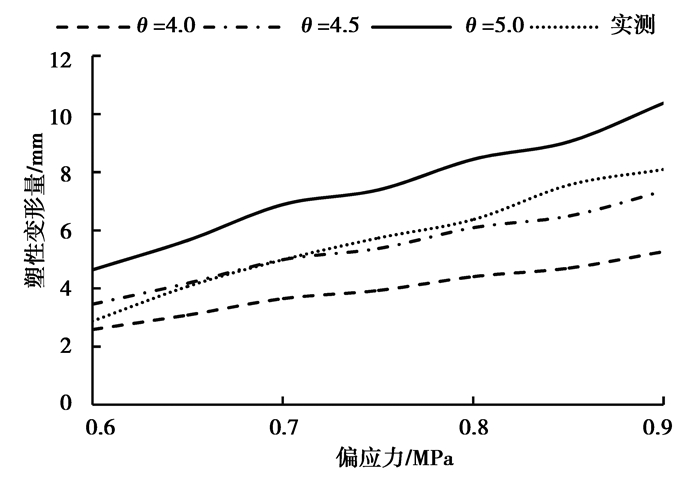
为验证改进Duncan-Chang模型的准确性,依托试验段进行现场检测,得到不同压应力下未养生水泥稳定碎石基层的塑性变形量,并将θ取4、4.5、5时的模型预测值进行了对比,计算结果如图 1所示。
|
图 1 预测值与实测值对比 Fig. 1 Comparison between predicted and observed values |
由图 1可知,塑性变形量随偏应力的增加呈线性增加趋势,当偏应力增大到塑性变形达到极限值时,基层会发生破坏。在极限偏应力与初始切线模量相同的情况下,调节因子θ能有效地调节模型应力-应变的变化速度,弥补了Duncan-Chang模型的缺陷,随着调节因子θ的增大,塑性变形量增大,增长速度增快,因此,在其他条件相同的条件下,调节因子θ与塑性变形量的增长速度呈正相关。当θ=4.5时,改进模型的塑性变形量预测值与实测值有很高的相关性,可以用来预测未养生水泥稳定碎石基层施工期内的变形值,预测公式如下
| $ {\varepsilon _1} = \frac{{{\sigma _1} - {\sigma _3}}}{{K\;{P_{\rm{a}}}{{\left( {\frac{{{\sigma _3}}}{{{P_{\rm{a}}}}}} \right)}^n}}}/{\left[ {1 - \frac{{\left( {{\sigma _1} - {\sigma _3}} \right)(1 - \sin \varphi ){R_{\rm{f}}}}}{{2c\;\cos \varphi + 2{\sigma _3}\sin \varphi }}} \right]^{4.5}}。$ | (7) |
大厚度底基层双层连续摊铺采用全幅流水作业,2台摊铺机同时作业,一台摊铺下底基层,一台摊铺上底基层,2台摊铺机之间留有一定工作空间,便于碾压设备及时压实水泥稳定混合料。由于水泥稳定下底基层未经过一定龄期的养生,强度难以达到传统摊铺对于下承层的要求,故在进行上底基层施工时,施工车辆作用在未经养生的水稳基层上会对道路造成塑性车辙破坏,从而影响平整度质量。通过分析荷载作用次数对塑性变形的影响,建立大厚度水稳底基层塑性变形模型。
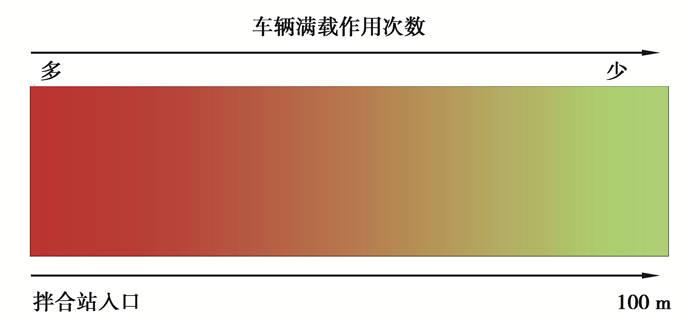
2.1 荷载作用次数对塑性变形的影响施工段每隔100 m设置出入便道,便于运输车辆、摊铺机不间断施工,尽可能减少施工车辆对底基层的影响。整个施工过程中的荷载作用次数分布如图 2所示。图中红色表示车辆满载下作用次数较多,绿色表示车辆满载下作用次数较少。从图中2可得,离入口越近,作用次数越多,因此入口处承受的满载下作用次数最多。
|
图 2 荷载作用次数分布 Fig. 2 Distribution of load times |
一辆运料车在现场摊铺的长度可以由公式(8)计算
| $ L = \frac{T}{{\rho HW}}, $ | (8) |
式中:L为一辆运料车摊铺长度, m;T为一车水稳混合料的重量, t;ρ为水稳混合料堆积密度, g·cm-3;H为路面松铺厚度,m;W为摊铺宽度,m。
则路面最不利位置施工荷载作用次数为
| $ N = \frac{{1\;000}}{L}, $ | (9) |
式中:N为运料车作用次数;T=45 t,ρ=1.6g/cm3,H=22.5 cm,W=11.25m,由公式(8)、(9)计算可知,一车料大约摊铺11.11 m左右,100 m大约需要9车料,即路面最不利位置需经过9次运输车的重复荷载作用。
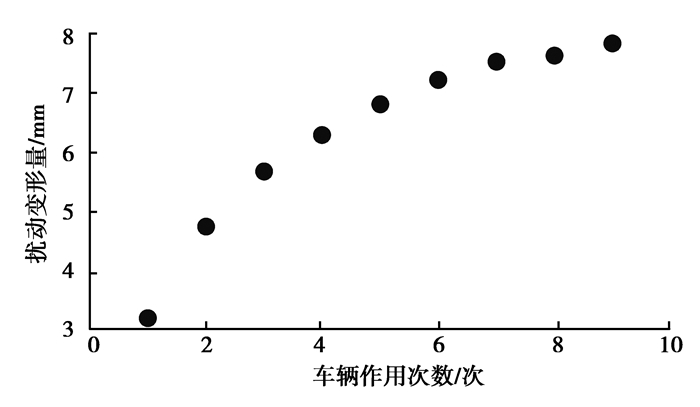
在试验段上取断面K130+040,采用3 m直尺对路段横向进行连续3尺检测;上层摊铺过程中,每次在运输车辆压过后,对上次测量的3个断面,采用3 m直尺进行横向连续3尺检测,以确定运输车辆对摊铺层的平整度扰动情况。检测结果如图 3所示。
|
图 3 实测扰动变形量随车辆作用次数的变化关系 Fig. 3 Relationship between measured disturbance deformation and the vehicle action times |
由图可得,实际工况下扰动位移量随运输车辆作用次数的增加而增加,且增加速度越来越慢,最终逐渐趋向于固定值,竖向变形不再增加。荷载作用最初5次内完成的变形量达到了总变形量的80%以上,之后变形量增长速率明显变缓,最大变形量大约在8 mm左右。
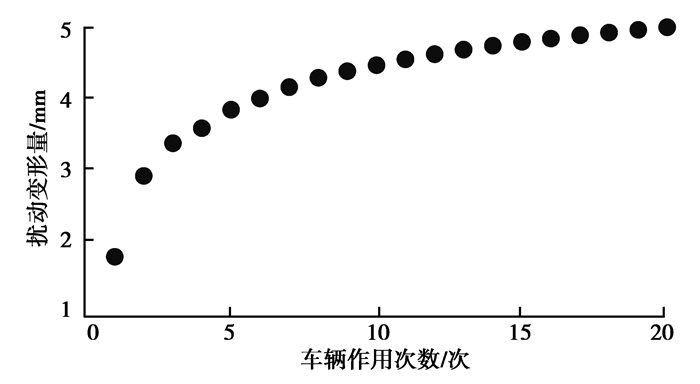
同时通过MTS810材料试验机对水稳碎石试件进行室内重复加载试验[16]。加载波形设定为:半正弦波,0.1 s加载时间,0.9 s间歇时间;应力水平1.0 MPa;荷载作用不少于12次;压实度不小于97%,试验材料参数及级配如表 1所示。为保证试验准确性,在试验开始前,设置正弦荷载的最小荷载为最大荷载的15%,并以最小荷载对试件预加载,使试件和压头加载设备之间接触良好。对数据进行处理后,建立扰动量与荷载作用次数关系如图 4。
|
图 4 室内试验扰动变形量随车辆作用次数的变化关系 Fig. 4 Relationship between disturbance deformation and the vehicle action times in laboratory tests |
由室内试验可得,荷载作用最初8次内完成的变形量达到了总变形量的80%以上,之后变形量增长速率明显变缓,最大变形量大约在5 mm左右。室内试验下的塑性变形较工地实测变化缓慢,是因为施工现场情况复杂,施工及检测影响因素较多,因此会产生一定变异性。
2.2 建立基层塑性变形模型选择Visser、Wolff作为预估模型,并结合实测数据建立相应函数关系式,得到双层摊铺模式下下承层施工位移预估模型模型参数。
| $ \varepsilon = (cN + a)\left( {1 - {{\rm{e}}^{ - bN}}} \right), $ | (10) |
式中:ε为材料累计变形量;N为重复荷载加载次数;a, b, c为材料参数。
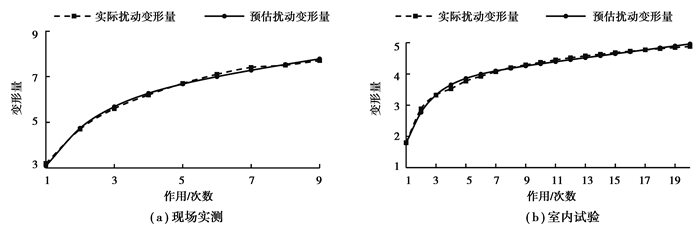
采用数据分析软件对室内模拟试验及现场实测数据参数进行非线性回归拟合,拟合结果与实测值对比如见图 5。模型参数a,b,c的拟合结果见表 4。
|
图 5 预测值与实测值对比 Fig. 5 Comparison between predicted and observed values |
| 表 4 模型参数拟合结果 Table 4 Model parameter fitting results |
将施工位移预估模型运用于现场实测、室内试验的结果预测中,均能得到高精度的预测结果,说明该模型适用于双层摊铺模式下下承层施工位移预估,可以用于指导施工从而保证施工质量。
3 基于塑性变形的平整度控制研究与传统摊铺工艺相比,大厚度连续摊铺由于下层施工扰动变形较大,未经过处理难以达到传统摊铺的控制标准。笔者研究了平整度传递规律,给出了基于大厚度基层连续摊铺的平整度控制标准。
3.1 平整度传递规律在理想状态下,平整度一般由路基开始,逐层向上传递,随结构层数的增加而呈指数降低。当路基平整度为β土,底基层、基层、面层等结构层的松铺系数分别为λ1λ2…λn,则路基平整度传递到某一结构层的影响量为[17]
| $ {\beta _{传递}} = \left( {1 - \frac{1}{{{\lambda _1}}}} \right)\left( {1 - \frac{1}{{{\lambda _2}}}} \right) \cdots \left( {1 - \frac{1}{{{\lambda _n}}}} \right){\beta _{土}}, $ | (11) |
上式基于理想状态下提出平整度传递公式,但实际施工中需要考虑的影响因素较多,因此需进行平整度公式修正。根据路面施工技术规范,路基、基层、面层的平整度要求越来越严格,因此在传递过程中应减少影响量,结合相关学者研究,引入影响因素q,并根据正态分布理论确定保证率为1.86,标准差为0.9,得到修正后的平整度传递公式(12)
| $ {\beta _{面}} = {(1 - 1.86q)^{ - n}}\left( {1 - \frac{1}{{{\lambda _1}}}} \right)\left( {1 - \frac{1}{{{\lambda _2}}}} \right) \cdots \left( {1 - \frac{1}{{{\lambda _n}}}} \right){\beta _{土}}, $ | (12) |
将修正后的平整度传递公式引入到大厚度水稳基层连续摊铺施工中,设平整度由下基层开始传递,向上传递至上基层,n=1,得到平整度传递公式(13)
| $ {\beta _{上}} = {(1 - 1.86q)^{ - 1}}\left( {1 - \frac{1}{\lambda }} \right){\beta _{下}}, $ | (13) |
式中:β上为上基层平整度;λ为上基层的松铺系数,取1.25;β下为下基层平整度实测值;q为其他影响因素造成的影响量。
大厚度基层连续摊铺施工中,由于下承层塑性变形较大,严重影响了上基层的平整度控制。因此,除满足规范对基层平整度的要求外,还应根据平整度传递规律适当提高下承层的平整度控制要求。
3.2 双层连续摊铺平整度控制标准双层连续摊铺平整度检测包括上基层平整度检测和下基层平整度检测,当上基层施工时,施工车辆作用在未经养生的水稳基层上会对下基层造成塑性变形,影响平整度质量。为了研究施工车辆对双层连续摊铺下基层的扰动影响,在内蒙古省道203第8标段K108+780~108+880进行了平整度扰动检测,结果如表 5所示。
| 表 5 K108+780~K108+880底基层纵向平整度检测结果 Table 5 Test results of vertical flatness of subbase (mm) of K108+780~K108+880mm |
中国规范中要求高速、一级公路底基层摊铺平整度的控制标准为12 mm,但是根据道路施工平整度传递理论的分析可知,在双层连续摊铺施工中下基层平整度标准欠佳会传递到上层施工,从而增加上基层的平整度,甚至使上层平整度达不到规范要求。根据《公路工程质量检验评定标准》中平整度检测的保证率95%,对现场检测数据进行可靠度处理,利用Matlab拟合得到q=0.413 7,带入式(13)中可得到下式
| $ {\beta _{{\rm{上}}}} = \left( {1 - \frac{1}{\lambda }} \right) \times {(1 - 1.86 \times 0.2305)^{ - 1}}{\beta _{{\rm{下}}}}, $ | (14) |
依托工程试验段设计厚度为16 cm,松铺系数为1.25,β上为规范标准的12 mm,代入式(14)中并取整,可以得出β下=14mm。则在16 cm+16 cm底基层双层连续摊铺过程中,下层平整度质量控制标准下限为14 mm。
考虑大厚度基层连续摊铺上下层之间的施工扰动,根据上文平整度传递规律的研究可得,连续摊铺工艺的平整度控制应当比传统施工工艺要求更加严格。因此,对连续摊铺平整度控制提出以下原则:连续摊铺层中、下层应按下一级层位施工标准进行平整度控制,其它层位按照传统摊铺施工标准进行控制,具体控制标准见表 6。
| 表 6 平整度质量控制标准 Table 6 quality control standards of flatness |
研究对大厚度基层连续摊铺下产生的塑性变形进行基于改进的Duncan-Chang模型分析,并进行了大量室内剪切试验及试验路平整度实测试验,得到以下结论:
1) 根据D-P屈服条件,得到水稳混合料的屈服极限为220 kPa,即当偏应力≤220 kPa时,水稳混合料基层处于弹性阶段,当偏应力>220 kPa时,塑性变形开始累积。
2) 改进了Duncan-Chang模型,引入调节因子θ,计算分析了半刚性基层连续摊铺工况下基层塑性变形,得到了未养生水泥稳定碎石基层施工期内的变形值预测公式。
3) 通过分析荷载作用次数对基层塑性变形的影响,得到双层摊铺模式下下承层施工位移预估函数。
4) 通过研究半刚性基层平整度传递规律,建立了平整度扰动预估模型,并提出连续摊铺施工技术的平整度控制标准。
| [1] |
Bruglachner H, Jordan S, Schmidt M, et al. New electrolytes for electrochemical double layer capacitors I[J]. Journal of New Materials for Electrochemical Systems, 2006, 9(3): 209-220. |
| [2] |
Grossmann S, Weyrauch T, Saal S, et al. Internal electrical field distribution in double layer polymer stacks as studied by electroabsorption[J]. Optical Materials, 1998, 9(4): 236-239. |
| [3] |
李晋鹏, 王伟. 大厚度一次整幅摊铺水稳基层施工技术应用研究[J]. 公路, 2016(06): 56-61. LI Jingpeng, WANG Wei. Application research on construction technology of large thickness single paving water stabilized base course[J]. Highway, 2016(06): 56-61. (in Chinese) DOI:10.3969/j.issn.1671-8879.2016.06.008 |
| [4] |
乔志, 王选仓, 张志芳, 等. 半刚性基层双层连续摊铺层间结合状态[J]. 交通运输工程学报, 2016(03): 28-34. QIAO Zhi, WANG Xuancang, ZHANG Zhifang, et al. Interlayer combination state of double-layer continuous paving semi-rigid base[J]. Journal of Traffic And Transportation Engineering, 2016(03): 28-34. (in Chinese) DOI:10.3969/j.issn.1671-1637.2016.03.004 |
| [5] |
乔志, 王选仓, 徐子涛, 等. 半刚性基层双层连续摊铺施工组织工艺研究[J]. 中国公路学报, 2016(03): 41-47. QIAO Zhi, WANG Xuancang, XU Zitao, et al. Study on construction organization process of continuous double-layer paving semi-rigid base[J]. China Journal of Highway and Transport, 2016(03): 28-34. (in Chinese) |
| [6] |
Liu Zh Y, Liu J Y, Wang Zh Q, et al. Compressive strength and frost heave resistance of different types of semi-rigid base materials after freeze-thaw cycles[J]. Sciences in Cold and Arid Regions, 2015, 7(4): 365-369. |
| [7] |
Herndo, VAL M A D. Guidelines for the design of semi-rigid long-life pavements[J]. International Journal of Pavement Research and Technology, 2016, 9(2): 121-1277. DOI:10.1016/j.ijprt.2016.03.003 |
| [8] |
Wu J, Liang J, Adhikari S. Dynamic response of concrete pavement structure with asphalt isolating layer under moving loads[J]. Journal of Traffic and Transportation Engineering (English Edition), 2014, 1(6): 439-447. DOI:10.1016/S2095-7564(15)30294-4 |
| [9] |
Hou T S, Wang W, Luo Y S, et al. Mechanical behavior of light-weight soil under consolidated drained shear condition[J]. Marine Georesources & Geotechnology, 2014, 32(3): 264-276. |
| [10] |
Li Y L, Li S Y, Ding Z F, et al. The sensitivity analysis of Duncan-Chang E-B model parameters based on the orthogonal test method[J]. Journal of Hydraulic Engineering, 2013, 39(S2): 79-85. |
| [11] |
汪智慧, 陈晨. 基于扰动状态理论的沈阳砾砂修正邓肯-张模型[J]. 沈阳建筑大学学报(自然科学版), 2017, 33(01): 68-76. WANG Zhihui, CHEN Chen. The modified Duncan-chang model for gravelly sand in Shenyang based on the disturbed state concept[J]. Journal of Shenyang Jianzhu University(Natural Science), 2017, 33(01): 68-76. (in Chinese) |
| [12] |
沈启鹏, 吴道祥, 胡雪婷, 等. 基于应力应变曲线类型的邓肯张模型修正[J]. 合肥工业大学学报(自然科学版), 2017, 40(9): 1264-1268. SHEN Qipeng, WU Daoxiang, Hu Xueting, et al. Duncan-chang model modification based on stress-strain curve type[J]. Journal of Hefei University of Technology (Natural Science), 2017, 40(9): 1264-1268. (in Chinese) DOI:10.3969/j.issn.1003-5060.2017.09.022 |
| [13] |
蒋应军, 陈浙江, 李寿伟, 等. 级配碎石塑性变形特性及其安定行为的数值模拟[J]. 同济大学学报(自然科学版), 2015, 43(06): 872-876. JIANG Yingjun, CHEN Zhejiang, LI Shouwei, et al. Plastic deformation characteristics and numerical simulation of shakedown behavior of graded broken stone[J]. Journal of Tongji University (Natural Science), 2015, 43(06): 872-876. (in Chinese) |
| [14] |
郑春婷, 蔡燕燕, 戚志博, 等. 基于回归分析法的改进Duncan-Chang模型研究[J]. 武汉理工大学学报, 2012, 34(04): 108-112. ZHENG Chunting, CAI Yanyan, QI Zhibo, et al. Use regression analysis to study the improved Duncan-Chang model[J]. Journal of Wuhan University of Technology, 2012, 34(04): 108-112. (in Chinese) DOI:10.3963/j.issn.1671-4431.2012.04.024 |
| [15] |
王伟, 卢廷浩, 周干武. 黏土非线性模型的改进切线模量[J]. 岩土工程学报, 2007, 29(3): 458-462. WANG Wei, LU Tinghao, ZHOU Ganwu. Improved tangent modulus of nonlinear soil model[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(3): 458-462. (in Chinese) DOI:10.3321/j.issn:1000-4548.2007.03.025 |
| [16] |
Mazaheripour H, Rui F, Ye G, et al. Microstructure-based prediction of the elastic behaviour of hydrating cement pastes[J]. Applied Sciences, 2018, 8(3): 442. DOI:10.3390/app8030442 |
| [17] |
马建, 赵祥模, 贺拴海, 等. 路面检测技术综述[J]. 交通运输工程学报, 2017, 17(05): 121-137. MA Jian, ZHAO Xiangmo, HE Shuanhai, et al. Review of pavement detection technology[J]. Journal of Traffic and Transportation Engineering, 2017, 17(05): 121-137. (in Chinese) DOI:10.3969/j.issn.1671-1637.2017.05.012 |
 2019, Vol. 42
2019, Vol. 42


