2. 直升机传动技术国防科技重点实验室, 湖南 株洲 412002
2. National Key Laboratory of Defence Science and Technology on Helicopter Transmission, Zhuzhou 412002, Hunan, P. R. China
传统波束形成(CB, conventional beamforming)是将声源所在平面划分为有限个网格点,然后利用一定几何形状排列的麦克风阵列测量得到声压信号,再通过延时求和算法对每个网格点进行聚焦从而增强真实声源方向的信号形成主瓣,同时衰减其他方向的干扰信号形成旁瓣[1-2],使阵列具有指向性。传统波束形成算法的输出结果理论上是声源分布与阵列点传播函数的卷积,阵列传声器采样的有限性和离散性使其点传播函数无法等于理想的δ函数,不仅在真实声源位置输出具有一定宽度的主瓣,还在非声源位置输出旁瓣。宽的主瓣影响声源定位的准确性,而旁瓣的出现则污染了成像结果,使真实声源难以被辨别。因此,寻找高分辨、高计算效率的声源识别方法成为了国内外学者研究的重点。
美国NASA的Brooks[3]于2004年提出了经典的反卷积声源成像方法(DAMAS, the deconvolution approach for the mapping of acoustic sources),该方法通过高斯塞德尔迭代法求解传统波束形成输出和声源分布之间构造的线性方程组,使成像结果有了显著提升,然而其变量多、计算量大、耗时长[4-6]的问题一直限制着DAMAS的实际应用。2008年,Yardibi等[7]利用声源的稀疏特性改进了DAMAS逆问题的求解方法,提出了稀疏约束反卷积(SC-DAMAS, sparsity constrained deconvolution approach for the mapping of acoustic sources)。2015年,Padois等[8]将正交匹配追踪算法(OMP, orthogonal matching pursuit)应用于DAMAS逆问题的求解提出了正交匹配追踪反卷积声源识别方法(OMP-DAMAS, orthogonal matching pursuit applied to the deconvolution approach for the mapping of acoustic sources inverse problem),进一步提升了反卷积方法的识别性能。
OMP算法是属于贪婪算法的一种典型稀疏信号重构方法[9]。原理是将信号在过完备字典矩阵中进行分解,其按照一定的贪婪法则寻找字典中与信号最匹配的原子,最终将信号表示成这些原子的稀疏组合。OMP算法由于其计算量小,求解速度快[10]的优点具有重要的研究应用价值。2011年,Peillot等[11]将OMP算法应用于压缩感知声源识别,研究结果显示OMP算法的分辨率相较于波束形成有明显的提高。2016年,宁方立等[12-13]基于压缩感知声源识别方法研究OMP算法对不同类型声源的分辨率以及对噪声的鲁棒性并识别了空间声源。虽然对OMP算法应用于压缩感知声源识别的相关研究已取得较多成果,但关于OMP-DAMAS波束形成声源识别结果随声源频率、迭代次数、信噪比等参数变化规律的研究还很鲜见。
笔者研究了反卷积OMP-DAMAS波束形成声源识别方法,并基于MATLAB实现相应算法。通过仿真计算4个单极子点声源在不同识别方法下的成像结果,分析其定位精度和分辨能力,探究OMP-DAMAS成像结果随迭代次数、信号频率、信噪比等参数的变化规律,对该技术的运用具有重要的指导意义。基于扬声器的声源识别实验验证了仿真分析的结论。
1 理论 1.1 反卷积波束形成传统波束形成采用一定顺序排列的传声器阵列接受声压信号,通过延迟求和算法对声源平面离散的各网格点进行反向聚焦,从而增强来波方向的信号,衰减其他方向的信号,进而识别声源。
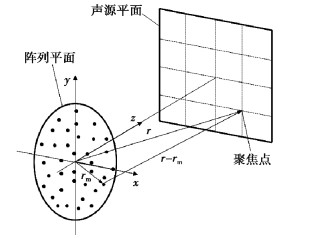
反卷积波束形成通过网格点和传声器分布的几何关系确定点声源在不同网格点时对其他网格点位置产生的波束形成声压贡献量,在传统波束形成输出和声源分布矢量之间引入正定约束,通过求解线性方程组将传统波束形成输出结果转化为更加精确的声源分布矢量。传统波束形成的输出量[6]为
|
图 1 波束形成声源识别布局图 Fig. 1 Beamforming configuration |
| $ \mathit{\boldsymbol{b}}(\mathit{\boldsymbol{r}}) = \frac{{{\mathit{\boldsymbol{v}}^{\rm{T}}}(\mathit{\boldsymbol{r}})\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{v}}^*}(\mathit{\boldsymbol{r}})}}{{{\mathit{\boldsymbol{w}}^{\rm{T}}}(\mathit{\boldsymbol{r}})\mathit{\boldsymbol{l}}{\mathit{\boldsymbol{w}}^*}(\mathit{\boldsymbol{r}})}}, $ | (1) |
式中:C为传声器接收声压信号的全互谱矩阵;l为所有元素均为1的矩阵;v=vm(r)为聚焦点为r的导向列向量;w=[|vm|]2;上标T和*分别表示转置和共轭。vm(r)表示第m个传声器的导向矢量,其表达式为
| $ {\mathit{\boldsymbol{v}}_m}(\mathit{\boldsymbol{r}}) = {{\rm{e}}^{ - jk|r - rm|}}/\left| {\mathit{\boldsymbol{r}} - {\mathit{\boldsymbol{r}}_m}} \right|, $ | (2) |
在非相干声源条件下,全互谱矩阵C可以表示为各声源单独作用时传声器接收声压信号的互谱矩阵之和,为
| $ \mathit{\boldsymbol{C}} = \sum\nolimits_{\mathit{\boldsymbol{r}}'} \mathit{\boldsymbol{C}} \left( {{\mathit{\boldsymbol{r}}^\prime }} \right) = \sum\nolimits_{\mathit{\boldsymbol{r}}'} q \left( {{\mathit{\boldsymbol{r}}^\prime }} \right){\mathit{\boldsymbol{v}}^*}\left( {{\mathit{\boldsymbol{r}}^\prime }} \right){\mathit{\boldsymbol{v}}^{\rm{T}}}\left( {{\mathit{\boldsymbol{r}}^\prime }} \right), $ | (3) |
式中:r′为声源位置向量; q(r′)为r′处源强。将式(3)代入式(1)得到:
| $ \left\{ \begin{array}{l} \;\;\;\;\;\;\;\;b(\mathit{\boldsymbol{r}}) = \sum\nolimits_{r'} q \left( {{\mathit{\boldsymbol{r}}^\prime }} \right){\mathop{\rm psf}\nolimits} \left( {\mathit{\boldsymbol{r}}|{\mathit{\boldsymbol{r}}^\prime }} \right), \\ {\mathop{\rm psf}\nolimits} \left( {\mathit{\boldsymbol{r}}|{\mathit{\boldsymbol{r}}^\prime }} \right) = \frac{{{\mathit{\boldsymbol{v}}^{\rm{T}}}(\mathit{\boldsymbol{r}}){\mathit{\boldsymbol{v}}^*}\left( {{\mathit{\boldsymbol{r}}^\prime }} \right){\mathit{\boldsymbol{v}}^{\rm{T}}}\left( {{\mathit{\boldsymbol{r}}^\prime }} \right){\mathit{\boldsymbol{v}}^*}(\mathit{\boldsymbol{r}})}}{{{\mathit{\boldsymbol{w}}^{\rm{T}}}(\mathit{\boldsymbol{r}})l{w^*}(\mathit{\boldsymbol{r}})}}, \end{array} \right. $ | (4) |
其中,psf(r|r′)称为阵列点传播函数,表示当仅有r′位置处存在单位源强的点声源时,其对r位置处产生的波束形成声压贡献量,当r=r′时,psf=1。可见,r位置处的波束形成输出量可以表示成各声源点在该点的波束形成声压贡献乘以对应源强后再求和。根据此关系,反卷积算法构建了波束形成输出结果、阵列点传播函数和声源分布之间的线性方程组,为
| $ \mathit{\boldsymbol{b}} = \mathit{\boldsymbol{Aq}}, $ | (5) |
式中:b=[b(r)]为N维波束形成输出列向量,N为网格点数目;A=[psf(r|r′)]为N×N维的点传播函数矩阵;q为N维的声源分布列向量;其中A、b已知,q未知。对式(5),DAMAS方法采用高斯赛德尔迭代法求解,而SC-DAMAS则通过对声源分布矢量施加l1范数正则化约束,最小化波束形成输出误差,使q趋近于真实声源分布。
1.2 正交匹配追踪OMP算法正交匹配追踪每次迭代均会在字典矩阵A中找到与信号b相关系数[13]最大的原子,将信号在选定原子的方向上进行正交投影得到残差矢量,则信号可以由该原子与残差矢量线性表示。显然残差矢量随迭代次数的增加逐渐收敛。经过一定次数的迭代后便可得到原始信号在已选原子下的近似稀疏表示,即q。通过OMP算法求解DAMAS逆问题的步骤如下[8, 14-15]:
1) 初始化t=1,残差rt-1=b,支撑集Jt-1=∅(空集),矩阵Λt-1=0。
2) 寻找索引λ=arg maxl |AHrt-1|。
3) 令Jt=Jt-1∪λ,Λt=Λt-1∪aλ,(aλ为A的第λ列向量)。
4) 计算最小二乘解
| $ {{\mathit{\boldsymbol{\hat \theta }}}_t} = \arg \;\mathop {\min }\limits_{{\theta _t}} {\left\| {{\mathit{\boldsymbol{b}}} - {{\mathit{\boldsymbol{\Lambda }}}_t}{{\mathit{\boldsymbol{\theta }}}_t}} \right\|_2}。$ |
5) 更新残差矢量
6) t=t+1,回到步骤(3)直到达到终止条件i等于迭代次数S。
7) 获得声源强度矢量估计值q在Jt处有非零值,其值为
式中:l=1, …, N,为声源分布矢量的索引;J为最终的索引设置;迭代次数S为声源数目的估计值,可以通过残差矢量的l2范数随迭代次数的收敛情况确定[8, 11]。q的稀疏性取决于OMP算法的迭代次数,即q中非零元素的个数等于OMP算法的迭代次数。OMP算法理论上并不能获得解析解,不同于SC-DAMAS,其目标函数的收敛速度与信号的稀疏程度有关。当信号足够稀疏时,其表现出相当高的求解效率。
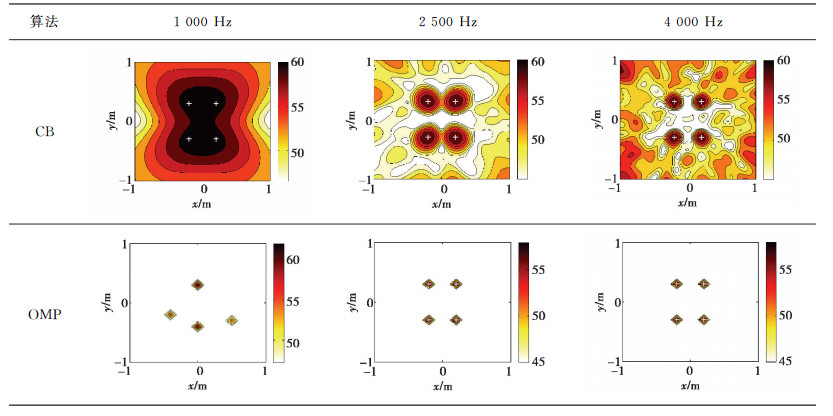
2 数值仿真基于OMP-DAMAS波束形成理论,设计相应的声源识别算法,模拟计算声源所在平面的识别成像结果并与传统波束形成识别结果进行对比。假设阵列所在平面为x-y平面,以阵列中心为原点,阵列前方为z轴正方向,采用直径为0.65 m的36通道Comb阵列识别阵列前方2 m×2 m的平面区域,声源平面距离阵列1 m,将声源平面离散为21×21个网格点。仿真假设声源为4个非相干单极子点声源,其坐标为(0.2, -0.3, 1)、(-0.2, -0.3, 1)、(0.2, 0.3, 1)、(-0.2, 0.3, 1)m,分别计算声源频率为1 000、2 500和4 000 Hz情况下的成像结果,有效声压均为0.02 Pa,对应声压级为60 dB,成像结果参考基准声压进行分贝转化,设置显示动态范围为15 dB。
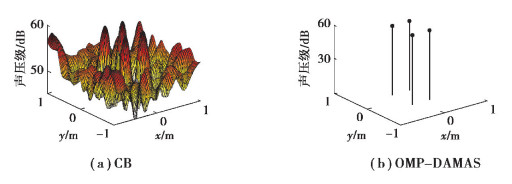
仿真结果如表 1所示,图中真实声源位置用白色十字标出,高幅值黑点为“主瓣”指示了声源所在位置。在非声源位置出现幅值较高的点为“旁瓣”使成像结果恶化,成像结果不清晰。对非相干声源的识别结果显示,2 500 Hz和4 000 Hz时的各图均在真实声源位置出现了主瓣,声源被有效定位。其中传统波束形成输出大量旁瓣,且主瓣宽度大,成像污染严重,而OMP-DAMAS输出较小的主瓣宽度,且无旁瓣出现,其分辨率更高,成像更加清晰。图 2为声源频率为4 000 Hz情况下的传统波束形成和OMP-DAMAS主瓣宽度对比结果。由图 2可以看到,传统波束形成输出的主瓣宽度大,定位精度低,而OMP-DAMAS的主瓣宽度小,能更加精确地定位声源。对不同声源频率的识别结果显示,OMP-DAMAS对2 500 Hz和4 000 Hz声源均能够准确定位,而对1 000 Hz声源的定位结果则严重偏离了声源实际位置。其成像规律满足“中高频效果好”的特性。
| 表 1 4个声源识别成像图 Table 1 Imaging diagram of four acoustic sources |
|
图 2 CB和OMP-DAMAS主瓣宽度对比图 Fig. 2 Comparison diagram of mainlobe width between CB and OMP-DAMAS |
为探究迭代次数对OMP-DAMAS成像结果的影响规律,固定声源频率为2 500 Hz,在添加SNR=15 dB高斯白噪声的情况下计算不同迭代次数下的识别结果,如图 3所示。图 3(a)迭代次数小于声源数目时,OMP-DAMAS仅识别出了部分声源,而图 3(c)迭代次数超过声源数目时,OMP-DAMAS又会在非声源位置重构出虚假声瓣。理论上OMP-DAMAS获得准确的成像结果依赖于对声源数目的正确估计。但实际上当信噪比较高时,由于重构出的旁瓣声压级较低,因此可以通过设置合适的动态范围以避免旁瓣污染。
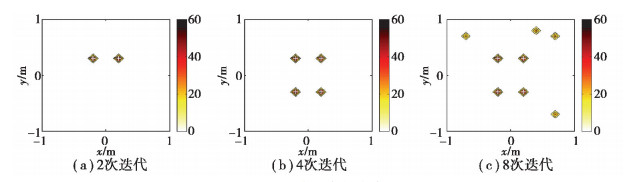
|
图 3 不同迭代次数成像结果 Fig. 3 Imaging results of different iteration number |
为进一步分析OMP-DAMAS对噪声的鲁棒性,固定声源频率为2 500 Hz,分别添加SNR为-5、0、15 dB高斯白噪声计算其成像结果,如图 4所示。由仿真结果可知,当信噪比高于0 dB时,OMP-DAMAS均能准确识别声源,而当信噪比为-5 dB时,OMP-DAMAS的识别结果与实际位置出现了较大偏差,这是由于噪声相比声源信号起主导作用,对信号影响过大,使OMP-DAMAS无法识别出真实声源。
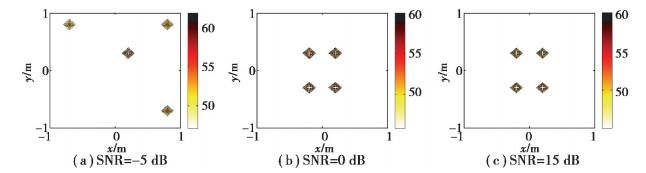
|
图 4 不同信噪比成像结果 Fig. 4 Imaging results of different SNR |
由上述仿真结果可知,声源频率和信噪比均对OMP-DAMAS识别准确度有重要影响。为同时量化由声源频率和信噪比2个因素引起的计算偏差,随机布置4个声源位置,有效声压均为0.02 Pa,固定迭代次数为4次,用式(6)定义的偏差值来衡量识别准确度。
| $ \sigma = {\rm{||}}\mathit{\boldsymbol{b}} - {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_4}{\mathit{\boldsymbol{\widehat \theta }}_4}{\rm{|}}{{\rm{|}}_2}。$ | (6) |
图 5为模拟计算的偏差值随声源频率和信噪比变化的结果,其中横坐标为声源频率,其范围从1 000 Hz变化到4 000 Hz,纵坐标为信噪比,其范围从-10 dB变化到15 dB。由图 5可知,当声源频率高于2 300 Hz,信噪比大于0 dB时,偏差值经过4次迭代后已经几乎收敛为0。
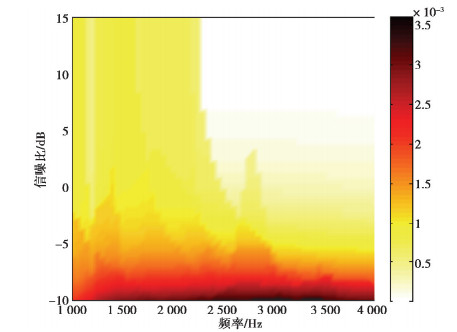
|
图 5 偏差值随声源频率和信噪比变化的结果 Fig. 5 Result of deviation value varying against signal frequency and SNR |
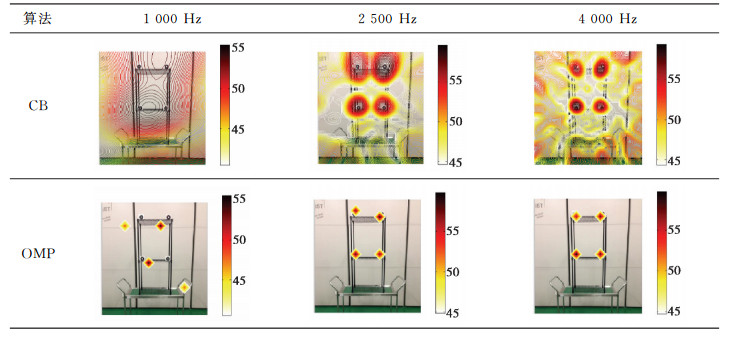
仿真计算结果表明,反卷积波束形成OMP-DAMAS声源识别方法能够准确识别声源并具备高分辨率和高定位精度的优势,其适用于对中高频声源的定位且对噪声的适应性较好,在信噪比高于0 dB的情况下均能获得准确的识别结果。采用4个扬声器在半消声室环境下进行声源识别试验,辐射声音频率范围为500~6 500 Hz,试验现场如图 6所示。

|
图 6 试验布置图 Fig. 6 Experement configuration |
试验采用Brüel & Kjær公司、0.65 m阵列直径、集成4958型传声器的36通道Comb阵列接收阵列前方声信号,4个扬声器坐标分别为(0.2, 0, 1), (-0.2, 0, 1),(0.2, 0.6, 1),(-0.2, 0.6, 1)m,设置动态范围为15 dB。各传声器接收的声信号被PULSE 3560D型数据采集系统同时采集并传输到PULSE LABSHOP软件中进行频谱分析,得传声器信号的互功率谱矩阵,导入MATLAB软件中利用编写的声源识别算法进行成像。这里设置声源计算平面尺寸为2 m×2 m,距离阵列1 m,划分为21×21个网格点。对不同声源频率的测量数据进行计算后成像,得到试验结果如表 2所示。
| 表 2 4个声源识别试验结果图 Table 2 Experemental imaging diagram of four acoustic sources |
从表 2可以看出,OMP-DAMAS对2 500 Hz以及4 000 Hz的声源均能准确识别,其主瓣宽度远小于传统波束形成方法,并能有效抑制旁瓣,极大地提高了分辨率。对于1 000 Hz的声源,由于传统波束形成的主瓣已经完全融合无法分辨出声源位置,进而OMP-DAMAS的识别结果亦不准确。总体上讲,OMP-DAMAS的声源识别性能优于传统波束形成。
4 结论研究了正交匹配追踪反卷积波束形成声源识别方法,仿真计算了传统波束形成和OMP-DAMAS对不同条件下多声源的识别结果,分析了其性能优劣。探究了OMP-DAMAS成像结果随声源频率、迭代次数和信噪比的变化规律并进行了声源识别试验验证。取得了如下主要结论:
1) 相比于传统波束形成方法,OMP-DAMAS能够有效缩减主瓣宽度,抑制旁瓣水平,成像结果更加清晰。
2) OMP-DAMAS重构的声源个数取决于迭代次数。
3) OMP-DAMAS与传统波束形成一样,均具有对中高频识别效果好而对低频效果较差的特点。其对噪声具有较好的适应性,对文中的阵列而言,在声源频率高于2 300 Hz,信噪比高于0 dB时均能获得准确的识别结果。
| [1] |
Batel M, Marroquin M, Hald J, et al. Noise source location techniques-Simple to advanced applications[J]. Sound and Vibration, 2003, 37(3): 24-36. |
| [2] |
褚志刚, 杨洋, 倪计民, 等. 波束形成声源识别技术研究进展[J]. 声学技术, 2013, 32(5): 430-435. CHU Zhigang, YANG Yang, NI Jimin, et al. Review of beamforming based sound source identification techni-ques[J]. Technical Acoustics, 2013, 32(5): 430-435. (in Chinese) |
| [3] |
Brooks T F, Humphreys W M. A deconvolution approach for the mapping of acoustic sources (DAMAS) determined from phased microphone arrays[J]. Journal of Sound and Vibration, 2006, 294(4/5): 856-879. |
| [4] |
杨洋, 褚志刚, 江洪, 等. 反卷积DAMAS2波束形成声源识别研究[J]. 仪器仪表学报, 2013, 34(8): 1779-1786. YANG Yang, CHU Zhigang, JIANG Hong, et al. Research on DAMAS2 beamforming sound source identific-ation[J]. Chinese Journal of Scientific Instrument, 2013, 34(8): 1779-1786. (in Chinese) DOI:10.3969/j.issn.0254-3087.2013.08.014 |
| [5] |
William M H. Extension of DAMAS phased array processing for spatial coherence determination (DAMAS-C)[C]. 12th AIAA/CEAS Aeroacoustics Conference (27th AIAA Aeroacoustics Conference), Cambridge, MA, 8-10 May 2006.
|
| [6] |
杨洋, 褚志刚. 四种典型波束形成声源识别清晰化方法[J]. 数据采集与处理, 2014, 29(2): 316-326. YANG Yang, CHU Zhigang. Four typical clearness methods for beamforming acoustic source identification[J]. Journal of Data Acquisition & Processing, 2014, 29(2): 316-326. (in Chinese) DOI:10.3969/j.issn.1004-9037.2014.02.025 |
| [7] |
Yardibi T, Li J, Stoica P, et al. Sparsity constrained deconvolution approaches for acoustic source mapping[J]. Journal of the Acoustical Society of America, 2008, 123(5): 2631-2642. DOI:10.1121/1.2896754 |
| [8] |
Padois T, Berry A. Orthogonal matching pursuit applied to the deconvolution approach for the mapping of acoustic sources inverse problem[J]. Journal of the Acoustical Society of America, 2015, 138(6): 3678-3685. DOI:10.1121/1.4937609 |
| [9] |
Tropp J A. Greed is good:Algorithmic results for sparse approximation[J]. IEEE Transactions on Information Theory, 2004, 50(10): 2231-2242. DOI:10.1109/TIT.2004.834793 |
| [10] |
杨真真, 杨震, 孙林慧, 等. 信号压缩重构的正交匹配追踪类算法综述[J]. 信号处理, 2013, 29(4): 486-496. YANG Zhenzhen, YANG Zhen, SUN Linhui, et al. A survey on orthogonal matching pursuit type algorithms for signal compression and reconstruction[J]. Signal Processing, 2013, 29(4): 486-496. (in Chinese) DOI:10.3969/j.issn.1003-0530.2013.04.011 |
| [11] |
Peillot A, Ollivier F, Chardon G, et al. Localization and identification of sound sources using "compressive sampling" techniques[C]. 18th International Congress on Sound and Vibration, Rio de Janeiro, Brazil, 10-14 July 2011, 1-8.
|
| [12] |
宁方立, 卫金刚, 刘勇, 等. 压缩感知声源定位方法研究[J]. 机械工程学报, 2016, 52(19): 42-52. NING Fangli, WEI Jingang, LIU Yong, et al. Study on sound sources localization using compressive sensing[J]. Journal of Mechanical Engineering, 2016, 52(19): 42-52. (in Chinese) |
| [13] |
Ning F L, Wei J G, Qiu L F, et al. Three-dimensional acoustic imaging with planar microphone arrays and compressive sensing[J]. Journal of Sound and Vibration, 2016, 380: 112-128. DOI:10.1016/j.jsv.2016.06.009 |
| [14] |
Davis G M, Mallat S, Zhang Z. Adaptive time-frequency decompositions with matching pursuits[J]. Optical Engineering, 1994, 33(7): 2183-2191. DOI:10.1117/12.173207 |
| [15] |
Pati Y C, Rezaifa R, Krishnaprasad P S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition[C]. Proceeding of 27th Annual Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, USA, 1-3 November 1993: 40-44.
|
 2019, Vol. 42
2019, Vol. 42