从野外采集的原始地震信号中包含着大量有用信息,但是其中也夹杂着各种各样的噪声,尤其随着勘探深度的增加,工区地质情况变得更加复杂,噪声与有用信息相互交织,严重干扰着对其分析处理。所以,对采集的原始地震信号进行去噪变得尤为重要[1]。
信号分解理论被广泛应用于地震信号去噪领域。常规经验模态分解(EMD, empirical mode decomposition)[3-4]算法是将信号分解为不同频率的IMF分量,而噪声主要存在于高频分量中,去除高频分量,对余下低频分量进行重构得到去噪后的信号。但是由于高频分量中也含有有效信息,因此,杨凯等[2]将EMD算法与小波变换模极大值去噪方法相结合,较好地去除了地震信号中的随机噪声。王姣等[5]采用完备集合经验模态分解(CEEMD, complete ensemble empirical mode decomposition)对地震信号随机噪声压制进行研究,对CEEMD分解后筛选出来的噪声较多的高频IMF分量用小波阈值[6-7]进行去噪,更好地保留了有效信息。由于EMD分解过程中容易造成模态混叠,而后改进的集合经验模态分解(EEMD, ensemble empirical mode decomposition)[8]中原始信号容易被污染,造成重构误差大。CEEMD对原始信号添加正负高斯白噪声以解决EEMD中存在的问题,然而其本质并没有改变,通过EMD独立分解添加正负高斯白噪声构成新信号,再将每次独立分解后对应的IMF分量进行加总平均运算,但是其单个IMF分量中依旧含有部分噪声。为了解决以上问题,笔者在EEMD和CEEMD基础上,引进一种全新的分解算法:自适应完备集合经验模态分解(CEEMDAN, complete ensemble empirical mode decomposition with adaptive noise)[9-10],该算法不仅解决了EEMD与CEEMD算法分解过程中残余噪声会从高频分量向低频分量传递的问题,而且运算效率、精确性及完备性都有所提升。原始信号经CEEMDAN分解成不同频率的IMF分量后,利用样本熵自适应筛选出需要处理的高频分量,根据噪声和有用信息与原始信号的相关性不同,实现对高频分量中的噪声系数定位,利用能量熵[11]选取噪声主区间,用高频分量中噪声主区间的噪声系数方差作为阈值,对其进行阈值去噪。将处理后的高频分量与筛选出的低频分量进行重构, 更好地保留有用信息,压制随机噪声。
1 CEEMDAN去噪原理 1.1 CEEMDAN分解原理CEEMDAN是在EEMD和CEEMD的基础上发展而来,EEMD分解时不对残留噪声进行隔离,对不同噪声单独分解后加总平均运算,导致高阶IMF分量中的残留噪声向低阶传递。CEEMD虽然通过对原始信号添加正负高斯白噪声,使原始信号保持了连续性,但是其本质与EEMD一样,分解后每一IMF分量中仍含有部分噪声。而CEEMDAN通过两种方法实现残余噪声隔离:第一,改变辅助噪声。添加经EMD分解后辅助噪声的IMF分量,而不是直接添加正负成对的高斯白噪声;第二,改变分解流程。EEMD是对不同噪声单独分解成各阶IMF分量后,进行加总平均运算。而CEEMDAN是信号中夹杂着的各种噪声分解出第一阶IMF分量后,立刻进行加总平均运算,得出最终的第一阶IMF分量,去除后对余下残差继续上述操作。避免了残余噪声从高阶向低阶的传递[12]。CEEMDAN分解原理如下[13]。
设Ej(·)为EMD分解后的第j阶模态分量。
步骤1 求第一阶IMF分量。将正负成对高斯白噪声(-1)qξ0ni(t)加入到原始信号x(t)中,构成新信号,其中q为系数,取q=1, 2,ξ0为幅值,i为添加辅助噪声的次数,其值取i=1, 2, …, N/2,对新信号进行EMD分解第一阶IMF分量u1(t):E(x(t)+(-1)qξ0ni(t))=u1i(t)+r1i,EMD分解后得到第一阶IMF分量,EMD不再分解,此时对产生的N个IMF分量进行加总平均运算得到:
步骤2 求第二阶IMF分量。在残差r1(t)中加入i=1, 2, …, N/2次正负成对高斯白噪声(-1)qξ0ni(t),构成新信号,进行EMD分解得到对应的第一阶模态分量u1i(t),由此运算得到:
步骤3 对步骤1~2进行重复操作,得出需要的IMF分量以及残差,直至信号为单调函数不能再被分解,则分解完成,信号为
CEEMDAN去噪算法思想是原始信号经CEEMDAN分解成K个依次从高频到低频的IMF分量,噪声是一种频率较高的信号,主要存在于高频分量中,去除高频分量,保留剩余低频分量进行重构,得到去噪后的信号为
| $ S(t) = \sum\limits_{i = k + 1}^K {{u_i}} (t), $ |
式中,i=(k+1)~K为低频分量。
算法的要点是找到高频分量与低频分量的界值k,需人为判定,并不准确,同时高频分量中的有用信息也被舍弃,导致重构后去噪效果并不理想。故文中在此基础上提出了CEEMDAN自适应阈值去噪算法。
2 CEEMDAN自适应阈值去噪原理原始信号经CEEMDAN分解出若干个从高频到低频的IMF分量,传统去噪算法去除高频分量,对余下低频分量重构以达到去噪目的,效果并不理想,而且高频分量需人为剔除并不精确。由于样本熵是度量时间序列复杂性的方法,原始信号是一种无序紊乱的信号,因此噪声含量越高,信号的时间序列复杂性越高,则样本熵越大;噪声含量越低,信号的时间序列复杂性越低,则样本熵越小。计算每个IMF分量的样本熵,并对其加总平均计算均值,IMF分量样本熵大于均值的为高频分量,小于均值的为低频分量,对高频分量实现了自适应选取。经过数据仿真,发现高频分量中主要成分为噪声,但仍旧存在有用信息,为保证去噪效果更好,需进一步对选取出的高频分量去噪。由于有用信息和噪声与原始信号的相关性不同,对高频分量与原始信号相关性分析,找出相关系数大的位置,为有用信息位置,其他为噪声位置,把有用信息的位置系数清零,将其划分为若干个区间,用其他系数计算每个IMF分量能量熵,计算每一区间的能量熵,选取能量熵最大子区间作为噪声的主区间,用对应的IMF分量噪声系数计算噪声方差,构造阈值,对高频分量进行阈值去噪。阈值去噪后的高频分量与未进行处理的低频分量重构,得到最终的去噪信号。文中算法对高频分量进行了自适应选取与阈值去噪,提高了信噪比,并更好地保留了有用信息。文中算法关键步骤如下。
2.1 样本熵划分高频分量Richman和Moorman在2000年提出了样本熵的概念,它针对近似熵中自身数据匹配易造成误差做出了相应的改进[14]。样本熵特性是数据或信号复杂性越高,则熵值越大,反之,复杂性越低,熵值越小。利用这一特性对IMF分量进行判断,求各个IMF分量样本熵,加总平均计算均值作为高频分量与低频分量的阈值,其样本熵大于阈值的为复杂性高的高频分量,含噪声程度大,小于阈值的为复杂性低的低频分量,是信号中的有用信息。样本熵具体算法如下[15]:
1) 设采样点数为M的原始信号为x(t)={x1, x2, …, xM},并且给定嵌入维数u和相似容限r,参照原始信号对其重构,重构一个u维向量X(i)={xi, xi+1, …, xi+u-1},1≤i≤M-u;
2) 定义dij为X(i)和X(j)对应元素之差绝对值的最大值的距离,计算X(i)和X(j)之间的距离dij(1≤j≤M-u, j≠i);
3) 统计dij小于r的个数num(dij<r)。定义Biu(r)为:Biu(r)=num(dij<r)/(M-u-1);
4) 对Biu(r)求平均值Bu(r);
5) 再对维数u+1重复上述步骤得到Biu+1(r)和Bu+1(r);
6) 样本熵的表达式为:SampEn(u, r, M)=
计算IMF分量与原始信号的相关性系数,则相关系数大的位置为有用信息位置,其他为噪声位置,并把有用信息的位置系数清零,实现噪声的定位。
相关系数计算原理:
定义Ri(n)为第i个IMF分量ui(n)与x(n)的相关系数为
| $ {R_i}(n) = \frac{1}{M}\sum\limits_{m = 1}^M {{u_i}} (m) \cdot x(n + m), $ | (1) |
式中:x(n)、ui(n)为信号x(t)和IMF分量ui(t)的离散化表示,n=1, …, M。
为使相关系数与IMF分量系数具有可比性,定义规范化相关系数为
| $ N{R_i}(n) = {R_i}(n)\sqrt {\frac{{\sum\limits_{n = 1}^M {{u_i}} (n)}}{{\sum\limits_{n = 1}^M {{R_i}} (n)}}} 。$ | (2) |
对比各IMF分量的规范化相关系数与各IMF分量系数,得到有效信息和噪声的IMF分量系数位置。
2.2.2 基于能量熵的噪声主区间确定方法经过CEEMDAN分解出的k个高频分量的能量为
| $ {E_k} = \sum\limits_{n = 1}^M {{{\left| {{u_k}(n)} \right|}^2}} 。$ | (3) |
将模态分量|uk(n)|等分成l个区间,任一区间的能量表示为
| $ {E_{ki}} = \sum\limits_{n = 1 + (i - 1)M/l}^{i*M/l + 1} {{{\left| {{u_k}(n)} \right|}^2}} , i = 1, \cdots , l。$ | (4) |
某一模态分量中的一个区间的能量Eki在该模态分量总能量Ek的概率为
| $ {p_{ki}} = \frac{{{E_{ki}}}}{{{E_k}}}。$ | (5) |
求得第i个区间的能量熵为
| $ {S_{ki}} = - {p_{ki}}\ln \;{p_{ki}}。$ | (6) |
构造第k个模态分量的能量熵序列:
| $ {S_k} = \left\{ {{S_{k1}}, \cdots , {S_{kl}}} \right\}。$ | (7) |
选取Sk中能量熵最大子区间,即为噪声主区间,记为
| $ {S_{km}} = \max \left\{ {{S_{k1}}, \cdots , {S_{kl}}} \right\}。$ | (8) |
计算噪声主区间的IMF分量系数的平均值,作为噪声方差为
| $ {\sigma _k} = \frac{1}{{M/l}}\sqrt {\sum\limits_{n = m \cdot M/l}^{m \cdot M/1} {{u_k}} (n)} , i = 1, \cdots , l。$ | (9) |
则第k个IMF分量的阈值Tk为
| $ {T_k} = {\sigma _k}\sqrt {2\log (M)} /\log (k + 1)。$ | (10) |
Step1:用CEEMDAN算法对信号进行分解,得到频率从高到低的IMF分量;
Step2:计算各个IMF分量的样本熵,求其均值,并根据样本熵理论,选取比均值大的高频分量进行下一步处理,保留比均值小的低频分量;
Step3:相关性分析。根据式(1)与式(2)分别计算各高频分量与原始信号的相关系数及其规范化相关系数,规范化相关系数大于各高频分量系数的位置为有效信息,小于的为噪声,分别记录其位置;
Step4:计算噪声方差。对Step3中记录的有效信息位置系数置0,保留噪声位置系数,得到新的系数构成的IMF分量,其采样点数与原来一致,将得到新系数的IMF分量分成l等份,求各等份区间的能量熵,选取能量熵最大子区间系数,作为噪声主区间,按照式(3)计算该区间系数的平均值σk,作为第k个IMF分量的噪声方差;
Step5:计算阈值。按照式(4)计算第k个IMF分量的阈值Tk;
Step6:根据Step5求出的阈值Tk,利用软阈值函数对Step2中选出的高频分量系数进行阈值处理,得到新的IMF分量系数;
Step7:重构。将经过阈值处理后的高频分量与Step2中保留的低频分量进行重构,得到去噪信号。
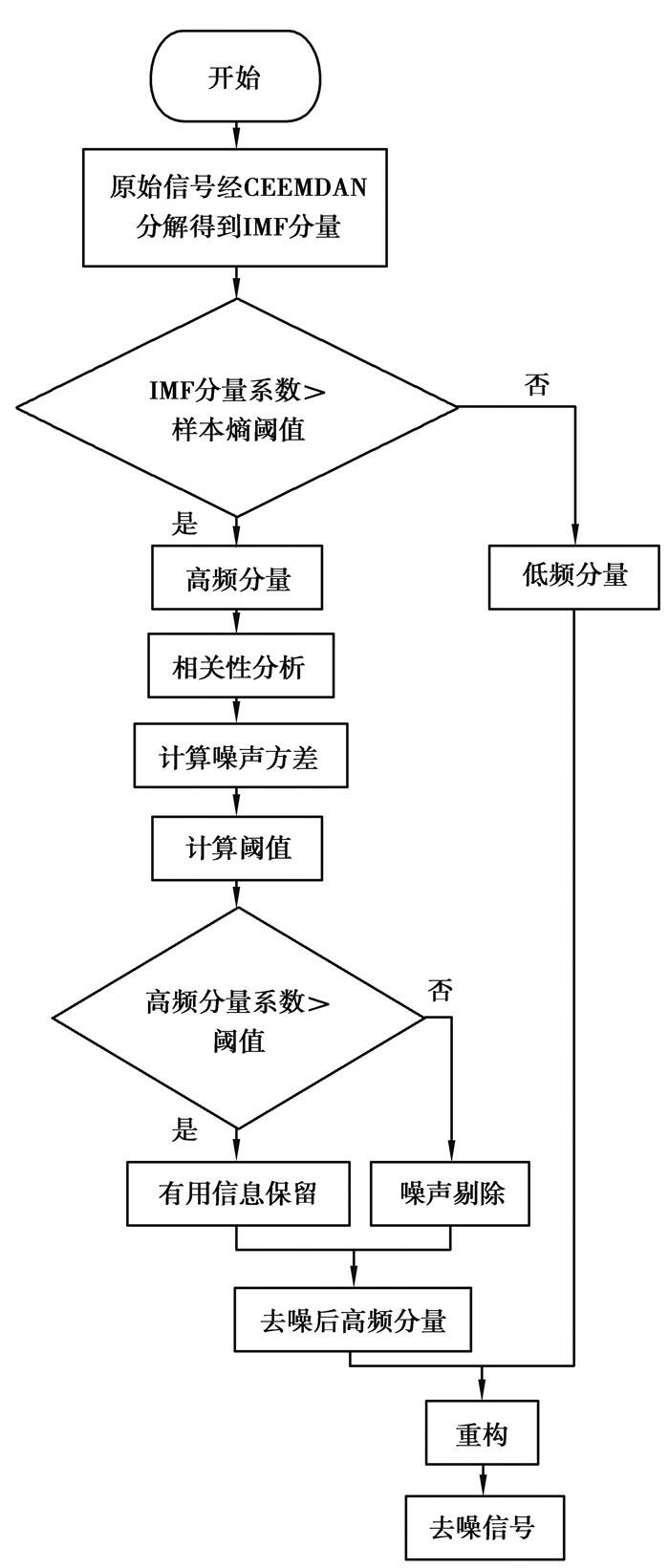
CEEMDAN自适应阈值去噪算法流程图如图 1所示。
|
图 1 CEEMDAN自适应去噪算法流程图 Fig. 1 Flow chart of CEEMDAN adaptive denoising algorithm |
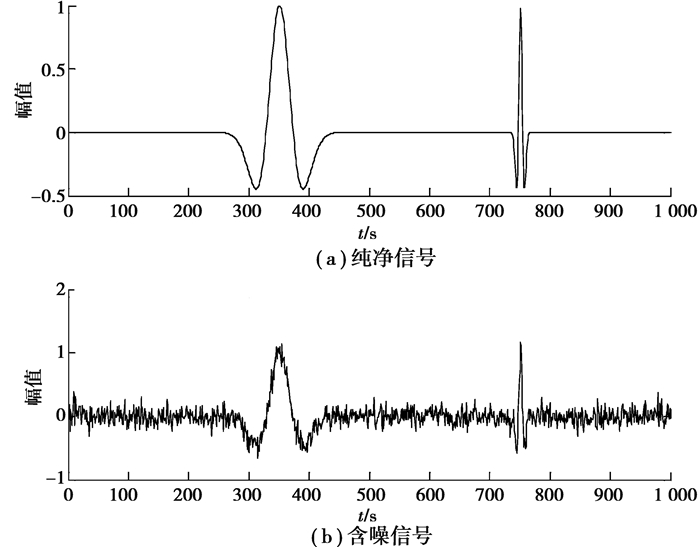
Ricker子波[16]是地震勘探中常用的子波类型,用其构造出由2层不同介质组成的模拟地震信号,时域为1 000 s,时宽为1 s,采样率1 kHz。图 2为Ricker子波构造的纯净信号和加入信噪比为5 dB高斯白噪声后的含噪信号。图 3为原始信号经CEEMDAN分解出11层IMF分量中的前7层IMF分量。图 4为CEEMDAN去噪算法,EMD去噪算法和本文改进CEEMDAN去噪算法去噪效果的对比。
|
图 2 纯净信号及含噪信号 Fig. 2 Pure signal and noise signal |
|
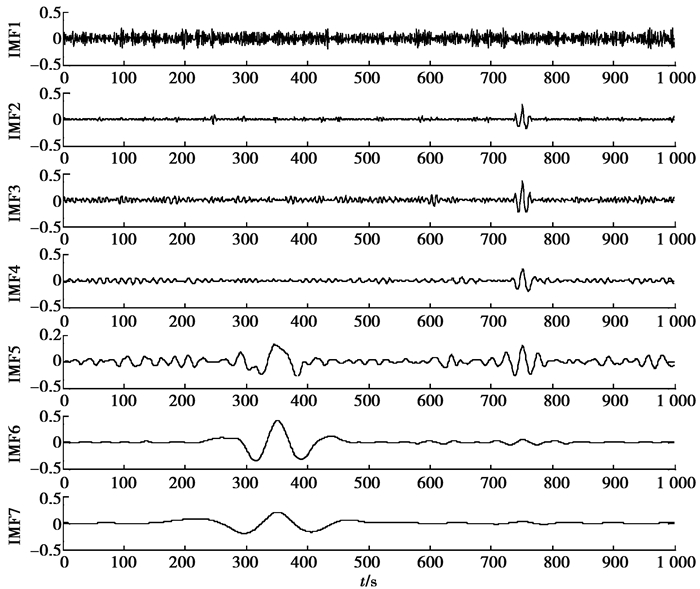
图 3 CEEMDAN分解出的前7层IMF分量 Fig. 3 The first seven layers of IMF components decomposed by CEEMDAN |
|
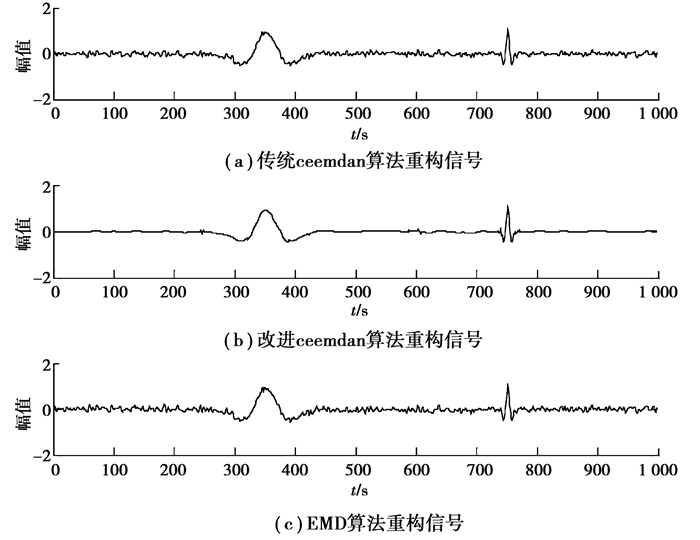
图 4 去噪效果对比 Fig. 4 Comparison of noise removal effect |
从图 3可以看出,IMF1中有用信息完全被噪声淹没,而IMF2-IMF5中包含部分有用信息,但也包含了噪声。从图 4可以看出,EMD去噪算法去噪效果不理想,去噪后信号中依旧含有大量随机噪声,CEEMDAN去噪算法相比于EMD去噪算法去噪后信噪比有所提升,但是少量随机噪声依旧存在,文中提出的CEEMDAN自适应阈值去噪算法,信噪比有了大幅提升,SNR=15.07,Ricker子波更为平滑,去噪效果显著。表 1为对纯净信号加入信噪比为0.5,1.0,2.0,5.0 dB的噪声时,3种去噪算法去噪后信噪比以及均方误差的对比结果。经过对比,文中去噪算法相比于CEEMDAN去噪算法和EMD去噪算法信噪比提升了近2倍。
| 表 1 噪声不同时去噪效果对比 Table 1 Comparison of noise removal effect with different noise |
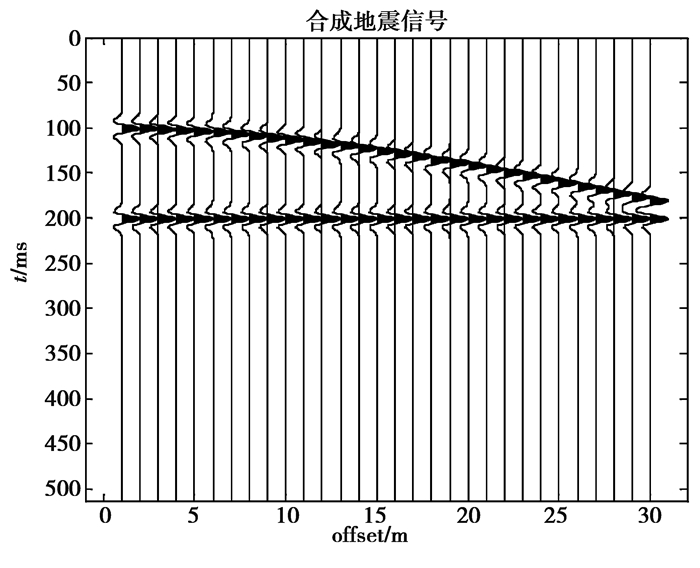
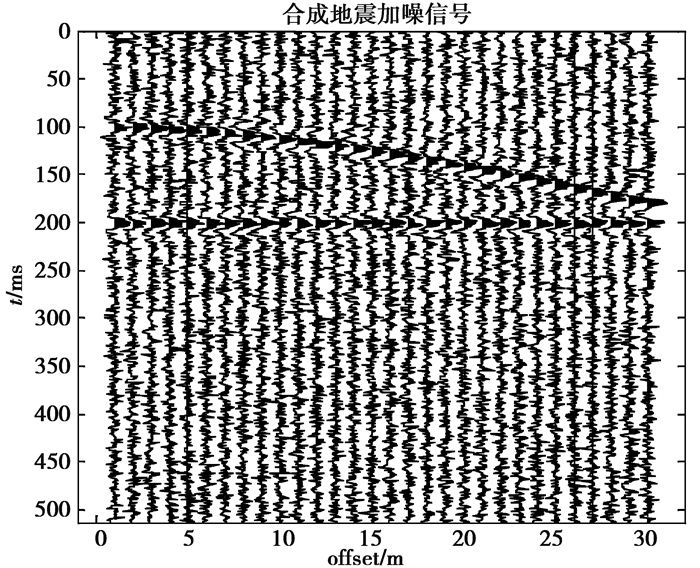
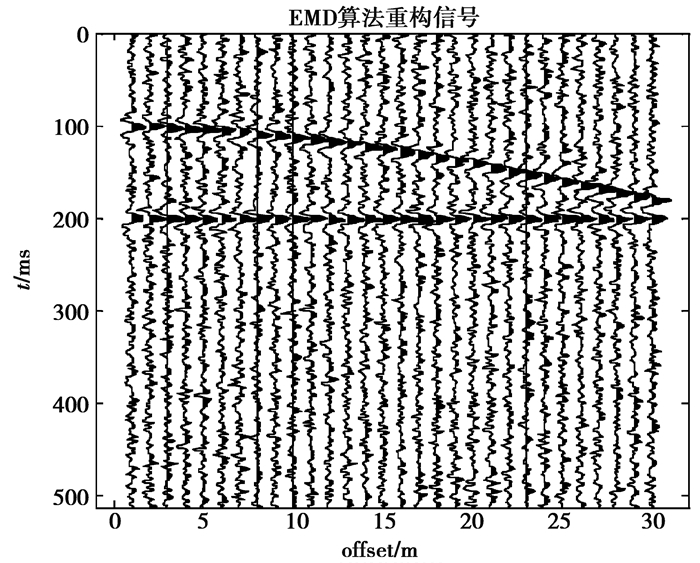
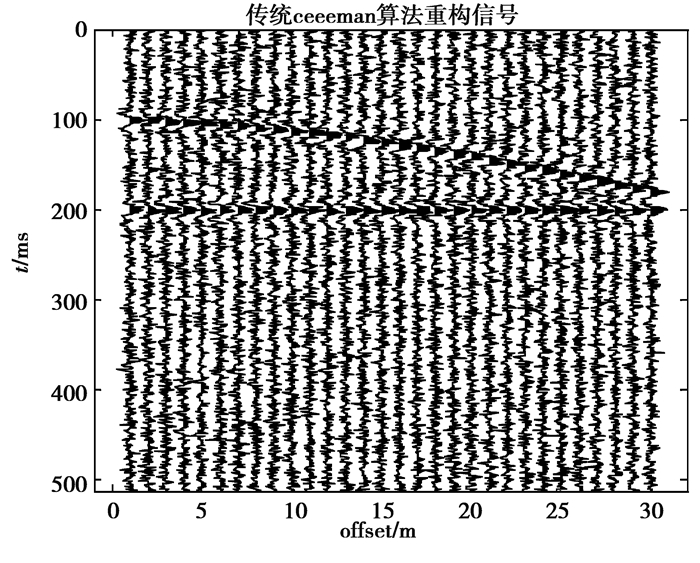
由低频Ricker子波与高频Ricker子波合成楔形地震模型。图 5为反射层上层速度为2 000 m/s,下层速度为3 000 m/s,深度为100 m,最小偏移距离10 m,记录时间长度512 ms,密度1,采集道数30的合成地震信号。图 6~图 9中横坐标offset为地震道。加入信噪比为2 dB的高斯白噪声构成的合成地震加噪信号如图 6所示。图 7为EMD去噪算法去噪后信噪比为2.34 dB的地震剖面图。图 8为CEEMDAN去噪算法去噪后信噪比为3.56 dB的地震剖面图。图 9为文中去噪算法去噪后信噪比为6.54 dB的地震剖面图。
|
图 5 合成地震信号二维剖面图 Fig. 5 2d profile of synthetic seismic signals |
|
图 6 合成地震加噪信号二维剖面图 Fig. 6 2d profile of synthetic seismic noise signal |
|
图 7 EMD去噪剖面图 Fig. 7 The section after denoising by EMD |
|
图 8 CEEMDAN去噪剖面图 Fig. 8 The section after denoising by CEEMDAN |
|
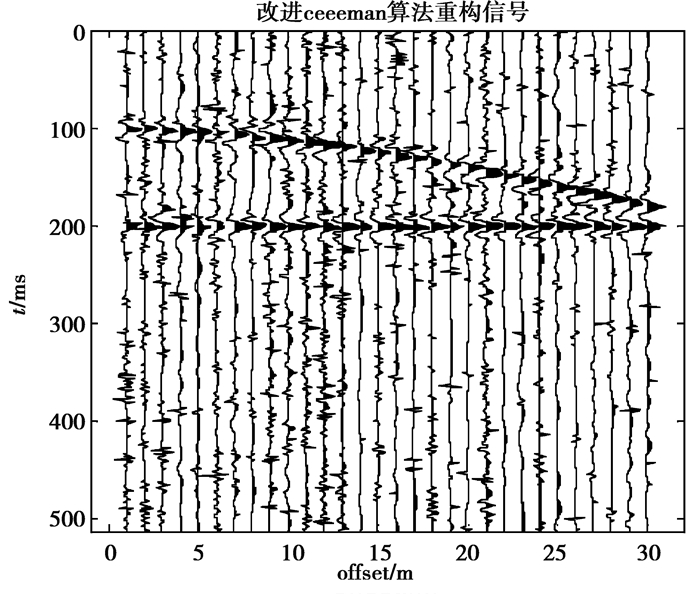
图 9 文中去噪剖面图 Fig. 9 The section after denoising by the algorithm proposed in this paper |
观察图 7~图 9,CEEMDAN去噪算法与EMD去噪算法对合成地震加噪信号去噪后,同相轴周边噪声污染效应降低,但有效能量损失现象依然存在,本文去噪算法对其去噪后,同相轴周边平稳有序,有效能量损失的现象得以改进,去噪效果更优。
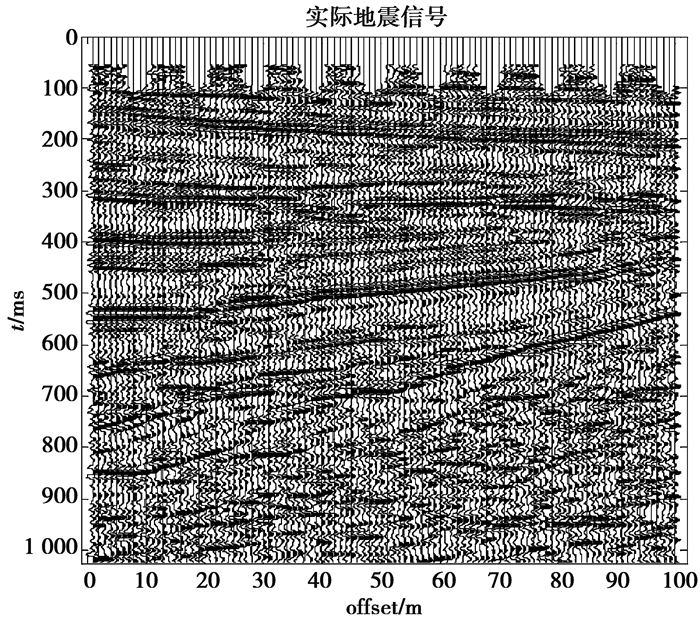
4 实际地震信号去噪采用某地区实际地震信号分别用3种去噪算法进行去噪处理。图 10为100道信号,每道采样点为1024,采样间隔为2 ms的实际地震信号。图 11~图 13分别为CEEMDAN去噪算法、EMD去噪算法以及文中改进CEEMDAN去噪算法对实际地震信号去噪后的剖面图。
|
图 10 实际地震信号剖面图 Fig. 10 Actual seismic profile |
|
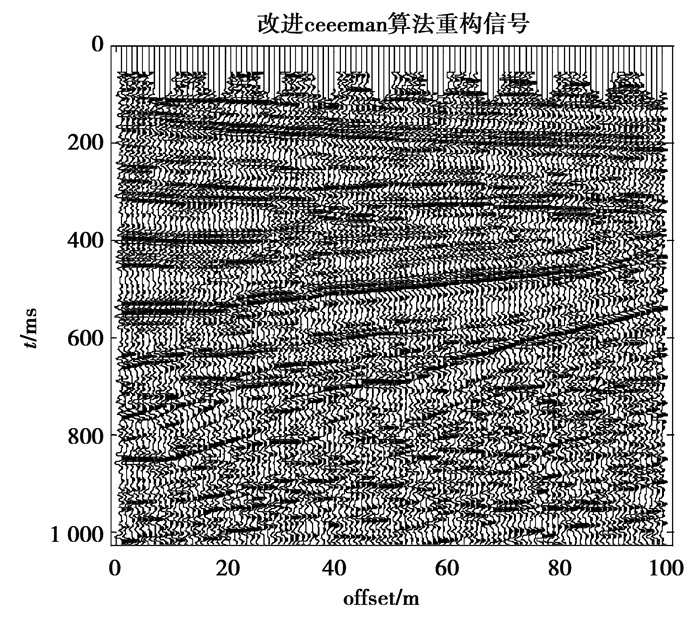
图 11 CEEMDAN去噪信号剖面图 Fig. 11 Signal profile after denoising by CEEMDAN |
|
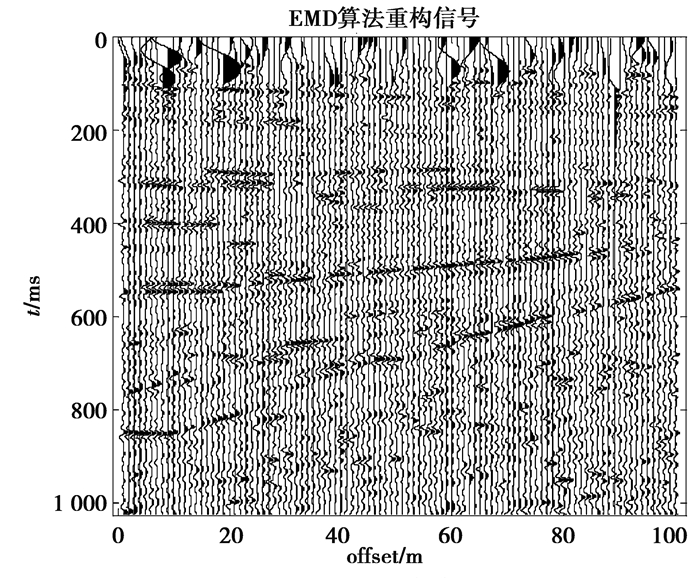
图 12 EMD算法去噪信号剖面图 Fig. 12 Signal profile after denoising by EMD algorithm |
|
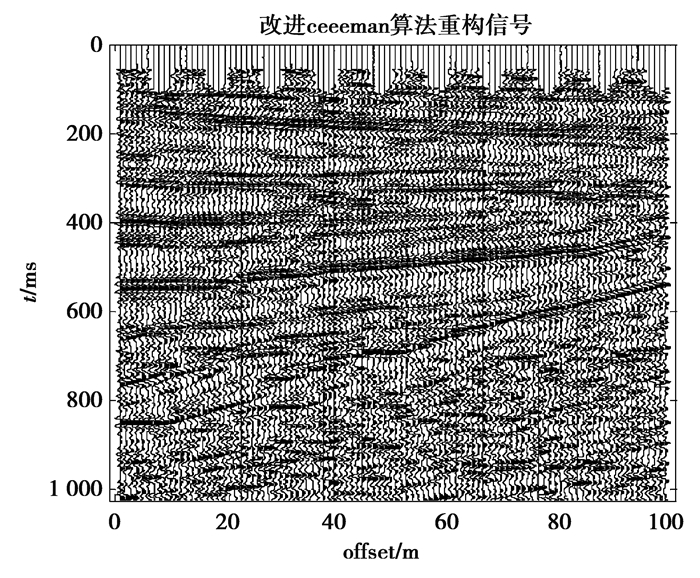
图 13 文中算法去噪剖面图 Fig. 13 The denoising profile of the algorithm presented in this paper |
观察3种去噪算法去噪后的剖面图,可以看出,图 11中同相轴仍被大量噪声淹没。图 12中噪声污染区削弱,但同相轴不再清晰,有效能量损失。图 13中同相轴清晰连续,更好地清除了同相轴周边的噪声污染,保留有用信息,去除噪声。
5 结论经过上述分析对比,文中提出的CEEMDAN自适应阈值去噪算法优于传统CEEMDAN和EMD通过分解信号直接去除高频分量进行重构的算法。去噪算法对分解出的IMF分量,利用样本熵自适应划分高频分量与低频分量,对划分出的高频分量相关性检测及定位,去除有用信息系数,保留噪声信号系数后,求其能量熵,计算阈值,对高频分量阈值去噪,与被划分出的低频分量进行重构,得到去噪信号。研究采用的CEEMDAN算法能够避免模态混叠,做到噪声隔离。在模拟、合成和实际地震信号的去噪实验中,证明了文中去噪算法在去噪效果与有用信号保留能力等方面都优于传统去噪算法。
| [1] |
刘霞, 黄阳, 黄敬, 等. 基于经验模态分解(EMD)的小波熵阈值地震信号去噪[J]. 吉林大学学报(地球科学版), 2016, 46(1): 262-269. LIU Xia, HUANG Yang, HUANG Jing, et al. Wavelet entropy threshold seismic signal denoising based on empirical mode decomposition (EMD)[J]. Journal of Jilin University(Earth Science Edition), 2016, 46(1): 262-269. (in Chinese) |
| [2] |
杨凯, 刘伟. 基于改进EMD的地震信号去噪[J]. 西南石油大学学报(自然科学版), 2012, 34(4): 75-82. YANG Kai, LIU Wei. Random noise attenuation of seismic signal based on improved EMD[J]. Journal of Southwest Petroleum University(Seience& Technology Edition), 2012, 34(4): 75-82. (in Chinese) DOI:10.3863/j.issn.1674-5086.2012.04.010 |
| [3] |
Li H G, Hu Y, Li F C, et al. Succinct and fast empirical mode decomposition[J]. Mechanical Systems and Signal Processing, 2017, 85: 879-895. DOI:10.1016/j.ymssp.2016.09.031 |
| [4] |
Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactionson Signal Processing, 2014, 62(3): 531-544. |
| [5] |
王姣, 李振春, 王德营, 等. 基于CEEMD的地震数据小波阈值去噪方法研究[J]. 石油物探, 2014, 53(2): 164-172. WANG Jiao, LI Zhenchun, WANG Deying, et al. A method for wavelet threshold denoising of seismic data based on CEEMD[J]. Geophysical Prospecting for Petroleum, 2014, 53(2): 164-172. (in Chinese) DOI:10.3969/j.issn.1000-1441.2014.02.006 |
| [6] |
李文, 刘霞, 段玉波, 等. 基于小波熵和相关性的高分辨率阈值去噪方法[J]. 数据采集与处理, 2013, 28(3): 371-375. LI Wen, LIU Xia, DUAN Yubo, et al. High-resolutiont threshold denoising method based on wavelet entropy and correlation[J]. Journal of Data Acquisition & Processing, 2013, 28(3): 371-375. (in Chinese) DOI:10.3969/j.issn.1004-9037.2013.03.020 |
| [7] |
Rosso O A, Blanco S, Yordanova J, et al. Wavelet entropy:anew tool for analysis of short duration brain electrical signals[J]. Journal of Neuroscience Methods, 2001, 105(1): 65-75. DOI:10.1016/S0165-0270(00)00356-3 |
| [8] |
Wu Q M, Wang J, Peng X Y, et al. Fault diagnosis of rotating machinery using Gaussian process and EEMD-treelet[J]. International Journal of Adaptive Control and Signal Processing, 2019, 33(1): 52-73. DOI:10.1002/acs.2952 |
| [9] |
Li Y X, Li Y A, Chen X, et al. A new underwater acoustic signal denoising technique based on CEEMDAN, mutual information, permutation entropy, and wavelet threshold denoising[J]. Entropy, 2018, 20(8): 563. DOI:10.3390/e20080563 |
| [10] |
Bouhalais M L, Djebala A, Ouelaa N, et al. CEEMDAN and OWMRA as a hybrid method for rolling bearing fault diagnosis under variable speed[J]. The International Journal of Advanced Manufacturing Technology, 2018, 94(5/6/7/8): 2475-2489. |
| [11] |
张杏莉, 卢新明, 贾瑞生, 等. 基于变分模态分解及能量熵的微震信号降噪方法[J]. 煤炭学报, 2018, 43(2): 356-363. ZHANG Xingli, LU Xinming, JIA Ruisheng, et al. Micro-seismic signal denoising method based on variational mode decomposition and energy entropy[J]. Journal of China Coal Society, 2018, 43(2): 356-363. (in Chinese) |
| [12] |
Zhou Z B, Lin L, Li S X. International stock market contagion:A CEEMDAN wavelet analysis[J]. Economic Modelling, 2018, 72: 333-352. DOI:10.1016/j.econmod.2018.02.010 |
| [13] |
李锋, 林阳阳, 赵辉, 等. 基于CEEMDAN-SVM的液压泵故障诊断方法研究[J]. 液压与气动, 2016(1): 125-129. LI Feng, LIN Yangyang, ZHAO Hui, et al. Fault diagnosis of hydraulic pump based on CEEMDAN-SVM[J]. Chinese Hydraulics & Pneumatics, 2016(1): 125-129. (in Chinese) DOI:10.11832/j.issn.1000-4858.2016.01.026 |
| [14] |
刘颜明.基于变分模态分解的滚动轴承故障诊断系统研究[D].大庆: 东北石油大学, 2018. LIU Yanming. Research on bearing fault diagnosis system based on variational mode decomposition[D]. Daqing: Northeast Petroleum University, 2018. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10141-2009040519.htm |
| [15] |
黄阳.基于经验模态分解的轴承故障诊断系统研究[D].大庆: 东北石油大学, 2016. HUANG Yang. Research on bearing fault diagnosis system based on empirical mode decomposition[D]. Daqing: Northeast Petroleum University, 2016. (in Chinese) |
| [16] |
Wang Y H. The ricker wavelet and the lambert w function[J]. Geophysical Journal International, 2015, 200(1): 111-115. DOI:10.1093/gji/ggu384 |
 2019, Vol. 42
2019, Vol. 42


