燃气发电锅炉燃烧过程一般由燃料、送风、引风3个子控制系统调节。燃料控制系统用于调节进入锅炉炉膛的燃料量,以控制主蒸汽压力大小;送风控制系统主要调节进入炉膛的风量,保证合适的煤气和空气配比,促进煤气充分燃烧;引风控制系统主要通过控制引风量大小保证送风和引风风量之间的平衡,维持锅炉炉膛负压稳定[1]。燃料控制系统对主蒸汽压力控制至关重要,而控制主蒸汽压力稳定是锅炉系统稳定运行的保证。火力发电厂的锅炉将水变为高温高压蒸汽,推动汽轮机旋转做功,进而产生电能。蒸汽压力过高或过低都会影响汽机设备,甚至产生安全事故,而锅炉蒸汽压力又是一个大滞后、不确定性、大干扰的系统,当出现煤气热值或压力变化,主蒸汽压力设定值变化等扰动时,主蒸汽压力很可能出现超调、震荡或压力过低的现象,且需要很长时间调节,不利于机组稳定运行[2]。
常用的PID控制算法简单,易于实现,但对于锅炉这种复杂的控制对象控制效果不理想。目前,Smith预估控制是一种对锅炉等大滞后系统有效的控制方法,但Smith预估器要求要有精确的被控对象数学模型,而工业对象的参数往往具有很强的不确定性[3]。为此,许多学者先后提出过多种改进方案:王宝忠等[4]利用RBF神经网络整定参数的PID控制器和基本Smith预估控制器结合,但并未解决系统参数变化的控制问题;韩立强等[5]通过在基本的Smith预估器基础上加入一个中间微分反馈环节,对参数变化附加一个校正作用,但当系统滞后时间发生变化时,控制效果不够理想。
刘长良等[6]对Smith预估控制器进行了改进,使改进后的算法能够在辨识模型失配的情况下有效补偿辨识误差,大大降低了控制系统对模型参数变化的敏感性。研究将RBF神经网络整定参数的PID控制器和这种失配补偿型Smith预估控制器相结合,利用RBF神经网络的在线学习能力实时调整PID控制器参数,以适应对象特性经常性变化,并通过改进Smith预估器对模型参数变化被控系统中存在的纯滞后进行补偿。通过Matlab仿真和某钢厂150 t燃气锅炉应用表明,该方案对于火力发电锅炉主蒸汽压力控制具有很好的稳定性和抗干扰能力。
1 发电锅炉蒸汽压力模型燃气锅炉蒸汽压力的生成过程分为煤气燃烧过程和蒸汽形成过程,煤气经由煤气调节阀进入炉膛燃烧,使汽包中的水生产高温高压蒸汽进而推动汽轮机工作产生电能。
目前大多数燃气发电锅炉的主蒸汽压力控制系统以蒸汽压力为主要控制参数,以进入炉膛的煤气量为副调节参数,控制量也为煤气量而形成的串级控制系统。当锅炉煤气燃烧状态发生变化时,主蒸汽压力也会发生改变,通过调节煤气流量而改变锅炉燃烧状况,从而改变锅炉产汽量和蒸汽压力[7]。
煤气在锅炉炉膛内充分燃烧,产生热量,由引风机将高温控制引入烟道,将热量储存在烟道中的汽包管壁、过热器和换热器中。这里系统的输入值为煤气量,输出值为输入值煤气量所产生的热量,因此传递函数可表示为
| $ G_{1}(s)=\frac{K_{1}}{T_{1} s+1}, $ | (1) |
式中:K1为煤气燃烧产热的系数;T1为燃烧过程时间常数s。
高温烟气与汽包管壁经过剧烈的热传递使汽包生产饱和蒸汽。输入量为传递给汽包导管中汽水混合物的热量,输出了为主蒸汽压力,其传递函数可表示为
| $ G_{2}(s)=\frac{K_{2}}{T_{2} s+1} e^{-\tau_{2} s}, $ | (2) |
式中:K2为热量转化为蒸汽的放大系数;T2为蒸汽形成过程时间常数s;τ2为纯滞后时间s。
| $ G(s) = \frac{{{K_1}{K_2}}}{{\left( {{T_1}s + 1} \right)\left( {{T_2}s + 1} \right)}}{e^{ - {\tau _2}s}}。$ | (3) |
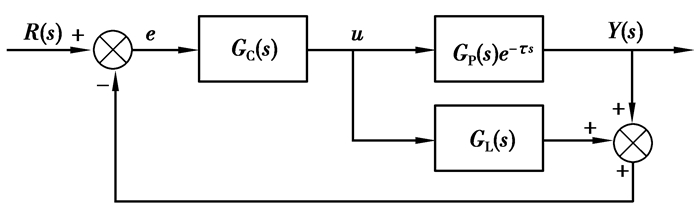
为了解决系统中存在的纯滞后问题,史密斯(Smith O J M)提出了一种预估补偿控制算法。该算法通过引入一个预估补偿环节,抵消系统中所含的纯滞后时间,使原被滞后的控制信号提前送到调节器,使调节器能够及时动作,从而加快系统调节速度并减小系统超调量[10-11]。基本型Smith预估补偿控制原理如图 1所示。
|
图 1 基本型Smith预估补偿控制框图 Fig. 1 Basic Smith Predictive Compensation Control Block Diagram |
其中:GC(s)为系统控制器,GP(s)e-τs为对象传递函数,GL(s)为Smith预估补偿器
| $ {G_L}(s) = {G_P}(s) \cdot \left( {1 - {e^{ - \tau s}}} \right)。$ | (4) |
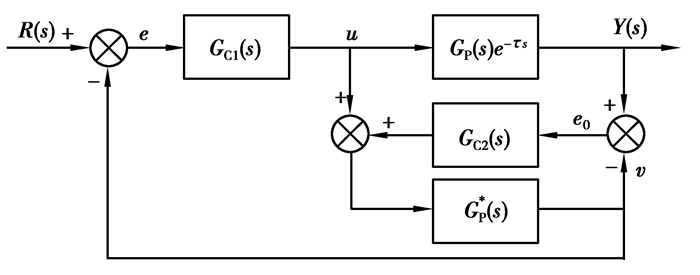
然而,这种Smith预估补偿控制器建立在精确的系统模型基础上,很容易受到被控系统参数变化的影响。为此,在系统中增加一个补偿控制器,用于补偿辨识模型失配时的误差,从而减小系统参数变化带来的不利影响。失配补偿型Smith预估控制原理如图 2所示[12]。
|
图 2 失配补偿型Smith预估控制系统框图 Fig. 2 Block diagram of mismatch compensation Smith predictive control system |
其中:GC1(s)为系统主控制器,可选用PID控制器;GP(s)e-τs为对象传递函数;G*(s)P为被控对象去掉滞后即GP(s)的辨识模型,GP*(s)和GP(s)之间允许存在一定的误差;GC2(s)为反馈补偿控制器,可以选用PI控制器。
主控制器GC1(s)的输出u经过GP*(s)后输出信号v,v和系统输出y之间存在一定的偏差,计算出这个偏差e0后经过GC2(s)反馈到GP*(s),再把GP*(s)的输出信号v反馈到系统输入端。这种控制方案能够补偿GP*(s)和对象真实模型失配时的误差,达到改善系统性能的作用。
从系统的给定与输出之间的关系计算传递函数为
| $ \begin{array}{l} \frac{{Y(s)}}{{R(s)}} = \frac{{{G_{C1}}(s){G_P}(s){e^{ - \tau \tau s}}\left[ {1 + {G_{C2}}(s)G_P^*(s)} \right]}}{{1 + {G_{C1}}(s){G_P}(s){e^{ - \tau s}}{G_{C2}}(s)G_P^*(s) + {G_{C1}}(s)G_P^*(s) + {G_{C2}}(s)G_P^*(s)}}\\ \;\;\;\;\;\;\; = \frac{{{G_{C1}}(s){G_P}(s){e^{ - \tau s}}}}{{1 + {G_{C1}}(s)G_P^*(s)\frac{{1 + {G_P}(s){G_{C2}}(s){e^{ - \tau s}}}}{{1 + {G_{C2}}(s)G_P^*(s)}}}} 。\end{array} $ | (5) |
于是得到特征方程如下
| $ 1+G_{C 1}(s) G_{P}^{*}(s) \frac{1+G_{P}(s) G_{C 2}(s) e^{-\tau s}}{1+G_{C 2}(s) G_{P}^{*}(s)}=0。$ | (6) |
当GC2(s)的模足够小时,可知
| $ 1+G_{P}(s) G_{C 2}(s) e^{-\tau s} \approx 1, $ | (7) |
| $ 1+G_{C 2}(s) G_{P}^{*}(s) \approx 1, $ | (8) |
于是公式(6)可近似为
| $ 1+G_{C 1}(s) G_{P}^{*}(s)=0, $ | (9) |
由式(9)可知,补偿控制器和被控系统的时滞不影响系统的稳定性,由式(5)可知,系统对模型参数的变化的敏感性也大大降低。由于GC2(s)、GP*(s)中都不含有被控对象的纯滞后时间,因此不必再辨识,只需辨识GP(s)即可,并且允许存在一定的辨识误差,改善了系统的控制性能。
3 RBF神经网络 3.1 RBF神经网络模型RBF神经网络是由Moody J和Darken C提出的一种特殊前馈型神经网络,能够由问题的确定网络拓扑结构,这种RBF神经网络不存在局部极小问题,具有快速收敛速度、网络规模小、逼近精度高等优点。
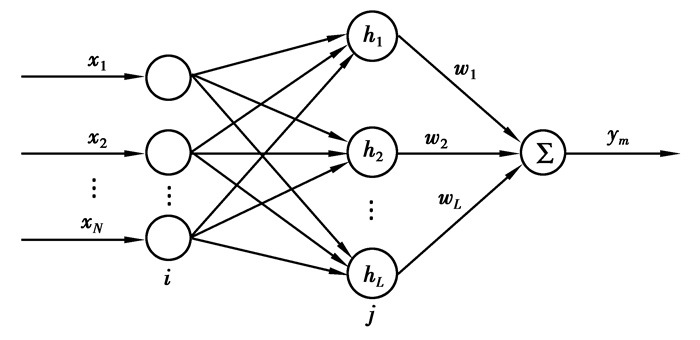
RBF神经网络具有3层网络结构,分为输入层、隐藏层和输出层,是一种前向网络。第一层为输入层,用于传递输入数据;中间层为隐含层,用于对输入层数据进行非线性计算;输出层用于对隐含层输出的数据进行线性计算[13]。其网络结构如图 3所示。
|
图 3 RBF神经网络结构图 Fig. 3 RBF Neural Network Structure Diagram |
图中,X=[x1, x2, …, xN]T为网络输入向量,W=[w1, w2, …, wL]T为隐含层与输出层之间的连接权值,H=[h1, h2, …, hL]T为网络的径向基向量,选取高斯函数作为径向基函数
| $ h_{j}=\exp \left(-\frac{\left\|\boldsymbol{X}-\boldsymbol{C}_{j}\right\|^{2}}{2 \sigma_{j}^{2}}\right), j=1,2, \cdots, L, $ | (10) |
式中:Cj=[cj1, cj2, …, cjN]T为隐含层第j个节点的中心向量;σj为第j个隐层节点径向基函数的宽度;
RBF 神经网络的输出层为隐含层所有节点加权之和,所以网络的输出为
| $ y_{m}=\sum\limits_{j=1}^{L} h_{j} w_{j}, j=1,2, \cdots L。$ | (11) |
神经网络优化的性能指标函数为
| $ E=\frac{1}{2}\left(y-y^{d}\right)^{2}, $ |
式中:y、yd分别为神经网络的实际输出和期望输出。
根据梯度下降法,网络的输出权值、隐含层节点中心向量以及基函数宽度为
| $ \Delta w_{j}=-\eta \frac{\partial E(k)}{\partial w_{j}}=\eta\left(y(k)-y^{d}(k)\right) h_{j}, $ | (12) |
| $ w_{j}(k)=w_{j}(k-1)+\Delta w_{j}+\alpha\left(w_{j}(k-1)-w_{j}(k-2)\right), $ | (13) |
| $ \Delta \boldsymbol{c}_{j i}=-\eta \frac{\partial E(k)}{\partial \boldsymbol{c}_{j i}}=\left(y(k)-y^{d}(k)\right) w_{j} h_{j} \frac{x_{i}-\boldsymbol{c}_{j i}}{\sigma_{j}^{2}}, $ | (14) |
| $ \boldsymbol{c}_{j i}(k)=\boldsymbol{c}_{j i}(k-1)+\Delta \boldsymbol{c}_{j i}+\alpha\left(\boldsymbol{c}_{j i}(k-1)-\boldsymbol{c}_{j i}(k-2)\right), $ | (15) |
| $ \Delta \sigma_{j}=-\eta \frac{\partial E(k)}{\partial \sigma_{j}}=\left(y(k)-y^{d}(k)\right) w_{j} h_{j} \frac{\left\|X-\boldsymbol{C}_{j}\right\|^{2}}{\sigma_{j}^{3}}, $ | (16) |
| $ \sigma_{j}(k)=\sigma_{j}(k-1)+\Delta \sigma_{j}+\alpha\left(\sigma_{j}(k-1)-\sigma_{j}(k-2)\right), $ | (17) |
其中:η∈[0, 1]为学习系数,α∈[0, 1]为动量因子。
对象输出对输入的敏感度Jacobian信息辨识算法如下
| $ \frac{\partial y(k)}{\partial u(k)} \approx \frac{\partial y^{d}(k)}{\partial u(k)}=\sum\limits_{j} w_{j} h_{j} \frac{c(1, j)-x_{1}}{\sigma_{j}^{2}}, $ | (18) |
式中,x1=u(k)。
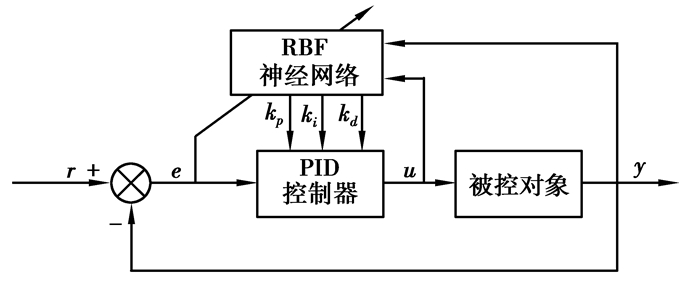
3.2 RBF网络PID参数整定原理由于神经网络能够以任意精度逼近任意函数,并且不依赖于被控对象的精确数学模型,将RBF神经网络与PID控制器相结合,利用RBF神经网络的自学习能力对传统PID控制器的参数进行整定。在RBF神经网络优化调整PID控制器的参数kp、ki、kd时,这些参数不再是一组固定的组合关系,而是根据RBF神经网络辨识情况随时调整的非线性关系,通过RBF神经网络的自学习能力得到PID控制器参数的最佳组合,从而实现PID控制器对系统的最优控制[14]。RBF网络整定PID参数控制系统框图如图 4所示。
|
图 4 RBF网络整定PID参数控制系统框图 Fig. 4 Block diagram of RBF network tuning PID parameter control system |
图中,r为系统给定值;y为系统实际输出值;PID采用增量式控制器
| $ \Delta u(k)=k_{P}[e(k)-e(k-1)]+k_{i} e(k)+k_{d}[e(k)-2 e(k-1)+e(k-2)], $ | (19) |
其中:e(k)=r(k)-y(k),kp、ki、kd即为PID控制器的参数:比例、积分和微分系数。
RBF神经网络性能指标为
| $ E(k)=\frac{1}{2}[r(k)-y(k)]^{2}=\frac{1}{2} e(k)^{2}, $ | (20) |
PID的三项输入为
| $ \begin{array}{l} {x_c}\left( 1 \right) = e\left( k \right) - e\left( {k - 1} \right),\\ {x_c}\left( 2 \right) = e\left( k \right),\\ {x_c}\left( 3 \right) = e\left( k \right) - 2e\left( {k - 1} \right) + e\left( {k - 2} \right)。\end{array} $ |
根据梯度下降法,kp、ki、kd的调整算法如下
| $ \Delta {k_p} = - {\eta _p}\frac{{\partial E}}{{\partial {k_p}}} = - {\eta _p}\frac{{\partial E}}{{\partial y}}\frac{{\partial y}}{{\partial u}}\frac{{\partial u}}{{\partial {k_p}}} = {\eta _\rho }e(k)\frac{{\partial y}}{{\partial u}}{x_c}(1), $ | (21) |
| $ \Delta k_{i}=-\eta_{i} \frac{\partial E}{\partial k_{i}}=-\eta_{i} \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial k_{i}}=\eta_{i} e(k) \frac{\partial y}{\partial u} x_{c}(2), $ | (22) |
| $ \Delta k_{d}=-\eta_{d} \frac{\partial E}{\partial k_{d}}=-\eta_{d} \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial k_{d}}=\eta_{d} e(k) \frac{\partial y}{\partial u} x_{c}(3), $ | (23) |
式中,ηp、ηi、ηd为PID参数的学习速率,
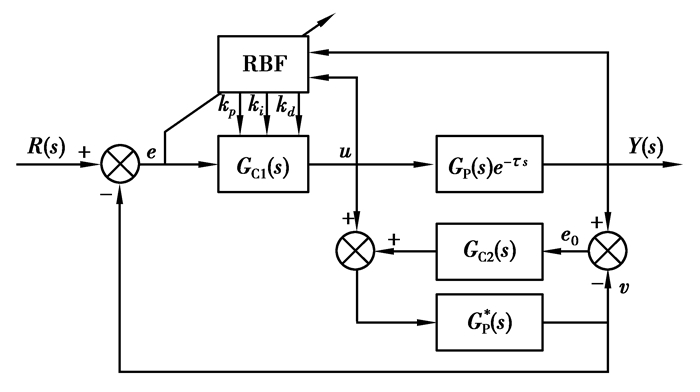
将RBF整定参数的PID控制器与失配补偿型Smith预估器相结合,构成了失配补偿型Smith-RBF控制系统,其结构如图 5所示。
|
图 5 失配补偿型Smith-RBF控制系统框图 Fig. 5 Block diagram of mismatch compensation Smith-RBF control system |
图 5所示控制系统中,通过失配补偿型Smith预估器对被控对象中所含的纯滞后进行补偿,降低了系统对被控对象模型参数变化的敏感性,同时利用RBF神经网络整定主控制器参数,能够更好的消除纯滞后项所带来的影响,以取得更好的控制效果。
5 仿真分析与现场应用 5.1 仿真分析为了验证上述控制算法的有效性,选取某钢厂发电3车间150 t燃气发电锅炉主蒸汽压力控制系统作为被控对象,其传递函数为
| $ G(s)=\frac{10}{400 s^{2}+50 s+1} e^{-35 s}, $ | (24) |
该系统由于干扰等原因,其模型参数会在一定范围内发生变化。取采样时间为1 s,系统输入为单位阶跃函数。RBF神经网络结构取为3-6-1,取其输出权值向量初值为10,隐含层节点中心向量初值为35,基函数宽度初值为30,学习系数η=0.2,动量因子α=0.15,PID参数学习速率ηP=ηi=ηd=0.05。控制器GC2(s)选用PI控制器,用试凑法整定GC2(s)参数,得:KP2=0.3、Ki2=0.01。为了证明所设计方案的有效性,利用常规PID单回路控制、基本型Smith预估和RBF神经网络相结合(基本型Smith-RBF)2种控制方案与所设计的失配补偿型Smith和RBF网络相结合(失配补偿型Smith-RBF)的方案仿真结果进行比较。
1) 当辨识模型参数准确时,即对系统模型的辨识结果取为:

|
图 6 模型参数精确时仿真图 Fig. 6 Simulation Diagram with Precise Model Parameters |
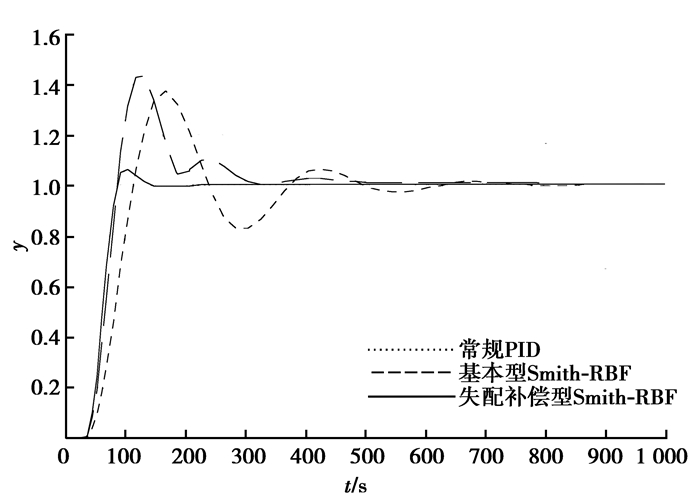
2) 被控对象模型参数发生变化时,其传递函数变为
|
图 7 模型参数变化时仿真图 Fig. 7 Simulation Diagram with Variable Model Parameters |
由图 6可知,在系统模型参数不变、辨识模型精确的情况下,失配补偿型Smith-RBF控制方案能够达到比较好的控制效果,而基本型Smith-RBF控制方案存在一定的超调,常规PID控制方案超调大,调节时间长。如图 7所示,当系统模型参数发生变化时,基本型Smith-RBF控制方案存在较大的超调,且调节时间长,而失配补偿型Smith-RBF控制方案受到的影响较小,控制效果良好。表明失配补偿型Smith-RBF有效的克服了基本型Smith预估器易受模型参数变化的影响的缺陷,获得了良好的控制效果。
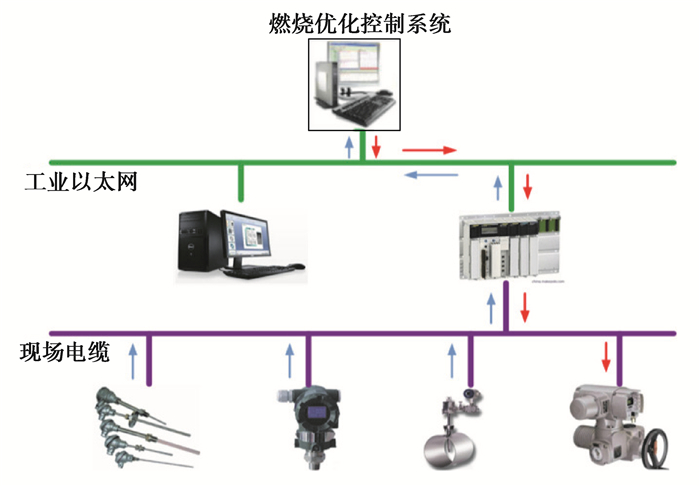
5.2 工程应用某钢发电3车间150 t燃气发电锅炉控制系统为浙大中控DCS系统,额定发电功率为42 MW。本项目在不改变原系统结构和硬件配置的情况下,增加一台工控机作为燃气锅炉主蒸汽压力优化控制系统,优化控制系统通过OPC协议从DCS系统读取锅炉燃烧控制有关参数,优化控制系统与原DCS系统连接结构框图如图 8所示。
|
图 8 燃烧优化控制系统结构 Fig. 8 Structure of combustion optimization control system |
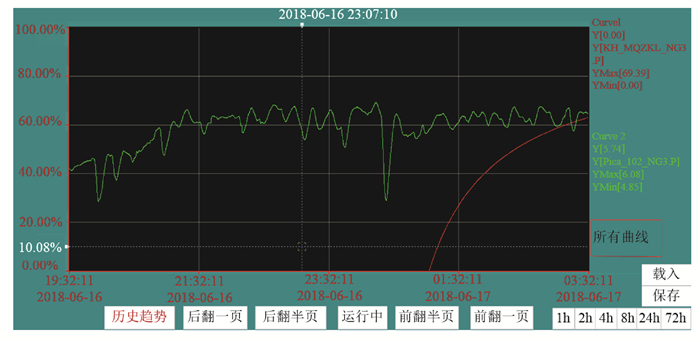
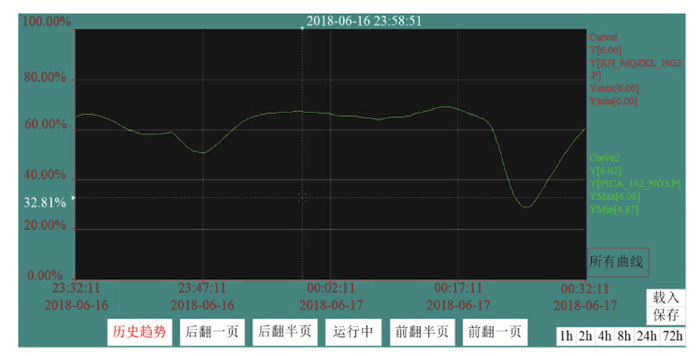
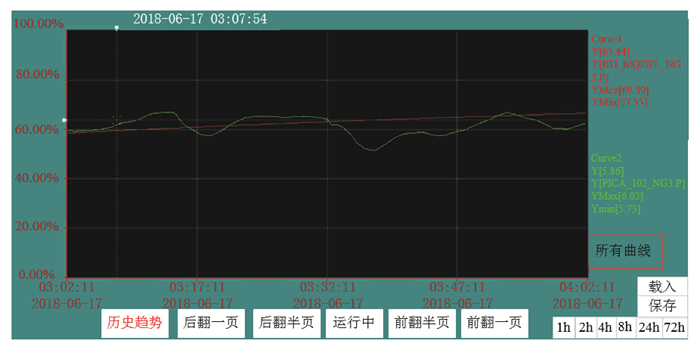
燃烧优化系统用于控制燃气锅炉的燃烧优化,调节煤气用量和煤气配比,其主控制回路为主蒸汽压力控制。燃烧优化控制系统通过工业以太网与DCS管理员站连接,通过Kepware OPC软件进行数据通讯,使用力控组态软件进行算法和组态编程。图 9为燃烧优化控制系统采集的传统PID控制与失配补偿Smith预估及RBF神经网络控制的主蒸汽压力对比曲线,图中红色曲线为燃烧优化控制系统中主蒸汽压力控制回路投入使用时间的积分,当主蒸汽压力控制回路投入时红色曲线不为0,且随投入使用的时间逐渐累积。图 9中绿色曲线为主蒸汽压力,主蒸汽压力设定点为5.9 MPa,红色曲线起始时刻为失配补偿Smith预估及RBF神经网络控制算法投入主蒸汽控制回路的时间,图 9的时间长度为8 h。由图 9可以看出,当主蒸汽压力控制回路投入所设计的算法时,主蒸汽压力曲线更平稳,无较大波动,且主蒸汽压力超调不超过6.0 MPa,在煤气压力波动的一定范围内,主蒸汽压力最低不低于5.8 MPa。由图 10和图 11可以看出,当煤气压力突然发生变化时,采用失配补偿Smith预估及RBF神经网络控制算法的优化控制系统能够很快的抑制煤气扰动,相对于PID控制,具有更快的快速性和稳定性,保证了主蒸汽压力的稳定。
|
图 9 主蒸汽压力控制对比曲线 Fig. 9 Contrast Curve of Main Steam Pressure Control |
|
图 10 煤气扰动时PID控制的主蒸汽压力曲线 Fig. 10 Main Steam Pressure Curve of PID Control under Gas Disturbance |
|
图 11 煤气扰动时失配补偿Smith预估及RBF神经网络控制的主蒸汽压力曲线 Fig. 11 Smith Prediction of Mismatch Compensation for Gas Disturbance and Main Steam Pressure Curve Controlled by RBF Neural Network |
针对模型参数经常变化的火力燃气发电锅炉控制系统中存在的纯滞后问题,将失配补偿型Smith预估控制器与RBF神经网络整定PID参数相结合,提出了一种失配补偿型Smith-RBF控制方案。仿真结果和现场工程应用效果表面,失配补偿型Smith-RBF控制方案对模型精度要求明显降低,有效改善了模型参数变化及纯滞后系统的控制问题,具有良好的抗干扰性,达到了满意的控制效果。
| [1] |
沈霞, 张丽香, 王晓伟. 基于TDOF MD PID的循环流化床锅炉主蒸汽压力控制系统研究[J]. 热力发电, 2014(5): 94-97. SHEN Xia, ZHANG Lixiang, WANG Xiaowei. TDOF MD PID based main steam pressure control system in circulating fluidized bed boilers[J]. Thermal Power Generation, 2014(5): 94-97. (in Chinese) DOI:10.3969/j.issn.1002-3364.2014.05.094 |
| [2] |
Sivakumar L, Jims S H, Dharmalingam S. An investigation on the efficacy of classical tuning algorithm to satisfy advanced requirements:control of main steam pressure during fuel switching and load disturbances in coal fired boilers[J]. Ifac Papersonline, 2016, 49(1): 443-449. DOI:10.1016/j.ifacol.2016.03.094 |
| [3] |
李俊利, 杨绍武, 袁平, 等. 基于动态矩阵控制的燃煤锅炉蒸汽压力控制[J]. 控制工程, 2016, 23(11): 1685-1689. LI Junli, YANG Shaowu, YUAN Ping, et al. Steam pressure control of coal fired boiler based on dynamic matrix control[J]. Control Engineering of China, 2016, 23(11): 1685-1689. (in Chinese) |
| [4] |
王宝忠, 宋冬锋, 刘卫法. 基于Smith预估补偿与RBF神经网络的改进PID控制[J]. 现代电子技术, 2011, 34(5): 153-157. WANG Baozhong, SONG Dongfeng, LIU Weifa. Improved PID control based on smith predictive compensation and RBF neural network[J]. Modern Electronics Technique, 2011, 34(5): 153-157. (in Chinese) DOI:10.3969/j.issn.1004-373X.2011.05.047 |
| [5] |
韩立强, 李志宏. 一种改进结构的Smith预估器及在轧机AGC中的应用[J]. 河北大学学报(自然科学版), 2004, 24(2): 130-134. HAN Liqiang, LI Zhihong. A improved smith predictor and its application for AGC in the roll[J]. Journal of Hebei University, 2004, 24(2): 130-134. (in Chinese) DOI:10.3969/j.issn.1000-1565.2004.02.005 |
| [6] |
刘长良, 马增辉. Smith预估模型参数仿真分析及多目标优化[J]. 系统仿真学报, 2014, 26(8): 1706-1712. LIU Changliang, MA Zenghui. Simulation analysis and multi-objective optimization of smith-predictor parameters tuning[J]. Journal of System Simulation, 2014, 26(8): 1706-1712. (in Chinese) |
| [7] |
张晓宇, 付林, 沈炯, 等. 基于在线支持向量机的锅炉动态建模方法研究[J]. 中国电机工程学报, 2017, 37(增1): 123-128. ZHANG Xiaoyu, FU Lin, SHEN Jiong, et al. Study on dynamic modeling method of boiler based on on-line support vector machine[J]. Proceedings of the Csee, 2017, 37(S1): 123-128. |
| [8] |
Ma J, Eason J P, Dowling A W, et al. Development of a first-principles hybrid boiler model for oxy-combustion power generation system[J]. International Journal of Greenhouse Gas Control, 2016, 46: 136-157. DOI:10.1016/j.ijggc.2015.12.036 |
| [9] |
Sampath R, Dhami S S, Srivastava S. A virtual model of steam turbine power generation unit[J]. International Journal of Performability Engineering, 2016, 46: 136-157. |
| [10] |
刘长良, 马增辉. 过热汽温系统的Smith预估器参数多目标优化控制[J]. 模式识别与人工智能, 2015, 28(3): 282-288. LIU Changliang, MA Zenghui. Multi-objective optimization control of smith-predictor parameters in superheated steam temperature system[J]. Pattern Recognition and Artificial Intelligence, 2015, 28(3): 282-288. (in Chinese) |
| [11] |
Mai N T, Yamada K. A design method for stabilizing modified smith predictor for multiple-input/multiple-output non-minimum phase time-delay plants with multiple time-delays[J]. Icic Express Letters, 2014, 8(3): 915-920. |
| [12] |
汪秉文, 李国宽, 姜新. 一种改进的Smith预估补偿方法[J]. 华中理工大学学报, 1999(12): 33-35. WANG Bingwen, LI Guokuan, JIANG Xin. An improved smith predictor control method[J]. Journal of Huazhong University Ofence & Technology, 1999(12): 33-35. (in Chinese) |
| [13] |
Qiao J, Meng X, Li W. An incremental neuronal-activity-based rbf neural network for nonlinear system modeling[J]. Neurocomputing, 2018, 302(8): 1-11. |
| [14] |
Wang X W. Path planning and tracking for vehicle parallel parking based on preview BP neural network PID controller[J]. Transactions of Tianjin University, 2015, 21(3): 199-208. DOI:10.1007/s12209-015-2485-x |
| [15] |
Zhu H, Shen J, Su Z. RBF neural network regression model based on fuzzy observations[J]. Journal of Southeast University (English Edition), 2013, 29(4): 400-406. |
 2019, Vol. 42
2019, Vol. 42


 ,
,