近些年来,伴随着技术进步和劳动力成本提高,机械臂被广泛应用于工业生产的各个领域,扮演着越来越重要的作用。在机械臂的实际应用中,往往要求其能够快速且精确地跟踪期望轨迹,完成规定作业任务。然而,在实际工业现场环境,机械臂系统通常会面临模型参数摄动和外部扰动等不确定性因素的影响,如负载变化、摩擦力矩扰动以及系统外部扰动等。因此,实现机械臂的快速高精度跟踪控制是一个极具挑战性的问题。
为了抑制不确定性因素对机械臂跟踪控制性能的影响,人们对其跟踪控制问题进行广泛深入地研究,许多控制方法被应用于机械臂的跟踪控制。如鲁棒控制方法[1-2]、模型预测控制方法[3-5]、神经网络控制方法[6-8]、滑模控制方法[9-11]等。文献[1]提出了一种鲁棒H∞有限时间稳定控制方法,并应用于机械臂的轨迹跟踪控制,但该控制方法仅仅保证系统具有一定的扰动抑制水平,不能完全抑制系统扰动,且所设计的控制器保守性较大。文献[3]针对具有系统参数不确定性的柔性关节机械臂轨迹跟踪控制问题,提出一种自适应非线性模型预测控制算法,该设计算法过于复杂。文献[6]针对未知摩擦非线性会导致机械臂跟踪控制精度难以提高的问题, 建立了基于动态LuGre摩擦的机械臂模型,考虑系统参数未知和机械臂负载变化的情况下,设计了一种自适应模糊神经网络控制器,仿真结果验证了设计控制器的有效性。然而,神经网络控制方法的控制效果高度依赖于神经网络节点的数量,导致了更多的计算量和在线学习时间,使控制算法的实时性得不到保证,不利于设计控制算法的实际应用。文献[9]基于自适应模糊滑模控制算法,有效解决了存在结构化和非结构化不确定性的机械臂动力学模型控制器设计问题,证明了闭环系统的全局渐近稳定性。
在对机械臂的跟踪控制研究中,由于滑模控制方法具有控制器计算量小、对系统参数摄动和外部干扰具有很强的鲁棒性,使其特别适合机械臂系统的跟踪控制。然而,在传统的滑模控制方法中,由于采用线性滑模面系统状态无法做到有限时间收敛,为了加快系统状态的收敛速度,控制器往往需输出很大的控制量,这极易引起系统执行机构进入饱和状态,从而使得系统控制性能下降甚至引起整个闭环系统的不稳定。另外,相比于传统的滑模控制,有限时间滑模控制方法不仅能够保证系统跟踪误差的有限时间收敛和快速动态响应性能,具有更好的抗扰动能力[10-13]。
为了实现机械臂的有限时间跟踪控制,同时保证系统较强的抗干扰性能。考虑存在系统总和扰动的机械臂有限时间跟踪控制问题,利用有限时间滑模控制方法结合反步控制技术,提出了反步有限时间滑模控制算法。首先,通过将系统模型表示为严格反馈形式,进而利用三阶非线性扩张状态观测器的在线估计,实现系统总和扰动地有效补偿。结合反步有限时间滑模控制方法设计控制策略,实现机械臂轨迹跟踪误差可在有限时间内收敛到平衡点附近的领域。仿真结果表明,所提控制算法能够补偿总和扰动对系统跟踪性能的影响,提高系统的鲁棒性能,同时实现跟踪误差的快速收敛,便于控制器的实际应用。
1 机械臂动力学模型及轨迹跟踪问题描述对于n关节机械臂系统,如果考虑系统未建模动态、摩擦力及干扰的影响,其动力学模型[14]可表示为
| $ \boldsymbol{M}(\boldsymbol{q}) \ddot{\boldsymbol{q}}+\boldsymbol{C}(\boldsymbol{q}, \dot{\boldsymbol{q}})+\boldsymbol{G}(\boldsymbol{q})+\boldsymbol{d}(t)=\boldsymbol{\tau}, $ | (1) |
式中:
由于机械臂系统存在诸多不确定性因素,如负载扰动、测量噪声及系统外部扰动等,要想获得精确的系统模型是比较困难的。所以,实际系统的模型可以表示为名义系统模型和总和扰动项之和的形式
| $ {\mathit{\boldsymbol{M}}_0}\mathit{\boldsymbol{\ddot q}} + \mathit{\boldsymbol{\omega }}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}},\mathit{\boldsymbol{\ddot q}}},t \right) = \mathit{\boldsymbol{\tau }}, $ | (2) |
式中:M0=M-ΔM,M0为M的名义部分,可依据经验确定,M0为M的不确定部分;ω=[ω1, …, ωn]T=
控制目标为在考虑系统(2)总和扰动的情况下,设计多关节机械臂反步有限时间滑模控制器,实现多关节机械臂的位置矢量q对期望位置矢量qd的有限时间快速稳定跟踪控制。
2 控制器设计 2.1 三阶扩张状态观测器设计由式(2)可知,系统的总和扰动项是未知的,需要设计扩张状态观测器进行在线估计。
设
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot x}}}_1} = {\mathit{\boldsymbol{x}}_2}\\ {{\mathit{\boldsymbol{\dot x}}}_2} = \mathit{\boldsymbol{M}}_0^{ - 1}\tau + {\mathit{\boldsymbol{x}}_3}\\ {{\mathit{\boldsymbol{\dot x}}}_3} = \mathit{\boldsymbol{h}} \end{array} \right., $ | (3) |
在机械臂控制系统中,为了检测各关节的位置信息,一般各关节都安装有位置传感器。假设各关节位置传感器的输出矢量可表示为yp,那么系统的输出方程可表示为
| $ {\mathit{\boldsymbol{y}}_{\rm{p}}} = \mathit{\boldsymbol{q}}。$ | (4) |
为了实现对系统的关节位置、关节速度及扩张状态矢量的估计,由式(3)、(4)扩张状态观测器可设计为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{e}}_1} = {z_1} - {\mathit{\boldsymbol{y}}_{\rm{p}}}\\ {\mathit{\boldsymbol{e}}_2} = {z_2} - {\mathit{\boldsymbol{x}}_{\rm{2}}}\\ {\mathit{\boldsymbol{e}}_3} = {z_3} - {\mathit{\boldsymbol{x}}_{\rm{3}}}\\ {{\dot z}_1} = {z_2} - {\mathit{\boldsymbol{K}}_1}{\mathit{\boldsymbol{e}}_1}\\ {{\dot z}_2} = {z_3} - {\mathit{\boldsymbol{K}}_2}\mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{e}}_1}} \right) + \mathit{\boldsymbol{M}}_0^{ - 1}\mathit{\boldsymbol{\tau }}\\ {{\dot z}_3} = - {\mathit{\boldsymbol{K}}_3}\mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{e}}_1}} \right) \end{array} \right., $ | (5) |
式中:e1=[e11, …, e1n]T,e2=[e21, …, e2n]T,e3=[e31, …, e3n]T分别表示扩张状态观测器对关节位置、关节速度及扩张状态矢量的观测误差矢量;
K1=diag{k11, …, k1n},k1i>0,
K2=diag{k21, …, k2n}, k2i>0,
K3=diag{k31, …, k3n},k3i>0,i=1, 2, …, n为正定的扩张状态观测器增益矩阵;
F(e1)=[f1(e11), …, fn(e1n)]T为非线性函数矢量,其中fi(e1i)具有如下形式
| $ {f_i}\left( {{e_{1i}}} \right) = \left\{ {\begin{array}{*{20}{l}} {{{\left| {{\mathit{\boldsymbol{e}}_{1i}}} \right|}^\alpha }{\mathop{\rm sign}\nolimits} \left( {{\mathit{\boldsymbol{e}}_{1i}}} \right),}&{\left| {{\mathit{\boldsymbol{e}}_{1i}}} \right| > \sigma ;}\\ {{\mathit{\boldsymbol{e}}_{1i}}/{\sigma ^{1 - \alpha }},}&{\left| {{\mathit{\boldsymbol{e}}_{1i}}} \right| \le \sigma ,} \end{array}} \right. $ | (6) |
式中:i=1, …, n;0 < a < 1;σ>0为待整定参数。
由文献[15-17]可知,只要通过合理选择三阶扩张状态观测器增益矩阵K1,K2,K3,系统(5)就能很好地估计系统(3)中的状态变量,估计误差矢量ei(i=1, 2, 3)的各元素可以收敛到原点很小的领域内。
2.2 反步有限时间滑模控制律设计针对系统模型(2),下面结合反步设计思想和有限时间滑模控制技术进行控制律设计,具体设计步骤为
步骤1
为了应用反步设计思想,首先定义跟踪误差矢量ε1=[ε11, …, ε1n]T=x1-qd,并假设期望位置矢量qd充分光滑,则ε1的一阶导数可表示为
| $ \dot{\boldsymbol{\varepsilon}}_{1}=\left[\dot{\boldsymbol{\varepsilon}}_{11}, \cdots, \boldsymbol{\dot { \varepsilon }}_{1 n}\right]^{\mathrm{T}}=\dot{\boldsymbol{x}}_{1}-\dot{\boldsymbol{q}}_{\mathrm{d}}, $ | (7) |
对于x1子系统,设计虚拟控制输入为
| $ {\mathit{\boldsymbol{\varepsilon }}_2} = {\lambda _1}{\mathit{\boldsymbol{\varepsilon }}_1} + {\mathit{\boldsymbol{x}}_2} - {\mathit{\boldsymbol{q}}_{\rm{d}}} + \beta {\mathop{\rm sign}\nolimits} {\left( {{\mathit{\boldsymbol{\varepsilon }}_1}} \right)^\varphi }, $ | (8) |
式中,λ1=diag{λ11, …, λ1n},λ1i>0,β=diag{β1, …, βn},βi>0,i=1, 2, …, n为待设计的对角参数矩阵;
0 < φ < 1为待设计的正常数;sign(ε1)φ=[ε11φsign(ε11), …, ε1nφsign(ε1n)]T。
定义Lyapunov函数
| $ {\mathit{\boldsymbol{V}}_1} = \frac{1}{2}\mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}{\mathit{\boldsymbol{\varepsilon }}_1}, $ | (9) |
对V1求时间的导数并结合式(7)、(8)可得
| $ {\mathit{\boldsymbol{\dot V}}_1} = \mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}{\mathit{\boldsymbol{\dot \varepsilon }}_1} = \mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}\left( {{\mathit{\boldsymbol{x}}_2} - {{\mathit{\boldsymbol{\dot q}}}_d}} \right) = \mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}\left( {{\mathit{\boldsymbol{\varepsilon }}_2} - {\lambda _1}{\mathit{\boldsymbol{\varepsilon }}_1} - \mathit{\boldsymbol{\beta }}{\rm{sign}}{{\left( {{\mathit{\boldsymbol{\varepsilon }}_1}} \right)}^\varphi }} \right) = - \mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_1}{\mathit{\boldsymbol{\varepsilon }}_1} + \mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}{\mathit{\boldsymbol{\varepsilon }}_2} - \mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}\mathit{\boldsymbol{\beta }}{\rm{sign}}{\left( {{\mathit{\boldsymbol{\varepsilon }}_1}} \right)^\varphi }, $ | (10) |
故只要设计控制律使得ε2收敛到零,则可保证
步骤2
针对x2子系统,在扩张状态观测器对系统总和扰动估计的基础上,采用有限时间滑模控制技术设计控制律τ以改进普通反步滑模控制算法的性能。
由式(8)可知虚拟控制输入ε2由系统跟踪误差ε1及其一阶导数构成,故系统滑模面可设计为
| $ \boldsymbol{s}_{1}=\left[\begin{array}{ccc}{s_{11}} & {\cdots} & {s_{1 n}}\end{array}\right]^{\mathrm{T}}=\boldsymbol{\varepsilon}_2 。$ | (11) |
定义Lyapunov函数
| $ \boldsymbol{V}_{2}=\boldsymbol{V}_{1}+\frac{1}{2} \boldsymbol{s}_{1}^{\mathrm{T}} \boldsymbol{s}_{1}。$ | (12) |
对V2求时间的导数可得
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot V}}}_2} = {{\mathit{\boldsymbol{\dot V}}}_1} + \mathit{\boldsymbol{s}}_1^{\rm{T}}{{\mathit{\boldsymbol{\dot s}}}_1} = - \mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}{\mathit{\boldsymbol{\lambda }}_1}{\mathit{\boldsymbol{\varepsilon }}_1} + \mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}{\mathit{\boldsymbol{\varepsilon }}_2} - \mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}\mathit{\boldsymbol{\beta }}{\rm{sign}}{{\left( {{\mathit{\boldsymbol{\varepsilon }}_1}} \right)}^\varphi } + }\\ {\mathit{\boldsymbol{s}}_1^{\rm{T}}\left( {{\lambda _1}{{\mathit{\boldsymbol{\dot \varepsilon }}}_1} + \mathit{\boldsymbol{M}}_0^{ - 1}\tau + {\mathit{\boldsymbol{x}}_3} - {{\ddot q}_d} + {{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\beta }}_1}\varphi {{\left| {{\mathit{\boldsymbol{\varepsilon }}_{11}}} \right|}^{\varphi - 1}}{{\mathit{\boldsymbol{\dot \varepsilon }}}_{11}},}&{ \cdots ,}&{{\mathit{\boldsymbol{\beta }}_n}\varphi {{\left| {{\mathit{\boldsymbol{\varepsilon }}_{1n}}} \right|}^{\varphi - 1}}{{\mathit{\boldsymbol{\dot \varepsilon }}}_{1n}}} \end{array}} \right]}^{\rm{T}}}} \right),} \end{array} $ | (13) |
控制律τ设计为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tau }} = {\mathit{\boldsymbol{M}}_0}\left( { - {\mathit{\boldsymbol{\varepsilon }}_1} - {\mathit{\boldsymbol{\lambda }}_1}{{\mathit{\boldsymbol{\dot \varepsilon }}}_1} + {{\mathit{\boldsymbol{\ddot q}}}_d} - {z_3} - {{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\beta }}_1}\varphi {{\left| {{\mathit{\boldsymbol{\varepsilon }}_{11}}} \right|}^{\varphi - 1}}{{\mathit{\boldsymbol{\dot \varepsilon }}}_{11}},}&{ \cdots ,}&{{\mathit{\boldsymbol{\beta }}_n}\varphi {{\left| {{\mathit{\boldsymbol{\varepsilon }}_{1n}}} \right|}^{\varphi - 1}}{{\mathit{\boldsymbol{\dot \varepsilon }}}_{1n}}} \end{array}} \right]}^{\rm{T}}} - } \right.}\\ {\left. {{\kappa _{\rm{d}}}{\rm{sign}}\left( {{\mathit{\boldsymbol{s}}_1}} \right) - {\kappa _{\rm{t}}}{\rm{sign}}{{\left( {{\mathit{\boldsymbol{s}}_1}} \right)}^\varphi }} \right),} \end{array} $ | (14) |
将控制律(14)代入式(13)可得
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot V}}}_2} = {{\mathit{\boldsymbol{\dot V}}}_1} + \mathit{\boldsymbol{s}}_1^{\rm{T}}{{\mathit{\boldsymbol{\dot s}}}_1} = - \mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}{\lambda _1}{\mathit{\boldsymbol{\varepsilon }}_1} - \mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}\beta {\rm{sign}}{{\left( {{\mathit{\boldsymbol{\varepsilon }}_1}} \right)}^\varphi } + \mathit{\boldsymbol{s}}_1^{\rm{T}}\left( {{\mathit{\boldsymbol{x}}_3} - {\mathit{\boldsymbol{z}}_3}} \right) - }\\ {\mathit{\boldsymbol{s}}_1^{\rm{T}}\left[ {{\kappa _{\rm{d}}}{\mathop{\rm sign}\nolimits} \left( {{\mathit{\boldsymbol{s}}_1}} \right) + {\kappa _{\rm{t}}}{\mathop{\rm sign}\nolimits} {{\left( {{\mathit{\boldsymbol{s}}_1}} \right)}^\varphi }} \right] \le }\\ { - \mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}\beta {\mathop{\rm sign}\nolimits} {{\left( {{\mathit{\boldsymbol{\varepsilon }}_1}} \right)}^\varphi } + \sum\limits_{i = 1}^n {\left| {{\mathit{\boldsymbol{s}}_{1i}}} \right|} \left| {{e_{3i}}} \right| - {\kappa _{\rm{d}}}\sum\limits_{i = 1}^n {\left| {{\mathit{\boldsymbol{s}}_{1i}}} \right|} - {\kappa _{\rm{t}}}\mathit{\boldsymbol{s}}_1^{\rm{T}}{\mathop{\rm sign}\nolimits} {{\left( {{\mathit{\boldsymbol{s}}_1}} \right)}^\varphi },} \end{array} $ | (15) |
式中,κd,κt>0为待设计的控制器参数。当选择κd>max{|e3i|}, i=1, …, n,则
| $ {\mathit{\boldsymbol{\dot V}}_2} \le - \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{\beta }}_i}} {\left| {{\mathit{\boldsymbol{\varepsilon }}_{1i}}} \right|^{\varphi + 1}} - {\kappa _t}\sum\limits_{i = 1}^n {{{\left| {{\mathit{\boldsymbol{s}}_{1i}}} \right|}^{\varphi + 1}}} \le 0, $ | (16) |
因此,由Lyapunov稳定性理论可知,在控制律式(14)作用下可保证系统状态x1对期望信号qd的稳定跟踪。
2.3 有限时间稳定性分析引理1 如果0 < p < 2,则下面的不等式成立[18-20]
| $ {\left( {b_1^2 + b_2^2 + \cdots + b_n^2} \right)^{\frac{p}{2}}} \le {\left| {{b_1}} \right|^p} + {\left| {{b_2}} \right|^p} + \cdots + {\left| {{b_n}} \right|^p}。$ | (17) |
引理2 假设存在一个连续正定的函数V(t),满足以下微分方程[21]
| $ \dot{\boldsymbol{V}}(t) \leqslant-\zeta \boldsymbol{V}^{\mu}(t), \forall t>0, \boldsymbol{V}\left(t_{0}\right)>0, $ | (18) |
式中,ζ>0,0 < μ < 1是常数。则对应任意给定的t0,存在有限时间t0,使得以下式子成立
| $ \boldsymbol{V}^{1-\mu}(t) \leqslant \boldsymbol{V}^{1-\mu}\left(t_{0}\right)-\zeta(1-\mu)\left(t-t_{0}\right), t_{0} \leqslant t \leqslant t_{1}, $ | (19) |
| $ \boldsymbol{V}(t) \equiv 0, \forall t \geqslant t_{1}, $ | (20) |
式中,
定理1 对于考虑总和扰动情况的多关节机械臂系统(2)及滑模面(11),设计三阶扩张状态观测器(5)和控制律(14),当控制器参数满足κd>max{|e3i|}, i=1, …, n时,可保证系统滑模面s1在有限时间内收敛到零。
证 若设ρ=min{βi, κt}, i=1, …, n,则由式(16)及引理1可得
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot V}}}_2} \le - \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{\beta }}_i}{{\left| {{\mathit{\boldsymbol{\varepsilon }}_{1i}}} \right|}^{\varphi + 1}}} - {\kappa _{\rm{t}}}\sum\limits_{i = 1}^n {{{\left| {{\mathit{\boldsymbol{s}}_{1i}}} \right|}^{\varphi + 1}}} \\ \;\;\;\; \le - \sum\limits_{i = 1}^n {\rho \left( {{{\left| {{\mathit{\boldsymbol{\varepsilon }}_{1i}}} \right|}^{\varphi + 1}} + {{\left| {{\mathit{\boldsymbol{s}}_{1i}}} \right|}^{\varphi + 1}}} \right)} \\ \;\;\;\; \le - \rho \sum\limits_{i = 1}^n {{{\left( {{{\left| {{\mathit{\boldsymbol{\varepsilon }}_{1i}}} \right|}^2} + {{\left| {{\mathit{\boldsymbol{s}}_{1i}}} \right|}^2}} \right)}^{\frac{{\varphi + 1}}{2}}}} \\ \;\;\;\; = - \rho {2^{\frac{{\varphi + 1}}{2}}}\mathit{\boldsymbol{V}}_2^{\frac{{\varphi + 1}}{2}}, \end{array} $ | (21) |
因此,依据引理2,存在有限时间t1当满足t>t1时V2=0,从而在控制律(14)的作用下可以保证系统滑模面s1有限时间内收敛于零。
证毕。
定理2 在系统滑模面s1于有限时间内收敛到零后,对于考虑总和扰动情况下的多关节机械臂系统(2),其位置矢量q将在有限时间内实现对期望位置矢量qd的稳定跟踪。
证 在滑模面s1于有限时间内收敛到零后,由式(8)、(11)可知,在滑模面上
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot V}}}_1} = \mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}{{\mathit{\boldsymbol{\dot \varepsilon }}}_1} = - \mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}\left( {{\lambda _1}{\mathit{\boldsymbol{\varepsilon }}_1} + \mathit{\boldsymbol{\beta }}{\mathop{\rm sign}\nolimits} {{\left( {{\mathit{\boldsymbol{\varepsilon }}_1}} \right)}^\varphi }} \right)\\ \;\;\;\; = - \mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}{\lambda _1}{\mathit{\boldsymbol{\varepsilon }}_1} - \mathit{\boldsymbol{\varepsilon }}_1^{\rm{T}}\mathit{\boldsymbol{\beta }}{\mathop{\rm sign}\nolimits} {\left( {{\mathit{\boldsymbol{\varepsilon }}_1}} \right)^\varphi }\\ \;\;\;\; = - \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{\lambda }}_{1i}}} {\left| {{\mathit{\boldsymbol{\varepsilon }}_{1i}}} \right|^2} - \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{\beta }}_i}} {\left| {{\mathit{\boldsymbol{\varepsilon }}_{1i}}} \right|^{\varphi + 1}}\\ \;\;\;\; \le - \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{\beta }}_i}} {\left| {{\mathit{\boldsymbol{\varepsilon }}_{1i}}} \right|^{\varphi + 1}}\\ \;\;\;\; \le \sum\limits_{i = 1}^n \eta {\left| {{\mathit{\boldsymbol{\varepsilon }}_{1i}}} \right|^{\varphi + 1}}\\ \;\;\;\; \le - \eta {\left( {\sum\limits_{i = 1}^n {\mathit{\boldsymbol{\varepsilon }}_{1i}^2} } \right)^{\frac{{\varphi + 1}}{2}}} = - \eta {2^{\frac{{\varphi + 1}}{2}}}\mathit{\boldsymbol{V}}_1^{\frac{{\varphi + 1}}{2}}, \end{array} $ | (22) |
式中,η=min{βi}, i=1, …, n。
因此,依据引理2可知,多关节机械臂系统(2)的位置矢量q将在有限时间内稳定至期望位置矢量qd。
证毕。
注1 由于控制律(14)中符号函数的存在将引起系统状态在到达滑模面后出现来回穿越滑模面的现象,产生抖振问题,影响控制器的实际应用。为了抑制抖振问题可以采用如下形式的饱和函数[22]代替符号函数。
| $ {\mathop{\rm sat}\nolimits} \left( {{\mathit{\boldsymbol{s}}_1}} \right) = \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{s}}_1}/\gamma ,}&{\left| {{\mathit{\boldsymbol{s}}_1}} \right| \le \gamma ;}\\ {{\mathop{\rm sign}\nolimits} \left( {{\mathit{\boldsymbol{s}}_1}} \right),}&{\left| {{\mathit{\boldsymbol{s}}_1}} \right| > \gamma ,} \end{array}} \right. $ | (23) |
式中,γ为边界层厚度。
3 数值仿真以二关节机械臂为验证对象,其动力学模型[14]为
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_{11}}\left( \mathit{\boldsymbol{q}} \right)}&{{\mathit{\boldsymbol{M}}_{12}}\left( \mathit{\boldsymbol{q}} \right)}\\ {{\mathit{\boldsymbol{M}}_{21}}\left( \mathit{\boldsymbol{q}} \right)}&{{\mathit{\boldsymbol{M}}_{22}}\left( \mathit{\boldsymbol{q}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\ddot q}}}_1}}\\ {{{\mathit{\boldsymbol{\ddot q}}}_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_{11}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)}&{{\mathit{\boldsymbol{C}}_{12}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)}\\ {{\mathit{\boldsymbol{C}}_{21}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)}&{{\mathit{\boldsymbol{C}}_{22}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot q}}}_1}}\\ {{{\mathit{\boldsymbol{\dot q}}}_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{G}}_1}\left( \mathit{\boldsymbol{q}} \right)}\\ {{\mathit{\boldsymbol{G}}_2}\left( \mathit{\boldsymbol{q}} \right)} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{d}}_1}\left( t \right)}\\ {{\mathit{\boldsymbol{d}}_2}\left( t \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\tau }}_1}}\\ {{\mathit{\boldsymbol{\tau }}_2}} \end{array}} \right], $ | (24) |
式中,正定惯性矩阵各元素为
| $ \boldsymbol{M}_{11}(\boldsymbol{q})=\left(m_{1}+m_{2}\right) l_{1}^{2}+m_{2} l_{2}^{2}+2 m_{2} l_{1} l_{2} \cos \left(\boldsymbol{q}_{2}\right), $ |
| $ \boldsymbol{M}_{12}(\boldsymbol{q})=m_{2} l_{2}^{2}+m_{2} l_{1} l_{2} \cos \left(\boldsymbol{q}_{2}\right), $ |
| $ \boldsymbol{M}_{21}(\boldsymbol{q})=m_{2} l_{2}^{2}+m_{2} l_{1} l_{2} \cos \left(\boldsymbol{q}_{2}\right), $ |
| $ \boldsymbol{M}_{22}(\boldsymbol{q})=m_{2} l_{2}^{2}; $ |
离心力和哥氏力矩阵各元素为
| $ \boldsymbol{C}_{11}(\boldsymbol{q}, \dot{\boldsymbol{q}})=-m_{2} l_{1} l_{2} \sin \left(\boldsymbol{q}_{2}\right) \dot{\boldsymbol{q}}_{2}, $ |
| $ \boldsymbol{C}_{12}(\boldsymbol{q}, \dot{\boldsymbol{q}})=-m_{2} l_{1} l_{2} \sin \left(\boldsymbol{q}_{2}\right)\left(\dot{\boldsymbol{q}}_{1}+\dot{\boldsymbol{q}}_{2}\right), $ |
| $ \boldsymbol{C}_{21}(\boldsymbol{q}, \dot{\boldsymbol{q}})=m_{2} l_{1} l_{2} \sin \left(\boldsymbol{q}_{2}\right) \dot{\boldsymbol{q}}_{1}, $ |
| $ \boldsymbol{C}_{22}(\boldsymbol{q}, \dot{\boldsymbol{q}})=0; $ |
重力项矢量各元素为
| $ \boldsymbol{G}_{1}(\boldsymbol{q})=\left(m_{1}+m_{2}\right) l_{1} g \cos \left(\boldsymbol{q}_{2}\right)+m_{2} l_{2} g \cos \left(\boldsymbol{q}_{1}+\boldsymbol{q}_{2}\right), $ |
| $ \boldsymbol{G}_{2}(\boldsymbol{q})=m_{2} l_{2} g \cos \left(\boldsymbol{q}_{1}+\boldsymbol{q}_{2}\right); $ |
仿真中对象参数设定为m1=2.2 kg,m2=0.8 kg,l1=0.15 m,l2=0.1 m。
为了验证所提反步有限时间滑模控制算法的有效性,分别对如下2种控制算法进行仿真对比研究,即
算法1:为所提控制算法,其滑模面和控制律分别如式(11)、(14)所示。
算法2:带总和扰动补偿的普通反步滑模控制算法,其滑模面及控制律分别设计如下
| $ \boldsymbol{s}_{2}=\lambda_{2} \boldsymbol{\varepsilon}_{1}+\boldsymbol{x}_{2}-\dot{\boldsymbol{q}}_{\mathrm{d}}, $ | (25) |
| $ \tau = {\mathit{\boldsymbol{M}}_0}\left( { - {\mathit{\boldsymbol{\varepsilon }}_1} - {z_3} - {\mathit{\boldsymbol{\lambda }}_2}{{\mathit{\boldsymbol{\dot \varepsilon }}}_1} + {{\mathit{\boldsymbol{\ddot q}}}_{\rm{d}}} - {\kappa _{\rm{f}}}{\mathop{\rm sign}\nolimits} \left( {{\mathit{\boldsymbol{s}}_1}} \right)} \right), $ | (26) |
式中,λ2=diag{λ21, …, λ2n},λ2i>0,i=1, 2, …, n;控制器参数κf>max{|x3i|}, i=1, …, n,其中x3i为系统总和扰动的第i个分量。
为便于对比分析,仿真中2种控制算法的初始条件和控制器部分参数设置相同。机械臂各关节的期望轨迹为qd=0.2sin(t)0.3cos(t);各关节的初始位置设定为qd(0)=0.10.2;扩张状态观测器的参数设置为
假设机械臂系统所受的外部扰动信号为
| $ \left[\begin{array}{c}{d_{1}(t)} \\ {d_{2}(t)}\end{array}\right]=\left[\begin{array}{c}{0.1 \sin (t)+0.01} \\ {0.2 \cos (t)+0.02}\end{array}\right], $ | (27) |
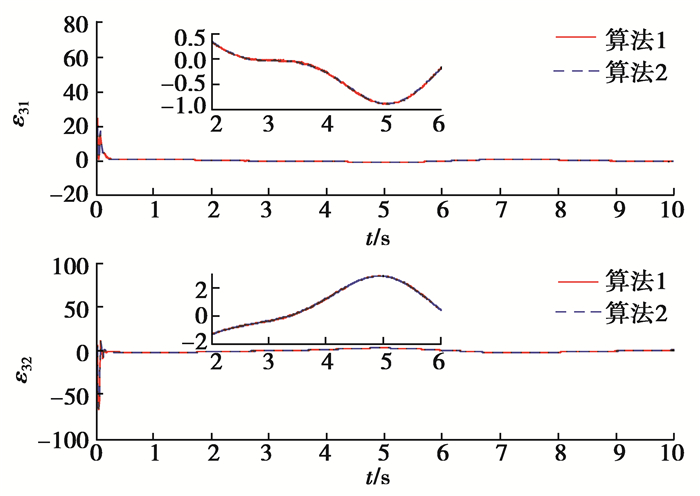
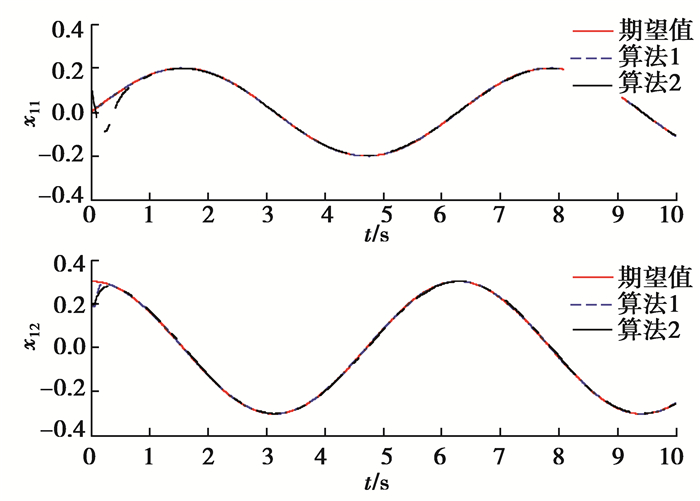
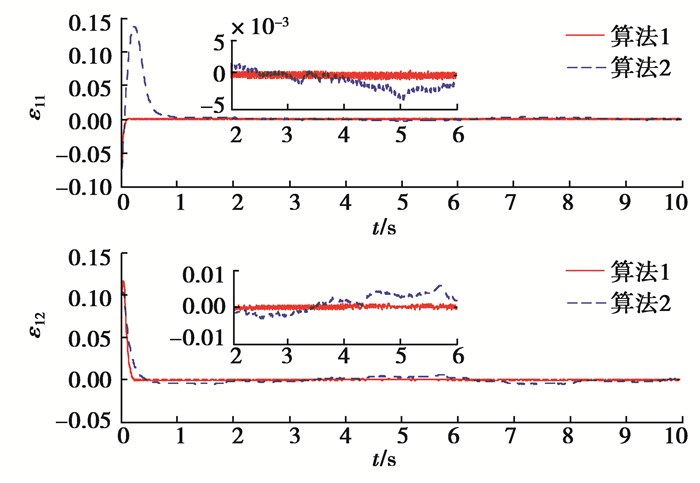
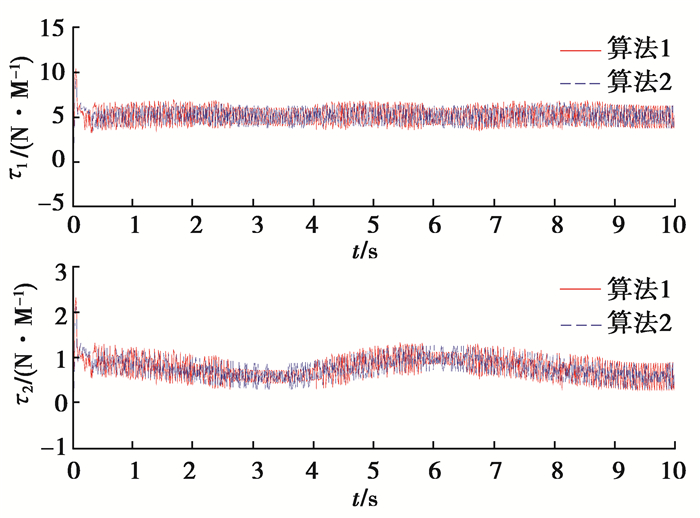
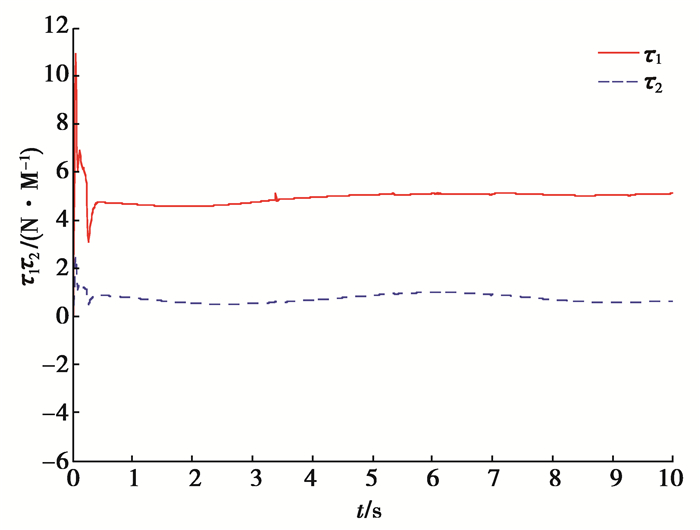
仿真结果如图 1~图 5所示。图 1为2种算法对系统总和扰动的估计误差曲线;图 2为2种算法的状态响应曲线;图 3为2种算法的跟踪误差曲线;图 4为2种算法的控制信号;图 5为算法1改进的控制信号。由图 1可见在2种算法中三阶扩张状态观测器均能较好地实现对系统总和扰动的估计,即通过合理选择观测器的参数,系统总和扰动估计误差可以控制在较小的范围内,充分体现了扩张状态观测器对系统总和扰动的估计能力,提高了系统的鲁棒性能;由图 2、图 3可见相比于算法2,算法1在存在系统总和扰动的情况下,能够实现对期望轨迹的有限时间跟踪,具有更短的收敛时间以及很小的稳态误差, 保持了较好的动态性能,算法2收敛速度相对较慢,稳态误差相对较大,且跟踪误差变化曲线存在一定波动;由图 5可知当用饱和函数代替符号函数后可有效抑制系统控制信号的抖振问题,确保控制信号是连续的。
|
图 1 2种算法的总和扰动估计误差 Fig. 1 Thetotal disturbance estimation errors of two algorithms |
|
图 2 2种算法的状态响应曲线 Fig. 2 The state response curves of two algorithms |
|
图 3 2种算法的跟踪误差曲线 Fig. 3 The tracking error curves of two algorithms |
|
图 4 2种算法的控制信号 Fig. 4 The control signals of two algorithms |
|
图 5 算法1改进的控制信号 Fig. 5 The modified control signals of algorithm 1 |
为了更好地说明所提算法的跟踪误差控制性能,定义跟踪误差的绝对值积分为
| $ {\rm{EAI}} = \int_0^T {\left| {{\varepsilon _{1i}}} \right|{\rm{d}}t} ,\left( {i = 1,2,T\;为仿真时间} \right), $ | (28) |
表 1为2种算法的跟踪误差性能比较。
| 表 1 2种控制算法的跟踪误差性能比较 Table 1 Tracking error performance comparison of two methods |
从表 1可以看出算法1具有更小的EAI值,取得了对期望轨迹的精确跟踪性能。基于以上对比分析可知针对考虑总和扰动情况下的多关节机械臂的跟踪控制问题,所提的基于反步有限时间滑模控制算法相比于普通反步滑模控制算法具有更好的控制性能。
4 结论针对考虑总和扰动情况下的多关节机械臂轨迹跟踪控制问题,提出了一种基于扩张状态观测器的反步有限时间滑模控制方法。将系统的部分内部动态、参数摄动和外部扰动看成系统的总和扰动,并通过三阶扩张状态观测器加以实时估计,得到总和扰动的估计值。然后,在此基础上设计反步有限时间滑模控制器。仿真结果表明与普通反步滑模控制相比所提算法具有更快的收敛速度和更高的控制精度。
| [1] |
Liu H, Tian X, Wang G, et al. Robust H∞ finite-time stability control of a class of nonlinear systems[J]. Applied Mathematical Modelling, 2016, 40(4): 5111-5122. |
| [2] |
Anne D, Guillaume J L, Yassine H. Robust control of a planar manipulator for flexible and contactless handling[J]. Mechatronics, 2012, 22(6): 852-861. DOI:10.1016/j.mechatronics.2012.05.003 |
| [3] |
Schnelle F, Eberhard P. Adaptive nonlinear model predictive control design of a flexible-link manipulator with uncertain parameters[J]. Acta Mechanica Sinica, 2017, 33(3): 529-542. DOI:10.1007/s10409-017-0669-4 |
| [4] |
Durmus B, Temurtas H, Yumusak N. A study on industrial robotic manipulator model using model based predictive controls[J]. Journal of Intelligent Manufacturing, 2009, 20(2): 233-241. DOI:10.1007/s10845-008-0221-2 |
| [5] |
Dubay R, Hassan M, Li C, et al. Finite element based model predictive control for active vibration suppression of a one-link flexible manipulator[J]. Isa Transactions, 2014, 53(5): 1609-1619. DOI:10.1016/j.isatra.2014.05.023 |
| [6] |
徐智浩, 李胜, 张瑞雷, 等. 基于LuGre摩擦模型的机械臂模糊神经网络控制[J]. 控制与决策, 2014, 29(6): 1097-1102. XU Zhihao, LI Sheng, ZHANG Ruilei, et al. Fuzzy-neural-network control for robot manipulators with LuGre friction model[J]. Control and Decision, 2014, 29(6): 1097-1102. (in Chinese) |
| [7] |
Yang R, Yang C, Chen M, et al. Discrete-time optimal adaptive rbfnn control for robot manipulators with uncertain dynamics[J]. Neurocomputing, 2017, 234(2): 107-115. |
| [8] |
Kumar N, Sharma S P, Sharma S P. Neural network-based nonlinear tracking control of kinematically redundant robot manipulators[J]. Mathematical & Computer Modelling, 2011, 53(9): 1889-1901. |
| [9] |
Veysi M, Soltanpour M R. Voltage-base control of robot manipulator using adaptive fuzzy sliding mode control[J]. International Journal of Fuzzy Systems, 2017, 19(5): 1430-1443. DOI:10.1007/s40815-016-0234-5 |
| [10] |
Mondal S, Mahanta C. Adaptive second order terminal sliding mode controller for robotic manipulators[J]. Journal of the Franklin Institute, 2014, 351(4): 2356-2377. DOI:10.1016/j.jfranklin.2013.08.027 |
| [11] |
Corradini M L, Fossi V, Giantomassi A, et al. Discrete time sliding mode control of robotic manipulators:development and experimental validation[J]. Control Engineering Practice, 2012, 20(8): 816-822. DOI:10.1016/j.conengprac.2012.04.005 |
| [12] |
Zhao Z, Yang J, Li S. Finite-time super-twisting sliding mode control for mars entry trajectory tracking[J]. Journal of the Franklin Institute, 2015, 352(11): 5226-5248. DOI:10.1016/j.jfranklin.2015.08.022 |
| [13] |
Ding S, Li S. Stabilization of the attitude of a rigid spacecraft with external disturbances using finite-time control techniques[J]. Aerospace Science & Technology, 2009, 13(4): 256-265. |
| [14] |
Tran M D, Kang H J. Adaptive terminal sliding mode control of uncertain robotic manipulators based on local approximation of a dynamic system[J]. Neurocomputing, 2017, 228(2): 231-240. |
| [15] |
Castaneda H, Salas-Pena O S. Extended observer based on adaptive second order sliding mode control for a fixed wing UAV[J]. Isa Transactions, 2017, 66(1): 226-323. |
| [16] |
Lu K, Xia Y, Shen G. Sliding mode control for mars entry based on extended state observer[J]. Advances in Space Research, 2017, 60(9): 2009-2020. DOI:10.1016/j.asr.2017.06.014 |
| [17] |
Chen Q, Yu L, Nan Y. Finite-time tracking control for motor servo systems with unknown dead-zones[J]. Journal of Systems Science & Complexity, 2013, 26(6): 940-956. |
| [18] |
Barambones O, Etxebarria V. Energy-based approach to sliding composite adaptive control for rigid robots with finite error convergence time[J]. International Journal of Control, 2002, 75(5): 352-359. DOI:10.1080/00207170110112241 |
| [19] |
Tang Y. Terminal sliding mode control for rigid robots[J]. Automatica, 1998, 34(1): 51-56. DOI:10.1016/S0005-1098(97)00174-X |
| [20] |
Song Z, Sun K. Adaptive backstepping sliding mode control with fuzzy monitoring strategy for a kind of mechanical system[J]. Isa Transactions, 2014, 53(1): 125-133. DOI:10.1016/j.isatra.2013.07.017 |
| [21] |
Sun Y, Wu X, Bai L. Finite-time synchronization control and parameter identification of uncertain permanent magnet synchronous motor[J]. Neurocomputing, 2016, 207(5): 511-518. |
| [22] |
王芳, 宗群, 田栢苓, 等. 再入飞行器带有干扰观测器的有限时间控制[J]. 控制理论与应用, 2016, 33(11): 1527-1534. WANG Fang, ZONG Qun, TIAN Bailing, et al. Finite time control design for re-entry hypersonic vehicle with disturbance observer[J]. Control Theory & Applications, 2016, 33(11): 1527-1534. (in Chinese) |
 2019, Vol. 42
2019, Vol. 42

