全动力换挡传动变速系统是实现拖拉机自动化、正向智能化的重要标志之一。目前全动力换挡式拖拉机大多由国外企业生产,如New Holland公司的Power command动力换挡变速器、John Deere公司的7230型拖拉机等[1-2],国内的洛阳一拖、雷沃重工则有部分动力换挡拖拉机在小批量生产。
动力换挡是通过控制几对离合器之间切换来实现,与汽车的双离合换挡类似,但因为负载工作状况更加恶劣、复杂,有关拖拉机的换挡控制策略的研究尚存在许多不足。米兰理工的Tanelli等[3-4]分析了动力换挡和换向过程,提出以换挡各过程拖拉机速度变化幅度为换挡品质优化目标,通过优化离合器起始压力,得出最佳换挡过程。Kim等[5]分析了影响动力换挡的因素如换挡时拖拉机速度、质量及变速器输入轴阻尼减震器等,为分析换挡时提供了参考。文献[6-8]则主要针对汽车的使用工况,以燃油经济性为目标来制定换挡控制策略,以冲击度为目标来完成换挡过程的实现和换挡品质的改善。
在中国,席志强等[9]提出以换挡时变速器输出转速和输出扭矩为拖拉机换挡指标,并以此对换挡时离合器重叠时间加以优化,得到最优策略;王东青[10]匹配了部分动力换挡变速器,针对换挡过程建立了液压系统、传动系统的Dymola模型并仿真。马彪等[11]对升挡离合器与降挡离合器的联合控制进行研究,减小了换挡波动。在工程车辆领域陈宁等[12]对工程车辆的换挡品质进行了研究,提出了以冲击度和传动系动载荷为目标,得到4种改善控制方法。但上述文献都没有考虑拖拉机实际工作条件状况,也没有考虑拖拉机换挡点经常处于调速阶段,柴油机在换挡过程中的转矩变化非常大,导致离合器在闭合时容易产生很大的冲击度。针对这些问题,笔者提出离合器同步阶段油压控制方法,以车速变化量、冲击度及滑摩功等为评价指标,采用遗传算法对拖拉机动力换挡过程进行分析设计,制定换挡控制方法。
1 动力学模型的建立拖拉机动力换挡变速传动系统是由发动机、动力换挡变速箱、副变速箱及减速机构等组成,基本结构如图 1所示。
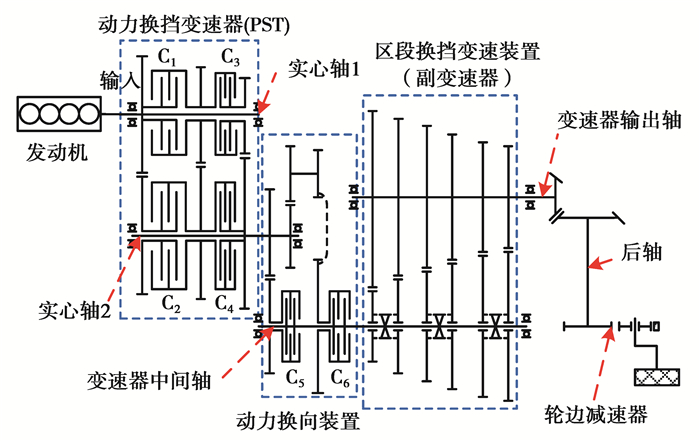
|
图 1 动力换挡变速箱基本结构图 Fig. 1 Basic structure of the power shift gearbox |
发动机参数通过实验数据查表而来,发动机扭矩视为油门开度与转速的函数,表示为式(1)。这里采用的发动机为玉柴YC4EG160-50(EJ400),额定转速为2 500 r/min;最高输出扭矩为600 N·m。
| $ {T_{\rm{e}}} = f(\alpha , {n_{\rm{e}}}), $ | (1) |
式中:Te为发动机输出转矩,N·m;α为油门开度,%;ne为发动机转速,r/min。
湿式多片离合器仿真模型的控制量是离合器油压压力[13],输出是其传递的转矩。其在接合过程中转矩的传递特性为:
间隙消除阶段
| $ {T_{\rm{c}}} = 0。$ | (2) |
滑摩阶段
| $ {T_{\rm{c}}} = {\rm{sign}}({n_{\rm{c}}} - {n_{\rm{e}}})\cdot \mu \cdot Z\cdot S\cdot (P - {P_0})\cdot {R_{\rm{c}}}。$ | (3) |
锁止阶段
| $ {T_{\rm{c}}} = {T_{\rm{e}}}。$ | (4) |
式(2)~(4)中:Tc为离合器传递的转矩;nc为离合器从动盘转速;μ为离合器的动态摩擦系数;Z为离合器摩擦面数;S为离合器活塞作用面积,m2;P,P0分别为离合器接合油压和初始油压,Pa;Rc为离合器的等效摩擦半径,m。
拖拉机作业时所受阻力∑F由牵引阻力Ft、滚动阻力Ff、坡道阻力Fi和加速阻力Fa组成, 可表示为
| $ \sum F = {F_{\rm{t}}} + {F_{\rm{f}}} + {F_{\rm{i}}} + {F_{\rm{a}}}。$ | (5) |
1) 牵引阻力。
拖拉机作业时,牵引阻力主要是农具所受的土壤阻力,根据土壤实验的研究结果,土壤阻力可以表示为
| $ {F_{\rm{t}}} = {B_1}\cdot {b_{\rm{n}}}\cdot v + {B_2}\cdot {a_{\rm{n}}}\cdot {b_{\rm{n}}}, $ | (6) |
式中:v为拖拉机作业速度;B1,B2为作业阻力系数;an为耕深,cm;bn为耕宽,m。
2) 滚动阻力。
拖拉机的滚动阻力系数f和当前滑移率s有直接关系[14],不同土壤(混凝土、硬耕土壤、中耕土壤、软耕土壤)上滚动阻力系数与滑移率的关系为
| $ f = {A_1}\cdot s - {A_2}\cdot {s^2} + {A_3}\cdot {s^3} - {A_4}\cdot {s^4} + {A_5}\cdot {s^5} - {A_6}\cdot {s^6}, $ |
式中:Ai(i=1,2,…,6)为相关系数,见表 1。
| 表 1 土壤系数取值 Table 1 Value of soil coefficient |
拖拉机作业过程中所受的滚动阻力为
| $ {F_{\rm{f}}} = G\cdot f\cdot \cos\;\beta , $ | (7) |
式中:G为拖拉机重力,N; f为滚动阻力系数;β为作业过程中的道路坡度角,rad。
3) 坡道阻力。
拖拉机行驶时的坡道阻力为
| $ {F_{\rm{i}}} = G\cdot \sin\;\beta 。$ | (8) |
4) 加速阻力。
拖拉机行驶时的加速阻力为
| $ {F_{\rm{a}}} = \delta \cdot m\cdot a, $ | (9) |
式中:m为拖拉机质量,kg;a为作业过程中的加速度,m/s2;δ为旋转质量换算系数。
1.2 换挡过程动力学模型以东方红负载换挡拖拉机结构为依据进行换挡过程研究,建立了动力学模型。图 2为此结构的动力学模型,图中,ωc1, ωc2,ωc3,ωc4分别为离合器1,2,3,4从动盘角速度(rad/s),其余变量在方程式中说明。在1挡升2挡时,离合器C1,C2分别为分离、接合离合器,离合器C3闭合,C4断开;而在4挡降3挡时,离合器C1,C2分别为接合、分离离合器,离合器C3断开,C4闭合。副变速箱在升降挡时均处于1挡状态下。
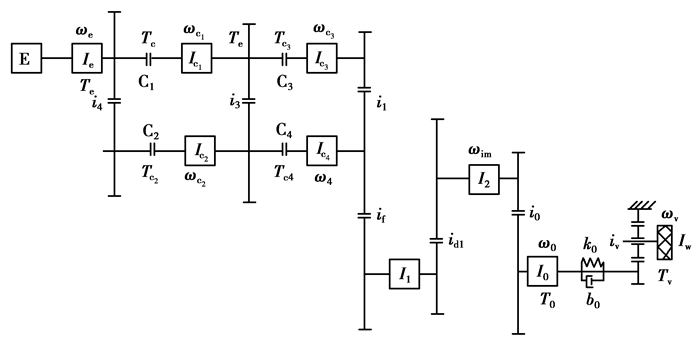
|
图 2 动力换挡系统动力学模型 Fig. 2 Dynamics model of the power shift system |
1) 换挡前后动力学方程。
| $ \left\{ \begin{array}{l} {T_{\rm{e}}} = {T_{{{\rm{c}}_1}}} + \frac{{{T_{{{\rm{c}}_2}}}}}{{{i_4}}};\\ {T_{{{\rm{c}}_1}}},{T_{{{\rm{c}}_2}}} = \left\{ \begin{array}{l} 0,\;分离;\\ {T_{{\rm{engage}}}}{\rm{,}}\;{\rm{闭合;}} \end{array} \right.\\ ({T_{{{\rm{c}}_1}}} \cdot {i_1} + \frac{{{T_{{{\rm{c}}_2}}} \cdot {i_1}}}{{{i_3}}}){i_{{\rm{d}}1}} \cdot {i_{\rm{f}}} - \frac{{{T_0}}}{{{i_0}}} = {I_{{\rm{eq}}}} \cdot \frac{{{\rm{d}}{\omega _{{\rm{im}}}}}}{{{\rm{d}}t}};\\ {T_0} \cdot {i_{\rm{v}}} - {T_{\rm{w}}} = {I_{\rm{w}}}\cdot\frac{{{\rm{d}}{\omega _{\rm{v}}}}}{{{\rm{d}}t}};\\ {T_0} = {k_0}({\theta _0} - {\theta _{\rm{v}}}\cdot{i_{\rm{v}}}) + {b_0}({\omega _0} - {\omega _{\rm{v}}}\cdot{i_{\rm{v}}})。\end{array} \right. $ | (10) |
式(10)为1挡升2挡前后动力学方程式:Tc1,Tc2为离合器C1,C2传递的转矩;T0为后轴传递的转矩;Tengage是指离合器闭合时传递的转矩,可由式(4)得出;Tw为车轮受到的阻力矩(N·m);i1,i2,i3,i4,if,id1,i0,iv分别为1挡、2挡、3挡、4挡、正向或反向齿轮、副变速箱1挡、主减速器、轮边减速器传动比;k0为后轴刚度(N·m)/rad;b0为后轴阻尼(N·m·s)/rad;θ0,θv为后轴和车轮转动角度,rad;ω0,ωv,ωim分别为后轴、车轮、变速器输出轴的转动角速度。其中
| $ {i_2} = \frac{{{i_1} \cdot {i_4}}}{{{i_3}}}。$ |
Iw为车轮的转动惯量(kg·m2),Ieq为等效到变速器输出轴的转动惯量,升挡前值为
| $ {I_{{\rm{eq}}}} = ({I_{\rm{e}}} + {I_{{{\rm{c}}_1}}} + {I_{{{\rm{c}}_3}}}){({i_1}\cdot {i_{{\rm{d1}}}}\cdot {i_{\rm{f}}})^2} + {I_1}i_{{\rm{d1}}}^2 + {I_2} + \frac{{{I_0}}}{{i_0^2}}。$ |
升挡后值为
| $ {I_{{\rm{eq}}}} = {I_{\rm{e}}}{({i_2}\cdot {i_{{\rm{d1}}}}\cdot {i_{\rm{f}}})^2} + {I_{{{\rm{c}}_2}}}\cdot \frac{{i_1^2i_{\rm{f}}^2i_{{\rm{d1}}}^2}}{{i_3^2}} + {I_{{{\rm{c}}_3}}}i_1^2i_{\rm{f}}^2i_{{\rm{d1}}}^2 + {I_1}i_{{\rm{d1}}}^2 + {I_2} + \frac{{{I_0}}}{{i_0^2}}。$ |
其中,Ie,Ic1,Ic2,Ic3,I1,I2,I0分别为发动机和飞轮、离合器C1从动盘、离合器C2从动盘、离合器C3从动盘、变速器中间轴、变速器输出轴、主轴的转动惯量。
| $ \left\{ \begin{array}{l} {T_{\rm{e}}} = {T_{{{\rm{c}}_1}}} + \frac{{{T_{{{\rm{c}}_2}}}}}{{{i_4}}};\\ {T_{{{\rm{c}}_1}}}, {T_{{{\rm{c}}_2}}} = \left\{ \begin{array}{l} 0, \;分离;\\ {T_{{\rm{engage}}}}{\rm{, }}\;{\rm{闭合;}} \end{array} \right.\\ ({T_{{{\rm{c}}_1}}} \cdot {i_3} + {T_{{{\rm{c}}_2}}}){i_{{\rm{d}}1}} \cdot {i_{\rm{f}}} - \frac{{{T_0}}}{{{i_0}}} = {I_{{\rm{eq}}}} \cdot \frac{{{\rm{d}}{\omega _{{\rm{im}}}}}}{{{\rm{d}}t}};\\ {T_0}\cdot {i_{\rm{v}}} - {T_{\rm{w}}} = {I_{\rm{w}}}\cdot \frac{{{\rm{d}}{\omega _{\rm{v}}}}}{{{\rm{d}}t}};\\ {T_0} = {k_0}({\theta _0} - {\theta _{\rm{v}}}\cdot {i_{\rm{v}}}) + {b_0}({\omega _0} - {\omega _{\rm{v}}}\cdot {i_{\rm{v}}})。\end{array} \right. $ | (11) |
式(11)为4挡降3挡前后动力学方程式,Ieq降挡前值为
| $ {I_{{\rm{eq}}}} = ({I_{\rm{e}}} + {I_{{{\rm{c}}_1}}}){({i_3}\cdot {i_{{\rm{d1}}}}\cdot {i_{\rm{f}}})^2} + {I_{{{\rm{c}}_4}}}i_{\rm{f}}^2i_{{\rm{d1}}}^2 + {I_1}I_{{\rm{d1}}}^2 + {I_2} + \frac{{{I_0}}}{{i_0^2}}。$ |
降挡后值为
| $ {I_{{\rm{eq}}}} = {I_{\rm{e}}}{({i_4}\cdot {i_{{\rm{d1}}}}\cdot {i_{\rm{f}}})^2} + \left( {{I_{{{\rm{c}}_2}}} + {I_{{{\rm{c}}_4}}}} \right)i_{\rm{f}}^2i_{{\rm{d1}}}^2 + {I_1}i_{{\rm{d1}}}^2 + {I_2} + \frac{{{I_0}}}{{i_0^2}}。$ |
2) 换挡过程中动力学方程式。
| $ \left\{ \begin{array}{l} {T_{\rm{e}}} = {T_{{{\rm{c}}_1}}} - \frac{{{T_{{{\rm{c}}_2}}}}}{{{i_4}}} = {I_{\rm{e}}} \cdot \frac{{{\rm{d}}{\omega _{\rm{e}}}}}{{{\rm{d}}t}};\\ {T_{{{\rm{c}}_1}}}, {T_{{{\rm{c}}_2}}} = \left\{ \begin{array}{l} 0, \;分离;\\ {T_{{\rm{slip}}}}{\rm{, }}\;{\rm{滑摩;}} \end{array} \right.\\ ({T_{{{\rm{c}}_1}}} \cdot {i_1} + \frac{{{T_{{{\rm{c}}_2}}} \cdot {i_1}}}{{{i_3}}}){i_{{\rm{d}}1}} \cdot {i_{\rm{f}}} - \frac{{{T_0}}}{{{i_0}}} = {I_{{\rm{eq}}}} \cdot \frac{{{\rm{d}}{\omega _{{\rm{im}}}}}}{{{\rm{d}}t}};\\ {T_0}\cdot {i_{\rm{v}}} - {T_{\rm{w}}} = {I_{\rm{w}}}\cdot \frac{{{\rm{d}}{\omega _{\rm{v}}}}}{{{\rm{d}}t}};\\ {T_0} = {k_0}({\theta _0} - {\theta _{\rm{v}}}\cdot {i_{\rm{v}}}) + {b_0}({\omega _0} - {\omega _{\rm{v}}}\cdot {i_{\rm{v}}})。\end{array} \right. $ | (12) |
式(12)为1挡升2挡过程中动力学方程式:Tslip为离合器滑摩时所传递扭矩,可由式(3)得出;ωe为发动机输出角速度。
| $ {I_{{\rm{eq}}}} = {I_{{{\rm{c}}_2}}}\cdot \frac{{i_1^2i_{\rm{f}}^2i_{{\rm{d1}}}^2}}{{i_3^2}} + ({I_{{{\rm{c}}_2}}} + {I_{{{\rm{c}}_3}}})i_1^2i_{\rm{f}}^2i_{{\rm{d1}}}^2 + {I_1}i_{{\rm{d1}}}^2 + {I_2} + \frac{{{I_0}}}{{i_0^2}}。$ |
| $ \left\{ \begin{array}{l} {T_{\rm{e}}} = {T_{{{\rm{c}}_1}}} - \frac{{{T_{{{\rm{c}}_2}}}}}{{{i_4}}} = {I_{\rm{e}}} \cdot \frac{{{\rm{d}}{\omega _{\rm{e}}}}}{{{\rm{d}}t}};\\ {T_{{{\rm{c}}_1}}}, {T_{{{\rm{c}}_2}}} = \left\{ \begin{array}{l} 0, \;分离;\\ {T_{{\rm{slip}}}}{\rm{, }}\;{\rm{滑摩;}} \end{array} \right.\\ ({T_{{{\rm{c}}_1}}} \cdot {i_3} + {T_{{{\rm{c}}_2}}}){i_{{\rm{d}}1}} \cdot {i_{\rm{f}}} - \frac{{{T_0}}}{{{i_0}}} = {I_{{\rm{eq}}}} \cdot \frac{{{\rm{d}}{\omega _{{\rm{im}}}}}}{{{\rm{d}}t}};\\ {T_0}\cdot {i_{\rm{v}}} - {T_{\rm{w}}} = {I_{\rm{w}}}\cdot \frac{{{\rm{d}}{\omega _{\rm{v}}}}}{{{\rm{d}}t}};\\ {T_0} = {k_0}({\theta _0} - {\theta _{\rm{v}}}\cdot {i_{\rm{v}}}) + {b_0}({\omega _0} - {\omega _{\rm{v}}}\cdot {i_{\rm{v}}})。\end{array} \right. $ | (13) |
式(13)为4挡降3挡过程中动力学方程式,Ieq值为:Ieq=(Ic2+Ic4)·if2id12+Ic1·i32if2id12+I1id12+
换挡过程中需要对接合与分离离合器油压进行精确控制, 同时对发动机进行协调控制[15]。由于离合器在接合过程中容易形成扭矩突变,造成较大冲击度,影响离合器寿命和驾驶感受,所以笔者在接合离合器同步阶段制定了离合器同步方法。
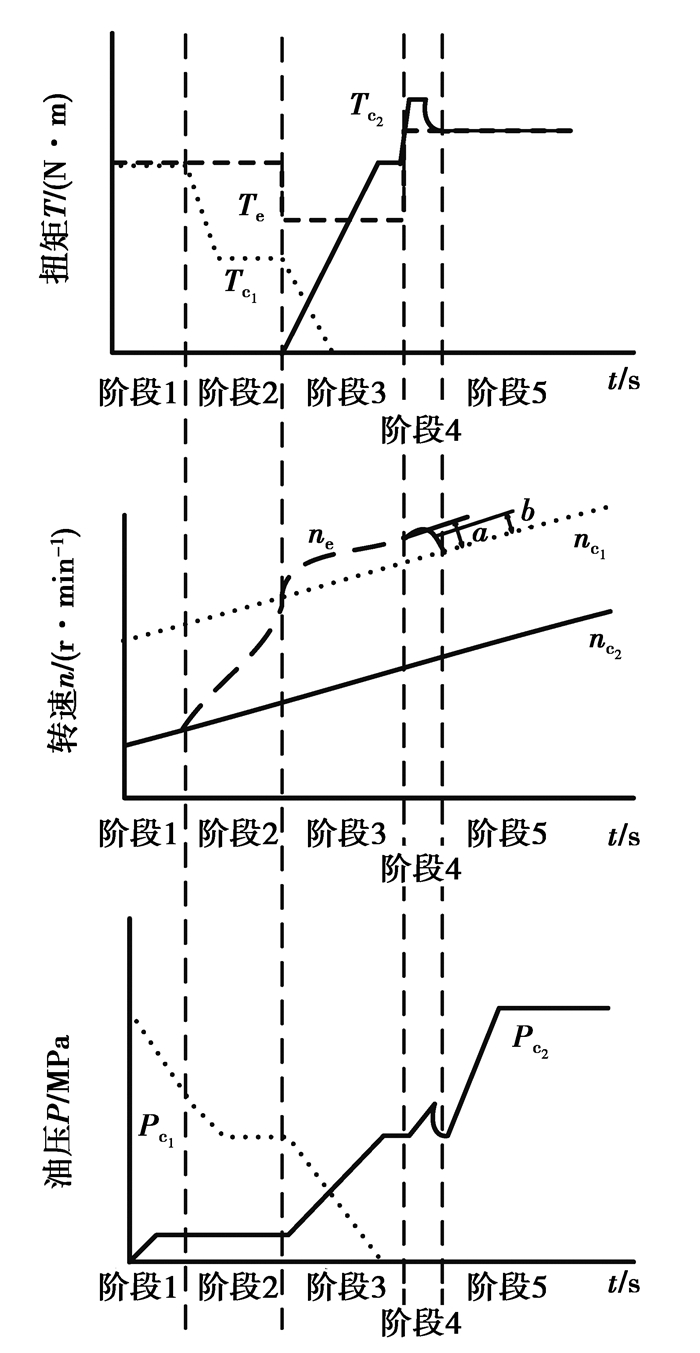
2.1 升挡过程在升挡过程中,动力换挡过程分为换挡准备、转矩相、惯性相、离合器同步、换挡结束阶段,如图 3所示的1~5阶段。图中Pc1,Pc2为离合器C1,C2的油压,nc1,nc2为离合器C1,C2从动盘转速,a,b为离合器转速差界限。
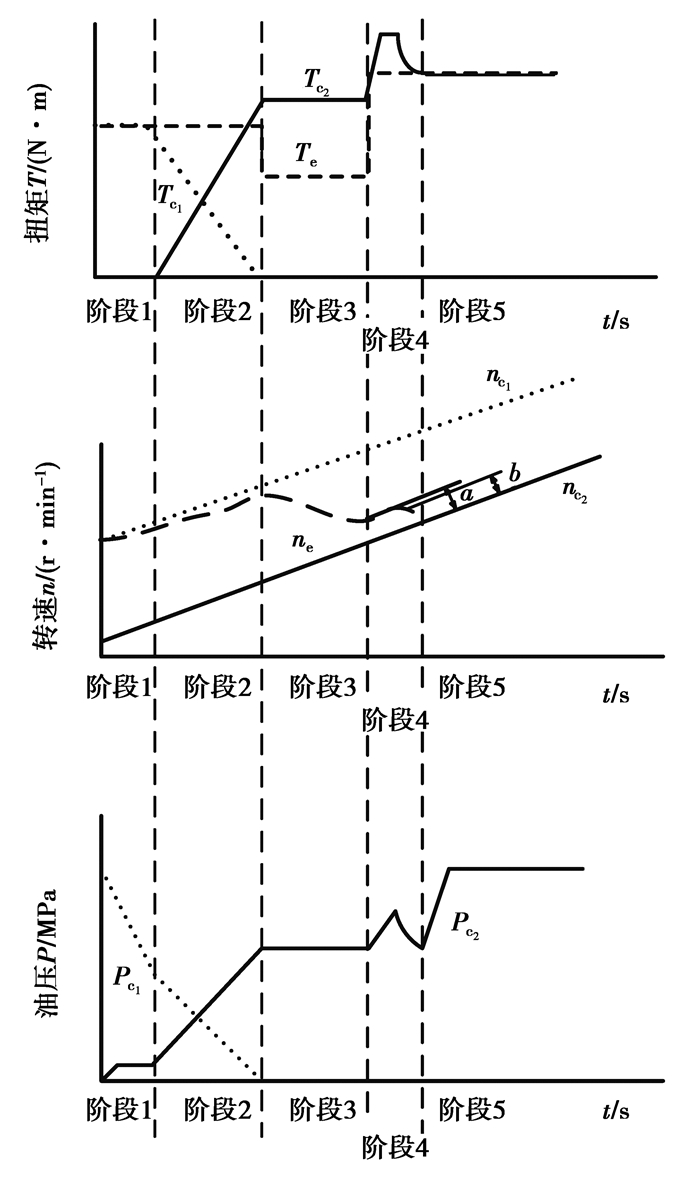
|
图 3 升挡过程示意图 Fig. 3 Schematic diagram of the upshift process |
在换挡准备阶段,分离离合器开始以最快速度分离油压,而接合离合器则以最快速度充油至即将滑摩的阶段。当分离离合器至将要滑摩时进入阶段2(转矩相)。
转矩相:接合离合器采用开环控制,通过以油门开度和发动机当前扭矩为输入,以油压变化率为输出的模糊控制,同时以当前挡位数为修正量的控制方法。而分离离合器采用滑转率闭环PID控制,保证分离离合器主、从动盘角速度差保持在一定范围,当分离离合器油压降为0时进入阶段3(惯性相)。
惯性相:此阶段需要对发动机转速进行调节,故采用闭环PID控制。目标角速度设定为接合离合器从动盘角速度,以目标转速和实际角速度差为输入,以电子油门开度为输出的PID控制,具体过程如图 4所示。接合离合器油压到达目标值后不再增加。目标值为惯性相开始前发动机扭矩Te′对应的油压,同时为使拖拉机在换挡过程中转速变化小,目标值Te′·i(当前传动比)需与阻力进行比较,若小于阻力矩,则取阻力矩对应的油压。当接合离合器转速差为a时,进入阶段4(离合器同步阶段)。图 4中Δωc1为离合器C1主、从动盘角速度差;Δω_target为离合器C1目标角速度差;ωe_target为目标发动机输出角速度。
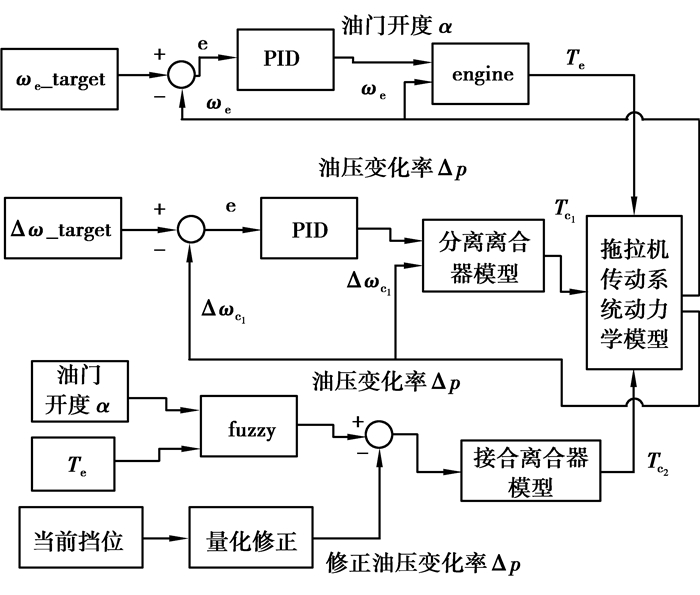
|
图 4 控制方法示意图 Fig. 4 Schematic diagram of the control method |
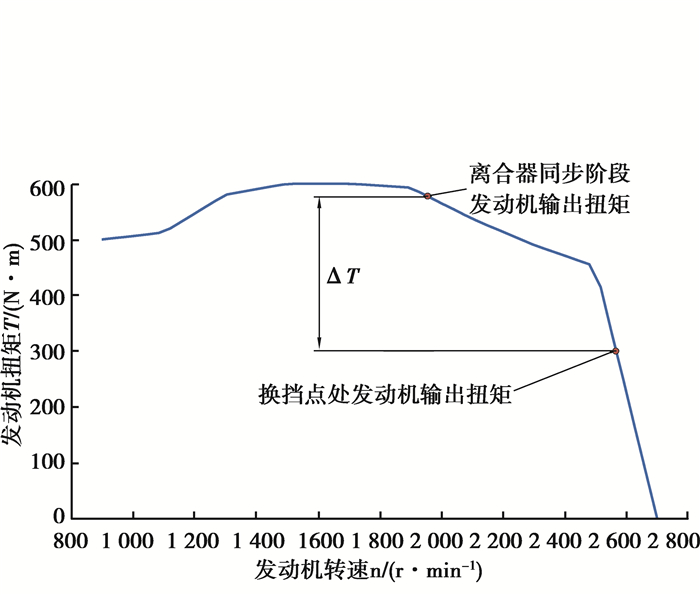
离合器同步阶段:进入阶段4之后,发动机转速闭环控制结束,此时油门开度回到换挡前初值,由于发动机转速变化大,输出转矩与惯性相开始前相比也很大,如图 5所示。
|
图 5 发动机扭矩变化示意图 Fig. 5 Schematic diagram of engine torque changes |
需判断离合器传递扭矩与发动机扭矩的大小从而改变离合器压力, 控制策略为
| $ \Delta T = {T_{{\rm{e\_a}}}} - {T_{{\rm{c\_a}}}}\left\{ \begin{array}{l} \ge 0, 离合器压力以转矩相速度增加至{T_{\rm{e}}} + c所对应压力;\\ < 0\left\{ \begin{array}{l} {T_{{\rm{c\_a}}}} - {T_{{\rm{e\_a}}}} \le c, 离合器压力保持不变;\\ {T_{{\rm{c\_a}}}} - {T_{{\rm{e\_a}}}} > c, 离合器压力减小至{T_{\rm{e}}} + c所对应压力。\end{array} \right. \end{array} \right. $ |
式中:Tc_a为离合器主、从动盘转速差满足条件a时离合器转矩;Te_a为条件a时刻对应的发动机转矩;ΔT为发动机输出扭矩与接合离合器传递扭矩差值;c为常数。
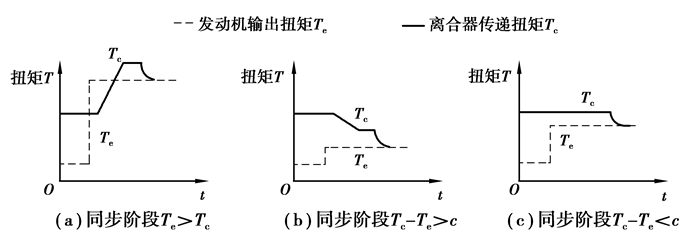
当接合离合器转速差到达界限b时,则减小离合器油压P以减小转矩突变。扭矩控制策略为
| $ {T_{\rm{c}}} = {T_{\rm{e}}} + k({n_{\rm{c}}} - {n_{\rm{e}}}), $ | (14) |
式中k为斜率,表达式如式(15)所示。
| $ k = \left\{ \begin{array}{l} c/\Delta n, \;\Delta T \ge 0\\ ({T_{{\rm{e\_b}}}} - {T_{{\rm{c\_b}}}})/\Delta n, \;\Delta T < - c;\\ c/\Delta n, \;\Delta T > - c < 0。\end{array} \right. $ | (15) |
式中:Δn为条件b的阈值;Tc_b为离合器主、从动盘转速差达到界限b时离合器转矩;Te_b为达到界限b时刻对应的发动机转矩。离合器油压P由式(3)(14)(15)推出,同步阶段控制示意图如图 6所示,主要作用是让离合器转矩逐渐减小到与发动机转矩相等。
|
图 6 同步阶段控制策略示意图 Fig. 6 Schematic diagram of the synchronization phase control strategy |
换挡结束阶段:当接合离合器的转速差Δω2≤ ε时,接合离合器即接合,此时Tc=Te,接合离合器以最快速度充油至油压上限,换挡结束。
2.2 降挡过程在降挡过程中,动力换挡过程分为换挡准备、惯性相、转矩相、离合器同步、换挡结束阶段。如图 7所示的1~5阶段。
|
图 7 降挡过程示意图 Fig. 7 Schematic diagram of the downshift process |
换挡准备阶段:分离离合器油压以最快速度减少,接合离合器油压升高到即将滑摩状态。到分离离合器至滑摩状态时进入阶段2(惯性相)。
惯性相:分离离合器油压在保证冲击度条件下降低至设定值P2,使分离离合器处于滑摩状态,发动机转速上升;接合离合器油压保持不变。当发动机转速ne与接合离合器从动盘转速相等时,惯性相结束,进入阶段3(转矩相)。
转矩相:采用升挡转矩相相同的控制方法即分离离合器油压以接合离合器相同的油压变化率减少至零;发动机通过与升挡过程同样闭环PID控制进行转速调节。当接合离合器转速差满足条件a时,进入离合器同步阶段。
离合器同步阶段:控制方法与升挡相同。
降挡结束阶段:接合离合器以最大速度增加油压至上限,换挡结束。
2.3 换挡过程仿真通过MATLAB.simulink软件建立了仿真过程,拖拉机结构的仿真参数见表 2。
| 表 2 拖拉机结构仿真参数 Table 2 Tractor structure simulation parameters |
拖拉机作业过程的仿真条件见表 3。
| 表 3 作业过程仿真参数 Table 3 Operation process simulation parameters |
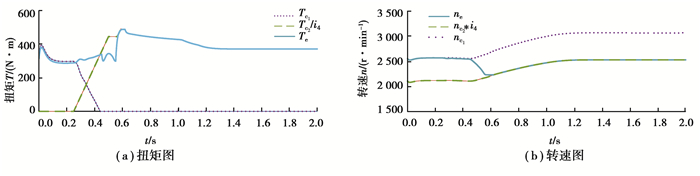
1挡升2挡的仿真结果如图 8~9所示,从中可见所制定的控制策略得到的结果良好,换挡过程中车速变化幅度小,冲击度在20 m/s3之内,滑摩功为3 100 J,油门开度变化见图 9(a)。
|
图 8 升挡过程扭矩、转速结果 Fig. 8 Torque and speed results in the upshift process |
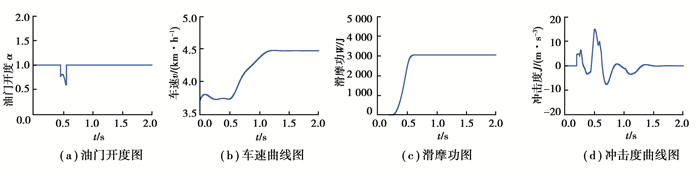
|
图 9 升挡过程其他指标结果 Fig. 9 Results of other indicators in the upshift process |
4挡降3挡的仿真结果如图 10~11所示,降挡过程中车速变化幅度小,冲击度在20 m/s3之内,滑摩功为8 000 J。
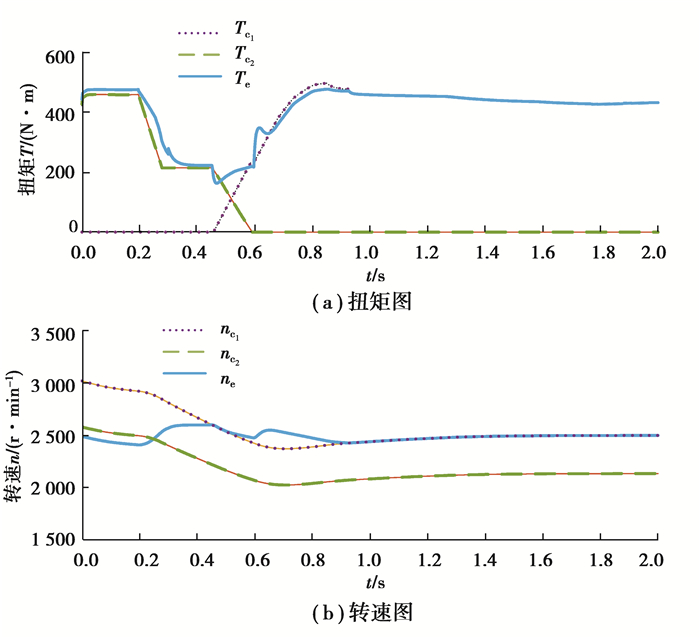
|
图 10 降挡过程扭矩转速结果 Fig. 10 Torque and speed results in the downshift process |
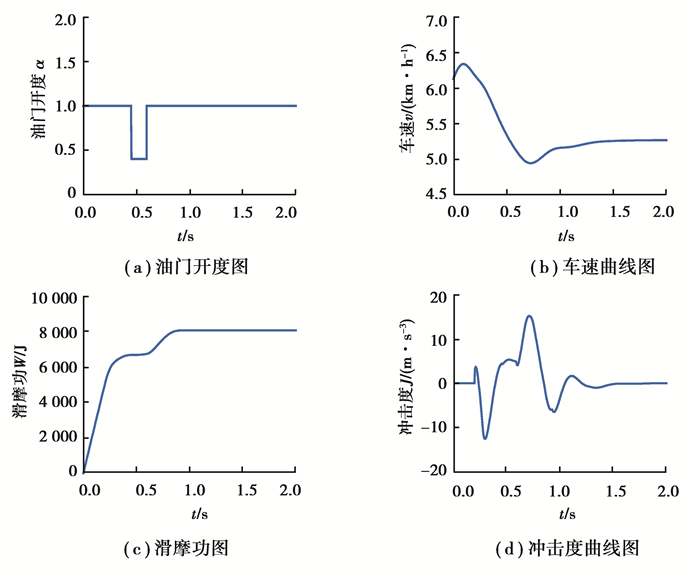
|
图 11 降挡过程其他指标结果 Fig. 11 Results of other indicators in the downshift process |
拖拉机换挡的主要指标就是作业质量,即拖拉机换挡过程中的车速变化。
1) 变速器输出转速变化量。
变速器输出转速变化量Δωt是在换挡过程结束前变速器输出轴的转速变化值,见图 12,可以看出拖拉机在换挡过程中速度变化范围,以此评价拖拉机作业质量的好坏。
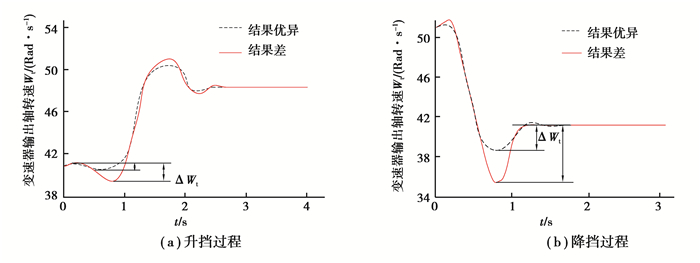
|
图 12 变速器输出转速取值 Fig. 12 Output speed value of transmission |
2) 冲击度。
冲击度J主要描述的是拖拉机纵向加速度变化,舒适度标准为17.64 m/s3,其计算公式为
| $ J = \frac{{{\rm{d}}a}}{{{\rm{d}}t}} = \frac{{{\rm{d}}v}}{{{\rm{d}}{t^2}}} = r \cdot \frac{{{\rm{d}}{\omega _{\rm{v}}}}}{{{\rm{d}}{t^2}}} = r \cdot {i_{\rm{v}}} \cdot \frac{{{\rm{d}}{T_0}}}{{{\rm{d}}t}}。$ | (16) |
3) 换挡时间。
动力换挡的换挡时间t不能太短,也不能太长。好的换挡品质要求换挡平稳的前提下,尽可能减少换挡时间。对于双离合变速器,国内外研究认为,最佳换挡时间为0.5~0.8 s;而拖拉机由于换挡传递扭矩更大,需要的时间也更多。
4) 滑摩功。
离合器在换挡过程中的接合与分离中存在滑摩状态,此时会产生滑摩功W,其表达式为
| $ W = \int_{{t_1}}^{{t_2}} {\left( {{T_{\rm{c}}} \cdot \Delta \omega } \right){\rm{d}}t, } $ | (17) |
式中:t1,t2分别为离合器滑摩开始、结束时间;Δω为离合器主、从动盘转速差。
3.2 换挡目标的确定不同换挡品质指标的加权系数采用层次分析法[16]进行确定。在分析法中,首先确定目标层,拖拉机换挡品质主要是改善作业质量,其次才是驾驶感受。
根据专家经验,得到经验系数矩阵,进行处理可得系数矩阵
| $ \mathit{\boldsymbol{M}} = \left[ \begin{array}{l} 0.547\\ 0.295\\ 0.099\\ 0.059 \end{array} \right], $ |
再对矩阵M进行一致性检验,可得各评价指标的加权系数表(表 4)。
| 表 4 加权系数表 Table 4 Weighting factor table |
确定各指标加权系数之后即可确定目标函数,以最优换挡品质为优化目标,以转矩相分离离合器油压变化率PID控制参数为优化变量,可得升挡过程优化函数。
| $ \left\{ \begin{array}{l} \min \;F\left( X \right) = 0.547 \cdot \frac{{\Delta {\omega _{\rm{t}}}}}{{\Delta {\omega _{{\rm{range}}}}}} + 0.295 \cdot \frac{j}{{{j_{{\rm{range}}}}}} + 0.099 \cdot \frac{t}{{{t_{{\rm{range}}}}}} + 0.059 \cdot \frac{W}{{{W_{{\rm{range}}}}}}, \\ X = [{X_1}, {X_2}, {X_3}], \\ {X_1} = {K_{\rm{P}}}, \\ {X_2} = {K_{\rm{I}}}, \\ {X_3} = {K_{\rm{D}}}, \\ X_i^{\rm{L}} \le {X_i} \le X_{^i}^{\rm{U}}。\end{array} \right. $ | (18) |
降挡时,优化目标不变,但是在惯性相分离离合器的滑摩油压P的取值会影响到换挡品质,所以优化变量增加,所得函数为
| $ \left\{ \begin{array}{l} \min \;F\left( X \right) = 0.547 \cdot \frac{{\Delta {\omega _{\rm{t}}}}}{{\Delta {\omega _{{\rm{range}}}}}} + 0.295 \cdot \frac{j}{{{j_{{\rm{range}}}}}} + 0.099 \cdot \frac{t}{{{t_{{\rm{range}}}}}} + 0.059 \cdot \frac{W}{{{W_{{\rm{range}}}}}}, \\ X = [{X_1}, {X_2}, {X_3}, {X_4}], \\ {X_1} = {K_{\rm{P}}}, \\ {X_2} = {K_{\rm{I}}}, \\ {X_3} = {K_{\rm{D}}}, \\ {X_4} = {P_2}, \\ X_1^{\rm{L}} \le {X_1} \le X_2^{\rm{U}}。\end{array} \right. $ | (19) |
式(18)(19)中:X1为PID控制参数KP;X2为PID控制参数KI;X3为PID控制参数KD;X4为降挡过程中分离离合器滑摩油压P2。XiU和XiL为优化变量的上下限,Δωrange,jrange,trange,Wrange为换挡目标的期望范围的最大值与最小值之差,其中Δωrange的取值根据换挡时最大车速变化范围确定,PID控制参数的取值范围如表 5所示,降挡时的滑摩油压P2则以换挡前分离离合器的传递扭矩对应的油压为上限,下限均取上限值的0.1倍。取值区间如表 5所示。
| 表 5 换挡指标取值范围 Table 5 Range of shift indicators |
选取初始种群规模(population size)为500,交配概率(crossover fraction)为0.8, 变异概率(migration fraction)为0.2,进化代数(generations)升挡优化选取60、降挡优化选取60进行仿真优化。
在重负荷全油门作业下升挡过程优化结果为:适应度函数的优化过程如图 13~14所示,随着遗传代数的增加,适应度值不断收敛,升挡超过30代、降挡超过40代后趋于平稳,该值即最佳适应度值,此时优化得到的参数结果如表 6所示。
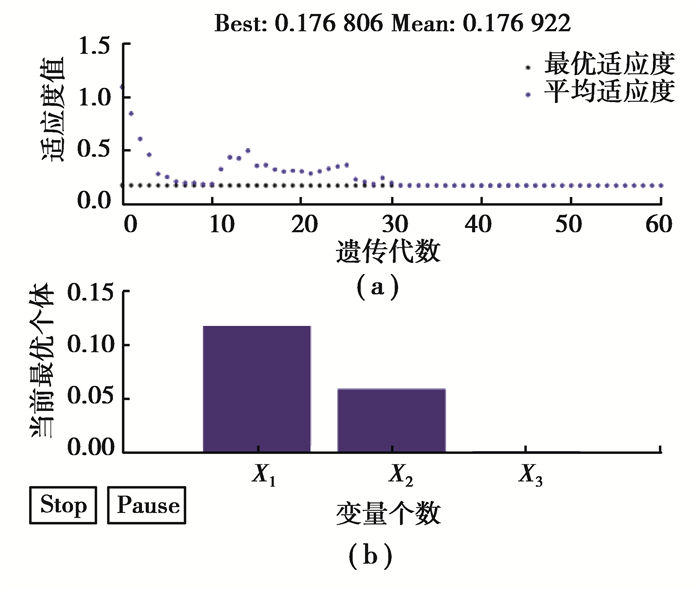
|
图 13 升挡过程优化结果 Fig. 13 Optimization results of the upshift process |
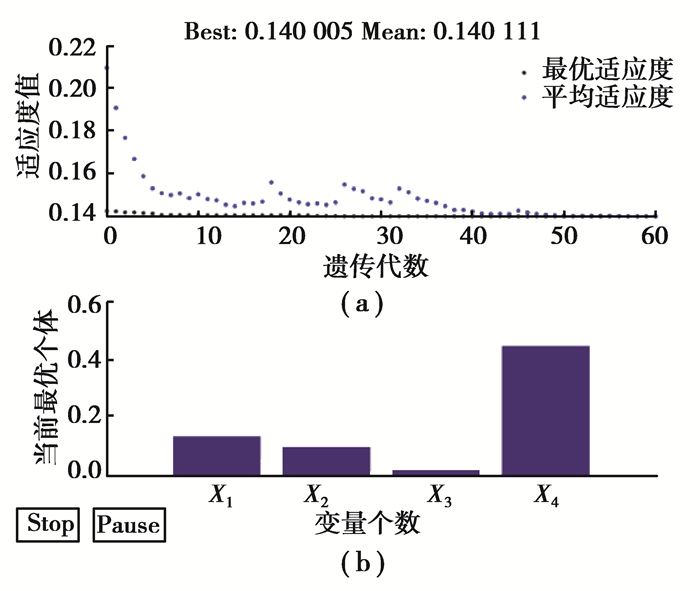
|
图 14 降挡过程优化结果图 Fig. 14 Optimization results of the downshift process |
| 表 6 优化结果 Table 6 Optimization results |
1挡升2挡过程优化前后对比结果如图 15所示,可知优化后的车速波动量较优化前减少20%,最大冲击度增加10%,换挡时间略增加0.3 s, 滑摩功增加1 500 J。
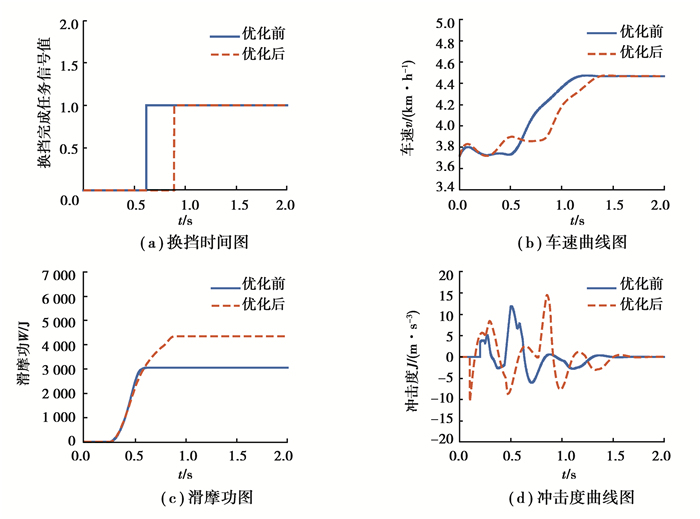
|
图 15 升挡换挡指标优化前后对比图 Fig. 15 Comparison of upshifting index before and after optimization |
4挡降3挡过程优化前后对比结果如图 16所示,可得优化后当车速波动减少20%时,冲击度增加15%,换挡时间增加0.1 s,滑摩功增加5%。
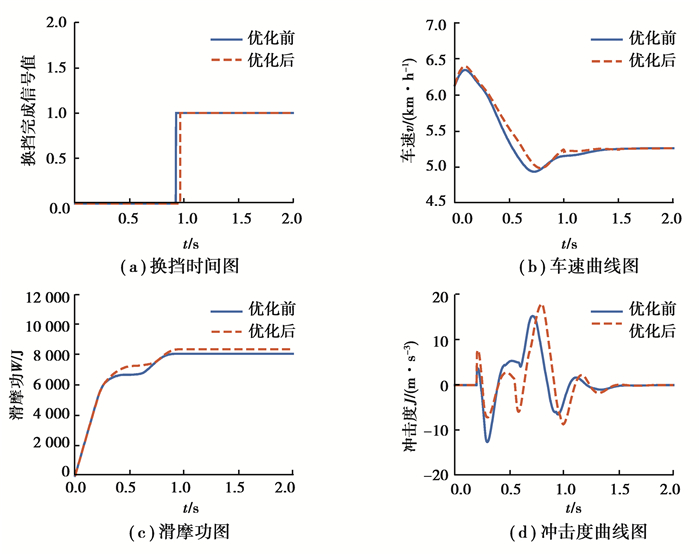
|
图 16 降挡换挡指标优化前后对比图 Fig. 16 Comparison of downshifting index before and after optimization |
1) 针对换挡过程发动机扭矩变化幅度大导致接合离合器在接合时产生扭矩突变的问题提出的同步阶段控制方法,在离合器同步阶段将要结束时,根据发动机输出扭矩调整油压,减小离合器闭合时扭矩突变,能够在滑摩功、换挡时间增加不大下将冲击度控制在舒适标准之内。
2) 采用发动机与离合器的PID联合控制方法,对整个拖拉机控制系统开发有借鉴意义。
3) 以变速器输出转速变化量、冲击度等为拖拉机作业过程换挡指标对拖拉机换挡过程中扭矩相分离离合器油压变化PID控制参数进行了优化,结果如下:拖拉机换挡过程中速度变化幅值减小20%,作业质量得到提高;冲击度小幅度增加但在20 m/s3以内,换挡过程舒适性有所保证;滑摩功、换挡时间有所增加,但均保持在标准范围内,滑摩功不超过1.3 kJ,换挡时间不超过1 s。
| [1] |
席志强, 周志立. 拖拉机自动变速器应用现状与技术分析[J]. 机械传动, 2015, 39(6): 187-195. XI Zhiqiang, ZHOU Zhili. Application status and technical analysis of automatic transmission on tractor[J]. Journal of Mechanical Transmission, 2015, 39(6): 187-195. (in Chinese) |
| [2] |
Eike C R, Stoever G T. Case MX Magnum Transmission Controls: International Off-Highway & Powerplant Congress & Exposition[C/OL].SAE International, 1999.[2018-12-15].https://doi.org/10.4271/1999-01-2811.
|
| [3] |
Tanelli M, Panzani G, Savaresi S M, et al. Transmission control for power-shift agricultural tractors:design and end-of-line automatic tuning[J]. Mechatronics, 2011, 21(1): 285-297. |
| [4] |
Manzoni V, Tanelli M, Savaresi S M, et al. Automatic end-of-line tuning for a motion inverter in agricultural tractors[J]. Control Engineering Practice, 2010, 18(11): 1342-1355. DOI:10.1016/j.conengprac.2010.05.011 |
| [5] |
Kim D C, Kim K U, Park Y J, et al. Analysis of shifting performance of power shuttle transmission[J]. Journal of Terramechanics, 2007, 44(1): 111-122. DOI:10.1016/j.jterra.2006.04.001 |
| [6] |
Liu Y G, Qin D T, Jiang H, et al. A systematic model for dynamics and control of dual clutch transmissions[J]. Journal of Mechanical Design, 2009, 131(6): 061012. DOI:10.1115/1.3125883 |
| [7] |
Goetz M, Levesley C, Crolla A. Dynamics and control of gearshifts on twin-clutch transmissions[J]. Proceedings of the Institution of Mechanical Engineers, Part D:Journal of Automobile Engineering, 2005, 219(8): 951-963. DOI:10.1243/095440705X34720 |
| [8] |
Galvagno E, Velardocchia M, Vigliani A. Dynamic and kinematic model of a dual clutch transmission[J]. Mechanism and Machine Theory, 2011, 46(6): 794-805. DOI:10.1016/j.mechmachtheory.2011.01.013 |
| [9] |
席志强, 周志立, 张明柱, 等. 拖拉机动力换挡变速器换挡特性与控制策略研究[J]. 农业机械学报, 2016, 47(11): 350-357. XI Zhiqiang, ZHOU Zhili, ZHANG Mingzhu, et al. Shift characteristics and control strategy of powershift transmission on tractor[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(11): 350-357. (in Chinese) DOI:10.6041/j.issn.1000-1298.2016.11.047 |
| [10] |
王东青.拖拉机负载换挡变速箱性能的研究[D].北京: 中国农业大学, 2014. WANG Dongqing. Study on the performance of agricultural tractor powershift transmission[D]. Beijing: China Agricultural University, 2014. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10019-1015500616.htm |
| [11] |
马彪, 关万俊, 陈漫, 等. 联合油压控制的DCT升挡控制策略研究[J]. 重庆大学学报, 2015, 38(4): 24-30, 37. MA Biao, GUAN Wanjun, CHEN Man, et al. Study on DCT up-shift control strategy with united control[J]. Journal of Chongqing University, 2015, 38(4): 24-30, 37. (in Chinese) |
| [12] |
陈宁, 赵丁选, 于微波. 改善动力换挡变速箱换挡品质的研究[J]. 机床与液压, 2004, 32(10): 29-31. CHEN Ning, ZHAO Dingxuan, YU Weibo. Study on improving shift quality of powershift transmissions[J]. Machine Tool & Hydraulics, 2004, 32(10): 29-31. (in Chinese) DOI:10.3969/j.issn.1001-3881.2004.10.011 |
| [13] |
刘文, 王青松, 林腾蛟, 等. 基于响应面试验设计的湿式离合器优化策略[J]. 重庆大学学报, 2018, 41(6): 9-23. LIU Wen, WANG Qingsong, LIN Tengjiao, et al. Optimization strategy of wet clutch based on response surface test design[J]. Journal of Chongqing University (Natural Science Edition), 2018, 41(6): 9-23. (in Chinese) |
| [14] |
Kolator B, Białobrzewski I. A simulation model of 2WD tractor performance[J]. Computers and Electronics in Agriculture, 2011, 76(2): 231-239. |
| [15] |
刘振军, 董小洪, 秦大同, 等. 双离合器自动变速换挡品质分析与控制[J]. 重庆大学学报, 2010, 33(5): 29-34. LIU Zhenjun, DONG Xiaohong, QIN Datong, et al. Analysis and control on shift quality of dual-clutch transmission[J]. Journal of Chongqing University(Natural Science Edition), 2010, 33(5): 29-34. (in Chinese) |
| [16] |
邓雪, 李家铭, 曾浩健, 等. 层次分析法权重计算方法分析及其应用研究[J]. 数学的实践与认识, 2012, 42(7): 93-100. DENG Xue, LI Jiaming, ZENG Haojian, et al. Research on computation methods of AHP wight vector and its applications[J]. Mathematics in Practice and Theory, 2012, 42(7): 93-100. (in Chinese) DOI:10.3969/j.issn.1000-0984.2012.07.012 |
 2019, Vol. 42
2019, Vol. 42

