在Czochralski(Cz)提拉法生产晶体过程中,由于Marangoni-热毛细对流的存在会引起熔体界面温度和杂质浓度的波动,进而影响固液界面形状以及杂质在晶体中的分布,甚至引起物性参数的变化。为了提高晶体生长质量,人们对Marangoni-热毛细对流的产生及发展机理进行了深入研究,在此基础上探索削弱Marangoni-热毛细对流的方法。Ueno等[1]实验发现,在不同的垂直温度梯度和水平温度梯度下会出现5种不同的热毛细对流结构。Sakhy等[2]通过数值模拟进一步表明,规则的流胞主要是由Marangoni-热毛细作用引起的。Touihri等[3]的研究则考虑了更多的因素,探索了同时存在底部加热和自由表面散热的圆柱形液层内的热毛细浮力对流。除了传热之外,传质同样会对热毛细对流产生影响,张利等[4]发现,热毛细对流和表面蒸发相互耦合、相互影响。
系统旋转常常用来削弱自由表面的温度波动,以此获得均匀的温度场。Jou等[5]发现,由于科氏力的作用,旋转能够削弱热对流,提高流动的稳定性。Li等[6]研究了液池旋转对环形浅液池内硅熔体流型转变过程的影响。Shi等[7]通过线性稳定性分析证实了液池旋转能够增强流动的稳定性。Sim等[8]进一步研究指出,当Ta数较小时,旋转对流动的影响很小;当Ta数较大时,流动结构将会发生变化。Zhang等[9]确定了不同转速下环形浅液池中热毛细对流失稳的临界热流密度,发现临界热流密度随转速的增加而增大。Yin等[10]对低转速旋转液池中的热毛细对流进行了深入研究,确定了流动失稳临界条件,并且利用能量分析进一步阐明了流动失稳的机理。
除了液池旋转外,磁场的加入也可以有效地削弱表面张力引起的热对流, 而不同类型的磁场削弱效果也不尽相同。在环形液池中,轴向磁场对径向流动的削弱效果明显,当磁场强度超过某一临界值时,三维震荡流动将变成轴对称稳定流动[11]。对于径向流动,轴向磁场的削弱效果比会切磁场的削弱效果更好[12],但是会切磁场对改善晶体生长中的径向偏析更为有利[13-14]。横向旋转磁场能够搅拌熔体内的周向流动,并且削弱轴向流动,可以有效地控制浮区法晶体生长中的热表面张力流[15]。磁场也有一些负面效应。Yao等[16]的研究发现,施加的磁场较小时,反而会削弱流动的稳定性。Hoshikawa等[17]实验研究表明,轴向磁场能够改善硅晶体轴向电阻率的均匀性,同时也会增加其轴向含氧量,导致杂质的偏析。不少学者耦合了磁场和旋转进行研究。Zhou等[18]指出,在一定强度的旋转磁场作用下,当晶体和坩埚旋转方向相同时,熔体和晶体中氧浓度含量最低。Takagi等[19]的数值模拟研究表明,在较缓慢的液池速度下添加较小强度的轴向磁场,其耦合作用对热流体波的削弱效果甚至比高液池转速单独作用的削弱效果更好。
虽然旋转和磁场都会对Marangoni-热毛细对流产生一定的削弱作用,但是又都有其局限性,因此,研究耦合液池旋转和轴向磁场作用下的Marangoni-热毛细对流特性将是一种新的尝试。为了与工业实际生产过程更为接近,考虑了底部加热和自由表面辐射散热的影响。
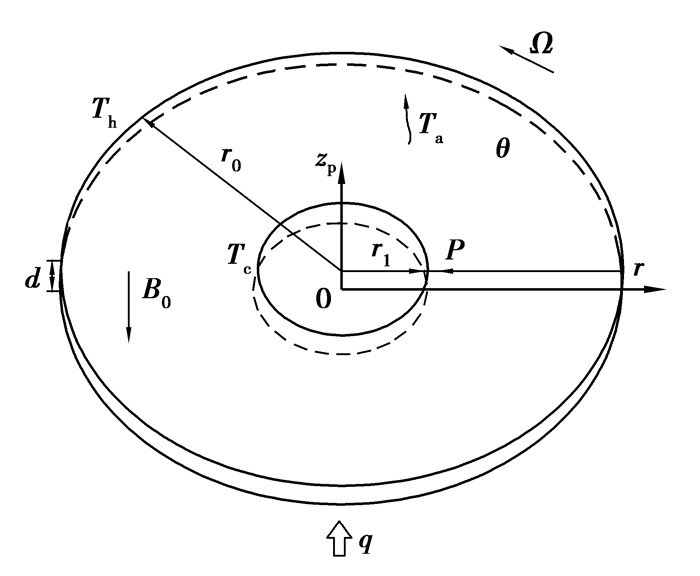
1 数学物理模型图 1为环形浅液池的物理模型。环形浅液池的内半径、外半径、液池深度分别表示为ri,ro,d,其中ri=15 mm,ro=50 mm,d=3 mm。研究介质硅熔体充满整个环形浅液池,它的物性参数如表 1所示。液池内壁面温度、外壁面温度、水平温差分别表示为Tc,Th,ΔT,其中Tc=1 683 K,Th=1 696 K,ΔT=Th-Tc。环形浅液池顶部为平整的自由表面,对外辐射换热(环境温度Ta=1 599 K),底部均匀加热,热流密度为q。液池围绕Z轴逆时针旋转,角速度为Ω(Ω≤3 r/min),同时有静态磁场沿Z轴负方向穿过硅熔体,其强度用B0表示。
|
图 1 环形浅液池物理模型 Fig. 1 Configuration of system |
为了简化计算,需要忽略一些次要影响因素,做如下假设:1)硅熔体的密度几乎不发生变化,可以认为是不可压缩牛顿流体;2)液池内硅熔体流速较低,液池尺寸较小,所有流动均可认为是层流;3)液池内硅熔体与外界没有质量交换,且流动缓慢,可以认为自由表面平整无变形;4)热毛细力作用仅存在于硅熔体的自由表面,固壁处均满足无滑移边界条件;5)表面张力为温度的线性函数,其他物性参数均考虑为常数;6)所有边界均视为电绝缘边界。
根据上述假设,无量纲控制方程如下:
| $ \nabla \cdot V = 0, $ | (1) |
| $ \frac{{\partial V}}{{\partial \tau }} + V \cdot \nabla V = - \nabla P + {\nabla ^2}V + F, $ | (2) |
| $ \frac{{\partial \Theta }}{{\partial \tau }} + V \cdot \nabla \Theta = \frac{1}{{Pr}}{\nabla ^2}\Theta 。$ | (3) |
式(2)中,F代表洛伦兹力,其无量纲分量为
| $ {F_{\rm{R}}} = - H{a^2}\left( {\frac{1}{R}\frac{{\partial \varphi }}{{\partial \theta }} + {V_{\rm{R}}}} \right){e_{\rm{R}}}, $ | (4) |
| $ {F_\theta } = - H{a^2}\left( { - \frac{{\partial \varphi }}{{\partial R}} + {V_\theta }} \right){e_\theta }, $ | (5) |
| $ {F_Z} = 0。$ | (6) |
其中,f为电势,由下述方程确定
| $ {\nabla ^2}\varphi = \nabla \cdot \left( {\mathit{\boldsymbol{V}} \times \mathit{\boldsymbol{B}}} \right)。$ | (7) |
边界条件为:
自由表面(Z=D, Ri<R<Ro, 0≤θ≤2π)
| $ \frac{{\partial {V_{\rm{R}}}}}{{\partial Z}} = - \frac{{Ma}}{{\mathit{Pr}}}\frac{{\partial \Theta }}{{\partial R}},\frac{{\partial {V_\theta }}}{{\partial Z}} = - \frac{{Ma}}{{\mathit{Pr}}}\frac{{\partial \Theta }}{{R\partial \theta }},\frac{{\partial \Theta }}{{\partial Z}} = - {H_{\rm{R}}}\left( {\Theta - {\Theta _{\rm{a}}}} \right),{V_{\rm{Z}}} = 0,\frac{{\partial \varphi }}{{\partial Z}} = 0; $ | (8) |
底部(Z=0, Ri<R<Ro, 0≤θ≤2π)
| $ \frac{{\partial \Theta }}{{\partial Z}} = - Q,{V_{\rm{R}}} = {V_{\rm{Z}}} = 0,{V_\theta } = R{e_{\rm{R}}} \cdot R,\frac{{\partial \varphi }}{{\partial Z}} = 0; $ | (9) |
内壁面(0≤Z≤D, R=Ri, 0≤θ≤2π)
| $ \Theta = 0,{V_{\rm{R}}} = {V_{\rm{Z}}} = 0,{V_\theta } = R{e_{\rm{R}}} \cdot {R_{\rm{i}}},\frac{{\partial \varphi }}{{\partial R}} = 0; $ | (10) |
外壁面(0≤Z≤D, R=Ro, 0≤θ≤2π)
| $ \Theta = 1,{V_{\rm{R}}} = {V_{\rm{Z}}} = 0,{V_\theta } = R{e_{\rm{R}}} \cdot {R_{\rm{o}}},\frac{{\partial \varphi }}{{\partial R}} = 0; $ | (11) |
初始条件(τ=0):
| $ \tau = 0,\Theta = 0,{V_{\rm{R}}} = {V_{\rm{z}}} = {V_\theta } = 0,\varphi = 0; $ | (12) |
控制方程中的V、P、Θ、B、ϕ、Pr和Ha分别是无量纲速度、压力、温度、磁场强度、电势、普朗特数和哈特曼数,边界条件中的Q、τ、HR、ReR和Ma分别是无量纲热流密度、时间、辐射换热系数、旋转雷诺数和Marangoni数,其定义式如下,
| $ V = \frac{v}{{\nu /\left( {{r_{\rm{o}}} - {r_{\rm{i}}}} \right)}},P = \frac{p}{{\rho {\nu ^2}/{{\left( {{r_{\rm{o}}} - {r_{\rm{i}}}} \right)}^2}}},\Theta = \frac{{T - {T_{\rm{c}}}}}{{{\mathit{\Delta}} T}},B = \frac{B}{{{B_0}}},\varphi = \frac{\varphi }{{\nu {{\rm{B}}_0}}}。$ | (13) |
| $ \mathit{Pr} = \frac{\nu }{a},Ha = {B_{\rm{o}}}\left( {{r_{\rm{o}}} - {r_{\rm{i}}}} \right)\sqrt {\sigma /(\rho \nu )} ,Q = \frac{q}{{\lambda {\mathit{\Delta}} T/\left( {{r_{\rm{o}}} - {r_{\rm{i}}}} \right)}},\tau = \frac{t}{{{{\left( {{r_{\rm{o}}} - {r_{\rm{i}}}} \right)}^2}/\nu }}。$ | (14) |
| $ {H_{\rm{R}}} = \frac{{\varepsilon \sigma \left( {{r_{\rm{o}}} - {r_{\rm{i}}}} \right)}}{\lambda }\left( {{T^2} + T_a^2} \right)\left( {T + {T_a}} \right),R{e_{\rm{R}}} = \frac{{2{\rm{ \mathsf{ π} }}\mathit{\Omega }{{\left( {{r_{\rm{o}}} - {r_{\rm{i}}}} \right)}^2}}}{{60\nu }},Ma = \frac{{{\gamma _T}{\mathit{\Delta}} T\left( {{r_{\rm{o}}} - {r_{\rm{i}}}} \right)}}{{\mu \alpha }}。$ | (15) |
在低转速的浅液池中,浮力的影响可以忽略不计[6, 20],在控制方程中忽略了浮力项。
控制方程采用有限差分法离散处理,对流项采用QUICK格式,扩散项采用二阶中心差分格式,压力速度耦合采用PISO算法,压力插值采用PRESTO算法。网格采用90R×40Z×120θ的非均匀网格,时间步长为4.52×10-8~4.52×10-6。
为了验证网格的独立性,在Ma=1 798、Q=1.514、ReR=464和Ha=20 (ΔT=13 K, q=3.6 W/cm2, Ω=1 r/min, B0=13.8 mT)时,取不同的网格进行计算,结果如表 2所示。考虑到计算精度和计算成本,选取90R×40Z×120θ的网格是合理的。为了验证程序的正确性,模拟计算了与Zhang等[9]的图 7(a)相同的工况,结果如图 2(a)所示。可以发现,与Zhang等[9]的计算结果十分吻合。
| 表 2 网格独立性验证 Table 2 Verification of grid independence |
|
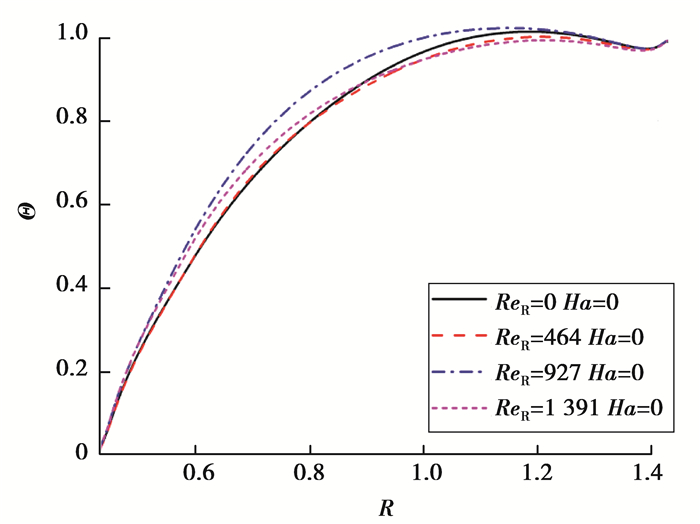
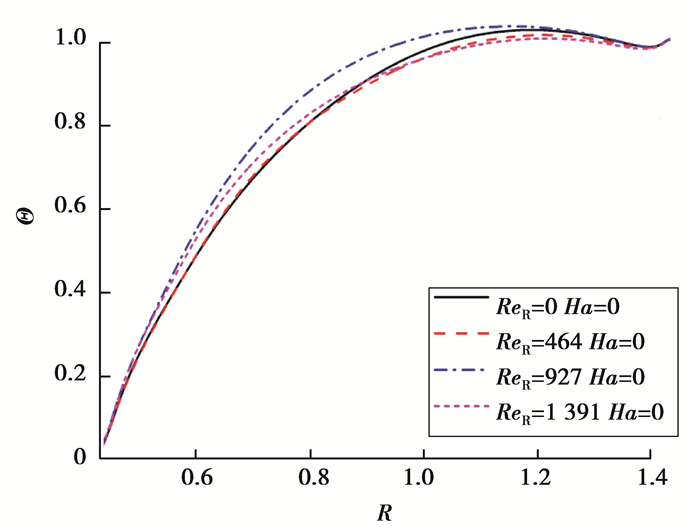
图 7 Ha=0时θ=0处自由表面上温度的径向分布 Fig. 7 Radial distribution of temperature on the free surface at θ=0 when Ha=0 |
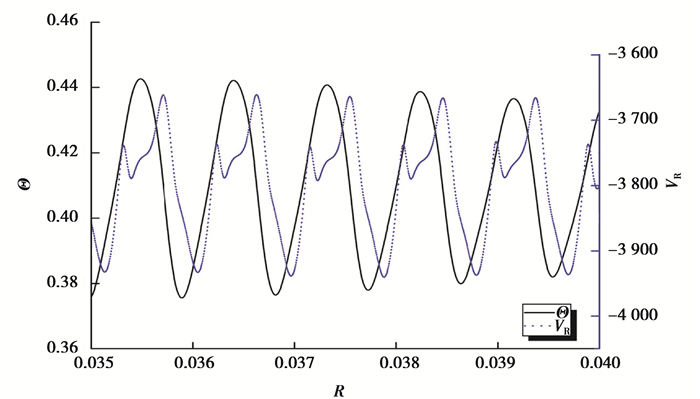
底部热流Q的存在会导致Marangoni对流,水平温差ΔT的存在会导致热毛细对流,当两者同时存在时,则会产生Marangoni-热毛细对流。当底部无因次热流密度Q或Marangoni数超过相应的某一临界值时,硅熔体内将会出现三维振荡状态的Marangoni-热毛细对流。图 3中曲线显示了自由表面监测点P(R=0.571,θ=0,Z=0.086)在Ma=1 798、Q=1.514、ReR=0和Ha=0时的径向速度和温度的时变曲线。从图中可以发现,径向速度曲线和温度曲线均表现为周期性振荡,但是温度的振荡稍微超前于径向速度的振荡。
|
图 3 ReR=0和Ha=0时监测点P处温度和径向速度随时间的变化 Fig. 3 Ranges of temperature and radial velocity at the monitoring point P when ReR=0 and Ha=0. |
定义温度波动δΘ和R-Z截面上的流函数ψ分别如下,
| $ \delta \Theta (R,\theta ,Z) = \Theta (R,\theta ,Z) - \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int 2 {{\rm{ \mathsf{ π} }}_0}\Theta (R,\theta ,Z){\rm{d}}\theta , $ | (16) |
| $ {V_{\rm{R}}} = \frac{1}{R}\frac{{\partial \psi }}{{\partial Z}},{V_Z} = - \frac{1}{R}\frac{{\partial \psi }}{{\partial R}}。$ | (17) |
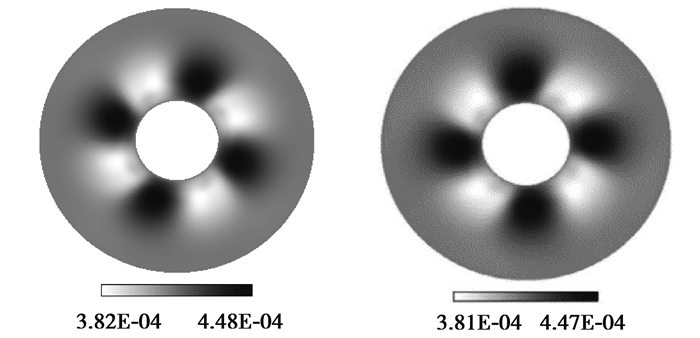
从图 4(a)可以看到,自由表面温度波动呈花瓣状结构,波数m=11,此时流动的不稳定性主要集中在内壁附近,并且在由内壁向外壁传播的同时逐渐减弱。图 5(a)进一步给出了R-Z截面上的等流函数线分布,这里,逆时针流向为正,顺时针流向为负。可以看到,内壁面附近存在一个逆时针方向的流胞,而外壁面附近存在一个顺时针方向的流胞,并且逆时针方向的流胞占主导地位。由于底部热流的存在,自由表面的径向温度分布不再是单调递增,而是先增大、后减小,在外壁附近达到最大值,由此形成2个分别指向内、外壁的温度梯度,进而产生2个反向的表面张力梯度。在表面张力梯度的驱动下,自由表面的流体从最高温度点处分别流向内、外壁,然后,在底部形成相反方向的回流,最终产生2个反向的流胞。同时,可以看到在外壁附近的表面上还有一个微小的逆时针流胞,这主要是因为自由表面的辐射散热,使得外壁面附近的熔体温度略低于外壁面温度,形成了一个由内壁面指向外壁面的温度梯度。为了更好地了解熔体内部的流动,图 6(a)给出了R=0.571处,θ-Z截面上的周向速度分布。由于周向温度分布不均匀,导致存在沿逆时针和顺时针方向(逆时针为正,顺时针为负)的2个区域,并且2个区域在周向上交替出现。此时,沿逆时针方向的流动和沿顺时针方向的流动强度相当。

|
图 4 Ha=0时自由表面温度波动δΘ Fig. 4 Snapshots of temperature fluctuation on the free surface when Ha=0 |

|
图 5 Ha=0时θ=0处R-Z截面上的流函数:(a)ReR=0; (b)ReR=464; (c)ReR=927; (d)ReR=1391 Fig. 5 Pseudo streamlines on the R-Z plane at θ=0 when Ha=0: |

|
图 6 Ha=0时R=0.571处θ-Z截面上周向速度分布:(a)ReR=0; (b)ReR=464; (c)ReR=927; (d)ReR=1 391 Fig. 6 Snapshots of the circumferential velocity on the θ-Z plane at R=0.571 when Ha=0: |
液池旋转时,硅熔体不仅受到热毛细力作用,还受到科氏力作用,其温度场和流场都会发生相应变化。此时,流动仍然保持三维振荡流动,但自由表面温度波动和周向速度波动都发生了变化,如图 4所示。液池开始缓慢旋转之后,自由表面温度的花瓣状波动结构转变为热流体波结构,随着ReR数的不断增大,热流体波的波数发生变化,由4个减少为3个。当ReR数较小时,液池旋转之后,由于外力扰动,温度波动反而增大,导致流动不稳定性增强。此现象与Hu等[21]的研究结果基本相符。同时,文中模拟结果还发现,即使将ReR数增加到足够大,旋转也并非总是能够削弱流动的不稳定性。这主要是因为多流胞的存在,科氏力削弱径向顺时针流动的同时增强了径向逆时针流动。观察图 5可以发现,外壁附近的小流胞会随着ReR数的增大而扩大,当ReR足够大时(如ReR=1 391),流胞已经扩展到整个液池深度。旋转对硅熔体的周向流速也有显著的影响。图 6展示了硅熔体的周向速度在θ-Z截面上的分布随ReR数的变化。对比图 6(a)、6(b)、6(c)可以发现,逆时针方向的流动随着ReR数的增大而明显增强,顺时针方向的流动随着ReR数的增大而明显减弱。当ReR数足够大时(如ReR=1 391),顺时针流动消失,周向上只存在逆时针方向流动。由此表明,旋转能够使熔体的周向流动趋于稳定。不仅如此,在ReR数较大时,旋转还能够降低最高温度,使径向温度梯度变得更均匀[22],如图 7所示。
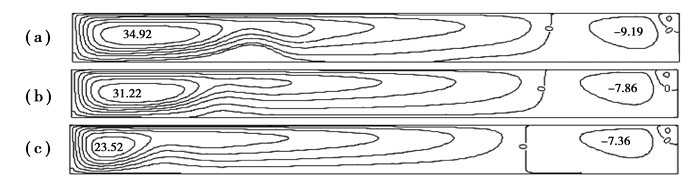
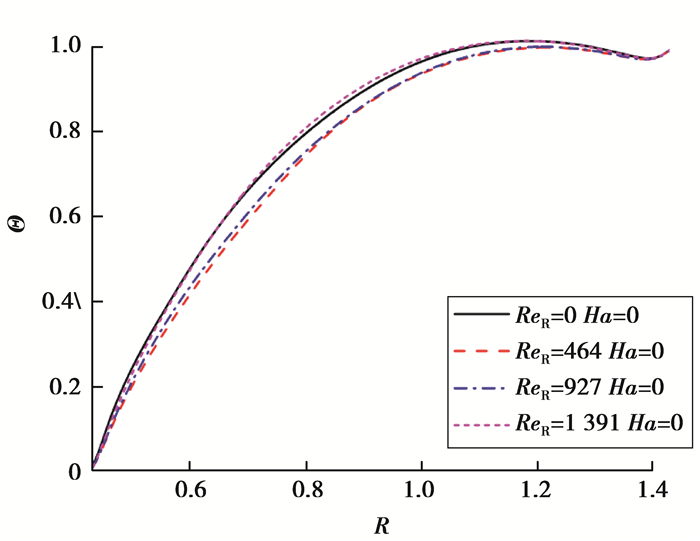
2.3 轴向磁场对三维振荡流动的影响当Ha数较小时,自由表面的温度波动变为m=4的直条幅状的热流体波,此时,温度波动并不会沿周向传播,如图 8(a)所示。将图 4(a)和图 8(a)中的温度波动幅度进行对比,可以发现,施加的磁场较弱(Ha数较小)时,引入的洛伦兹力反而使得流动的不稳定性增强。这与Yao等[16]的结论基本一致。随着Ha数的增大,自由表面温度波动随Ha数的增大而减小,当Ha数足够大时(如Ha=60),自由表面温度几乎没有波动,流动的不稳定性被极大地削弱,流场变得均匀,表现为轴对称稳态。进一步分析发现,磁场对强流动的削弱效果更明显,而对微弱流动几乎没有影响,如图 8所示。R-Z截面上顺时针和逆时针流动都被削弱,如图 9所示。轴向磁场对硅熔体的周向流动也有显著的影响,图 10展示了周向速度在θ-Z截面上的分布。对比图 10(a)、10(b)、10(c)可以发现,周向速度随着Ha数的增大而逐渐减小,并且趋于均匀。轴向磁场虽然对流动的不稳定性有很好的削弱作用,同时也会增加自由表面温度径向分布的不均匀性[23],如图 11所示。
|
图 8 ReR=0时某时刻自由表面温度波动 Fig. 8 Snapshots of temperature fluctuation on the free surface when ReR=0 |
|
图 9 ReR=0时某时刻R-Z截面上的等流函数线:(a) Ha=20; (b) Ha=40; (c) Ha=60 Fig. 9 Pseudo streamlines on the R-Z plane at θ=0 when ReR=0: (a) Ha=20; (b) Ha=40; (c) Ha=60. |

|
图 10 ReR=0时R=0.571处θ-Z截面上周向速度分布:(a)Ha=20; (b)Ha=40; (c)Ha=60 Fig. 10 Snapshots of the circumferential velocity on the θ-Z plane at R=0.571 when ReR=0: (a)Ha=20; (b)Ha=40; (c)Ha=60. |
|
图 11 ReR=0时θ=0处自由表面上温度的径向分布 Fig. 11 Radial distribution of temperature on free surface at θ=0 when ReR=0 |
表 3给出了耦合液池旋转和轴向磁场作用下三维振荡流动自由表面温度波动。分析表中数据可知,在相同Ha数下,自由表面温度波动随ReR数的增大而减小,这与液池旋转单独作用时有显著差别;当ReR数不变时,随着Ha数的增大,自由表面温度波动逐渐减小。轴向磁场单独作用时,磁场强度变化对流动不稳定性的影响也有相同的趋势,但是其对流动不稳定性的削弱效果更加显著。当ReR数不为0时,使流动保持稳态的最小Ha数为50。当Ha=50时,ReR数的变化对R-Z截面的流动强度几乎没有影响。进一步分析发现,自由表面上温度的径向分布也几乎不受ReR数变化的影响,如图12所示。但是,周向速度却受ReR数变化的影响显著,其大小与ReR数近似正比关系。θ-Z截面上的周向速度方向与ReR数的大小无关,均为逆时针方向。在同一ReR数下,液池底部周向速度的大小近似于自由表面的1/2。当磁场强度较大时(Ha=50),在不同液池转速下,q=0处,硅熔体的周向速度沿Z轴的分布如图13所示。特别的,当ReR=242时,周向速度沿Z轴的分布极其规律,近似线性分布。结合温度分布和周向速度分布规律可以发现,当ReR=242、Ha=50时,硅熔体的速度场和温度场都相对均匀。因此,ReR=242、Ha=50是能够使硅熔体的流动保持轴对称稳态的最佳组合。
| 表 3 不同Ha数下ReR=927、464、232、0时自由表面温度波动范围 Table 3 Ranges of temperature fluctuation on the free surface at various Ha when ReR=0, 232, 464, 927.under vvavariousat various Ha when ReR=927, 464, 232, 0. |
利用三维数值模拟了液池转速和轴向磁场对双温度梯度下浅液池内硅熔体流动的影响,得到如下结论:1)底部热流的存在会使自由表面的最高温度出现在内、外壁之间,导致R-Z截面产生双流胞结构。2)仅存在液池旋转时,ReR数的增大会强化径向的逆时针方向的流动,削弱顺时针方向流动。虽然液池旋转能够改善硅熔体内速度场的周向均匀性和温度场的径向均匀性,即使ReR数足够大,三维振荡流动也不会转变为轴对称稳态。3)轴向磁场对硅熔体的径向和轴向流动有明显的削弱作用,并且削弱效果随着Ha数的增大而显著增强。当Ha数足够大时,三维振荡流动将转变为轴对称稳态流动。4)液池旋转和轴向磁场能够相互加强对三维非稳态流动的削弱作用,在较小轴向磁场作用下施加旋转就会出现轴对称稳态流动。
| [1] |
Murata Y, Kurosawa T, Ueno I, et al. Thermocapillary convection in a thin liquid layer with a temperature gradient inclined to a free surface:linear flow case[J]. Jasma Journal of the Japan Society of Microgravity Application, 2002, 19. |
| [2] |
Es Sakhy R, El Omari K, Le Guer Y, et al. Rayleigh-Bénard-Marangoni convection in an open cylindrical container heated by a non-uniform flux[J]. International Journal of Thermal Sciences, 2014, 86: 198-209. DOI:10.1016/j.ijthermalsci.2014.06.036 |
| [3] |
Touihri R, El Gallaf A, Henry D, et al. Instabilities in a cylindrical cavity heated from below with a free surface. Ⅰ. Effect of Biot and Marangoni numbers[J]. Physical Review E, 2011, 84(5): 056302. |
| [4] |
张利, 吴春梅, 李友荣, 等. 表面蒸发对环形液池内稳态热毛细对流的影响[J]. 重庆大学学报, 2017, 40(7): 1-8. ZHANG Li, WU Chunmei, LI Yourong, et al. Effect of surface evaporation on steady thermocapillary convection in an annular pool[J]. Journal of Chongqing University, 2017, 40(7): 1-8. (in Chinese) |
| [5] |
Jou J J, Kung K Y, Hsu C H. Effects of Coriolis force and surface tension on Bénard-Marangoni convective instability[J]. International Journal of Heat and Mass Transfer, 1997, 40(6): 1447-1458. DOI:10.1016/S0017-9310(96)00172-X |
| [6] |
Li Y R, Xiao L, Wu S Y, et al. Effect of pool rotation on flow pattern transition of silicon melt thermocapillary flow in a slowly rotating shallow annular pool[J]. International Journal of Heat and Mass Transfer, 2008, 51(7/8): 1810-1817. |
| [7] |
Shi W Y, Li Y R, Ermakov M K, et al. Stability of thermocapillary convection in rotating shallow annular pool of silicon melt[J]. Microgravity Science and Technology, 2010, 22(3): 315-320. DOI:10.1007/s12217-010-9194-9 |
| [8] |
Sim B C, Zebib A. Effect of free surface heat loss and rotation on transition to oscillatory thermocapillary convection[J]. Physics of Fluids, 2002, 14(1): 225-231. DOI:10.1063/1.1428323 |
| [9] |
Zhang Q Z, Peng L, Wang F, et al. Thermocapillary convection with bidirectional temperature gradients in a shallow annular pool of silicon melt:Effects of ambient temperature and pool rotation[J]. International Journal of Heat and Mass Transfer, 2016, 101: 354-364. DOI:10.1016/j.ijheatmasstransfer.2016.05.015 |
| [10] |
Yin L M, Zeng Z, Qiu Z H, et al. Linear stability analysis of thermocapillary flow in a slowly rotating shallow annular pool using spectral element method[J]. International Journal of Heat and Mass Transfer, 2016, 97: 353-363. DOI:10.1016/j.ijheatmasstransfer.2016.02.031 |
| [11] |
李友荣, 刘英杰, 彭岚, 等.轴向磁场对环形浅液池内硅熔体热毛细对流的影响[C]//2006中国工程热物理学会传热传质学学术会议, 2006. LI Yourong, LIU yingjie, PENG lan, et al. Effect of axial magnetic field on thermocapillary convection of silicon melt in shallow annular pool[C]//Conference on Heat and Mass transfer of the Chinese Society of Engineering Thermophysics, 2006.(in Chinese) http://www.cnki.com.cn/Article/CJFDTotal-RGJT201606006.htm |
| [12] |
Peng L, Gong H. Effects of static magnetic fields on melt flow in detached solidification[J]. Transactions of Nonferrous Metals Society of China, 2015, 25(3): 936-943. DOI:10.1016/S1003-6326(15)63682-2 |
| [13] |
李亮, 曾忠, 姚丽萍, 等. 组合线圈磁场下的液桥热表面张力流[J]. 工程力学, 2012, 29(8): 39-44. LI Liang, ZENG Zhong, YAO Liping, et al. Thermocapillary flow in liquid bridge under magnetic field generated by combined coil configurations[J]. Engineering Mechanics, 2012, 29(8): 39-44. (in Chinese) |
| [14] |
Chen C B, Zeng Z, Mizuseki H, et al. Thermocapillary convection of liquid bridge under axisymmetric magnetic fields[J]. Materials Transactions, 2008, 49(11): 2566-2571. DOI:10.2320/matertrans.MB200830 |
| [15] |
姚丽萍, 曾忠, 张永祥. 微重力环境下横向旋转磁场对热表面张力流的影响[J]. 重庆大学学报(自然科学版), 2012, 35(3): 115-120. YAO Liping, ZENG Zhong, ZHANG Yongxiang. Effects of transverse rotating magnetic field on thermocapillary flow under microgravity[J]. Journal of Chongqing University(Natural Science Edition), 2012, 35(3): 115-120. (in Chinese) |
| [16] |
Yao L P, Zeng Z, Zhang Y, et al. Influence of rotating magnetic field strength on three-dimensional thermocapillary flow in a floating half-zone model[J]. Heat and Mass Transfer, 2012, 48(12): 2103-2111. DOI:10.1007/s00231-012-1051-5 |
| [17] |
Hoshikawa K, Kohda H, Hirata H. Homogeneous dopant distribution of silicon crystal grown by vertical magnetic field-applied czochralski method[J]. Japanese Journal of Applied Physics, 1984, 23(1): L37-L39. |
| [18] |
Zhou X M, Huang H L. Numerical simulation of Cz crystal growth in rotating magnetic field with crystal and crucible rotations[J]. Journal of Crystal Growth, 2012, 340(1): 166-170. |
| [19] |
Takagi Y, Okano Y, Minakuchi H, et al. Combined effect of crucible rotation and magnetic field on hydrothermal wave[J]. Journal of Crystal Growth, 2014, 385(1): 72-76. |
| [20] |
Shi W Y, Imaishi N. Hydrothermal waves in differentially heated shallow annular pools of silicone oil[J]. Journal of Crystal Growth, 2006, 290(1): 280-291. |
| [21] |
Hu K X, He M, Chen Q S. Instabilities of thermocapillary flows between counter-rotating disks[J]. Procedia Engineering, 2015, 126: 54-57. DOI:10.1016/j.proeng.2015.11.177 |
| [22] |
Hur M J, Han X F, Song D S, et al. The influence of crucible and crystal rotation on the sapphire single crystal growth interface shape in a resistance heated czochralski system[J]. Journal of Crystal Growth, 2014, 385: 22-27. DOI:10.1016/j.jcrysgro.2013.05.041 |
| [23] |
张发云, 罗玉峰, 李云明, 等. 磁场应用在硅晶体生长过程中的研究进展[J]. 材料导报, 2013, 27(13): 15-19. ZHANG Fayun, LUO Yufeng, LI Yunming, et al. Research and development on magnetic field application in the process of silicon crystal growth[J]. Materials Review, 2013, 27(13): 15-19. (in Chinese) DOI:10.3969/j.issn.1005-023X.2013.13.003 |
 2019, Vol. 42
2019, Vol. 42