2. 林同棪国际工程咨询(中国)有限公司, 重庆 401121
2. T. Y. Lin International Engineering Consulting(China) Co., Ltd, Chongqing 401121, P. R. China
斜拉桥及悬索桥在现代桥梁中具有举足轻重的地位,而拉索在其受力过程中扮演着至关重要的角色,但随着工业化的发展,拉索所处工作环境变得越来越恶劣,当起防护作用的PE套发生破损后,拉索将直接暴露在包含各种腐蚀介质的空气中,在交变应力和各种腐蚀介质共同作用下,拉索将会发生锈蚀并使其力学性能退化,而腐蚀将会产生蚀坑,蚀坑部位产生的应力集中也会加速拉索使用功能的衰退[1],如果空气中存在氯离子,由于氯离子的局部酸化催化作用,会进一步加快拉索腐蚀速率。目前,国内通过元胞自动机对金属腐蚀进行模拟的研究并不多,且大多数元胞自动机模型并未考虑到氯离子的影响,如李磊等[2]建立了模拟金属在湿大气环境下初期腐蚀行为的元胞自动机模型,通过引入的演化规则和元胞类型,分析得到了两类重要参数对腐蚀过程的影响并得到了腐蚀过程主要离子的浓度分布图;何乐儒等[3]以飞机结构为研究对象,利用MATLAB编程建立了模拟无防护层和有防护层金属表面局部腐蚀的元胞自动机模型,并引入了3种参数建立了腐蚀速率的参数化模型,通过对模型的分析得到了各种参数对腐蚀速率及腐蚀形貌的影响;郭东旭等[4]针对外界环境作用下金属表面容易形成坑蚀而致使结构性能退化这一问题建立了金属局部腐蚀的三维元胞自动机模型,利用模型分析在不同腐蚀溶液浓度和温度条件下结构表面蚀坑随时间的变化过程,为预测结构的剩余强度及服役寿命提供了可能。P. Cordoba-Torres等[5]提出了一种模拟电极介观尺度行为的元胞自动机模型, 并通过研究发现金属表面在形态上变得不均匀;其次,粗糙度与活性溶解位点的特定分布有关,但在元胞自动机模型中并未引入氯离子;Zenkri等[6]提出了一种基于空间分离电化学反应、扩散、溶液中和,氧化层被动性质的腐蚀随机CA建模方法,发现阳极和阴极区域的自发空间分离与表面裸露的金属和钝化金属有关,这种分离也与更快的腐蚀速率有关,文中也未提及过氯离子。Stafiej等[7]对基于元胞自动机的腐蚀和钝化模型进行了简要的研究,以空间分离的阳极和阴极反应模型为基础,给出了一种由非保护膜的点状损伤和非初始平面损伤发展成空腔的模拟结果;陈梦成等[8]采用元胞自动机方法对腐蚀环境下钢材的腐蚀行为进行了模拟,定义了元胞自动机模型的局部演化规则,确定了能够真实反映蚀坑形貌的模拟条件。虽然二者都对腐蚀产生的蚀坑进行了模拟,但模拟产生的蚀坑形貌与实际有所出入,文中在模拟腐蚀性元胞侵蚀金属元胞时,将其侵蚀移动方向分为切线方向和非切线方向,并加大了切线方向的接触概率,因此,模拟产生的蚀坑与实际情况更加接近。
虽然利用元胞自动机模拟金属腐蚀损伤演化进程已有不少研究成果,但是现有元胞自动机多是针对钢板、铝板等“平面状”构件,很难模拟圆形截面构件不同位置处蚀坑的形状;由于腐蚀机理不同,现有成果很少关注氯离子对钢材锈蚀过程的加速作用。鉴于此,文中通过引入氯离子元胞以考虑氯离子对钢丝腐蚀的加速作用,通过定义“元胞切向移动规则”实现了圆形截面不同位置的坑蚀进程的模拟。
1 元胞自动机简介元胞自动机(cellular automata,CA),是一种时间、空间、状态都离散,空间相互作用和时间因果关系为局部的网格动力学模型,具有模拟复杂系统时空演化过程的能力,不同于一般的动力学模型,元胞自动机不是由严格定义的物理方程或函数确定,而是用一系列模型构造的规则构成。元胞自动机的时间和空间都处于离散状态,随着时间的推移,系统不断产生演化;系统中的元胞空间由一个个离散的且具有有限状态的元胞网格组成,每个元胞在元胞空间中根据自身和邻居元胞的当前状态以及定义的局部规则决定下一时刻自身或者邻居元胞的状态、元胞空间在每一个时刻呈现出不同的内容,整个元胞自动机系统表现为在离散的空间和时间上根据局部规则进行演化的复杂动力学系统[9-12]。
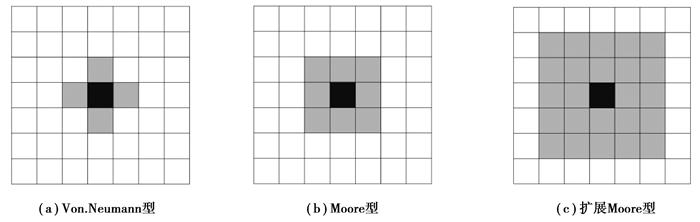
元胞自动机最重要的3个元素为元胞状态、元胞邻居和局部规则。元胞状态是元胞本身具有的性质,任何一个元胞自动机都必须赋予每个元胞一种特定的涵义,被赋予了特定涵义的元胞有规律地排列起来组成元胞空间,并在这个离散的空间中各个元胞的元胞状态根据所定义的局部规则随着时间的变化而变化,也就意味着某一时刻的元胞状态是由上一个时刻元胞状态以及元胞邻居所确定的。元胞邻居是元胞周围邻近元胞及其元胞状态的集合,代表着决定元胞演化规则的周边环境[13],常用的元胞邻居模型有3种:Von.Neumann型、Moore型、扩展Moore型[14],如图 1所示。
|
图 1 元胞邻居类型 Fig. 1 Cell neighbor type |
元胞自动机之所以能很好地模拟腐蚀进程,是因为其在数学上的严格定义,元胞状态、元胞邻居和局部规则皆以函数的形式给出。局部规则是决定元胞自动机成功与否最重要的因素,它是保证演化过程顺利进行的一种明确的动力学函数,通常表示为R={R1, R2, ...Rm},一旦确定了初始位置,给定初始条件,那么元胞的初始状态便可确定为Φ(l, t),即元胞在l位置处t时刻的状态,而在下一时刻具体演化过程可通过函数表示为
| $ \mathit{\Phi }\left( {l, t + 1} \right) = {R_j}\left[ {\mathit{\Phi }\left( {l, t} \right), \mathit{\Phi }\left( {l + {\delta _1}, t} \right), \mathit{\Phi }\left( {l + {\delta _2}, t} \right), ...\mathit{\Phi }\left( {l + {\delta _n}, t} \right)} \right], $ | (1) |
式中:Φ(l, t+1)表示初始元胞在下一时刻的元胞状态;Rj表示规则R集合中的某一种局部规则,Φ(l+δi, t)则便是邻居元胞的状态。
2 模拟拉索腐蚀的元胞自动机模型 2.1 拉索钢丝电化学腐蚀机制拉索钢丝表面一旦受到破损产生初始蚀坑,且空气中包含Cl-,那么阳极区的Fe2+会与空气中的Cl-形成络合物FeCl+,并在蚀坑表面形成FeCl2的盐膜,由质量转移引起的阳离子的减少小于阳极反应的增加,因此,凹坑的内部保持其中酸性环境,蚀坑可以继续增长。
蚀坑演化过程中阳极区的反应如下
| $ {\rm{Fe}} \to {\rm{F}}{{\rm{e}}^{{\rm{2 + }}}}{\rm{9 + 2}}{{\rm{e}}^{\rm{ - }}}。$ | (2) |
蚀坑内氧离子的水解及Cl-在腐蚀过程中的局部酸化以及催化原理如下
| $ {\rm{F}}{{\rm{e}}^{{\rm{2 + }}}}{\rm{ + }}{{\rm{H}}_{\rm{2}}}{\rm{O = FeO}}{{\rm{H}}^{\rm{ + }}}{\rm{ + }}{{\rm{H}}^{\rm{ + }}}, $ | (3) |
| $ {\rm{FeC}}{{\rm{l}}^{\rm{ + }}}{\rm{ + }}{{\rm{H}}_{\rm{2}}}{\rm{O = FeO}}{{\rm{H}}^{\rm{ + }}}{\rm{ + }}{{\rm{H}}^{\rm{ + }}}{\rm{ + C}}{{\rm{l}}^{\rm{ - }}}, $ | (4) |
| $ {\rm{FeC}}{{\rm{l}}_{{\rm{2(aq)}}}}{\rm{ + }}{{\rm{H}}_{\rm{2}}}{\rm{O = FeO}}{{\rm{H}}^{\rm{ + }}}{\rm{ + }}{{\rm{H}}^{\rm{ + }}}{\rm{ + 2C}}{{\rm{l}}^{\rm{ - }}}。$ | (5) |
从上式中可以发现,整个过程中Cl-并没有消耗,但释放出的H+降低了蚀坑内的pH值,使其处于酸性环境下工作,进一步加快蚀坑的增长,因此,拉索钢丝在具有Cl-的环境下工作会加快其腐蚀进程。
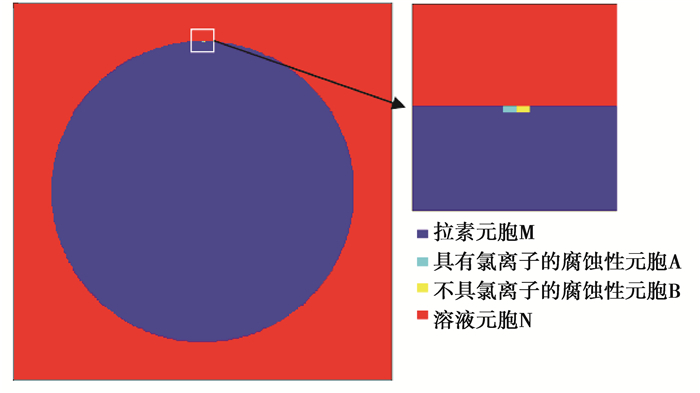
2.2 元胞类型的定义当拉索的PE套在长时间工作后发生破损,拉索钢丝直接暴露在空气中,外界腐蚀环境和疲劳荷载的耦合作用会加速拉索的腐蚀。为模拟拉索钢丝的腐蚀进程,文中将拉索和与其接触的外界腐蚀溶液定义成按局部规则进行演化的空间和时间上均离散的动力学系统。将拉索和与其接触的外界腐蚀溶液离散成500×500的有序网格,设定钢丝区域内的相关网格为金属元胞(图 2内的蓝色区域),钢丝周围其他区域设定为不具备腐蚀能力的溶液元胞N(图 2内的红色区域),初始腐蚀位置处仅设置2个相邻的腐蚀性元胞(图 2内用绿色表示的含氯离子的腐蚀元胞A和用黄色表示的不含氯离子的腐蚀元胞B)。
|
图 2 元胞自动机及初始腐蚀位置 Fig. 2 cellular automata and initial corrosion location |
为了更好地模拟拉索在外界环境影响下腐蚀的演化进程,元胞自动机以Moore型(见图 1)作为元胞邻居模型,并引入了4种类型的元胞:溶液元胞N包围在拉索钢丝周围,不具备腐蚀和移动能力;拉索元胞M能够被具有腐蚀性的元胞侵蚀掉,在演化进程中不具备移动能力,自始至终保持固定不变的位置;腐蚀性元胞分为含有氯离子的腐蚀元胞A和不含氯离子的腐蚀元胞B,腐蚀元胞具有移动能力,可以向周围移动扩散并侵蚀元胞M,考虑到氯离子具有局部酸化催化作用[15],故有氯离子存在的区域其腐蚀进程通常较快,为了区分腐蚀元胞A和B并探究氯离子对拉索腐蚀的影响,特引入2种元胞的腐蚀概率Pa和Pb(Pa>Pb)。元胞N环绕在拉索周围,由多种元胞随机排列组成,其中,包括元胞A和元胞B。
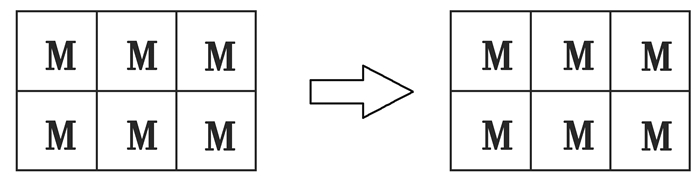
2.3 局部规则的定义拉索腐蚀是一个非常复杂的过程,不仅要考虑在发生腐蚀过程中各种化学反应的影响,同时还应考虑周边环境的影响和各种参数的随机性。元胞自动机定义了4种不同类型的元胞以及腐蚀概率Pa和Pb,在此基础上将腐蚀性溶液浓度c引入该模型中,c代表腐蚀性元胞(元胞A与元胞B的总和)与溶液元胞的比值,并将c/(c+1)作为腐蚀性元胞(元胞A和元胞B)能够在演化过程中接触到元胞M的概率;同时,以各种局部规则所产生的效应近似模拟拉索在实际环境中的腐蚀进程。为了更准确模拟拉索腐蚀的演化过程,使蚀坑更接近真实形貌,引入了如下4种局部规则进行模拟,如图 3~图 6所示。
|
图 3 局部规则:拉索元胞移动规则 Fig. 3 Local rules: cable cell movement rules |
|
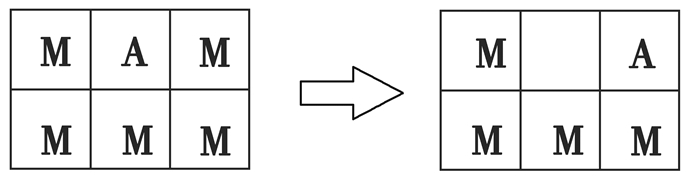
图 4 局部规则:腐蚀元胞移动规则 Fig. 4 Local rules: corrosion cell movement rules |
|
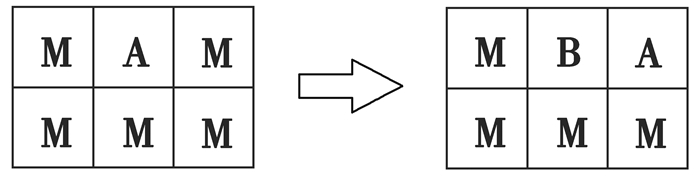
图 5 局部规则:腐蚀规则1 Fig. 5 Local rules: corrosion rules 1 |
|
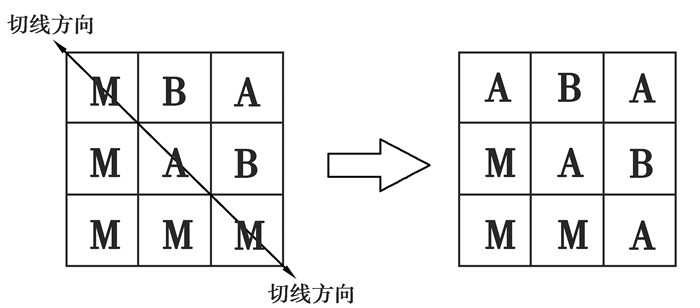
图 6 局部规则:腐蚀规则2 Fig. 6 Local rules: corrosion rules 2 |
1) 拉索元胞M在演化过程中始终处于静止状态,不具备移动能力。
2) 具有氯离子的腐蚀性元胞A以及无氯离子的腐蚀性元胞B在演化过程的每一个时间步长中可以向上、下、左、右移动,当其周围存在空位时,在下一个时间步长内,元胞A或元胞B会以一定的概率向空位移动占据空位,其原本位置变为空位或被其他腐蚀性元胞占据。
3) 当腐蚀性元胞周围存在拉索元胞M时,在下一个时间步长内,元胞A或元胞B会以接触概率c/(c+1)向元胞M所占据的网格移动,然后分别以腐蚀概率Pa或者Pb占据其所在网格实现对拉索的侵蚀,其原本所占据的网格变为空位或被其他腐蚀性元胞占据。
4) 为了使模拟的拉索钢丝蚀坑形貌更接近真实的“椭球状”,假定腐蚀中心元胞向钢丝表面切向方向移动的概率较非切线方向大,即同一个时间步长内,元胞A或元胞B以2c/(c+1)的接触概率向切线方向元胞M所占据的网格移动,而以c/(c+1)的接触概率向非切线方向移动。
如图 6所示,中心元胞A切线方向的金属元胞只有2个,而非切线方向的金属元胞有3个,如果中心元胞A仍然以c/(c+1)的概率接触金属元胞,那么接触到非切线方向金属元胞的总概率就是3c/(c+1),接触到切线方向金属元胞的总概率就是2c/(c+1),蚀坑形貌就会表现出深度较深而直径比较短的特征,不符合蚀坑实际形貌,而实际蚀坑形貌更接近的“椭球状”,深度较浅而直径较长,因此,切线方向总接触概率必须大于非切线方向总接触概率。如果元胞A或元胞B向切线方向每个金属元胞移动的接触概率为2c/(c+1),那么切线方向金属元胞总接触概率就可以达到4c/(c+1),大于非切线方向总接触概率,模拟出的蚀坑形貌则表现出直径较长而深度较浅的特征,符合实际蚀坑“椭球状”的形貌。
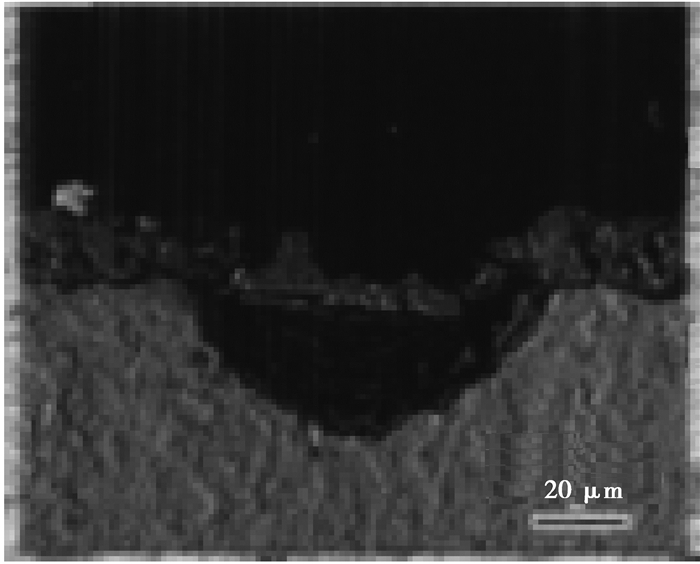
3 钢丝坑蚀元胞自动机模拟结果及分析 3.1 蚀坑形貌的模拟当拉索长时间暴露在空气中工作时会产生电化学腐蚀,表面会出现大大小小的蚀坑,这些蚀坑截面形状近似于半椭圆形[2],如图 7所示,为了使CA模型产生的蚀坑形貌更加接近于实际,经过多次对参数进行修改,当腐蚀性溶液浓度c=0.6,腐蚀概率Pa=0.8以及腐蚀概率Pb=0.5时,CA模型模拟产生的蚀坑最接近实际状况,如图 8所示。
|
图 7 蚀坑实际形貌 Fig. 7 Actual shape of the etch pit |
|
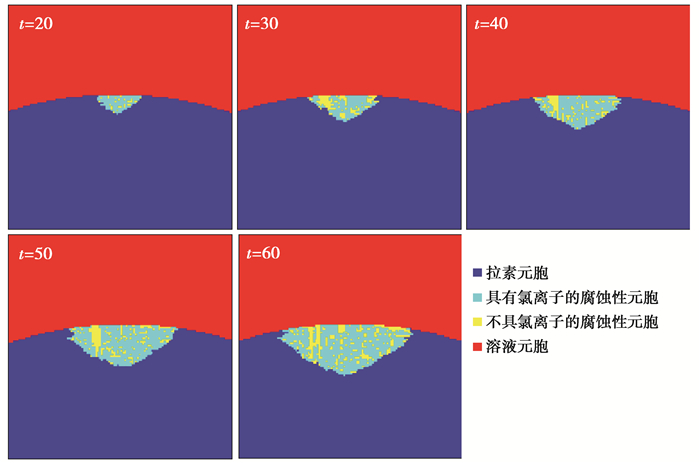
图 8 各时间步长CA模拟产生的蚀坑形貌 Fig. 8 The shape of the etch pit generated by CA simulation of each time step |
从图中可以看出,在任何时间步长内,CA模型模拟产生的蚀坑始终保持半椭圆形的形状,这与实际蚀坑也是十分吻合的,证明了虽然CA模型是利用概率事件对实际腐蚀过程进行模拟,但利用该模型模拟拉索钢丝表面蚀坑的演化进程仍是可行的;观察各个时间步长内蚀坑的形貌可以发现,随着时间的推移,蚀坑的深度以及半径也在不断变大,这也符合拉索在实际环境中受到腐蚀作用时蚀坑形貌随时间变化的趋势,也证明了CA模型模拟的蚀坑形貌不仅仅是在某一个时刻呈现出半椭圆形的形状,而是在整个模拟腐蚀演化进程中始终保持着与实际情况相接近的方式进行演化发展,进一步验证了CA模型的可行性。文中CA模型包含4种类型的元胞,观察每个时间步长内不同类型元胞的时空演化趋势可以发现,在蚀坑内仅存在元胞A和元胞B 2种腐蚀性元胞,这是由局部规则所导致的,元胞M会在c/(c+1)的概率下被腐蚀性元胞接触到并以概率Pa或Pb遭到侵蚀,一旦元胞M受到腐蚀元胞的侵蚀,那么其格位将会被该种类型的元胞所占据,所以蚀坑中仅存在2种腐蚀元胞;通过对蚀坑内这2种腐蚀元胞数目的比较,不难发现,元胞A的数目明显多于元胞B的数目,这是由于在相同接触概率下,元胞A侵蚀元胞M的腐蚀概率Pa大于元胞B所对应的腐蚀概率Pb,元胞A侵蚀过后所占据的格位也较多,体现出元胞A中氯离子的局部酸化催化作用。鉴于CA模型模拟拉索腐蚀演化进程的可行性,通过调整元胞自动机运行规则尽量匹配试验结果,即可实现不同腐蚀时长下拉索蚀坑形状(深度、长轴和短轴长度)的蒙特卡洛模拟,结合拉索腐蚀加速试验结果扩充蚀坑样本,最终实现腐蚀钢丝力学行为的统计描述。
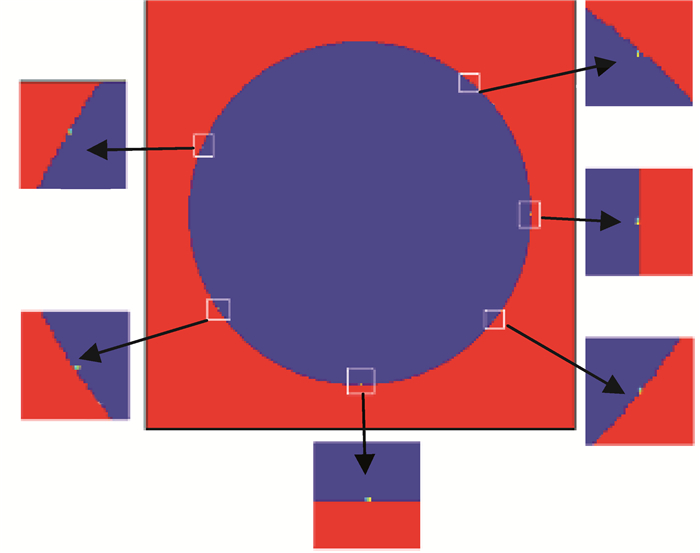
在实际环境中,拉索钢丝表面往往会出现多个蚀坑,且蚀坑位置也是随机分布,在钢丝表面随机选取如图 9所示的初始腐蚀位置,同样取腐蚀性溶液浓度c=0.6,腐蚀概率Pa=0.8以及腐蚀概率Pb=0.5,腐蚀时间步长t=60时,元胞自动机模拟产生的蚀坑如图 10所示,从图中可以看出,腐蚀无论发生在钢丝表面任何位置,其蚀坑形貌始终保持着近似半椭圆形的形状,与实际蚀坑形貌相吻合。因此,对于圆形截面的拉索钢丝,一旦确定了初始腐蚀位置,适当加大中心元胞与切线方向上的邻居元胞的接触概率,蚀坑形貌也就越接近真实形貌。
|
图 9 截面各位置初始腐蚀位置 Fig. 9 Initial corrosion position at each position of the section |

|
图 10 截面各位置蚀坑形貌 Fig. 10 The shape of the etch pit at each position of the section |
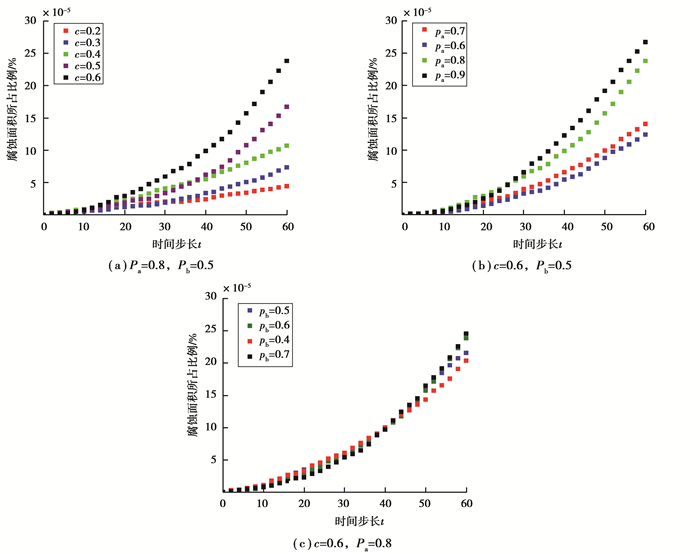
CA模型引入腐蚀性溶液浓度c及元胞A的腐蚀概率Pa和元胞B的腐蚀速率Pb 3个变量作为控制蚀坑形貌的参数,为了探究这3种参数对蚀坑形貌的影响,控制腐蚀性溶液浓度c及元胞A的腐蚀概率Pa和元胞B的腐蚀速率Pb 3个变量中某2个变量不变,改变第3个变量,提取60个时间步长内的腐蚀面积,用以描述腐蚀速率,并绘制不同浓度下腐蚀面积随时间变化的趋势,如图 11所示,可以看出图 11中腐蚀面积随时间变化的变化趋势符合幂函数关系。在电化学腐蚀中,用腐蚀面积表示的腐蚀速率满足时间的幂函数关系[16-19],进一步验证了该模型的正确性。
|
图 11 不同参数下腐蚀面积随时间变化曲线 Fig. 11 Change curve of corrosion area with time under different parameters |
观察图 11(a)可以发现,随着时间步长的增加,钢丝腐蚀面积不断变大,且腐蚀速率随腐蚀进程的演化而逐步增快,这意味着一旦钢丝腐蚀出现蚀坑,钢丝腐蚀面积越来越大的同时其腐蚀速率也将越来越快,原因可能是:随着腐蚀进程的发展,蚀坑表面积越来越大,更多的腐蚀性溶液进入蚀坑内,导致其腐蚀速率加快;而当腐蚀概率Pa和Pb保持一个定值,相同时间内钢丝腐蚀面积随腐蚀性溶液浓度c增大而增大;溶液浓度对钢丝腐蚀初期的腐蚀速率的影响并不显著,但高浓度会导致钢丝后期腐蚀速率明显加快。
从图 11(b)和图 11(c)中可以发现:当腐蚀概率Pa为0.6或0.7时,60个时间步长内钢丝腐蚀面积随时间的变化大致相同,但当概率达到0.8后,其腐蚀速率明显大于概率取0.7时所对应曲线;无氯离子的腐蚀元胞的腐蚀概率Pb对钢丝腐蚀速率的影响不大,对比图 11(b)不难发现,在拉索腐蚀的过程中具有氯离子的腐蚀性元胞具有主导地位,而不具有氯离子的腐蚀性元胞对腐蚀演化发展所做的贡献不及前者,这可能是由于氯离子对电化学反应的催化作用使得含有氯离子的腐蚀元胞的腐蚀速率和数量占比均大于不含氯离子的腐蚀元胞造成的,因此,在实际工程中,应重点关注周边环境氯离子的浓度,控制并减少周边环境中氯离子的浓度是减缓拉索腐蚀的有效途径。
4 结论利用元胞自动机模型模拟拉索钢丝的电化学腐蚀进程,将电化学腐蚀系统中的关键元素抽象成4种类型的元胞,并通过定义的局部规则在介观尺度对拉索腐蚀演化进程进行模拟,分析了腐蚀性溶液浓度c及腐蚀概率Pa和Pb 3个参数对钢丝腐蚀进程的影响。
1) 当元胞自动机特征参数选取合理,并适当加大中心元胞与切线方向上的邻居元胞的接触概率,元胞自动机模拟产生的蚀坑形貌与实际蚀坑形貌十分接近;
2) 钢丝腐蚀面积随时间不断变大的同时腐蚀速率也将逐步增快,表明一旦钢丝腐蚀出现蚀坑,钢丝腐蚀面积越来越大的同时其腐蚀速率也将越来越快;
3) 在拉索腐蚀的过程中具有氯离子的腐蚀性元胞具有主导地位,无氯离子的腐蚀元胞的腐蚀概率对钢丝腐蚀速率的影响不大,控制并减少周边环境中氯离子的浓度是减缓拉索腐蚀的有效途径。
| [1] |
黄克智, 肖纪美. 材料的损伤断裂机理和宏微观力学理论[M]. 北京: 清华大学出版社, 1999. HUANG Kezhi, XIAO Jimei. Damage and fracture mechanism of materials and macro-mechanical theory[M]. Beijing: Tsinghua University Press, 1999. (in Chinese) |
| [2] |
李磊, 李晓刚, 肖葵, 等. 金属在湿大气环境下初期腐蚀行为的元胞自动机模拟[J]. 中国腐蚀与防护学报, 2010, 30(2): 114-118. LI Lei, LI Xiaogang, XIAO Kui, et al. Cellular automata simulation on the early stages of metal corrosion in moist atmospheric environment[J]. Journal of Chinese Society for Corrosion and Protection, 2010, 30(2): 114-118. (in Chinese) |
| [3] |
何乐儒, 殷之平, 黄其青, 等. 模拟金属表面局部腐蚀的CA方法[J]. 航空材料学报, 2015, 35(2): 54-63. HE Leru, YIN Zhiping, HUANG Qiqing, et al. Simulation of local corrosion on metal surface with CA method[J]. Journal of Aeronautical Materials, 2015, 35(2): 54-63. (in Chinese) |
| [4] |
郭东旭, 任克亮, 王燕昌, 等. 金属局部腐蚀的三维元胞自动机模型[J]. 力学与实践, 2014, 36(4): 447-452. GUO Dongxu, REN Keliang, WANG Yanchang, et al. Three-dimensional cellular automata model for predicting local corrosion[J]. Mechanics in Engineering, 2014, 36(4): 447-452. (in Chinese) |
| [5] |
Córdoba-Torres P, Nogueira R P, Miranda L, et al. Cellular automaton simulation of a simple corrosion mechanism:mesoscopic heterogeneity versus macroscopic homogeneity[J]. Electrochimica Acta, 2001, 46(19): 2975-2989. DOI:10.1016/S0013-4686(01)00524-2 |
| [6] |
Zenkri, Caprio D, Pérez-Brokate, et al. Contribution of cellular automata to the understanding of corrosion phenomena[J]. Condensed Matter Physics, 2017, 20(3): 33802. DOI:10.5488/CMP.20.33802 |
| [7] |
Stafiej J, Caprio D, Bartosik. Corrosion-passivation processes in a cellular automata based simulation study[J]. The Journal of Supercomputing, 2013, 65(2): 697-709. DOI:10.1007/s11227-013-0933-8 |
| [8] |
陈梦成, 温清清. 钢材腐蚀损伤过程的元胞自动机模拟[J]. 中国腐蚀与防护学报, 2018, 38(1): 68-73. CHEN Mengcheng, WEN Qingqing. Cellular automata simulation of corrosion process for steel[J]. Journal of Chinese Society for Corrosion and Protection, 2018, 38(1): 68-73. (in Chinese) |
| [9] |
Caprio D, Vautrin C, Stafiej J, et al. Morphology of corroded surfaces:Contribution of cellular automaton modelling[J]. Corrosion Science, 2011, 53(1): 418-425. DOI:10.1016/j.corsci.2010.09.052 |
| [10] |
Lishchuk S V, Akid R, Worden K, et al. A cellular automaton model for predicting intergranular corrosion[J]. Corrosion Science, 2011, 53(8): 2518-2526. DOI:10.1016/j.corsci.2011.04.027 |
| [11] |
Chopard B, Droz M. Cellular automata modeling of physical systems[M]. Cambridge: Cambridge University Press, 1998.
|
| [12] |
郭东旭.基于三维元胞自动机方法的金属腐蚀损伤模拟[D].银川: 宁夏大学, 2014. GUO Dongxu. Simulation of metal corrosion based on the three-dimensional cellular automaton method[D]. Yinchuan: Ningxia University, 2014.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10749-1014225206.htm |
| [13] |
郭洪民, 刘旭波, 杨湘杰. 元胞自动机方法模拟微观组织演变的建模框架[J]. 材料工程, 2003, 31(8): 23-27, 48. GUO Hongmin, LIU Xubo, YANG Xiangjie. Model framework for microstructure evolution modeling with cellular automata[J]. Journal of Materials Engineering, 2003, 31(8): 23-27, 48. (in Chinese) DOI:10.3969/j.issn.1001-4381.2003.08.007 |
| [14] |
马俊军, 蔺鹏臻. 混凝土箱梁氯离子扩散效应分析与寿命预测的CA模型[J]. 长江科学院院报, 2019, 36(6): 121-126. MA Junjun, LIN Pengzhen. Cellular automata model of chloride ion diffusion and life prediction of concrete box girder[J]. Journal of Yangtze River Scientific Research Institute, 2019, 36(6): 121-126. (in Chinese) |
| [15] |
徐叶波.钢筋腐蚀电化学损伤的分数微分与元胞自动机识别方法[D].哈尔滨: 哈尔滨工业大学, 2013. XU Yebo. Identification methods based on fractional differentiation and cellular automata for the electrochemical corrosion damage of steel bar[D]. Harbin: Harbin Institute of Technology, 2013. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10213-1014003214.htm |
| [16] |
王慧, 吕国志, 张有宏. 蚀坑生长演化过程的元胞自动机模拟[J]. 腐蚀科学与防护技术, 2008, 20(6): 472-475. WANG Hui, LYU Guozhi, ZHANG Youhong. Cellular automaton simulations of corrosion pit growth[J]. Corrosion Science and Protection Technology, 2008, 20(6): 472-475. (in Chinese) DOI:10.3969/j.issn.1002-6495.2008.06.021 |
| [17] |
王慧, 吕国志, 王乐, 等. 金属表面腐蚀损伤演化过程的元胞自动机模拟[J]. 航空学报, 2008, 29(6): 1490-1496. WANG Hui, LYU Guozhi, WANG Le, et al. Cellular automaton simulations of surface corrosion damage evolution[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(6): 1490-1496. (in Chinese) DOI:10.3321/j.issn:1000-6893.2008.06.013 |
| [18] |
Malki B, Baroux B. Computer simulation of the corrosion pit growth[J]. Corrosion Science, 2005, 47(1): 171-182. DOI:10.1016/j.corsci.2004.05.004 |
| [19] |
Pidaparti R M, Palakal M J, Fang L. Cellular automation approach to model aircraft corrosion pit damage growth[J]. AIAA Journal, 2004, 42(12): 2562-2569. DOI:10.2514/1.2092 |
 2019, Vol. 42
2019, Vol. 42

