近年来，基于射频(RF)能量采集的认知无线网络(RF EH-CRN)受到了广泛关注，可对可用频谱进行重复使用并可对射频能量进行收集开发^[1]。根据次用户(SU)访问授权频谱的方法，射频认知无线网络中的次用户主要采用交织(Interweave)、覆盖(Overlay)和重叠(Underlay)模式^[2]。在交织和覆盖模式下，次用户需要消耗所采集的较多能量进行频谱感知并与主用户间进行协作^[3-7]。在重叠模式下，只要对主用户的干扰未超过其抗干扰阈值，次用户即可使用所采集的能量进行并行数据传输^[8-10]。

射频认知无线网络中的主用户通常通过所采集的能量进行自供电，无需外接专用供电通道。此外，由于射频源传输功率波动或信道衰落的存在，主用户所采集的能量将是动态或不稳定的。RF EH-CRN的主要目标之一为最大限度提高射频认知无线网络的能量效率(EE)，其定义为数据传输吞吐量与总能耗之间的比值。在文献[11]中，笔者首次考虑通过优化感知时间和传输功率最大限度地提高交织式射频认知无线网络的能量效率。在文献[12]中，作者对次用户网络的能量效率进行优化，次用户发射机需根据主用户的感知结果动态调整传输功率。由于不需要消耗能量进行频谱感知和协作，特别是当主用户大部分时间处于活跃状态时，Underlay射频能量收集认知无线网络将是能量效率更高的架构，可应用于很多实际场景，如无线传感网络^[8]。目前尚未充分研究在服务质量(QoS)保证下的Underlay射频能量收集认知无线网络的能量效率最大化问题。更具体地说，对次用户传输时间和功率的复杂约束条件和变量耦合会对优化方案设计带来巨大挑战。

综上所述，研究具有3个主要贡献。首先，在能量、干扰和服务质量约束下对Underlay模式下的射频认知无线网络能量效率最大化问题进行了建模，解决了该场景下能量效率最大化这种非线性分式规划问题。其次，假设了次用户在上一时隙传输完成后存在剩余能量可进行利用，则次用户使用能量的灵活性将得到提高，并能更全面得考虑认知无线网络射频能量收集等自供电应用场景。最后，基于Dinkelbach和拉格朗日对偶等方法，提出可提高能量效率资源分配的新算法，对传输时间和发射功率进行联合优化，并在不同场景下进行了仿真验证。

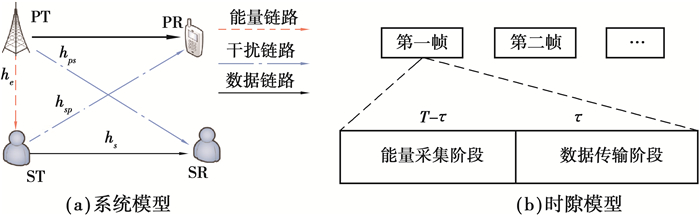
1 系统模型

Underlay模式下的RF EH-CRN系统如图 1(a)所示，由次用户发射机(ST)和次用户接收机(SR)组成的次用户网络与由主用户发射机(PT)和主用户接收机(PR)组成的主用户网络并存。主用户发射机首先采集由主用户发射机射频信号发出的能量，然后在相同频带作为主用户发射机同次用户接收机通信。支持3种链路，即能量链路(PT-ST)、干扰链路(PT-SR和ST-PR)和数据链路(ST-SR和PT-PR)。假定主用户发射机和主用户接收机在授权频谱始终处于相互通信状态。所有信道会出现块衰落，各分块的衰落状态维持不变，但分块之间会发生变化。假定次用户接收机有稳定供电，次用户发射机完全由采集的射频能量自行供电。此外，次用户发射机在半双工模式下工作，即可分别进行采集能量或传输数据但无法同时完成。如图 1(b)所示，一帧数据(次用户发射机的时间设为T)分为2个时隙，即能量采集时隙T-τ和数据传输时隙τ。

1) 能量采集时隙：次用户发射机在T-τ内采集能量，所采集的能量用E_h表示，

$ {E_h} = \eta {h_e}{P_t}(T - \tau ), $

(1)

其中：η表示ST的能量收集效率；h_e为从PT到ST能量链路的信道增益；P_t为PT恒定的发射功率。

2) 数据传输时隙：ST向SR发射数据信号所消耗的能量不能超过包括收集能量E_h和初始剩余能量Q_e的总可用能量，该条件可被归纳为能量因果约束^[1]如下

$ \left( {P + {P_c}} \right)\mathit{\boldsymbol{\tau }} \le {E_h} + {Q_e}, $

(2)

其中，P和P_c分别指次用户发射机的传输功率和电路功耗。由于次用户发射机在重叠模式下与主用户发射机共享频谱，必须限制次用户发射机的传输功率以便确保次用户发射机和主用户接收机之间的干扰低于主用户的可接受阈值，即干扰约束^[1]如下

$ P{h_{sp}} \le {P_I}, $

(3)

其中：P_I系指主用户接收机的允许干扰的峰值；h_sp系指干扰链路(ST-PR)的信道增益。次用户网络吞吐量可根据下列公式(4)计算

$ R(\mathit{\boldsymbol{\tau }},P) = \mathit{\boldsymbol{\tau }}{\log _2}\left( {1 + \frac{{P{h_s}}}{{{P_t}{h_{ps}} + {\sigma ^2}}}} \right), $

(4)

其中：h_s系指数据链路(ST-SR)的信道增益；h_ps系指链路(PT-SR)的信道增益；σ²系指次用户接收机的噪音功率。

为确保次用户网络的服务质量，需达到公式(5)中要求的次用户发射机的最低吞吐量R_min。

$ R(\mathit{\boldsymbol{\tau }} ,P) \ge {R_{\min }}, $

(5)

值得注意的是，能量采集和干扰均与主用户网络和次用户网络之间的距离有关，需考虑小尺度诉衰落，信道增益可表示为h_X=|G_X|²D^-a(X=e, sp, ps, s)，其中α系指路径损耗指数；D系指距离；G_X系指单位平均值的指数分布随机变量^[2]。

3) 能量效率最大化：次用户发射机所消耗的总能量E_c(τ, P)由2部分组成：第一部分为能量采集时隙内信道传播衰减所造成的能量损耗，另一部分为传输时间内信息传输所消耗的能量。因此，总耗能E_c(τ, P)可根据下列公式(6)进行计算

$ {E_c}(\mathit{\boldsymbol{\tau }} ,P) = {P_H}(T - \mathit{\boldsymbol{\tau }} ) + \left( {P + {P_c}} \right)\mathit{\boldsymbol{\tau }} , $

(6)

需注意，P_H(T-τ)表示主用户发射机ST中的能量采集电路带来的电路能量损耗，P_c为ST发射电路带来的能量损耗。结合公式(2)-(6)，射频认知无线网络的能量效率可根据下列公式(7)进行计算

$ \begin{array}{l} OP1:\mathop {\max }\limits_{\mathit{\boldsymbol{\tau }},P} EE(\mathit{\boldsymbol{\tau }},P) = \frac{{R(\mathit{\boldsymbol{\tau }} ,P)}}{{{E_c}(\mathit{\boldsymbol{\tau }} ,P)}}{\rm{,}}\\ {\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{. }}\left\{ {\begin{array}{*{20}{l}} {{\rm{式}}(2),(3),(5)}\\ {C4:0 < \mathit{\boldsymbol{\tau }} < T,0 < P < {P_{\max }}} \end{array}} \right., \end{array} $

(7)

其中，P_max系指认知系统授权的次用户发射机的最大传输功率。

2 解决方法和算法描述

由于OP1的目标函数为非凸函数且待优化变量τ和P的积出现在约束(2)中，因此OP1属于非凸问题。为实现OP1，引入了新变量e并定义为$ P = \frac{e}{\tau }$，即为次用户发射机传输数据实际所使用的能量。接着将e代入公式(2)-(6)后，OP1可进一步转换为公式(8)，

$ \begin{array}{l} OP2:\mathop {\max }\limits_{\mathit{\boldsymbol{\tau }},e} EE(\mathit{\boldsymbol{\tau }},e) = \frac{{R(\mathit{\boldsymbol{\tau }} ,e)}}{{{E_c}(\mathit{\boldsymbol{\tau }} ,e)}}{\rm{,}}\\ {\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{. }}\left\{ {\begin{array}{*{20}{l}} {C1:e + {P_c}\mathit{\boldsymbol{\tau }} \le \eta {h_e}{P_t}(T - \mathit{\boldsymbol{\tau }} ) + {Q_e}}\\ {C2:e{h_{sp}} \le \mathit{\boldsymbol{\tau }} {P_I}}\\ {C3:R(\mathit{\boldsymbol{\tau }} ,e) \ge {R_{\min }}}\\ {C4:0 < \mathit{\boldsymbol{\tau }} < T,e > 0} \end{array}} \right., \end{array} $

(8)

其中，$ R\left( {\tau , e} \right) = \tau {\rm{lo}}{{\rm{g}}_2}\left( {1 + \frac{e}{\tau }\gamma } \right)$和$ \gamma = \frac{{{h_s}}}{{{P_t}{h_{ps}} + {\sigma ^2}}}$系指能量约束、干扰约束和吞吐量约束，分别对应公式(2)，(3)和(5)。

由于吞吐量函数$ R\left( {\tau , e} \right) = \tau {\rm{lo}}{{\rm{g}}_2}\left( {1 + \frac{e}{\tau }\gamma } \right)$是函数$ f\left( e \right) \buildrel \Delta \over = {\rm{lo}}{{\rm{g}}_2}\left( {1 + e\gamma } \right)$的透视变换(perspective transformation)。众所周知，由于log对数函数是凹的，所以f(e)是一个关于e的凹函数。由于透视变换可保持函数的凹凸性，因此$ R\left( {\tau , e} \right) = \tau {\rm{lo}}{{\rm{g}}_2}\left( {1 + \frac{e}{\tau }\gamma } \right)$仍然是关于τ和e的凹函数。同时，EE_c(τ, e)显然是关于τ和e的仿射函数(affine function)。因此，OP2中目标函数EE(τ, e)是凹函数与仿射函数之间的比值。因此，使用著名的Dinkelbach方法^[13]，可将OP2转换成参数化的凹函数最大化问题，求得表示形式如下

$ \begin{array}{*{20}{c}} {OP3:\max \mathop {f(q)}\limits_{\mathit{\boldsymbol{\tau }},e} = R(\mathit{\boldsymbol{\tau }} ,e) - q{E_c}(\mathit{\boldsymbol{\tau }} ,e),}\\ {{\rm{s}}{\rm{.t}}{\rm{. }}C1,C2,C3,C4,} \end{array} $

(9)

其中q∈R⁺为一个参数。只要存在一个q^*使得f(q^*)=0，则EE(τ, e)在OP2中可取得最大值。此外，EE(τ, e)的最大值等于q^*[13]。显然，OP3是一个关于τ和e的凸优化问题并且满足Slater条件，因此可以解决其对偶(Dual)问题来代替原问题。根据约束条件C1和C3，OP3的部分拉格朗日函数(partial lagrangian function)可表示如下

$ L(\mathit{\boldsymbol{\tau }} ,e,\lambda ,v) = R(\mathit{\boldsymbol{\tau }} ,e) - q{E_c}(\mathit{\boldsymbol{\tau }} ,e) - \lambda \left( {e + {P_c}\mathit{\boldsymbol{\tau }} - \eta {h_e}{P_t}(T - \mathit{\boldsymbol{\tau }} ) - {Q_e}} \right) + \\ v\left( {R(\mathit{\boldsymbol{\tau }} ,e) - {R_{\min }}} \right), $

(10)

其中，τ和υ分别是与约束条件C1和C3有关的非负对偶变量。接着，OP3的拉格朗日对偶函数可求得如下

$ g(\lambda ,v) = \mathop {\max }\limits_{\mathit{\boldsymbol{\tau }} ,e \ge 0} L(\mathit{\boldsymbol{\tau }} ,e,\lambda ,v)。$

(11)

最终，OP3的对偶问题可描述为

$ D(\lambda ,v) = \mathop {\max }\limits_{\mathit{\boldsymbol{\tau }} ,e \ge 0} g\left( {\lambda ,v} \right)。$

(12)

定理1：对给定的EE(τ, e)，EE(τ, e)，EE(τ, e)，最优传输时间和能量分配可由下式求得

$ {\mathit{\boldsymbol{\tau }} ^*} = {\left[ { - \frac{{{e^*}\gamma W(\vartheta )}}{{W(\vartheta ) + 1}}} \right]^ + }, $

(13)

其中，$ \vartheta = - {\rm{exp}}\left( {\frac{{\zeta {\rm{ln}}2}}{{1 + \upsilon }}} \right)$，W(·)表示Lambert W函数且(x)⁺=max(0, x)^[14]。

$ {e^*} = \min {\left[ {{\mathit{\boldsymbol{\tau }} ^*}\left( {\frac{1}{\gamma } - \frac{{1 + v}}{{\ln 2(q + \lambda )}},\frac{{{\mathit{\boldsymbol{\tau }} ^*}{P_I}}}{{{h_{sp}}}}} \right)} \right]^ + }, $

(14)

证明：OP3是凸优化问题并且满足Slater条件。因此，τ和e的最优值必然满足KKT条件(Karush-Kuhn-Tucker)，该条件相应描述给出如下

$ {\left. {\frac{{\partial L(\mathit{\boldsymbol{\tau }} ,e,\lambda ,v)}}{{\partial \mathit{\boldsymbol{\tau }}}}} \right|_{\mathit{\boldsymbol{\tau }} = {\mathit{\boldsymbol{\tau }}^*}}} = 0, $

(15)

$ {\left. {\frac{{\partial L(\mathit{\boldsymbol{\tau }} ,e,\lambda ,v)}}{{\partial e}}} \right|_{e = {e^*}}} = 0, $

(16)

从公式(15)可以得到

$ \ln \left( {1 + \frac{{{e^*}}}{{{\mathit{\boldsymbol{\tau }} ^*}}}\gamma } \right) - \frac{{\frac{{{e^*}}}{\mathit{\boldsymbol{\tau }} }\gamma }}{{1 + \frac{{{e^*}}}{{{\mathit{\boldsymbol{\tau }} ^*}}}\gamma }} = \frac{{\zeta \ln 2}}{{1 + v}}, $

(17)

其中ζ=qP_H-qP_c-λP_c-ληh_eP_t。接着，由于Lambert W函数与f(z)=ze^z之间存在求逆关系^[14]，利用此函数来求得τ^*。最后，式(13)给出所得到的解。

同时，通过计算式(16)可得到

$ {e^*} = {\mathit{\boldsymbol{\tau }} ^*}\left( {\frac{1}{\gamma } - \frac{{1 + v}}{{\ln 2(q + \lambda )}}} \right), $

(18)

由于e^*也同时受限于OP2中的干扰功率约束C2，则可通过公式(14)得到最优值e^*。

遗憾的是，从式(13)-(14)可以看出，在每个迭代中τ^*和e^*耦合在一起。为避免直接求解这种含耦合变量的问题，在算法内循环中引入一种迭代方法。首先在给定e值下利用式(13)计算τ，然后在上一步求得τ的条件下利用式(14)得到e，直到收敛到一定精度。随后，利用次梯度算法(sub-gradient algorithm)可求得最小化函数g(λ, v)的最优对偶变量λ^*和v^*。特别的，λ值和υ值可基于以下算法过程进行迭代更新直到收敛

$ {\lambda ^{(k + 1)}} = {\lambda ^{(k)}} - a\nabla L\left( {{\lambda ^{(k)}}} \right), $

(19)

$ {v^{(k + 1)}} = {v^{(k)}} - a\nabla L\left( {{v^{(k)}}} \right), $

(20)

其中∇L(λ^(k))=-(e^*+P_cτ^*-ηh_eP_t(T-τ^*)-Q_e)，且∇L(v^(k))=τ^*log₂$ \left( {1 + \frac{{{e^*}}}{{{\tau ^*}}}\gamma } \right)$-R_min，a表示第k次迭代时使用的步长。最后，在迭代的外循环升级q值。只要满足f(q^*)=0或f(q^*)≤ε，即可得到原问题的最优资源分配策略和最大能效。相应的解法可概括为算法1，算法1伪代码如表 1，

值得注意的是，由于τ和e遵循KKT条件且在算法内循环中被迭代优化，此二变量将收敛到拉格朗日对偶变量λ和υ下的最优值。同时由OP3的凸性(Convexity)可知，对于任意给定q值，能保证变量λ和υ可收敛到最优解^[13]。总之，所提算法与文献[14-15]中所述Dinkelbach结构的收敛性一致，具有的快速收敛速率。

3 仿真实验结果

笔者给出了仿真实验结果以分析拟定资源分配算法的性能。次用户网络与主用户网络之间的相对距离约为5 m，路径损耗指数为2，其他参数分别设置为η=0.8、T=1、σ²=-65 dBm、P_{I, k}=P_{c, k}=0.01 W、∀k、P_t=20 W、P_I=2 W和R_min=1 bps/Hz。

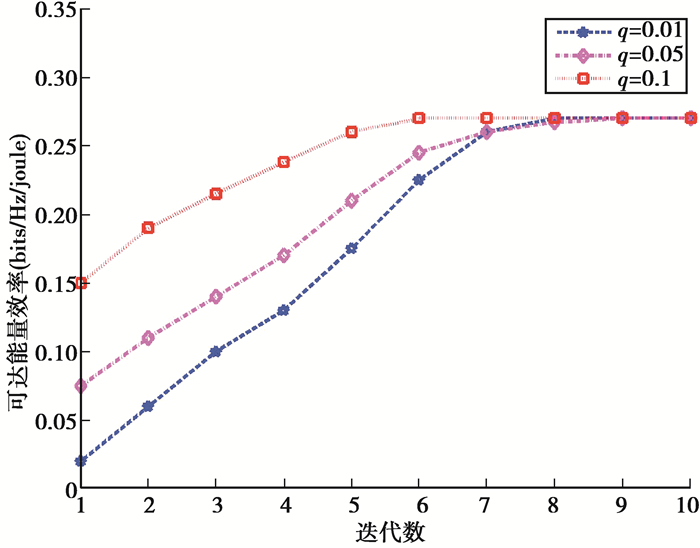
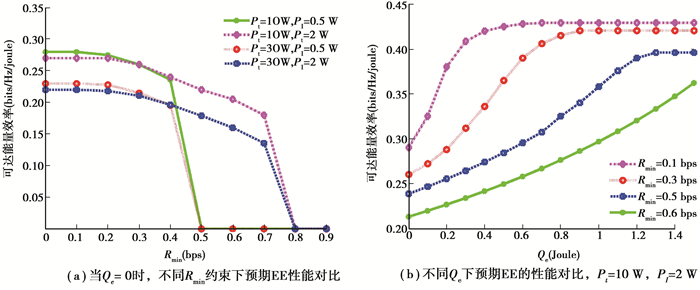
图 2说明了该算法的收敛速度。显而易见的是，该算法收敛速度快但对初值不敏感，且符合Dinkelbach方法的收敛性判据^[13]。图 3(a)说明了在不同主用户网络不同P_t、P_I和最低吞吐量R_min设置值约束条件下的能量效率性能比较。可清楚看到，当R_min最小时，能量效率达到最大。这意味着在优化能量效率的过程中，次用户发射机总是尽量少发送数据以便节省能量。当R_min增加时，能量效率将会降低。尽管R_min作为约束条件增加了，但将会导致吞吐量和能耗量同时提高，且能耗量的提高将大于吞吐量的提高，所以仍然会导致能量效率在总体趋势下的降低。此外，P_T相同但P_I不同时，能源效率相同。尽管因P_I增大会导致传输功率P的范围增大，但系统一旦达到R_min，传输功率P将不再增加。另外，能源效率将会随P_T增加而降低。这是因为若P_T越大，对次用户接收机的干扰越大，传输时间τ会延长因此R_min吞吐量会降低，则传输功率P会提高直至达到R_min吞吐量要求，致使次用户发射机消耗更多能量。最后，当次用户网络干扰强度足够大并且P_I较大或足够大时(达到一定门限时)，次用户发射机ST可能无法满足任何约束条件，RF EH-CRN能量效率最大化的优化问题将无法求解，则能量效率有可能会大幅降低或直接降至0左右，系统能量效率将会受到大幅度影响。从图 3(a)同时也能看出，当P_t较小为10 W时，系统能效消失的R_min门限更高，约为0.7，而当P_t更大时，门限约为0.4，这也与之前能效降至零的说法一致。图 3(b)分析了在不同初始能量值Q_e约束条件下的能源效率性能对比。首先，当Q_e=0时，次用户发射机ST完全依赖能量采集以满足最低吞吐量约束R_min，能量效率随R_min的增加而增加，该结果与图 3(a)中的分析结果一致。可以看到，能量效率随剩余能量Q_e的增加而提高。其原因在于，当Q_e增加时，需要耗费在采集能量阶段的时间更少，而同一时隙分配给传输数据的时间则会增加，从而可有效降低传输功率和总耗能。最后，当Q_e继续增加并能满足R_min约束需求，次用户发射机无需对采集能量进行时间分配而直接进行数据传输，能量效率将不再发生变化。

在实际应用中，需要根据不同的工作场景和指标需求，进行相对合理的吞吐量阈值的选择以满足相应的QoS保证，同时在优化问题中提出相应的约束条件。由于吞吐量和能量效率之间存在相互影响，一般来说，一个实际系统不能对这2个目标同时进行最大化考虑，必须进行权衡。因此：a)对于需要进行长时间工作的自供电应用场景，如无线传感网络等，则只需基于考虑满足基本QoS保证的吞吐量约束，再基于此来解决能量效率最大化问题；b)当无线网络需要尽可能大的系统总吞吐量时，则将系统吞吐量最大化的作为优化目标，而不需将能量效率目标作为主要问题。因此，必须依照具体应用场景来进行吞吐量和能量效率方面的权衡。

4 结论

笔者对Underlay模式下射频能量收集认知无线网络的能源效率最大化问题进行了建模和求解。针对不同的实际应用和工作场景需求进行适合的吞吐量阈值选择以满足相应的QoS需求，并同时反映到优化问题中相应的约束条件中去。基于ST保留有上一时隙传输后的剩余能量作为初始能量的假设，对节能传输和服务质量之间的关系进行了权衡。并基于Dinkelbach等方法得到优化算法，对传输时间和发射功率进行联合优化，求得了最优传输时间和发射功率，达到次用户网络能量效率最大化。仿真实验结果表明，能源效率优化和吞吐量需求之间存在相互竞争的关系，同时发现，主用户网络场景的设置和次用户供电电池初始能量等因素，会对射频能量收集认知无线网络的能量效率和QoS保证产生较大影响。