b. 重庆医科大学 附属儿童医院 放射科, 重庆 400000
b. The Department of Radiology, Children's Hospital Affiliated to Chongqing Medical University, Chongqing 400000, P. R. China
骨龄检测是评估儿童青少年生长发育、内分泌和新陈代谢问题的一种常见的临床手段,通过对左手X光片的骨成熟度进行评估获得[1-2]。由于人工评估方式耗时、主观性强,因此,基于计算机技术的骨龄自动评估引起了广泛关注。骨龄评估过程中首先需要对输入X光片进行预处理,包括背景抑制,放射标记、杂质和噪声的去除[3],这些无关因素会影响骨龄评估的准确性。预处理主要分为以下几个步骤:图像增强、手骨分割和图像归一化,其中手骨分割是影响骨龄评估精度与稳定性的重要步骤。手骨图像中的感兴趣区域(ROI, region of interest)是骨龄诊断中关注的有用区域,而ROI的分割也是医学图像分割研究的难点[4]。由于医学图像的复杂性和特殊性,去除骨龄X射线图像中的无关因素,从背景中实现手骨区域的定位与提取极其困难和复杂。
目前手骨分割的方法主要分为传统方法和基于深度学习的方法。文献中常用的传统方法包括阈值法、区域法和边界法[5-6]。仅使用图像灰度特征,忽略了图像的空间结构信息,导致阈值分割方法存在局限性[7];而区域生长和边缘检测容易造成欠分割和过分割。这3种方法必须结合使用才能产生较好的分割结果[8-9]。由于手骨图像包含大量软组织,部分前景与背景灰度差异较小,导致传统分割方法的鲁棒性较差。杨莉等[10]利用边缘检测算子结合形态学操作提取手骨边缘,但结果存在欠分割和大量伪边缘。Lee等[11]和胡鸿婷等[12]利用Otsu结合形态学获取手形二值图像,结果鲁棒性较差。Su等[13]利用直方图提取手形,指骨近端出现大量缺失。Simu等[14]通过实验比较基本分割算法(如Otsu、最大熵阈值分割、聚类等)和改进后的分割算法(如多级阈值分割等)用于手骨分割的性能,
实验结果表明这些方法都会造成部分骨骼信息的缺失。自从深度学习技术成功应用于视网膜血管的分割后[15],深度神经网络开始被广泛应用于医学图像的分割。Lee等[16]使用LeNet-5网络自动定位手形区域,然后创建手形标记,实现手骨分割。但是大部分手形掩码标记需要人工进行填充和提取。在Kaggle平台上的全自动骨龄识别比赛中,Iglovikov等[17]使用U-Net网络分割手骨。但是该方法中的标签制作和网络训练都非常耗时且复杂。训练过程中需要手动剔除分割效果不好的图像进行反复训练,对于最后预测结果中分割质量不佳的图片也需要再次进行手动处理。总之,相比传统分割方法的简单性和普适性,利用神经网络完成手骨分割复杂度较高,耗时长,如何选择网络结构也是一大难题。
考虑以上因素,提出一种复杂度低且自动处理能力强的手骨分割方法。在传统阈值分割方法的基础上,结合机器学习中的Softmax回归模型拟合最佳分割阈值,再利用区域生长法提取完整手形。该方法弥补了传统分割方法鲁棒性差的缺陷,也避免了使用神经网络带来的复杂性。实验证明Softmax回归模型拟合的阈值稳定可靠,基于该阈值取得了理想的分割结果;在100张测试集上的平均分割准确率为97%,具有较好的鲁棒性,可以完成自动化的手骨分割处理。
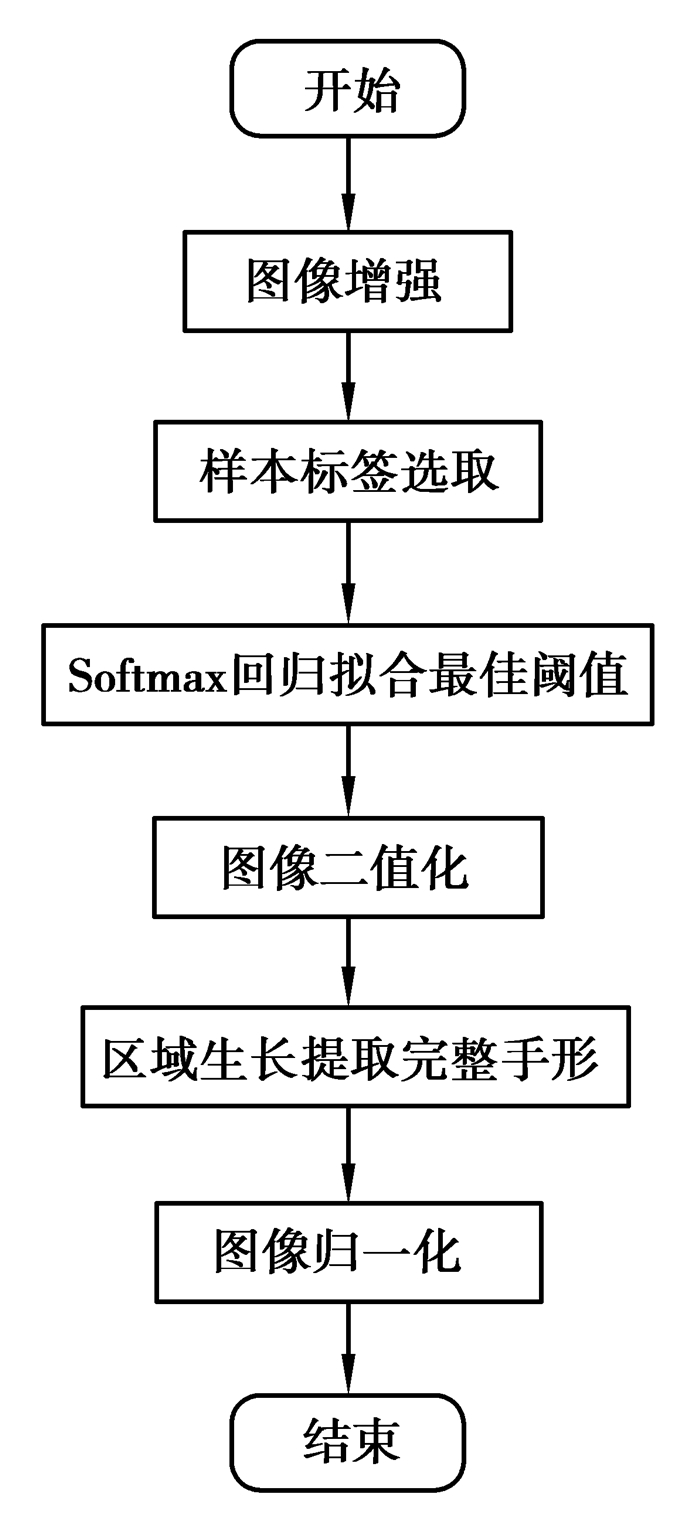
1 基于Softmax回归模型的手骨分割Softmax回归是线性回归在多分类问题上的扩展,主要用于处理多分类问题。研究将不同图片的最佳阈值作为分类类别,将直方图作为特征进行训练,用Softmax回归模型预测同类型图片的最佳阈值。通过最佳阈值对图像进行二值化处理,再使用区域生长法提取手形,归一化处理后即可完成手骨分割。实验流程如图 1所示。
|
图 1 实验方法流程图 Fig. 1 The flow chart of experimental method |
由于采集的手骨图像是3颜色通道的RGB彩色图像,所以首先把该手骨图像转化为灰度图像以方便进行二值化分割。然后采用中值滤波去除手骨图像中的部分噪声,如果仍然有小斑块噪声,采用核为7×7的开运算消除小斑块。
1.2 Softmax回归模型拟合最佳阈值 1.2.1 Softmax回归模型图像直方图是对一幅图像灰度分布的统计描述,图像灰度级范围为0~255。将每个灰度级上的像素个数作为特征,所以每幅图片有256个特征。类标签为最佳阈值,所以一共有256个分类。假设有m个训练样本,样本集合则为
| $ A = \left\{ {({x^{(1)}}, {y^{(1)}}), ({x^{(2)}}, {y^{(2)}}), \cdots , ({x^{(m)}}, {y^{(m)}})} \right\}, $ | (1) |
其中:x(i)为输入特征,x(i)∈Rn+1(n=255);y(i)∈{1, 2, …, k}为类标签(k=256)。每个样本估计其所属的类别概率为P(y=j|x)(j=1, …, k)。根据广义线性模型,推导出其假设函数如下[18-19]
| $ \begin{array}{l} {\mathit{\boldsymbol{h}}_\mathit{\boldsymbol{w}}}({x^{(i)}}) = \left[ {\begin{array}{*{20}{c}} {P({y^{(i)}} = 1|{x^{(i)}};\mathit{\boldsymbol{w}})}\\ {P({y^{(i)}} = 2|{x^{(i)}};\mathit{\boldsymbol{w}})}\\ \vdots \\ {P({y^{(i)}} = k|{x^{(i)}};\mathit{\boldsymbol{w}}) } \end{array}} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{{\sum\limits_{j = 1}^k {{e^{\mathit{\boldsymbol{w}}_j^{\rm{T}}{x^{(i)}}}}} }}\left[ {\begin{array}{*{20}{c}} {{e^{\mathit{\boldsymbol{w}}_1^{\rm{T}}{x^{(i)}}}}}\\ {{e^{\mathit{\boldsymbol{w}}_2^{\rm{T}}{x^{(i)}}}}}\\ \vdots \\ {{e^{\mathit{\boldsymbol{w}}_k^{\rm{T}}{x^{(i)}}}}} \end{array}} \right], \end{array} $ | (2) |
hw(x(i))表示第i个样本的预测函数,估计x的每种分类结果出现的概率。hw(x(i))输出的这个k维向量表示对k个类标签估计的概率值。
| $ \mathit{\boldsymbol{w}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{w}}_1^{\rm{T}}}\\ {\mathit{\boldsymbol{w}}_2^{\rm{T}}}\\ \vdots \\ {\mathit{\boldsymbol{w}}_k^{\rm{T}}} \end{array}} \right]。$ | (3) |
由于每张图片尺寸大小、像素值分布不同,得到的直方图差异较大,所以可能导致模型在拟合数据时出现较大偏差。即使模型在训练集上的拟合效果好,也不具有泛化能力,所以需要对直方图进行归一化处理。将每个灰度等级上的像素个数除以所有灰度级上像素总数最多的个数,如公式(4)所示
| $ x_j^{(i)} = \frac{{x_j^{(i)}}}{{\max {x^{(i)}}}}, $ | (4) |
xj(i)为第i个训练数据灰度级为j的像素个数, maxx(i)为灰度级上像素总数最多的像素个数。
1.2.2 Softmax回归求解Softmax回归算法在进行训练时是对其损失函数求极大似然估计,可采用梯度下降法或牛顿法进行求解。Softmax回归算法的损失函数如公式(5)所示
| $ J\left( \mathit{\boldsymbol{w}} \right) = - \frac{1}{m}\left[ {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^k {T{{({y^{(i)}})}_j}\cdot{\rm{log}}\frac{{{e^{\mathit{\boldsymbol{w}}_j^{\rm{T}}{x^{(i)}}}}}}{{\sum\limits_{l = 1}^k {{e^{\mathit{\boldsymbol{w}}_l^{\rm{T}}{x^{(i)}}}}} }}} } } \right]。$ | (5) |
该损失函数衡量真实类别与预测类别的相似性,训练模型参数的目标是使J(w)最小化。上式中T(y(i))j为指示函数,当y(i)属于第j类时T(y(i))j=1,否则为0。
| $ J\left( \mathit{\boldsymbol{w}} \right) = - \frac{1}{m}\left[ {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^k {T{{({y^{(i)}})}_j}\cdot{\rm{log}}\frac{{{e^{{\mathit{\boldsymbol{w}}}_j^{\rm{T}}{x^{(i)}}}}}}{{\sum\limits_{l = 1}^k {{e^{{\mathit{\boldsymbol{w}}}_j^{\rm{T}}{x^{(i)}}}}} }}} } } \right] + \frac{\lambda }{2}\sum\limits_{i = 1}^k {\sum\limits_{j = 0}^n {\mathit{\boldsymbol{w}}_{ij}^2} } 。$ | (6) |
这时损失函数变为凸函数,有唯一解且Hessian矩阵可逆,可以采用梯度下降法或牛顿法求解。对J(w)求偏导
| $ {\nabla _w}_jJ\left( \mathit{\boldsymbol{w}} \right) = - \frac{1}{m}\sum\limits_{i = 1}^m {[{x^{(i)}}((\mathit{\boldsymbol{T}}{{({y^{(i)}})}_j} - P({y^{(i)}} = j|{x^{(i)}};\mathit{\boldsymbol{w}}))] + \lambda {\mathit{\boldsymbol{w}}_j}, } $ | (7) |
这里采用梯度下降法,结合训练数据对权重w进行更新,求出w的最优解,如公式(8)所示
| $ {\mathit{\boldsymbol{w}}_j} = {\mathit{\boldsymbol{w}}_j} + \alpha {\nabla _\mathit{\boldsymbol{w}}}J\left( \mathit{\boldsymbol{w}} \right), $ | (8) |
α为学习率。
训练完成后,用w对测试数据做前向传播,每个测试数据得到k个值,选取其中最大值所对应的阈值作为模型预测的最佳阈值。
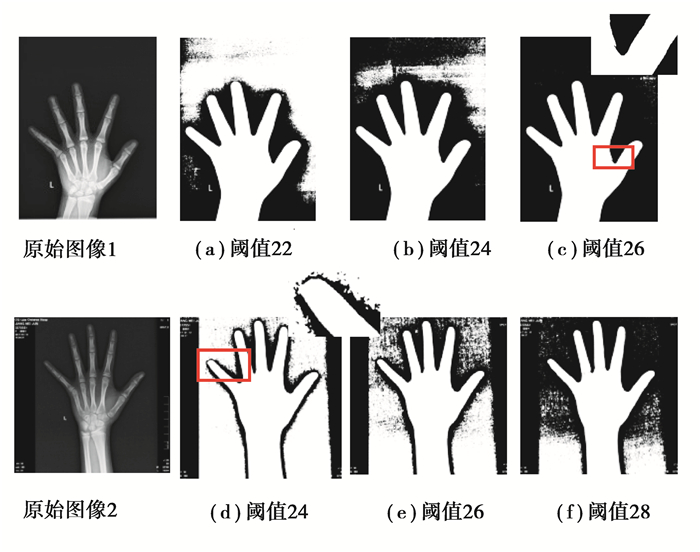
1.2.3 最佳阈值选取在训练Softmax回归模型拟合最佳分割阈值前,需要手动选取使得分割效果最好的阈值作为模型训练的标签。在最佳阈值选取过程中,经过实验测试发现,最佳阈值大部分低于图像像素均值。所以在像素均值2边以阈值间隔为2分别生成20幅不同的二值图像,根据二值图像的分割效果找出最佳阈值。实验测试结果显示,选取的阈值越大于最佳阈值,欠分割(分割的手形不完整)越严重,越小于最佳阈值则过度分割(手形与背景粘连)越严重;所以若二值图像在最大阈值情况下还存在过度分割,则将阈值增大再从中选取;若最小阈值情况下图像二值图存在欠分割,则将阈值减小再从中选取最佳阈值。最佳阈值的选取有2个标准:1)能对手形区域进行正确分割;2)手形没有失去过多细节。如图 2所示,对于2幅灰度图像,图(a)和图(e)中手形与背景只是恰好分离;图(c)手形边缘不平滑;图(d)指骨远端边缘与背景相连(红色矩形框标注,细节图如图像右上角所示)。而图(b)与图(f)手形与背景完全分离且没有缺失细节特征。因为模型是概率预测,如果预测值有偏差,那么预测结果与最佳阈值之间的误差至少为1。所以为考虑模型的拟合误差,选取(b)图和(f)图的阈值作为2幅图像的最佳阈值。
|
图 2 最佳阈值选取 Fig. 2 Selection of the optimal threshold |
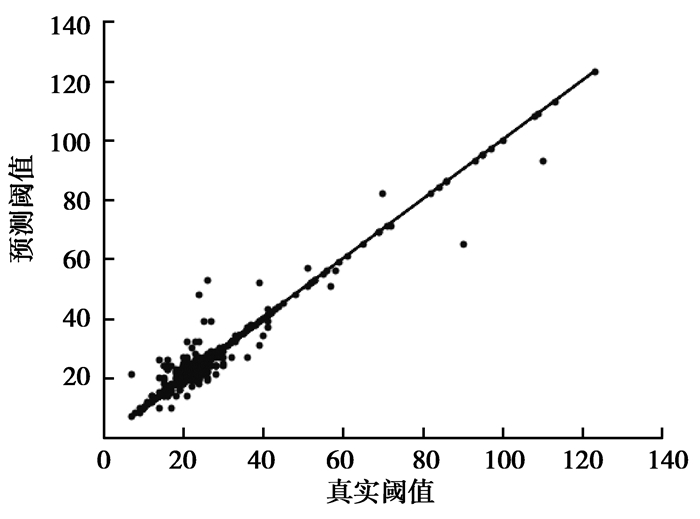
训练过程中,λ和α的初始值设置为0.1,通过迭代20万次后达到收敛。模型预测出的最佳阈值与真实最佳阈值之间的关系如图 3所示。
|
图 3 数据拟合图 Fig. 3 Data fitting diagram |
图中横坐标为人工选取的最佳阈值,纵坐标为模型预测出的最佳阈值。从图中可以看出,所选取的测试样本的所有最佳阈值都小于140,大部分阈值集中在10—40范围内。图中预测值围绕真实值波动,只有少部分预测值偏离直线。这是因为样本数据中有少量图片存在大量无关因素,如不相关的骨骼、首饰、边框等干扰信息,导致这些样本与其余样本区别太大,使得在拟合过程中出现偏差。但这种图片数量较少,并且实验过程中这种图片也能够通过预测出的阈值进行分割。从图中可以看出数据整体的拟合效果较好,没有出现过拟合的情况,说明模型的预测结果可靠。
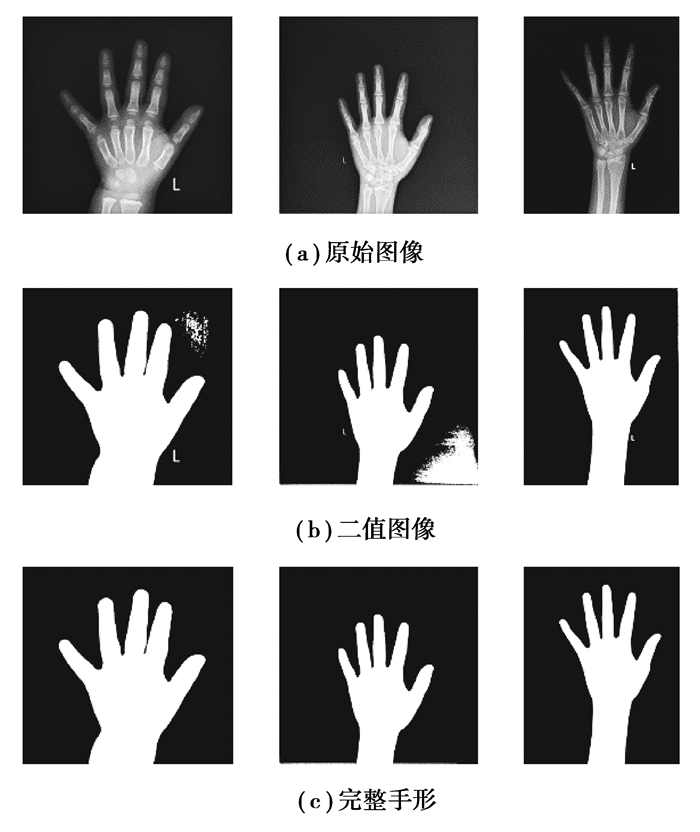
1.3 图像二值化与手形提取模型训练完毕后,统计每张图片的直方图,通过模型拟合即可预测出每张手骨图像的最佳分割阈值;并利用拟合的最佳阈值对图像进行二值化操作。如图 4(b)所示,二值化后的图像存在非手骨轮廓区域和噪声。
|
图 4 图像二值化与手形提取 Fig. 4 Image binarization and hand extraction |
图像分割过程中,对ROI的提取常采用区域生长法,最大连通区域法或边缘检测法。由于二值图像的手形区域不一定是最大连通域或最大轮廓,所以为了得到较好的分割率,采用区域生长法提取手形。该方法可以对具有相似性质的区域进行分割,只关注ROI,手形周围的噪声对提取没有影响。该方法根据选取的初始种子点和阈值生成连通区域[20-21]ROI,其算法描述如下
1) 将图片的中心像素点作为种子点;
2) 创建与图像大小相同的矩阵V,并将每个点置为False;
3) 以手形轮廓边缘为生长停止条件,在手形区域内生长,对手掌内像素值不为0的点(i, j)进行标记,标记为V[i, j]=True;
4) 遍历矩阵V,若V[i, j]≠True,即该点在手形区域外, 这时将原图对应点的值改为0,提取出完整手形。手形提取结果如图 4(c)所示。
1.4 图像归一化因为实验中使用的所有数据样本大小不一,为了统一样本,方便后期骨龄的自动识别,将分割后的手骨图像尺寸归一化为256×256。具体步骤如下:
1) 获得手形外接矩形的长和宽并标记为H、W;
2) 裁掉多余的边缘使手形居中;
3) 比较H、W,通过填充边缘使整个图形为正方形,扩展长度为|H-W|/2,这样保证图像缩小为256×256时不会对原图进行拉伸变换。
2 实验结果与分析本实验中所使用的骨龄X射线图像总计500张,其中训练集400张,测试集100张。年龄分布为1—18岁,图片大小各异,全部由重庆医科大学附属儿童医院放射科扫描获得,所有图片全部匿名化处理并已获得授权。研究实验环境为CPU@1.60GHz,Windows 10,Python2.7,OpenCV3。训练集和测试集从每个年龄段中随机选择,确保实验数据的选取具有多样性和泛化性。实验结果如图 5所示(随机从测试集中不同年龄段选取6张图像进行展示)。手骨图像类型包含:1)含有干扰因素,包括不相干的手骨、文字、边框(如图 5中第1、5、6列图像);2)手骨图像的位置不正(如图 5中第2、6列图像);3)低对比度(如图 5中第3列图像);4)只含有放射标记(如图 5中第4列图像)。

|
图 5 基于Softmax回归模型的手骨分割 Fig. 5 Hand bone segmentation based on Softmax regression |
从图 5中可以看出通过Softmax回归拟合的最佳阈值可以正确分离手骨与背景,且手骨的细节信息保存完整,利用区域生长法即可提取完整手形。而且对于一些特殊的骨龄X射线图像,如存在大量干扰因素,手骨位置不正或手骨区域对比度低,该方法也能取得较好的分割结果。
为了测试算法的分割精度,基于上述测试集,将softmax回归拟合最佳阈值的分割方法与文献中常用的阈值分割方法:Otsu、直方图平均、最大信息熵进行比较,部分实验结果如图 6所示。图 6中用红色矩形框标注部分表示完全不能分割出手骨或分割效果不理想的区域,如欠分割、过分割和手形边缘不光滑等。从图 6的实验结果可以看出,Otsu分割效果最差。欠分割严重,指骨信息大量丢失,基本不能提取出完整手形;最大熵分割效果较差,部分手骨图像完全不能分割(如图(c)中第3幅图像所示),少部分图像也存在欠分割和过分割;直方图均值分割结果比Otsu和最大熵阈值分割结果好,但大部分手形边缘不平滑。综上,这3种分割方法都会造成部分图像完全不能分割,且欠分割的情况也较为严重。据统计,测试集中Otsu、最大熵、直方图均值完全不能分割的图像数量分别为40、19、1。而基于Softmax回归分割方法的所有图像都能完成手骨的完整提取,欠分割和过分割较少,分割结果最理想。

|
图 6 4种分割方法的手形二值图像结果比较 Fig. 6 Comparison of hand masks segmentation results under four segmentation methods |
为了更加客观地评价各方法的分割效果,采取定量的方式计算分割图像的性能指标。分割准确率采用最常见的指标相似系数DSC(dice similarity coefficient)[22]进行定量评价,分割金标准为手骨的GT(ground truth)图像。此外,还计算了分割图像整体的过分割率和欠分割率[23]。
DSC值衡量GT图像与分割图像的相似度,公式如下
| ${\rm{DSC}} = \frac{{2\left| {X \cap Y} \right|}}{{\left| X \right| + \left| Y \right|}}, $ | (9) |
其中X代表GT图像,Y表示分割结果图像过分割率是指分割图像在GT图像参考面积之外的像素点的比率,公式如下
| $ OX = \frac{{{O_s}}}{{X + {O_s}}}, $ | (10) |
其中Os表示不应包含在分割结果中的像素点个数。
欠分割率是分割图像在GT图像参考面积中欠缺的像素点的比率,公式如下
| $ UX = \frac{{{U_s}}}{{X + {O_s}}}, $ | (11) |
Us表示本应包含在分割结果中实际却不在分割结果中的像素点个数。
在100张测试集上的计算结果如表 1所示,所有结果取平均值。
| 表 1 3种分割方法在测试集上的平均DSC值、过分割率和欠分割率 Table 1 The average DSC over-segmentation rate and under-segmentation rate of the four segmentation methods applied on the testing set |
由表 1可以看出,使用Softmax回归方法得到的DSC值最高,平均分割准确率为0.97,欠分割率最低,过分割率比Otsu和直方图均值法稍高,但都接近于0。过分割率稍高的原因是在选取最佳阈值时,一旦预测出的最佳阈值低于人工选取的最佳阈值,用预测值对图像进行二值化后可能会导致手形与背景相连从而产生过分割。这种情况可以考虑在保证图像分割质量的前提下,选取较大的阈值作为最佳阈值而得到改善。3种传统阈值分割方法中直方图均值方法的DSC值最高;Otsu的DSC值最低,且欠分割严重;最大熵阈值的过分割率最高。综合分析,通过Softmax回归拟合阈值并结合区域生长分割手骨的方法无论从主观还是客观的角度都优于其他3种方法,分割效果最理想,具有较好的鲁棒性。
3 讨论笔者提出了通过Softmax回归模型拟合最佳阈值进行图像分割的方法,并成功应用于骨龄X射线图像中手骨的分割,为医学图像的分割提供了新的思路。使用Softmax回归模型进行训练前,通过对输入参数-图像直方图进行归一化处理,有效防止了回归模型在拟合最佳阈值时出现漂移值的情况,提高了模型的拟合能力。最大的亮点在于将阈值的拟合问题变为分类问题,使得最终预测的结果在一定范围内,相对于线性回归模型来说能极大地减小误差并且提高数据的泛化能力。实验结果表明该方法比传统的阈值分割方法能获得更理想的手骨分割结果。传统的阈值分割最大的缺陷就是欠分割率高,鲁棒性差,在医学图像的分割应用上具有一定的局限性。而使用Softmax回归模型克服了这个缺陷,在拟合的最佳阈值分割基础上结合基于区域的分割,与单一的阈值分割方法相比有效降低了欠分割率。与深度学习的方法相比,Softmax回归模型比深度神经网络更加简单,算法的时间复杂度降低,数据处理更加快捷。且最重要的一点是基于神经网络的分割方法对手骨图像的边缘识别效果差,容易造成误分割,而本方法不存在此现象。另外,研究方法对于复杂的手骨图像也表现出较好的分割性能,说明该方法具有抗干扰能力和鲁棒性。由于方法具有实时性和较高的精确度,所以该算法可用于临床手骨图像的分割,可以快速准确的为骨龄识别研究提供大量可靠的预处理数据样本。
算法存在的不足是特征参数的处理还有待改进。因为参数之间数值上差距过大,所以改善参数的分布可以有效提高算法性能。研究将阈值的拟合问题转化为分类问题所使用的算法可以不限于所使用的Softmax回归,还可以是其他分类算法。作者的下一步工作是尝试使用更多分类算法并且结合机器学习中的集成学习方法进一步提高分割的准确率。
| [1] |
Spampinato C, Palazzo S, Giordano D, et al. Deep learning for automated skeletal bone age assessment in X-ray images[J]. Medical Image Analysis, 2017, 36: 41-51. DOI:10.1016/j.media.2016.10.010 |
| [2] |
Bunch P M, Altes T A, Mcilhenny J, et al. Skeletal development of the hand and wrist:digital bone age companion a suitable alternative to the greulich and pyle atlas for bone age assessment?[J]. Skeletal Radiology, 2017, 46(6): 785-793. DOI:10.1007/s00256-017-2616-7 |
| [3] |
Gertych A, Zhang A, Sayre J, et al. Bone age assessment of children using a digital hand atlas[J]. Computerized Medical Imaging and Graphics, 2007, 31(4-5): 322-331. DOI:10.1016/j.compmedimag.2007.02.012 |
| [4] |
王超, 王浩, 王伟, 等. 基于优化ROI的医学图像分割与压缩方法研究[J]. 重庆邮电大学学报(自然科学版), 2015, 27(02): 279-284. WANG Chao, WANG Hao, WANG Wei, et al. Research on medical image segmentation and compression method based on optimized ROI[J]. Journal of Chongqing University of posts and Telecommunications:Natural Science Edition, 2015, 27(02): 279-284. (in Chinese) |
| [5] |
Khan M W. A survey:image segmentation techniques[J]. International Journal of Future Computer and Communication, 2014, 3(2): 89-93. |
| [6] |
Zuva T, Olugbara O, Ojo S, et al. Image segmentation, available techniques, developments and open issues[J]. Canadian Journal on Image Processing and Computer Vision, 2011, 2(3): 20-29. |
| [7] |
陈乔松, 冉会琼, 闫亚星, 等. 基于数据场和水平集演化的图像分割[J]. 重庆邮电大学学报(自然科学版), 2018, 30(2): 257-264. CHEN Qiaosong, RAN Huiqiong, YAN Yaxing, et al. Image segmentation based on data field and level set evolution[J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2018, 30(2): 257-264. (in Chinese) |
| [8] |
Li C, Wang X, Eberl S, et al. Supervised variational model with statistical inference and its application in medical image segmentation[J]. IEEE Transactions on Biomedical Engineering, 2015, 62(1): 196-207. DOI:10.1109/TBME.2014.2344660 |
| [9] |
Munoz X, Freixenet J, Cufi X, et al. Strategies for image segmentation combining region and boundary information[J]. Pattern Recognition Letters, 2003, 24(1-3): 375-392. DOI:10.1016/S0167-8655(02)00262-3 |
| [10] |
杨莉, 王运琼, 胡蓉蓉, 等. 骨龄自动评测系统中骨骼边缘提取方法研究[J]. 计算机应用与软件, 2009, 26(5): 266-269. YANG Li, WANG Yunqiong, HU Rongrong, et al. Study on bone edge extraction in automatic bone age measurement system[J]. Computer Applications and Software, 2009, 26(5): 266-269. (in Chinese) DOI:10.3969/j.issn.1000-386X.2009.05.088 |
| [11] |
Lee S, Choi M, Choi H S, et al. FingerNet: deep learning-based robust finger joint detection from radiographs[C]//IEEE Biomedical Circuits and Systems Conference. Atlanta, USA: IEEE, 2015: 1-4. https://ieeexplore.ieee.org/document/7348440
|
| [12] |
胡婷鸿, 火忠, 刘太昂, 等. 基于深度学习实现维吾尔族青少年左手腕关节骨龄自动化评估[J]. 法医学杂志, 2018, 34(1): 27-32. HU Hongting, HUO Zhong, LIU Taiang, et al. The automatic assessment of bone age of the left wrist joint of uygur adolescents was realized based on deep learning[J]. Journal of Forensic Medicine, 2018, 34(1): 27-32. (in Chinese) DOI:10.3969/j.issn.1004-5619.2018.01.006 |
| [13] |
Su L, Fu X, Zhang X, et al. Delineation of carpal bones from hand X-ray images through prior model, and integration of region-based and boundary-based segmentations[J]. IEEE Access, 2018, 6: 19993-20008. DOI:10.1109/ACCESS.2018.2815031 |
| [14] |
Simu S, Lal S. A study about evolutionary and non-evolutionary segmentation techniques on hand radiographs for bone age assessment[J]. Biomedical Signal Processing and Control, 2017, 33: 220-235. DOI:10.1016/j.bspc.2016.11.016 |
| [15] |
Liskowski P, Krawiec K. Segmenting retinal blood vessels with deep neural networks[J]. IEEE Transactions on Medical Imaging, 2016, 35(11): 2369-2380. DOI:10.1109/TMI.2016.2546227 |
| [16] |
Lee H, Tajmir S, Lee J, et al. Fully automated deep learning system for bone age assessment[J]. Journal of Digital Imaging, 2017, 30(4): 427-441. DOI:10.1007/s10278-017-9955-8 |
| [17] |
Halabi S S, Prevedello L M, Kalpathy-Cramer J, et al. The RSNA pediatric bone age machine learning challenge[J]. Radiology, 2019, 290(2): 498-503. DOI:10.1148/radiol.2018180736 |
| [18] |
周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 53-57. ZHOU Zhihua. Machine learning[M]. Beijing: Tsinghua University Press, 2016: 53-57. (in Chinese) |
| [19] |
赵志勇. Python机器学习算法[M]. 北京: 电子工业出版社, 2017: 27-32. ZHAO Zhiyong. Python machine learning algorithm[M]. Beijing: Electronic Industry Press, 2017: 27-32. (in Chinese) |
| [20] |
Adams R, Bischof L. Seeded region growing[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994, 16(6): 641-647. DOI:10.1109/34.295913 |
| [21] |
Jeevakala S, Brintha T, Rajeswaran R. A novel segmentation of cochlear nerve using region growingalgorithm[J]. Biomedical Signal Processing, 2018, 39: 117-129. DOI:10.1016/j.bspc.2017.07.014 |
| [22] |
Chang H, Zhuang A H, Valentino D J, et al. Performance measure characterization for evaluating neuroimage segmentation algorithms[J]. Neuro Image, 2009, 47(1): 122-135. |
| [23] |
Hachouf F, Seghir Z A, Zeggari A. A generic methodology for image segmentation evaluation[C]//2nd International Conference on Information & Communication Technologies. Damascus, Syria: IEEE, 2006, 1: 1794-1799. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1684658
|
 2019, Vol. 42
2019, Vol. 42


