2. 合肥学院 电子信息与电气工程系, 安徽 合肥 230601
2. Department of Electronic Information and Electrical Engineering, Hefei University, Hefei 230601, Anhui, P. R. China
回转窑由于其大型烧结能力,是冶金、环保、化工和水泥等领域的核心设备。输出熟料的品质直接受制于其烧成带的温度,因此常被作为被控变量,应用于当前大多数水泥回转窑的自动或手动控制策略中[1]。然而,窑内恶劣的环境无法精确测量烧成带温度。近年来,通过对水泥回转窑烧成带火焰图像进行燃烧状况认知的策略被广泛研究[2-7]。文献[2-3]基于图像分割技术,获取烧成带火焰图像中的温度场和熟料烧结状态信息,以识别烧成状态;文献[4-7]在预处理环节采用Gabor滤波器提取纹理特征,面向具有不同纹理特性的感兴趣区域(火焰区域和物料区域),增强其可区分性,继而分别提取其色彩、全局形态和局部形态特征,实现火焰图像燃烧状况的融合识别,避免图像分割技术的缺陷。然而,受制于图像质量和识别方法等客观因素,以及不同层次的特征表征了认知对象的不同分析层面,异构的特征则表征了不同的分析视角,如何获取有确定映射关系的多层次和多样性特征,以适用于海量火焰图像样本尚需深入研究。
人工看火模式从模式识别的角度可归结为:操作员借助丰富的经验、反复比对由整体到局部多层次差异化视觉特征、实时评测多态认知结果的可信度,从而判别燃烧状况。传统基于机器视觉的燃烧状况识别模型可归结为一个具有不确定火焰图像输入和不确保燃烧状况输出的开环认知系统,其不变的特征空间和分类准则,以及认知结果的后验评测特性,与人实时评测认知结果可信度自寻优调节特征空间及其分类准则的思维存在显著差异。文献[4-9]分别介绍了反馈机制在水泥回转窑燃烧状况识别、青梅品级分类、人体健康评测等领域的有效应用。目前具有反馈机制的闭环认知系统模型的研究仍处于探索阶段。
近年来,随着神经网络训练算法的本质改变,以深度学习为代表的人工智能理论研究与应用受到了前所未有的关切[10-12]。卷积神经网络(CNN, convolutional neural networks)中卷积池化的交替运算可以提取由浅到深的语义特征,这与人类面向不同认知对象由全局到局部获取分析认知信息的渐进认知模式保持一致[13-14]。然而,试凑的网络架构所生成的特征空间中差异认知信息不明确,开环认知模式下的特征空间和分类准则一旦构建不再更新,这与人类认知思维存在显著差异,加之softmax层泛化能力的不足,以及深层神经网络中面向同一输入的不同卷积核操作必然使得输出特征空间冗余。因此,当面对奇异样本或分类面附近的相似样本时,学习模型的可达性和可信性恶化。
未来5年迁移学习将成为人工智能领域的关注重点。其采用多任务共享知识,并根据新任务更新学习模型的机制[15-16],与人类认知策略一致。然而,认知结果可信度的实时评测尚需深入研究。因此,为了克服已有燃烧状况识别方法中模型泛化能力的不足,以及深层神经网络结构的缺陷,模仿人类认知模式,基于已有工作基础[4-7]借鉴迁移学习和闭环控制理论思想,探索了一种基于深度迁移学习的回转窑燃烧状况智能感知机制和计算方法。首先,采用自优化调节的机制构建卷积神经网络的架构(ASCNN, adaptive structure convolutional neural networks),建立火焰图像由全局到局部具有确定映射关系的非结构化动态特征空间。其次,针对特征空间的冗余,基于特征可区分性测度指标和变精度粗糙集理论,从信息论的角度在不确定信息条件下,面向可区分性约束条件,建立自优化特征表征的回转窑燃烧状况认知决策信息系统,增强燃烧状况非结构化简约可分特征空间的可解释性。再次,将简约全连接特征向量送至具有万局逼近能力的随机配置网络分类器(SCN, stochastic configuration networks),建立火焰图像燃烧状况的分类决策准则。最后,模仿人类反复推敲比对的认知模式,构建语义误差熵评测指标,实时量测火焰图像燃烧状况认知结果的不确定性,构建基于不确定认知结果测度指标约束的动态迁移学习机制,实现燃烧状况多层次差异化特征空间及其分类准则的自寻优调节和重构。针对某水泥厂2#回转窑的火焰图像数据开展了实验研究,实验结果表明了所构建的基于深度迁移学习的火焰图像燃烧状况智能感知模型较已有文献方法和图像分割方法对于水泥回转窑燃烧状况精确认知的可行性和优越性。
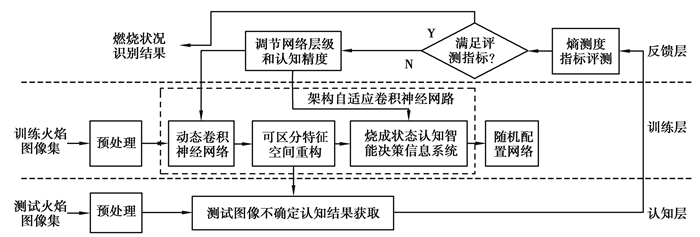
1 基于深度迁移学习的燃烧状况智能感知模型如图 1所示,提出的基于深度迁移学习的火焰图像燃烧状况智能感知模型采用3层实时信息交互结构。
|
图 1 基于深度迁移学习的燃烧状况智能感知模型构建 Fig. 1 Construction of intelligent cognitive model of burning state based on deep transfer learning |
1) 训练层面向预处理后的火焰图像,基于反馈层熵测度指标下达的网络层级,通过迁移学习共享较深层特征空间知识,动态增加卷积层构建更深层次特征空间,基于可区分性测度指标和变认知精度认知智能决策信息系统实现火焰图像变精度简约差异化特征空间获取,送入随机配置网络获取燃烧状况的认知结果,为认知层提供简约差异化特征空间和分类准则的构建标准。
2) 认知层基于训练层提供的构建标准,获取特定网络层级和认知精度条件下测试火焰图像燃烧状况的不确定认知结果,为反馈层的熵测度指标提供启发式反馈信息。
3) 反馈层实时评测测试火焰图像不确定燃烧状况认知结果的可信度,针对不满足的样本通过迁移学习自寻优调节卷积网络层级和认知精度,构建燃烧状况更深层次差异化特征空间及其分类准则以再认知。
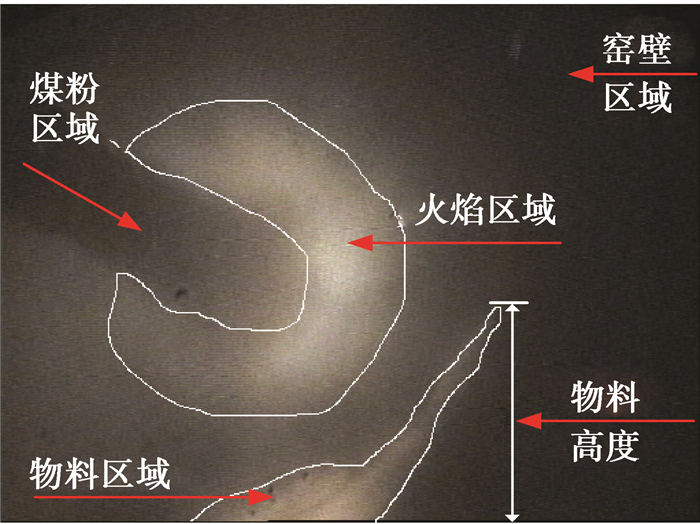
2 基于深度迁移学习的水泥回转窑燃烧状况智能感知算法 2.1 水泥回转窑烧结过程火焰图像回转窑烧成带火焰图像如图 2所示,基于文献[6]可构建自适应的Gabor滤波器组,对感兴趣区域滤波使得其更具可区分性。训练火焰图像的尺寸在预处理后被归一化为256×256。
|
图 2 烧成带火焰图像 Fig. 2 A burning zone flame image |
CNN采用卷积池化交叉的多层网络架构,提取从浅到深的语义特征。相邻卷积池化层具有相同的特征图个数,视为一个网络层级组合。设训练火焰图像集U,n为U的样本个数,采用l个交替的卷积池化层结构时,可获取训练火焰图像样本Ui∈U, i∈[1, n]的gl个特征图。在某个网络层级内,卷积核个数的增加意味着输入的多个视角表征。然而,在有限论域条件下,视角的增加使得信息量趋于饱和。因此,定义极大信息熵指标获取网络层级为l时,U的具有充分信息量的最小特征图空间Xl=[X1l, …, Xgll]T[9]
| $ \left\{ \begin{array}{l} \mathop {{\rm{max}}}\limits_{{g_l}} \;H(B({X^l})) = \mathop {{\rm{max}}}\limits_{{g_l}} \left( { - \sum\nolimits_{q = 1}^{{\delta _l}} {\frac{{\left| {{\varphi _q}} \right|}}{{\left| {{X^{l - 1}}} \right|}}lo{g_2}\frac{{\left| {{\varphi _q}} \right|}}{{\left| {{X^{l - 1}}} \right|}}} } \right), \\ {\rm{s}}{\rm{.t}}.\;\;\;\;\;\;\;0 < {\delta _l} \le {g_l} \end{array} \right. $ | (1) |
其中:H(B(Xl))为Xl的信息熵;B(Xl)={φ1, …, φδl}为Xl基于等价关系划分而成的商集。
2.3 可区分性特征空间重构深层神经网络所构建的特征空间数据结构性能与网络层级输出特征图密切相关,越多的特征图数量意味着越相似的相邻特征图。因此,为了消除冗余的特征图空间,特征图的选取应是构建深层神经网络中必不可少的一部分,以增强特征图空间的可解释性。针对网络层级为l时动态卷积网络提取的火焰图像动态特征图集合Xl,可区分性测度指标Qj评测每个特征图对多类别火焰图像的可区分能力
| $ {Q_j} = 2 \times \frac{{\sum\limits_{a = 1}^{{s_c} - 1} {\sum\limits_{b = a + 1}^{{s_c} - 1} {({\mathit{\boldsymbol{M}}_{a, j}} - {\mathit{\boldsymbol{M}}_{b, j}})\mathit{\boldsymbol{C}}_{a, b, j}^{ - 1}{{({\mathit{\boldsymbol{M}}_{a, j}} - {\mathit{\boldsymbol{M}}_{b, j}})}^{\rm{T}}}} } }}{{{s_c} \times ({s_c} - 1)}}, $ | (2) |
其中:Ma, j、Mb, j和Ca, b, j分别表示网络层级为l时,Xl的第a类火焰图像和第b类火焰图像所提取特征图集合的均值矩阵及其协方差矩阵;sc为燃烧状况类别数。基于文献[8]可构建Xl的gl个候选特征图子集[8]
| $ \left\{ {X_{{u_1}}^l} \right\}, \left\{ {X_{{u_1}}^l, X_{{u_2}}^l} \right\}, \cdots , \left\{ {X_{{u_1}}^l, X_{{u_2}}^l, \cdots , X_{ugl}^l} \right\}。$ | (3) |
特征之间的相关性是认知的关键。面向相同输入的特征图内部也可能存在冗余信息,致使识别性能恶化。信息论中的变精度粗糙集理论可以模仿人类自优化调节认知精度的模式,增强特征空间中差异认知特征的比例,以构建特定认知精度条件下的训练火焰图像认知决策信息系统Sβl={U, A, V, f},以约简特征图信息[8],其中β为认知精度;A=
机器学习模型的基本要求是它的学习能力,即通过样本学习实现表达复杂信号的能力。针对随机算法训练的多层感知机模型,由于参数的随机化使得随机权向量函数连接网络(RVFL, random vector functional-link net)无法确保其逼近能力。SCN自优化设置参数,并根据输出残差在随机输入权值和偏移的约束条件下生成新的随机基函数,确保学习模型的万局逼近能力。SCN可以等效为一个单隐层前馈神经网络
| $ \varphi (\mathit{\boldsymbol{\tilde X}}_\beta ^l, \vartheta ) = \sum\nolimits_{j = 1}^{{n_b}} {{\vartheta _j}\hbar ({w_j}\cdot\mathit{\boldsymbol{\tilde X}}_\beta ^l + {b_j}), } $ | (4) |
其中:ϑ=[ϑ1, …, ϑnb]为输出权值;
| $ {\zeta _j} = \frac{{{{(\mathit{\boldsymbol{e}}_{j - 1}^{\rm{T}}({U_i})\cdot{\mathit{\boldsymbol{A}}_j}({U_i}))}^2}}}{{A_j^{\rm{T}}({U_i})\cdot{\mathit{\boldsymbol{A}}_j}({U_i})}} - (1 - v - {\mu _j})\mathit{\boldsymbol{e}}_{j - 1}^{\rm{T}}({U_i}){e_{j - 1}}({U_i}) > 0, $ | (5) |
其中,Aj=ħj(wj·
| $ \hat \vartheta = {\mathit{\boldsymbol{A}}^\mathit{\dagger }}\mathit{\boldsymbol{O}} = {({\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}})^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{O}}, $ | (6) |
其中:A=[A1, …, Aj];A†是A的Moore-Penrose广义逆;O为训练火焰图像的输出矩阵[17]。在深层神经网络(ASCNN+SCN)的学习过程中,其参数需要迭代优化以适应输入端的多样化数据集,生成泛化的特征空间及其分类准则。笔者采用交替优化的策略调节深层神经网络参数。
在前向传播过程中,基于深层神经网络,在反馈层下达的网络层级和认知精度条件下,获取输入火焰图像的动态简约差异化特征空间。基于公式(4)-(6),逐渐增加SCN隐含层节点数,直至满足预设定的最大隐含层节点数或误差容许值,获取输出燃烧状况认知结果O。设P表示输入火焰图像集的真实类别,则不确定燃烧状况认知结果的输出误差
若SCNs预设定的误差容许值未能达到,且隐藏节点数增加至最大值时,则开始反向更新,SCN的输出误差e反向传播至输入端的误差ex为
| $ \mathit{\boldsymbol{e}}x = w({(\mathit{\boldsymbol{\hat \vartheta }} {\mathit{\boldsymbol{e}}^\mathit{\dagger }})^\mathit{\dagger }}({(\mathit{\boldsymbol{\hat \vartheta }} {\mathit{\boldsymbol{e}}^\mathit{\dagger }})^\mathit{\dagger }}(1 - {(\mathit{\boldsymbol{\hat \vartheta }} {\mathit{\boldsymbol{e}}^\mathit{\dagger }})^\mathit{\dagger }}))), $ | (7) |
这里选择sigmoid作为基函数。对ex中由Sβl压缩的元素处补充零元素,使得扩充后的向量维度与Xxl相同,采用逆映射策略将简约差异化特征图空间映射至原特征图空间大小,最后更新CNN中的参数。在一次反向更新过程完成后,前向传播过程重新启动,再次获取动态简约差异化特征空间,并重新构建SCN分类器。交替重复上述过程,直至满足SCN预设定的条件,或达到最大迭代优化次数时,输出燃烧状况认知结果。
2.5 燃烧状况不确定认知结果语义误差熵评测指标传统采用后验统计的方法无法实时评测火焰图像燃烧状况的不确定认知结果,为了模拟人类反复推敲比对的思维模式,需要构建误差评测指标,以实时评测燃烧状况认知结果的可信性,为特征空间及其分类准则的自优化调节提供量化依据,在多层次差异化简约特征空间建模的信息论与不确定燃烧状况认知结果评测的认知论之间构建等价的熵形式测度关系。
设经由预处理得到的测试火焰图像集为T,Ti∈T, i∈[1, N],在动态卷积层数为l,认知精度为β,简约差异化特征Fcl, βw的第ω次反馈认知结果为Zl, βw(Zl, βw∈[1, sc])。基于潜在语义分析[9]可将深层次高阶抽象特征Fcl, βw映射为语义空间向量fcl, βw=[fcl, β, 1w, …, fcl, β, sw]。将fcl, βw与同类别训练样本集的深层次高阶抽象特征的语义向量矩阵fcUl, βw相减,构建语义误差矩阵Kl, βw:
| $\mathit{\boldsymbol{K}}_{l, \beta }^w = {1_{{n{{T_i}}} \times 1}} \times \mathit{\boldsymbol{fc}}_{l, \beta }^w - {\mathit{\boldsymbol{fc}}_{U_{l, \beta }^w}}, $ | (8) |
其中,Ul, βw表示与Ti的燃烧状况认知结果相同类别的训练样本个数。则测试样本Ti的不确定燃烧状况认知结果语义误差熵可定义为
| $ H_{l, \beta }^w = - \frac{{\left| {\mathit{\boldsymbol{K}}_{l, \beta }^w} \right|}}{{m_{l, \beta }^w}}{\rm{lo}}{{\rm{g}}_2}\frac{{\left| {\mathit{\boldsymbol{K}}_{l, \beta }^w} \right|}}{{m_{l, \beta }^w}}, $ | (9) |
熵值越大表示测试样本的不确定燃烧状况认知结果可信性越低,需要动态增加卷积层级,在更深层次特征空间中进行燃烧状况再认知,反之亦然。
2.6 基于迁移学习的燃烧状况认知反馈调节机制传统燃烧状况认知模型可以被视为一个具有不确定火焰图像输入和不确保燃烧状况输出的开环认知系统,其不变的特征空间及其分类准则使得认知模型面向不同样本的泛化能力不足。因此,基于火焰图像不确定燃烧状况认知结果语义误差熵测度指标评测认知结果的可信度,若可信则输出作为最终认知结果,否则实时自主决策β和l,利用迁移学习实现特征空间和分类准则的自寻优反馈调节,实现火焰图像的优化再认知。自优化调节准则如下所示:
1) 若Ti的第w次燃烧状况认知结果的熵测度指标Hl, βw≤Δ(Δ是认知误差阈值),则表示参数集(βw和lw)最优适用于当前火焰图像,输出认知结果作为最终结果。
2) 若Hl, βw>Δ,表示当前不确定燃烧状况认知结果粗略符合要求,首先调节β,如果依旧无法满足阈值则增加l,利用迁移学习共享已学习的较深层次神经网络模型参数,单独训练增加的动态卷积层,在下一次反馈认知过程中挖掘可信度较低的火焰图像更深层次的认知特征,重新构建SCN以再次认知。此外,若动态卷积层级l>lmax时仍不能满足Δ,输出反馈认知过程中最小Hl, βw所对应的认知结果作为火焰图像的最终认知结果,避免系统陷入死循环。
| $\left\{ \begin{array}{l} {\beta _{w + 1}} = {\beta _w} + \frac{{H_{l, \beta }^w}}{w} \times e\left( {1 - _{i \in \left( {1, N} \right)}^{\ \ \ \min }H_{l, \beta }^w} \right) \times {\rm{lg}}\;w, \\ {\beta _1} = 0.5, {\beta _w} \in \left[ {0.5, 1} \right], \end{array} \right. $ | (10) |
| $ {l_{w + 1}} \leftarrow {l_w} + {10^{H_{l, \beta }^w}}, {l_w} \in [1, {l_{{\rm{max}}}}]。$ | (11) |
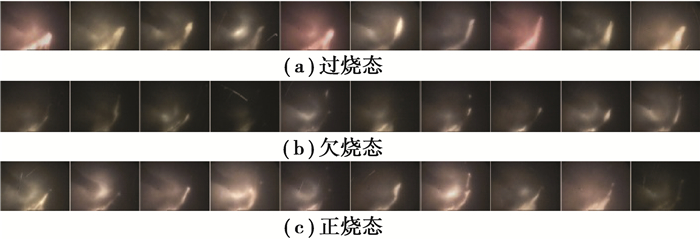
为验证基于深度迁移学习的水泥回转窑燃烧状况智能感知机制和计算方法的可行性,获取多种工况条件下某水泥厂1号窑的燃烧状况火焰图像,图像的大小为512×384。如图 3所示选取4 150幅图像,包括685幅过烧态、1 789幅欠烧态和1 676幅正烧态构建数据集合。1 000次bootstrapping方法获取平均燃烧状况的认知结果。火焰图像的燃烧状况标签由操作专家给出。
|
图 3 典型烧成带火焰图像样本 Fig. 3 Some typical burning zone flame image samples |
动态卷积层级的最大值lmax=5,ASCNN的训练数据重复轮数为100。较RVFL采用固定的[-1, 1]的范围,SCN中wj和bj的取值范围λ从预设定的集合{0.5, 1, 5, 10, 30, 50, 100}中自动选取。隐含层节点个数最大值设置为nb=2 000,10次独立实验获取最优的参数组合。Δ过低会导致燃烧状况的误识率较高,过高则产生不必要的反馈认知过程,设置Δ=0.2。所有实验在CPU i7-8700K,16G内存,GTX1080Ti的环境下运行。
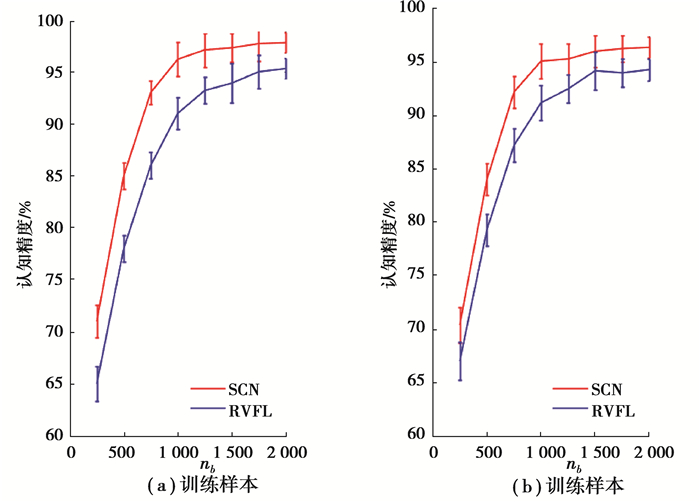
3.2 实验结果图 4给出了在动态卷积层级l=4和认知精度β=0.9的条件下,当采用不同nb时,训练火焰图像和测试火焰图像燃烧状况认知精度的均值及其标准差变化曲线。从图中可以明显看出,在每一个隐含层节点个数处,SCN的性能都优于RVFL。需要指出的是,当nb不断增大直至过拟合后,认知结果中SCN的性能同样优于RVFL。随着nb的增加,认知精度呈现单调递增趋势,当nb达到1 000时认知精度进入稳定区域,这一结果表明SCN建立了火焰图像输入简约差异化特征空间与输出燃烧状况类别之间的非线性关系,不同的基函数构建了不同的输入特征图空间,过多的基函数则会造成过拟合现象。
|
图 4 关于不同nb的SCN与RVFL认知精度比较(a)训练样本(b)测试样本 Fig. 4 Comparison of cognitive accuracy between SCNs and RVFLs with different nb (a)Training dataset(b)Testing dataset |
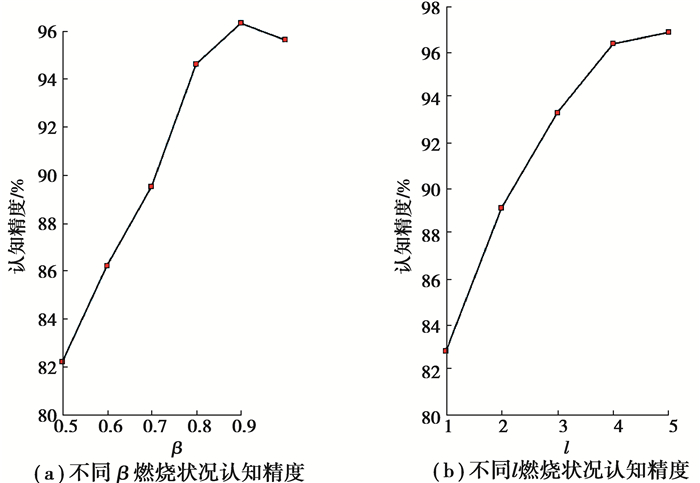
图 5给出了在某次实验中测试火焰图像集的燃烧状况认知精度关于不同卷积层级l和认知精度β的变化曲线,其中每个点均源于最优SCN参数的输出。如图所示,如图所示,通过调节β,可以控制有限论域条件下不同认知精度特征对火焰图像的适用程度。当内层β最优时,燃烧状况的认知性能随着l的增大呈现先递增后平稳的趋势,这是由于随着深层神经网络层级的加深,可以引入更强的非线性关系以提取更深层次的高阶抽象特征表征输入图像。然而,当动态网络层级达到一定的深度时,计算复杂度剧增,并可能会引入冗余信息致使性能饱和。测试样本中不可信的样本,包括被错误认知的样本以及被正确认知的样本但可信度较低,则基于反馈层调节机制动态增加卷积网络层,提取更深层次的抽象细节特征,并重新构建SCN分类器以再次认知。
|
图 5 燃烧状况认知精度和不同的β和l Fig. 5 Burning state cognitive accuracy vs. different β and l |
基于感兴趣区域全局形态的反馈认知算法[4]、基于感兴趣区域局部形态特征的反馈认知算法[5]、融合特征的燃烧状况认知算法[7]、基于多源特征的燃烧状况融合认知算法[6]、基于CNN的燃烧状况认知算法。1 000次实验的平均认知结果如表 1所示,所有数据均采用均值±±标准差的形式。
| 表 1 燃烧状况不同认知方法性能的比较 Table 1 Comparison of performance of different cognitive methods for burning states |
从表 1中可以看出,算法较其他算法性能更优,平均认知精度达到96.26%,相比于其它算法认知精度提高1%~5%。具有自寻优反馈调节机制算法的认知精度较无反馈开环认知系统性能更优,此外,深层神经网络较其他特征提取方法可以提取更为抽象的语义特征以表征火焰图像的燃烧状况。研究所提出的火焰图像燃烧状况智能感知算法能够根据不同认知需求,实时评测不确定燃烧状况认知结果的可信度,利用迁移学习动态生成多层面差异化简约特征空间,并构建具有万局逼近能力的SCN分类器,实现燃烧状况的优化反馈认知。
4 结论研究提出了一种基于深度迁移学习的水泥回转窑火焰图像燃烧状况智能感知方法,平均识别率达到96.26%。首先基于特征可分性测度指标和认知决策信息系统获取动态卷积神经网络的简约差异化特征空间,增强简约特征空间的可解释性;然后将简约全连接层特征向量送给具有万局逼近能力的SCN,建立具有强泛化能力的火焰图像燃烧状况分类准则;最后,基于认知结果语义误差熵评测指标,实时度量火焰图像的不确定燃烧状况认知结果,构建基于不确定认知结果测度指标约束的动态迁移学习机制,实现火焰图像燃烧状况多层次差异化特征空间及其分类准则的自寻优调节和重构,在多次反馈认知过程中模仿人类实时评测认知结果反复推敲比对的认知模式。特征空间的充分性表征将是下一步的工作重点。
| [1] |
Jarvensivu M, Saari K, Jamsa-Jounela S L. Intelligent control systemof an industrial lime kilnprocess[J]. Control Engineering Practice, 2001, 9(6): 589-606. DOI:10.1016/S0967-0661(01)00017-X |
| [2] |
Sun P, Chai T Y, Zhou X J. Rotary kiln flame image segmentation based on FCM and Gabor wavelet based texture coarseness[C]//Proc of World Congress on Intelligent Control and Automation. Chongqing: China, IEEE, 2008: 7615-7620. https://ieeexplore.ieee.org/document/4594586
|
| [3] |
姜慧研, 崔晓亮, 周晓杰, 等. 基于改进的双快速行进法的图像分割方法[J]. 系统仿真学报, 2008, 20(3): 803-810. JIANG Huiyan, CUI Xiaoliang, ZHOU Xiaojie, et al. Image segmentation based on improved dual fast marching method[J]. Journal of System Simulation, 2008, 20(3): 803-10. |
| [4] |
陈克琼, 王建平, 李帷韬, 等. 具有仿反馈机制的图像模式分类认知[J]. 中国图象图形学报, 2015, 20(11): 1500-1510. CHEN Keqiong, WANG Jianping, LI Weitao, et al. Image pattern cognition with simulated feedback mechanism[J]. Journal of Image and Graph-ics, 2015, 20(11): 1500-1510. DOI:10.11834/jig.20151109 |
| [5] |
陈克琼, 王建平, 李帷韬. 基于变粒度仿反馈机制的回转窑燃烧状况智能感知方法[J]. 模式识别与人工智能, 2015, 28(11): 1013-1022. CHEN Keqiong, WANG Jianping, LI Weitao. Variable granularity and simulated feedback mechanism based burning state intelligent cognitive method of rotary kiln sintering process[J]. Pattern Recognition and Artificial Intelligence, 2015, 28(11): 1013-1022. |
| [6] |
Li W T, Wang D H, Chai T Y. Flame image-based burning state recognition for sintering process of rotary kiln using heterogeneous features and fuzzy integral[J]. IEEE Transactions on Industrial Informatics, 2012, 8(4): 780-790. DOI:10.1109/TII.2012.2189224 |
| [7] |
Li W T, Wang D H, Chai T Y. Burning state recognition of rotary kiln using ELMs with heterogeneous features[J]. Neurocomputing, 2013, 102(2): 144-153. |
| [8] |
李帷韬, 曹仲达, 朱程辉. 基于深度集成学习的青梅品级智能反馈认知方法[J]. 农业工程学报, 2017, 23: 276-283. LI Weitao, CAO Zhongda, ZHU Chenghui. Intelligent feedback cognition of greengage grade based on deep ensemble learning[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017, 23: 276-283. |
| [9] |
Chen K, Wang J P, Li W T. An intelligent cognition method of human health states based on a variant knowledge granularity feedback mechanism[J]. IEEE Access, 2017, 5(1): 19570-19580. |
| [10] |
Bronstein M M, Bruna J, Lecun Y, et al. Geometric deep learning:going beyond euclidean data[J]. IEEE Signal Processing Magazine, 2017, 34(4): 18-42. DOI:10.1109/MSP.2017.2693418 |
| [11] |
Majumder N, Poria S, Gelbukh A, et al. Deep learning-based document modeling for personality detection from yext[J]. IEEE Intelligent Systems, 2017, 32(2): 74-79. DOI:10.1109/MIS.2017.23 |
| [12] |
Yang X, Kwitt R, Styner M, et al. Quicksilver:fast predictive image registration-a deep learning approach[J]. Neuroimage, 2017, 158: 378. DOI:10.1016/j.neuroimage.2017.07.008 |
| [13] |
周显恩, 王耀南, 朱青. 基于机器视觉的瓶口缺陷检测方法研究[J]. 电子测量与仪器学报, 2016, 30(5): 702-713. ZHOU Xian'en, WANG Yaonan, ZHU Qing. Research on defect detection method for bottle mouth based on machine vision[J]. Journal of Electronic Measurement and Instrumentation, 2016, 30(5): 702-713. |
| [14] |
司朋举, 胡伟. 一种改进的神经网络车牌识别算法研究[J]. 电子测量技术, 2016, 39(10): 100-103. SI Pengju, HU Wei. Research on an improved neural network license plate recognition algorithm[J]. Electronic Measurement Technology, 2016, 39(10): 100-103. DOI:10.3969/j.issn.1002-7300.2016.10.025 |
| [15] |
Zuo H, Zhang G, Pedrycz W, et al. Fuzzy regression transfer learning intakagi-sugenofuzzy models[J]. IEEE Transactions on Fuzzy Systems, 2017, 25(6): 1795-1807. DOI:10.1109/TFUZZ.2016.2633376 |
| [16] |
Bussas M, Sawade C, Kühn N, et al. Varying-coefficient models for geospatial transfer learning[J]. Machine Learning, 2017, 106(3): 1-22. |
| [17] |
Wang D. H., Li M. Stochastic configuration networks:fundamentals and algorithms[J]. IEEE Transactions on Cybernetics, 2017, 47(10): 3466-3479. DOI:10.1109/TCYB.2017.2734043 |
 2019, Vol. 42
2019, Vol. 42


