2a. 重庆大学 建筑城规学院, 重庆 400030;
2b. 重庆大学 山地城镇建设与新技术教育部重点实验室, 重庆 400030;
2c. 重庆大学 规划设计研究院有限公司, 重庆 400030
2a. Faculty of Architecture and Urban Planning, Chongqing University, Chongqing 400030, P. R. China;
2b. Key Laboratory of New Technology for Construction of Cities in Mountain Area, Chongqing University, Chongqing 400030, P. R. China;
2c. Chongqing University Planning & Design Institute Co., Ltd., Chongqing University, Chongqing 400030, P. R. China
城镇经济发展推动城市商圈的高速建设,商圈空间环境展现出人员密集、流线庞杂、功能复合的建设态势。步行路网是承担商圈空间联系、人流输送的交通媒介,也是重要的展示交往与活动空间,正逐步向立体化、复合化发展。商圈步行路网因而暴露出可达性差、脆弱性高、联系不足等现实问题,其防灾减灾矛盾日益突出。深化商圈步行路网可靠性研究,对了解步行路网结构特征,保障商圈安全,指导商圈步行系统建设有着重要意义。
针对商圈步行路网的安全研究,何晓丽将灰关联分析法运用于商业中心区的避难道路,以避难道路为对象开展实证[1]。苏薇采用层次分析法构建城市商业中心区避难疏散评价模型,确定控制要项与控制因子,建立评价指标体系[2]。总体而言,当前商圈路网可靠性研究主要聚焦于灾害情景的安全性评价,研究对象多针对单段道路或单个交叉口,且较少将其视为整体路网进行考虑。
复杂网络分析法为交通网络可靠性研究提供了新思路,闫慧丽[3]、李聪颖[4]运用复杂网络理论与分析方法对慢行网络进行结构层次的划分。张勇[5]、万丹[6-7]、王志强[8]、隋东[9]等分别将复杂网络运用于城市道路、公交、轨道交通[10-11]、航空网络,分析网络的小世界特征[12]和无尺度特征,对网络进行选择性攻击与随机失效条件下的可靠性分析。
基于复杂网络理论的路网系统可靠性研究已在区域与城市尺度积累一定成果,微观片区尺度的研究较少;宏观的大规模网络研究多关注于分析结果的规律性特征,忽视了网络模型与现实情景间的仿真模拟关系;相关研究大多为针对可靠性结论的单一评价,较少对现实路网提出优化策略。为此,文中以商圈步行路网的安全可靠性为现实情境,基于复杂网络理论与分析方法创新性地设计了步行路网故障模拟与可靠性研究方案,改进网络建模方法,并以重庆市五大商圈三维立体步行路网为研究对象构建网络模型,通过个案分析与对比分析,进行步行路网可靠性评价研究[13-14],并提出优化建议。
1 城市商圈步行路网复杂网络构建 1.1 商圈步行路网特征大多现实网络都具有2个基本特性,即增长性和偏好依附性[15],商圈步行路网也具备该特点。一方面,城市商圈的扩容提质,必然带来步行路网规模的增长;另一方面,偏好依附性表现为网络具有强者愈强的规则,商圈步行系统网络化、立体化、功能复合化的发展态势使得网络重要节点成为整体网络的中心,聚集人民各类商业娱乐活动,其重要性进一步巩固。
因此,城市商圈步行路网具有复杂网络的基本特性,基于复杂网络理论的拓扑规则适用于商圈步行网络模型的构建。
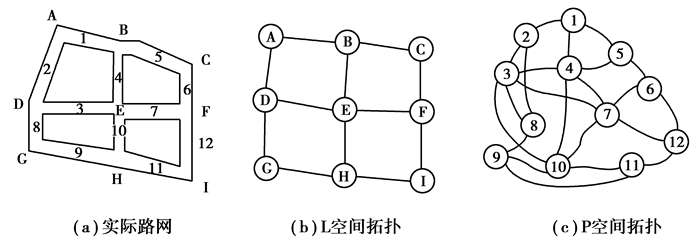
1.2 商圈步行复杂网络模型构建方法 1.2.1 道路复杂网络基本建模方法网络模型通过节点与节点间的相互关联来构建,步行路网主要包括交叉口和路段2个基本要素,将路网抽象为网络模型,可将交叉口作为节点、交叉口间的路段作为边,构建L空间网络模型,即“原始法”;也可将路段视为节点、路段间交叉口视为边,构建P空间网络,也称“对偶法”(图 1)。
|
图 1 道路网2种拓扑结构示意图 Fig. 1 Road network topology diagram |
商圈步行路网是由地面层与地上、地下层组成的三维立体路网。地面层路网以道路路段为核心,地上、地下层路网以与地面相连接的出入口为核心:这是由于灾害发生时,非地面层人流需要通过天桥、地道出入口设施向地面疏散,因此相对于地上、地下层的内部路径联系,立体步行路网地上、地下层通往地面层的交通联系更为重要。
因此,笔者对P空间法进行改良,以地面路段、地上地下连接口为节点,以节点之间是否交接为关系,构建商圈步行复杂网络,深层次的反映商圈步行网络拓扑结构关系。步行网络语义模型如图 2所示。

|
图 2 商圈步行路网语义模型 Fig. 2 Semantic model of pedestrian network of business district |
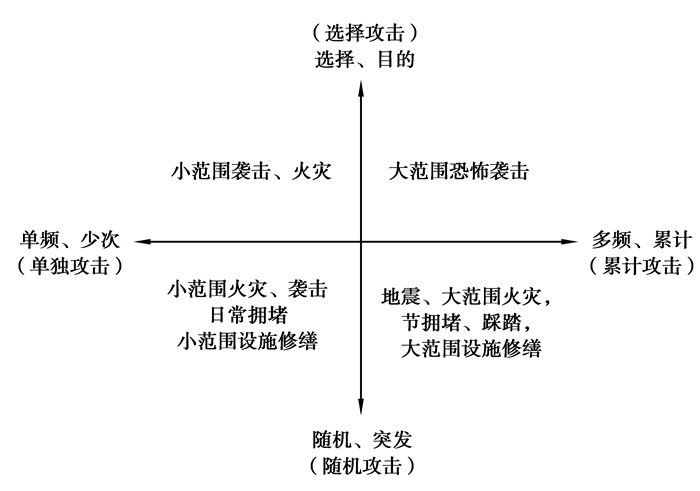
城市商圈步行路网可能遭受的外界冲击或破坏,如自然灾害、恐怖袭击、运营故障、设施维修乃至火灾等,其发生原因和破坏程度有所不同。自然灾害导致的破坏具有较强的随机性,恐怖袭击通常表现出较强的选择性,道路拥堵等运营故障是小规模、小范围的,而大型故障如大面积火灾、大范围基础设施维修等影响范围广、危害较大。按照破坏或故障的选择性与随机性,单频与多频,商圈步行路网灾害可分为4类(图 3)。
|
图 3 商圈步行路网灾害的四象限分析 Fig. 3 Four-quadrant analysis of pedestrian network disasters in commercial district |
步行路网在面临破坏的情况下,整体路网有被分裂为若干子网络的风险,因此路网是否连通、在多大程度上保持其连通性是衡量网络可靠性的基础;此外,人流从单条路段到达至其他任意路段的快慢,反映了灾害情境下的可达效率,也是反映该路网可靠性的重要指标。因此,步行路网在灾害背景下,以连通程度与连通效率,来测度步行路网的可靠性。
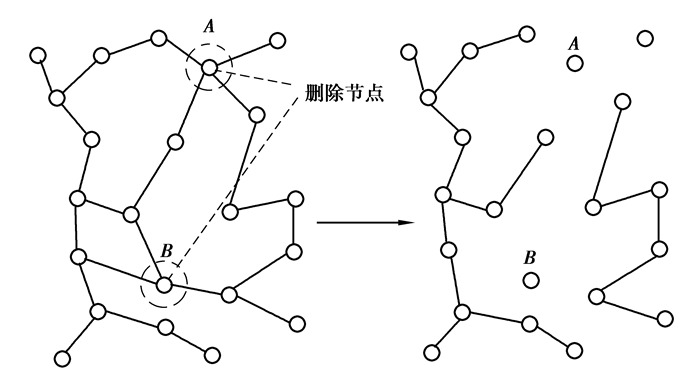
2.2 网络攻击与可靠性指标构建 2.2.1 网络攻击模式步行路网在故障情景下面临的破坏,抽象到网络拓扑模型中,就是网络节点或边的破坏,即网络攻击(图 4);这一分析手段可以实现对路网灾害的定量、动态模拟,通过对不同情景灾害的网络连通程度与整体效率变化,评判步行路网可靠性。
|
图 4 网络攻击示意图 Fig. 4 Network attack schematic |
1) 选择攻击与随机攻击。
随机攻击(failure)是每次随机性的移除网络的一个节点或边,且网络中每个节点或边被移除的概率相同;选择性攻击(attack)是网络的节点按一定的规则被破坏。节点度数与介数是描述网络中节点或边特征的重要指标,是选择攻击采用的大小顺序的重要依据①。一般而言,随机攻击是由网络自身原因引起的故障,用以测度网络的容错能力;选择性攻击则代表了有目的性的破坏,用以测度网络的抗攻击能力。
① 节点i的度定义为与该节点连接的其他节点的数目,度值越大,表示节点i与其他节点直接连通的节点越多。节点i的介数表达节点在结构中承担“中介”作用的能力,如果某节点总是处于其余节点相互联系的最短路径上,其中介中心度较高。
2) 累计攻击与单独攻击。
累计攻击指依次移除网络节点,直至所有节点被全部删除,累计攻击可分选择攻击与随机攻击2种模式,前者根据网络节点的度值高低依次加以攻击,后者随机选择网络节点进行攻击,且各次攻击结果通常存在差异。
单独攻击指每次仅对网络中单个节点进行删除,考察单个节点的脆弱性。单独攻击将网络节点按照度值由高到低的顺序排列而依次攻击。
2.2.2 可靠性指标构建商圈步行路网受到攻击后的结构变化,主要体现为网络平均最短距离和网络规模的变化[16],即路网连通效率与连通程度的变化。因此,文中选用网络效率测度路网连通效率,以最大连通子图相对大小测度路网连通程度,进而评价路网的可靠性。
1) 网络连通效率。
网络中节点i与j之间距离越远,效率越低。连通效率定义为i与j之间距离dij的倒数,εij=1/dij。网络连通效率需反映网络中所有节点对之间效率的整体情况,包括绝对效率与相对相率。绝对效率是所有节点对之间连通效率之和,相对连通效率是绝对效率的标准化,从而对不同规模网络的效率进行比较,文中采用相对连通效率,计算公式为
| $ {E_{{\rm{re}}}} = \frac{2}{{N\left( {N - 1} \right)}}\sum\limits_{i \ne j} {{{\rm{\varepsilon}} _{ij}}} , $ | (1) |
式中:Ere代表网络的相对效率;N为网络节点总数;εij为节点i、j间的网络效率。
2) 最大连通子图的相对大小。
最大连通子图的相对大小S可称为相对连通概率,即网络受到攻击后分裂为若干独立的子网络或节点,幸存下的网络中,其中规模最大的连通子网络,其所含的节点数占原网络节点数,计算公式为
| $S = \frac{{N\prime }}{N}, $ | (2) |
式中:N′表示网络遭受攻击后剩余最大连通子图的节点数;N为原网络节点数。
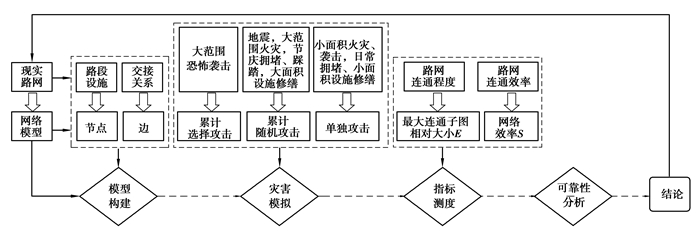
3 路网故障模拟与可靠性研究方案研究运用复杂网络分析方法,从现实路网与网络模型的关系出发,通过模型构建、灾害模拟、指标测度3个方面完成复杂网络对现实路网的仿真模拟,以网络的可靠性计算结果进行商圈步行路网的可靠性评价。步行路网故障模拟与可靠性分析技术路线如图 5所示。
|
图 5 步行路网故障模拟与可靠性分析技术路线 Fig. 5 Technical route of failure simulation and evaluation of pedestrian network |
模型构建阶段,以地面道路、地上地下出入口设施为节点,以节点之间是否交接为边构建复杂网络模型;灾害模拟阶段,以累计选择攻击、累计随机攻击与单独攻击的网络攻击方法模拟现实步行网络遭受的路网故障;指标测度阶段,以网络效率S与最大连通子图的相对大小E作为现实路网连通效率与连通程度的测度指标,反映路网在遭受攻击后,网络拓扑结构发生的变化。
4 实例分析 4.1 研究靶区重庆市城市空间为典型的多中心、组团式模式,形成以五大商圈为核心,多点发展的商圈格局;商圈步行路网规模较大、扩张迅速、与复杂的地形相结合,是典型的立体步行路网,因此文中选取重庆五大商圈步行路网为研究对象。
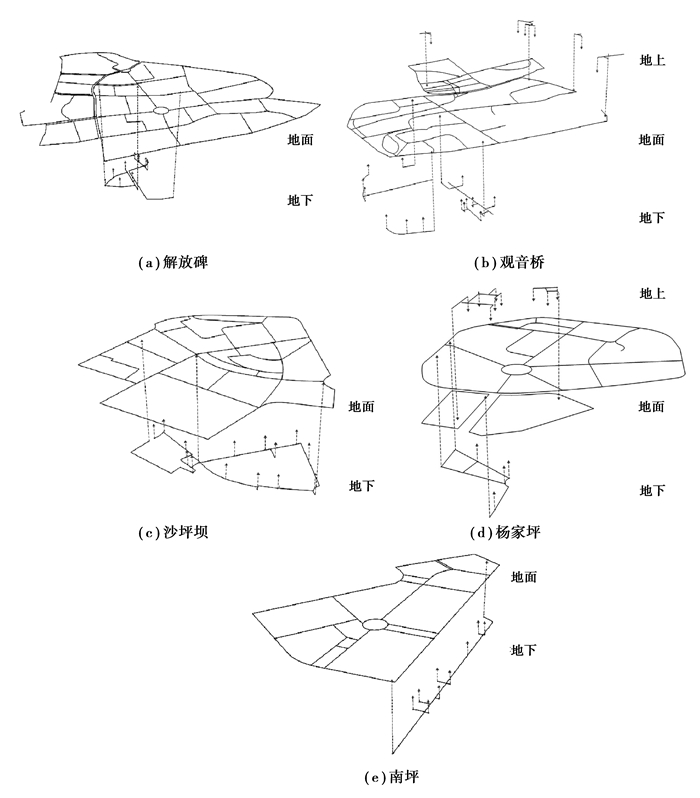
以现场调研为数据源,将商圈步行系统抽象为线型网络(图 6)。解放碑、沙坪坝、南坪商圈路网包括地面与地下2层;观音桥、杨家坪商圈路网包括地面、地下、地上3层。解放碑、沙坪坝、南坪内部区域无地形或建筑阻隔,其地面路网可以相互连通;而观音桥、杨家坪因交通干道穿行被划分为若干片区,地面路网无法完全连通。
|
图 6 五大商圈步行系统抽象网络 Fig. 6 Abstract network of pedestrian system in 5 business district |
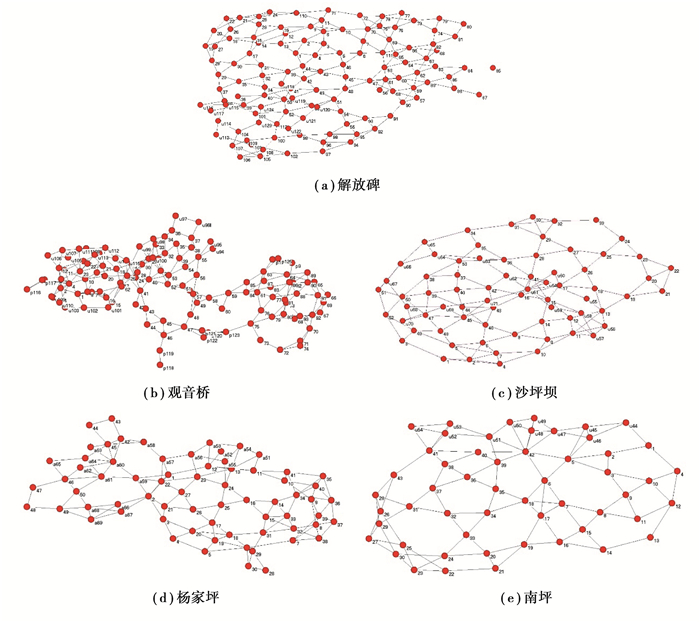
依照前述语义,在复杂网络分析软件中生成网络模型(图 7)。五大网络节点个数由大到小依次为观音桥(125)、解放碑(124)、沙坪坝(71)、杨家坪(69)、南坪(54);网络边个数由大到小依次为解放碑(386)、观音桥(380)、沙坪坝(226)、杨家坪(219)、南坪(168)。图 7显示,解放碑、沙坪坝、南坪节点分布较为均质化,观音桥、杨家坪网络体现出一定的组团特点。
|
图 7 五大商圈步行网络模型构建 Fig. 7 Network model construction of top 5 business district |
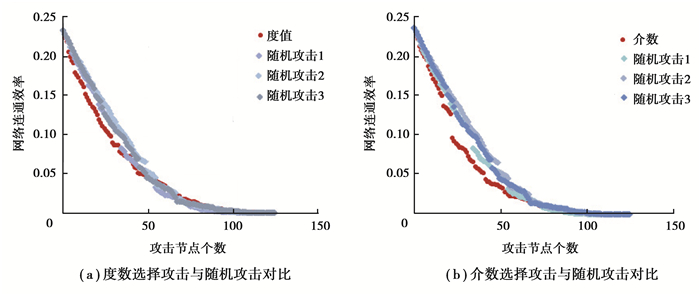
以解放碑商圈路网为例,图 8反映了在度数选择攻击与随机攻击、介数选择攻击与随机攻击对比下解放碑路网网络效率的变化。数据分析可知,网络效率下降为原有网络的1/2时,度数、介数与随机攻击②3者所需攻击的节点比例分别为17.7%,17.7%,22.6%;效率降为1/4时,节点比例分别为34.7%,29.0%,36.3%;效率降为0时,节点比例分别93.5%,91.1%,95.2%。效率下降时所需攻击的节点数越多,网络越稳定。因此,解放碑网络效率在选择攻击下的可靠性较低,在随机攻击下可靠性较高;3种攻击模式下稳定性由大到小为随机攻击、度数选择攻击、介数选择攻击。比较而言,网络在介数攻击时可靠性较低。
|
图 8 解放碑网络选择攻击与随机攻击下网络效率变化 Fig. 8 The comparison of network efficiency curve between selective attack and random attack of typical network |
② 采用随机攻击的平均值
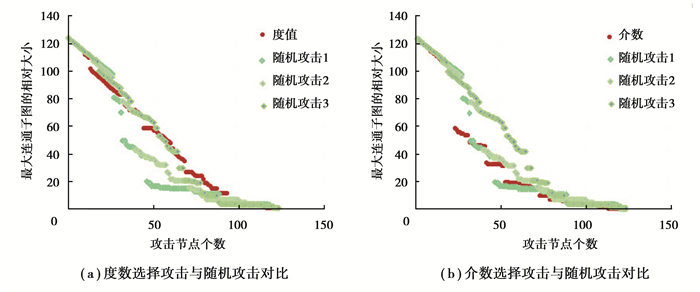
4.3.2 累计攻击下最大连通子图的相对大小变化以解放碑商圈路网为例,图 9反映了在度数选择攻击与随机攻击、介数选择攻击与随机攻击时最大连通子图的相对大小的变化,随机攻击与选择攻击下曲线无明显差异。数据分析可知,最大连通子图大小下降为原有网络的1/2时,度数、介数2者所需攻击的节点比例分别为35.5%,17.7%;子图大小降为1/4时,节点比例分别为55.6%,41.9%。指标下降时所需攻击的节点数越多,网络越稳定。3种攻击模式下稳定性由大到小为度数选择攻击、随机攻击、介数选择攻击。比较而言,网络在介数攻击时可靠性较低。
|
图 9 解放碑网络选择攻击与随机攻击下最大连通子图相对大小变化 Fig. 9 The comparison of maximal connected subgraph curve betwee n selective and random attack of typical network |
图 10反映了解放碑网络节点在单独攻击时网络连通效率的变化,该图横坐标为节点度数,度值自左向右逐次降低;纵坐标反映了移除该节点后网络效率呈现出的整体上扬趋势。表明从高度值点向低度值点过渡时,单一节点对网络效率的影响逐渐弱化。

|
图 10 解放碑步行网络单独攻击下网络效率变化 Fig. 10 The network efficiency curve at single attack and of typical network |
波动较大的曲线表明,在依次移除各个节点时,网络效率的变化差异巨大;这意味着网络中的某些节点对网络效率起到了关键性的影响,而且这些关键节点并不都是高度值点,还包括了部分低度值点。
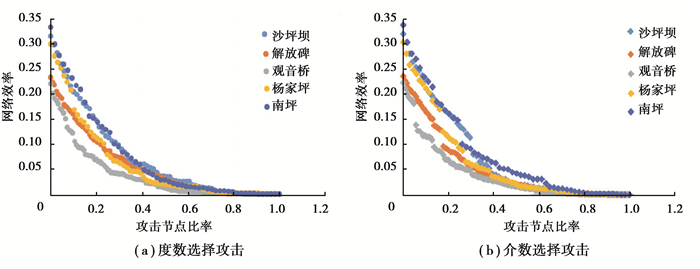
4.4 步行网络可靠性对比分析 4.4.1 累计攻击下网络效率变化图 11反映了选择攻击下的五大商圈步行网络的可靠性对比,数据分析可知,在度数攻击下,欲使网络效率降为初始水平的1/2,则各步行网络需要移除的节点占比由高到低分别为沙坪坝、解放碑、南坪、杨家坪、观音桥(18.3%、17.7%、16.7%、13%、10.4%);欲使网络效率降为初始水平的1/4,则各步行网络需要移除的节点占比由高到低分别为解放碑、沙坪坝、南坪、杨家坪、观音桥(34.7%、33.8%、33.3%、26.1%、24.0%)。将网络规模和初始网络效率相近的解放碑与观音桥对比,后者的网络效率下降更快,其稳定性更差;将网络规模和初始网络效率相近的杨家坪、沙坪坝、南坪对比,前者的网络效率下降最快,稳定性最差。
|
图 11 五步行网络在累计攻击下的网络效率变化比较 Fig. 11 Network efficiency change comparison of the 5 Facility network under cumulative attack |
介数攻击下,欲使网络效率降为初始水平的1/2,则各步行网络需移除的节点百分比从高到低依次为沙坪坝、南坪、解放碑、杨家坪、观音桥(21.1%、18.5%、17.7%、17.4%、10.4%);欲使网络效率降为初始水平的1/4,则各步行网络需移除的节点百分比从高到低依次为沙坪坝、南坪、解放碑、杨家坪、观音桥(32.4%、31.5%、29.0%、27.5%、25.6%)。介数攻击时五大网络的效率变化与度数攻击时结果相似,观音桥、杨家坪网络稳定性较弱。
综上,在度数攻击下,网络效率可靠性最高为沙坪坝网络,解放碑、南坪、杨家坪次之,观音桥最低;在介数攻击下,可靠性最高为沙坪坝网络,南坪、解放碑、杨家坪次之,观音桥最低。总体而言,以网络效率为度量,在介数选择攻击下解放碑相对更为脆弱,在度数选择攻击下南坪网络相对更为脆弱;而无论是哪类攻击,沙坪坝的可靠性相对较高,观音桥的可靠性相对较低。
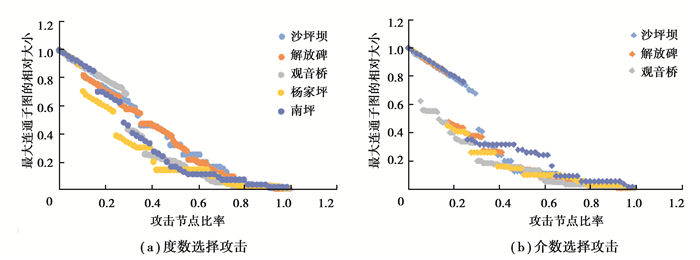
4.4.2 累计攻击下最大连通子图的相对大小变化图 12分别为度数攻击与介数攻击下,商圈步行网络的最大子图相对大小的变化曲线。
|
图 12 五步行网络在累计攻击下的最大连通子图变化比较 Fig. 12 Maximal connected subgraph change comparison of 5 facility network under cumulative attack |
如图 12所示,在度数攻击下,将各个步行网络中的节点按照度值排列由高到低进行移除,则在初始攻击阶段,解放碑、杨家坪最先崩溃,随着攻击继续沙坪坝、南坪也开始崩溃,而观音桥稳定性最强;进入攻击后期,沙坪坝、解放碑逐渐表现出较强的稳定性,而观音桥、南坪、杨家坪则较为脆弱。在介数攻击下,初始阶段南坪、解放碑、沙坪坝、杨家坪较为稳定,观音桥则迅速崩溃;而在攻击中后期,南坪表现出较强的稳定性,其余网络稳定性均表现一般。
综上,度数攻击下,网络连通程度的可靠性最高为沙坪坝网络,观音桥、南坪、解放碑次之,杨家坪最低;介数攻击下,可靠性最高为南坪网络,沙坪坝、解放碑、杨家坪次之,观音桥最低。总体而言,以连通子图为度量,观音桥、沙坪坝网络在介数攻击时更脆弱,南坪、杨家坪网络在度数攻击时更脆弱。
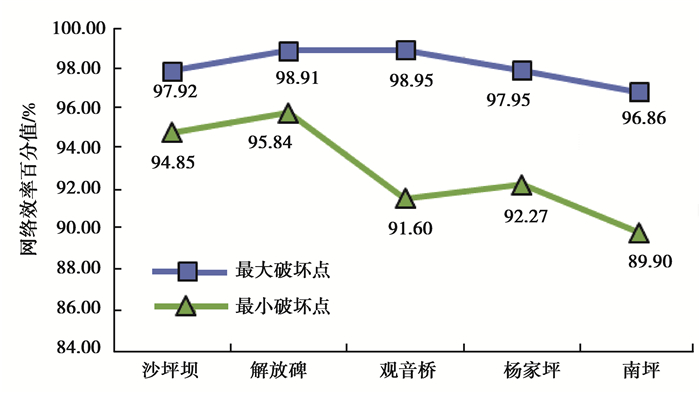
4.4.3 单独攻击下网络效率变化网络中各个节点的移除对整体网络效率的影响均不同,文中将移除某节点后网络效率下降最大的节点与移除后效率下降最小的点分别定义为“最大破坏点”与“最小破坏点”,图 13反映了五大商圈网络分别移除这两个节点后的网络效率变化。
|
图 13 最大破坏点或最小破坏点的移除产生的网络效率变化对比 Fig. 13 Network efficiency variations induced by removal of maximal breaking node and minimal breaking node |
如图 13所示,最小破坏点的移除对较大规模网络影响较小,对较小规模网络则影响较大,最小破坏点移除后网络效率下降最为显著的为南坪网络。最强破坏点移除所产生的影响则与网络规模的大小关系较弱,观音桥、南坪、杨家坪最大破坏点移除的影响较大,解放碑、沙坪坝影响较小,进一步表明二者的较高稳定性,而观音桥网络则因为“薄弱点”的存在,不可靠因素较高,稳定性较差。
5 结论与讨论 5.1 主要结论 5.1.1 沙坪坝网络可靠性相对较高,杨家坪、观音桥可靠性相对较低五大商圈在度数与介数攻击状态下,网络效率与最大连通子图的相对大小的变化曲线数据可知,总体而言,沙坪坝、南坪网络可靠性较好,观音桥、杨家坪网络可靠性较差。结合实际路网,观音桥、杨家坪步行路网均由南北2部分组成,连接南北两部分路网的通道较少,在攻击状态下极易破坏,对整体网络可靠性产生较大影响。
5.1.2 攻击状态网络效率初期下降更迅速,重建状态网络效率后期提升更迅速攻击状态下,网络少量节点移除即可引发网络效率的指数型下降,如观音桥在介数选择攻击下,移除1/10的节点,网络效率便迅速将至原来的1/2。因此,路网故障应尽可能强预防、快抢修,避免因几处故障引发整体网络的全线崩溃。
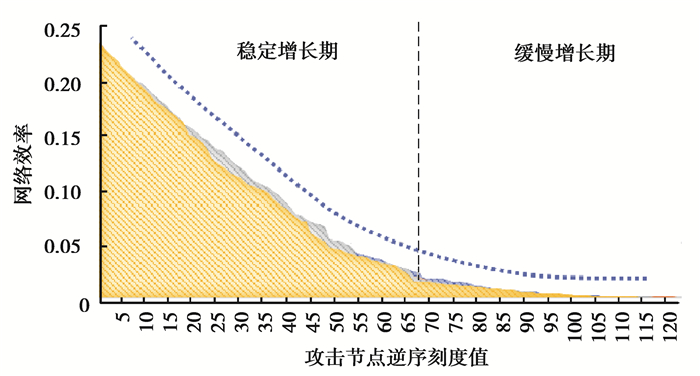
反之,将网络攻击的横坐标逆序排列,将节点增加视为时间轴模拟路网的重建过程。曲线变化显示,网络效率的增加经历了缓慢增长与稳定增长2个阶段:初始阶段效率提升较为缓慢;而随着节点数量的持续增加,效率提升速度明显加快。计算表明对于存在地理空间边界的商圈步行路网,网络规模扩大能极大的提升网络效率;因此增加地面路段、天桥地道设施,是增加可靠性、提升效率的重要途径。
|
图 14 节点逆序排列下的解放碑步行网络重建模拟 Fig. 14 The simulation of Jiefangbei pedestrian network reconstruction by nodes reverse order |
网络效率与最大连通子图的相对大小,均可以测度网络可靠性。选取网络效率进行测度,无论度数选择攻击还是介数选择攻击,该指标均大幅下降,而随机攻击时小幅度下降,表明了路网连通效率在选择攻击下具有脆弱性,随机攻击下表现出鲁棒性。选取最大连通子图的相对大小进行测度,在介数攻击时指标大幅下降,度数攻击时小幅下降,表明路网连通程度在介数攻击时脆弱性高,度数攻击时具有鲁棒性。这是由于高度值点代表着同时与多个路段相连的道路,其在路网中较少成为几个子网络的唯一通道,相比一般节点,移除单个高值点而导致网络分裂的概率较低。而高介值点代表着中介性较强的路段,在网络中起着较高的中介与桥梁的作用,该点的移除会直接造成网络的崩溃。
攻击状态下两类指标的曲线形态不同,网络效率曲线通常呈现由跌落到平缓、由快到慢的指数下降,最大连通子图呈现“阶梯-断崖-阶梯-断崖”,总体平缓、局部跌落的下降模式。两类曲线反映出所有节点的移除均能对路网的总体效率产生较大影响,而关键节点的移除对于路网的分裂与否产生较大影响。
不同网络对度数选择攻击与介数选择攻击的敏感性不同,如观音桥在介数攻击下相对更脆弱,南坪网络在度数攻击下更脆弱。
5.1.4 大规模网络单点攻击时易呈现鲁棒性,小规模网络单点攻击时易呈现脆弱性网络单独攻击下,移除单个节点对较小规模网络破坏性更大,表明单独点攻击的破坏性的强弱与网络规模的大小负相关。现实世界中,小规模网络因其节点数量的限制,使得每个节点的重要性都不可忽视,节点的移除、增加或改变均对网络结构产生较大的影响;大规模网络对单个节点的移除则具有一定的鲁棒性。
5.2 启示 5.2.1 路网规划建设提升路网网络效率与连通度是提高路网可靠性的重要手段。针对提升网络效率,“减少断头路、连接枝状路、形成环状路”可增强路段之间的可达性,有助于整体效率的提升;其次,在理想网络模型中,以三边形为基础单位的网络,节点间距离最短、效率最高,因此,在现实路网中,可根据实际条件尽可能增加路段之间的联系。针对连通度的提升,主要避免“桥”的产生,即2个子网络中仅有唯一通道,在现实路网中,当网络被分为多个分区时,需通过地道、天桥、电梯、人行横道等设施,增强路网连通性。
5.2.2 路网综合管理商圈路网中重要路段或设施的保护预防管理与应急抢修提升整体路网可靠性的主要途径。在路网综合管理中,可根据路段度值与介值的高低,可划分道路等级,对主要路段和设施进行重点管理,包括针对性的无障碍设施设置、标识设置、安全管理、节假日人流管制等措施。
| [1] |
周铁军, 何晓丽, 王大川, 等. 基于灰关联分析法的商业中心区避难道路安全评价研究:以重庆市沙坪坝商业中心为例[J]. 西部人居环境学刊, 2013, 28(6): 1-5. ZHOU Tiejun, HE Xiaoli, WANG Dachuan, et al. The study on safety evaluation of evacuation road in commercial centre based on grey relational analysis:a case of Sha Pingba commercial centre in Chongqing[J]. Human Settlements Forum in West China, 2013, 28(6): 1-5. (in Chinese) |
| [2] |
苏薇.山地城市商业中心区避难疏散评价与控制策略研究[D].天津: 天津大学, 2012. SU Wei. Study on evaluation and control strategy of refuge evacuation in commercial center districts of mountainous cities[D]. Tianjin: Tianjin University, 2012. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10056-1013039429.htm |
| [3] |
闫慧丽.基于复杂网络理论的城市慢行交通网络特性研究[D].西安: 长安大学, 2012. YAN Huili. Research on the characteristics of urban slow mode transportation network based on theory of complex network[D]. Xi'an: Chang'an University, 2012. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10710-1013019161.htm |
| [4] |
李聪颖.城市慢行交通规划方法研究[D].西安: 长安大学, 2011. LI Congying. Research on planning method of urban pedestrian and bicycle traffic[D]. Xi'an: Chang'an University, 2011.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10710-1012142582.htm |
| [5] |
张勇, 杨晓光. 城市路网的复杂网络特性及可靠性仿真分析[J]. 系统仿真学报, 2008, 20(2): 464-467, 513. ZHANG Yong, YANG Xiaoguang. Complex network property and reliability simulation analysis of urban street networks[J]. Journal of System Simulation, 2008, 20(2): 464-467, 513. (in Chinese) |
| [6] |
Wan D, Huang Y, Feng J, et al. Understanding topological and spatial attributes of bus transportation networks in cities of Chongqing and Chengdu[J]. Mathematical Problems in Engineering, 2018, 2018: 1-14. |
| [7] |
万丹.重庆城市公交系统复杂网络模型及可靠性规划研究[D].重庆: 重庆大学, 2017. WAN Dan. Study on reliability planning of complex network model of Chongqing bus system[D]. Chongqing: Chongqing University, 2017. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10611-1017723115.htm |
| [8] |
王志强, 徐瑞华. 基于复杂网络的轨道交通路网可靠性仿真分析[J]. 系统仿真学报, 2009, 21(20): 6670-6674. WANG Zhiqiang, XU Ruihua. Reliability simulation analysis of urban rail transit networks based on complex network[J]. Journal of System Simulation, 2009, 21(20): 6670-6674. (in Chinese) |
| [9] |
隋东, 康金霞. 基于复杂网络理论的中国航路网络抗毁性分析[J]. 哈尔滨商业大学学报(自然科学版), 2016, 32(3): 295-302. SUI Dong, KANG Jinxia. Analysis of China air route networks invulnerability based on complex networks[J]. Journal of Harbin University of Commerce(Natural Sciences Edition), 2016, 32(3): 295-302. (in Chinese) DOI:10.3969/j.issn.1672-0946.2016.03.010 |
| [10] |
邓良凯, 石亚灵, 张弘, 等. 城市群城际铁路站点空间网络研究[J]. 城市发展研究, 2017, 24(8): 64-70, 99. DENG Liangkai, SHI Yaling, ZHANG Hong, et al. Research on spatial network of intercity railway station in urban agglomeration[J]. Urban Development Studies, 2017, 24(8): 64-70, 99. (in Chinese) |
| [11] |
邓良凯, 石亚灵, 冯洁.京津冀城际铁路站点网络结构演变特征分析[C]//2018城市发展与规划论文集.2018. DENG Liangkai, SHI Yaling, FENG Jie. Analysis on evolution characteristics of network structure of beijing-tianjin-hebei intercity railway station[C]//2018 Urban Development and Planning Proceedings. 2018. (in Chinese) http://cpfd.cnki.com.cn/Article/CPFDTOTAL-BJBD201807001064.htm |
| [12] |
黄勇, 肖亮, 胡羽, 等. 社会网络分析法在城镇工程基础设施健康评价中的应用[J]. 重庆大学学报, 2015, 38(3): 39-46, 166. HUANG Yong, XIAO Liang, HU Yu, et al. The application of social network analysis in the infrastructure project evaluation of urban health[J]. Journal of Chongqing University, 2015, 38(3): 39-46, 166. (in Chinese) |
| [13] |
向宏, 张瑜, 胡海波. 大数据与安全可视化[J]. 重庆大学学报, 2016, 39(2): 71-81. XIANG Hong, ZHANG Yu, HU Haibo. Big data and security visualization[J]. Journal of Chongqing University, 2016, 39(2): 71-81. (in Chinese) |
| [14] |
叶建红, 陈小鸿, 俞梦骁, 等. 个体特征对步行通道行人最大通过量的影响[J]. 同济大学学报(自然科学版), 2015, 43(12): 1834-1840. YE Jianhong, CHEN Xiaohong, YU Mengxiao, et al. Impact analysis of individual characteristics on pedestrian maximum volume[J]. Journal of Tongji University(Natural Science), 2015, 43(12): 1834-1840. (in Chinese) DOI:10.11908/j.issn.0253-374x.2015.12.011 |
| [15] |
de Bona A A, Fonseca K V O, Rosa M O, et al. Analysis of public bus transportation of a brazilian city based on the theory of complex networks using the P-space[J]. Mathematical Problems in Engineering, 2016, 2016: 1-12. |
| [16] |
赵玲, 邓敏, 王佳璆, 等. 应用复杂网络理论的城市路网可靠性分析[J]. 测绘科学, 2013, 38(3): 83-86. ZHAO Ling, DENG Min, WANG Jiaqiu, et al. Reliability analysis of urban street network based on complex network theory[J]. Science of Surveying and Mapping, 2013, 38(3): 83-86. (in Chinese) |
 2019, Vol. 42
2019, Vol. 42


