1b. 湖南科技大学 煤矿安全开采湖南省重点实验室, 湖南 湘潭 411201;
1c. 湖南科技大学 资源环境与安全工程学院, 湖南 湘潭 411201;
2. 河南理工大学 安全工程学院, 河南 焦作 454000
1b. Hunan Province Key Laboratory of Safe Mining Techniques of Coal Mines, Hunan University of Science and Technology, Xiangtan 411201, Hunan, P. R. China;
1c. School of Resource Environment and Safety Engineering, Hunan University of Science and Technology, Xiangtan 411201, Hunan, P. R. China;
2. School of Safety Science and Engineering, Henan Polytechnic University, Jiaozuo 454000, Henan, P. R. China
新型射流的研发是水射流技术的一个重要发展方向。喷嘴是水射流技术的核心构件,直接关系射流束的形状与发散特性,因此喷嘴形状的改变将会形成新型的水射流。近年来,在一些特殊用途中形成了一些特殊出口形状的喷嘴,诸如三角形、正方形、椭圆形等,这些非圆形出口的喷嘴统称为异形喷嘴。
国内外诸多学者对异形喷嘴的水射流展开过研究。何小婷[1]采用圆形喷嘴和方形喷嘴进行了砂砖试块的冲蚀实验,结果表明在一定条件下方形喷嘴的冲蚀深度和体积均大于圆形喷嘴。禹言芳等[2]对圆形、椭圆、正方、十字、三角5种形状喷嘴的射流卷吸特性进行数值模拟研究,获得了不同形状喷嘴的射流轴向最大时均速度均随轴向位置增大呈幂函数关系衰减的规律。杨敏官等[3]提出将中心体喷嘴与正方形出口、三角形出口和圆形出口3种喷嘴组合以产生更好的空化射流效果的思路。Rouly等[4]设计了一种长短轴参数可变的椭圆形喷嘴结构,以此来获得高压、低发散的水射流,并在此基础上设计了圆形、矩形和椭圆形3种喷嘴用来传输切削液。结果表明圆形喷嘴的传输性能最好,但需要更高的入口压力[5]。文献[6]采用高速摄影技术观测了圆形、三角形、正方形3种喷嘴形式下射流空间流态,发现圆形喷嘴喷头射程最远,三角形喷嘴喷头射程最短。恽强龙等[7]研究了异形喷嘴情况下液气射流泵的水力性能,表明圆形喷嘴较异形喷嘴需要的工作压力较低。部分学者采用粒子图像测速(PIV)技术对不同形状喷嘴的射流流场进行了测量,分析了不同形状对射流流动特性的影响规律[8]。李栋等[9]同时考虑了异形喷嘴形状及压力的改变对射流形态变化的影响。另外一些学者采用数值模拟的方法对异形喷嘴内部流场[10]及内部热质传递规律[11, 12]进行了研究。异形喷嘴被用于农业喷洒具有良好的特性,受到了诸多的关注[13]。
上述文献表明,以往对异形喷嘴的研究主要聚焦在射流速度、流场形态与热质传递等方面,少有文献提及到异形喷嘴的冲击性能及其影响规律。唐川林等[14]虽然通过改变喷嘴出口形状来增强脉冲射流打击力,但其获得的是腔内压力峰值的变化规律。赵欣[15]分析了正三边形、正四边形和圆心喷嘴在不同压力下的射流打击力,然而其所述的打击力为射流作用于物体的总作用力,并不能直接表征射流破碎物料的能力。对物料破碎起决定性作用的是射流作用于物料单位面积上的冲击力,即压强。因此在上述研究的基础上,笔者拟采用实验研究的手段对不同形状喷嘴水射流的中心冲击力(中心压强)开展研究。
1 实验设计 1.1 基本原理高压水射流冲击物体表面时,流体的速度和方向均会发生改变,其动量必然随之改变。该过程中损失的动量将会以冲击力F的形式作用于物体表面。根据动量定理可以获得F的计算公式如下
| $ F = \rho Qv(1 - {\rm{cos}}\theta ), F = \rho Qv(1 - {\rm{cos}}\theta ), $ | (1) |
式中:ρ为流体的密度,kg/m3;Q是射流的流量,L/min;v为流体的速度,m/s;θ是流体冲击物体后的返流方向与物体壁面的夹角。然而式(1)计算出的冲击力F是水射流作用于物体表面的总冲击力,并不能直接表征其破碎物体的能力。水射流在物体表面产生的水锤压力Pwh才是诱导物体初始破碎核形成的关键作用力[16-17]
| $ {P_{{\rm{wh}}}} = \rho Cv, $ | (2) |
式中C为冲击波的传播速度。后续产生的滞止压力Ps是物体破碎发展的直接作用力
| $ {P_{\rm{s}}} = \frac{1}{2}\rho {v^2}。$ | (3) |
因此,水射流作用于物体单位面积上的冲击力才是物体破碎的表征。笔者拟采用试验手段来测定不同形状喷嘴下水射流的冲击压强P。即首先测试出水射流的总冲击力F,然后再根据P=F/A计算出冲击压强,其中A为水射流作用于物体表面的总面积。总冲击力F通过一定的测试手段容易获得,然而作用面积A却变化较大。另外,根据图 1所示的非淹没水射流结构可以知道,水射流自喷嘴喷出后,流体与周围静止的气体必然要发生动量与能量的交换,导致水射流边界速度不断降低,从而在射流截面上形成中心速度大、边界速度小的梯度。这种速度梯度变化会导致射流截面上冲击压强的分布不均,从而不能直接采用P=F/A的方法来计算冲击压强。
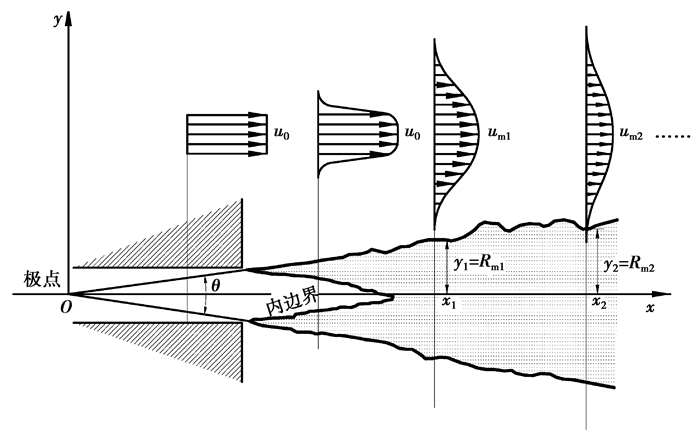
|
图 1 非淹没水射流结构图 Fig. 1 The structure of unsubmerged water jet |
假设水射流某一截面(如图 1中的轴向x1处)中心处的冲击压强为Pm,则该截面上任意一点的冲击压强Py可表示为[18]
| $ \frac{{{P_y}}}{{{P_{\rm{m}}}}} = 1 - 3{\left( {\frac{y}{{{R_x}}}} \right)^2} + 2{\left( {\frac{y}{{{R_x}}}} \right)^3}, $ | (4) |
式中:y是该截面上某一点与射流轴心的垂直距离,Rx是该截面上射流的半径。对式(4)进行变化可以获得该截面任意一点冲击压强Py表示形式
| $ {P_y} = (1 - 3{Y^2} + 2{Y^3}){P_{\rm{m}}}, $ | (5) |
式中,Y=y/Rx,且Y∈(-1,1)。因此,该截面所受到的总的冲击力可以表示为
| $ F = \int_{ - Y}^Y {(1 - 3{Y^2} + 2{Y^3})} {P_{\rm{m}}}{\rm{d}}y = 2\left( {Y - {Y^3} + \frac{{{Y^4}}}{2}} \right){P_{\rm{m}}}。$ | (6) |
在无量纲量Y足够小的情况下,对式(6)略去高阶项可以得到
| $ F \approx 2Y{P_{\rm{m}}}。$ | (7) |
因此可由式(7)计算获得射流中心的冲击压强Pm≈F/2Y。该计算公式对于所有呈中心对称或轴对称形状的喷嘴均适用。
1.2 实验喷嘴设计本实验设计了5种出口形状的喷嘴,分别为圆形、正方形、椭圆形、十字形与正三角形。根据出口面积相同的原理,设定所有喷嘴出口的截面面积S=π mm2,从而可以依次计算出5种喷嘴的结构尺寸,如表 1所示,其中圆形喷嘴的直径2 mm为这5种形状喷嘴的当量直径。所有喷嘴的内部均采用收敛段与直线段相结合的结构,如图 3所示。其中L1为直线段的长度,L2为总喷嘴的长度,α为收敛段的张角,Φ为喷嘴的外直径,R为喷嘴的当量直径,各种形状喷嘴的详细尺寸见表 1。根据表 1所示的参数,采用线切割的加工方式制备出如图 2所示的喷嘴实物。
| 表 1 喷嘴结构参数 Table 1 The structural parameters of nozzle |

|
图 2 5种喷嘴出口形状及尺寸 Fig. 2 The shape and size of the five different nozzles |
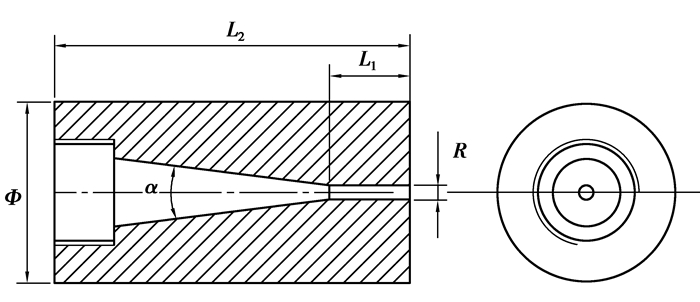
|
图 3 喷嘴结构示意图 Fig. 3 Overall structure of nozzle |
为了精确测试不同喷嘴形状下水射流的冲击力,自主设计了如图 4所示的水射流冲击力测试实验平台。该平台由两个子系统组成,分别为水射流发生系统与数据采集系统。
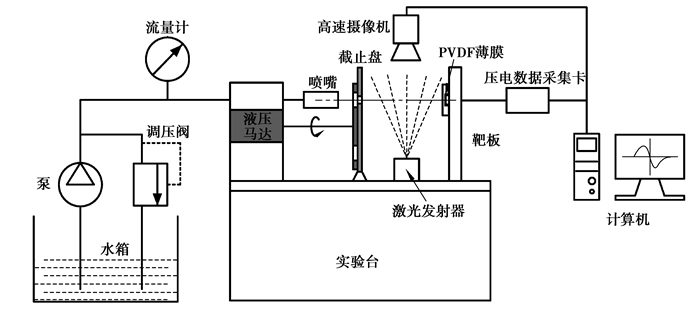
|
图 4 水射流冲击力测试系统示意图 Fig. 4 The sketch of the impacting pressure testing system for water jet |
水射流发生系统由水箱、乳化泵、电磁流量计与特制喷嘴组成。为了消除乳化泵加压过程的影响,本实验采用旋转截止盘来获取截断式脉冲水射流。具体操作步骤为:在乳化泵加压未稳定之前,使喷嘴避开截止盘的孔口,等待乳化泵稳定至实验设定的压力后开启液压马达,以200 r/min的转速带动截止盘旋转从而形成稳定压力的脉冲水射流。
数据采集系统是本实验的核心部分。首先,采用PVDF薄膜传感器来获取水射流冲击的电量变化。PVDF薄膜压电传感器与其他压力传感器相比,具有电量高、结构灵巧、极高响应频率、线性范围广和低噪影响等特性。本实验采用美国Dynasen公司生产的PVF4.040-EK型PVDF压电薄膜传感器。该传感器的直径为0.5 mm,厚度约为0.1 mm,采样频率为100 MHz,且可以直接承受高达10 GPa的冲击荷载。因此,可以计算出无量纲变量Y=0.5 mm/2 mm=0.25,代入式(5),可以得到Py≈0.84Pm。计算结果表明,采用该PVDF传感器来测量冲击压力时,所测得的冲击压强P≥0.84Pm。这是在未考虑射流发散情况下的结果,若考虑射流的发散性,Rx>2 mm,所测试的冲击压强更加大于0.84倍的中心压强。鉴于PVDF薄膜上受到的冲击压强与中心冲击压强接近,因此本实验采用式(7)来计算水射流的中心冲击压强。针对PVDF采集的数据,采用高频数据采集卡进行放大整形,并将最终数据传输至计算机保存。另外,试验拟采用日本Olympus公司生产的i-SPEED-TR型高速摄像机捕捉不同形状喷嘴的水射流撞击平面靶体瞬间的图像,并采用该高速摄像机的配套软件i-SPEEDViewer对图像进行二值化处理来提取水射流的扩散形态。
2 实验结果分析及讨论 2.1 不同形状喷嘴水射流的冲击形态特征图 5为二值化处理后不同形状喷嘴的水射流冲击平面靶板的扩散形态。不同喷嘴形状水射流的射流前端呈现出极大的差异性:圆形喷嘴射流前端类似伞状结构,这是由射流横截面上中心速度大边缘速度小的梯度所导致的;方形喷嘴的射流前端较圆形喷嘴更加发散,未有出现明显的伞状结构;十字形喷嘴射流前端出现了伞状结构,但更加尖锐,且宽度明显比圆形喷嘴的小;三角形喷嘴的射流前端较为紧凑,出现了类似伞状的前端结构;椭圆形喷嘴的射流前端出现了明显的伞状结构,但最为发散、尺寸最大。通过射流前端的形状可以推测出,方形喷嘴和椭圆形喷嘴的射流结构较为发散,圆形喷嘴和三角形喷嘴次之,十字形喷嘴射流结构较为收敛,但其尺寸最小。
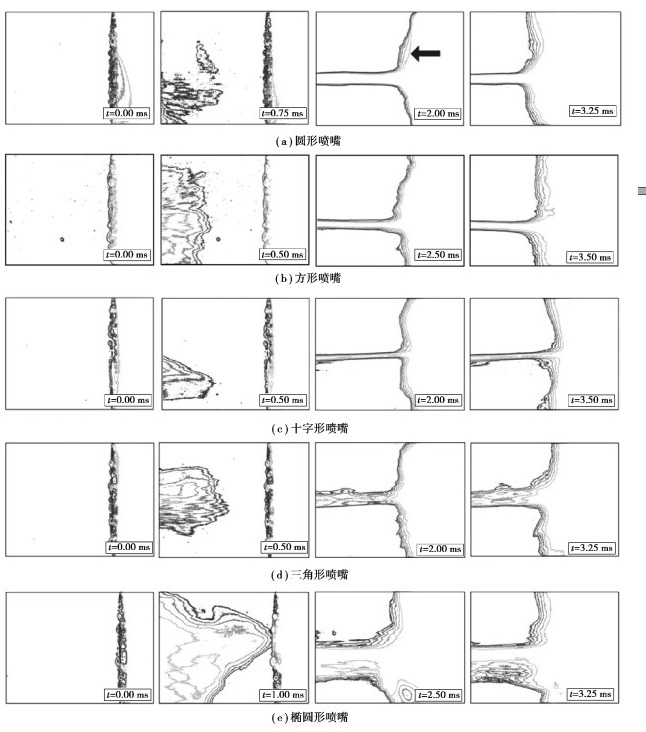
|
图 5 水射流冲击平面靶板的扩展形态 Fig. 5 The diffusion form of water jet impacting flat target |
另外从图 5还可以看出,当射流接触到平面靶板的瞬间,高速流体在撞击中心区域附近迅速形成隆起,如图 5(a)中t=2.00 ms的黑色箭头所示。随着冲击的继续,隆起部分的流体迅速向外移动,并最终形成t=3.25 ms时刻的流动形态。分析表明,高速流体撞击固体靶板时会产生冲击波,一部分冲击波能量以球面波的形式向固体内部传播,另一部分冲击波能量以激波的形式反向射流向流体内部传播,使流体边缘产生扰动。在液固接触的瞬间,撞击后的流体会向外扩散,同时产生的冲击波也会向四周传播。如果冲击波对流体边缘产生扰动时流体还未来得及扩散,此时便会在扰动的区域产生图中的隆起[19]。根据文献[20],在隆起的区域会产生极高的冲击压力,即水锤压力。因此,隆起区域的范围越大、持续时间越长,射流冲击靶板产生的水锤压力越大。根据图 5所示,圆形喷嘴与方形喷嘴的水射流冲击靶板后产生的隆起较为明显,十字形和三角形喷嘴水射流次之,而椭圆形喷嘴撞击靶板后产生的隆起范围最小。
采用i-SPEEDViewer软件测量出不同形状喷嘴水射流的可视直径Ds,并采用靶板的直径Db对其进行无量纲处理,获得图 6所示的无量纲射流直径D=Ds/Db。根据图 6所示,椭圆形喷嘴水射流的可视直径较其他喷嘴射流的直径大3~4倍,圆形喷嘴、方形喷嘴与三角形喷嘴水射流的直径几乎一致,而十字形喷嘴水射流的直径较小,约为圆形喷嘴水射流直径的一半。
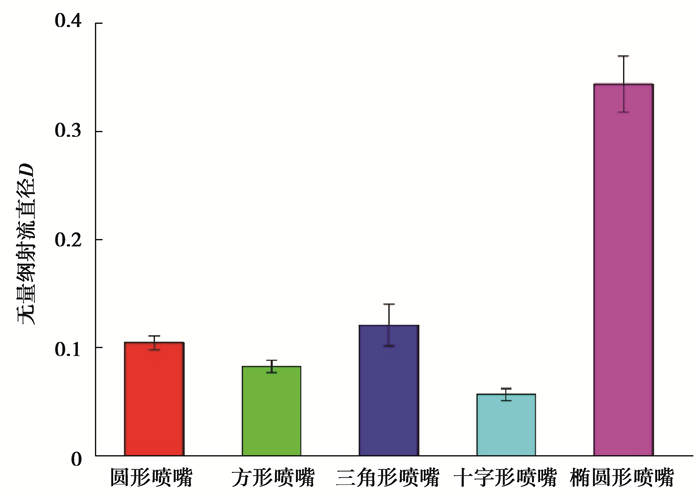
|
图 6 不同形状喷嘴的射流直径 Fig. 6 The jet diameters of different nozzles |
根据图 5所示射流冲击靶板后的扩展规律可以推断,水射流的速度对其扩展规律影响较大,最终导致其冲击压力变化较大。依次选择射流速度为100,150,200 m/s作为实验速度来开展测试实验。根据公式v≈44.7
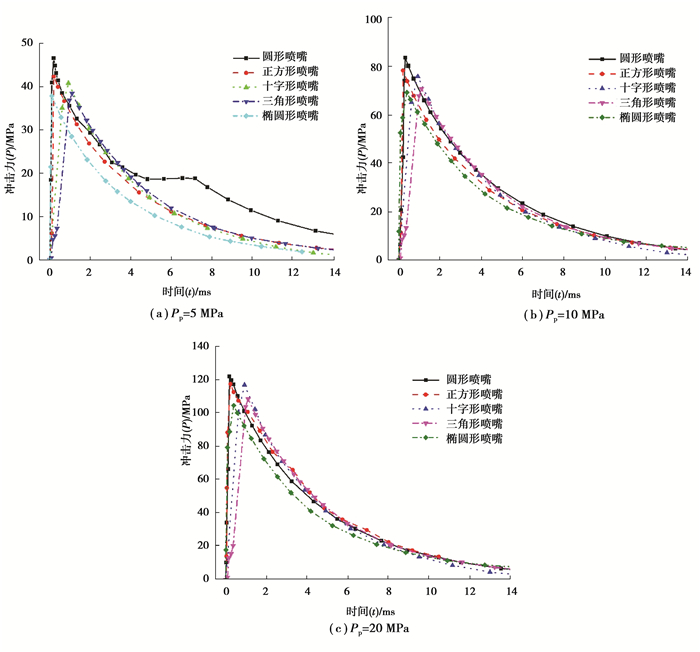
|
图 7 水射流冲击平面靶板的压力曲线 Fig. 7 The pressure profile of water jet impacting target |
根据图 7所示的冲击压力曲线,不同喷嘴形状的高压水射流在冲击固体靶板后极短的时间内(约为0.2 ms),靶板所受冲击压力迅速升高至峰值压力,随后逐渐衰减至较小的稳定值。这一现象完全符合以往对水射流冲击压力的研究结果,即水锤压力阶段与滞止压力阶段。至于图 7(a)中圆形喷嘴的冲击压力曲线在4~8 ms时出现了异常变化规律,根据现场实验情况,分析认为这是由于PVDF薄膜传感器出现了损坏所导致的。这一段异常变化不会影响水射流冲击压力的总体变化规律。由于本实验采用的是截断式脉冲水射流,每一脉冲段的水射流极短,因此后续的滞止压力持续时间较短。
根据冲击压力曲线图可以看出,在相同的系统泵压下,圆形喷嘴水射流的峰值冲击压力最大,正方形喷嘴水射流次之,随后三角形喷嘴、十字形喷嘴和椭圆形喷嘴水射流的峰值冲击压力依次降低。随着水射流冲击靶板的持续,不同形状喷嘴水射流的冲击压力逐渐趋于一致,这就是所谓的滞止压力阶段。然而与传统的滞止压力不同的是,本文实验获得的滞止压力并没有稳定在一个固定的值,而是逐渐衰减至零。造成这种差异的主要原因有两个:一是本实验采用的截断脉冲水射流持续时间较短;二是截断水射流的形状并非规整均匀的,而是呈首部大、尾部小的梭形[22]。
测试数据表明,在相同工况下不同形状喷嘴的水射流冲击平面靶板时产生的峰值冲击压力有所差异。根据射流冲击靶板后的扩展形态可知,水射流集束性越好,冲击产生隆起区域的范围便会越广,最终冲击产生的峰值压力也就越大。因此综合来看,圆形喷嘴喷射的水射流在冲击靶面前,射流束较为均匀,集束性较好;正方形喷嘴喷射的射流较圆形喷嘴有所发散,但总体来说集束性较好;正三角形喷嘴喷射的水射流虽然较为均匀,但其形态出现了明显的不对称性,射流束偏向一方;十字形喷嘴与椭圆形喷嘴喷射的水射流较前三种喷嘴喷射的水射流出现了明显的发散,这两种喷嘴喷射的水射流在撞击靶面前的射流束极不均匀,尤其是椭圆形喷嘴的水射流出现了较大的发散。
2.3 泵压对峰值冲击压力的影响规律高压水射流的峰值压力(即水锤压力)对其冲击性能影响巨大,而系统泵压是峰值压力的重要影响因素之一。为了探究不同形状喷嘴水射流的冲击峰值压力与泵压的关系,选取了5,10,20 MPa的系统泵压来开展实验,获取了不同形状喷嘴水射流的峰值压力大小与峰值压力持续时间随系统泵压的变化规律。
图 8所示为峰值压力大小随系统泵压的变化曲线。根据图 8所示,所有形状喷嘴水射流的峰值冲击压力均随着系统泵压的增大而呈现非线性的增加趋势。具体表现为在系统泵压较小时(如系统泵压小于10 MPa时)峰值压力随系统泵压的增加而快速增加,当系统泵压逐渐增大后(如大于10 MPa),峰值压力随泵压递增的速度稍有降低。
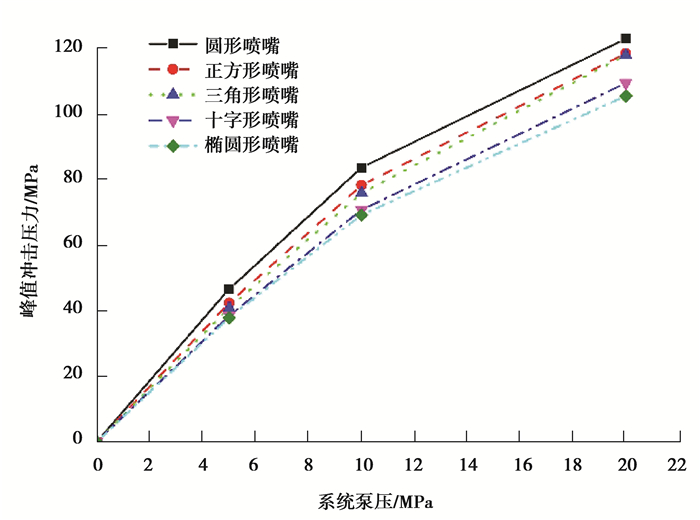
|
图 8 泵压与峰值压力的关系曲线 Fig. 8 The relationship between pump pressure and peak pressure |
图 9所示为峰值压力持续时间随系统泵压的变化规律。根据图 9所示,对于特定喷嘴形状的水射流,其峰值压力的持续时间随泵压的增加几乎保持不变。圆形喷嘴水射流的峰值压力持续时间最长,约为1.1 ms,正方形喷嘴次之,约为1 ms,其他3种形状喷嘴水射流的峰值压力持续时间大小相当,约为0.2 ms。
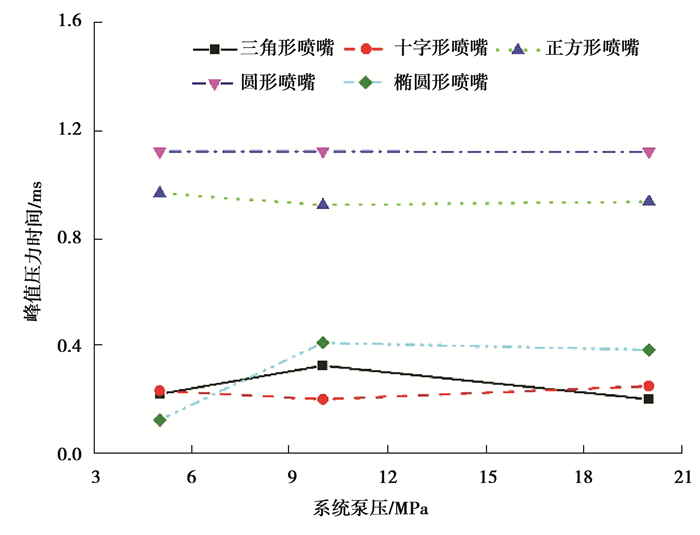
|
图 9 泵压与峰值压力持续时间的关系曲线 Fig. 9 The relationship between pump pressure and duration of peak pressure |
设计了3种形状的喷嘴,在自主设计的水射流冲击力测试平台上开展了冲击测试实验,采用PVDF薄膜传感器直接获取冲击压力,采用高速摄像机捕捉射流扩展形态。研究结果表明:
1) 在相同的工况下,圆形喷嘴水射流的集束性最好,其冲击平面靶板瞬间产生的隆起区域最广,由此诱导产生的中心冲击压力最大,依次是正方形、三角形与十字形喷嘴,椭圆形喷嘴的水射流形态最为发散,其中心冲击压力最小;
2) 不同形状喷嘴水射流的峰值冲击压力均随着系统泵压的增加而呈现非线性的递增趋势,但所有喷嘴形状水射流的峰值压力持续时间随着泵压的改变而几乎保持不变。
研究结果可为水射流喷嘴的选型提供一定的理论依据。但由于实验组数和论文篇幅的限制,只选择了3组压力开展了测试实验,对于超高压条件下不同形状喷嘴的冲击特性有待进一步研究。
| [1] |
何小婷.不同喷嘴形状的自振脉冲喷嘴数值模拟与实验研究[D].株洲: 湖南工业大学, 2014. HE Xiaoting. Numerical simulation and experimental research on self-excited oscillation pulsed nozzle of different nozzle shape[D]. Zhuzhou: Hunan University of Technology, 2014.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-11535-1014365044.htm |
| [2] |
禹言芳, 李春晓, 孟辉波, 等. 不同形状喷嘴的射流流动与卷吸特性[J]. 过程工程学报, 2014, 14(4): 549-555. YU Yanfang, LI Chunxiao, MENG Huibo, et al. Flow and entrainment characteristics of jet from different shape nozzles[J]. The Chinese Journal of Process Engineering, 2014, 14(4): 549-555. (in Chinese) |
| [3] |
杨敏官, 肖胜男, 康灿, 等. 出口形状对中心体喷嘴射流性能的影响[J]. 流体机械, 2011, 39(5): 13-19. YANG Minguan, XIAO Shengnan, KANG Can, et al. Influence of outlet profile on performance of central-body nozzle[J]. Fluid Machinery, 2011, 39(5): 13-19. (in Chinese) DOI:10.3969/j.issn.1005-0329.2011.05.004 |
| [4] |
Rouly E, Warkentin A, Bauer R. Design and testing of low-divergence elliptical-jet nozzles[J]. Journal of Mechanical Science and Technology, 2015, 29(5): 1993-2003. DOI:10.1007/s12206-015-0420-7 |
| [5] |
Rouly E, Bauer R J, Warkentin A. An investigation into the effect of nozzle shape and jet pressure in profile creepfeed grinding[J]. Proceedings of the Institution of Mechanical Engineers, Part B:Journal of Engineering Manufacture, 2017, 231(7): 1116-1130. DOI:10.1177/0954405415584960 |
| [6] |
周小引, 李红, 蒋跃. 低压喷头异形喷嘴水量分布均匀性试验研究[J]. 排灌机械工程学报, 2017, 35(5): 448-453. ZHOU Xiaoyin, LI Hong, JIANG Yue. Study on water distribution uniformity of non-circular nozzles at low pressure[J]. Journal of Drainage and Irrigation Machinery Engineering, 2017, 35(5): 448-453. (in Chinese) |
| [7] |
恽强龙, 向清江, 李红. 几种异形喷嘴喷射的液气射流泵性能试验研究[J]. 流体机械, 2011, 39(11): 1-4, 16. YUN Qianglong, XIANG Qingjiang, LI Hong. Experimental study on the performance of liquid jet gas pump with non-circular nozzle[J]. Fluid Machinery, 2011, 39(11): 1-4, 16. (in Chinese) DOI:10.3969/j.issn.1005-0329.2011.11.001 |
| [8] |
陈冬林, 贠英, 米建春, 等. 菱形自由射流与圆形自由射流流动特性的粒子图像测速研究[J]. 中国电机工程学报, 2012, 32(17): 76-81. CHEN Donglin, YUN Ying, MI Jianchun, et al. Particle image velocimetry measurements of turbulent jets issuing from diamond and circular orifice plates[J]. Proceedings of the CSEE, 2012, 32(17): 76-81. (in Chinese) |
| [9] |
李栋, 卢晓江, 赵欣. 异形喷嘴低压射流形态的实验研究[J]. 轻工机械, 2006, 24(3): 18-20. LI Dong, LU Xiaojiang, ZHAO Xin. Experimental study on low pressure jet characteristic of the non-circle jet nozzle[J]. Light Industry Machinery, 2006, 24(3): 18-20. (in Chinese) DOI:10.3969/j.issn.1005-2895.2006.03.007 |
| [10] |
左海宁, 白璐, 周家日, 等. 异形喷嘴内部流场的可视化研究[J]. 湖南工业大学学报, 2013, 27(1): 43-47. ZUO Haining, BAI Lu, ZHOU Jiari, et al. Visualization research on the internal flow field of non-circle nozzle[J]. Journal of Hunan University of Technology, 2013, 27(1): 43-47. (in Chinese) DOI:10.3969/j.issn.1673-9833.2013.01.010 |
| [11] |
Singh D, Premachandran B, Kohli S. Effect of nozzle shape on jet impingement heat transfer from a circular cylinder[J]. International Journal of Thermal Sciences, 2015, 96: 45-69. DOI:10.1016/j.ijthermalsci.2015.04.011 |
| [12] |
Vinze R, Chandel S, Limaye M D, et al. Influence of jet temperature and nozzle shape on the heat transfer distribution between a smooth plate and impinging air jets[J]. International Journal of Thermal Sciences, 2016, 99: 136-151. DOI:10.1016/j.ijthermalsci.2015.08.009 |
| [13] |
魏洋洋, 袁寿其, 李红, 等. 异形喷嘴变量喷头水力性能试验[J]. 农业机械学报, 2011, 42(7): 70-74. WEI Yangyang, YUAN Shouqi, LI Hong, et al. Hydraulic performance experiment of the variable-rate sprinkler with non-circle nozzle[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(7): 70-74. (in Chinese) |
| [14] |
唐川林, 王晓明, 胡东, 等. 自振脉冲喷嘴中异形结构对射流振荡频率的影响[J]. 矿山机械, 2015, 43(1): 15-20. TANG Chuanlin, WANG Xiaoming, HU Dong, et al. Influence of special-outlet self-exciting oscillation pulsed nozzle on oscillation frequency[J]. Mining & Processing Equipment, 2015, 43(1): 15-20. (in Chinese) |
| [15] |
赵欣.异形喷嘴射流特性的实验研究[D].天津: 天津科技大学, 2005. ZHAO Xin. Experimental study on the jet characteristic of non-circle jet nozzle[D]. Tianjin: Tianjin University of Science & Technology, 2005.(in Chinese) http://www.cnki.com.cn/Article/CJFDTotal-QGJX200504006.htm |
| [16] |
司鹄, 王丹丹, 李晓红. 高压水射流破岩应力波效应的数值模拟[J]. 重庆大学学报(自然科学版), 2008, 31(8): 942-945, 950. SI Hu, WANG Dandan, LI Xiaohong. Stress wave effect in numerical simulation on rock breaking under high-pressure water jet[J]. Journal of Chongqing University(Natural Science Edition), 2008, 31(8): 942-945, 950. (in Chinese) |
| [17] |
Lu Y Y, Huang F, Liu X C, et al. On the failure pattern of sandstone impacted by high-velocity water jet[J]. International Journal of Impact Engineering, 2015, 76: 67-74. DOI:10.1016/j.ijimpeng.2014.09.008 |
| [18] |
黄飞.水射流冲击瞬态动力特性及破岩机理研究[D].重庆: 重庆大学, 2015. HUANG Fei. On the transient dynamics of water jet impinging target and the mechanism of water jet breaking rock[D]. Chongqing: Chongqing University, 2015.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10611-1015971066.htm |
| [19] |
Huang F, Li S Q, Zhao Y L, et al. Study on lateral jetting range during an arc-curved jet impacting nonplanar solid surfaces[J]. Journal of Fluids Engineering, 2018, 140(10): 101-102. |
| [20] |
Bowden F P, Field J E. The brittle fracture of solids by liquid impact, by solid impact, and by shock[J]. Proceedings of the Royal Society of London Series A:Mathematical, Physical and Engineering Sciences, 1964, 282(1390): 331-352. DOI:10.1098/rspa.1964.0236 |
| [21] |
黄飞, 卢义玉, 李树清, 等. 高压水射流冲击速度对砂岩破坏模式的影响研究[J]. 岩石力学与工程学报, 2016, 35(11): 2259-2265. HUANG Fei, LU Yiyu, LI Shuqing, et al. Influence of velocity of high-pressure water jet on failure patterns of sandstone[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(11): 2259-2265. (in Chinese) |
| [22] |
陆朝晖.高压脉冲水射流流场结构的数值模拟及破硬岩机理研究[D].重庆: 重庆大学, 2012. LU Zhaohui. CFD modeling on flow-field structure of high pressure pulse water jet and its hard rock fragmentation mechanism[D]. Chongqing: Chongqing University, 2012.(in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10611-1012047346.htm |
 2019, Vol. 42
2019, Vol. 42


