柔性作业车间调度问题(FJSP, flexible job-shop scheduling problem)是一种由经典作业车间调度问题(JSP, Job shop schedule problem)扩展而来的NP-hard问题,比JSP更加贴近真实生产加工环境。自1990年提出以来就备受研究人员和技术人员的关注。
与传统作业车间相比,柔性作业车间调度减少了加工过程中对机器的约束,增加机器柔性,扩大可行域搜索范围,是较作业车间调度更复杂的NP难问题。在过去30年中,随着计算机科学技术的不断进步,诸如模拟退火、禁忌搜索、遗传算法、粒子群算法等元启发式方法广泛应用于求解FJSP问题,且取得了良好的效果,诸如Nouiri等[1]采用粒子群优化算法(PSO, particle swarm optimization)求解该FJSP问题,使最大完成时间最小;Driss等[2]在改进染色体表达方式,且引入不同交叉、变异策略的基础上提出一种新的遗传算法(NGA, new genetic algorithm)求解FJSP。
近年来随着互联网技术的飞速发展,许多新的群体智能算法不断涌现,如Mirjalili等[3]模拟灰狼的领导模式及狩猎机制提出灰狼算法(GWO, grey wolf optimize);研究了蚁狮的捕猎模式,提出蚁狮算法(ALO, ant lion optimizer)[4]。Neshat等[5]根据鱼群的群体行为提出一种人工鱼群算法(AFSA, artificial fish-swarm algorithm)。
这些新算法的出现为求解FJSP提供了新的思路。Jiang等[6]提出一种以最大完工时间最小为目标的混合GWO算法,建立FJSP的离散空间与GWO连续空间的映射关系,并引入变邻域搜索策略提高算法的全局能力实现问题求解;GE等[7]提出了一种高效的基于分布估计的人工鱼群模型(AFSA-ED),以获得智能调度策略;Gao等[8]通过改进种群初始化策略,并引入新的和声生成规则,提出一种求解FJSP的有效离散和声搜索算法。
鲸鱼群算法是由Zeng等[9]提出一种新的自然启发元启发式算法,算法模拟鲸鱼群狩猎行为,用于求解函数优化问题。针对FJSP问题特点,对鲸鱼群算法进行改进,通过设计鲸鱼个体位置表达方式及距离计算方式,引入协同搜索“较优且较近”鲸鱼策略和变邻域搜索算法,成功将鲸鱼群算法用于求解FJSP问题,取得了较好的结果。
1 柔性作业车间调度问题概述柔性作业车间调度问题,即n个工件{J1, ..., Jn}在m台机器{M1, ..., Mn}上进行加工[10]。每个工件包含一道或多道工序,每道工序可以在一台或多台机器上进行加工,在不同机器上加工所需加工时间可以不同,同一工件不同加工工序之间的加工顺序固定。因此,柔性作业车间调度问题包括机器选择和工序排序2个子问题。通过为每个工件的每道工序安排合适的加工机器,确定每台机器上各工序的最佳加工顺序及相应开始加工、结束加工时间,实现诸如最大完工时间等性能指标的优化[11]。
柔性作业车间调度按可选加工机器集分为完全柔性作业车间调度和部分柔性作业车间调度。完全柔性作业车间调度,指每个工件的每道工序均可在任意一台机器上进行加工;若存在某一个工件的某一道工序不能在某台机器上进行加工,则为部分柔性作业车间调度[12]。
在加工过程中,调度方案还需满足以下约束条件:
•同一台机器上同一时刻只能加工一个工件。
•同一工件的同一道工序在同一时刻只能被一台机器加工。
•每个工件的每道工序一旦开始加工,不可中断。
•不同工件之间优先级相同。
•同一工件的不同工序之间存在加工顺序约束,不同工件的不同工序之间无顺序约束。
•所有工件在零时刻均可以被加工。
以最大完工时间最小为目标函数,其公式表示形式如下
| $ \min C_{M}=\min \left(\max \left(C_{k}\right)\right) 1 \leqslant k \leqslant m, $ | (1) |
式中:m为机器数;Ck为机器k的加工完成时间。
表 1为一个包含2个工件共5道工序,5台机器部分柔性作业调度问题的加工机器和加工时间表。其中数字为工序在对应机器上所需加工时间,“—”表示该工序不可在此机器上进行加工。若表 1中不含“—”,则为完全柔性作业车间调度问题。
| 表 1 部分柔性作业车间调度问题实例 Table 1 Example of partial FJSP |
鲸鱼群算法是一种新型群体智能优化算法,源于鲸鱼群利用超声波通信进行捕食的群体行为,由Zeng等[9]于2017年提出。算法基本原理如下:首先在定义域内随机生成一组解作为初始种群,种群中的每个个体为一条鲸鱼。然后根据种群中各鲸鱼的适应度值和所在位置,依次为每条鲸鱼搜索“优且最近”的目标鲸鱼,即适应度更优的鲸鱼个体中距离待移动个体最近的鲸鱼。每条鲸鱼均以其目标鲸鱼为导向以某种方式进行移动,产生新一代种群。
2.2 基本步骤鲸鱼群算法框架如图 1所示。首先,随机初始化鲸鱼群,鲸鱼群中每条鲸鱼代表解空间中的一个候选解。然后,为种群中的每个个体依次寻找“较优且最近”的鲸鱼,其中个体优劣程度通过优化目标定义的适应度函数评价,2条鲸鱼之间的距离采用欧式距离进行计算。

|
图 1 鲸鱼群算法框架 Fig. 1 The general frame of Whale Swarm Algorithm |
若“较优且最近”鲸鱼存在,则按照公式(2)以“较优且最近”的鲸鱼为目标移动;否则,鲸鱼个体位置保持不变。
| $ x_{i}^{t+1}=x_{i}^{t}+\operatorname{rand}\left(0, \rho_{0} \cdot \mathrm{e}^{-\eta \cdot d X \cdot Y}\right) \cdot\left(y_{i}^{t}-x_{i}^{t}\right), $ | (2) |
其中:X为待移动鲸鱼的位置信息;xit+1和xit分别为鲸鱼X的第i个元素在第t+1次、t次迭代后所在位置;Y为鲸鱼X的“较优且最近”鲸鱼,yit为鲸鱼Y的第i个元素在第t次迭代后所在位置;dX, Y为X鲸鱼和Y鲸鱼之间的距离;ρ0为超声波源的强度,一般情况ρ0=2;η为超声波衰减系数,其值由目标函数决定,一般情况下由公式η= -20·ln 0.25/dmax算得近似值,在实验的基础上调整至最优值或近似最优值;rand(0, ρ0*e-η*dX, Y)为介于0和ρ0*e-η*dX, Y间的随机数。
由公式(2)可知,当鲸鱼X与“较优且最近”鲸鱼Y之间距离很近时,鲸鱼X会积极地向鲸鱼Y随机移动;否则,鲸鱼X会消极地向鲸鱼Y随机移动。
3 改进鲸鱼群算法求解FJSP 3.1 改进鲸鱼群算法流程通过设计一种新的距离计算方式,并引入协同式搜索策略改进鲸鱼群算法,结合基于关键路径的变邻域搜索算法提出改进鲸鱼群算法。
该算法流程如图 2所示,具体流程如下

|
图 2 改进鲸鱼群算法流程 Fig. 2 Flow chart of improved Whale Swarm Algorithm |
Step 1:参数设置。确定种群规模和最大迭代次数。
Step 2:初始化种群并评价种群中个体的适应度值。
Step 3:判断是否满足终止条件。若满足,则输出当前最优解;否则,转到Step 4;
Step 4:依次遍历鲸鱼群,对种群内每一个鲸鱼个体寻找其“较优且较近”鲸鱼。若“较优且较近”鲸鱼存在,转到Step 5,否则,转到Step 6;
Step 5:待移动鲸鱼与“较优且较近”的鲸鱼以JBX交叉方式移动至新位置。评价新个体,并将新个体中的较优个体取代原鲸鱼,转到Step 7。
Step 6:随机选择工序排序编码中的2道工序,若属于同一工件,则重新选择对应加工机器;否则,交换两工序的位置,并重新安排对应加工机器。转Step 7。
Step 7:判断是否遍历种群中的所有鲸鱼个体。若满足条件,则转到Step 8;否则,选择未进行遍历操作的鲸鱼个体转到Step 4;
Step 8:对此时种群中的最好个体,利用所述2种邻域结构进行变邻域搜索,求得较优解后更新原来个体,转到Step 2。
3.2 个体编码与解码根据FJSP的特征模型,采用基于机器编码(MS)和基于工序编码(OS)的双层编码方式[10]对鲸鱼个体进行编码。以表 1所示问题为例,编码结果如图 3所示。基于机器编码从第一个工件的第一道加工工序开始直到最后一个工件的最后一道加工工序依次分配加工机器,数字N为对应工序可选机器集内的第N台机器;基于工序的编码中数字代表工件号,出现次数为对应工件的加工工序。
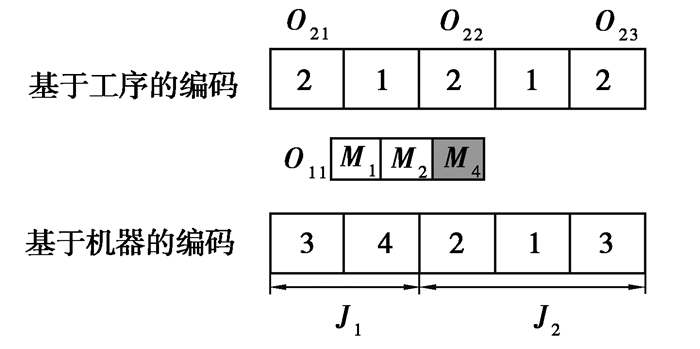
|
图 3 鲸鱼个体编码 Fig. 3 Encoding of individual Whales |
初始解的质量对于鲸鱼个体的优劣紧密相关,随机初始化生成的鲸鱼群质量普遍偏低,在求解过程中效率较低。引入文献[13]提出的全局搜索和局部搜索方法,同随机方法按比例生成鲸鱼个体组成初始鲸鱼群。其权值分配为:全局搜索60%,局部搜索30%,随机生成10%。
3.4 个体位置表达方式及距离计算由于上述编码方案产生的鲸鱼种群属于离散问题,鲸鱼群算法中提出的距离公式适用于求解连续型问题,不能直接用于离散型问题求解。因此,提出一种新的距离计算方法:依次比较2条鲸鱼个体对同一工件的同一道工序在机器选择和加工次序上的不同,各差值之和为二者间的距离值。
对鲸鱼X进行主动调度解码得到每道工序的加工机器mijX,及其在加工机器上的加工次序sijX,则工序Oij的位置信息为(mijX, sijX), 表示第Oij道工序是机器mijX上的第sijX道加工任务,以此类推得到所有工序的位置信息,通过公式(3)得到距离值。其中,系数ρ用来反应加工机器的选择差异。若鲸鱼X,Y为工序Oij选择相同机器加工,则ρ=1;否则
| $ D=\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{k} \rho \cdot\left|s_{i j}^{Y}-s_{i j}^{X}\right|, $ | (3) |
式中:D为2条鲸鱼之间的距离;sijy和sijx分别为工序Oij在鲸鱼Y、鲸鱼X个体中在各自加工机器上的加工次序;n为工件数;k为工件i的加工工序数;当mijy=mijx时,ρ=1;否则
以表 1为例,要得到鲸鱼个体间距离,首先需获取鲸鱼个体的位置信息,鲸鱼个体位置表达方法如下:图 4中鲸鱼A和鲸鱼B分别代表 2条不同的个体,即2个不同的调度方案,分别将每条鲸鱼解码为主动调度,得到鲸鱼A和鲸鱼B的甘特图如图 5所示。由每台机器的加工任务集,确定每道工序的加工机器和它在加工机器上的加工顺序。如图 6所示,鲸鱼A中,工序O11安排在机器5的第一个加工任务,记为(5,1);工序O12安排在机器1的第一个加工任务,记为(1,1)。同理依次读取剩余各工序的加工信息得到鲸鱼A的位置信息为:(5,1),(1,1),(4,1),(3,1),(3,2);鲸鱼B的位置信息为:(2,1),(5,1),(1,1),(5,2),(3,1)。由公式3.1计算可得,鲸鱼A和鲸鱼B之间的距离为

|
图 4 鲸鱼个体实例 Fig. 4 examples of individual whales |
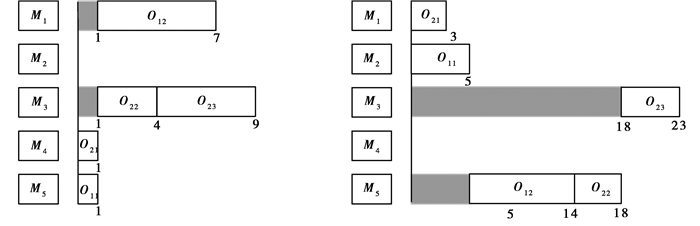
|
图 5 鲸鱼A和鲸鱼B解码甘特图 Fig. 5 Gantt charts of whale A and B |

|
图 6 鲸鱼A和鲸鱼B位置信息 Fig. 6 positions of whale A and B |
鲸鱼群算法的核心步骤为鲸鱼个体通过其“较优且最近”的鲸鱼进行移动。从而实现种群的进化,寻得最优解。但是对于柔性作业车间调度这类离散型车间调度问题,这种方法不能保证鲸鱼个体在其“较优且最近”鲸鱼引导下按照移动规则移动形成的新个体优于原个体,因此在原算法中加入协同式搜索,将目标鲸鱼从一条扩大为多条,形成目标鲸鱼群。即搜索距鲸鱼X“较优且较近”的多条目标鲸鱼。“较近”距离定义方法为:依次计算鲸鱼X同种群中其他鲸鱼之间的距离,获取其中的最大距离值(maxdis)和最小距离值(mindis),实验结果显示,当距离取为maxdis和mindis的平均值时,搜索效果较好,故“较近”距离取二者均值,即鲸鱼X同种群中其余个体最近距离和最远距离的平均值。之后,生成鲸鱼X的副本鲸鱼X’,鲸鱼X’按照移动规则依次向目标鲸鱼移动产生新个体,若新个体的适应度由于鲸鱼X,则以新个体替代鲸鱼X,实现鲸鱼个体向更优的方向移动。搜索“较优且较近”鲸鱼具体步骤如图 7。

|
图 7 寻找“较优且较近”的鲸鱼的伪代码 Fig. 7 The pseudo code of finding a whale's "better and nearest" whale |
协同式寻找“较优且较近”的鲸鱼策略能够有效避免种群陷入局部最优,提高算法的全局搜索能力。
3.6 个体移动规则个体移动采用LI等[14]提出的JBX交叉方式。基于工序编码移动操作:将工件集随机分为2个部分,工件集1和工件集2。从目标鲸鱼群中选取一条目标鲸鱼同待移动鲸鱼共同组成父代个体P1, P2,同时生成2条空白个体作为移动后的子鲸鱼C1, C2。然后将P1个体中工件集1所含工序对应保留至子鲸鱼C1,其余按照剩余工件在P2个体内的顺序依次填充;将P2个体中工件集2所含工序对应保留至子鲸鱼C2中,其余按照剩余工件在P1个体内的顺序依次填充。
基于机器编码移动操作:子鲸鱼保留对应父代鲸鱼的机器编码部分,基于概率进行变异,即随机生成λ,若λ≤0.5, 则替换为另一父代机器编码中的对应机器;否则保持不变。其中,C1子鲸鱼只对工件集2所含工序的机器进行概率选择,工件集1所含工序的加工机器保持不变;C2子鲸鱼只对工件集1所含工序的机器进行概率选择,工件集2所含工序的加工机器保持不变。
4 变邻域搜索策略在上述优化算法的基础上融入基于关键路径的变邻域搜索算法,增强鲸鱼群算法的局部搜索能力。基本思想为:在局部搜索范围内系统化地改变多个邻域结构。从初始解出发,按照不同的邻域结构依次搜索直到找到更好的解或迭代次数满足终止条件。
4.1 析取图模型析取图模型G=(N, A, E)由Balas[15]提出,其中N是由总工序数构成的节点集,每个节点的权值为此节点在对应加工机器上的加工时间;A是连接同一工件相邻工序的有向弧集,用于描述工序之间的加工顺序约束;E是同一台加工机器上相邻工序之间的析取弧集。E中析取弧均为双向,且由每台机器上的析取弧子集共同构成。对于机器而言,一个调度方案等于为析取弧集中对应的双向弧选择一个方向。一个环就是从一个工序出发到此工序终止的路径。在完成析取弧集内所有析取弧方向的选择后,若析取图模型中不包含任何有向环,且所有选择均为非循环,则称之为一个可行调度。
为生成和调度方案对应的可行调度,避免析取图中生成有向环,将鲸鱼个体解码所得甘特图和析取图模型相结合,按照甘特图主动解码所得每台机器上的加工任务顺序选择对应析取弧方向,生成非循环有向图。如图 8为图 4中鲸鱼B个体的析取图模型,“0”和“*”分别代表开始节点和结束节点。由图 5鲸鱼B的甘特图可知各加工机器的加工任务集。机器1上的加工任务为{O21},机器2上的加工任务为{O11},机器3上的加工任务为{O23},机器4上的加工任务为空集,机器5上的加工任务为{O12,O22}。根据机器5上加工任务的排序,选择由O12节点指向O22节点的析取弧,得到同甘特图相对应的有向图,如图 9所示。

|
图 8 鲸鱼B析取图模型 Fig. 8 Disjunctive graph model of whale B |

|
图 9 鲸鱼B有向图 Fig. 9 The oriented graph of whale B with direction |
该方法能够有效避免有向环的形成,从而避免析取图模型生成不可行调度,减少计算机计算复杂度,降低计算时间。
在非循环有向图中,从开始到结束的最长路径称为关键路径。关键路径上的工序被称为关键工序。同一台机器上相邻关键工序组成关键块。通过移动关键工序,改变最大完工时间。关键工序的确定方法如下:假设JP(q)表示工序q在同一工件上的前一道工序,JS(q)表示工序q在同一工件上的后一道工序;MP(q)表示工序q在同一机器上加工的前一道工序,MS(q)表示工序q在同一机器上加工的后一道工序;pq为工序q在机器上完成加工所需时间;sE(q)和cE(q)分别为q的最早开工和最早完工时间,且cE(q)=sE(q)+pq;sL(q)和cL(q)分别为q的最晚开工和最晚完工时间,且cL(q)=sL(q)+pq。从0节点开始依次计算每道工序的最早开工时间,sE(q)=max{cE[JP(q)], cE[MP(q)]};之后从*节点开始依次寻找每个节点工序的最晚开工时间,cL(q)=min{sL[JS(q)], sL[MS(q)]}。若工序的最早开工时间和最晚开工时间相等,则该工序为关键工序。
若可行调度方案中存在多条关键路径,则需对每一条关键路径都进行移动,实现对最大完工时间[1]键工序进行移动,不对非关键工序做任何改变。
4.2 邻域结构变邻域算法的寻优性能较大程度上取决于邻域结构的设计。设计了2种基于关键路径的邻域结构,通过对关键工序产生小的扰动,增加算法的局部搜索能力,尽可能缩短最大完工时间。
4.2.1 基于工序的邻域结构基于工序的邻域结构通过改变关键块中工序的排列顺序生成邻域解,不改变关键工序对应机器的分配。邻域解产生过程如下:依次遍历每个关键块,若关键块只包含一道关键工序则不交换;若包含2个关键工序,则交换此2个工序;若包含2个以上关键工序,则只交换块首2道工序。若待交换的2个工序属于同一工件,按照加工顺序约束不进行交换。
4.2.2 基于机器的邻域结构基于机器的邻域结构通过改变关键工序对应的加工机器缩短加工时间,以尽可能减小最大完工时间,获得邻域解。邻域解产生过如下:在每条关键路径中随机选择一道工序,然后选择其可加工机器集内加工时间最短的机器,更新鲸鱼个体基于机器编码。该邻域结构不改变原鲸鱼个体对工序的排序结果,只对加工机器进行重新安排。
5 仿真实验鲸鱼群优化算法采用C++语言编程实现,程序运行环境为:intel i5处理器,3 470 CPU,主频3.20 GHZ,内存为4.00 GB。为了测试算法性能,选取了由Brandimate[13]提出的BRdata实例。10个问题由工件数从10~20,机器数从4~15进行组合。每组问题的工序数从5~15。
为了使计算结果更具有效性和一般性,避免误差干扰,对每个问题实例连续运行10次。算法运行过程中,种群数量根据问题规模进行多次调整,得到使运算效果最佳的种群数量,范围在100~500不等。种群最大迭代次数为200。算法对BRdata基准实例的测试结果如表 2所示,并与文献[16]所提FJS MATSLO+算法(2013年),文献[1]所提DPSO算法(2018年),文献[17]所提HGWO算法(2018年),文献[18]所提Heuristic算法(2014年)进行对比,以验证WSA算法的有效性和可行性。表中WSA代表提出的鲸鱼群优化算法。
| 表 2 BRdata算例计算结果统计与对比 Table 2 Summary of results: BRdata |
表中,n×m代表对应问题的工件数和机器数。LB和UB代表目前已知最有下届和最优上界。比较研究算法与其他文献中提出算法相较当前最优值的累计偏差,公式表示为
| $ \mathrm{dev}=\sum\limits_{i=1}^{10} \mathrm{dev}_{i} $ | (4) |
其中devi=(UBi-Cimax)/UBi, devi为第i个问题算法计算结果偏差值,UBi为第i个问题的目前最优上届,Cimax为第i个问题算法计算所得最大完工时间。
从表 2中可以看出提出的改进鲸鱼群算法和其他文献所提算法相比,在5个问题上优于PSO,6个问题优于HGWO计算得到的最优值,相比FJS MATSLO+和Heuristic存在较大优势。对比与目前最优解的相对偏差值,WSA算法相较其他算法偏差较低,即表示整体上提出的鲸鱼群优化算法优FJS MATSLO+等其他4个算法。图 10为标准实例Mk06求出的最优解调度甘特图。
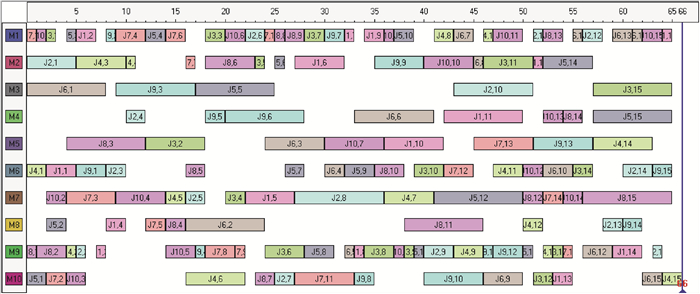
|
图 10 Mk06标准算例甘特图 Fig. 10 Gantt chart of Mk06 |
从实验结果可以看出,将鲸鱼群算法改进并融合变邻域搜索算法,提出改进鲸鱼群算法在求解单目标柔性作业车间调度问题取得了较好的结果,为连续问题算法求解离散性问题的改进方式提供了一种新思路,同时也为单目标柔性作业车间调度问题的求解提供了一种新方法。
6 结论以最大完工时间为目标,提出了一种求解FJSP问题的有效WSA算法。基于二维向量编码和种群混合初始化方案,优化了个体位置表达方式及相应距离计算方法,引入协同搜索策略扩大鲸鱼个体移动搜索区域,增强了算法的全局搜索能力。同时,提出了一种基于关键路径的邻域搜索策略,根据机器选择和工序排序2个子问题,设计了2种对应的邻域结构,增强算法局部搜索能力。实验结果表明,研究提出的算法具有良好的可行性和有效性。
研究只对单目标柔性作业车间调度问题进行了讨论,在实际生产中还存在资源受限、机器负荷等诸多约束因素。因此,未来可根据不同车间调度模型,对鲸鱼群算法进行进一步的改进,以满足实际工程优化问题的需要。
| [1] |
Nouiri M, Bekrar A, Jemai A, et al. An effective and distributed particle swarm optimization algorithm for flexible job-shop scheduling problem[J]. Journal of Intelligent Manufacturing, 2018, 29(3): 603-615. DOI:10.1007/s10845-015-1039-3 |
| [2] |
Driss I, Moussk N, Lahhoun A. A new genetic algorithm for flexible job-shop scheduling problems[J]. Journal of Mechanical Science and Technology, 2015, 29(3): 1273-1281. DOI:10.1007/s12206-015-0242-7 |
| [3] |
Mirjalili S, Mirjalili S M, Lewis A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. DOI:10.1016/j.advengsoft.2013.12.007 |
| [4] |
Seyedali Mirjalili. The ant lion optimizer[J]. Advances in Engineering Software, 2015, 83: 80-98. DOI:10.1016/j.advengsoft.2015.01.010 |
| [5] |
Neshat M, Sepidnam G, Sargolzaei M, et al. Artificial fish swarm algorithm: a survey of the state-of-the-art, hybridization, combinatorial and indicative applications[J]. Artificial Intelligence Review, 2014, 42(4): 965-997. DOI:10.1007/s10462-012-9342-2 |
| [6] |
姜天华. 混合灰狼优化算法求解柔性作业车间调度问题[J]. 控制与决策, 2018, 33(3): 503-508. JIANG Tianhua. Flexible job shop scheduling problem with hybrid grey wolf optimization algorithm[J]. Control and Desicion, 2018, 33(3): 503-508. (in Chinese) |
| [7] |
Hongwei G, Liang S. Intelligent scheduling in flexible job shop environments based on artificial fish swarm algorithm with estimation of distribution[C/OL]2016 IEEE Congress on Evolutionary Computation (CEC), New York, USA: IEEE, 2016(2016-11-21)[2019-09-25].https://ieeexplore.ieee.org/document/7744198.
|
| [8] |
Gao K Z, Suganthan P N, Pan Q K, et al. Discrete harmony search algorithm for flexible job shop scheduling problem with multiple objectives[J]. Journal of Intelligent Manufacturing, 2016, 27(2): 363-374. DOI:10.1007/s10845-014-0869-8 |
| [9] |
Zeng B, Gao L, LI X. Whale swarm algorithm for function optimization[J]. International Conference on Intelligent Computing, 2017, 10631: 624-639. |
| [10] |
Gao L, Peng C, Zhou C, et al. Solving flexible job shop scheduling problem using general particle swarm optimization[C]//36th International Conference on Computers and Industrial Engineering, ICC and IE 2006(2006).[s.l.]: IEEE, 3018-3027.
|
| [11] |
Ho N B, Tay J C, Lai M K. An effective architecture for learning and evolving flexible job-shop schedules[J]. European Journal of Operational Research, 2007, 179(2): 316-333. DOI:10.1016/j.ejor.2006.04.007 |
| [12] |
张国辉.柔性作业车间调度方法研究[D].武汉: 华中科技大学, 2009. ZHANG Guohui. Research on methods for flexible job shop scheduling problems.[D]. Wuhan: Huazhong University of Science and Technology, 2009. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10487-2010042175.htm |
| [13] |
张国辉, 高亮, 李培根, 等. 改进遗传算法求解柔性作业车间调度问题[J]. 机械工程学报, 2009, 45(7): 145-151. ZHANG Guohui, GAO Liang, Li Peigen, et al. Improved genetic algorithm for flexible job shop scheduling problem[J]. Journal of Mechanical Engineering, 2009, 45(7): 145-151. (in Chinese) |
| [14] |
Li X, Gao L. An effective hybrid genetic algorithm and tabu search for flexible job shop scheduling problem[J]. International Journal of Production Economics, 2016, 174: 93-110. DOI:10.1016/j.ijpe.2016.01.016 |
| [15] |
Balas E. Machine sequencing via disjunctive graphs: an implicit enumeration algorithm[J]. Operations Research, 1969, 17(6): 941-957. DOI:10.1287/opre.17.6.941 |
| [16] |
Henchiri A, Ennigrou M. Particle swarm optimization combined with tabu search in a multi-agent model for flexible job shop problem[J]. International Conference in Swarm Intelligence, 2013, 7929: 385-394. |
| [17] |
姜天华. 混合灰狼优化算法求解柔性作业车间调度问题[J]. 控制与决策, 2018, 33(3): 503-508. JIANG Tianhua. The ixed grey wolf optimization algorithm for solving flexible job shop scheduling problem[J]. Control and Decision, 2018, 33(3): 503-508. (in Chinese) |
| [18] |
Ziaee, Mohsen. A heuristic algorithm for solving flexible job shop scheduling problem[J]. The International Journal of Advanced Manufacturing Technology, 2014, 71(1/2/3/4): 519-528. |
 2020, Vol. 43
2020, Vol. 43


