2. 首都经济贸易大学 管理工程学院, 北京 101149
2. School of Management Engineering, Capital University of Economics and Business, Beijing 100070 P. R. China
近年来,物流企业数量逐年增加。由于很多企业的城市物流配送体系采取单独配送模式,导致车辆使用数及行驶里程逐年增加,车辆空载率高、配送线路重合等问题日益严重,既不符合绿色物流的发展,也不利于提高物流配送效率。构建城市物流共同配送体系,实现多个企业物流配送资源共享,能够有效降低物流配送成本、提高配送效率[1]。构建物流共同配送体系涉及到共同配送中心选址[2]和多个层级节点之间的车辆路径优化[3-4]问题,该问题可以归结为多层级选址路径问题。
国内外关于选址路径问题的研究成果可以按照节点类型分为单层级选址路径问题、两层级选址路径问题和多层级选址路径问题。
单层级的选址路径问题指网络中只包含两类节点:配送中心和需求点。如城市物流中心选址路径问题[5],考虑污染物排放的选址路径问题[6],带时间窗的多车型选址路径问题[7],自提点选址和路径规划问题[8]等。求解单层级选址路径问题的主要算法是自适应大邻域搜索算法[5-6]、混合进化搜索算法[7]、改进的蚁群算法[8]等。
两层级的选址路径问题指网络中包含三类不同节点:物流中心、配送中心和客户点,在规划配送路径时,不仅需要确定物流中心和配送中心之间的路径,还需要确定配送中心和最终客户点之间的路径。求解两层级选址路径问题主要采用聚类方法[9]、混合遗传算法[10]、多目标粒子群算法[11]和分层级优化方法[12-13]等。
多层级选址路径问题指网络中至少包含三类不同的节点。黄凯明等[14]针对三层级设施选址路径规划问题提出量子进化算法。
城市物流共同配送网络包含三类节点:物流中心、配送中心和客户点,两种类型的车辆路径,即从物流中心到配送中心的大型运输车配送路径、从配送中心到客户点的小型运输车配送路径。构建共同配送体系,需要解决共同配送中心选址问题和两层级的配送路径规划问题,该问题属于两层级带容量限制的选址路径规划问题。
文中以北京市奶制品共同配送问题为例,研究共同配送选址路径优化问题。具体包括:从备选点中选择配送中心并进行两层级的配送路径规划;建立共同配送的选址路径问题的混合整数规划模型,并设计求解模型的算法。结合北京市奶制品配送现状,构建北京市奶制品共同配送网络体系,通过模拟计算验证共同配送模式的优越性,并验证文中模型和算法的有效性。
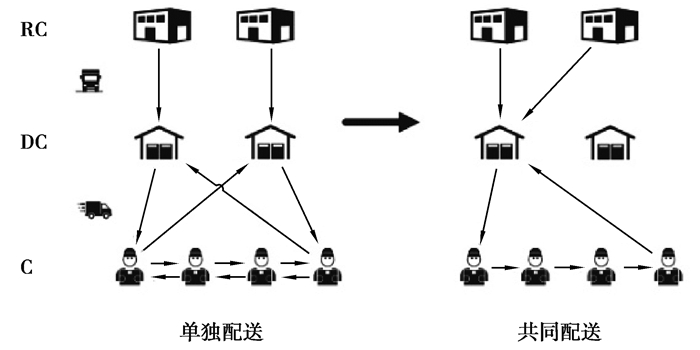
1 北京市奶制品配送现状北京市共有82家大型商超销售奶制品,奶制品供应商都采取单独配送模式,由于不同品牌奶制品供应商面对的客户群体相似,配送路径雷同或重复现象严重,导致总配送里程和配送成本居高不下。如图 1所示,当2个供应商单独配送时,需要从2个配送中心经过不同的配送路径为同一批顾客点配送各自的奶制品。如果2个供应商采取共同配送模式,只需要建立1个共同配送中心,并将2条配送路径整合为1条,就可以有效降低物流成本。
|
图 1 单独配送和共同配送示意图 Fig. 1 Independent distribution and joint distribution |
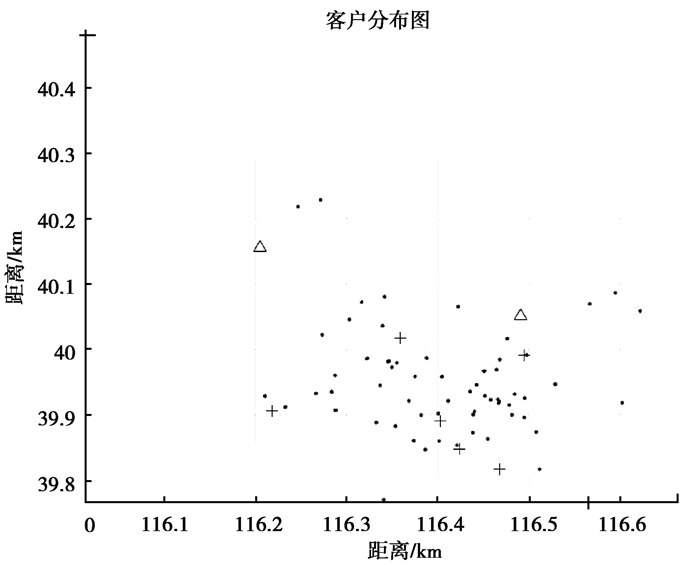
文中以伊利和蒙牛两大品牌的奶制品为例开展研究。两大品牌奶制品在北京地区的物流中心(RC)位置坐标如表 1所示;两种奶制品的配送中心(DC)位置坐标、容量、日常运行费用等信息如表 2所示;北京市内的82家商超(C)的地理位置如图 2所示;两种奶制品的销售量如表 3所示;从物流中心到配送中心使用的一级车和从配送中心到客户点使用的二级车的荷载量和固定成本(即车辆折旧费、检修费和人工费等)如表 4所示。
| 表 1 两种奶制品的物流中心地理坐标 Table 1 Geographical coordinates of logistics centers for two types of dairy products |
| 表 2 两种奶制品配送中心的相关信息 Table 2 Information of two dairy distribution centers |
|
图 2 RC、DC和C的位置坐标图(‘.’表示客户点;‘+’表示备选共同配送中心;‘△’表示物流中心) Fig. 2 Location coordinates of RC, DC and C ('. 'represents customer point, '+' represents alternative common distribution center, '△'represents logistics center) |
| 表 3 各商超(C)编号及两种奶制品的销售量(单位:盒) Table 3 Serial number of each supermarket (C) and sales volume of two types of dairy products (unit: box) |
| 表 4 两种运输车的相关信息 Table 4 Information of two types of vehicles |
目前,蒙牛和伊利供应商均采取单独配送模式为北京市的82家商超提供配送服务,其中,蒙牛拥有1家配送中心(DC1),伊利拥有7家配送中心(DC2, …, DC8)。由于从物流中心到配送中心使用一级车配送,其运输费率(即单位运输距离运价,每公里费用)为6元/km,从配送中心到商超使用二级车配送,其运输费率为9元/km。为了便于管理,两家供应商均采取固定线路配送模式(即每天的配送线路相同)。整个物流活动的总成本如表 5所示。
| 表 5 单独配送相关费用汇总 Table 5 Relevant costs of independent distribution |
根据以上分析,这两家奶制品供应商单独配送时的总成本为50.706万元。两家供应商共使用一级车3辆,二级车15辆,车辆总使用费用3万元;第一层级由物流中心到配送中心的配送总里程为312.93 km,第二层级由配送中心到需求点的配送总里程为1 209.75 km,总配送路线成本为1.277万元;配送中心固定运行成本为46.428万元。
2 共同配送选址路径问题描述和模型建立 2.1 共同配送选址路径问题描述文中以北京市奶制品共同配送问题为例,将共同配送选址路径问题转化为两层级带容量限制的选址路径问题。共同配送网络包括三类节点和两个层级相邻节点之间的配送路径。三类节点分别为各品牌奶制品的物流中心(RC)、共同配送中心(DC)、客户点(C);两个层级的配送路径包括RC到DC的配送路径和DC到C的配送路径。其中,涉及的成本包括共同配送中心的运行成本、车辆的固定成本和路径运输成本等。问题是如何确定共同配送中心DC的位置和RC-DC、DC-C的配送路径,才能使总费用最低。
为了简化问题,做出如下假设:
1) 一个RC只能提供一种产品,且RC提供的产品类型编号与物流中心序号相同;
2) 各种产品单独配送时使用的配送中心均可作为候选共同配送中心,即候选共同配送中心DC位置已知,每个候选配送中心容量有限,且固定运行成本已知;
3) 不同层级节点之间使用的运输车类型已知,即RC-DC使用一级车运输,DC-C使用二级车运输。两种车型的数量充足、车容量及单位运输费率已知;
4) 每个C的所有产品需求只能由1辆二级车提供服务;
5) 不考虑越级配送。即一级车只能由RC出发,将单一产品运送到DC;二级车只能由DC出发,可以同时将多种产品运送到多个C。
2.2 符号说明定义以下符号:
I:物流中心集合(即产品类型集合);
J:备选配送中心集合;
K:客户点集合;
Ai1={pis1:pis1=ij1j2, ..., jri; i∈I; j1, ..., jr∈J}:物流中心i到配送中心的配送路径集合,每一条路径均从物流中心i出发,经过一个或多个配送中心j1j2, ..., jr,最后返回物流中心i;
V(pis1):从物流中心i出发的第s条配送路径pis1经过的所有配送中心的集合;
dis1:从物流中心i出发的第s条配送路径pis1总长度;
Aj2={pjt2:pjt2=jk1k2, ..., krj; j∈J; k1, ..., kr∈K}:从配送中心j到客户点的配送路径集合,每一条路径均从配送中心j出发,依次经过若干客户点k1k2, ..., kr,最后返回配送中心j;
V(pjt2):从配送中心j出发的第t条配送路径pjt2服务的所有客户点集合;
djt2:从配送中心j出发的第t条配送路径pjt2总长度;
gj:备选配送中心j的固定运行成本;
Rj:备选配送中心j的容量;
h1:一级车辆的固定动用成本;
h2:二级车辆的固定动用成本;
Q1:由物流中心出发为共同配送中心提供服务的一级车容量;
Q2:由共同配送中心出发为客户点提供配送服务的二级车容量;
c1:一级车的单位运输费率;
c2:二级车的单位运输费率;
qki:客户k对产品i的需求量。
定义以下决策变量:
| $ x_{j}=\left\{\begin{array}{l} {1} &备选配送中心j被选中\\ {0}&否则 \end{array}\right.\\ y_{is}^1=\left\{\begin{array}{l} {1} &从物流中心i出发的第s条配送路线被选中\\ {0}&否则 \end{array}\right.\\ y_{jt}^2=\left\{\begin{array}{l} {1} &从配送中心j出发的第t条配送路线被选中\\ {0}&否则 \end{array}\right. $ |
fij:从物流中心i出发的车辆为配送中心j配送产品i的数量。
2.3 混合整数规划模型共同配送选址路径问题可以表示成如下混合整数规划模型:
| $ \min w=\sum\limits_{j\in J}{g_j}x_j+h_1\sum\limits_{i\in I}{\sum\limits_{p_{is}^{1}\in A_{i}^{1}}y_{is}^{1}}+h_2\sum\limits_{j\in J}{\sum\limits_{p_{jt}^{2}\in A_{j}^{2}}{y_{jt}^{2}}}\\+c_1\sum\limits_{i\in I}{\sum\limits_{p_{is}^{1}\in A_{i}^{1}}d_{is}^{1}y_{is}^{1}}+c_2\sum\limits_{j\in J}{\sum\limits_{p_{jt}^{2}\in A_{j}^{2}}{d_{jt}^{2}}}y_{jt}^{2}。$ | (1) |
s.t.
| $ \sum\limits_{j \in J} f_{i j} \leqslant Q_{1} \sum\limits_{p_{i s}^{1} \in A_i^1} y_{i s}^{1}, i \in I。$ | (2) |
| $ y_{j t}^{2} \sum\limits_{k \in V\left(p_{j t}^{2}\right)} \sum\limits_{i \in I} q_{k}^{i} \leqslant Q_{2}, p_{j t}^{2} \in A_{j}^{2}, j \in J。$ | (3) |
| $ \sum\limits_{j \in J} \sum\limits_{p_{j t}^{2}\in A_{j}^{2}, k\in V(p_{j t}^{2})} y_{j t}^{2}=1, k \in K。$ | (4) |
| $ f_{i j}=\sum\limits_{p_{j t}^{2}\in A_{j}^{2}, k\in V(p_{j t}^{2})} y_{j t}^{2} q_{k}^{i}, i \in I, j \in J。$ | (5) |
| $ \sum\limits_{i \in I} f_{i j} \leqslant R_{j} x_{j}, j \in J。$ | (6) |
| $ y_{j t}^{2} \leqslant x_{j} \quad p_{j t}^{2} \in A_{j}^{2}, j \in J。$ | (7) |
| $ f_{i j} \geqslant 0 \quad i \in I, j \in J。$ | (8) |
| $ x_{j} \in\{0, 1\}, j \in J。$ | (9) |
| $ y_{i s}^{1} \in\{0, 1\}, p_{i s}^{1} \in A_{i}^{1}。$ | (10) |
| $ y_{j t}^{2} \in\{0, 1\}, p_{j t}^{2} \in A_{j}^{2}。$ | (11) |
模型的目标函数(1)表示极小化总成本,其中,第1项表示共同配送中心的固定运行成本,第2项和第3项分别表示第1层级和第2层级运输车辆的固定动用成本,第4项和第5项分别表示第1层级和第2层级车辆路径配送成本。
约束条件(2)表示从物流中心i运往各个配送中心的产品i之和不超过从物流中心i出发的所有配送车辆的容量之和;约束条件(3)表示从配送中心j出发的任一条配送路径上的所有客户点对各种产品的总需求量不超过二级车的容量;约束条件(4)表示对于任意客户点k,恰好有一辆从配送中心出发的车辆(被选中的配送路径)为其提供服务;约束条件(5)表示从物流中心i运往配送中心j的产品i总量等于从配送中心j运往各个客户点的产品i总量(运量平衡约束);约束条件(6)表示从物流中心运往配送中心j的各种产品之和,不超过配送中心j的容量限制,且如果配送中心j未被选中,则物流中心的产品不可能运往该配送中心;约束条件(7)表示如果从配送中心j出发的一条配送线路被选中, 则备选配送中心j必被选中;约束条件(8)~(11)是决策变量取值约束。
3 算法设计共同配送选址路径问题属于NP难问题,对于大规模问题,无法在短时间内通过直接求解混合整数规划模型得到全局最优解。文中设计三阶段启发式算法求解模型。
3.1 第一阶段:将客户点划分为若干客户集在构建大规模共同配送网络时,为减少从共同配送中心到客户点的配送成本(即二级车辆的固定动用成本和行驶成本),通常会将邻近的终端客户聚集在一起由一辆二级车提供配送服务[9]。在考虑二级车容量限制的前提下,采用基于遗传算法的带容量约束的K-means聚类算法,将客户点划分为尽可能少的客户集,使得每一个客户恰好被划分到一个客户集中,且每个客户集对各种产品的总需求量不超过二级车容量(即满足约束条件(3)和(4))。
由于K-means聚类算法需要确定聚类数,根据目标函数表达式中的第2项,聚类数目越少,二级车的固定动用成本越小。考虑到二级车容量限制,可以根据公式(12)确定最少聚类数目cn:
| $ c n=\left\lceil\sum\limits_{k=1}^{K} q_{k} / Q\right\rceil。$ | (12) |
Step1.1 确定初始聚类中心:从k个客户中随机选取cn个客户作为初始的聚类中心;
Step1.2 分配客户到各个类中:根据每个客户坐标,计算该客户到所有聚类中心的距离。在满足配送车容量限制条件下,将客户分配至离它最近的类,并更新该类的总需求量;若最近类的剩余容量无法满足该客户的需求,则将该客户分配给离它次近的类;以此类推,直到为每个客户分配类别;
Step1.3 更新聚类中心:根据每一类客户点的位置及需求量,采用精确重心法计算各个类重心,并将其作为新的聚类中心坐标;
Step1.4 重复步骤Step1.2和Step1.3,直到聚类中心不再发生变化。
3.1.2 基于遗传算法的带容量约束的K-means聚类算法为克服K-means算法对初始聚类中心的依赖性,将遗传算法和K-means聚类算法相结合(KBGA,k-means clustering algorithm based on genetic algorithm)[15],求解客户点聚类问题。
算法的基本思想:从样本中随机选取cn个客户点位置作为初始聚类中心,计算客户点对应的聚类结果;将每一组聚类中心用浮点数编码为染色体;根据聚类结果计算适应度函数值;对每一代种群对应的聚类中心编码执行遗传算法操作,产生新的聚类中心;然后对新的聚类中心执行K-means算法,找到聚类问题的最终解。
KBGA算法的具体基本步骤:
Step2.1 设置遗传算法参数:种群规模sizepop,最大迭代次数MAXGEN,选择概率GGAP,交叉概率Pc,变异概率Pm;
Step2.2 种群初始化:从样本中随机选取cn个客户点位置作为初始聚类中心,并对每一个类中心进行浮点数编码。重复sizepop次,得到初始种群;
Step2.3 对当前种群的每个个体(每组类中心),按照带容量约束的K-means聚类算法步骤Step1.2计算客户点的聚类结果;
Step2.4 计算适应度:适应度函数定义为类间距之和,计算群体中每个个体的适应度;根据适应度计算每个个体的选择概率;
Step2.5 按照轮盘赌法选择sizepop个个体进入交配池;按照交叉概率Pc选择一部分个体执行交叉操作;按照变异概率选择一部分个体执行变异操作,生成下一代种群;同时采取精英保留策略将类间距最小的个体直接保留至下一代;
重复执行步骤Step2.3~2.5,直到达到最大迭代次数。将最后一代群体中适应度最大的个体对应的聚类中心作为最优聚类中心;
Step2.6 对最优聚类中心执行带容量约束的K-means聚类算法的步骤Step1.3~1.4,得到最优聚类结果和客户点分类矩阵。
3.1.3 最优聚类数的确定聚类数目越少,动用的车辆数越少,但每辆车的行驶距离将增大,车辆的行驶成本将增加,故最少聚类数目不一定对应总成本最低的配送方案。为找到对应总成本最低的配送方案,需要确定最优聚类数目,文中利用轮廓分析法[16]从多个备选的聚类数目中选择最优聚类数。
假设按照公式(12)计算出的最少聚类数为cn,则备选聚类数目定义为:cn,cn+1,cn+2,cn+3,cn+4,cn+5。对每一种聚类数目,按照KBGA算法计算聚类结果,并进行轮廓分析,具体步骤为:
Step3.1 计算每个客户点i与簇内其它客户点之间的平均距离(即内聚度)a(i);
Step3.2 计算每个客户点i与最近簇中所有客户点之间的平均距离(即分离度)b(i);
Step3.3 将分离度与内聚度之差除以二者中较大的数,得到客户点i的轮廓系数,计算公式如下:
| $ s^{(i)}=\frac{b^{(i)}-a^{(i)}}{\max \left\{b^{(i)}, a^{(i)}\right\}}。$ | (13) |
轮廓系数的取值在-1~1之间。当内聚度与分离度相等时,轮廓系数为0。当b≫a时,轮廓系数近似取到1,此时分类效果最佳;轮廓系数为负值时,表示该客户点分类错误。
对每一种聚类结果分别计算各个客户点的轮廓系数;选择平均轮廓系数尽可能大、轮廓系数为负的客户点数尽可能少的聚类结果对应的聚类数作为最优聚类数。
3.2 第二阶段:确定共同配送中心位置及第二层级配送路径利用TSP问题的算法计算从各个DC出发为每个客户集配送产品的最优路径和配送成本(对应目标函数(1)第5项的值)。在此基础上,将共同配送中心选址和第2层级配送路径优化问题简化为配送中心选址和客户集分配问题,建立数学模型并利用Lingo软件求解。得到共同配送中心的选址结果和从共同配送中心到客户点的配送路径,以及各个共同配送中心为客户点配送的各种类型产品总量。
由于每个客户集只需要一辆二级车服务,因此共同配送中心j为客户集m提供服务的最优路径,即为由配送中心j和客户集m组成的TSP问题的最优解。根据TSP问题的算法可以得到配送中心j为客户集m提供服务的最优配送路径pjm2和路径总长度djm2。
根据以上分析,将客户聚类后,从配送中心到客户点的配送车辆固定动用成本为常数。在不考虑第一层级配送成本的前提下,根据模型目标函数中的配送中心选址成本和第二层级配送路径成本,将共同配送中心选址和第二层级配送路径优化问题转化为共同配送中心选址和客户集指派问题。
令M={1, 2, ..., cn}表示客户集m序号集合;Emi表示客户集m对第i种商品的总需求量;djm2表示从备选配送中心j出发为客户集m配送商品的最优配送路径长度。
定义决策变量:
| $ x_{j}=\left\{\begin{array}{l} {1}& 备选配送中心j被选中\\ {0}&否则 \end{array}\right. $ |
| $ z_{jm}=\left\{\begin{array}{l} {1}& 共同配送中心j为客户集m提供配送服务\\ {0}&否则 \end{array}\right. $ |
则共同配送中心选址和客户集分配问题可以表示成如下0~1线性规划模型:
| $ \min w=\sum\limits_{j \in J} g_{j} x_{j}+c_{2} \sum\limits_{j \in J} \sum\limits_{m \in M} d_{j m}^{2} z_{j m}。$ | (14) |
| $ {\rm s.t.}\\ ~~~~~~\sum\limits_{m \in M} \sum\limits_{i \in I} E_{m}^{i} z_{j m} \leqslant R_{j} x_{j}, j \in J。$ | (15) |
| $ \sum\limits_{j \in J} z_{j m}=1, m \in M。$ | (16) |
| $ z_{j m} \leqslant x_{j}, j \in J, m \in M。$ | (17) |
| $ x_{j}, z_{j m}=\{0, 1\}, j \in J, m \in M。$ | (18) |
目标条件(14)表示极小化配送共同配送中心选址成本和第二层级配送路径成本之和;约束条件(15)表示所有分配给共同配送中心j的客户集的总需求量不超过配送中心j的容量(该约束等价于混合整数规划模型中的约束条件(5)(6));约束条件(16)表示一个客户集恰好由一个共同配送中心提供服务(该约束等价于混合整数规划模型中的约束条件(4));约束条件(17)表示若共同配送中心j未被选中则不会有分配给它的客户集(该约束等价于混合整数规划模型中的约束条件(7));约束条件(18)为决策变量取值约束。
由于0~1线性规划模型式(14)~式(18)的决策变量和约束条件并不多,可以直接用Lingo软件求解。
3.3 第三阶段:确定第一层级的配送路径根据第二阶段计算结果,按照公式(19)计算每个共同配送中心服务的所有客户点对各种产品的总需求量。
| $ B_{j}^{i}=\sum\limits_{m \in M} E_{m}^{i} z_{j m}, j \in J, i \in I。$ | (19) |
考虑一级车辆固定动用成本和从RC到选中的DC的配送成本,在满足一级车容量约束(约束条件(2))的情况下使目标函数(1)中的第2项和第4项之和尽可能小的第一层级配送路径优化问题,等价于从各个RC到选中的DC的带容量约束的VRP问题。可直接利用精确求解或启发式算法求出从各个物流中心到共同配送中心的最优配送路径。
4 实例求解与结果分析根据两大品牌奶制品供应商的物流基地、配送中心,以及北京市82家商超位置及销售量等基础数据。考虑到不同品牌奶制品的共同配送会增加诸如管理费等相关费用,故设二级车的运输费率为15元/km,一级车的运输费率仍为6元/km。利用文中方法求解结果如下。
4.1 将82家商超聚类成客户集为商超提供配送服务的二级车容量为7 500盒;82家商超对两种奶制品的总需求为70 615盒;根据式(12)得到最低聚类数为10;根据KBGA算法依次计算cn∈{10, 11, 12, 13, 14, 14}的聚类结果。
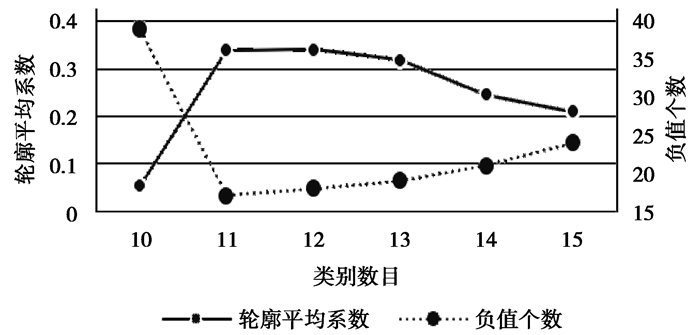
对每一聚类结果使用式(13)计算轮廓系数,统计平均轮廓系数和轮廓系数为负值的客户点个数,分析2个指标随聚类数的变化关系,如图 3所示,横坐标表示聚类数,纵坐标分别表示平均轮廓系数和轮廓系数为负值的客户点个数。
|
图 3 不同聚类数对应的轮廓系数分析图 Fig. 3 Contour coefficient analysis diagram of different cluster numbers |
由图 3可知,随着聚类数的增加,平均轮廓系数呈现先增后减趋势、轮廓系数取负值的点的个数呈现先减后增的趋势,综合考虑2个指标可得聚类数为11时聚类效果最佳。第一阶段只考虑客户需求量和配送车容量,在满足车容量约束下根据类间距对客户文中根据轮廓分析结果,考虑cn的3个较优选择,即cn∈{11, 12, 13}。
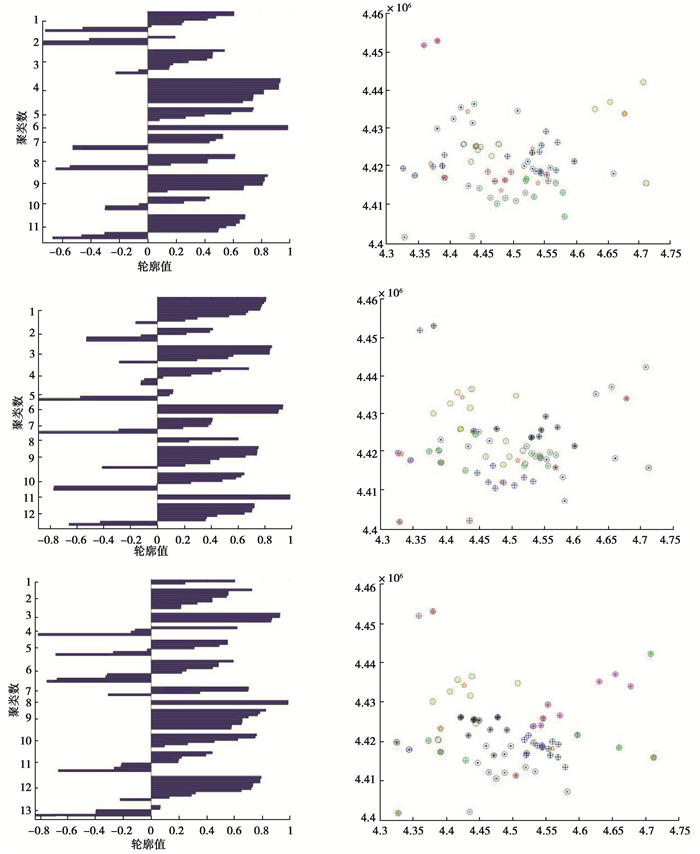
图 4为客户分类结果和轮廓值关系图,其中,第一列表示每类中各点的轮廓系数,第二列为对应聚类数的客户聚类情况。
|
图 4 客户分类结果和轮廓值(五角星为聚类中心) Fig. 4 Classification results of customers and the contour values (each star represents a cluster center) |
根据轮廓系数将客户划分为正负2组,聚类数为11、12、13时,轮廓系数介于0~0.6的客户点数较多,轮廓系数为负的客户点较少,故聚类数为11、12、13时聚类效果较优。
聚类数为cn=11、12、13时,轮廓系数为负值的客户点分别是17、18、19个,与聚类数为13的情景相比,聚类数为11或12时轮廓系数的异常值较少,且轮廓系数在0.6以上的客户点较多。基于以上观察,可以认为聚类数为11时的效果最优,聚类数为12时结果优于聚类数为13的结果。
4.2 共同配送中心选址路径规划结果对于cn∈{11, 12, 13}的聚类结果,分别计算从每个备选配送中心到各个客户集的最优配送路径的长度。根据模型(14)~(18),利用Lingo软件编程求解,最终得到4个共同配送中心和对应的客户集分配方案,以及从共同配送中心到客户集的最优配送路径。
分别计算4个共同配送中心服务的客户集对两种奶制品的总需求量,作为共同配送中心的需求量。利用TSP问题的精确算法计算从每个物流中心出发为4个共同配送中心配送奶制品的最优路径。详细求解结果如表 6~表 9所示。其中,表 6列出各种聚类数对应的共同配送中心选址结果和总选址费用。表 7~表 9分别列出不同聚类数对应的第1层级和第2层级配送路径信息。第1列为路径类型或配送车辆出发点,第2列为详细的路径信息,第3、4列分别列出每条路径的长度和对应的配送成本,最后一列为动用车辆的固定成本。
| 表 6 不同聚类数对应的共同配送中心选址结果 Table 6 Location results of joint distribution centers based on different number of clusters |
| 表 7 聚类数为11的路径规划结果 Table 7 Routing results with cluster number 11 |
| 表 8 聚类数为12的路径规划结果 Table 8 Routing results with cluster number 12 |
| 表 9 聚类数为13的路径规划结果 Table 9 Routing results with cluster number 13 |
根据表 7~表 9的结果可以进一步计算得到三种聚类数对应的总成本,如表 10所示。由表 10可以看出,聚类数为11时总成本最低。总里程数为627.4 km;选中的共同配送中心为DC2、DC3、DC5和DC6,共同配送中心总运行成本为22.57万元;从物流中心到共同配送中心需动用2辆一级车,总成本为1万元;从共同配送中心到客户点需动用11辆二级车,总成本为1.1万元;总配送路线成本为0.79万元。
| 表 10 基于三种不同聚类数的结果比较 Table 10 Comparison of the results based on three kinds of clustering numbers |
选取聚类数为11的计算结果与单独配送方案进行对比,结果如表 11所示。由表 11可以看出,共同配送比单独配送总成本节省约25万元(约占总成本的49.79%);配送中心数量减少4家;由物流中心到配送中心的车辆行驶里程节省约145 km(约占46.28%);由配送中心到客户点的车辆行驶里程节省约750 km(约62.04%);总路线成本节省约0.49万元,大约降低38%。可以看出,采取共同配送策略可减少配送中心数量、配送车辆使用量、配送总里程;降低配送成本,整合社会资源,达到节能减排的总目标。
| 表 11 奶制品共同配送与单独配送方案的对比分析 Table 11 Comparative analysis of joint distribution and independent distribution schemes for dairy products |
多类型产品共同配送选址路径问题属于NP难问题。从算例的求解过程可以看出,对于大规模问题,三阶段算法的第一阶段首先通过对需求点进行聚类,将大规模问题转化为若干个小规模问题。因此,算法的第二和第三阶段需要求解的配送中心选址问题和两层级路径规划相关的TSP问题以及VRP问题的规模都不大,即使直接利用商业软件求解,也会很快得到精确最优解。文中设计的三阶段算法可以用于求解大规模共同配送中心选址路径规划问题。
5 结论文中以北京市奶制品配送问题为场景,研究了共同配送选址路径优化问题,建立了两层级带容量限制的选址路径问题(2E-CLRP)的数学模型,并设计了求解模型的三阶段算法。利用北京市奶制品配送问题实际数据进行模拟计算,得出奶制品共同配送中心选址和配送路径规划方案;通过与单独配送模式进行对比可以发现,采取共同配送模式可以有效减少配送中心数量和配送车辆使用量,降低配送车辆行驶里程和配送成本。文中的模型和算法为解决共同配送的物流网络构建和优化问题提供决策依据。可直接推广,用于解决其它产品共同配送网络规划问题。
在研究共同配送问题时做了一些必要的简化假设,未来可以从以下几个方面对问题进行深入研究:1)对随机需求下的共同配送中心选址和配送路径优化问题进行研究;2)根据模型的结构,设计精确算法求全局最优解;3)根据客户点的需求选择合适的车型安排配送路径,减少车辆空载率。
| [1] |
霍红, 臧旭, 徐玲玲. 农资共同配送成本分摊模型问题研究[J]. 江苏农业科学, 2017, 45(20): 352-354. HUO Hong, ZANG Xu, XU Lingling. Study on the cost allocation model of joint distribution of agricultural materials[J]. Jiangsu Agricultural Sciences, 2017, 45(20): 352-354. (in Chinese) |
| [2] |
宾厚, 曾琴云, 王欢芳. 城市共同配送中心选址研究:基于生态位和混合整数规划法视角[J]. 贵州财经大学学报, 2016(4): 86-93. BIN Hou, ZENG Qinyun, WANG Huanfang. Research on the model of city joint distribution center location: based on niche fitness and mixed integer programming perspective[J]. Journal of Guizhou University of Finance and Economics, 2016(4): 86-93. (in Chinese) DOI:10.3969/j.issn.1003-6636.2016.04.009 |
| [3] |
倪霖, 刘凯朋, 涂志刚. 考虑同时取送货的城市快递共同配送路径优化[J]. 重庆大学学报, 2017, 40(10): 30-39. Ni Lin, LIU Kaipeng, TU Zhigang. Optimization on vehicle routing problem with simultaneous pickup-delivery for urban express joint distribution[J]. Journal of Chongqing University, 2017, 40(10): 30-39. (in Chinese) DOI:10.11835/j.issn.1000-582X.2017.10.004 |
| [4] |
葛显龙, 薛桂琴. 不确定环境下多品类共同配送路径优化[J]. 计算机工程与应用, 2019, 55(9): 264-270. GE Xianlong, XUE Guiqin. Multi-products joint distribution vehicle routing optimization with uncertain circumstance[J]. Computer Engineering and Applications, 2019, 55(9): 264-270. (in Chinese) |
| [5] |
Koç Ç, Bektaş T, Jabali O, et al. The impact of depot location, fleet composition and routing on emissions in city logistics[J]. Transportation Research Part B: Methodological, 2016, 84: 81-102. DOI:10.1016/j.trb.2015.12.010 |
| [6] |
Demir E, Bektaş T, Laporte G. An adaptive large neighborhood search heuristic for the Pollution-Routing Problem[J]. European Journal of Operational Research, 2012, 223(2): 346-359. DOI:10.1016/j.ejor.2012.06.044 |
| [7] |
Koç Ç, Bektaş T, Jabali O, et al. The fleet size and mix location-routing problem with time windows: Formulations and a heuristic algorithm[J]. European Journal of Operational Research, 2016, 248(1): 33-51. |
| [8] |
周翔, 许茂增, 吕奇光, 等. 基于客户点行政地址的自提点选址—路径优化[J]. 计算机集成制造系统, 2019, 25(8): 2069-2078. ZHOU Xiang, XU Maozeng, LYU Qiguang, et al. Location-routing problem of pickup point based on administrative address of customer points[J]. Computer Integrated Manufacturing Systems, 2019, 25(8): 2069-2078. (in Chinese) |
| [9] |
Wang Y, Assogba K, Liu Y, et al. Two-echelon location-routing optimization with time windows based on customer clustering[J]. Expert Systems With Applications, 2018, 104: 244-260. DOI:10.1016/j.eswa.2018.03.018 |
| [10] |
周林, 康燕, 宋寒, 等. 送提一体与终端共享下的最后一公里配送选址—路径问题[J]. 计算机集成制造系统, 2019, 25(7): 1855-1864. ZHOU Lin, KANG Yan, SONG Han, et al. Location-routing problem for last mile delivery with simultaneous home delivery and customer's pickup based on terminal sharing[J]. Computer Integrated Manufacturing Systems, 2019, 25(7): 1855-1864. (in Chinese) |
| [11] |
邱晗光, 李海南, 宋寒. 需求依赖末端交付与时间窗的城市配送自提柜选址—路径问题[J]. 计算机集成制造系统, 2018, 24(10): 2612-2621. QIU Hanguang, LI Hainan, SONG Han. Reception box locating-vehicle routing problems in urban distribution considering demand depending on last-mile delivery and time slots[J]. Computer Integrated Manufacturing Systems, 2018, 24(10): 2612-2621. (in Chinese) |
| [12] |
Boccia M, Crainic T G, Sforza A, et al. A metaheuristic for a two echelon location-routing problem[C]//Experimental Algorithms. Berlin, Heidelberg: Springer Berlin Heidelberg, 2010: 288-301.
|
| [13] |
Zhao Q W, Wang W, d Souza R. A heterogeneous fleet two-echelon capacitated location-routing model for joint delivery arising in city logistics[J]. International Journal of Production Research, 2018, 56(15): 5062-5080. DOI:10.1080/00207543.2017.1401235 |
| [14] |
黄凯明, 卢才武, 连民杰. 三层级设施选址-路径规划问题建模及算法研究[J]. 系统工程理论与实践, 2018, 38(3): 743-754. HUANG Kaiming, LU Caiwu, LIAN Minjie. Research on modeling and algorithm for three-echelon location-routing problem[J]. Systems Engineering-Theory & Practice, 2018, 38(3): 743-754. (in Chinese) |
| [15] |
吴香庭.基于遗传算法的K-means聚类方法的研究[D].青岛: 山东科技大学, 2010. WU Xiangting.Study of K-means clustering based on genetic algorithm[D].Qingdao: Shandong University of Science and Technology, 2010. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10294-2007047178.htm |
| [16] |
Struyf A, Hubert M, Rousseeuw P. Clustering in an object-oriented environment[J]. Journal of Statistical Software, 1996, 1(4): 1-30. |
 2020, Vol. 43
2020, Vol. 43

