2. 重庆大学 机械工程学院, 重庆 400044;
3. 鲁东大学 信息与电气工程学院, 山东 烟台 264005;
4. 河南农业大学 信息管理学院, 郑州 450002
2. College of Mechanical Engineering, Chongqing University, Chongqing 400044, P. R. China;
3. School of Information and Electrical Engineering, Ludong University, Yantai 264005, Shandong, P. R. China;
4. College of Information and Management Science Henan Agricultural University, Zhengzhou 450002, P. R. China
并行机调度是对多台机器的资源配置和作业排序,以及单台机器上工件的加工顺序进行优化研究。根据机器特征分为同构并行机和不相关并行机。由于机器新旧程度、规格、型号等不同,导致加工速度不同,并且相同工件的作业切换时间也不同。目前,多数的并行机生产调度研究主要是同构并行机调度研究,不能有效地解决实际生产调度问题,文中研究的不相关并行机成组调度问题具有实际应用价值。
Lee Jae-Ho等[1]提出禁忌搜索算法解决排序和机器依赖作业切换时间的不相关并行机调度问题,数学模型为Rm|Sijk|ΣTj,Rm表示不相关并行机,Sijk表示机器和排序依赖作业切换时间,ΣTj表示总拖延时间,以最小化总拖延为优化目标。Chen J F[2]研究了加工限制和作业切换的不相关并行机最小化最大拖延时间,文中提出了一种高效的基于引导启发式搜索,记录更新和禁忌列表的方法。Chen J F [3]研究了排序和机器依赖作业切换时间并考虑工期约束的不相关并行机调度问题,提出一种有效的启发式模拟退火算法基于修正作业切换导致的拖延成本,设计提高了算法参数。Zeidi J R等[4]研究了排序依赖作业切换时间的不相关并行机调度问题。考虑了工期约束,以最小化拖延和提早完工成本为目标,应用遗传模拟退火集成的元启发式算法进行求解。Lee J H等[5]以最小化拖延时间为优化目标,应用禁忌搜索算法求解了机器和排序依赖作业切换时间的不相关并行机调度问题。Lin S W等[6]为解决不相关并行机调度问题,提出了一种混合人工蜂群(HABC)算法,以最小化完工时间为优化目标。Gedik R等[7]研究了排序独立作业切换时间并考虑工期约束的不相关并行机生产调度问题,提出约束规划(CP)模型。轩华等[8]研究了以最小化最大完工时间为目标的不相关并行机环境下带恶化工件的车间调度问题,建立了数学规划模型,应用改进遗传算法进行模型求解。C M Nogueira J P等[9]研究了最小化总提早和拖延惩罚的不相关并行机调度问题,考虑了机器、排序依赖作业切换时间和释放时间3个因素。提出了基于贪婪随机自适应搜索过程(GRASP)启发式的算法。Lin S W等[10]针对排序依赖作业切换时间和不相关并行机调度问题,提出了一个简单的迭代贪婪式启发算法来求解最小化总拖延目标。Diana R O M等[11]针对排序依赖作业切换时间和不相关并行机调度问题,提出了免疫算法来求解最小化完工时间的优化目标。刘美瑶等[12]针对考虑预防性维修的分布式不相关并行机调度问题,以最小化最大完工时间为优化目标,提出了一种新型人工蜂群算法进行问题求解。
上述文献主要分别以最小化完工时间和最小化总拖延为优化目标构建了模型,研究了不相关并行机调度问题,个别文献考虑了排序依赖作业切换时间。研究主要应用了遗传算法(GA)、模拟退火算法(SA)、禁忌搜索算法(TS)、粒子群优化算法(PSO)、人工蜂群(ABC)算法等智能算法进行求解作业车间调度问题。然而单一智能算法在复杂优化问题求解方面各自存在一定的劣势,导致算法的优化结果不够好。比如,遗传算法实现算子的参数选择大部分靠经验,如交叉率和变异率等参数设置,并且遗传算法对初始种群的选择具有一定依赖性,可以结合一些启发算法进行改进。禁忌搜索算法和模拟退火算法是基于个体的元启发式算法,其中,禁忌搜索算法受禁忌长度、特赦规则和候选集大小的影响。模拟退火算法存在收敛速度慢,执行时间长,算法性能与初始值有关及参数敏感等问题。粒子群算法和人工蜂群算法是基于群体的元启发式算法,其中粒子群算法对于离散的优化问题处理不佳,容易陷入局部最优。为此,国内外学者提出基于融合思想的智能算法改进策略[13]。
为满足客户的个性化需求,多品种、小批量的生产模式成为离散制造企业的主要生产模式,该模式导致了频繁的作业切换和大量的作业切换时间,并且不同作业排序的不相关并行机的作业切换时间和加工时间不等,对于产品生产周期和生产效率都有影响。因此,文中研究了排序依赖作业切换时间不相关并行机调度问题,应用GATS混合算法进行问题求解,通过实例验证了混合算法的寻优能力。
1 问题描述研究基于成组技术的排序依赖作业切换时间的不相关并行机调度问题,优化目标为最小化总拖延时间,根据工件加工所需资源的相似性进行工件成组,要确定所有工件组在各机器上的分配,以及确定同一台机器上的各工件组以及组内的排列顺序,不同的排列顺序,产生不同的作业切换时间,以及不同的总拖延时间(Ti)。该问题的数学规划模型(Rm/sijm/ΣTi)可以描述为,有n个工件组在m台机器上加工,调度优化决策包括2个阶段,一是工件组—机器的匹配优化,二是根据工期和作业切换时间对分配到机器上的工件组以及组内工件的加工排序进行优化。文中应用了遗传禁忌搜索(GATS)算法进行模型求解,对不同规模的问题分别对比人工蜂群(ABC)算法和遗传模拟退火(GASA)算法进行案例研究。
2 模型构建 2.1 模型假设文中提出如下假设:1)所有机器在t=0时刻都可以使用;2)假设工件同时到达,不考虑机器的等待时间;3)每台机器的加工速度不同,相同工件在不同机器上的加工时间不同;4)每个工件在操作中不能中断;5)每台机器每次最多加工一个工件;6)工件没有加工特权;7)假设工件可以在任意机器上加工;8)排在机器第一位加工工件存在初始作业切换时间。
2.2 参数及变量描述具体参数及变量如表 1所示。
| 表 1 参数及变量表 Table 1 Parameters and variables |
优化目标
| $ \min \text { mize } \sum\limits_{i \in G} T_{i}, $ | (1) |
满足
| $ \sum\limits_{i=0}^{n} x_{i k}=1, k=1, 2, \cdots, m, $ | (2) |
| $ \sum\limits_{j=1}^{n} y_{i j k} \leqslant x_{i k}, j \neq i, i=0, 1, \cdots, n ; j=1, 2, \cdots, n ; k=1, 2, \cdots, m, $ | (3) |
| $ \sum\limits_{i=0}^{n} y_{i j k}=x_{j k}, j \neq i, i=0, 1, \cdots, n ; j=1, 2, \cdots, n ; k=1, 2, \cdots, m, $ | (4) |
| $ \sum\limits_{j=1}^{n} y_{0 j k}=1, i=0 ; j=1, 2, \cdots, n ; k=1, 2, \cdots, m, $ | (5) |
| $ C_{j} \geqslant C_{i}+p_{j k}+y_{i j k}-M \times\left(1-y_{i j k}\right), \\j \neq i, i=0, 1, \cdots, n, j=1, 2, \cdots, n, $ | (6) |
| $ C_{0}=0, $ | (7) |
| $ C_{j} \geqslant 0 . j=1, 2, \cdots, n, $ | (8) |
| $ T_{i}=\max \left\{C_{i}+d_{i}, 0\right\}, $ | (9) |
其中,式(2)说明每个工件只能在一台机器上加工1次;式(3)和式(4)说明2个工件恰好在同一台机器上紧前和紧后加工;式(5)说明每台机器都存在初始作业切换时间;式(6)紧前紧后工件完工时间包含作业切换时间;式(7)设排在第一位加工工件前有虚拟工件,其完工时间为0;式(8)每个工件都被加工;式(9)计算每个工件的拖延时间。
3 算法设计将GA和TS算法各自优点紧密结合起来,能够得到具有较强的全局搜索能力和局部搜索能力的遗传禁忌搜索算法(GATS)。GA和TS算法整合起来,能够优缺点互补。李大卫等[14]将禁忌搜索算法的记忆思想融入到遗传算法的搜索过程中,形成新的重组算法,并把禁忌搜索算法作为遗传算法的变异算子。方叶祥等[15]研究了基于遗传禁忌算法的双资源约束下并行生产线调度研究,交叉算子中引入了记忆功能,来避免早熟现象,对于交叉产生的个体,根据设置禁忌表确定被舍弃还是接受,引入藐视准则来保留优良个体。采用禁忌搜索算法作为变异算子,把一个要变异的染色体作为禁忌搜索的输入,把禁忌搜索得到的解作为变异的新个体。将TS独有的记忆功能引入GA的搜索过程中,利用TS爬山能力强的优点,使用TS改进GA的爬山能力,构建新的交叉算子,TSR算子作为交叉算子。把TS作为GA的变异算子TSM。遗传禁忌算法(GATS)结合了具有多出发点的GA,以及具有爬山能力强和记忆功能特点的TS,保持了GA具有多出发点的优势,克服了GA爬山能力差的缺点。
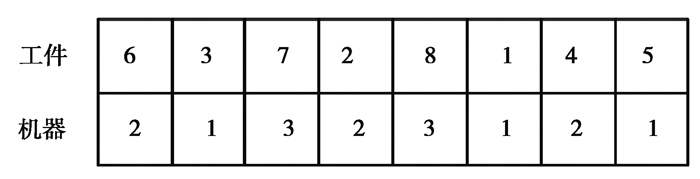
3.1 种群初始化初始的染色体设计方案能有效缩短算法运行时间,向量整数规划元启发算法是典型的染色体应用于并行机调度问题。一个n个数列的两行排列应用于染色体表达,n表示工件数量,第一行数列表示工件的一种排列,从1~n,第二行的每个元素对应第一种群由染色体的规模种群组成,每一条染色体就是问题的一种候选方案。适当行每个工件加工的机器,同一台机器上第一行越早出现的工件表示排在越靠前的位置进行加工。染色体的表达如图 1所示。工件分配如图 2所示。工件交叉操作如图 3所示。
|
图 1 染色体表示 Fig. 1 Chromosome representation |
|
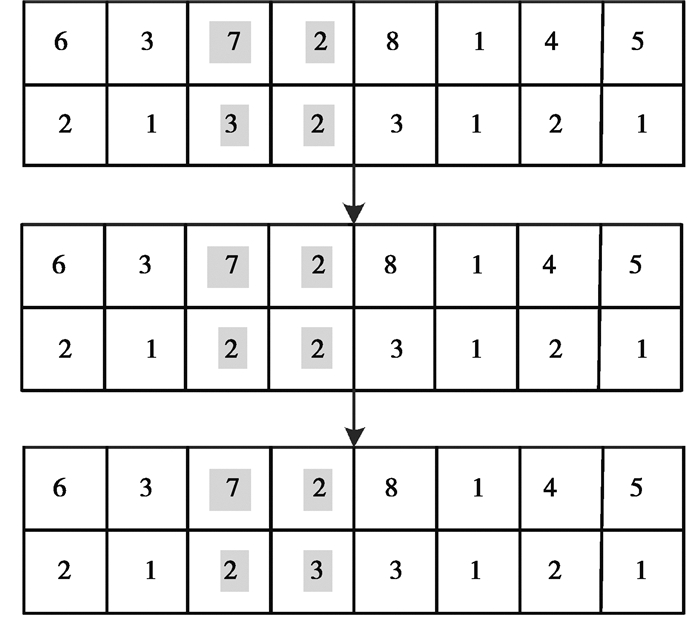
图 2 工件分配 Fig. 2 Jobs reallocation |
|
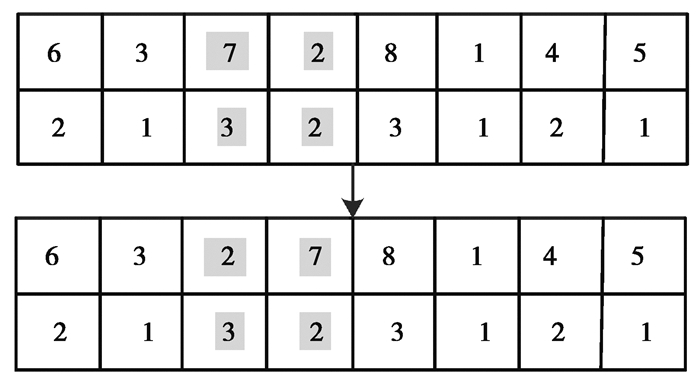
图 3 工件交叉操作 Fig. 3 Jobs crossover operator |
每条染色体评价的适应度函数为
| $ f(x)=\frac{1}{1+\sum\limits_{i=1}^{n} \max \left\{C_{i}-d_{i}, 0\right\}}, x=1, 2, \cdots, pop_\text {size }, $ | (14) |
式中,f(x)是种群中第x条染色体的适应度函数值;
禁忌搜索算法搜索的最优解比较依赖初始解。遗传算法通过选择、交叉、变异等操作产生的可行解作为禁忌搜索算法的初始解,能够有效的缩短禁忌搜索时间。禁忌搜索算法再根据工件加工优先指标对初始解进行优化排序。考虑将优先权指标值最大的工件首先安排在机器上加工。修正的优先权指标[16]表示为。
| $ I_{j}(t, i)=\frac{1}{p_{j k}} \exp \left(-\frac{\max \left(d_{j}-p_{j k}-t, 0\right)}{k_{1} \bar{p}}\right) \exp \left(-\frac{s_{i j k}}{k_{2} \bar{s}}\right), $ | (18) |
其中:Ij(t, i)表示工件j在t时刻的优先权指标,i是t时刻最后一个在机器上完成的工件,t时刻最大指标值的工件被选择加工;pjk是工件j在机器k上的加工时间;sijk是在机器k上工件j安排在工件i紧后加工,排序依赖机器的作业切换时间;dj是工件j的工期;k1和k2是标度参数,由τ,R,η,μ确定。τ为工期松紧系数,R为工期阈值因子,η为作业切换时间效率系数,μ为工件—机器因子。
| $ k_{1}=1.2 \ln (\mu)-R, $ | (19) |
| $ k_{2}=\frac{\tau}{A \sqrt{\eta}}, $ | (20) |
如果τ < 0.5,则式(19)中k1还要减去0.5;如果τ < 0.8,式(20)中A=1.8,当τ>=0.8,则A=2;如果η < 0.5并且μ>5,则k1还要减去0.5。
| $ \tau=1-\left(\frac{\bar{d}}{C_{\max }}\right), $ | (21) |
其中:d为平均工期;Cmax为最大完工时间,如果τ接近1说明生产调度任务很紧密,完工时间无限大。
工期阈值因子计算为
| $ R=\left(d_{\max }-d_{\min }\right) / C_{\max }, $ | (22) |
其中:dmin为最小工期;dmax为最大工期。
作业切换时间效率系数计算为
| $ \eta=\bar{s} / \bar{p}, \bar{s}, $ | (23) |
其中:s为平均作业切换时间; p为平均加工时间。
| $ \bar{p}_{i}=\sum\limits_{k=1}^{m} p_{i k} / m。$ | (24) |
工件—机器因子(μ)计算为
| $ \mu=N / M, $ | (25) |
其中:N为工件数;M为机器数;μ是一台机器上加工工件的平均数[18]。这些参数具体值依赖实际问题。对于规模较大的工件排序,Cmax较难计算,采用估算公式[16]。
| $ \hat{C}_{\max }=\left(\beta\bar{s}+\bar{p}\right) \mu, \beta \leqslant 1, $ | (26) |
其中:β是针对μ充分大时给出的评估因子(比如μ≥5),其计算公式为
| $ \beta=0.4+\frac{10}{\mu^{2}}-\frac{\eta}{7}。$ | (27) |
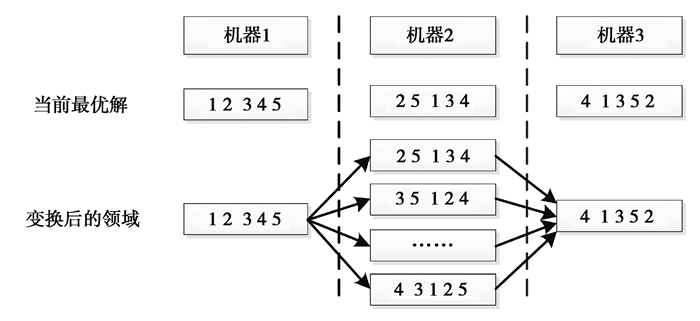
邻域映射为对换2种工件的加工顺序位置的2—opt,由于多个机器,每个机器上的工件位置顺序都可以变换,也存在同时变化的情况,比较复杂。文中生成了一个1~m的随机整数,由这个随机整数确定变化哪个机器上的工件以及各机器上的先后顺序[2-3]。比如,有3台机器(m=3),5种工件(n=5)的情况,在某次由当前最优解产生其邻域时,产生1~3的随机整数位2,则变化第2台机器的位置顺序。具体邻域生成方法如图 4所示。
|
图 4 邻域产生方法 Fig. 4 Neighborhood generated method |
禁忌搜索算法包括8种领域生成方法。都是基于交换和插入方法。n*m个操作的基因表示,代表一次操作的优化组合,n个工件m台机器。机器的拖延时间是指分配到该台机器上加工的所有工件的总拖延时间。带下标的工件组是指分配在某台机器上连续延迟或者早到的工件群。
Step1:子工件组再分配,基于插入方法。从最大拖延机器上任意选择的子工件组中移动一组连续工件,将它们插入到最小拖延机器上。这里所说的连续的工件组,是指从任意选择的子工件组里第一个工件开始。
Step2:工件再分配。这种方法与子工件组再分配方法相同,只不过工件替代了工件组被选择和插入。也就说分配到最大拖延机器上的工件从原始位置被移动,并且插入到任意位置,其分配的排序是在最小化拖延机器上,分配到最大拖延机器上的工件是被随意选择的。
Step3:子工件组和子工件组链再分配。从最大拖延机器上选择的子工件组被任意分配到中间机器,并且另外的子工件组从中间机器上被再分配到最小化拖延机器上。
Step4:子工件组和工件链再分配。这种方法与子工件组和子工件组链再分配是一样的。只是从中间机器上被选择的是一个工件而不是一个工件组,其被再分配到最小化拖延机器上。
Step5:工件和工件链再分配。方法与子工件组与子工件组链的再分配方法相同,只是两个再分配(从最大拖延机器到中间机器和从中间机器到最大拖延机器)对象是工件而不是工件组。
Step6:子工件组和子工件组交换。基于交换方法生成邻域方案,通过选择两个子工件组并且互相交换。特别是,从最大拖延机器上选择一个子工件组与另外任意机器上的子工件组进行交换。
Step7:机器间的工件交换。这种方法与子工件组交换相同,但是指的是两个工件交换而不是子工件组交换。也就是说,从最大拖延机器上选择一个工件与任意其他机器上的工件进行交换。
Step8:分配在一台机器上的工件间的交换。这种方法与机器间的工件和工件交换方法一样,只是交换的两个工件是任意机器上分配的工件。
3.5 交叉、变异操作将禁忌搜索的记忆功能引入到遗传算法的交叉算子中,即TSR的交叉过程具有高适应值的子代进入到下一代的机会很大,但不是所有的高适应值的子代一定都进入到下一代,因为TSR使用了禁忌表,可以限制适应值相同的子代出现次数,使得群体中尽可能保持染色体结构的多样性,避免早熟现象。
将禁忌搜索作为遗传算法的变异算子,即TSM输入一个解(染色体)作为初始解,经TSM作用,返回再输出另一个解。TSM是一个搜索过程,需要评价函数确定移动值,并根据移动值和禁忌表决定接受哪个移动,即确定接受哪个输出解,TSM搜索过程中可以接受劣解,TSM具有极强的爬山能力。
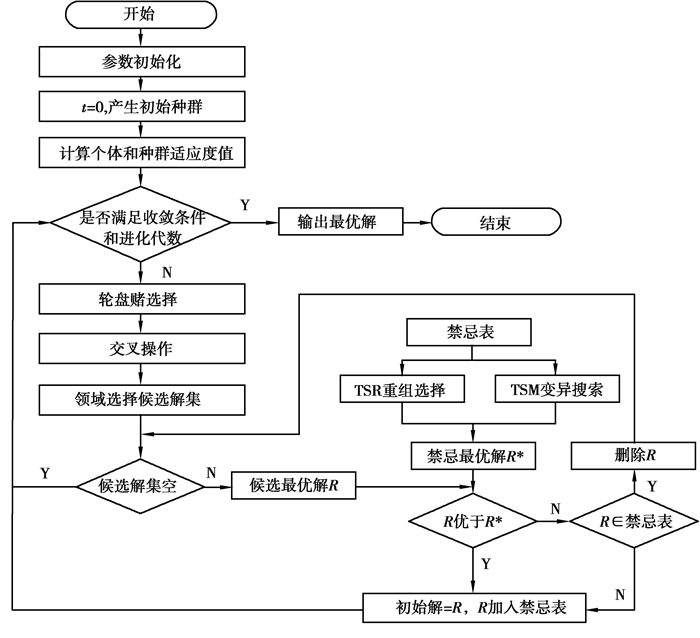
遗传禁忌搜索算法的具体流程图如图 5所示。
|
图 5 遗传禁忌搜索算法流程图 Fig. 5 The flow chart of GATS algorithm |
研究基于成组技术的排序依赖作业切换时间的不相关并行机调度问题(Rm|sijm|ΣTi)。以最小化总拖延时间为优化调度目标,即Minimize ΣTi。对于大规模问题,由于完工时间不能准确计算,根据最小的加工时间和作业切换时间对其进行估算,工期阈值因子(R)为[0.4, 1],工期松紧系数(τ)为[0.4, 0.8],具体参数设置[1, 3, 4, 10],如表 2所示。
| 表 2 参数设置 Table 2 Parameter settings |
| $ C_{\max }=\left(\sum\limits_{j \in F} \sum\limits_{k \in M}\left(p_{i k}+\left(\sum\limits_{i \in F} S_{i j k}\right) / F / M\right) / M\right.。$ |
根据田口试验得出最优参数组合为Npop=60,Ngen=150,Pc=0.6,Pm=0.12,Ps=0.25,L=10,ns=15。Chen[3]创建了960个试验问题,考虑了6个因子:工件数量(N),机器数量(M),工件组数量(F),工期优先因子(τ),工期范围因子(R),重要客户工件优先度因子(P)。文中借鉴了文献[3]考虑了5个因子:工件数量(N),机器数量(M),工件组数量(F),工期松紧系数(τ),工期阈值因子(R),假设工件重要程度相同。表 3分别包含4种工件数(N),3种机器数(M),2种工件组数量(F),2种工期松紧系数(τ),2种工期阈值因子(R)。生成5个实例,测试数据集为4×3×2×2×2=96个测试问题,总的测试实例为4×3×2×2×2×5=480个。
| 表 3 ABC算法与GATS算法对比结果 Table 3 Comparison between the results of the ABC and GATS algorithms |
GATS算法分别对比了ABC算法[20]和GASA算法[4]。算法运行机器性能参数为PC上CORE i3 M 380,CPU 2.53 GHz,内存为6.00 GB,运行软件为Matlab R2010a。所有导入数据从Excel 2010读取,结果以Excel形式表现,运行时间指主程序的运行时间,不包括导入数据的时间。不同规模数据各测试20次,计算结果表示为4个参数:目标最小值(Min.sol),目标平均值(Avg.sol),目标最大值(Max.sol)和平均值提高率(%)。GATS算法和ABC算法对比结果如表 3所示,GATS算法和GASA算法对比结果如表 4所示。
| 表 4 GASA算法与GATS算法对比结果 Table 4 Comparison between the results of the GASA and GATS algorithms |
根据计算结果,大多数的试验问题是工期松紧系数较大即紧工期(比如τ=0.8),工期阈值比较小(比如R=0.4),总体来说,GATS算法的性能是好于ABC算法和GASA算法,3种算法最优解的最小值、最大值、平均值如表 3和表 4所示。总拖延时间随着工件数和机器数的增加而增加。当R=0.4,τ=0.8时,总拖延时间也在增加,GATS算法比GASA算法和ABC算法的目标最优解平均值分别提高了11.90%和9.93%,GATS算法的最小、最大、平均总拖延时间分别为4 644.94, 4 784.68,4 699.41。虽然, GATS算法有些最优目标平均值没有GASA算法结果好,但是总的平均值提高率总的平均为8.56,结果标明GATS算法优于GASA算法。
5 结束语在实际生产中由于机器新旧程度、规格型号的差异导致机器的加工速率不同,因此,文中研究了基于成组技术的最优作业切换的不相关并行机调度问题,考虑了工期以及排序依赖作业切换时间等约束条件,以最小化总拖延为优化目标。首先,应用成组技术确定了所有工件组在各机器上的分配;其次,确定了同一台机器上的各工件的排列顺序。工件组之间存在切换时间,不同的加工顺序,作业切换时间不同,并且相同工件在不同机器上的切换时间不同。应用GATS算法进行问题求解,引用相关文献案例对不同规模的调度问题对比了ABC算法和GASA算法运行结果,结果显示文中采用的GATS算法具有很好的寻找最优解的能力。
| [1] |
Lee J H, Yu J M, Lee D H. A tabu search algorithm for unrelated parallel machine scheduling with sequence-and machine-dependent setups: minimizing total tardiness[J]. The International Journal of Advanced Manufacturing Technology, 2013, 69(9/10/11/12): 2081-2089. |
| [2] |
Chen J F. Minimization of maximum tardiness on unrelated parallel machines with process restrictions and setups[J]. The International Journal of Advanced Manufacturing Technology, 2006, 29(5/6): 557-563. |
| [3] |
Chen J F. Scheduling on unrelated parallel machines with sequence-and machine-dependent setup times and due-date constraints[J]. The International Journal of Advanced Manufacturing Technology, 2009, 44(11/12): 1204-1212. |
| [4] |
Zeidi J R, Mohammad Hosseini S. Scheduling unrelated parallel machines with sequence-dependent setup times[J]. The International Journal of Advanced Manufacturing Technology, 2015, 81(9/10/11/12): 1487-1496. |
| [5] |
Lee J H, Yu J M, Lee D H. A tabu search algorithm for unrelated parallel machine scheduling with sequence-and machine-dependent setups: minimizing total tardiness[J]. The International Journal of Advanced Manufacturing Technology, 2013, 69(9/10/11/12): 2081-2089. |
| [6] |
Lin S W, Ying K C. ABC-based manufacturing scheduling for unrelated parallel machines with machine-dependent and job sequence-dependent setup times[J]. Computers & Operations Research, 2014, 51: 172-181. |
| [7] |
Gedik R, Rainwater C, Nachtmann H, et al. Analysis of a parallel machine scheduling problem with sequence dependent setup times and job availability intervals[J]. European Journal of Operational Research, 2016, 251(2): 640-650. DOI:10.1016/j.ejor.2015.11.020 |
| [8] |
轩华, 秦莹莹, 王薛苑, 等. 带恶化工件的不相关并行机调度优化[J]. 系统仿真学报, 2019, 31(5): 919-924. XUAN Hua, QIN Yingying, WANG Xueyuan, et al. Optimization for unrelated parallel machine scheduling with deteriorating jobs[J]. Journal of System Simulation, 2019, 31(5): 919-924. (in Chinese) |
| [9] |
C M Nogueira J P, Arroyo J E C, Villadiego H M M, et al. Hybrid GRASP heuristics to solve an unrelated parallel machine scheduling problem with earliness and tardiness penalties[J]. Electronic Notes in Theoretical Computer Science, 2014, 302: 53-72. DOI:10.1016/j.entcs.2014.01.020 |
| [10] |
Lin S W, Lu C C, Ying K C. Minimization of total tardiness on unrelated parallel machines with sequence-and machine-dependent setup times under due date constraints[J]. The International Journal of Advanced Manufacturing Technology, 2011, 53(1/2/3/4): 353-361. |
| [11] |
Diana R O M, de França Filho M F, de Souza S R, et al. An immune-inspired algorithm for an unrelated parallel machines' scheduling problem with sequence and machine dependent setup-times for makespan minimisation[J]. Neurocomputing, 2015, 163: 94-105. DOI:10.1016/j.neucom.2014.06.091 |
| [12] |
刘美瑶, 雷德明.基于新型人工蜂群算法的分布式不相关并行机调度[J/OL].控制理论与应用: 1-9.http://kns.cnki.net/kcms/detail/44.1240.TP.20191022.1723.012.html. New artificial bee colony for distributed unrelated parallel machine scheduling[J]. Control Theory & Applications: 1-9.http://kns.cnki.net/kcms/detail/44.1240.TP.20191022.1723.012.html. (in Chinese) |
| [13] |
王凌. 智能优化算法及其应用[M]. 北京: 清华大学出版社, 2004. WANG Ling. Intelligent optimization algorithms with applications[M]. Beijing: Tsinghua University Press, 2004. (in Chinese) |
| [14] |
李大卫, 王莉, 王梦光. 遗传算法与禁忌搜索算法的混合策略[J]. 系统工程学报, 1998, 13(3): 28-34. LI Dawei, WANG Li, WANG Mengguang. Genetic algorithm and tabu search: a hybrid strategy[J]. Journal of Systems Engineering, 1998, 13(3): 28-34. (in Chinese) |
| [15] |
方叶祥, 钱存华, 蒋南云, 等. 基于遗传禁忌算法的双资源约束下并行生产线调度研究[J]. 运筹与管理, 2007, 16(5): 153-158. FANG Yexiang, QIAN Cunhua, JIANG Nanyun, et al. Scheduling of parallel production lines based on hybrid genetic-tabu search algorithm for dual-resource constrained[J]. Operations Research and Management Science, 2007, 16(5): 153-158. (in Chinese) DOI:10.3969/j.issn.1007-3221.2007.05.032 |
| [16] |
戚峰, 俞晶菁, 黄召杰. 基于禁忌搜索算法求解车间作业调度问题[J]. 兰州交通大学学报, 2011, 30(3): 79-85. QI Feng, YU Jingjing, HUANG Zhaojie. Solving a job-shop scheduling problem based on a tabu search algorithm[J]. Journal of Lanzhou Jiaotong University, 2011, 30(3): 79-85. (in Chinese) DOI:10.3969/j.issn.1001-4373.2011.03.019 |
| [17] |
Lee Y H, Pinedo M. Scheduling jobs on parallel machines with sequence-dependent setup times[J]. European Journal of Operational Research, 1997, 100(3): 464-474. DOI:10.1016/S0377-2217(95)00376-2 |
| [18] |
Lee Y H, Pinedo M. Scheduling jobs on parallel machines with sequence-dependent setup times[J]. European Journal of Operational Research, 1997, 100(3): 464-474. DOI:10.1016/S0377-2217(95)00376-2 |
| [19] |
Diana R O M, de Souza S R, Filho M F F. A Variable Neighborhood Descent as ILS local search to the minimization of the total weighted tardiness on unrelated parallel machines and sequence dependent setup times[J]. Electronic Notes in Discrete Mathematics, 2018, 66: 191-198. DOI:10.1016/j.endm.2018.03.025 |
| [20] |
Ying K C, Lin S W. Unrelated parallel machines scheduling with sequence-and machine-dependent setup times and due date constraints[J]. International Journal of Innovational Computing Information and Contro, 2012(8): 1-19. |
 2020, Vol. 43
2020, Vol. 43

