1b. 中原工学院 电子信息学院, 郑州 450007;
2. 杭州电子 科技大学 自动化学院, 杭州 310018
1b. School of Electronic Information, Zhongyuan University of Technology, Zhengzhou 450007, P. R. China;
2. School of Automation, Hangzhou Dianzi University, Hangzhou 310018, P. R. China
随着互联网技术的发展,文本数据在维度和样本数量上都出现了指数增长,对多维数据进行高效且有效的分析变得越来越具有挑战性,而基于机器学习的分类技术以其能够从海量数据中自动发现模式和知识的能力得到广泛应用。这其中极限学习机(Extreme learning machine,ELM)方法作为一种新型高效的单隐含层前馈神经网络学习方法,克服了传统的基于梯度下降法的BP网络参数多、速度慢的缺点,已成为学者们研究的热点。
为了达到多维数据的最佳分类效果,如何选择最少最有效的特征和最优的ELM分类器参数成为分类器设计的关键。文献[1]使用粒子群算法优化隐含层节点数,文献[2]提出了基于遗传算法(GA)的KELM分类器参数优化方法,文献[3]利用改进的人工蜂群算法优化极限学习机的参数,有效改善了分类模型的效果。文献[4]将极限学习机与粒子群算法相结合,用于优化极限学习机相关参数,并将该模型应用于山洪的预测。文献[5]提出了一种基于遗传算法的wrapper特征选择方法,并利用极限学习机,建立了ICU并行死亡率预测模型。文献[6]将改进粒子群算法MPSO和极限学习机相结合,利用MPSO对单隐层前馈神经网络的隐节点参数进行优化。文献[7]采用灰太狼优化智能算法优化极限学习机相关参数,构建了一个有效的KELM模型。文献[8]提出一种改进粒子群优化算法,并将该算法用于优化极限学习机的惩罚系数和核宽,以提高模型预测精度和泛化性能。文献[9]采用改进的花朵授粉算法优化ELM预测模型的初始参数,提高了准确率和运行效率。可以看出,对于特征个数的选择和ELM分类器参数的优化问题,相关研究已经非常深入,但同时实现特征和ELM分类器参数选择的研究并不多见。为了获得更优的分类效果,文中结合参数少、鲁棒性强的人工蜂群算法,同时完成高维数据的特征选择和ELM分类器参数的寻优。
1 极限学习机原理极限学习机是由Huang等[10]于2004年提出的前馈、单隐含层快速神经网络算法。
对于一个含有N个不同的训练样本集{(xi, yi)|xi∈Rn, yi∈Rm},其隐含层网络的激活函数为g(x),ELM分类模型可表示为
| $ f = \sum\nolimits_{f = 1}^L {{\beta _j}G\left( {{W_j} \cdot {X_i} + {b_j}} \right) = {Y_i}, i = 1, 2, \ldots , N} , $ | (1) |
其中,L为隐层节点数;G(x)为激励函数;Wj=[wj1, wj2, …wjm]T为第j个隐层节点与输入节点的权重向量;βj=[βj1, βj2, …βjn]T为第j个隐层节点与输出节点的权重向量;bj为第j个隐层节点的偏置。ELM训练步骤如下:
1) 设定隐含层网络的节点数,随机设定输入层网络和隐含层网络的连接权重W和隐含层网络节点的阈值b;
2) 选择一个无限可微的函数,作为隐含层网络的激活函数,并计算隐含层输出矩阵H;
3) 计算输出层权值β。
显然在训练分类器过程中,隐含层和输出层之间的连接权值通过解方程组方式一次性确定, 而隐含层节点数L需要设置,输入层和隐含层的全连接权值W、隐含层激活函数阈值b等参数可以随机生成或手动调整。为了保证最优分类效果,文中引入人工蜂群算法,同时对W、b和数据特征数联合寻优,从而得到最优分类器。
2 基于蜂群算法的分类器优化人工蜂群算法(artificial bee colony algorithm,ABC)是由土耳其学者Karaboga于2005年提出的一种新型群智能优化算法。该方法搜寻最优解的过程可分为3个阶段。第一是采蜜蜂阶段:采蜜蜂执行邻域搜索,并基于贪婪准则评估适应度值;之后是观察蜂阶段,它依据采蜜蜂阶段获得的解的质量好坏,执行同采蜜蜂相同的搜索;最后是侦察蜂阶段,当解更新次数达到局部搜索上限时,蜂的角色发生转换,放弃旧解,采用随机全局搜索方式生成一个新解。3个阶段搜索完成后,最终保留寻找到的最优解。
2.1 解的编码及更新在利用ABC算法进行分类器优化时,解向量由ELM分类器的参数W、b和特征向量f三部分组成,且均为[-1, 1]间的实数编码,解的编码形式如下:
| $ \begin{array}{l} x = \left[ {{w_{11}}, {w_{12}}, \cdots {w_{1n}}, {w_{21}}, {w_{22}}, \cdots {w_{2n}}, \cdots , {w_{l2}}} \right., \\ \;\;\;\;\;\;\;\;\left. { \cdots {w_{ln}}, {b_1}, {b_2}, \cdots {b_l}, {f_1}, {f_2} \cdots {f_n}} \right], \end{array} $ | (2) |
其中,n、l分别为输入网络、隐含网络节点数。
在解的更新过程,从W、b、f三部分中分别随机选择一维同时进行更新,如式(3)所示,式中α、β为区间[-1, 1]之间的随机数。
| $ {v_{ij}} = {x_{ij}} + \alpha \left( {{x_{ij}} - {x_{kj}}} \right) + \beta \left( {{\rm{Rpo}}{{\rm{p}}_{ij}} - {x_{ij}}} \right), $ | (3) |
其中:, k≠i,Vij为更新后第i个解的第j维,xij为第i个解的第j维,Rpopij为帕累托解集中第i个解的第j维。
2.2 适应度函数构造适应度函数用于衡量待优化解的质量,也就是分类器的性能。文中是以数据特征个数最少、分类器精度最高这样2个相互矛盾的指标为目标,如式(4)所示:
| $ \left\{ {\begin{array}{*{20}{l}} {{f_1} = N, }\\ {{f_2} = \alpha (1 - {\rm{Train Acc}}) + \beta (1 - {\rm{TestAcc }}), } \end{array}} \right. $ | (4) |
其中, N为选中的特征个数,TrainAcc、TestAcc分别为训练集和测试集正确率,在适应度函数中兼顾训练集和测试集的正确率,主要是防止训练过程中出现过拟合或者欠拟合。权重α、β取值为0.4和0.6。
2.3 算法步骤文中采用5折交叉验证评估算法的性能,算法最终的输出为最优参数集合和最佳特征组合子集。算法流程如图 1所示:
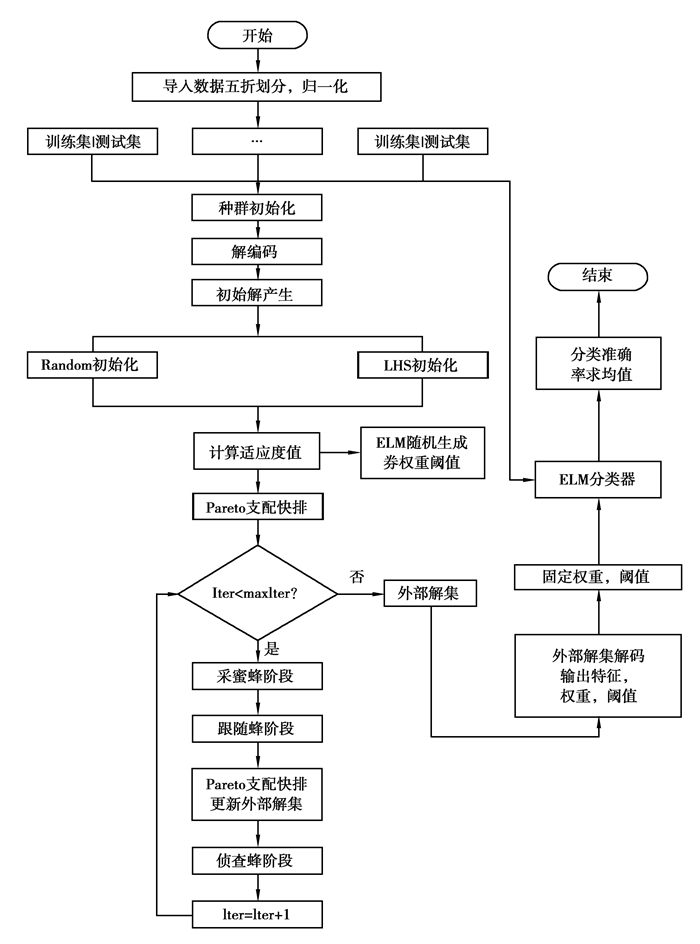
|
图 1 MOABC-ELM算法流程图 Fig. 1 Flowchart of MOABC-ELM |
步骤1:归一化数据集,并按5折划分,其中训练集和测试集样本数比例为4:1。
步骤2:初始化MOABC算法参数,生成初始解。针对ABC算法随机初始化方式(Random)产生的解分布不均匀问题,采用拉丁超立方体采样(LHS)方式生成初始解[12]。
步骤3:计算初始解的适应度函数值,快速Pareto支配排序形成初始解集。
步骤4:采蜜蜂阶段,更新解的维度得到新解,根据新解的适应度,确定新、旧解的Pareto支配关系,若旧解被新解支配,则存储新解,反之,旧解维持不变。
步骤5:跟随蜂阶段,计算跟随蜂跟随采蜜蜂的概率。若随机生成的概率小于当前采蜜蜂的概率,则占用一个跟随蜂去采蜜蜂所在的解进行更新,过程和步骤4采蜜蜂阶段类似。
步骤6:侦察蜂阶段:某一个解的领域搜索次数大于预设次数的蜜蜂角色转换为侦察蜂,并将所对应的解用随机生成的解替换。
步骤7:当前搜索的最优解用外部档案进行存储。若外部档案中解的数目大于预设档案集数目,则根据拥挤距离来删除最劣解或者最拥挤的解。之后返回第3步继续循环,直到满足设定的搜索次数。
步骤8:输出帕累托外部档案集,对其求平均值,并解码平均解生成的参数,将其带入模型,对优化后的分类器进行实验评估。
3 实验验证 3.1 实验数据描述为了检验提出算法的分类性能,选用UCI机器学习数据库中的6个代表性数据集[13]进行测试,分别为HAR、Wine、Iris、Breast Tissue、Statlog heart、Banknote,具体信息如表 1所示。
| 表 1 实验数据集 Table 1 The experimental datasets |
算法运行在Matlab 2016b版本上,运行环境为Windows7操作系统、Intel core i5处理器、主频3.3 GHz、内存4 GB。算法参数设置为种群规模200、最大循环次数为100、同一位置维度更新极限次数为100,ELM隐层激活函数为Radbas。
为了确定隐含层节点数对分类结果的影响,这里设置节点数分别为5、10、15、20、25、30,并分别考察不同的隐层神经元数目下ELM分类器的优化结果。由图 2可以看出,随着节点数和特征个数的增加,错误率总体呈减小趋势,但并不一定是特征个数和节点数越多,错误率就越低。从结果出发,按照特征数和错误率两者均最小的原则,为不同的数据集选择各自ELM分类器的节点数目,结果如表 2所示。
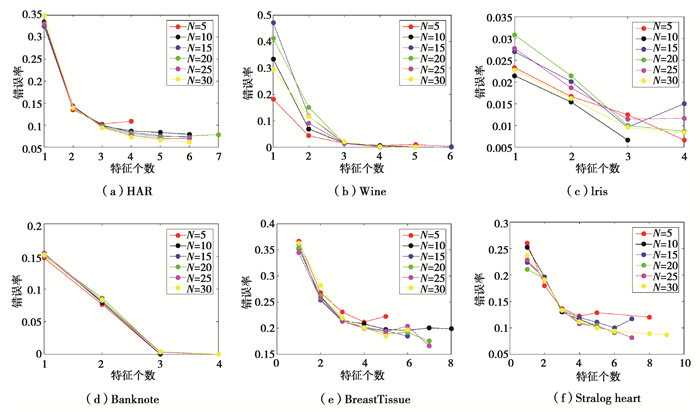
|
图 2 不同节点数下Pareto优化结果 Fig. 2 Theoptimization results with different nodes of ELM |
| 表 2 不同数据集的节点数设置 Table 2 The selection of nodes of ELM under different datasets |
为了评估算法的性能,基于选定的ELM神经元节点数,利用基于LHS初始化和传统随机初始化方法的人工蜂群算法去寻优特征个数和分类器参数,对生成的Pareto最优解所对应的适应度求平均值,其结果如图 3所示。由图 3可知,2种初始化方法对应的多目标优化算法均能取得较好的效果。优化后的特征子集有多个选择,特征数目和错误率之间的权衡可以由用户自行选择。而当特征数目最少或最多时,分类错误率都不是最低。这也从一个侧面说明,解决这种问题使用多目标优化算法是最佳选择。
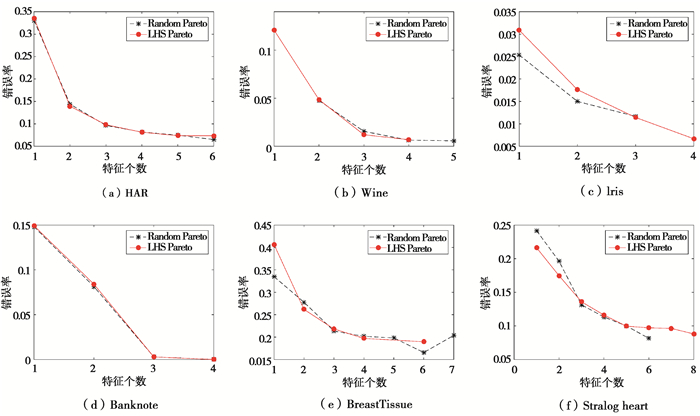
|
图 3 两种初始化方式结果对比 Fig. 3 Thecomparisons of results corresponding todifferent initialization methods |
为了验证优化连接权值和阈值对结果产生的影响,图 4列出了2种优化方式的Pareto结果图,其中蓝色折线(F_Pareto)代表只优化特征个数而手动选择ELM分类器参数的情况,而红色折线(FWB_Pareto)表示文中所采用的同时优化特征和ELM模型输入层和隐含层直间的连接权值、隐含层的阈值的方法。从图 4可以看出,FWB_Pareto方法相比F_Pareto方法,在特征个数相同的情况下,错误率更低,分类精度更高。证明了文中所提出方法的有效性。
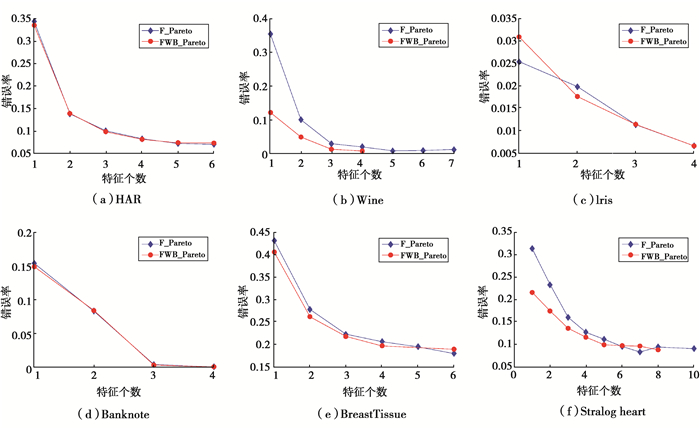
|
图 4 2种优化方式下Pareto优化结果 Fig. 4 The optimization results with two methods |
为了更进一步验证文中方法的先进性,不考虑Wine、Iris、Banknote等3个数据集分类准确率为100%的情况,只在表 3中列出另外3个数据集的分类结果,并与其它文献对应结果进行了对比。从表 3可以看出,文中所用方法相比于参考文献的方法,能够在保证更少特征个数的前提下,有效地将正确率提升5%甚至更多。
| 表 3 文中与文献的结果对比 Table 3 The comparison of results in this paper and previous literatures |
文中将多目标蜂群算法应用于多维数据分类问题中,对如何同时完成特征选择和极限学习机的参数优化进行了探讨。通过UCI数据集的测试,特征个数少且分类错误率低,结果证明了所提出的方法的有效性。
| [1] |
Han F, Zhao M R, Zhang J M. An improved incremental error minimized extreme learning machine for regression problem based on particle swarm optimization[J]. International Conference on Intelligent Computing, 2015(8): 94-100. |
| [2] |
Han F, Zhao M R, Zhang J M. An improved incremental error minimized extreme learning machine for regression problem based on particle swarm optimization[M]//Lecture Notes in Computer Science. Cham: Springer International Publishing, 2015: 94-100.
|
| [3] |
何敏, 刘建伟, 胡久松. 遗传优化核极限学习机的数据分类算法[J]. 传感器与微系统, 2017, 36(10): 141-143. HE Min, LIU Jianwei, HU Jiusong. Genetic optimization kernel-based extreme learning machine data classification algorithm[J]. Transducer and Microsystem Technologies, 2017, 36(10): 141-143. (in Chinese) |
| [4] |
赵虎, 左开伟, 覃永震. 改进人工蜂群算法优化ELM分类模型[J]. 计算机测量与控制, 2016, 24(10): 251-254. ZHAO Hu, ZUO Kaiwei, QIN Yongzhen. Improved artificial bee colony optimize ELM classification model[J]. Computer Measurement & Control, 2016, 24(10): 251-254. (in Chinese) |
| [5] |
Bui D T, Ngo P T Thi, Pham T D, et al. A novel hybrid approach based on a swarm intelligence optimized extreme learning machine for flash flood susceptibility mapping[J]. Catena, 2019, 179: 184-196. DOI:10.1016/j.catena.2019.04.009 |
| [6] |
Krishnan G S, Sowmya K S. A novel GA-ELM model for patient-specific mortality prediction over large-scale lab event data[J]. Applied Soft Computing, 2019, 80: 525-533. DOI:10.1016/j.asoc.2019.04.019 |
| [7] |
Nayak D R, Dash R, Majhi B. Discrete ripplet-Ⅱ transform and modified PSO based improved evolutionary extreme learning machine for pathological brain detection[J]. Neurocomputing, 2018, 282: 232-247. DOI:10.1016/j.neucom.2017.12.030 |
| [8] |
Wang M J, Chen H L, Li H Z, et al. Grey wolf optimization evolving kernel extreme learning machine: Application to bankruptcy prediction[J]. Engineering Applications of Artificial Intelligence, 2017, 63: 54-68. DOI:10.1016/j.engappai.2017.05.003 |
| [9] |
盛晓晨, 史旭东, 熊伟丽. 改进粒子群优化的极限学习机软测量建模方法[J]. 计算机应用研究, 2020, 37(6). SHENG Xiaochen, SHI Xudong, XIONG Weili. Soft sensor modeling for extreme learning machine based on improved particle swarm optimization[J]. Application Research of Computers, 2020, 37(6). (in Chinese) |
| [10] |
牛培峰, 李进柏, 刘楠, 等. 基于改进花授粉算法和极限学习机的锅炉NOx排放优化[J]. 动力工程学报, 2018, 38(10): 782-787. NIU Peifeng, LI Jinbai, LIU Nan, et al. NOx emission optimization of a boiler based on improved flower pollination algorithm and extreme learning machine[J]. Journal of Chinese Society of Power Engineering, 2018, 38(10): 782-787. (in Chinese) |
| [11] |
Huang G B, Zhou H, Ding X, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2012, 42(2): 513-529. DOI:10.1109/TSMCB.2011.2168604 |
| [12] |
Cui L Z, Li G H, Zhu Z X, et al. A novel artificial bee colony algorithm with an adaptive population size for numerical function optimization[J]. Information Sciences, 2017, 414: 53-67. DOI:10.1016/j.ins.2017.05.044 |
| [13] |
Evangelaras H, Koutras M V. On second order orthogonal Latin hypercube designs[J]. Journal of Complexity, 2017, 39: 111-121. DOI:10.1016/j.jco.2016.10.007 |
| [14] |
A Frank, Asuncion. UCI machine learningrepository.https: //archive.ics.uci.edu/ml/index.php
|
| [15] |
Ling H, Qian C X, Kang W C, et al. Combination of Support Vector Machine and K-Fold cross validation to predict compressive strength of concrete in marine environment[J]. Construction and Building Materials, 2019, 206: 355-363. DOI:10.1016/j.conbuildmat.2019.02.071 |
| [16] |
Shinmoto Torres R L, Ranasinghe D C, Shi Q F. Evaluation of wearable sensor tag data segmentation approaches for real time activity classification in elderly[M]//Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering. Cham: Springer International Publishing, 2014: 384-395.
|
| [17] |
Liyao Ma, SebastienDestercke, Yong Wang. Online active learning of decision trees with evidential data[J]. Pattern Recognition, 2016, 52: 33-45. DOI:10.1016/j.patcog.2015.10.014 |
| [18] |
Karegowda A G. Enhancing BPN Performance using GA identified significant features: a case study for categorization of heart statlog dataset[C].Foundation of Computer Science (FCS), 2013, IC2IT(1): 1-4.
|
 2020, Vol. 43
2020, Vol. 43


