2. 重庆工程职业技术学院 电气工程学院, 重庆 402260
2. School of Electrical Engineering, Chongqing Vocational Institute of Engineering, Chongqing 402260, P. R. China
近年来, 随着无线传感器网络(WSNs, wireless sensor networks)技术的成熟, 带来了信息感知领域的革命[1-3]。WSNs包含数据采集、存储、融合与处理以及通信等功能, 通常具有大规模和高密度的节点分布; 而且, 无线传感器节点常被布设在复杂环境中[4-6]。因此, 通过更换电池来延长网络寿命的方法是不现实的。为此, 提高传感器节点的能量利用率, 优化WSNs能耗管理, 以此来延长网络生存期显得格外重要; 同时, 无线传感器网络节点能量的获取是延长网络生存周期的根本途径。因此, 可获能无线传感器网络(EH-WSNs, energy-harvesting wireless sensor networks)成为该领域的研究热点[7-11]。EH-WSNs的理想目标是平衡所获能量与节点工作耗能。因此, 需要平衡所获能量与节点工作的耗能, 使其有能量富裕以维持网络持续工作, 实现不间断数据传输。
综上, 针对WSNs中基于预测算法的能量分配与管理机制的不足(没有考虑前期的历史获能情况及节点获能与节点耗能的匹配问题), 研究太阳能可充电无线传感器网络中能耗管理, 提出基于历史获能的能量中性管理机制, 以提高传感器节点的能量利用率并延长网络生存期。
1 自动跟踪太阳能的节点获能模型太阳能可充电传感器节点需要解决2个问题:一是如何提高太阳能电池板的获能效率[12]; 二是如何充分利用来之不易的能量[13]。
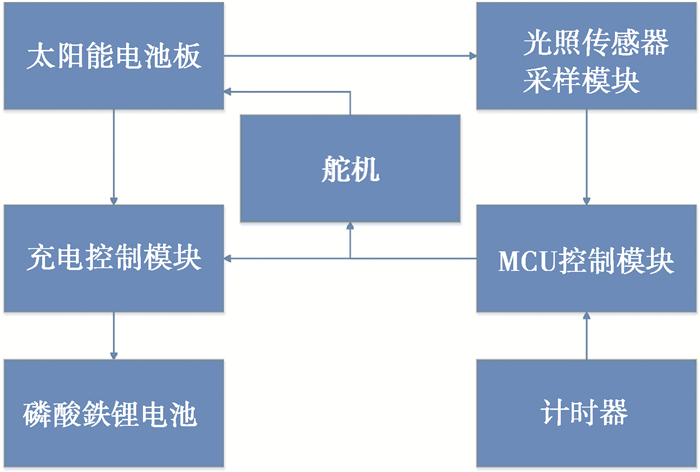
为了提高节点获能效率, 利用现有的太阳能电池, 采取动态跟踪太阳光技术, 实时调整太阳能电池板的高度角与方位角, 最大化地吸收太阳能[14]。采用性价比较高的普通太阳能电池板、光敏传感器BH1750及减速电机构建了如图 1所示的自动跟踪太阳能节点获能模型。
|
图 1 太阳能可充电传感器节点电池模型 Fig. 1 Solar rechargeable sensor node battery model |
为了充分利用来之不易的能量, 使节点工作时的耗能小于等于节点获能, 确保节点一直处于能量中性状态(即确保节点有足够的能量不至于衰亡)。为此, 针对太阳能可充电无线传感器节点, 提出基于历史获能水平的能量中性管理机制(ENMM-HHE, energy neutral management mechanism based on historical harvested energy)[15], 利用该机制, 根据历史操作周期(OC, operation cycle)中由太阳能转化而来的可用能量, 调节当前操作周期(OC)中节点工作占空比。
将一天(24 h), 分割为N个较小的时隙, 其中N∈{1, 2, 3, …, n}。规定每个时隙的时间跨度相等, 并且以符号Tslt来表示, 用Toc来表示一个操作周期, 它表示从第1个时隙到第N个时隙的时间跨度[16]。因此可得时隙与操作周期的关系如下
| $ {T_{oc}} = N{T_{{\rm{slt}}}}, $ | (1) |
在此规定N=24。节点在第k个时隙所收集的太阳能Eh(k)是可以通过一个积分公式计算出来的, 其中被积函数是太阳能收集功率Ph(k), 则有
| $ {E_h}\left( k \right) = \int t + {T_{{\rm{slt}}}}{P_h}\left( k \right){\rm{d}}t, $ | (2) |
由此, 节点的历史获能可由式(2)求得。然而, 未来某时隙的Ph(k)是在变化的, 所以Ph(k)的预测误差必然存在, 因而由此计算得到的Eh(k)也必然存在一定的误差[17]。但历史数据是具体的, 引入实时历史数据来设计能量分配管理机制, 可克服上述预测误差影响。
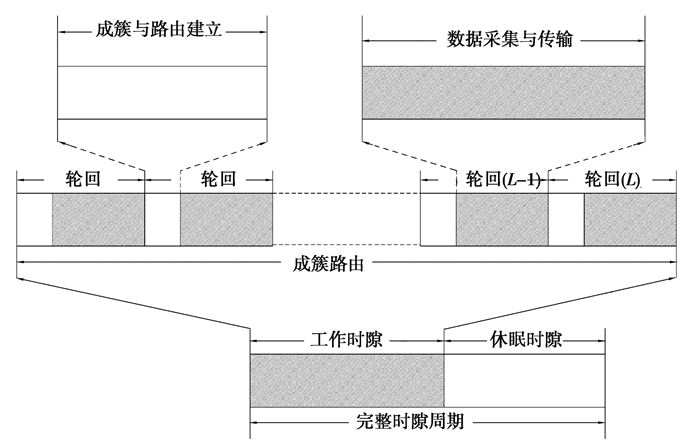
网络数据传输时间、簇重构时间以及路由建立时间的具体关系如图 2所示。
|
图 2 节点活动状态时间片构成 Fig. 2 The time slice of nodes active state |
在每一个分簇轮中, 任何一个传感器节点担任的角色只有2种, 要么被选为簇头节点, 要么成为簇普通节点。节点充当2种不同角色时所消耗的能量分别记为Ech(i)和Ecm(i)。假定监测区域中布置了q个WSNs节点, 自组织形成无线传感器网络, 同时假设监测区域被分成了p簇单元。定义q/p为一个轮周期数(RC, round cycle), 整个轮周期的时间用标记Trc表示[17]。则有
| $ {T_{{\rm{rc}}}} = \left( {q/p} \right){T_r}, $ | (3) |
在式(3)中Tr代表轮周期中一轮所持续的时间。现设法计算出第k个时隙中第m个轮周期的单个节点i所消耗的能量, 并记为Erc(m, k)(i)。则有
| $ E_{{\rm{rc}}}^{\left( {m,k} \right)}\left( i \right) = \sum\limits_{l = 1}^u {E_{{\rm{ch}}}^{\left( {l,m,k} \right)}} \left( i \right) + \sum\limits_{j = 1}^{q/p - u} {E_{{\rm{cm}}}^{\left( {j,m,k} \right)}} \left( i \right), $ | (4) |
在式(4)中:
| $ E_{{\rm{rc}}}^{\left( {m,k} \right)}\left( i \right) \ne E_{{\rm{rc}}}^{\left( {m + 1,k} \right)}\left( i \right),\left( {m = 1,2,3, \cdots } \right), $ | (5) |
因此, 可以得到节点i在第k个时隙中所消耗的总能量Ectalk(i)
| $ E_{{\rm{ctal}}}^k\left( i \right) = \sum\limits_{m = 1}^L {E_{{\rm{rc}}}^{\left( {m,k} \right)}\left( i \right)} , $ | (6) |
式(6)中L代表第k个时隙中轮周期的次数, 很显然它随着占空比的变化而变化。根据前面的理论可以得到L
| $ L = \left\{ \begin{array}{l} \left[ {\frac{{\eta {T_{{\rm{slt}}}}}}{{{T_{{\rm{rc}}}}}}} \right],\left( {\frac{{\eta {T_{{\rm{slt }}}}}}{{{T_{{\rm{rc}}}}}} - \left[ {\frac{{\eta {T_{{\rm{slt }}}}}}{{{T_{{\rm{rc}}}}}}} \right] < 0.5} \right),\\ \left[ {\frac{{\eta {T_{{\rm{slt}}}}}}{{{T_{{\rm{rc}}}}}}} \right] + 1,\left( {\frac{{\eta {T_{{\rm{slt}}}}}}{{{T_{{\rm{rc}}}}}} - \left[ {\frac{{\eta {T_{{\rm{slt}}}}}}{{{T_{{\rm{rc}}}}}}} \right] \ge 0.5} \right), \end{array} \right. $ | (7) |
在式(7)中, 一旦所有传感器节点部署完成之后, Trc便是一个固定值。η(ηmin≤η≤1)在此处表示占空比, 它其实就是单个节点在一个时隙中分别处于活动状态与睡眠状态时所占比例的反应。ηmin代表满足网络服务要求的最小占空比。因为占空比在一定程度上反映了网络的数据通信量, 过低的占空比自然满足不了用户对数据的需求。[x]表示对括弧内的函数做取整运算。至此, 在一个操作周期(OC)中节点i所消耗的总能量
| $ E_{{\rm{coc}}}^{{n_{oc}}}\left( i \right) = \sum\limits_{k = 1}^N {E_{{\rm{ctsl}}}^k} \left( i \right) = \sum\limits_{k = 1}^N {\sum\limits_{m = 1}^L {E_{{\rm{rc}}}^{\left( {m,k} \right)}} } \left( i \right), $ | (8) |
Erc(m, k)(i)代表第k个时隙中第m个轮周期中, 单个节点i所消耗的能量。结合式(3)~(8), 可以得到Ecocnoc(i)的另一种形式如下
| $ E_{{\rm{coc}}}^{{n_{oc}}}\left( i \right) = \sum\limits_{k = 1}^N {\sum\limits_{m = 1}^L {\left( {\sum\limits_{l = 1}^u {E_{{\rm{ch}}}^{\left( {l,m,k} \right)}} \left( i \right) + \sum\limits_{j = 1}^{q/p - u} {E_{{\rm{cm}}}^{\left( {j,m,k} \right)}} \left( i \right)} \right)} } , $ | (9) |
式(9)中, L由式(7)确定。通过式(9)易知:节点i在任何一个操作周期(OC)中所消耗的总能量Ecocnoc(i)与占空比η(ηmin≤η≤1)之间具有正相关性。因此, 可以通过调节占空比η来控制节点i在一个操作周期(OC)中所消耗的能量。
改进的方法是:保证节点i在同一个操作周期(OC)内占空比η恒定不变, 而不同的操作周期(OC)内可不同, 因为不同操作周期(OC)之间的关联性并不强。但是, 即使是同一个节点i在不同轮周期内所消耗的能量Erc(m, k)(i)也是不同的; 并且在同一个轮周期内, 不同的节点所消耗的能量Erc(m, k)(i)也应该是不同的。尽管要设法保证η在同一操作周期内(OC)为固定值, 而下面的关系依然存在
| $ E_{{\rm{copc}}}^{{n_{oc}}}\left( i \right) \ne E_{{\rm{copc}}}^{{n_{oc}}}\left( {i + 1} \right)\;\;\;\left( {i = 1,2,3, \cdots } \right), $ | (10) |
| $ E_{{\rm{copc}}}^{{n_{oc}}}\left( i \right) \ne E_{{\rm{copc}}}^{{n_{oc}} + 1}\left( i \right)\;\;\;\left( {i = 1,2,3, \cdots } \right), $ | (11) |
为了达到能量中性操作的状态, 给出任何操作周期(OC)内的能量中性约束条件如下[18]
| $ E_{{\rm{coc}}}^{{n_{oc}}}\left( i \right) \le E_{{\rm{hoc}}}^{{n_{oc}}}\left( i \right), $ | (12) |
在式(12)中, Ehocnoc(i)表示节点i在一个操作周期(OC)中通过太阳能收集装置所收集的能量, 然后这些能量被储能装置存储起来后再供给节点使用。
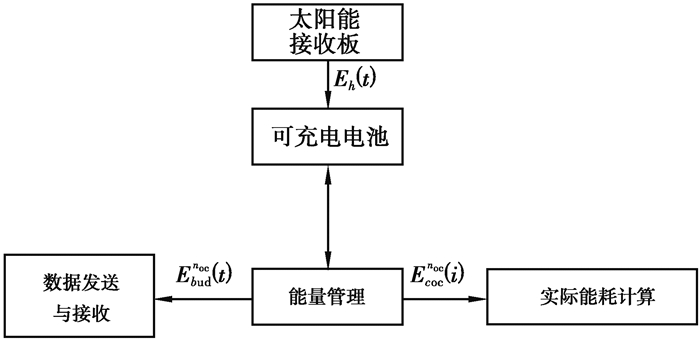
现提出一种实践性更强的能量分配机制, 它是建立在上一操作周期(OC)获能基础之上的[19]。具体关系如图 3所示。
|
图 3 能量收集与预算的过程 Fig. 3 Process of Energy Harvesting and Budgeting |
图 3粗略的描述了从能量收集到能量预算分配的处理过程。能量管理设备实时掌握着电池能量水平值, 并为节点精确分配电池所存储的能量。同时真实耗能计算设备可以准确计算出在一个操作周期(OC)内所消耗的能量。
在一个操作周期(OC)内, 为了高效利用所分配的能量Ebudnoc(i), 并且考虑到为下一个操作周期(OC)所分配的能量
| $ E_{{\rm{coc}}}^{{n_{oc}}}\left( i \right) = E_{{\rm{bud}}}^{{n_{oc}}}\left( i \right) = E_{{\rm{hoc}}}^{{n_{oc}}}\left( i \right), $ | (13) |
正如式(10)与(11)所反应的, 因为随机分簇的缘由, 不同节点的Ecocnoc(i)往往不同, 所以即使可以调节占空比η在一个操作周期内保持恒定, 等式Ecocnoc(i)=Ebudnoc(i)也很难实现。这就需要根据历史获能与耗能来计算一个操作周期(OC)中占空比η的固定值为多少。
假设每一个节点i在上一个邻近的操作周期(OC)中, 它的能量消耗功率Pcnoc(i)是一个固定值。根据这个假设, 可以得到一个轮周期内节点i的平均耗能, 其计算式如下
| $ E_{{\rm{avec}}}^{{n_{oc}}}\left( i \right) = \frac{{\left( {q/p} \right){T_r}E_{{\rm{coc}}}^{{n_{oc}}}\left( i \right)}}{{{\eta _{{n_{oc}}}}N{T_{{\rm{slt}}}}}}, $ | (14) |
在此规定ηnoc(ηmin≤ηnoc≤1)在一个操作周期(OCnoc)中保持固定值。如前所述网络中有q个太阳能可充电传感器节点, 那么还可以获得所有节点在同一个操作周期(OCnoc)中的平均耗能
| $ E_{{\rm{avec}}}^{{n_{oc}}} = \frac{1}{q}\sum\limits_{i = 1}^q {E_{{\rm{avec}}}^{{n_{oc}}}\left( i \right)} , $ | (15) |
因此, 一旦下一操作周期(OCnoc+1)中预算分配的能量
| $ {\eta _{{n_{oc}} + 1}} = \min \left( {\max \left( {\frac{{\left( {q/p} \right){T_r}E_{{\rm{bud}}}^{{n_{oc}} + 1}}}{{{T_{oc}}E_{{\rm{avec}}}^{{n_{oc}}}}},{\eta _{\min }}} \right),1} \right), $ | (16) |
式(16)中, 函数min(·)和max(·)分别表示取括弧中变量的最小值与最大值。所以结合公式(7)、(9)、(14)、(15)、(16), 可以计算出在操作周期(OCnoc+1)中节点i所消耗的能量
| $ \left\{ \begin{array}{l} E_{{\rm{coc}}}^{{n_{oc}} + 1}\left( i \right) = \sum\limits_{k = 1}^N {\sum\limits_{m = 1}^{L_{{n_{oc}} + 1}} {\left( {\sum\limits_{l = 1}^u {E_{{\rm{ch}}}^{\left( {l,m,k} \right)}} \left( i \right) + \sum\limits_{j = 1}^{q/p - 1} {E_{{\rm{cm}}}^{\left( {j,m,k} \right)}} \left( i \right)} \right)} } ,\\ {L_{{n_{oc}} + 1}} = \left\{ \begin{array}{l} \left[ {\frac{{{\eta _{{n_{oc}} + 1}}{T_{{\rm{slt}}}}}}{{{T_{{\rm{rc}}}}}}} \right]\;\;\;\;\;\;\;\left( {\frac{{{\eta _{{n_{oc}} + 1}}{T_{{\rm{slt}}}}}}{{{T_{{\rm{rc}}}}}} - \left[ {\frac{{{\eta _{{n_{oc}} + 1}}{T_{{\rm{slt}}}}}}{{{T_{{\rm{rc}}}}}}} \right] < 0.5} \right),\\ \left[ {\frac{{{\eta _{{n_{oc}} + 1}}{T_{{\rm{slt}}}}}}{{{T_{{\rm{rc}}}}}}} \right] + 1\;\;\;\left( {\frac{{{\eta _{{n_{oc}} + 1}}{T_{{\rm{slt}}}}}}{{{T_{{\rm{rc}}}}}} - \left[ {\frac{{{\eta _{{n_{oc}} + 1}}{T_{{\rm{slt}}}}}}{{{T_{{\rm{rc}}}}}}} \right] \ge 0.5} \right), \end{array} \right.\\ {\eta _{{n_{oc}} + 1}} = \min \left( {\max \left( {\frac{{\left( {q/p} \right){T_r}E_{{\rm{bud}}}^{{n_{oc}} + 1}}}{{{T_{oc}}E_{{\rm{avec}}}^{{n_{oc}}}}},{\eta _{\min }}} \right),1} \right) \end{array} \right. $ | (17) |
在式(17)中, q和p分别代表监测区域中部署的太阳能传感器节点总数和预先设定的每一轮中簇单元总数。因此, 可变的轮数Lnoc+1也能反应出相应时隙中的轮周期数目。根据式(1)可得N=Toc/Tslt, 它表明了一个操作周期(OC)中有多少个时隙。通过式(17)可以抽象出如下函数式
| $ E_{{\rm{coc}}}^{{n_{oc}} + 1}\left( i \right) = f\left( {E_{{\rm{coc}}}^{{n_{oc}}}\left( i \right)} \right), $ | (18) |
由式(18)可知, 如果能获得过去任何一个操作周期(OCnoc)中节点的历史耗能Ecocnoc(i), 那么就可以计算出下一个操作周期(OCnoc+1)中节点需要消耗的能量
| $ {f_\Delta }\left( {{\eta _{{n_{oc}}}}} \right) = E_{{\rm{coc}}}^{{n_{oc}}}\left( i \right) - E_{{\rm{bud}}}^{{n_{oc}}}\left( i \right), $ | (19) |
在此从结论出发探寻结论成立所需的条件, 假定
| $ {f_\Delta }\left( {{\eta _{{n_{oc}}}}} \right) = \left\{ \begin{array}{l} > 0\;\;\;\left( {{\eta _{{n_{oc}}}} > \eta _{{n_{oc}}}^ * } \right),\\ = 0\;\;\;\left( {{\eta _{{n_{oc}}}} = \eta _{{n_{oc}}}^ * } \right),\\ < 0\;\;\;\;\left( {{\eta _{{n_{oc}}}} < \eta _{{n_{oc}}}^ * } \right), \end{array} \right. $ | (20) |
根据前面的论述可知, 因为第k个时隙中第m个轮周期中, 单个节点i所消耗的能量Erc(m, k)(i)具有随机因素, 所以条件
| $ \left( {E_{{\rm{rc}}}^{\left( {m,k} \right)}\left( i \right) - E_{{\rm{avec}}}^{{n_{oc}}}\left( i \right)} \right) \sim N\left( {0,{\sigma ^2}} \right), $ | (21) |
在式(21)中, 某个轮周期内的耗能Erc(m, k)(i)与平均耗能Eavecnoc(i)的偏差(Erc(m, k)(i)-Eavecnoc(i))的均值取0是合理的, 而方差σ则表明了误差随均值的波动情况。
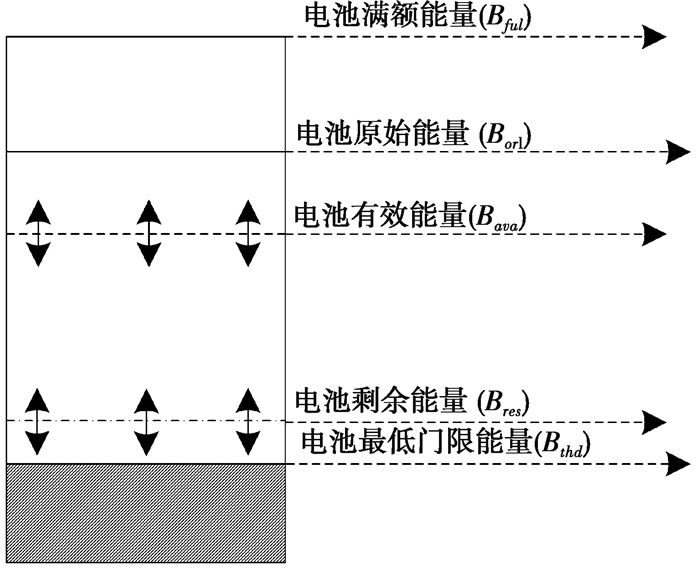
在此, 给出可充电电池能量电平分段模型, 如图 4所示。
|
图 4 电池能量水平分段模型 Fig. 4 The Model of Battery Energy Level Segmentations |
在图 4中, 自上而下的第二条实线代表在第一个操作周期(OC)中, 可充电传感器节点电池初始携带的能量水平, 记为(Borl)。第一条实线代表电池的容量Bful, 很明显它处在最高的位置是合理的。自上而下的第三条实线表示电池能量的阈值(Bthd), 被定义为在最初的第一个操作周期(OC)结束时电池的剩余能量, 并且从那时起这个值就是确定不变的了。图 4中, 在任一操作周期(OC)内, 任一节点i所消耗的能量是可以通过电池实时能量消耗计算设备推算得到。因为不同节点在相同操作周期(OC)中的能量消耗具有波动性, 所以采用平均能量消耗值来设定电池能量阈值(Bthd)。因此得到如下公式
| $ {B_{{\rm{thd}}}} = {B_{{\rm{orl}}}} - \frac{1}{q}\sum\limits_{i = 1}^q {E_{{\rm{coc}}}^1\left( i \right)} , $ | (22) |
为了对比不同操作周期(OC)的耗能情况, 将第一个操作周期(OC)中的占空比设置为1(η=1)。从第二个操作周期(OC)开始就有了太阳能通过光电转换来的能量, 这样可充电电池就可以根据历史获能与剩余能量水平, 来为节点在下一个操作周期(OC)的工作分配所需能量。除了第一个操作周期(OC)外, 在每个操作周期(OC)开始的时刻, 以符号(Bava)表示电池的可用能量水平, 它包含上一个操作周期结束时的电池的剩余能量(Bres)和收集的能量。据此可以得到能量预算值(Ebudnoc(i))的计算式如下
| $ \left\{ \begin{array}{l} E_{{\rm{bud}}}^{{n_{oc}}}\left( i \right) = B_{{\rm{ava}}}^{{n_{oc}}}\left( i \right) - {B_{{\rm{thd}}}},\\ B_{{\rm{ava}}}^{{n_{oc}}}\left( i \right) = E_h^{{n_{oc}} - 1}\left( i \right) + B_{{\rm{res}}}^{{n_{oc}} - 1}\left( i \right), \end{array} \right. $ | (23) |
在式(23)中,
| $ E_{{\rm{bud}}}^{{n_{oc}}} = \frac{1}{q}\sum\limits_{i = 1}^q {B_{{\rm{ava}}}^{{n_{oc}}}\left( i \right)} - {B_{{\rm{thd}}}}, $ | (24) |
根据式(8)和(19)可以推导出改进的方法, 用它可计算一个操作周期(OC)中所消耗的能量, 并进一步确定下一操作周期(OC)中的占空比[20-21]。这个公式的优点在于, 它考虑了实际能量消耗偏差对能量预算的影响。具体表达式为
| $ \begin{array}{l} E_{r - {\rm{coc}}}^{{n_{oc}}}\left( i \right) = E_{{\rm{coc}}}^{{n_{oc}}}\left( i \right) + {f_\Delta }\left( {{\eta _{{n_{oc}}}}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;2E_{{\rm{coc}}}^{{n_{oc}}}\left( i \right) - E_{{\rm{bud}}}^{{n_{oc}}}\left( i \right), \end{array} $ | (25) |
再结合式(23)与(24)可得
| $ E_{r - {\rm{coc}}}^{{n_{oc}}}\left( i \right) = 2E_{{\rm{coc}}}^{{n_{oc}}}\left( i \right) - B_{{\rm{ava}}}^{{n_{oc}}}\left( i \right) + {B_{{\rm{thd}}}}, $ | (26) |
因此, 更进一步结合式(14)、(15)、(16)、(24)和(26), 并借助当下操作周期(OCnoc)中改进的能量消耗公式Er-cocnoc(i), 可以推导出下一操作周期(OCnoc+1)中的占空比(ηnoc+1)
| $ {\eta _{{n_{oc}} + 1}} = \min \left( {\max \left( {\frac{{{\eta _{{n_{oc}}}}\sum\limits_{i = 1}^q {\left( {B_{{\rm{ava}}}^{{n_{ov}} + 1}\left( i \right) - {B_{{\rm{thd}}}}} \right)} }}{{\sum\limits_{i = 1}^q {\left( {2E_{{\rm{coc}}}^{{n_{oc}}}\left( i \right) - B_{{\rm{ava}}}^{{n_{oc}}}\left( i \right) + {B_{{\rm{thd}}}}} \right)} }},{\eta _{\min }}} \right),1} \right), $ | (27) |
如果平均能量超过了电池初始携带能量的水平线(即
| $ \left\{ {{L_{{n_{oc}} + 1}} = \left\{ \begin{array}{l} \left[ {\frac{{{\eta _{{n_{oc}} + 1}}{T_{{\rm{slt}}}}}}{{{T_{{\rm{rc}}}}}}} \right]\left( {\frac{{{\eta _{{n_{oc}} + 1}}{T_{{\rm{slt}}}}}}{{{T_{{\rm{rc}}}}}} - \left[ {\frac{{{\eta _{{n_{oc}} + 1}}{T_{{\rm{slt}}}}}}{{{T_{{\rm{rc}}}}}}} \right] < 0.5} \right),\\ \left[ {\frac{{{\eta _{{n_{oc}} + 1}}{T_{{\rm{slt}}}}}}{{{T_{{\rm{rc}}}}}}} \right] + 1\;\;\;\;\left( {\frac{{{\eta _{{n_{oc}} + 1}}{T_{{\rm{slt}}}}}}{{{T_{{\rm{rc}}}}}} - \left[ {\frac{{{\eta _{{n_{oc}} + 1}}{T_{{\rm{slt}}}}}}{{{T_{{\rm{rc}}}}}}} \right] \ge 0.5} \right), \end{array} \right.} \right. $ | (28) |
| $ \left\{ \begin{array}{l} {\eta _{{n_{oc}} + 1}} = \min \left( {\max \left( {\frac{{{\eta _{{n_{oc}}}}\sum\limits_{i = 1}^q {\left( {B_{{\rm{ava}}}^{{n_{oc}} + 1}\left( i \right) - {B_{{\rm{thd}}}}} \right)} }}{{\sum\limits_{i = 1}^q {\left( {2E_{{\rm{coc}}}^{{n_{oc}}}\left( i \right) - B_{{\rm{ava}}}^{{n_{oc}}}\left( i \right) + {B_{{\rm{thd}}}}} \right)} }},{\eta _{\min }}} \right),1} \right),\\ \left( {{\eta _1} = 1} \right), \end{array} \right. $ | (29) |
至此, 可以根据式(28)和(29)分别确定下一操作周期(OCnoc+1)中轮周期次数(Lnoc+1)和占空比(ηnoc+1), 这是基于电池历史获能和实时能量水平自适应调节节点下一操作周期(OCnoc+1)占空比机制的关键参数。
3 仿真分析考虑在实际应用中, 每个节点携带的初始能量至少要能满足, 一个操作周期(OC)中当占空比(DC)为1 h的耗能需求; 当然初始能量也不能达到电池的极限容量, 因为还要为太阳能转换而来的电能留有存储空间, 以免能量溢出。因此, 设置电池的初始能量为1 400 J, 其值是电池极限容量的70%。根据实际应用的需求设置最小占空比(DC ηmin)为0.1 (ηmin =0.1)。设定目标监测区域大小为20 000 m2(200 m×100 m), 其中部署的节点为1 000个。仿真参数设置如表 1所示, 仿真结果如图 5所示。
| 表 1 基本参数设置 Table 1 Basic parameters settings |
|
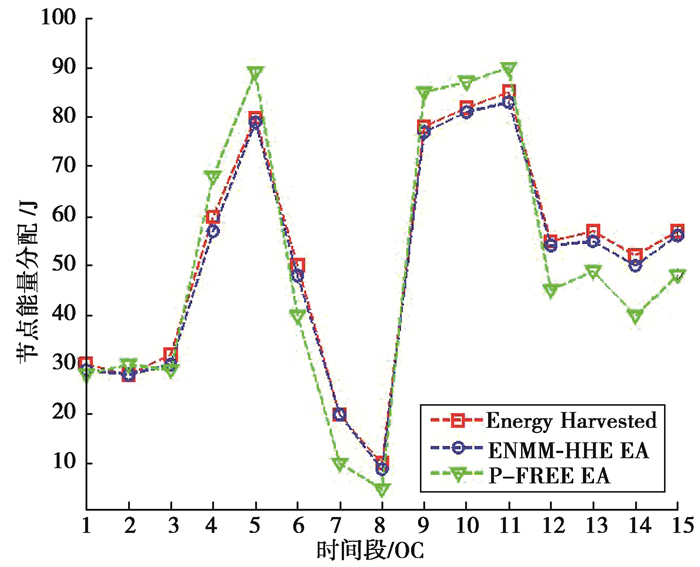
图 5 ENMM-HHE与P-FREE能量分配误差对比 Fig. 5 Comparison of energy assigning deviation between ENMM-HHE and P-FREE |
图 5中的绿色线(带三角形标记)代表P-FREE, 可以看出在获能差别不大且变化相对稳定时, P-FREE能量分配误差比ENMM-HHE稍微偏高; 但是在天气变化剧烈, 即获能变化差别较大时, P-FREE能量分配误差比ENMM-HHE要高出很多。这意味着要么能量分配过多耗能过快, 不得不使用电池初始携带能量, 长此下去必然影响电池寿命; 要么能量分配偏少, 造成能量浪费和利用率偏低。
而图 5中的蓝色曲线(带圆圈标记)代表ENMM-HHE的能量分配情况, 显而易见蓝色线紧随红色曲线的变化而变化, 并且始终位于红色线下方。这充分说明了ENMM-HHE的优势, 它根据节点历史获能情况(过去的一个操作周期)与剩余能量, 来调节下一操作周期(OC)中的占空比, 使之在每一个操作周期内保持恒定; 以这样的方式使收获的能量得到合理分配, 从而实现能量的高效利用。因此, 仿真结果验证了在能量分配管理方面, ENMM-HHE要优于P-FREE。
4 实验测试与分析采用实验室已有的三峡库区水质监测传感器节点进行获能工作实验。实验测试装置如图 6所示。在程序中设定每5 s完成一次数据的采集、处理与上传。

|
图 6 水质检测试验 Fig. 6 Water quality testing test |
测试时间从早上6:30到晚上18:30, 负载从30 Ω(中午太阳光最强时, 节点工作频繁, 占空比最大, 表现出负载电阻较小)到260 Ω(早晚太阳光最弱时, 节点工作迟缓, 占空比最小, 表现出负载电阻较大)。其测试结果如表 2所示。
| 表 2 晴天中固定式节点获能装置测量数据 Table 2 Fixed node energy harvester measurement data in sunny days |
经测量系统在数据收发时的电压为5.02 V, 电流为0.22 A(发信); 在其他时间系统的电压为5.04 V, 电流为0.11 A(发信)。根据如表 2中情况的晴天, 自动跟踪太阳光的节点获能装置的平均获能为49 776 J。计算可知, 如果水质检测系统全天候收发数据, 那么一天的平均耗能为95 420 J, 这时获能不足以支持系统耗能。通过收发数据的平均功率和节点的历史获能计算可得, 如果系统持续收发数据那么49 776 J的能量只能工作约12.51 h。这就要根据系统不同时间的耗能功率来匹配系统的耗能与获能。经计算如果一天(24)数据收发的总时间为1 h, 其他23 h的时间都不收发数据, 那么系统一天的全部耗能正好为49 776 J。因此, 设定系统每2 min开始的5 s收发数据, 这样保证功能完善, 其他时间处于休眠状态, 这样系统在当天的耗能正好小于等于节点在昨天的获能, 验证了历史获能的能量中性管理策略。
5 结语根据基于历史获能的能量中性管理机制, 设计了一种自适应跟踪太阳光的节点获能模型, 并在“三峡库区水质监测平台”上, 利用水质检测传感器节点进行试验。通过调节水质检测系统的数据收发频率(即占空比), 实现节点耗能与获能的平衡, 从而实现太阳能电池板大小与节点能耗的最佳匹配, 验证了基于历史获能的能量中性管理策略的可行性。
| [1] |
Xu G B, Shen W M, Wang X B. Applications of wireless sensor networks in marine environment monitoring: a survey[J]. Sensors, 2014, 14(9): 16932-16954. |
| [2] |
刘鸣. 无线传感器网络技术发展分析[J]. 信息通信, 2016, 29(6): 286-287. LIU Ming. Analysis of the development of wireless sensor network technology[J]. Information & Communications, 2016, 29(6): 286-287. (in Chinese) |
| [3] |
Atzori L, Iera A, Morabito G. The internet of things: a survey[J]. Computer Networks, 2010, 54(15): 2787-2805. |
| [4] |
吕雪. 无线传感器网络技术发展现状[J]. 信息通信, 2015(10): 169-170. LV Xue. Development status of wireless sensor network technology[J]. Information & Communications, 2015(10): 169-170. (in Chinese) |
| [5] |
Raghavendra C S, Sivalingam K M, Znati T. Wireless sensor networks[M/OL]. Boston, MA: Springer US, 2004[2018-09-25]. https: //doi.org/10.1007/b117506.
|
| [6] |
徐伟强, 吴铁军, 汪亚明, 等. 用于Ad Hoc网络的自适应多速率多播拥塞控制策略[J]. 软件学报, 2008(3): 769-778. XU Weiqiang, WU Tiejun, WANG Yaming, et al. Adaptive congestion control strategy for multirate multicast sessions in ad hoc networks[J]. Journal of Software, 2008(3): 769-778. (in Chinese) |
| [7] |
Miorandi D, Sicari S, de Pellegrini F, et al. Internet of things: vision, applications and research challenges[J]. Ad Hoc Networks, 2012, 10(7): 1497-1516. |
| [8] |
Xu G B, Shen W M, Wang X B. Applications of wireless sensor networks in marine environment monitoring: a survey[J]. Sensors, 2014, 14(9): 16932-16954. |
| [9] |
王伟.无线传感器网络若干关键技术研究[D].武汉: 华中科技大学, 2011. WANG Wei. Research on several key technologies of wireless sensor networks[D]. Wuhan: Huazhong University of Science and Technology, 2011. (in Chinese) |
| [10] |
Mainetti L, Patrono L, Vilei A. Evolution of wireless sensor networks towards the internet of things: A survey[C/OL]. SoftCOM 2011, 19th International Conference on Software, Telecommunications and Computer Networks.New York, USA: IEEE, 2011: (2011-11-01)[2018-09-25].https://ieeexplore.ieee.org/document/6064380?arnumber=6064380&tag=1.
|
| [11] |
何聪, 郭松涛. 可充电无线传感器网络的有向充电优化算法[J]. 重庆大学学报, 2019, 42(1): 88-97. HE Cong, GUO Songtao. Directed charging optimization algorithm in rechargeable wireless sensor networks[J]. Journal of Chongqing University, 2019, 42(1): 88-97. (in Chinese) |
| [12] |
芦浩. 太阳能光伏发电技术应用研究与普及[J]. 中国新技术新产品, 2016(16): 28-29. LU Hao. Application research and popularization of solar photovoltaic power generation technology[J]. New Technology & New Products of China, 2016(16): 28-29. (in Chinese) |
| [13] |
Kosunalp S, Cihan A. Harvesting solar energy for limited-energy problem in wireless sensor networks[C/OL]. 2017 25th Signal Processing and Communications Applications Conference (SIU). New York, USA: IEEE, 2017: (2017-06-29)[2018-09-28]https: //ieeexplore.ieee.org/document/7960535.
|
| [14] |
Ramya R, Saravanakumar G, Ravi S. Energy harvesting in wireless sensor networks[M]. India: Springer India, 2016: 841-843.
|
| [15] |
Zhang X X, Fan R, Yang X C, et al. Two tracking control method to improve solar cell photoelectric efficiency[C/OL]. 2016 Chinese Control and Decision Conference (CCDC), Northeastern University, IEEE Singapore Industrial Electronics Session: Editorial Department of Control and Decision Making, 2016[2018-11-25]. https://ieeexplore.ieee.org/abstract/document/7531396.
|
| [16] |
Yang L, Lu Y Z, Zhong Y C, et al. A hybrid, game theory based, and distributed clustering protocol for wireless sensor networks[J]. Wireless Networks, 2016, 22(3): 1007-1021. |
| [17] |
Basagni S, Naderi M Y, Petrioli C, et al. Wireless sensor networks with energy harvesting[M/OL]Mobile Ad Hoc Networking: Cutting Edge Directions, Second Edition. 2013-02-22.https://ieeexplore.ieee.org/document/6482731?denied.
|
| [18] |
潘泽中.能量采集无线传感器网络的能量预测及分簇算法[D].南昌: 华东交通大学, 2016. PAN Zezhong. Energy prediction and clustering algorithm in energy harvesting wireless sensor network[D]. Nanchang: East China Jiaotong University, 2016. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10404-1016900404.htm |
| [19] |
Peng S, Low C P. Throughput optimal energy neutral management for energy harvesting wireless sensor networks[C/OL]. 2012 IEEE Wireless Communications and Networking Conference (WCNC). New York, USA: IEEE, 2012: (2012-06-11)[2018-09-25].https://ieeexplore.ieee.org/document/6214186.
|
| [20] |
Babayo A A, Anisi M H, Ali I. A review on energy management schemes in energy harvesting wireless sensor networks[J]. Renewable and Sustainable Energy Reviews, 2017, 76: 1176-1184. |
| [21] |
杨柳.基于分簇结构的无线传感器网络节能路由协议研究[D].重庆: 重庆大学, 2016. YANG Liu. Study on cluster-based energy saving routing protocols for wireless sensor networks[D].Chongqing: Chongqing University, 2016. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10611-1016765753.htm |
 2020, Vol. 43
2020, Vol. 43


