2. 柳州日高汽车减振技术有限责任公司, 湖南 柳州 545000;
3. 华南理工大学 机械与汽车工程学院, 广州 510640
2. Liuzhou Rigo Automotive Vibration Reduction Technology Co. Ltd., Liuzhou, Hunan 545000, P. R. China;
3. School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510641, P. R. China
悬架缓冲块位于汽车悬架系统中,与螺旋弹簧并联形成非线性的弹性元件,其力学性能直接影响整车的平顺性和操稳性[1]。合理地设计缓冲块结构能够有效地提升汽车行驶的舒适性。
Dickson等[2]对缓冲块工作阶段橡胶的挤压特性进行了分析,总结出了缓冲块形状设计的一般原则和方法。Schudt等[3]以缓冲块的吸能特性为提升目标,设计了3种不同结构的缓冲块来改善其性能,但是这一改进依赖工程师的经验和时间,报道中没有提出优化缓冲块结构的方法。Sidhu等[4]研究了缓冲块在不同压缩条件下的疲劳特性,但并没有对缓冲块的结构进行优化。Caliskan等[5]、黄敏等[6]和Geisler等[7]计算了缓冲块的力-位移性能,研究了不同材料的本构模型对计算的影响,但没有对缓冲块的性能做出优化。黄舟等[8]对由天然橡胶、丁基橡胶和发泡橡胶等典型工程橡胶制造的缓冲块进行了研究,探究了不同橡胶材料的压缩变形行为,使用缓冲吸能水平、缓冲系数和吸能效率来评价缓冲块的吸能特性,但仅考虑了材料的影响,并没有从结构方面进行优化,具有局限性。张志飞等[9]以缓冲块的刚度曲线为目标,利用结构优化方法对汽车前保险杠缓冲块进行了结构优化设计。
综上所述,部分文章虽然分析了缓冲块的结构对其性能的影响,并根据工程经验提出了结构改进策略,但并未提出一种系统的优化方法来对缓冲块结构进行优化设计。笔者以悬架设计要求为基础,得出缓冲块性能的评价指标,使用结构优化方法对缓冲块的结构进行优化设计。以缓冲块的截面形状参数为设计变量,通过有限元仿真计算出不同结构缓冲块的性能参数,通过响应面法建立设计变量和性能参数的近似数学模型,以性能参数最优为目标,最后使用遗传算法解出最优的结构参数组合。所提出的方法对缓冲块的设计具有指导意义。
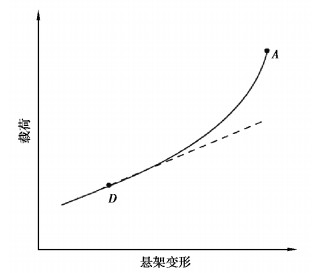
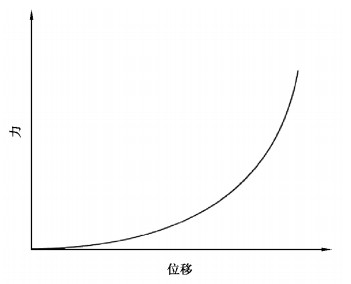
1 缓冲块性能评价指标根据悬架设计的要求,悬架的力-位移曲线应为非线性弹性特性曲线,如图 1所示。曲线中,D点处的刚度较小,并且其附近的刚度变化也较小,以使汽车在良好道路行驶时具有较好的行驶平顺性。而当悬架变形比较大时,刚度急剧增大,这样悬架系统能够吸收更多的能量。螺旋弹簧和缓冲块并联,其中螺旋弹簧的刚度为线性,缓冲块的刚度曲线为非线性,如图 2所示。
|
图 1 悬架弹性特性曲线 Fig. 1 Suspension elasticity curve |
|
图 2 缓冲块刚度曲线 Fig. 2 Stiffness curve of jounce bumper |
从缓冲块刚度曲线可以看出,主要的特性分为两个部分:①接触时低刚度——接触特性;②极限压缩后高刚度——吸能特性。本研究中使用这2个特性作为缓冲块性能的评价指标。
为了便于直观地衡量接触特性,定义悬架极限压缩量达到50%时的力值大小作为评价接触特性的指标,力值越小,接触特性越好。
吸能特性可由压缩力压缩量曲线下所包含的面积计算得出,即:
| $ W = \int_0^{{x_{{\rm{max}}}}} {F{\rm{d}}x} 。$ | (1) |
式中:F为极限力值;W为吸收的能量;x为压缩量;xmax为极限压缩量。
在已报道的文献中还提出了其他几种评价吸能特性的指标[10],如缓冲系数C和吸能效率E。
缓冲系数C定义为给定的峰值力Fpeak与在此峰值力下缓冲块可以吸收的能量W的比值,即:
| $ C = \frac{{{F_{{\rm{peak}}}}}}{W} = \frac{{{F_{{\rm{peak}}}}}}{{\int_0^{{x_{{\rm{max}}}}} {F{\rm{d}}x} }}。$ | (2) |
缓冲材料的吸能效率E为缓冲结构所吸收的能量W与对应力值Fpeak之比,即:
| $ C = \frac{W}{{{F_{{\rm{peak}}}}}} = \frac{{\int_0^{{x_{{\rm{max}}}}} {F{\rm{d}}x} }}{{{F_{{\rm{peak}}}}}}。$ | (3) |
这3个指标W、C和E都能反映出不同结构缓冲块的吸能特性。取其中E作为吸能特性的指标,E越大,吸能特性越好。
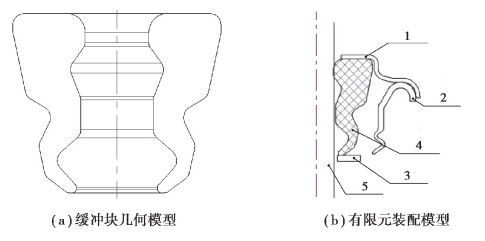
2 缓冲块性能计算与试验 2.1 缓冲块性能计算的有限元模型建立由于缓冲块的模型是轴对称模型[11],采用2D轴对称模型进行计算。一悬架减振器缓冲块几何模型和有限元装配模型如图 3所示。网格单元选择CAX4R,即轴对称线性缩减积分单元。线性缩减积分单元在数值上存在沙漏问题,需要验证求解过程中系统伪应变能(ALLAE)与系统弹性应变能(ALLSE)的比值是否在5%以内[12]。网格划分采用1 mm×1 mm四边形网格,共737个单元。相比于缓冲块的大变形,上杯罩、防尘罩、压头、活塞杆的变形可以忽略不计,故将其视为刚体。定义上杯罩、防尘罩、压头和活塞杆与缓冲块的接触均为面面接触,选择刚体为主面,缓冲块为从面,并选择有限滑移,刚体与缓冲块的摩擦系数设为0.2。随着压缩进行,缓冲块产生自接触,因此需要定义缓冲块的自接触,设置自接触摩擦系数为0.2。
|
1..上杯罩; 2.防尘罩; 3.压头; 4.缓冲块; 5.活塞杆 图 3 缓冲块的几何模型和有限元装配模型 Fig. 3 Geometric model of jounce bumper and assembly model of finite element model |
缓冲块常用的材料是天然橡胶。天然橡胶属于超弹性材料,假设其不可压缩,采用Mooney-Rivilin超弹性本构模型,通过单轴拉伸和压缩试验,利用最小二乘法拟合得到其模型材料常数[13-14],如表 1所示。
| 表 1 Mooney-Rivilin模型材料常数 Table 1 Mooney-Rivilin material constants |
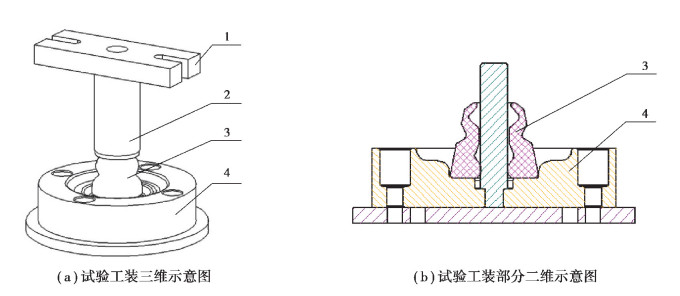
如图 4所示为缓冲块刚度性能测试工装示意图。金属压头按照减振器导向座上端面的尺寸设计,金属底座按照上杯罩进行设计,其外轮廓尺寸相同。测试时,固定金属底座,将缓冲块样件装配在金属底座的导向杆上,金属压头装配在金属连接板上,金属连接板固定在机台上端,机台上端施加向下的位移载荷对缓冲块进行挤压。设备的力传感器安装在机台上端,记录压缩过程中压缩力和压缩量的数据。
|
1.金属连接板; 2.金属压头; 3.缓冲块样件; 4.金属底座 图 4 测试缓冲块刚度性能的工装示意图 Fig. 4 Tooling diagram for testing the stiffness performance of the jounce bumper |
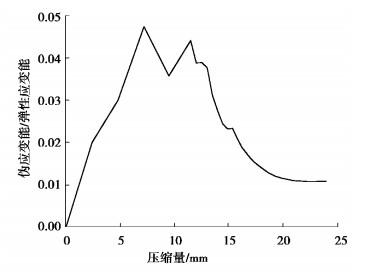
由于选择的线性缩减积分单元在数值上存在沙漏问题,提取计算过程中系统伪应变能(ALLAE)与系统弹性应变能(ALLSE)的值,绘制ALLAE与ALLSE的比值曲线,结果如图 5所示。从图 5可见,在整个分析过程中ALLAE与ALLSE的比值始终低于5%,表明求解过程中沙漏问题并不严重。
|
图 5 伪应变能与弹性应变能的比值 Fig. 5 Ratio of ALLAE to ALLSE |
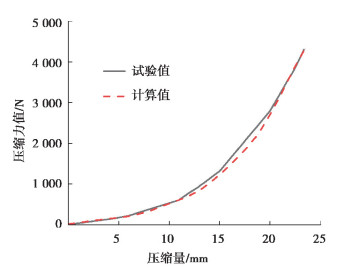
有限元法计算的结果和试验结果见图 6。从图中可以看出,计算和试验结果吻合,说明有限元模型是正确的。
|
图 6 缓冲块刚度曲线的计算值与试验值 Fig. 6 Calculated and test results of stiffness |
本研究中使用的分析方法是正交试验法[15]。通过缓冲块外形结构参数的不同组合计算出不同的性能指标,借助正交试验法来筛选出权重最高的结构参数。
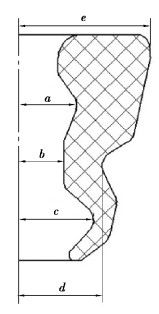
本研究的对象是某轻型轿车前悬架缓冲块。根据主机厂要求,缓冲块所受极限力值为5 400 N,缓冲块高度为49.4 mm。根据Schudt等[3]的报道,高度在40~60 mm的缓冲块外部宜采用一个凹槽的设计,如图 7所示。取其中5个尺寸作为正交设计的变量,各尺寸的变化范围如表 2所示。
|
图 7 缓冲块结构参数示意图 Fig. 7 Structural parameter diagram of the jounce bumper |
| 表 2 缓冲块的尺寸及其变化范围 Table 2 The sizes of the jounce bumper and their variation ranges |
利用L16(45)正交表安排正交试验[15],各因素的水平如表 3所示。
| 表 3 各因素的水平列表 Table 3 Values of the factors |
表 4为5因素4水平正交试验分配及结果。试验结果统计分析通常采用两种方法:直观分析法(极差分析法)和方差分析法。由于考虑的因素数较少,所以选用直观分析法对正交表计算结果进行分析[15]。
| 表 4 结构参数正交试验分配及有限元计算结果 Table 4 Value assignment of structural parameter orthogonal test and results by the finite element calculation |
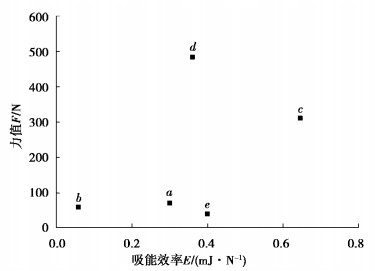
依据表 4有限元计算的性能指标计算值,计算得到吸能效率E和力值F的直观分析表,如表 5、表 6所示,分析得到评价指标吸能特性E和力值F对各结构参数的极差如图 8所示。
| 表 5 吸能效率直观分析表 Table 5 Intuitive analysis table of energy absorption efficiency |
| 表 6 压缩力值直观分析表 Table 6 Intuitive analysis table of compressive force value |
|
图 8 吸能特性与力值的极差分析结果 Fig. 8 Extreme results of energy absorption characteristics and force values |
在表 5~6中,Kij表示第
从极差图中可以看出,各因素对缓冲块性能影响大小的顺序是:尺寸c>尺寸d>尺寸e>尺寸a>尺寸b。选取影响力最高的3个结构参数,即尺寸c、尺寸d和尺寸e,进行下一步的响应面模型[16]建立。
4 缓冲块性能优化方法 4.1 响应面模型的建立为更好地建立响应面模型,采用Box-Behnken设计[17]对筛选出的结构参数重新进行分配试验。表 7所示为分配方案及计算结果。
| 表 7 结构参数Box-Behnken试验分配及结果 Table 7 Value assignment of Box-Behnken test for structural parameters and calculated results of E and F |
表中第0组为对照组,是初始设计结果。采用二阶多项式作为拟合响应面代理模型的函数形式,根据选择的3个主要结构参数,响应面代理模型可表示为:
| $ E = {a_0} + {a_1}c + {a_2}d + {a_3}e + {a_4}cd + {a_5}ce + {a_6}de + {a_7}{c^2} + {a_8}{d^2} + {a_9}{e^2},$ | (4) |
| $ F = {b_0} + {b_1}c + {b_2}d + {b_3}e + {b_4}cd + {b_5}ce + {b_6}de + {b_7}{c^2} + {b_8}{d^2} + {b_9}{e^2}。$ | (5) |
通过Design-Expert软件拟合后的系数如表 8所示。
| 表 8 响应面代理模型估计系数 Table 8 Estimation coefficient of response surface proxy model |
上述构建的响应面代理模型,吸能效率的相关系数r2值为0.990 7,力值的相关系数r2值为0.999 1,这表示由响应面模型预测的吸能效率和力值与计算值差别较小。
为了验证代理模型的准确度,在设计区间内随机选择了5个测试样本点,由ABAQUS有限元软件计算获得其性能指标(FEA),与响应面模型式(4)~(5)计算值对比,结果如表 9所示。
| 表 9 响应面模型测试样本点及相对误差 Table 9 Response surface model test sample points and relative errors |
从表 9可以看出,响应面模型的最大相对误差小于10%,预测精度较高,可以代替有限元模型进行优化计算。
4.2 单目标遗传算法优化方法为了更好地评价缓冲块的总体性能,定义性能指标P如下:
| $ P = \frac{{E - {E_0}}}{{{E_0}}} + \frac{{{F_0} - F}}{{{F_0}}}。$ | (6) |
式中:E0是对照组的吸能效率值,F0是对照组的压缩力值。P值表示相对于对照组,吸能效率的增加量与压缩力值的减少量的总和。P值最大,说明性能越好。
因此结构参数优化设计的目标,即优化设计问题可以描述为:
| $ \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\rm{max}}\;\;P}\\ {{\rm{s}}{\rm{.t}}{\rm{. }}\;14.5 \le c \le 16,}\\ {6.5 \le d \le 18.5,} \end{array}}\\ {27.5 \le e \le 29。} \end{array}} \right. $ | (7) |
使用isight软件中单目标遗传算法[18]进行优化,得出一个最优组合参数,如表 10所示。
| 表 10 优化后的结构参数组合 Table 10 Optimized combination of structural parameters |
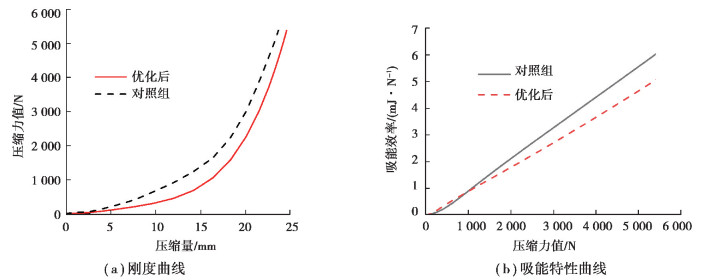
将优化后的参数组合输入到ABAQUS软件中进行计算,得出刚度曲线和吸能特性曲线并与对照组进行比较,结果见图 9。在恒定峰值力5 400 N压缩下,对照组吸能效率为5.95 mJ/N,力值为909.80 N;优化后的结构吸能效率为4.97 mJ/N,力值为466.88 N。优化后的缓冲块牺牲了14.3%的吸能特性,提升了47.9%的接触特性,综合作用使得缓冲块性能提升了34.6%。
|
图 9 结构优化前后对比 Fig. 9 Performance before and after structural optimization |
通过有限元仿真和试验,以及对缓冲块的性能进行研究,得出以下结论:
1) 以天然橡胶作为缓冲块的材料时,其压缩力值随着压缩量增加而增加,当压缩量在总长度40%左右时压缩力值剧烈增加,力位移曲线呈非线性。
2) 改变缓冲块结构参数对其性能影响明显,凹槽的深度越浅,缓冲块的吸能特性越好,接触特性越差;外径越大,缓冲块吸能特性越好,接触特性越差。吸能特性和接触特性相互矛盾,取折中的参数组合效果最好。
| [1] |
Dickson D G. A primer on jounce bumper design using microcellular polyurethane, [J/OL]. SAE Technical Paper, 2004: 2004-01-1541[2020-02-01]. https://doi.org/10.4271/2004-01-1541.
|
| [2] |
Dickson D G, Schranz S, Wolff M. Microcellular polyurethane jounce bumper design and the effects on durability[J/OL]. SAE Technical Paper, 2005: 2005-01-1714[2020-02-01]. https://doi.org/10.4271/2005-01-1714.
|
| [3] |
Schudt J A, Tsai M, Patil R, et al. Dual rate jounce bumper design[J/OL]. SAE Technical Paper, 2011: 2011-01-0791[2020-02-01]. https://doi.org/10.4271/2011-01-0791.
|
| [4] |
Sidhu R S, Ali A. Fatigue life of automotive rubber jounce bumper[J]. IOP Conference Series:Materials Science and Engineering, 2010, 11: 012008. |
| [5] |
Caliskan K, Konukseven I, Unlusoy Y S. Product-oriented material testing and FEA for hyperelastic suspension jounce bumper design[J]. International Journal of Design Engineering, 2010, 3(4): 374-391. DOI:10.1504/IJDE.2010.040523 |
| [6] |
黄敏, 黄舟, 贾东, 等. 基于压缩试验的两种橡胶材料本构模型分析[J]. 噪声与振动控制, 2018, 38(S2): 483-486. HUANG Min, HUANG Zhou, JIA Dong, et al. Analysis of constitutive models of two kinds of rubber materials based on compression test[J]. Noise and Vibration Control, 2018, 38(S2): 483-486. (in Chinese) |
| [7] |
Geisler R L, Patil R, Schudt J, et al. Recent applications of Abaqus/explicit in GM Chassis CAE[Z/OL]. 2010[2020-02-01]. https://pdfs.semanticscholar.org/4706/5bf24e94db9829d3142bc60b23023eb179ab.pdf.
|
| [8] |
黄舟, 贾东, 陈军红, 等. 工程橡胶压缩实验和缓冲特性分析[J]. 装备环境工程, 2018, 15(6): 27-32. HUANG Zhou, JIA Dong, CHEN Junhong, et al. Compression experiment and buffering characteristic analysis of engineering rubber products[J]. Equipment Environmental Engineering, 2018, 15(6): 27-32. (in Chinese) |
| [9] |
张志飞, 李勋, 徐中明, 等. 面向刚度曲线的汽车前保险杠缓冲块优化设计[J]. 重庆大学学报, 2016, 39(3): 21-27. ZHANG Zhifei, LI Xun, XU Zhongming, et al. The optimal design of the bumper absorber based on stiffness curve[J]. Journal of Chongqing University, 2016, 39(3): 21-27. (in Chinese) |
| [10] |
计宏伟, 王怀文. 基于高速图像测量技术的缓冲材料缓冲性能的表征[J]. 振动与冲击, 2011, 30(9): 216-220. JI Hongwei, WANG Huaiwen. Characterization of cushioning properties of cushioning materials based on high-speed image measurement technology[J]. Journal of Vibration and Shock, 2011, 30(9): 216-220. (in Chinese) DOI:10.3969/j.issn.1000-3835.2011.09.045 |
| [11] |
薛继明, 吴晓庆, 王焕功, 等. 有限元分析中轴对称问题研究与应用[J]. 机械工程师, 2014(4): 126-128. XUE Jiming, WU Xiaoqing, WANG Huan Gong, et al. Research and application of axisymmetric problems in finite element analysis[J]. Mechanical Engineer, 2014(4): 126-128. (in Chinese) DOI:10.3969/j.issn.1002-2333.2014.04.055 |
| [12] |
Dassault Systemes Simulia Corporation. Abaqus 6.14 documentation[Z/OL]. 2014[2020-02-01]. http://ivt-abaqusdoc.ivt.ntnu.no:2080/v6.14/index.html.
|
| [13] |
Miller K. Testing elastomers for hyperelastic material models in finite element analysis[R/OL]. Ann Arbor, MI, USA: Axel Products Inc., 2000[2020-02-01]. http://www.axelproducts.com/downloads/TestingForHyperelastic.pdf.
|
| [14] |
徐中明, 袁泉, 张志飞, 等. 基于超静定方程的橡胶材料本构模型参数识别[J]. 重庆大学学报, 2017, 40(2): 1-9. XU Zhongming, YUAN Quan, ZHANG Zhifei, et al. Parametric identification of constitutive model of rubber materials based on statically indeterminate equation[J]. Journal of Chongqing University, 2017, 40(2): 1-9. (in Chinese) |
| [15] |
刘瑞江, 张业旺, 闻崇炜, 等. 正交试验设计和分析方法研究[J]. 实验技术与管理, 2010, 27(9): 52-55. LIU Ruijiang, ZHANG Yewang, WEN Chongwei, et al. Study on the design and analysis methods of orthogonal experiment[J]. Experimental Technology and Management, 2010, 27(9): 52-55. (in Chinese) DOI:10.3969/j.issn.1002-4956.2010.09.016 |
| [16] |
刘文, 王青松, 林腾蛟, 等. 基于响应面试验设计的湿式离合器优化策略[J]. 重庆大学学报, 2018, 41(6): 9-23. LIU Wen, WANG Qingsong, LIN Tengjiao, et al. Optimization strategy of wet clutch based on response surface test design[J]. Journal of Chongqing University, 2018, 41(6): 9-23. (in Chinese) |
| [17] |
Ferreira S L C, Bruns R E, Ferreira H S, et al. Box-Behnken design:an alternative for the optimization of analytical methods[J]. Analytica Chimica Acta, 2007, 597(2): 179-186. DOI:10.1016/j.aca.2007.07.011 |
| [18] |
吴立华, 白洁, 左亚军, 等. 基于Matlab的遗传算法在结构优化设计中的应用[J]. 机电工程技术, 2017, 46(10): 44-47. WU Lihua, BAI Jie, ZUO Yajun, et al. Application of genetic algorithm based on Matlab in structural optimization design[J]. Mechanical & Electrical Engineering Technology, 2017, 46(10): 44-47. (in Chinese) DOI:10.3969/j.issn.1009-9492.2017.10.012 |
 2020, Vol. 43
2020, Vol. 43


