2. 桂林福达股份有限公司, 广西 桂林 541199
2. Guilin Fuda Co., Ltd., Guilin 541199, Guangxi, P. R. China
准双曲面齿轮具有重合度大、容差能力强、啮合稳定性高,且适用于大交角、可偏置安装等优点,广泛运用于航空、汽车、船舶等传动系统之中。与格里森制齿轮相比,奥利康制齿轮具有加工效率高、承载能力强及噪声低等优点。由于奥利康制齿轮加工为连续分度切削的过程, 刀头的结构、安装位置方向及刀盘摇台加工齿轮三者间的协调运动要求十分严格;同时,基于不同的参考基准,刀盘和切削参数是不相同的,造成奥利康制准双曲面齿轮齿面成形理论变得更加复杂。在现有研究中通常采用切屑方向基准进行齿面建模,而对于基于NS(neutral surface)法向基准的齿面建模几乎没有,因此有必要研究此基准下齿面数学模型的推导。
针对准双曲面齿轮齿面成形理论,国内外相关学者进行了一定的研究。Litvin[1]提出了局部综合法理论,为准双曲面齿轮相关研究奠定了基础。Fan[2-4]基于传统摇台式机床对格里森Spiroflex面滚加工方法进行了系统的分解。Shih等[5-6]提出了一种通用型准双曲面齿轮端面铣齿和端面滚齿的通用建模方法。方宗德等[7]利用常规格里森刀盘推到了弧齿齿面数学方程。郭晓东等[8]通过齿面测量机得到齿面点集,建立了反调优化齿轮模型。林希[9]通过CATIA进行切削仿真,建立了格里森制准双曲面齿轮副模型。王星星等[10]基于AutoCAD二次开发构建轮坯与刀盘实体,通过模拟刀具加工系统进行摆线齿准双曲面齿轮建模。江玉刚[11]、王星等[12]以数学推导为基础,建立了格里森制准双曲面齿轮理论工作齿面和刀尖圆弧段曲面数学方程。张卫青[13]、杜进辅[14]基于切削方向基准对摆线准双曲面齿轮齿面的离散化建模进行了研究。这些研究中有关准双曲面齿轮建模主要是通过模拟仿真和数学推导两种方法。大部分研究针对格里森制准双曲面齿轮且采用简化刀具进行齿面建模,而针对奥利康制准双曲面齿轮精确化建模,均采用切屑方向基准,对刀具基准的定义几乎没有介绍。因此,笔者基于刀具NS法向基准,从加工刀具的几何截面、结构出发,分析了奥利康三面刀具结构和安装位置,建立了包含刀尖圆弧段的刀盘数学模型;通过刀倾半展成法建立了成形法大轮和展成法小轮的加工坐标系,得到了在毛坯坐标系下刀具切削刃的切削轨迹面;根据大轮小轮的加工方法,推导了大小轮的齿面数学模型。通过与理论45点齿面进行齿面误差对比和通过有限元方法计算的实际接触印痕与KIMOS理论轮齿接触分析(TCA)、轮齿承载接触分析(LTCA)计算的接触印痕对比验证,验证了基于刀具NS法向基准的奥利康准双曲面齿轮建模的正确性。
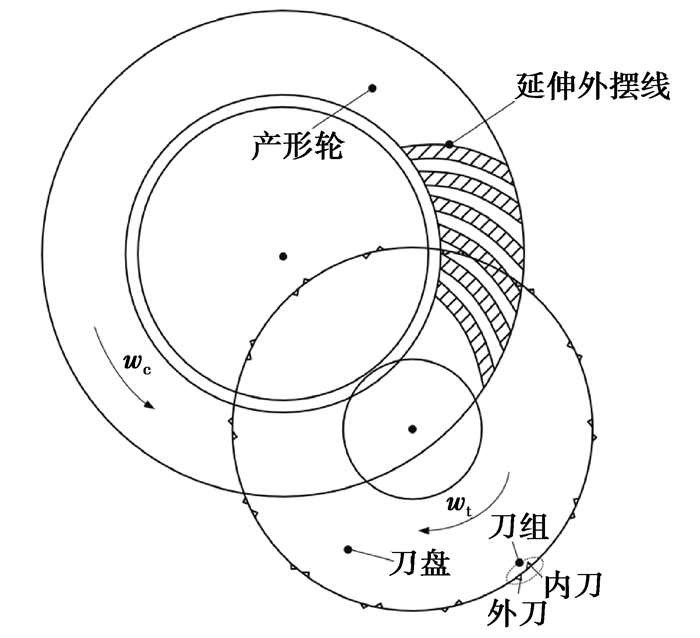
1 奥利康制准双曲面齿轮精确化建模奥利康制准双曲面齿轮采用端面滚齿法加工。图 1为奥利康制准双曲面齿轮端面滚齿的切齿原理,刀盘在自转的同时围绕基圆公转,形成延伸外摆线齿线。端面刀盘上有z0组刀齿,每组刀齿至少有一个内刀和一个外刀,分别用于加工轮齿的凸面和凹面。wc,wt分别为产形轮和刀盘角速度,产形轮由刀具切削刃在机床坐标系下的切削回转面构成。
|
图 1 奥利康准双曲面齿轮切齿原理 Fig. 1 Cutting principle of Oerlikon's hypoid gear |
准双曲面齿轮建模基准一般分为两种:切削方向基准和NS法向基准。NS法向基准建立在NS平面的法向方向,切削方向基准建立在切削曲线的相切方向,如图 2所示。图 3为奥利康刀具切削刃截面图,切削刃由主切削刃和刀尖圆弧段构成。

|
图 2 切削基准的定义 Fig. 2 Benchmark definition of cutting |
|
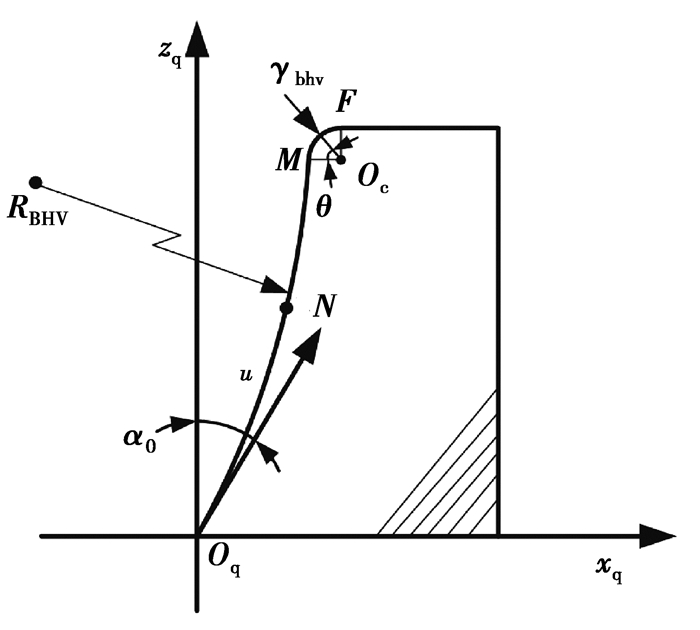
图 3 刀具切削刃截面 Fig. 3 Cutting edge section of cutting tool |
以左弦内刀为例,在坐标系Sq(xq, yq, zq)下,建立主切削刃和刀尖圆弧段的数学模型,其表达式如下:主切削刃(Oq—M段)
| $ {\mathit{\boldsymbol{r}}_{{\rm{q}}(u)}} = \left[ {\begin{array}{*{20}{c}} {2{R_{{\rm{BHV}}}}\sin \left( {\frac{u}{{2{R_{{\rm{BHV}}}}}}} \right)\sin \left( {{\alpha _0} - \frac{u}{{2{R_{{\rm{BHV}}}}}}} \right)}\\ 0\\ {2{R_{{\rm{BHV}}}}\sin \left( {\frac{u}{{2{R_{{\rm{BHV}}}}}}} \right)\cos \left( {{\alpha _0} - \frac{u}{{2{R_{{\rm{BHV}}}}}}} \right)}\\ 1 \end{array}} \right]。$ | (1) |
刀尖圆弧(M—F段)
| $ {\mathit{\boldsymbol{r}}_{q\left( \theta \right)}} = {\mathit{\boldsymbol{M}}_{\rm{D}}}{\mathit{\boldsymbol{M}}_{\rm{R}}}\left[ {\begin{array}{*{20}{c}} {{r_{{\rm{bhv}}}}\cos \theta }\\ 0\\ {{r_{{\rm{bhv}}}}\sin \theta }\\ 1 \end{array}} \right], $ | (2) |
其中
| $ {\mathit{\boldsymbol{M}}_{\rm{D}}} = \left[ {\begin{array}{*{20}{c}} {\cos \left( {{\alpha _0} - \frac{{{u_{\max }}}}{{{R_{{\rm{BHV}}}}}}} \right)}&0&{\sin \left( {{\alpha _0} - \frac{{{u_{\max }}}}{{{R_{{\rm{BHV}}}}}}} \right)}&0\\ 0&1&0&0\\ { - \sin \left( {{\alpha _0} - \frac{{{u_{\max }}}}{{{R_{{\rm{BHV}}}}}}} \right)}&0&{\cos \left( {{\alpha _0} - \frac{{{u_{\max }}}}{{{R_{{\rm{BHV}}}}}}} \right)}&0\\ 0&0&0&1 \end{array}} \right], $ | (3) |
| $ {\mathit{\boldsymbol{M}}_{\rm{R}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&{ - {r_{{\rm{bhv}}}} - {R_{{\rm{BHV}}}}}\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]。$ | (4) |
图中,Oq为刀具参考点,Oc为刀尖圆弧段圆心,M为刀尖圆弧与主切削刃的公切点。α0为参考点压力角,u为切削刃参考点到主切削刃任意一点N的弧长,umax为M点到参考点之间的弧长,RBHV为主切削刃圆弧半径,rbhv为刀尖圆弧半径,θ为刀尖圆弧段的角度。矩阵MD,MR为刀尖圆弧段转换至坐标系Sq(xq, yq, zq)的变换矩阵。
图 4为加工奥利康制齿轮的三面刀具(a)和刀盘模型(b)。坐标系Sq(xq, yq, zq)建立在前刀面刀具参考点上,St(xt, yt, zt)为刀盘回转坐标系,Sa,Sn,Ss和Sg均为辅助坐标系。其中,Sn(xn, yn, zn),Ss(xs, ys, zs)坐标系分别为刀盘切削方向基准和NS平面基准坐标系,NS法向基准与切削方向基准的夹角为γs。

|
图 4 端面滚齿刀盘模型 Fig. 4 Knife plant model of face-hobbed |
切削内刀与外刀切削刃参考点间的夹角为τs。切削刃通过刀具刀盘坐标变换得到St(xt, yt, zt)坐标系下的切削轨迹面。rt(u)为主切削刃段,rt(θ)为刀尖圆弧段,其表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{r}}_{\rm{s}}}(u) = {\mathit{\boldsymbol{M}}_{{\rm{sn}}}}\left( {{\gamma _{\rm{s}}}} \right){\mathit{\boldsymbol{M}}_{{\rm{na}}}}(\varepsilon ){\mathit{\boldsymbol{M}}_{{\rm{aq}}}}\left( {{\gamma _{\rm{a}}}} \right){\mathit{\boldsymbol{r}}_{\rm{q}}}(u),}\\ {{\mathit{\boldsymbol{r}}_{\rm{s}}}(\theta ) = {\mathit{\boldsymbol{M}}_{{\rm{sn}}}}\left( {{\gamma _{\rm{s}}}} \right){\mathit{\boldsymbol{M}}_{{\rm{na}}}}(\varepsilon ){\mathit{\boldsymbol{M}}_{{\rm{aq}}}}\left( {{\gamma _{\rm{a}}}} \right){\mathit{\boldsymbol{r}}_{\rm{q}}}(\theta )。} \end{array}} \right. $ | (5) |
| $ {\mathit{\boldsymbol{M}}_{{\rm{aq}}}} = \left[ {\begin{array}{*{20}{c}} {\cos {\gamma _{\rm{a}}}}&{\sin {\gamma _{\rm{a}}}}&0&0\\ {\sin {\gamma _{\rm{a}}}}&{\cos {\gamma _{\rm{a}}}}&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]。$ | (6) |
| $ {\mathit{\boldsymbol{M}}_{{\rm{na}}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&{\cos \varepsilon }&{ - \sin \varepsilon }&0\\ 0&{\sin \varepsilon }&{\cos \varepsilon }&0\\ 0&0&0&1 \end{array}} \right]。$ | (7) |
| $ {\mathit{\boldsymbol{M}}_{{\rm{sn}}}} = \left[ {\begin{array}{*{20}{c}} {\cos {\gamma _{\rm{s}}}}&{\sin {\gamma _{\rm{s}}}}&0&0\\ {\sin {\gamma _{\rm{s}}}}&{\cos {\gamma _{\rm{s}}}}&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]。$ | (8) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{r}}_{\rm{t}}}(u) = {\mathit{\boldsymbol{M}}_{{\rm{ts}}}}\left( {\delta ,{r_0},{\beta _{\rm{t}}},\beta } \right){\mathit{\boldsymbol{r}}_{\rm{s}}}(u),}\\ {{\mathit{\boldsymbol{r}}_{\rm{t}}}(\theta ) = {\mathit{\boldsymbol{M}}_{{\rm{ts}}}}\left( {\delta ,{r_0},{\beta _{\rm{t}}},\beta } \right){\mathit{\boldsymbol{r}}_{\rm{s}}}(\theta )。} \end{array}} \right. $ | (9) |
式中:γa为刀具前角;ε为刀具重磨角度;δ为刀齿方向角;ro为刀具参考点的回转半径;βt为刀具起始安装角。Maq, Mna, Msn和Mts分别为刀具前角、重磨角、主刃后角及刀盘坐标系的变换矩阵。Msn为NS法向基准坐标变换矩阵,Mna为切削方向基准坐标变换矩阵。
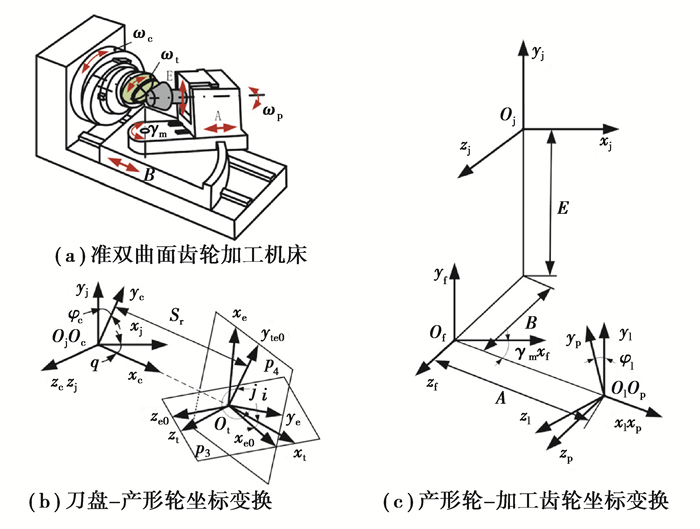
1.2 基于通用机床加工的准双曲面齿轮数学模型奥利康制准双曲面齿轮加工机床(如图 5(a)所示)主要由切削刀盘、刀倾装置、刀转装置、摇台、床位装置、垂直轮位装置及水平轮位装置几大部件构成。机床坐标系的主要参数有刀倾角、刀转角、径向刀位、角向刀位、滚比、床位、垂直轮位和水平轮位。在机床坐标系中,坐标系St(xt, yt, zt)、Sj(xj, yj, zj)和Sp(xp, yp, zp)分别固联在刀盘、机床和加工毛坯上。式(9)通过St(xt, yt, zt)到Sj(xj, yj, zj)的坐标变换(如图 5(b)所示),将刀具的回转切削面转换到机床坐标系下,得到虚拟产形轮的齿面方程;通过Sj(xj, yj, zj)到Sp(xp, yp, zp)的坐标变换(如图 5(c)所示),得到毛坯坐标系下刀具的切削轨迹面,表达式如下:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{r}}_{\rm{p}}}\left( {u,\beta ,{\phi _{{\rm{cl}}}},{\phi _{{\rm{c}}2}},{\varphi _1}} \right) = {\mathit{\boldsymbol{M}}_{{\rm{pl}}}}\left( {{\varphi _1}} \right),\\ {\mathit{\boldsymbol{M}}_{1{\rm{t}}}}\left( {i,j,{s_{\rm{r}}},q,E,B,\gamma ,A;{\phi _{{\rm{c1}}}},{\phi _{{\rm{c2}}}}} \right){\mathit{\boldsymbol{M}}_t}(\beta ){r_{\rm{t}}}(u),\\ {\mathit{\boldsymbol{r}}_{\rm{p}}}\left( {\theta ,\beta ,{\phi _{{\rm{cl}}}},{\phi _{{\rm{c}}2}},{\varphi _1}} \right) = {\mathit{\boldsymbol{M}}_{{\rm{pl}}}}\left( {{\varphi _1}} \right),\\ {\mathit{\boldsymbol{M}}_{1{\rm{t}}}}\left( {i,j,{s_r},q,E,B,\gamma ,A;{\phi _{{\rm{c}}1}},{\phi _{{\rm{c}}2}}} \right){\mathit{\boldsymbol{M}}_{\rm{t}}}(\beta ){r_{\rm{t}}}(\theta )。\end{array} \right. $ | (10) |
|
图 5 左旋准双曲面齿轮机床加工坐标系 Fig. 5 Machining coordinate system of left hypoid gear machine |
式中:M1t为机床的坐标变换;Mp1为毛坯旋转坐标系;Mt为刀盘旋转坐标系。β为刀盘旋转角度,ϕc1, ϕc2为摇台增量角。式(10)为超静定方程,需要根据其齿面成型方法减少求解量进行求解。
成形法加工时,摇台固定不动,摇台增量角为零,即ϕc1=0及ϕc2=0;展成法加工时,摇台增量角是随时间变化的,其摇台增量角ϕc1, ϕc2的表达式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\phi _{{\rm{cl}}}} = \beta \frac{{{z_0}}}{{{z_{\rm{p}}}}},}\\ {{\phi _{{\rm{c}}2}} = {\varphi _1}\frac{z}{{{z_{\rm{p}}}}}。} \end{array}} \right. $ | (11) |
式中:z, z0, zp分别代表毛坯齿数、刀具头数和产形轮齿数;ϕc1用于形成延伸外摆线,ϕc2用于齿面展成。
1.3 齿面啮合方程展成法加工时,齿面方程通过式(11)依旧超静定,需要经过啮合方程求解出各个刀盘旋转角下的摇台增量角或者毛坯旋转角进行求解。在毛坯坐标系Sp(xp, yp, zp)下,刀具的法向量和相对速度表达式为
| $ {\mathit{\boldsymbol{n}}_{\rm{p}}}\left( {u,\beta ,{\varphi _1}} \right) = \frac{{\frac{{\partial r\left( {u,\beta ,{\varphi _1}} \right)}}{{\partial u}} \times \frac{{\partial r\left( {u,\beta ,{\varphi _1}} \right)}}{{\partial \beta }}}}{{\left| {\frac{{\partial r\left( {u,\beta ,{\varphi _1}} \right)}}{{\partial u}} \times \frac{{\partial r\left( {u,\beta ,{\varphi _1}} \right)}}{{\partial \beta }}} \right|}}, $ | (12) |
| $ {\mathit{\boldsymbol{v}}_{\rm{p}}} = \frac{{\partial {r_{\rm{p}}}}}{{\partial {\varphi _1}}}{{\dot \varphi }_1}。$ | (13) |
基于齿轮啮合理论,齿轮的啮合方程为
| $ \mathit{\boldsymbol{f}}\left( {u,\beta ,{\varphi _1}} \right) = {\mathit{\boldsymbol{n}}_{\rm{p}}}{\mathit{\boldsymbol{v}}_{\rm{p}}} = {\mathit{\boldsymbol{n}}_{\rm{p}}}\left( {{{\dot \varphi }_1}\frac{{\partial {r_p}}}{{\partial {\varphi _1}}}} \right), $ | (14) |
式中:vp为刀具切削刃在毛坯坐标系Sp(xp, yp, zp)的速度;rp为刀具在毛坯坐标系Sp(xp, yp, zp)下的矢径;φ1为毛坯的旋转角;
对于右旋准双曲面齿轮齿面,采用右旋刀盘,加工刀盘逆时针旋转,刀具安装方向沿着切削方向;在机床坐标系中,刀盘安装于第1象限,毛坯安装于第4象限,摇台初始安装角、垂直轮位与左旋齿轮相反;毛坯旋转方向与左旋齿轮相反为顺时针旋转,以相同的求解方式可得到右旋齿轮在毛坯坐标系下的切削轨迹面方程。
1.4 准双曲面齿轮三维实体模型表 1为齿轮的基本参数,表 2为刀倾半展成法的大小轮机床基本参数。基于NS法向基准,通过刀倾半展成法加工,建立齿轮的实体模型。
| 表 1 齿轮基本参数 Table 1 Basic parameters of gear |
| 表 2 机床参数 Table 2 Machine parameters |
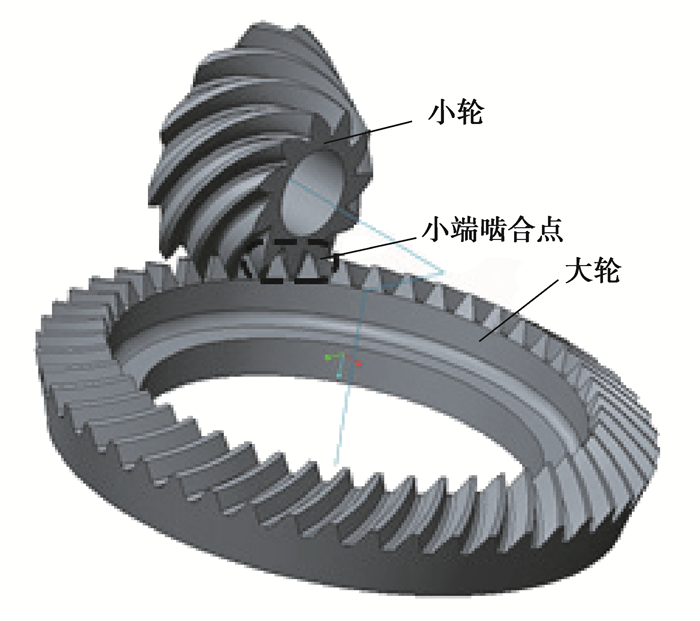
根据上文推导的齿面数学方程,依据表 1、表 2参数,得到在毛坯坐标系下的刀具切削轨迹面;通过CREO建立大小轮毛坯,运用边界混合得到凹凸面的轨迹面,进行布尔求解去除齿槽材料,得到大小齿轮的实体模型;根据安装参数得到准双曲面齿轮啮合实体装配模型,如图 6所示。
|
图 6 啮合实体装配模型 Fig. 6 The model of meshing solid assembly |
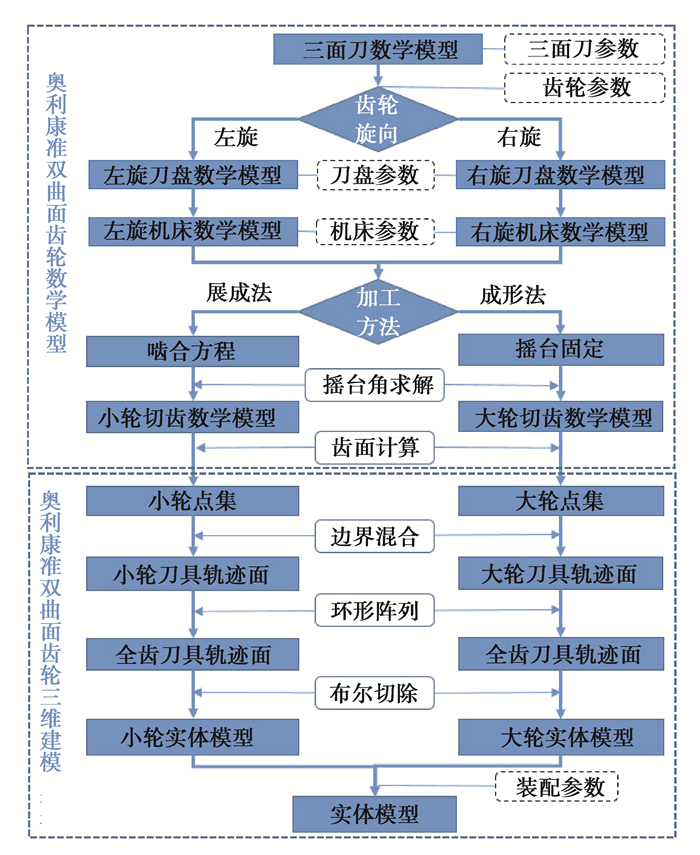
图 7为奥利康准双曲面齿轮啮合实体模型的精确数学建模流程,主要分为奥利康制齿轮齿面数学模型的建立和准双曲面齿轮三维实体建模两个部分。第一部分主要是基于刀具参考基准,从齿轮的加工出发,建立刀头、刀盘、机床、毛坯加工坐标系,推导出大小轮的切齿齿面数学模型;通过MATLAB编程计算得到大小轮的切削齿面点集。第二部分将得到的齿面点集导入三维设计软件CERO中,通过边界混合得到刀具切削轨迹面、刀具切削齿槽以及通过图纸建立齿轮的加工毛坯;通过环形阵列得到全齿切削齿槽,通过布尔求差,得到大小轮的实体模型;根据齿轮装配参数,得到奥利康准双曲面齿轮的啮合实体模型。
|
图 7 奥利康准双曲面齿轮建模流程 Fig. 7 Modeling process of Oerlikon's hypoid gear |
根据表 1,2所示奥利康制准双曲面齿轮基本参数与机床加工参数,通过KIMOS软件导入C27机床,加工出实际齿轮,并与经过齿面方程推导得到的大小轮数学模型对比,如图 8所示。

|
图 8 加工与数学齿轮模型 Fig. 8 Machine and mathematics model of pinion and gear |
通过KIMOS设计模块得到45点齿面点集,部分数据如表 3所示;通过齿面数学模型计算,求解齿轮点集,部分数据如表 4所示。在CREO软件中建立大小轮数学齿面实体模型,并导入45点数据,建立对比齿面,如图 9所示。图 9中蓝色齿面为小轮凹面理论45点构成的齿面,橙色为大轮凸面理论45点构成的齿面,灰色模型是通过齿面方程推导建立的大小轮实体模型。对比分析得出大小轮齿面基本重合,其中,小轮凹面最大误差位于小端偏齿顶处,其值为0.007 5 mm,最小误差点在大端齿根处,其值为-0.001 5 mm;大轮凸面最大误差为0.002 3 mm, 位于小端偏齿顶,最小误差为-0.000 5 mm,位于大端偏齿根。
| 表 3 Kimos理论齿面45点齿面坐标点集(部分) Table 3 Theory tooth surface 45 points set of Kimos (Portion) |
| 表 4 数学齿面坐标点集(部分) Table 4 Mathematical tooth surface points set (Portion) |

|
图 9 数学齿面与45点齿面对比 Fig. 9 Comparison of 45 points tooth surface |
通过ABAQUS加载特性分析得到大轮凸面的接触斑点与KIMOS轮齿接触分析(TCA)及承载接触分析(LTCA)在450 NM时计算的大轮凸面接触印痕进行对比,进一步验证齿面模型推导的准确性。KIMOS计算结果如图 10所示。

|
图 10 KIMOS理论TCA与LTCA印痕(大轮凸面) Fig. 10 Contact patterns (KIMOS) |
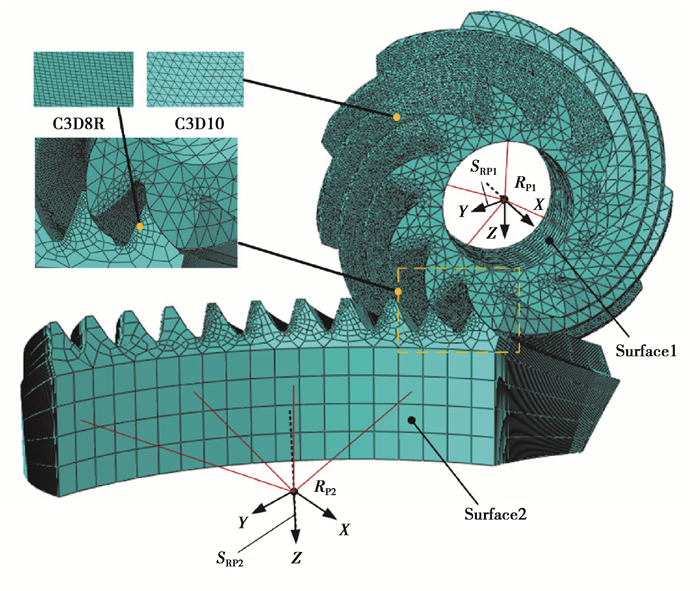
根据上文建立的齿轮实体模型,通过ABAQUS建立有限元啮合模型,如图 11所示,为节省计算时间,大轮选择11齿,小轮为全齿。RP1, RP2分别为小轮、大轮的参考耦合点;小轮凹面为主动接触面,大轮凸面为从动接触面,相互啮合齿面分别建立接触对,接触特性设置无摩擦、硬接触;采用预加载和正常啮合分析步来模拟齿轮的正常啮合过程。大轮扭矩450 NM,杨氏模量为210 GPa,泊松比为0.3。
|
图 11 有限元啮合模型 Fig. 11 Finite element meshing model |
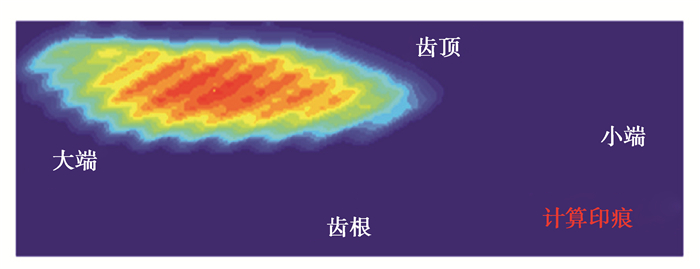
图 12为大轮凸面从啮入到啮出的3个时刻的瞬时接触线。图 13为大轮凸面的接触印痕。由图可知,KIMOS计算的理论TCA印痕与有限元计算印痕的位置基本一致;有限元计算的接触印痕与KIMOS通过LTCA计算的位置、大小基本一致,进一步验证了齿面的正确性。

|
图 12 瞬时接触线 Fig. 12 Instantaneous contact line |
|
图 13 有限元计算印痕 Fig. 13 Contact patterns (ABAQUS) |
在实际接触印痕的位置、大小设计过程中,热处理工艺以及轴系支撑变形等因素应当被考虑。通过调整刀具及机床参数,可以调整设计印痕的位置,确保在热处理变形及支撑变形之后,啮合印痕的区域位于齿中,提高齿轮的接触状态。
通过齿面对比和接触印痕的验证,基于刀具NS法向基准的准双曲面齿轮建模方法是准确可行的。
3 结论笔者从奥利康准双曲面齿轮的实际加工出发,研究了加工刀盘的结构和位置,建立了基于刀具NS法向基准的刀盘数学模型和奥利康制准双曲面齿轮实体模型,并进行了相关验证,提出了一套基于NS基准的建模流程。该方法对准双曲面齿轮的精确化建模提供了新的思路,为后续相关齿轮齿面的设计优化提供了基础,具有较强的实用价值。
| [1] |
Litvin F L. Michalec. Theory of gearing[M]. Washington, D. C.: NASA Reference Publication, 1989.
|
| [2] |
Fan Q. Computerized modeling and simulation of spiral bevel and hypoid gears manufactured by gleason face hobbing process[J]. Journal of Mechanical Design, 2006, 128(6): 1315-1327. DOI:10.1115/1.2337316 |
| [3] |
Fan Q. Advanced developments in computerized design and manufacturing of spiral bevel and hypoid gear drives[J]. Applied Mechanics and Materials, 2011, 86: 439-442. DOI:10.4028/www.scientific.net/AMM.86.439 |
| [4] |
Fan Q. Tooth surface error correction for face-hobbed hypoid gears[J]. Journal of Mechanical Design, 2010, 132(1): 61-69. |
| [5] |
Shih Y P, Fong Z H. Flank correction for spiral bevel and hypoid gears on a six-axis CNC hypoid generator[J]. Journal of Mechanical Design, 2008, 130(6): 876-877. |
| [6] |
Shih Y P. A novel ease-off flank modification methodology for spiral bevel and hypoid gears[J]. Mechanism and Machine Theory, 2010, 45(8): 1108-1124. DOI:10.1016/j.mechmachtheory.2010.03.010 |
| [7] |
方宗德, 曹雪梅, 沈云波. 弧线齿面齿轮的齿面设计与加工[J]. 航空动力学报, 2010, 25(1): 224-227. FANG Zongde, CAO Xuemei, SHEN Yunbo. Tooth surface design and manufacture for arcuate tooth trace face-gear[J]. Journal of Aerospace Power, 2010, 25(01): 224-227. (in Chinese) |
| [8] |
郭晓东, 张卫青, 张明德, 等. 螺旋锥齿轮切齿调整参数的精确反调[J]. 重庆大学学报, 2011, 34(3): 32-37. GUO Xiaodong, ZHANG Weiqing, ZHANG Mingde, et al. The machine setting reverse method of spiral bevel gear[J]. Journal of Chongqing University, 2011, 34(3): 32-37. (in Chinese) |
| [9] |
林希. 全工序法准双曲面齿轮建模与有限元分析[J]. 机械传动, 2017, 41(6): 159-163. LIN Xi. Modeling and finite element analysis of hypoid gear cutting by completed method[J]. Journal of Mechanical Transmission, 2017, 41(6): 159-163. (in Chinese) |
| [10] |
王星星, 李权才, 付丽, 等. 摆线齿准双曲面齿轮模拟加工系统建模[J]. 现代制造工程, 2013(07): 86-89. WANG Xingxing, LI Quancai, FU Li, et al. Modeling on simulation machining system of epicycloidal hypoid gears[J]. Modern Manufacturing Engineering, 2013(7): 86-89. (in Chinese) DOI:10.3969/j.issn.1671-3133.2013.07.021 |
| [11] |
江玉刚.基于精确齿面建模的弧齿锥齿轮有限元分析[D].杭州: 浙江大学, 2011. JIANG Yugang. Finite element analysis of spiral bevel gear based on precise tooth surface model[D]. Hangzhou: Zhejiang University, 2011. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10335-1011068846.htm |
| [12] |
王星, 方宗德, 李声晋, 等. HGT准双曲面齿轮精确建模和加载接触分析[J]. 四川大学学报(工程科学版), 2015, 47(4): 181-185. WANG Xing, FANG Zongde, LI Shengjin, et al. Precise modeling of HGT hypoid gear and loaded tooth contact analysis[J]. Journal of Sichuan University(Engineering Science Edition), 2015, 47(4): 181-185. (in Chinese) |
| [13] |
张卫青.螺旋锥齿轮端面滚齿加工的理论与实验[D].重庆: 重庆大学, 2016. ZHANG Weiqing. The face hobbing theory and experiments of hypoid gear[D]. Chongqing: Chongqing University, 2016. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10611-1017801776.htm |
| [14] |
杜进辅.摆线齿准双曲面齿轮齿面啮合性能分析及设计技术研究[D].西安: 西北工业大学, 2015. DU Jinfu. Tooth contact pattern analysis and design technology research of cycloid hypoid gears[D]. Xi'an: Northwestern Polytechnical University, 2015. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10699-1016909387.htm |
 2020, Vol. 43
2020, Vol. 43


