2. 重庆大学 输配电装备及系统安全与新技术国家重点实验室, 重庆 400044
2. State Key Laboratory of Power Transmission Equipment&System Security and New Technology, Chongqing University, Chongqing 400044, P. R. China
间谐波作为评定电能质量的一项参数指标,其检测的准确性将直接影响评定结果[1]。间谐波的小振幅和引起的信号周期变化,使得基于离散傅里叶变换DFT(discrete Fourier transform)的精确分析和检测相对困难,根本原因在于DFT对非同步采样的高敏感度[2]。
国际标准IEC 61000中采用10个工频周波进行间谐波测量,算法核心在于信号DFT后所对应的间谐波频谱“群”及“子群”划分,但无法就频率分量参数(频率、相位)进行测量。特别是在对间谐波进行非同步采样时,未就加Hanning窗DFT的检测算法进行深入阐述和探讨[3]。
为消除非同步情况下DFT存在的频谱泄露和栅栏效应,常采用加对称余弦窗的DFT频谱插值算法。一方面采用长时间窗口以获取更高的频率分辨率,降低其他频率分量的旁瓣衰减分量干扰,但显然增加了算法计算成本,且长时间窗口容易包含多个分段动态间谐波,使得测量结果出现偏差;另一方面采用旁瓣快速衰减的时间窗加权,以降低频谱泄露分量对插值算法的影响,但主瓣宽度的增加限制了其在短时间窗口内的应用,特别是在间谐波接近直流及各谐波分量时,相对低频的间谐波负频率频谱干扰使得插值算法存在较大误差[4-10]。
上述问题已引起了学术界的广泛关注,相继提出了多种插值算法。文献[11]在考虑负频率频谱干扰前提下,提出了基于相位差的测量算法,但明显无法满足短时采样窗口设定;文献[12]提出了三复谱线插值的矩阵解析算法,文献[13]进一步将其扩展应用于电力频率参数估计,并给出了最大旁瓣衰减窗下的通用解析式;文献[10]基于此思想并根据间谐波位置的不同,给出了3种基波同步采用下间谐波快速检测算法的解析式;对于直流分量存在时,上述插值算法的解析过程依然适应,文献[14]仿真结果显示,对照IEC三点和四点拟合方法,新算法在幅值和相位校正估计上具有更高的精度。
为在利用DFT进行间谐波快速检测时获得更为准确的检测结果,我们根据最大旁瓣衰减窗频谱特性,采用改进三谱线插值算法减少负频率频谱泄露分量的干扰,进而在参考IEC标准的特定信号周期截断条件下,实现低频及超低频间谐波的快速高精度检测。
1 计及负频率插值DFT 1.1 通用加最大旁瓣衰减窗下DFT考虑单个间谐波离散采样信号实数序列为:
| $ s(n) = {A_{{\rm{in}}}}\cos \left( {2{\rm{ \mathsf{ π} }}\frac{{{\lambda _{{\rm{in}}}}}}{N}n + {\theta _{{\rm{in}}}}} \right),n = 0,1, \cdots ,N - 1。$ | (1) |
式中:N为时域采样点数;Ain和θin分别为对应信号幅值和相位;归一化频率λin与频率分辨率Δf满足λin=NΔf;采样频率fS与频率分辨率满足Δf=fS/N。在非同步采样情况下,归一化频率满足λin=kin+δ,kin为整数,分数部分δ的取值范围为[-0.5, 0.5)。在进行加最大旁瓣衰减窗DFT后,对应于峰值谱线的离散频谱为:
| $ S\left( {{k_{{\rm{in}}}}} \right) = \frac{{{A_{{\rm{in}}}}}}{2}{{\rm{e}}^{{\rm{j}}{\theta _{{\rm{in}}}}}}W( - \delta ) + \frac{{{A_{{\rm{in}}}}}}{2}{{\rm{e}}^{ - {\rm{j}}{\theta _{{\rm{in}}}}}}W\left( {2{k_{{\rm{in}}}} + \delta } \right)。$ | (2) |
在采样点数满足N>>1且N>>|δ|时,H项的最大旁瓣衰减窗频谱W近似为[7]:
| $ \hat W(\delta ) \approx \frac{{N\sin ({\rm{ \mathsf{ π} }}\delta )}}{{{2^{2H - 2}}{\rm{ \mathsf{ π} }}}}{{\rm{e}}^{ - {\rm{j \mathsf{ π} }}\delta }}\frac{{(2H - 2)!}}{{\delta \prod\limits_{h = 1}^{H - 1} {\left( {{h^2} - {\delta ^2}} \right)} }}。$ | (3) |
从峰值谱线的离散频谱表达式(2)明显看出,对应正频率范围的峰值谱线包含有来自负频率分量的加权旁瓣衰减分量,即对正频率的频谱来说为泄露干扰。根据窗函数频谱特性还可知,当整数kin→0时,泄露分量逐渐增大,且在分数部分|δ|=0.5时,此分量相对最大。理想情况下,即不存在负频率频谱泄露,式(2)中第2部分为零,则利用峰值谱线与其临近谱线的频谱线性比例[7]可得到分数部分δ的估计如下:
| $ {R_{{\rm{ideal}}}} = \frac{{S\left( {{k_{{\rm{in }}}} \pm 1} \right)}}{{S\left( {{k_{{\rm{in }}}}} \right)}} \approx \frac{{|\hat W( - \delta \pm 1)|}}{{|\hat W( - \delta )|}} = \frac{{H - 1 \pm \delta }}{{H \mp \delta }}; $ | (4a) |
| $ \hat \delta = \pm \frac{{H{R_{{\rm{ideal }}}} - H + 1}}{{{R_{{\rm{ideal }}}} + 1}}。$ | (4b) |
若考虑负频率的频谱泄露干扰,即将式(3)带入式(2),稍作变换可得:
| $ S\left( {{k_{{\rm{in}}}}} \right) = \frac{{{A_{{\rm{in}}}}}}{2}{{\rm{e}}^{{\rm{j}}\left( {{\theta _{{\rm{in}}}} + {\rm{ \mathsf{ π} }}\delta } \right)}}|\hat W( - \delta )| + \frac{{{A_{{\rm{in}}}}}}{2}{{\rm{e}}^{ - {\rm{j}}\left( {{\theta _{{\rm{in}}}} + {\rm{ \mathsf{ π} }}\delta } \right)}}\left| {\hat W\left( {2{k_{{\rm{in}}}} + \delta } \right)} \right|, $ | (5) |
式中
| $ {S_{{\rm{re}}}}\left( {{k_{{\rm{in}}}}} \right) = \frac{{{A_{{\rm{in}}}}}}{2}\cos \left( {{\theta _{{\rm{in}}}} + {\rm{ \mathsf{ π} }}\delta } \right)\left( {|\hat W( - \delta )| + \left| {\hat W\left( {2{k_{{\rm{in}}}} + \delta } \right)} \right|} \right); $ | (6a) |
| $ {S_{{\rm{im}}}}\left( {{k_{{\rm{in}}}}} \right) = \frac{{{A_{{\rm{in}}}}}}{2}\sin \left( {{\theta _{{\rm{in}}}} + {\rm{ \mathsf{ π} }}\delta } \right)\left( {|\hat W( - \delta )| - \left| {\hat W\left( {2{k_{{\rm{in}}}} + \delta } \right)} \right|} \right)。$ | (6b) |
同理,对应次峰值谱线也具有如上所示的实部和虚部分解,即:
| $ {S_{{\rm{re}}}}\left( {{k_{{\rm{in}}}} \pm 1} \right) = \frac{{{A_{{\rm{in}}}}}}{2}\cos \left( {{\theta _{{\rm{in}}}} + {\rm{ \mathsf{ π} }}\delta } \right)\left( {|\hat W( - \delta \pm 1)| + \left| {\hat W\left( {2{k_{{\rm{in}}}} + \delta \pm 1} \right)} \right|} \right); $ | (7a) |
| $ {S_{{\rm{im}}}}\left( {{k_{{\rm{in}}}} \pm 1} \right) = \frac{{{A_{{\rm{in}}}}}}{2}\sin \left( {{\theta _{{\rm{in}}}} + {\rm{ \mathsf{ π} }}\delta } \right)\left( {|\hat W( - \delta \pm 1)| - \left| {\hat W\left( {2{k_{{\rm{in}}}} + \delta \pm 1} \right)} \right|} \right)。$ | (7b) |
为消去幅值和相位分量,将对应谱线的频谱实部和虚部分别相比,比例分别为:
| $ {R_{{\rm{re}}}} = \frac{{{S_{{\rm{re}}}}\left( {{k_{{\rm{in}}}} \pm 1} \right)}}{{{S_{{\rm{re}}}}\left( {{k_{{\rm{in}}}}} \right)}} = \frac{{|\hat W( - \delta \pm 1)| + \left| {\hat W\left( {2{k_{{\rm{in}}}} + \delta \pm 1} \right)} \right|}}{{|\hat W( - \delta )| + \left| {\hat W\left( {2{k_{{\rm{in}}}} + \delta } \right)} \right|}}; $ | (8a) |
| $ {R_{{\rm{im}}}} = \frac{{{S_{{\rm{im}}}}\left( {{k_{{\rm{in}}}} \pm 1} \right)}}{{{S_{{\rm{im}}}}\left( {{k_{{\rm{in}}}}} \right)}} = \frac{{|\hat W( - \delta \pm 1)| - \left| {\hat W\left( {2{k_{{\rm{in}}}} + \delta \pm 1} \right)} \right|}}{{|\hat W( - \delta )| - \left| {\hat W\left( {2{k_{{\rm{in}}}} + \delta } \right)} \right|}}。$ | (8b) |
对比式(8)和式(4a),若来自负频率分量的加权旁瓣衰减分量
为此,文献[15]提出了多种近似校正估计的计算方法,如式(9)所示,分别对应为算术均值、几何平均值、调和平均值和二次均值。仿真结果表明其中效果最好的是调和平均值
| $ \left\{ {\begin{array}{*{20}{l}} {{{\hat R}_{{\rm{est }}1}} = \frac{{{R_{{\rm{re}}}} + {R_{{\rm{im}}}}}}{2};}\\ {{{\hat R}_{{\rm{est}}2}} = \sqrt {{R_{{\rm{re}}}}{R_{{\rm{im}}}}} ;}\\ {{{\hat R}_{{\rm{est}}3}} = \frac{2}{{1/{R_{{\rm{re}}}} + 1/{R_{{\rm{im}}}}}};}\\ {{{\hat R}_{{\rm{est}}4}} = \sqrt {\frac{{R_{{\rm{re}}}^2 + R_{{\rm{im}}}^2}}{2}} 。} \end{array}} \right. $ | (9) |
为进一步提高基于插值DFT的低频率检测精度,考虑先进行如式(4b)的计算,然后再对实部和虚部的估计进行式(9)的多种平均计算。与前述两谱线的插值方法不同,首先采用广义的三谱线复数插值算法,即:
| $ {R_{3{\rm{i}}}} = \frac{{S\left( {{k_{{\rm{in}}}} + 1} \right) - S\left( {{k_{{\rm{in}}}} - 1} \right)}}{{S\left( {{k_{{\rm{in}}}} + 1} \right) - 2S\left( {{k_{{\rm{in}}}}} \right) + S\left( {{k_{{\rm{in}}}} - 1} \right)}}。$ | (10) |
利用式(4)中频谱线性比例关系,上式可化简为:
| $ {R_{3{\rm{i}}}} = \frac{{{\delta _{3{\rm{i}}}} - 2H{\delta _{3{\rm{i}}}}}}{{2\delta _{3{\rm{i}}}^2 - H}}。$ | (11) |
进一步求解得到δ3i,其对应实部和虚部的分数部分分别为:
| $ \left\{ \begin{array}{l} {\delta _{3{\rm{i\_re}}}} = Re \left[ {\frac{{(1 - 2H) \pm \sqrt {{{(1 - 2H)}^2} + 8HR_{3{\rm{i}}}^2} }}{{4{R_{3{\rm{i}}}}}}} \right];\\ {\delta _{3{\rm{i\_im}}}} = Im \left[ {\frac{{(1 - 2H) \pm \sqrt {{{(1 - 2H)}^2} + 8HR_{3{\rm{i}}}^2} }}{{4{R_{3{\rm{i}}}}}}} \right]。\end{array} \right. $ | (12) |
式(12)中正负号选取仅根据δ的取值范围即可决定,即选择满足|δ3i|≤0.5的值。对应实部和虚部的归一化频率分别为:λre=k±δ3i_re,λim=kim±δ3i_im。进而采用式(9)的均值算法进一步减小近似误差,即:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\hat \lambda }_{{\rm{est}}1}} = \frac{{{\lambda _{{\rm{re}}}} + {\lambda _{{\rm{im}}}}}}{2};}\\ {{{\hat \lambda }_{{\rm{est}}2}} = \sqrt {{\lambda _{{\rm{re}}}}{\lambda _{{\rm{im}}}}} ;}\\ {{{\hat \lambda }_{{\rm{est}}3}} = \frac{2}{{1/{\lambda _{{\rm{re}}}} + 1/{\lambda _{{\rm{im}}}}}};}\\ {{{\hat \lambda }_{{\rm{est4}}}} = \sqrt {\frac{{\lambda _{{\rm{re}}}^2 + \lambda _{{\rm{im}}}^2}}{2}} 。} \end{array}} \right. $ | (13) |
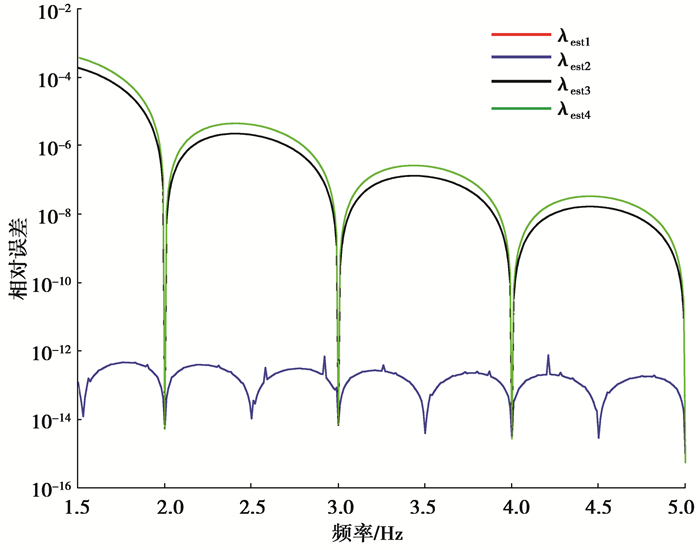
上述几种计算方法准确度的比较见图 1。其中,所加窗函数为2阶的最大旁瓣衰减窗(Hanning窗)信号频率范围为[1.5, 5.0]Hz,信号相位则以步长0.02π在[0, π)范围内变化,取误差最大时的估计结果。
|
图 1 随频率变化的相对误差 Fig. 1 Relative error with frequency |
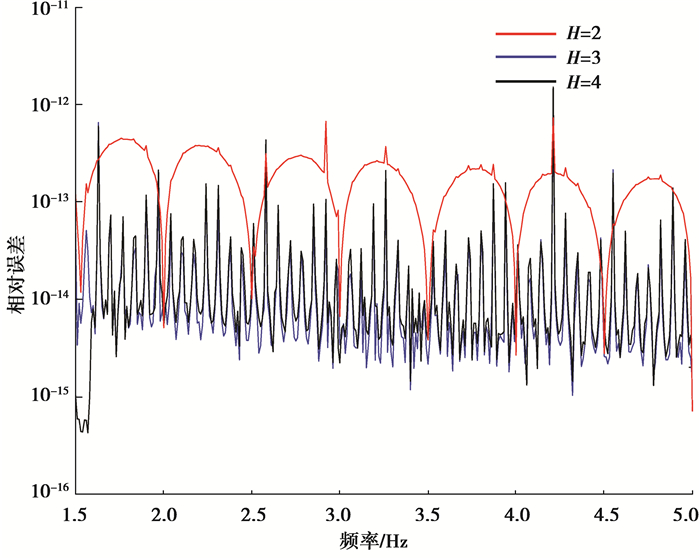
从上图可看出,与文献[15]中的结果不同,此处效果最好的是几何平均值,其误差最大不超过10-12;且值得特别注意的是被测频率处于k+0.5时频谱泄露最大,而基于几何平均值算法却能够将误差降低到与整周期采用时的同一水平。进一步对比不同时间窗函数下的校正精度,分别取H=3和H=4(窗函数对应参数如表 1所示),得到对应频率的校正相对误差结果如图 2所示。
| 表 1 最大旁瓣衰减窗系数 Table 1 The coefficients of maximum sidelobe decay window |
|
图 2 不同时间窗下误差比对 Fig. 2 Error comparison under different windows |
上图进一步说明了改进三谱线DFT插值算法在不同窗函数下的可适应性,且高阶窗函数更快速的旁瓣衰减性能使得在Hanning窗下的局部峰值误差得到进一步降低,其最大误差基本不超过10-13。
2.2 幅值和相位校正为求得幅值和相位,利用三角变换将式(6)的局部峰值谱线频谱改写为:
| $ \left\{ \begin{array}{l} {S_{{\rm{re}}}}\left( {{k_{{\rm{in}}}}} \right) = \frac{{{A_{{\rm{in}}}}}}{2}\cos \left( {{\theta _{{\rm{in}}}}} \right)\cos ({\rm{ \mathsf{ π} }}\delta )\left( {|\hat W( - \delta )| + \left| {\hat W\left( {2{k_{{\rm{in}}}} + \delta } \right)} \right|} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{A_{{\rm{in}}}}}}{2}\sin \left( {{\theta _{{\rm{in}}}}} \right)\sin ({\rm{ \mathsf{ π} }}\delta )\left( {|\hat W( - \delta )| + \left| {\hat W\left( {2{k_{{\rm{in }}}} + \delta } \right)} \right|} \right);\\ {S_{{\rm{im}}}}\left( {{k_{{\rm{in}}}}} \right) = \frac{{{A_{{\rm{in}}}}}}{2}\sin \left( {{\theta _{{\rm{in}}}}} \right)\cos ({\rm{ \mathsf{ π} }}\delta )\left( {|\hat W( - \delta )| - \left| {\tilde W\left( {2{k_{{\rm{in}}}} + \delta } \right)} \right|} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{A_{{\rm{in}}}}}}{2}\cos \left( {{\theta _{{\rm{in}}}}} \right)\sin ({\rm{ \mathsf{ π} }}\delta )\left( {|\hat W( - \delta )| - \left| {\hat W\left( {2{k_{{\rm{in}}}} + \delta } \right)} \right|} \right)。\end{array} \right. $ | (14) |
令
| $ \left[ {\begin{array}{*{20}{c}} {{b_1}}&{ - {b_2}}\\ {{b_3}}&{{b_4}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} x\\ y \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{S_{{\rm{re}}}}\left( {{k_{{\rm{in}}}}} \right)}\\ {{S_{{\rm{im}}}}\left( {{k_{{\rm{in}}}}} \right)} \end{array}} \right]. $ | (15) |
其中系数矩阵对应的参数分别为:
| $ \left\{ {\begin{array}{*{20}{l}} {{b_1} = \cos ({\rm{ \mathsf{ π} }}\delta )\left( {|\hat W( - \delta )| + \left| {\hat W\left( {2{k_{{\rm{in}}}} + \delta } \right)} \right|} \right);}\\ {{b_2} = \sin ({\rm{ \mathsf{ π} }}\delta )\left( {|\hat W( - \delta )| + \left| {\hat W\left( {2{k_{{\rm{in}}}} + \delta } \right)} \right|} \right);}\\ {{b_3} = \sin ({\rm{ \mathsf{ π} }}\delta )\left( {|\hat W( - \delta )| - \left| {\hat W\left( {2{k_{{\rm{in}}}} + \delta } \right)} \right|} \right);}\\ {{b_4} = \cos ({\rm{ \mathsf{ π} }}\delta )\left( {|\hat W( - \delta )| - \left| {\hat W\left( {2{k_{{\rm{in}}}} + \delta } \right)} \right|} \right)。} \end{array}} \right. $ | (16) |
采用最小二乘法可求解得到式(15)中的x和y,即:
| $ \left[ {\begin{array}{*{20}{l}} x\\ y \end{array}} \right] = \left\{ {{{\left[ {\begin{array}{*{20}{c}} {{b_1}}&{ - {b_2}}\\ {{b_3}}&{{b_4}} \end{array}} \right]}^{\rm{T}}}\left[ {\begin{array}{*{20}{l}} {{b_1}}&{ - {b_2}}\\ {{b_3}}&{{b_4}} \end{array}} \right]} \right\} - 1\left[ {\begin{array}{*{20}{l}} {{b_1}}&{ - {b_2}}\\ {{b_3}}&{{b_4}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{S_{{\rm{re}}}}\left( {{k_{{\rm{in}}}}} \right)}\\ {{S_{{\rm{im}}}}\left( {{k_{{\rm{in}}}}} \right)} \end{array}} \right]。$ | (17) |
进而得到幅值和相位的校正估计,分别为:
| $ {A_{{\rm{in}}}} = 2\sqrt {{x^2} + {y^2}} ,{\theta _{{\rm{in}}}} = \arctan \frac{y}{x}。$ | (18) |
值得注意的是:1)若求解频率偏移分量,式(16)中窗函数频谱应采用准确的理论表达式,而非式(3)中的近似表达式;2)在考虑白噪声的谱干扰情况下,若需要提高最小二乘法精度,可采用多谱线构成上述类似方程组进行求解,即扩展对应式(15)中左右参数矩阵。
3 仿真分析为验证算法对间谐波的检测性能,且考虑实际工况运行下噪声干扰,采用3个数字仿真进行分析。第1个为不同信噪比情况下的单频间谐波参数检测,第2和第3个将提出的改进方法与IEC及IEEE标准方法进行比对。
3.1 噪声对单一低频间谐波检测算法的性能影响为评估算法对噪声的敏感度,测试存在白噪声情况下信号频率估计的准确度,以确定该方法相对于Cramer-Rao下界(fCRB)的统计特性。首先通过经验均方根误差(empirical root mean square error,用eRMSE表示)确定估计方差,其定义为:
| $ {e_{{\rm{RMSE}}}}(v) = \sqrt {\frac{1}{K}\sum\limits_{k = 1}^K {{{(\hat v - v)}^2}} } 。$ | (19) |
式中:
|
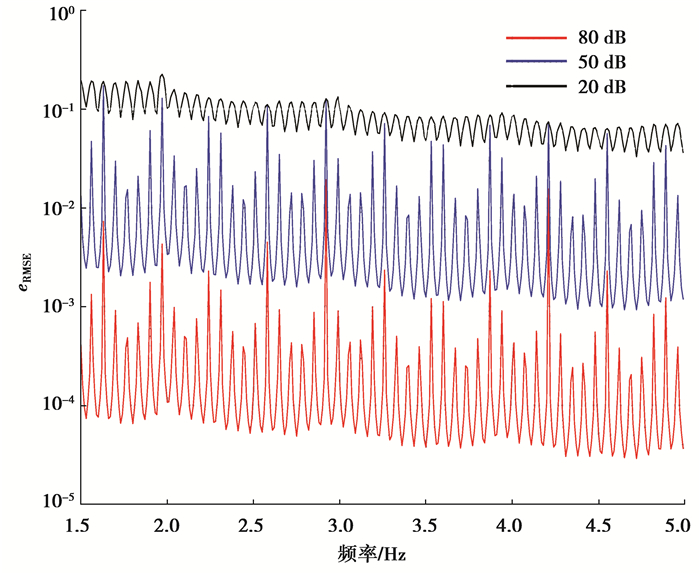
图 3 不同信噪比下的频率估计eRMSE Fig. 3 Frequency estimation eRMSE at different signal to noise ratios |
进一步根据采样频率及信噪比RSNR得到频率估计的Cramer-Rao下界[17]:
| $ {f_{{\rm{CRB}}}}(\hat v) = \frac{{3f_S^2}}{{{{\rm{ \mathsf{ π} }}^2}{R_{{\rm{SNR}}}}\left( {{N^3} - N} \right)}}。$ | (20) |
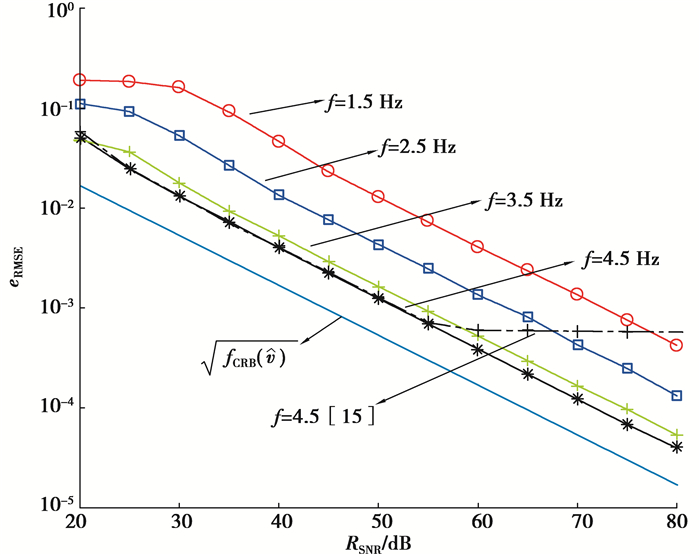
此处测试信噪比以步长5 dB在20~80 dB间逐渐变化,相位随机变化区间为[0, π),被测频率分别在1.5,2.5,3.5,4.5 Hz时的eRMSE与fCRB如图 4所示。
|
图 4 算法抗噪统计特性 Fig. 4 Anti-noise statistical characteristics of the algorithm |
从图 3看出,算法在低信噪比下依然能够稳定运行,且随着信噪比逐渐升高,负频率频谱泄露分量成为干扰的主要分量,因而算法的负频谱泄露抑制原理使得校正准确度逐步提升;而图 4进一步表明,随着被测频率逐渐增大,在其旁瓣泄露(f=(k+0.5)Δf)最大情形下依然能够逐渐逼近fCRB,即算法对噪声抑制具有一致性。作为对比,图 4中黑色虚线表示的为文献[15]算法的eRMSE,明显在信噪比大于55 dB时(此时干扰的主要分量为负频率频谱泄露分量)变得相对平坦,揭示对负频率频谱泄露分量的抑制性能已无明显提升。通过上述仿真表明,改进算法在噪声条件下比其原始算法更具鲁棒性。
3.2 与IEC间谐波检测比较IEC 61000以10个工频周波作为间谐波测量的信号截断长度,频率分辨率为5 Hz,其对应测量误差限为±5%[10],间谐波计算公式分为基波同步和非同步,分别为:
| $ \left\{ {\begin{array}{*{20}{l}} {Y_{{\rm{ig}}}^2 = \sum\limits_{k = 1}^{N - 1} {Y_{C,(N \times m) + k}^2} ;}\\ {Y_{{\rm{isg}}}^2 = \sum\limits_{k = 2}^{N - 2} {Y_{C,(N \times m) + k}^2} 。} \end{array}} \right. $ | (21) |
式中:N为截断周期,m为谐波次数,YC为对应谱线的有效值,Yig和Yisg为间谐波谱线“群”及“子群”对应的有效值。
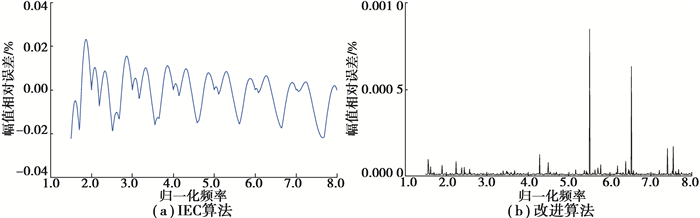
设置低频间谐波的归一化频率在[1.5, 8.0]Δf范围内以步长0.01Δf逐渐变化,相位随机变化区间为[0, π),则在60 dB信噪比下IEC算法与本研究中改进算法的间谐波幅值检测相对误差如图 5所示。图中的相对误差取相位变化范围内的误差最大值,此处仅进行单次随机噪声下的性能比较。
|
图 5 60 dB下幅值相对估计误差 Fig. 5 Relative error of amplitude estimation at 60 dB |
IEC谱线群算法在被测间谐波频率变化时误差波动较大;而我们的算法的误差基本稳定在0.001 0%以下。出现的局部极大值误差是单次噪声的随机性造成的;此处幅值校正估计误差明显由频率校正精度确定,因而若提高信噪比,则幅值相对误差将进一步提高。
3.3 与IEEE三参量拟合比较IEC 61000给出的间谐波检测公式(21)仅能给出幅值信息;而对于相位检测,此处以IEEE 1057三参量拟合算法作为本研究的算法相位校正的参考。假设间谐波频率已知,则IEEE 1057采用最小二乘拟合方式得到幅值及相位估计,即:
| $ \left[ {\begin{array}{*{20}{c}} {{A_{\cos }}}\\ {{A_{\sin }}} \end{array}} \right] = \left[ {{{\left( {{\Im ^T}\Im } \right)}^{ - 1}}\Im } \right]\left[ {\begin{array}{*{20}{c}} {s(0)}\\ \vdots \\ {s(N - 1)} \end{array}} \right]。$ | (22) |
式中:系数矩阵
| $ \Im = \left( {\begin{array}{*{20}{c}} {\left[ {\cos \left( {\frac{{2{\rm{ \mathsf{ π} }}\hat f}}{N}0} \right)} \right.}&{\left. {\sin \left( {\frac{{2{\rm{ \mathsf{ π} }}\hat f}}{N}0} \right)} \right]}\\ \vdots & \vdots \\ {\left[ {\cos \left( {\frac{{2{\rm{ \mathsf{ π} }}\hat f}}{N}(N - 1)} \right)} \right.}&{\left. {\sin \left( {\frac{{2{\rm{ \mathsf{ π} }}f}}{N}(N - 1)} \right)} \right]} \end{array}} \right)。$ | (23) |
对比式(22)和(15),IEEE 1057需要解析的方程为
|
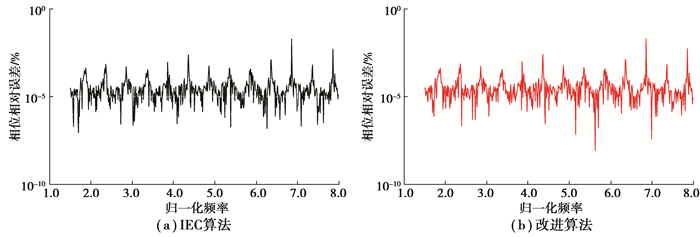
图 6 60 dB下相位相对估计误差 Fig. 6 Relative error of phase estimation at 60 dB |
从上图看出,本研究的改进算法在采用三离散谱线拟合的情况下,仍能够达到与IEEE采用N点拟合同样的精度。
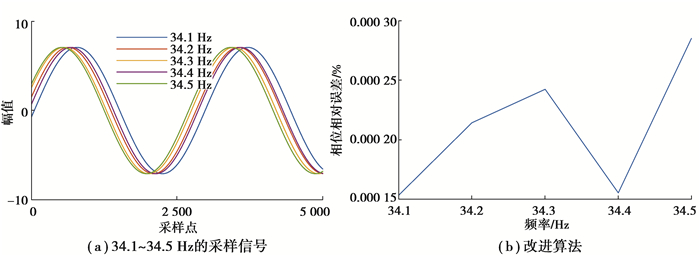
3.4 与实验结果比较为测试算法在实际电力信号检测中的性能,此处采用0.02级三相交直流仪表检定输出高精度电压功率信号,其频率以步长0.1 Hz依次设定为34.1~34.5 Hz,幅值有效值为5 V。利用采样频率高达100 kHz的IOtech进行离散信号采样。为验证算法性能,凸显算法对快速傅里叶变换(fast Fourier transform, FFT)后负频率泄漏分量干扰抑制能力,随机截取其中5 000采样点数据,如图 7(a)所示。采用改进算法分别进行1 000次独立频率估计,根据式(19)得到各频率点下平均误差如图 7(b)所示。从结果可以看出,实测信号下算法频率估计结果统计误差在0.000 3%以下,与前述理论仿真及统计结果一致。
|
图 7 实验信号及分析结果 Fig. 7 Experimental signal and analysis results |
1) 以信号加窗的DFT频谱分解为出发点,从谱线构成上剖析了负频率频谱泄露对插值校正的影响,进而在最大旁瓣衰减窗的频谱特性下,提出了抑制负频率频谱干扰的改进三谱线插值DFT算法,该算法适用于任意阶的最大旁瓣衰减窗。
2) 针对噪声干扰对谱线插值精度的影响,改进算法较原始算法在一定信噪比范围内精度有明显提升,进而可有效提高频率校正的精度,为后续幅值和相位估计校正奠定基础。
3) 将改进插值算法用于低频间谐波检测,并与IEC间谐波检测方法的幅值精度、IEEE三参量拟合算法的相位精度比较,结果显示改进算法的幅值精度较IEC算法有大幅度提升,相位精度与IEEE三参量拟合算法基本一致,但计算速度明显提升,因此具有很高的实际工程应用价值。
| [1] |
刘亚栋, 杨洪耕, 陈丽, 等. 非稳态谐波和间谐波检测的新方法[J]. 电网技术, 2012, 36(1): 170-175. LIU Yadong, YANG Honggeng, CHEN Li, et al. A new method to detect non-stationary harmonics and inter-harmonics[J]. Power System Technology, 2012, 36(1): 170-175. (in Chinese) |
| [2] |
Langella R, Testa A. Amplitude and phase modulation effects of waveform distortion in power systems[J]. Electrical Power Quality and Utilization Journal, 2007, 8(1): 25-32. |
| [3] |
International Electrotechnical Commission. General guide on harmonics and interharmonics measurements for power supply systems and equipment connected thereto: IEC61000-4-7[S]. Geneva: International Electrotechnical Commission, 2009.
|
| [4] |
Li Y F, Chen K F. Eliminating the picket fence effect of the fast Fourier transform[J]. Computer Physics Communications, 2008, 178(7): 486-491. DOI:10.1016/j.cpc.2007.11.005 |
| [5] |
毛育文, 涂亚庆, 张海涛, 等. 计及负频率影响的频谱分析方法及研究进展[J]. 电测与仪表, 2011, 48(5): 27-32. MAO Yuwen, TU Yaqing, ZHANG Haitao, et al. Advances and trends in spectrum analysis methodology with negative frequency contribution[J]. Electrical Measurement & Instrumentation, 2011, 48(5): 27-32. (in Chinese) DOI:10.3969/j.issn.1001-1390.2011.05.007 |
| [6] |
陈奎孚, 张森文, 郭幸福. 消除负频率影响的频谱校正[J]. 机械强度, 2004, 26(1): 25-28. CHEN Kuifu, ZHANG Senwen, GUO Xingfu. Spectrum rectifying with negative frequency contribution eliminating[J]. Journal of Mechanical Strength, 2004, 26(1): 25-28. (in Chinese) DOI:10.3321/j.issn:1001-9669.2004.01.006 |
| [7] |
Belega D, Petri D, Dallet D. Frequency estimation of a sinusoidal signal via a three-point interpolated DFT method with high image component interference rejection capability[J]. Digital Signal Processing, 2014, 24: 162-169. DOI:10.1016/j.dsp.2013.09.014 |
| [8] |
Belega D, Petri D, Dallet D. Accurate amplitude and phase estimation of noisy sine-waves via two-point interpolated DTFT algorithms[J]. Measurement, 2018, 127: 89-97. DOI:10.1016/j.measurement.2018.05.075 |
| [9] |
Diao R P, Meng Q F. Frequency estimation by iterative interpolation based on leakage compensation[J]. Measurement, 2015, 59: 44-50. DOI:10.1016/j.measurement.2014.09.039 |
| [10] |
王泽, 杨洪耕, 王佳兴, 等. 消除负频率影响的低频间谐波快速检测方法[J]. 电力自动化设备, 2015, 35(3): 140-145, 156. WANG Ze, YANG Honggeng, WANG Jiaxing, et al. Rapid low-frequency interharmonic detection with negative-frequency elimination[J]. Electric Power Automation Equipment, 2015, 35(3): 140-145, 156. (in Chinese) |
| [11] |
李醒飞, 李立, 寇科, 等. 全相位FFT时移相位差频谱校正分析及改进[J]. 天津大学学报(自然科学与工程技术版), 2016, 49(12): 1290-1295. LI Xingfei, LI Li, KOU Ke, et al. Analysis and improvement of time-shift phase difference spectral correction based on all-phase FFT[J]. Journal of Tianjin University (Science and Technology), 2016, 49(12): 1290-1295. (in Chinese) |
| [12] |
Chen K F, Cao X, Li Y F. Sine wave fitting to short records initialized with the frequency retrieved from Hanning windowed FFT spectrum[J]. Measurement, 2009, 42(1): 127-135. |
| [13] |
Borkowski J, Kania D, Mroczka J. Interpolated-DFT-based fast and accurate frequency estimation for the control of power[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12): 7026-7034. DOI:10.1109/TIE.2014.2316225 |
| [14] |
Wang Y, Wei W, Xiang J. Multipoint interpolated DFT for sine waves in short records with DC components[J]. Signal Processing, 2017, 131: 161-170. DOI:10.1016/j.sigpro.2016.08.013 |
| [15] |
Luo J F, Hou S C, Li X Y, et al. Generalization of interpolation DFT algorithms and frequency estimators with high image component interference rejection[J/OL]. EURASIP Journal on Advances in Signal Processing, 2016, 2016: 30(2016-03-05)[2019-07-25]. https://link.springer.xilesou.top/content/pdf/10.1186%2Fs13634-016-0330-6.pdf. DOI:10.1186/s13634-016-0330-6
|
| [16] |
Zhou W, Gan L Q, Xiao H, et al. Frequency estimators with high resistance to interference from image frequency components[J]. Journal of Algorithms & Computational Technology, 2018, 12(2): 147-158. |
| [17] |
Handel P. Properties of the IEEE-STD-1057 four-parameter sine wave fit algorithm[J]. IEEE Transactions on Instrumentation and Measurement, 2000, 49(6): 1189-1193. DOI:10.1109/19.893254 |
 2020, Vol. 43
2020, Vol. 43

