2. 中国电力工程顾问集团 西南电力设计院有限公司, 成都 610021
2. Southwest Electric Power Design Institute, China Power Engineering Consulting Corporation, Chengdu 610021, P. R. China
在四川、贵州、重庆、湖北等地区,存在不少跨越高山、峡谷、河流的输电线路,这些线路通常具有大档距大高差的特点,若线路处于覆冰区会出现脱冰跳跃问题,其导线脱冰时冰跳高度可能与常规线路不同。现有的导线脱冰跳跃高度计算公式几乎没有考虑大档距大高差线路的特点,因此有必要对其进行系统深入的研究,获得适用于不同档距和高差线路的工程设计简化计算公式。
一些学者采用模型实验方法模拟了导线的脱冰跳跃过程,研究了导线脱冰过程中冰跳高度和张力的变化[1-4],Morgan等[5]通过在一条实际线路上施加和释放集中载荷模拟了脱冰跳跃问题。脱冰跳跃模拟实验具有代价大、效率低、参数变化困难等缺点。Oertli[6]和Morgan等[5]通过建立理论简化模型,利用能量原理导出了导线冰跳高度的理论简化计算方法。伍川等[7]针对连续档导线脱冰问题,基于导线脱冰跳跃过程中的能量守恒和应力弧垂变化关系等,得到了计算导线脱冰跳跃高度的迭代方法。然而,这些理论模型和方法忽略了线路高差的影响,且没有考虑大档距线路导线脱冰后振动形态的影响。另一方面,有限单元法已经成为研究输电线路脱冰动力响应问题的重要手段[1, 8-15],这些工作大多关注各种参数对导线脱冰后振动特征的影响规律。Yan等[13]利用有限元方法,模拟研究了不同参数条件下导线的脱冰跳跃过程,并基于数值模拟结果,利用最小二乘线性回归方法,给出了计算脱冰跳跃高度的工程简化公式,但是该公式不适用于大档距大高差线路。
因此,研究同时适用于大档距大高差线路的导线冰跳高度计算方法或简化计算公式,具有重要的工程应用价值。
1 导线脱冰动力响应数值模型 1.1 典型线路结构及覆冰参数在连续档线路设计中,一般按等档距奇数档验算导线脱冰时的跳跃高度[1, 13]。已有的研究结果表明,对于奇数档线路,当中间档整档完全脱冰时导线的冰跳高度最大,而且当档数超过3档时,导线最大脱冰高度随档数的增加变化很小[13]。
我们将研究对象扩展到大档距大高差的情况,考虑到大档距大高差线路的特殊性,以5档连续档线路为对象,模拟研究导线脱冰时的动力响应。选择表 1所列典型输电线路作为计算对象,模拟在典型覆冰厚度和脱冰率情况下导线的动力响应,进而研究导线的脱冰跳跃高度。
| 表 1 典型线路结构及覆冰和脱冰参数 Table 1 Typical transmission line structure and parameters of ice-coating and ice-shedding |
已有的研究表明杆塔对冰跳高度影响很小,在此忽略杆塔的影响,仅建立导线有限元模型。以档距800 m的五档六分裂导线为例说明有限元建模方法。该线路导线型号为LGJ-1250/100,子导线截面为1 350.03 mm2,外径为47.85 mm,单位长度质量为4.01 kg/m;间隔棒型号为JZF-400,质量为7.50 kg;悬垂绝缘子串长17.32 m,总质量为5 150 kg;LX-4245悬垂联板质量37.86 kg,线夹总质量89.26 kg。
导线可视为柔索,采用索单元模拟,经计算,单元长度取0.5 m可以满足单元收敛性要求。将间隔棒等效为边长0.45 m、由直径0.05 m的圆杆构成的六边形框架,根据模型与实际间隔棒质量相等计算其等效密度。类似地将线夹也简化为边长0.45 m的六边形框架,计算其等效密度时,还需加上悬垂联板的质量。
导线的弹性模量为65.2 GPa,泊松比取0.3。绝缘子串、线夹和间隔棒等金具的弹性模量和泊松比分别取200 GPa和0.3。准确确定导线的阻尼十分困难,而阻尼对导线脱冰后振动的衰减过程影响较明显,但是其在一定的取值范围内对导线脱冰后第一个振动峰值影响很小,该峰值决定了导线的冰跳高度,在此取覆冰导线的阻尼比为2%。
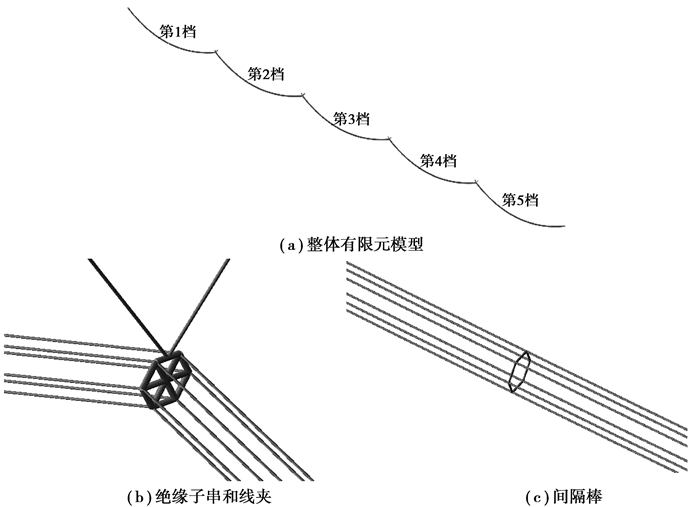
考虑作用于导线上的自重和覆冰载荷,假设覆冰均匀分布在导线表面,脱冰为整档瞬间脱落。脱冰前导线上总荷载可通过修改其等效密度来模拟,等效密度由导线自重和覆冰载荷确定。而脱冰载荷则可通过修改导线的惯性加速度来模拟,惯性加速度与导线脱冰率有关,具体模拟方法详见文献[9, 13]。所有悬垂绝缘子串与杆塔连接的端点线位移固定约束,可以绕悬挂点自由转动,线路两端与耐张塔相连,设置为固定约束,有限元模型如图 1所示。在数值模拟过程中,首先通过计算确定导线在自身重量和覆冰载荷作用下的平衡状态,该平衡状态下的应力和弧垂应满足导线在设定自然条件下应力弧垂表中给出的数据,然后再数值模拟研究在各种脱冰条件下导线产生的动力响应情况。
|
图 1 六分裂800 m档距五档线路导线有限元模型 Fig. 1 Finite-element model of a five-span line from 800 m span length and 0 m elevation difference with six-bundle conductor |
如图 2所示为六分裂导线800 m档距线路中间档脱冰时,1、2、3档中点的竖向位移时程。由于对称性,4、5两档的竖向位移时程分别与1、2档的相同。从图中可见,第3档脱冰时导线中点位移最大,其脱冰后先向上运动到最大冰跳高度,而其它档先向下运动然后上下振动。

|
图 2 六分裂800 m档距线路中间档脱冰时各档中点竖向位移响应 Fig. 2 Vertical displacement responses at midpoint of spans after ice shedding from 800 m span length and six-bundle conductor |
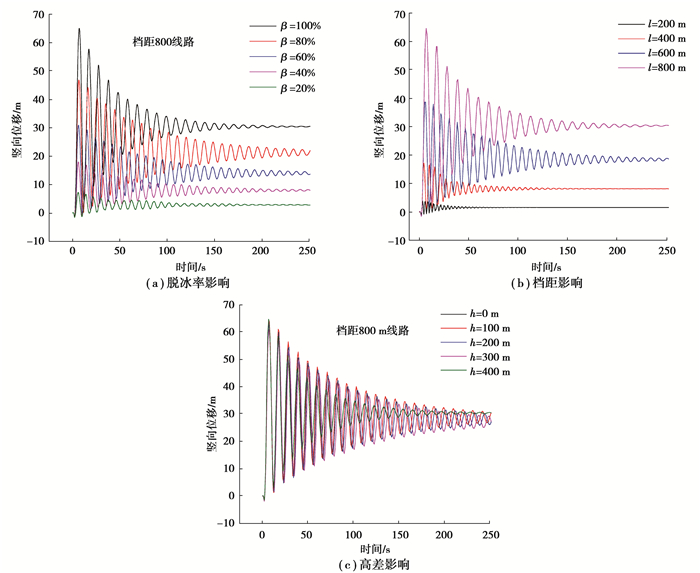
由图 3可以看出,导线脱冰产生的最大冰跳高度随脱冰率β增大而增大(图 3(a)),随档距l增大而增大(图 3(b)),随高差增大而减小(图 3(c))。
|
图 3 不同参数对脱冰档中点竖向位移响应的影响(六分裂五档线路) Fig. 3 Effect of different parameters on the vertical displacement response at midpoints of span after ice-shedding (six-bundle conductor and five-span line) |
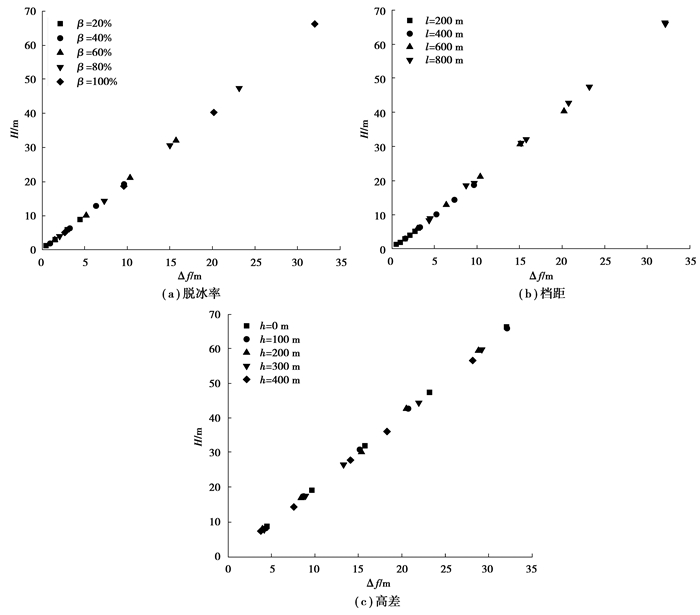
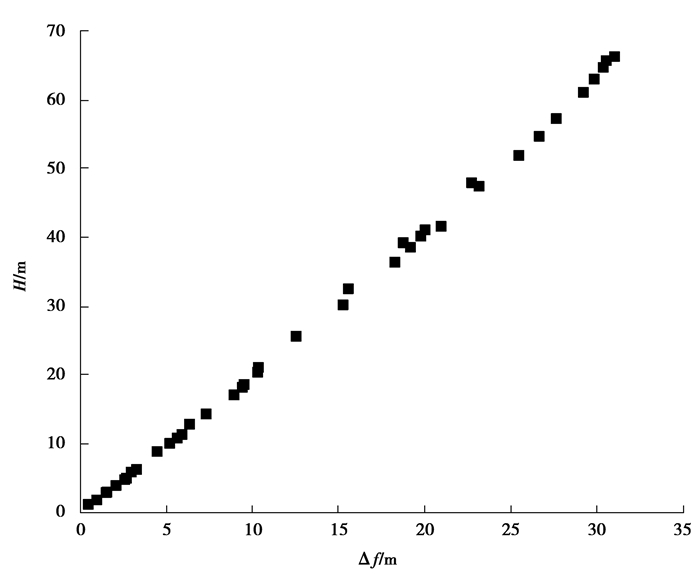
已有研究表明,由于导线的弧垂与档距、高差、张力和载荷有关,导线脱冰前后静止状态下的弧垂差与导线脱冰产生的最大跳跃高度之间存在一定的关系[13]。根据导线脱冰动力响应数值模拟结果,作出导线最大脱冰跳跃高度H与其脱冰前后静止状态弧垂差Δf之间的关系图,如图 4所示。整合所有参数条件下计算结果列于图 5中。从图中可见,在Δf较小时,H与Δf几乎呈线性关系。数据分析可知,Δf较小时对应档距和高差不大的情况,而Δf较大时对应大档距大高差情况,此时H与Δf不再是线性关系。因此有必要对已有的冰跳高度公式进行改进,考虑到导线脱冰跳跃高度受档距l和高差h的影响,对图 5中的数据进行拟合可得到如下改进计算公式:
| $ H=[1.75+(5 l-2 h) / 10000] \Delta f。$ | (1) |
|
图 4 不同参数条件下冰跳高度H随弧垂差Δf的变化 Fig. 4 Variation of jump height H with sag difference Δf under different parameters |
|
图 5 所有参数条件下冰跳高度H随弧垂差Δf的变化 Fig. 5 Variation of jump height H with sag difference Δf under all parameters |
Yan等[13]基于导线脱冰动力响应数值模拟结果,通过线性回归方法给出了如下导线冰跳高度简化计算公式:
| $ H=1.82 \Delta f。$ | (2) |
但该公式利用的数据没有包含大档距和大高差线路数值模拟结果。此外,中国输电线路设计规程[16]利用前苏联的计算公式
| $H=m(2-l / 1000) \Delta f。$ | (3) |
式中m是考虑导线部分脱冰引入的常数,在整档完全脱冰时取1.0。
采用理论简化分析模型,连续档线路均布载荷作用下导线的弧垂可由下式计算[17]:
| $ f=\frac{\gamma l^{2}}{8 \sigma \cos \varphi}。$ | (4) |
式中:γ为作用于导线的静止线载荷,这里包括自重和覆冰载荷;σ为导线最低点的水平应力;φ为有高差线路时两端绝缘子串悬挂点之间的仰角差。对于脱冰后的静止状态,γ和σ取决于脱冰率,因此可以由此计算得到脱冰后导线的弧垂。为此,在计算导线的脱冰高度时,首先用公式(4)计算导线脱冰前后的弧垂,进而得到弧垂差,再利用公式(1)(2)或(3)计算其冰跳高度。
3.2 冰跳高度公式的适应性下面分析比较前述几种导线冰跳高度计算公式。表 2所示为分别利用公式(1)~(3)和有限元模拟得到的不同参数条件下导线冰跳高度。可见,在线路的档距很小时,利用公式(1)~(3)和有限元方法计算得到的结果非常接近。但是,随着线路档距和高差增大,这些公式的计算结果差别也越来越大。公式(3)得到的结果明显小于其它计算结果,公式(2)的结果随档距和高差增大与有限元结果的偏离也越大,而我们的改进计算公式(1)在所有档距和高差变化范围内均与数值模拟结果非常接近,最大相对误差为4.09%,满足工程设计的要求。
| 表 2 利用不同公式和方法计算得到的冰跳高度 Table 2 Jump height calculated by different formulas and methods |
基于不同参数条件下导线的脱冰动力响应数值模拟结果,对导线冰跳高度简化计算公式进行了改进,得到适用于不同档距和高差线路的改进计算公式和以下结论:
1) 大档距大高差输电线路导线脱冰跳跃高度与线路的结构参数和覆冰载荷参数之间的关系较复杂,需要引入档距和高差的影响。
2) 基于数值模拟结果得到的导线脱冰跳跃高度改进计算公式不仅适用于小档距小高差的情况,也适用于大档距和大高差情况。
3) 在档距和高差不大的情况下,导线冰跳高度的计算可以采用以往的导线冰跳高度工程简化计算公式,但在大档距大高差情况下则需要利用我们的改进公式进行计算。
4) 本文中的导线冰跳高度改进计算公式为冰区大档距大高差线路设计提供了重要的依据。
| [1] |
Jamaleddine A, McClure G, Rousselet J, et al. Simulation of ice-shedding on electrical transmission lines using ADINA[J]. Computers & Structures, 1993, 47(4/5): 523-536. |
| [2] |
王璋奇, 齐立忠, 杨文刚, 等. 集中质量法模拟覆冰在架空线脱冰动张力实验中的适用性研究[J]. 中国电机工程学报, 2014, 34(12): 1982-1988. WANG Zhangqi, QI Lizhong, YANG Wengang, et al. Research on the applicability of lumped mass method for cable's dynamic tension in the ice shedding experiment[J]. Proceedings of the CSEE, 2014, 34(12): 1982-1988. (in Chinese) |
| [3] |
Meng X B, Hou L, Wang L M, et al. Oscillation of conductors following ice-shedding on UHV transmission lines[J]. Mechanical Systems and Signal Processing, 2012, 30: 393-406. DOI:10.1016/j.ymssp.2011.10.020 |
| [4] |
Kollar L E, Farzaneh M. Modeling sudden ice shedding from conductor bundles[J]. IEEE Transactions on Power Delivery, 2013, 28(2): 604-611. DOI:10.1109/TPWRD.2012.2227281 |
| [5] |
Morgan V T, Swift D A. Jump height of overhead-line conductors after the sudden release of ice loads[J]. Proceedings of the Institution of Electrical Engineers, 1964, 111(10): 1736. DOI:10.1049/piee.1964.0285 |
| [6] |
Oertli H. Oscillations de cables electriques aeriens apres la chute de surcharges[J]. Bulletin de l'Association Suisse des Electriciens, 1950, 41: 501-511. |
| [7] |
Wu C, Yan B, Zhang L, et al. A method to calculate jump height of iced transmission lines after ice-shedding[J]. Cold Regions Science and Technology, 2016, 125: 40-47. DOI:10.1016/j.coldregions.2016.02.001 |
| [8] |
Kollar L E, Farzaneh M. Vibration of bundled conductors following ice shedding[J]. IEEE Transactions on Power Delivery, 2008, 23(2): 1097-1104. DOI:10.1109/TPWRD.2007.915876 |
| [9] |
陈将, 严波, 陈科全. 重冰区架空输电线脱冰振动的数值模拟研究[J]. 重庆大学学报(自然科学版), 2007, 30(S0): 46-48. CHEN Jiang, YAN Bo, CHEN Kequan. Numerical simulation of the dynamic response of ice-shedding on overhead electrical transmission in cold regions[J]. Journal of Chongqing University (Natural Science Edition), 2007, 30(S0): 46-48. (in Chinese) |
| [10] |
陈勇, 胡伟, 王黎明, 等. 覆冰导线脱冰跳跃特性研究[J]. 中国电机工程学报, 2009, 29(28): 115-121. CHEN Yong, HU Wei, WANG Liming, et al. Research on ice-shedding characteristic of icing conductor[J]. Proceedings of the CSEE, 2009, 29(28): 115-121. (in Chinese) DOI:10.3321/j.issn:0258-8013.2009.28.019 |
| [11] |
Yang F L, Yang J B, Han J K, et al. Dynamic responses of transmission tower-line system under ice shedding[J]. International Journal of Structural Stability and Dynamics, 2010, 10(3): 461-481. |
| [12] |
Yang F L, Yang J B, Zhang Z F. Unbalanced tension analysis for UHV transmission towers in heavy icing areas[J]. Cold Regions Science and Technology, 2012, 70: 132-140. DOI:10.1016/j.coldregions.2011.07.008 |
| [13] |
Yan B, Chen K Q, Guo Y M, et al. Numerical simulation study on jump height of iced transmission lines after ice shedding[J]. IEEE Transactions on Power Delivery, 2013, 28(1): 216-225. DOI:10.1109/TPWRD.2012.2219324 |
| [14] |
Mirshafiei F, McClure G, Farzaneh M. Modelling the dynamic response of iced transmission lines subjected to cable rupture and ice shedding[J]. IEEE Transactions on Power Delivery, 2013, 28(2): 948-954. DOI:10.1109/TPWRD.2012.2233221 |
| [15] |
黄新波, 徐冠华, 肖渊, 等. 输电线路档距组合对覆冰导线脱冰跳跃的影响[J]. 高电压技术, 2015, 41(7): 2356-2361. HUANG Xinbo, XU Guanhua, XIAO Yuan, et al. Impact of transmission line span combination on ice-shedding of iced conductor[J]. High Voltage Engineering, 2015, 41(7): 2356-2361. (in Chinese) |
| [16] |
张殿生. 电力工程高压送电线路设计手册[M]. 2版. 北京: 中国电力出版社, 2003. ZHANG Diansheng. Design manual of high voltage transmission lines for electric engineering[M]. 2nd ed. Beijing: China Electric Power Press, 2003. (in Chinese) |
| [17] |
邵天晓. 架空送电线路的电线力学计算[M]. 2版. 北京: 中国电力出版社, 2003: 185-188. SHAO Tianxiao. Mechanics calculation of overhead transmission lines[M]. 2nd ed. Beijing: China Electric Power Press, 2003: 185-188. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43


