应力波在工程领域中,如地震波探测[1]、宇宙空间探索[2]、设备检测[3]、武器装备的破坏与防护[4-6]和地球物理勘探[7]以及医疗领域[8]等等都有广泛的应用。如:使用由高速冲击而产生的应力波探索材料的动态力学性能;利用应力波造成的破坏机制,发展防护装甲和破坏装甲的武器;通过爆炸引起的应力波的传播、以及应力波在界面上反射和折射等对地球的内部结构进行探索,识别地壳分布情况和勘探地球资源;在无损检测使用超声波;利用声波发射来监测裂缝的延伸扩展等,从而推动应力波理论进一步的深入研究和改善。所有这些都表明在地球科学、爆炸力学、冲击动力学和材料力学性能研究中应力波理论是重要研究基础。
应力波的研究开始于19世纪,由Navier首先建立了弹性体振动方程;其后弹性体中能够传递纵波和横波这一现象[9]被Poisson发现,据此得到了弹性力学的基本方程组;Cauchy给出了当应力应变为线性,材料为应变率无关时的应力波理论;从1862年到1955年,应力波的研究有了长足的进步,Clebsch建立了弹性体自由振动常规模型,在实验中由J. Hokinson第一次观测到粒子在导线中的运动过程[10],Pochhammer和Chree得到了应力波在杆中传播的精确的弹性方程[11-12],Rayleigh研究并得到了半无限空间中平面应变情况下的时空演化过程[13]。塑性波理论始于二战,其成果是在二战结束后才被发表。
弹性波理论的发展依赖于弹性力学的发展。根据弹性理论,研究应力波理论需要考虑到弹性体变形本构关系、几何关系以及边界条件等等。在传统的波动理论中纵波和横波都是满足二阶的双曲波动方程[14]。其后,随着科学技术的飞速进步,在面对一些实际的工程问题时,这些理论无法解决。在细观尺度时开始出现尺寸效应,于是在二十世纪六十年代,偶应力理论被提出并得到发展[15-18];然后变形梯度理论也随之被Fleck等[19]提出;以及随之而来的微极线弹性理论也被提出和发展[20-21],因此弹性理论的基本变量增加到了6个。
由于弹性理论的发展,应力波理论也有了新的认知。Georgiadis等[23-24]讨论了应力波弥散效应受到微结构的影响以及扭转表面波在半无限空间中的时空演化。Ottosen等[25]研究了包含微结构的含偶应力的Rayleigh波在线弹性介质中的传播;Parfitt和Eringen[26]研究了应力波在自由面上的反射,首先提出了应力波反射有4个独立的脉冲,并且都相互独立,同时还指出了在一些特定的材料中和某些特定临界频率时,其中有2个波会消失。
文中修正弹性应力波波动方程[27]是张量方程,第一步就是将该方程通过张量分析投影到曲线坐标系中。通过笛卡尔坐标系和曲线坐标系的转换关系,完成投影到柱坐标系的转换过程。投影到柱坐标系的目的是在实际的工程应用中有许多柱壳形结构,在柱坐标系下对这些结构进行分析比在笛卡尔坐标系中更方便简单。本文中计算的几何模型为无限长的空心圆柱结构,通过有限差分法计算求解应力波在该结构上沿柱面的传播情况。
1 修正的弹性应力波理论对于各向同性弹性体,在小变形假设的前提下,研究其应力波的时空演化过程。首先要研究弹性体的变形,变形的描述可用位移的右梯度。矢量的右梯度作为一个二阶张量,可以将其分解为一个对称的二阶张量与一个反对称的二阶张量之和。其中对称的二阶张量即为应变张量,反对称的二阶张量为转动张量如式(1)所示[27]:
| $ \mathit{\boldsymbol{u}}\nabla = \frac{1}{2}\left( {\mathit{\boldsymbol{u}}\nabla + \nabla \mathit{\boldsymbol{u}}} \right) + \frac{1}{2}\left( {\mathit{\boldsymbol{u}}\nabla - \nabla \mathit{\boldsymbol{u}}} \right) = \mathit{\boldsymbol{\varepsilon }} + \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}, $ | (1) |
式中:u为位移,ε为平动变形即应变,Ω为转动变形,传统的理论都将Ω忽略了。
应变张量又可以分解为偏量与球量之和,并且应变的分解唯一
| $ \mathit{\boldsymbol{\varepsilon }} = \mathit{\boldsymbol{e}} + \frac{1}{3}tr\varepsilon \mathit{\boldsymbol{I}} = \mathit{\boldsymbol{e}} + \frac{1}{3}\theta \mathit{\boldsymbol{I}}, $ | (2) |
式中:e为偏斜应变,它的对角线元素之和零,即迹为零,θ为体积应变,I为二阶单位张量,体积应变是一个标量。且偏量与球量是2个线性无关的二阶张量。如式(3)所示的胡克定律,它表示柯西应力与应变之间的线性本构关系。
| $ \mathit{\boldsymbol{\sigma }} = 2\mu \mathit{\boldsymbol{\varepsilon }} + \lambda tr\mathit{\boldsymbol{\varepsilon I}}。$ | (3) |
弹性体的动量守恒方程为:
| $ \nabla \cdot \mathit{\boldsymbol{\sigma }} + \rho \mathit{\boldsymbol{b}} = \rho \frac{{{\partial ^2}\mathit{\boldsymbol{u}}}}{{\partial {t^2}}}。$ | (4) |
联立方程(1)(2)(4)可以得出以位移为基本变量的纳维方程:
| $ \left( {\lambda + \mu } \right)\nabla \nabla \cdot \mathit{\boldsymbol{u}} + \mu {\nabla ^2}\mathit{\boldsymbol{u}} + \rho \mathit{\boldsymbol{b}} = \rho \frac{{{\partial ^2}\mathit{\boldsymbol{u}}}}{{\partial {t^2}}}。$ | (5) |
在这里需要注意的是,基于经典弹性力学,纳维方程忽略了转动变形的动量矩守恒方程,是基于应变描述平动变形的场方程。对纳维方程分别做左梯度、右梯度,并求和,然后引入方程(1)可以得:
| $ \left( {\lambda + \mu } \right)\nabla \nabla \theta + \mu {\nabla ^2}\mathit{\boldsymbol{\varepsilon }} = \rho \frac{{{\partial ^2}\mathit{\boldsymbol{\varepsilon }}}}{{\partial {t^2}}}。$ | (6) |
将(3)式代入(6)式可得:
| $ \left( {\lambda + \mu } \right)\nabla \nabla \theta + \frac{1}{3}\mu {\nabla ^2}\theta \mathit{\boldsymbol{I}} + \mu {\nabla ^2}\mathit{\boldsymbol{e}} = \frac{1}{3}\rho \frac{{{\partial ^2}\theta }}{{\partial {t^2}}}\mathit{\boldsymbol{I}} + \rho \frac{{{\partial ^2}\mathit{\boldsymbol{e}}}}{{\partial {t^2}}}。$ | (7) |
式(7)两端同时双点积一个二阶单位张量I得到体积波波动方程:
| $ \left( {\lambda + 2\mu } \right){\nabla ^2}\theta - \rho \frac{{{\partial ^2}\theta }}{{\partial {t^2}}} = 0, $ | (8) |
式中:λ与μ是拉梅参数,ρ为密度,
| $ {c_1} = \sqrt {\frac{{\lambda + 2\mu }}{\rho }} 。$ | (9) |
静水压力与体积应变的关系为:
| $ P = \left( {\lambda + \frac{2}{3}\mu } \right)\theta 。$ | (10) |
对式(8)两端同时乘以
| $ \mu {\nabla ^2}\mathit{\boldsymbol{e}} - \rho \frac{{{\partial ^2}\mathit{\boldsymbol{e}}}}{{\partial {t^2}}} = \left( {\lambda + \mu } \right)\left( {\frac{1}{3}{\nabla ^2}\theta \mathit{\boldsymbol{I}} - \nabla \nabla \theta } \right)。$ | (11) |
偏应变的本构关系:
| $ S = 2\mu \mathit{\boldsymbol{e}}。$ | (12) |
在式(11)中,发现其右端项不为零,是一个非齐次的双曲波动方程,偏应变的传播受体积应变的影响,是一个弱耦合的应力波方程。根据偏应变的本构关系,形变波的波速为:
| $ {c_2} = \sqrt {\frac{\mu }{\rho }} 。$ | (13) |
将波动方程(8)和(11)简化到一维情况时有:
| $ \left( {\lambda + 2\mu } \right)\frac{{{\partial ^2}\theta }}{{\partial {x^2}}} - \rho \frac{{{\partial ^2}\theta }}{{\partial {t^2}}} = 0, $ | (14) |
| $ \mu \frac{{{\partial ^2}e}}{{\partial {x^2}}} - \rho \frac{{{\partial ^2}e}}{{\partial {t^2}}} = - \frac{2}{3}\left( {\lambda + \mu } \right)\frac{{{\partial ^2}\theta }}{{\partial {x^2}}}。$ | (15) |
用式(14)乘以-2/3再与方程(15)相加,便可得到空间一维与时间相关的形变波的另一种形式:
| $ \mu \frac{{{\partial ^2}\hat e}}{{\partial {x^2}}} = \rho \frac{{{\partial ^2}\hat e}}{{\partial {t^2}}}。$ | (16) |
其中:
| $ \hat e = e - \frac{2}{3}\theta 。$ | (17) |
式(16)是标准双曲方程,波速c2,为形变波的第二部分,它单独成为一个脉冲,式(16)的波动变量为偏应变的第一个主值减去体积应变的三分之二。所以,在平面应力波的时空演化过程中,形变波随着时间的增加分成两个部分:其第一个部分和体积波复合在一起形成一个复合脉冲并且以波速c1向前运动;形变波第二部分单独成为一个脉冲以波速c2向前运动。由于波速c1大于c2,主波和次波的间距会随着时间相隔越来越远,主波是复合脉冲,所以主波引起的应力应变都会明显强于次波。在柱面波中,形变波同样会分成两部分,第一部分以波速c1与体积波一起传播,第二部分以波速c2传播。
2 柱坐标系下的修正的弹性应力波理论为了得到柱坐标系下的应力波的波动方程,需要使用张量分析方法中的坐标变换对前文中的波动方程进行推导,其详细过程不赘述。
柱坐标系下的Laplace微分算子
| $ \begin{array}{*{20}{c}} {{\nabla ^2} = \nabla \cdot \nabla = {\mathit{\boldsymbol{g}}^i} \cdot {\nabla _i}\left( {{\nabla _j}{\mathit{\boldsymbol{g}}^j}} \right) = {\mathit{\boldsymbol{g}}^i} \cdot {\nabla _{j,i}}{\mathit{\boldsymbol{g}}^j} = {\nabla _{j,i}}{g^{ij}} = \left( {{\nabla _{j,i}} - {\nabla _k}\mathit{\Gamma }_{ji}^k} \right){g^{ij}} = }\\ {\frac{{{\partial ^2}}}{{\partial {r^2}}} + \frac{1}{{{r^2}}}\frac{{{\partial ^2}}}{{\partial {\varphi ^2}}} + \frac{{{\partial ^2}}}{{\partial {z^2}}} - \frac{\partial }{{\partial r}}\mathit{\Gamma }_{\varphi \varphi }^r{g^{\varphi \varphi }} = \frac{{{\partial ^2}}}{{\partial {r^2}}} + \frac{1}{r}\frac{\partial }{{\partial r}} + \frac{1}{{{r^2}}}\frac{{{\partial ^2}}}{{\partial {\varphi ^2}}} + \frac{{{\partial ^2}}}{{\partial {z^2}}},} \end{array} $ | (18) |
式中:下标带“,”表示偏导数;带“;”则表示协变导数。基于此可以迅速的得到柱坐标系中体积波的波动方程:
| $ \frac{{{\partial ^2}\theta }}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial \theta }}{{\partial r}} + \frac{1}{{{r^2}}}\frac{{{\partial ^2}\theta }}{{\partial {\varphi ^2}}} + \frac{{{\partial ^2}\theta }}{{\partial {z^2}}} = \frac{\rho }{{\lambda + 2\mu }}\frac{{{\partial ^2}\theta }}{{\partial {t^2}}}。$ | (19) |
柱坐标系下的形变波波动方程更为复杂,首先需要将方程(11)改写为:
| $ {\nabla ^2}\mathit{\boldsymbol{e}} = \frac{\rho }{\mu }\frac{{{\partial ^2}\mathit{\boldsymbol{e}}}}{{\partial {t^2}}} + \frac{{\lambda + \mu }}{\mu }\left( {\frac{1}{3}{\nabla ^2}\theta \mathit{\boldsymbol{G}} - \nabla \nabla \theta } \right), $ | (20) |
式中,G为曲线坐标系中的度量张量。方程右端项在柱坐标系中为:
| $ {\nabla ^2}\theta = {\theta _{,j;i}}{g^{ij}} = \left( {{\theta _{,j,i}} - {\theta _{,k}}\mathit{\Gamma }_{ji}^k} \right){g^{ij}}, $ | (21) |
| $ \nabla \nabla \theta = {\mathit{\boldsymbol{g}}^i}{\nabla _i}\left( {{\theta _{,j}}{\mathit{\boldsymbol{g}}^j}} \right) = {\theta _{,j;i}}{\mathit{\boldsymbol{g}}^i}{\mathit{\boldsymbol{g}}^j} = \left( {{\theta _{,ij}} - {\theta _{,k}}\mathit{\Gamma }_{ij}^k} \right){\mathit{\boldsymbol{g}}^i}{\mathit{\boldsymbol{g}}^j}。$ | (22) |
由式(20)(21)(22)可得,形变波在曲线坐标系中的分量形式如下:
| $ {e_{ij;kl}}{g^{kl}} = \frac{1}{{c_2^2}}\frac{{\partial {e_{ij}}}}{{\partial {t^2}}} + \frac{{\lambda + \mu }}{\mu }\left( {\frac{1}{3}{\theta _{,l;k}}{g^{kl}}{g_{ij}} - {\theta _{,j;i}}} \right)。$ | (23) |
偏应变张量的协变导数为:
| $ {e_{ij;k}} = {e_{ij,k}} - {e_{lj}}\mathit{\Gamma }_{ki}^l - {e_{il}}\mathit{\Gamma }_{kj}^l。$ | (24) |
偏应变张量的二阶协变导数为:
| $ {e_{ij;k;l}} = {e_{ij;k,l}} - {e_{ij;m}}\mathit{\Gamma }_{lk}^m - {e_{mj;k}}\mathit{\Gamma }_{li}^m - {e_{im;k}}\mathit{\Gamma }_{lj}^m。$ | (25) |
因为偏应变的迹为零,所以得到形变波在柱坐标系下的有6个独立分量,分别表示为:
| $ {e_{rr;rr}} + \frac{1}{{{r^2}}}{e_{rr;\varphi \varphi }} + {e_{rr;zz}} = \frac{1}{{c_2^2}}\frac{{\partial {e_{rr}}}}{{\partial {t^2}}} + \frac{{\lambda + \mu }}{\mu }\left( {\frac{1}{3}{\nabla ^2}\theta {g_{rr}} - {\theta _{,r;r}}} \right), $ | (26) |
| $ {e_{\varphi \varphi ;rr}} + \frac{1}{{{r^2}}}{e_{\varphi \varphi ;\varphi \varphi }} + {e_{\varphi \varphi ;zz}} = \frac{1}{{c_2^2}}\frac{{\partial {e_{\varphi \varphi }}}}{{\partial {t^2}}} + \frac{{\lambda + \mu }}{\mu }\left( {\frac{1}{3}{\nabla ^2}\theta {g_{\varphi \varphi }} - {\theta _{,\varphi ;\varphi }}} \right), $ | (27) |
| $ {e_{zz;rr}} + \frac{1}{{{r^2}}}{e_{zz;\varphi \varphi }} + {e_{zz;zz}} = \frac{1}{{c_2^2}}\frac{{\partial {e_{zz}}}}{{\partial {t^2}}} + \frac{{\lambda + \mu }}{\mu }\left( {\frac{1}{3}{\nabla ^2}\theta {g_{zz}} - {\theta _{,z;z}}} \right), $ | (28) |
| $ {e_{r\varphi ;rr}} + \frac{1}{{{r^2}}}{e_{r\varphi ;\varphi \varphi }} + {e_{r\varphi ;zz}} = \frac{1}{{c_2^2}}\frac{{\partial {e_{r\varphi }}}}{{\partial {t^2}}} + \frac{{\lambda + \mu }}{\mu }\left( { - {\theta _{,\varphi ;r}}} \right), $ | (29) |
| $ {e_{rz;rr}} + \frac{1}{{{r^2}}}{e_{rz;\varphi \varphi }} + {e_{rz;zz}} = \frac{1}{{c_2^2}}\frac{{\partial {e_{rz}}}}{{\partial {t^2}}} + \frac{{\lambda + \mu }}{\mu }\left( { - {\theta _{,z;r}}} \right), $ | (30) |
| $ {e_{\varphi z;rr}} + \frac{1}{{{r^2}}}{e_{\varphi z;\varphi \varphi }} + {e_{\varphi z;zz}} = \frac{1}{{c_2^2}}\frac{{\partial {e_{\varphi z}}}}{{\partial {t^2}}} + \frac{{\lambda + \mu }}{\mu }\left( { - {\theta _{,z;\varphi }}} \right)。$ | (31) |
根据式(25)可以得到:
| $ \begin{array}{*{20}{c}} {{e_{rr;rr}} = {e_{rr;r,r}} - {e_{rr;m}}\mathit{\Gamma }_{rr}^m - {e_{mr;r}}\mathit{\Gamma }_{rr}^m - {e_{rm;r}}\mathit{\Gamma }_{rr}^m = {e_{rr;r,r}},}\\ {{e_{rr;\varphi \varphi }} = {e_{rr;\varphi ,\varphi }} - {e_{rr;m}}\mathit{\Gamma }_{\varphi \varphi }^m - {e_{mr;\varphi }}\mathit{\Gamma }_{\varphi r}^m - {e_{rm;\varphi }}\mathit{\Gamma }_{\varphi r}^m = {e_{rr;\varphi ,\varphi }} + r{e_{rr;r}} - \frac{2}{r}{e_{\varphi r;\varphi }},}\\ {{e_{rr;zz}} = {e_{rr;z,z}} - {e_{rr;m}}\mathit{\Gamma }_{zz}^m - {e_{mr;z}}\mathit{\Gamma }_{zr}^m - {e_{rm;z}}\mathit{\Gamma }_{zr}^m = {e_{rr;z,z}}。} \end{array} $ | (32) |
由式(24)有:
| $ \begin{array}{*{20}{c}} {{e_{rr;r}} = {e_{rr,r}} - {e_{lr}}\mathit{\Gamma }_{rr}^l - {e_{rl}}\mathit{\Gamma }_{rr}^l = {e_{rr,r}},}\\ {{e_{rr;\varphi }} = {e_{rr,\varphi }} - {e_{lr}}\mathit{\Gamma }_{\varphi r}^l - {e_{rl}}\mathit{\Gamma }_{\varphi r}^l = {e_{rr,\varphi }} - \frac{2}{r}{e_{r\varphi }},}\\ {{e_{rr;z}} = {e_{rr,z}} - {e_{lr}}\mathit{\Gamma }_{zr}^l - {e_{rl}}\mathit{\Gamma }_{zr}^l = {e_{rr,z}},}\\ {{e_{r\varphi ;\varphi }} = {e_{r\varphi ,\varphi }} - {e_{l\varphi }}\mathit{\Gamma }_{\varphi r}^l - {e_{rl}}\mathit{\Gamma }_{\varphi \varphi }^l = {e_{r\varphi ,\varphi }} - \frac{1}{r}{e_{\varphi \varphi }} + r{e_{rr}}。} \end{array} $ | (33) |
将式(33)替换式(32)可得:
| $ \begin{array}{*{20}{c}} {{e_{rr;rr}} = {e_{rr;r,r}} = {e_{rr,rr}},}\\ {{e_{rr;\varphi \varphi }} = {e_{rr,\varphi \varphi }} - \frac{4}{r}{e_{r\varphi ,\varphi }} + r{e_{rr,r}} - 2{e_{rr}} + \frac{2}{{{r^2}}}{e_{\varphi \varphi }},}\\ {{e_{rr;zz}} = {e_{rr;z,z}} = {e_{rr,zz}}。} \end{array} $ | (34) |
把(34)带入式(26)则有:
| $ {e_{rr;rr}} + \frac{1}{{{r^2}}}\left( {{e_{rr,\varphi \varphi }} - \frac{4}{r}{e_{r\varphi ,\varphi }} + r{e_{rr,r}} - 2{e_{rr}} + \frac{2}{{{r^2}}}{e_{\varphi \varphi }}} \right) + {e_{rr,zz}} = \frac{1}{{c_2^2}}\frac{{\partial {e_{rr}}}}{{\partial {t^2}}} + \frac{{\lambda + \mu }}{\mu }\left( {\frac{1}{3}{\nabla ^2}\theta {g_{rr}} - {\theta _{,r;r}}} \right)。$ | (35) |
需要注意的是上式中的每个张量分量可以表示为物理分量,因此上式表示为物理分量为:
| $ \frac{{{\partial ^2}{e_{rr}}}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial {e_{rr}}}}{{\partial r}} + \frac{1}{{{r^2}}}\frac{{{\partial ^2}{e_{rr}}}}{{\partial {\varphi ^2}}} + \frac{{{\partial ^2}{e_{rr}}}}{{\partial {z^2}}} - \frac{4}{{{r^2}}}\frac{{\partial {e_{r\varphi }}}}{{\partial \varphi }} - \frac{2}{{{r^2}}}{e_{rr}} + \frac{2}{{{r^2}}}{e_{\varphi \varphi }} = \frac{1}{{c_2^2}}\frac{{\partial {e_{rr}}}}{{\partial {t^2}}} + \frac{{\lambda + \mu }}{\mu }\left( {\frac{1}{3}{\nabla ^2}\theta - \frac{{{\partial ^2}\theta }}{{\partial {r^2}}}} \right)。$ | (36) |
即:
| $ {\nabla ^2}{e_{rr}} - \frac{4}{{{r^2}}}\frac{{\partial {e_{r\varphi }}}}{{\partial \varphi }} - \frac{2}{{{r^2}}}{e_{rr}} + \frac{2}{{{r^2}}}{e_{\varphi \varphi }} = \frac{1}{{c_2^2}}\frac{{\partial {e_{rr}}}}{{\partial {t^2}}} + \frac{{\lambda + \mu }}{\mu }\left( {\frac{1}{3}{\nabla ^2}\theta - \frac{{{\partial ^2}\theta }}{{\partial {r^2}}}} \right)。$ | (37) |
同理另外5个方程为:
| $ {\nabla ^2}{e_{\varphi \varphi }} + \frac{4}{{{r^2}}}\frac{{\partial {e_{r\varphi }}}}{{\partial \varphi }} + \frac{2}{{{r^2}}}{e_{rr}} - \frac{2}{{{r^2}}}{e_{\varphi \varphi }} = \frac{1}{{c_2^2}}\frac{{{\partial ^2}{e_{\varphi \varphi }}}}{{\partial {t^2}}} + \frac{{\left( {\lambda + \mu } \right)}}{\mu }\left( {\frac{1}{3}{\nabla ^2}\theta - \frac{1}{{{r^2}}}\frac{{{\partial ^2}\theta }}{{\partial {\varphi ^2}}} - \frac{1}{r}\frac{{\partial \theta }}{{\partial r}}} \right), $ | (38) |
| $ {\nabla ^2}{e_{zz}} = \frac{1}{{c_2^2}}\frac{{{\partial ^2}{e_{zz}}}}{{\partial {t^2}}} + \frac{{\lambda + \mu }}{\mu }\left( {\frac{1}{3}{\nabla ^2}\theta - \frac{{{\partial ^2}\theta }}{{\partial {z^2}}}} \right), $ | (39) |
| $ {\nabla ^2}{e_{r\varphi }} + \frac{2}{{{r^2}}}\frac{{\partial {e_{rr}}}}{{\partial \varphi }} - \frac{2}{{{r^2}}}\frac{{\partial {e_{\varphi \varphi }}}}{{\partial \varphi }} - \frac{4}{{{r^2}}}{e_{r\varphi }} = \frac{1}{{c_2^2}}\frac{{{\partial ^2}{e_{r\varphi }}}}{{\partial {t^2}}} - \frac{{\lambda + \mu }}{\mu }\left( {\frac{1}{r}\frac{{{\partial ^2}\theta }}{{\partial r\partial \varphi }} - \frac{1}{{{r^2}}}\frac{{\partial \theta }}{{\partial \varphi }}} \right), $ | (40) |
| $ {\nabla ^2}{e_{rz}} - \frac{2}{{{r^2}}}\frac{{\partial {e_{\varphi z}}}}{{\partial \varphi }} - \frac{1}{{{r^2}}}{e_{rz}} = \frac{1}{{c_2^2}}\frac{{{\partial ^2}{e_{rz}}}}{{\partial {t^2}}} - \frac{{\lambda + \mu }}{\mu }\frac{{{\partial ^2}\theta }}{{\partial r\partial z}}, $ | (41) |
| $ {\nabla ^2}{e_{\varphi z}} + \frac{2}{{{r^2}}}\frac{{\partial {e_{rz}}}}{{\partial \varphi }} - \frac{1}{{{r^2}}}{e_{\varphi z}} = \frac{1}{{c_2^2}}\frac{{{\partial ^2}{e_{\varphi z}}}}{{\partial {t^2}}} - \frac{{\lambda + \mu }}{\mu }\frac{1}{r}\frac{{{\partial ^2}\theta }}{{\partial \varphi \partial z}}。$ | (42) |
首先对前文所述的柱面波理论模型进行简化,如图 1所示轴向无限长的圆柱筒形结构,并设轴向为z,径向为r,周向为φ,考虑到波沿径向均匀膨胀或压缩,且轴向无限长,因此轴向z和周向φ对应力波的传播不产生干扰。然后得到简化后的柱坐标系下的应力波波动方程组。
| $ \frac{{{\partial ^2}\theta }}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial \theta }}{{\partial r}} = \frac{\rho }{{\lambda + 2\mu }}\frac{{{\partial ^2}\theta }}{{\partial {t^2}}}, $ | (43) |
| $ \frac{{{\partial ^2}{e_r}}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial {e_r}}}{{\partial r}} - \frac{2}{{{r^2}}}{e_r} + \frac{2}{{{r^2}}}{e_\varphi } = \frac{1}{{c_2^2}}\frac{{{\partial ^2}{e_r}}}{{\partial {t^2}}} + \frac{{\lambda + \mu }}{\mu }\left( { - \frac{2}{3}\frac{{{\partial ^2}\theta }}{{\partial {r^2}}} + \frac{1}{{3r}}\frac{{\partial \theta }}{{\partial r}}} \right), $ | (44) |
| $ \frac{{{\partial ^2}{e_\varphi }}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial {e_\varphi }}}{{\partial r}} + \frac{2}{{{r^2}}}{e_r} - \frac{2}{{{r^2}}}{e_\varphi } = \frac{1}{{c_2^2}}\frac{{{\partial ^2}{e_\varphi }}}{{\partial {t^2}}} + \frac{{\lambda + \mu }}{\mu }\left( {\frac{1}{3}\frac{{{\partial ^2}\theta }}{{\partial {r^2}}} - \frac{2}{{3r}}\frac{{\partial \theta }}{{\partial r}}} \right), $ | (45) |
| $ \frac{{{\partial ^2}{e_z}}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial {e_z}}}{{\partial r}} = \frac{1}{{c_2^2}}\frac{{{\partial ^2}{e_z}}}{{\partial {t^2}}} + \frac{{\lambda + \mu }}{\mu }\left( {\frac{1}{3}\frac{{{\partial ^2}\theta }}{{\partial {r^2}}} + \frac{1}{{3r}}\frac{{\partial \theta }}{{\partial r}}} \right)。$ | (46) |

|
图 1 无限长空心圆柱筒结构示意图 Fig. 1 Infinitely long hollow cylinder structure diagram |
柱面波在圆柱筒形结构中传播时遇到界面会发生应力波的入射、反射和透射等界面效应,以柱面波在加载面上波的激发以及在自由面上的反射为研究对象,首先将波阵面视为间断面,在间断面上有质量守恒方程为[28]:
| $ [\rho (\mathit{\boldsymbol{v}} - \mathit{\boldsymbol{c}})] \cdot \mathit{\boldsymbol{n}} = 0, $ | (47) |
式中:v表示质点运动速度;n表示间断面法线方向;方括号表示间断。间断面在向右移动时,用“+”表示间断面前面的量“-”表示间断面后面的量,于是可以进一步得到:
| $ {\rho ^ - }\left( {{v^ - } - c} \right) + \rho c = 0。$ | (48) |
运动间断面上的动量守恒方程为:
| $ [\rho \mathit{\boldsymbol{v}}(\mathit{\boldsymbol{v}} - \mathit{\boldsymbol{c}}) - \mathit{\boldsymbol{\sigma }}] \cdot \mathit{\boldsymbol{n}} = 0。$ | (49) |
分量形式为:
| $ \left[ {\rho {v^i}(v - c) - {\sigma ^{ij}}{n_j}} \right] = 0。$ | (50) |
考虑到波阵面方向和3个主应力方向一致,故式(50)进一步写作:
| $ \begin{array}{*{20}{c}} {\left[ {\rho {v^r}(v - c) - {\sigma ^{rr}}{n_r} - {\sigma ^{r\varphi }}{n_\varphi } - {\sigma ^{rz}}{n_z}} \right] = 0,}\\ {\left[ {\rho {v^\varphi }(v - c) - {\sigma ^{\varphi r}}{n_r} - {\sigma ^{\varphi \varphi }}{n_\varphi } - {\sigma ^{\varphi z}}{n_z}} \right] = 0,}\\ {\left[ {\rho {v^z}(v - c) - {\sigma ^{zr}}{n_r} - {\sigma ^{z\varphi }}{n_\varphi } - {\sigma ^{zz}}{n_z}} \right] = 0。} \end{array} $ | (51) |
由于仅考虑主应力故为:
| $ \begin{array}{*{20}{c}} {\left[ {\rho {v_r}(v - c) - {\sigma _{rr}}{n_r}} \right] = 0,}\\ {\left[ {\rho {v_\varphi }(v - c) - {\sigma _{\varphi \varphi }}{n_\varphi }} \right] = 0,}\\ {\left[ {\rho {v_z}(v - c) - {\sigma _{zz}}{n_z}} \right] = 0。} \end{array} $ | (52) |
将式(50)带入式(52)可进一步得:
| $ \sigma _{rr}^ - {n_r} = - \rho cv_r^ - ,\sigma _{\varphi \varphi }^ - {n_\varphi } = - \rho cv_\varphi ^ - ,\sigma _{zz}^ - {n_z} = - \rho cv_z^ - 。$ | (53) |
在只考虑主应力状态下则有:
| $ \sigma _r^ - = - \rho cv_r^ - ,\sigma _\varphi ^ - = - \rho cv_\varphi ^ - ,\sigma _z^ - = - \rho cv_z^ - , $ | (54) |
式(54)表示了主应力与质点速度的关系,其中ρc为波阻抗。
体积波和形变波的波阵面在传播的过程中,可以视作间断面,然后根据式(54)可得:
| $ v = - \frac{P}{{\rho {c_1}}},{v_1} = - \frac{{{S_r}}}{{\rho {c_2}}},{v_2} = - \frac{{{S_\varphi }}}{{\rho {c_2}}},{v_3} = - \frac{{{S_z}}}{{\rho {c_2}}}, $ | (55) |
式中:P为静水压力,Sr和Sφ为由形变波产生的2个主应力,v、v1和v2分别为体积波引起的质点运动速度和2个形变波主应力引起的质点运动速度,z方向的量不独立,在加载面上受到均布外在f(t),加载面速度为v(t),静水压力和偏应力的本构关系如下:
| $ P = \left( {\lambda + \frac{2}{3}\mu } \right)\theta ,{S_r} = 2\mu {e_r},{S_\varphi } = 2\mu {e_\varphi }。$ | (56) |
然后根据加载面上的平衡关系,则可以得到:
| $ P + S = f\left( t \right),{v_r} = v + {v_1},{v_\varphi } = v + {v_2}。$ | (57) |
联立方程(51)~(54)得到加载面上的边界条件:
| $ \left. \begin{array}{l} \theta (t) = \frac{{\left( {f + \rho {c_2}{v_r}} \right){c_1}}}{{\left( {\lambda + \frac{2}{3}\mu } \right)\left( {{c_1} - {c_2}} \right)}}\\ {e_r}(t) = \frac{{\left( {f + \rho {c_1}{v_r}} \right){c_2}}}{{2\mu \left( {{c_2} - {c_1}} \right)}}\\ {e_\varphi }(t) = \frac{{{c_2}\left( {f + \rho {c_1}{v_\varphi }} \right) + \rho c_2^2\left( {{v_r} - {v_\varphi }} \right)}}{{2\mu \left( {{c_2} - {c_1}} \right)}} \end{array} \right\}。$ | (58) |
然后推导自由面上的边界条件,同样在自由面上,在加载面上产生的2个波中形变波中的一部分随着体积波以波速c1前进,其余部分以波速c2前进,由于c2小于c1,所以它们随着时间相隔越来越远,于是第一个波就会先碰到自由面,并且它们的内力及速度的作用关系为:
| $ {\sigma _r} = - \rho {c_1}v_r^\prime ,{\sigma _\varphi } = - \rho {c_1}v_\varphi ^\prime 。$ | (59) |
自由面上力与速度的关系为:
| $ {P^\prime } = \rho {c_1}{v^\prime },S_r^\prime = \rho {c_2}v_1^\prime ,S_\varphi ^\prime = \rho {c_2}v_2^\prime 。$ | (60) |
在自由面上由力的平衡与速度的平衡可以得:
| $ \left. {\begin{array}{*{20}{l}} {{\sigma _r} + {P^\prime } + S_r^\prime = 0}\\ {{v_r} + {v^\prime } + v_1^\prime = {u_r}}\\ {{v_\varphi } + {v^\prime } + v_2^\prime = {u_\varphi }} \end{array}} \right\}。$ | (61) |
将式(56)(57)带入式(58)得到自由面上的边界条件如下:
| $ \left. \begin{array}{l} {\theta ^\prime }(t) = \frac{{\rho {c_1}{c_2}{u_r} + \left( {{c_1} + {c_2}} \right){\sigma _r}}}{{\left( {\lambda + \frac{2}{3}\mu } \right)\left( {{c_2} - {c_1}} \right)}}\\ e_r^\prime (t) = \frac{{\rho {c_1}{c_2}{u_r} + 2{c_2}{\sigma _r}}}{{2\mu \left( {{c_1} - {c_2}} \right)}}\\ e_\varphi ^\prime = \frac{1}{{2\mu }}\left( {\rho {c_2}{u_\varphi } + \frac{{{c_2}}}{{{c_1}}}{\sigma _\varphi } + \frac{{\rho {c_1}c_2^2{u_r} + {c_2}\left( {{c_1} + {c_2}} \right){\sigma _r}}}{{{c_1}\left( {{c_1} - {c_2}} \right)}}} \right) \end{array} \right\}。$ | (62) |
同样的由加载面激发的第二个波以波速c2前进,在碰到自由面时力与质点速度的关系为:
| $ {{\hat S}_r} = - \rho {c_2}{{\hat v}_r},{{\hat S}_\varphi } = - \rho {c_2}{{\hat v}_\varphi }。$ | (63) |
经过后反射产生体积波形变波,所以反射后质点内力与速度的关系为:
| $ {P^{\prime \prime }} = \rho {c_1}{v^{\prime \prime }},S_r^{\prime \prime } = \rho {c_2}v_1^{\prime \prime },S_\varphi ^{\prime \prime } = \rho {c_2}v_2^{\prime \prime }。$ | (64) |
同理根据力的平衡以及速度的平衡可得到如下关系式:
| $ \left. {\begin{array}{*{20}{l}} {{{\hat S}_r} + {P^{\prime \prime }} + S_r^{\prime \prime } = 0}\\ {{{\hat v}_r} + {v^{\prime \prime }} + v_1^{\prime \prime } = {{\hat u}_r}}\\ {{{\hat v}_\varphi } + {v^{\prime \prime }} + v_2^{\prime \prime } = {{\hat u}_\varphi }} \end{array}} \right\}。$ | (65) |
将式(63)(64)带入式(65)的到第二个波的边界条件如下:
| $ \left. \begin{array}{l} {\theta ^{\prime \prime }}(t) = \frac{{\rho {c_1}{c_2}{{\hat u}_r} + 2{c_1}{{\hat S}_r}}}{{\left( {\lambda + \frac{2}{3}\mu } \right)\left( {{c_2} - {c_1}} \right)}}\\ e_r^{\prime \prime }(t) = \frac{{\rho {c_1}{c_2}{{\hat u}_r} + \left( {{c_1} + {c_2}} \right){{\hat S}_r}}}{{2\mu \left( {{c_1} - {c_2}} \right)}}\\ e_\varphi ^{\prime \prime }(t) = \frac{1}{{2\mu }}\left( {\rho {c_2}{{\hat u}_\varphi } + {{\hat S}_\varphi } + \frac{{\rho {c_1}c_2^2{{\hat u}_r} + 2{c_1}{c_2}{{\hat S}_r}}}{{{c_1}\left( {{c_1} - {c_2}} \right)}}} \right) \end{array} \right\}。$ | (66) |
通过前文所述,只需要知道加载面上力和速度的初始条件,即可计算得到应力应变的值,应力的值只需将应变结果通过本构关系式(56)即可求得,以上内容即为应力波传播的完整过程。
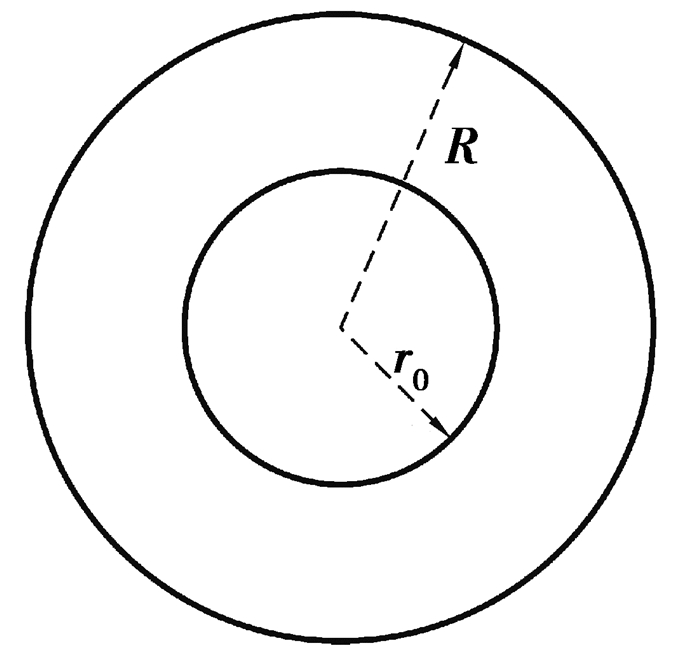
4 柱坐标系下的数值计算根据上面得到的修正的弹性应力波柱面波理论,对轴向无限长的空心圆柱结构进行应力波分析,其示意图如图 1所示,内径r0=5 mm,外径R=15 mm,切向角度为φ,轴向为z。由上文所述,轴向z和周向φ对应力波的传播不产生影响,只沿径向均匀膨胀,因此其简化如图 2所示,仅考虑径向对应力波传播的影响。即波动变量只是和r有关的函数。
|
图 2 柱面截面示意图 Fig. 2 Cylindrical cross- sectional schematic |
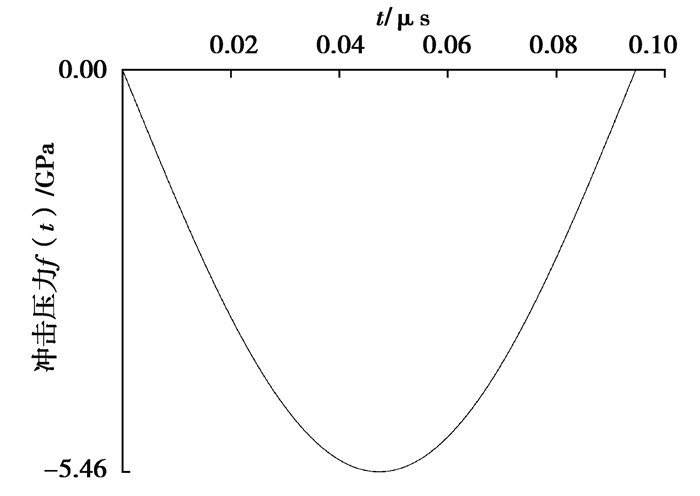
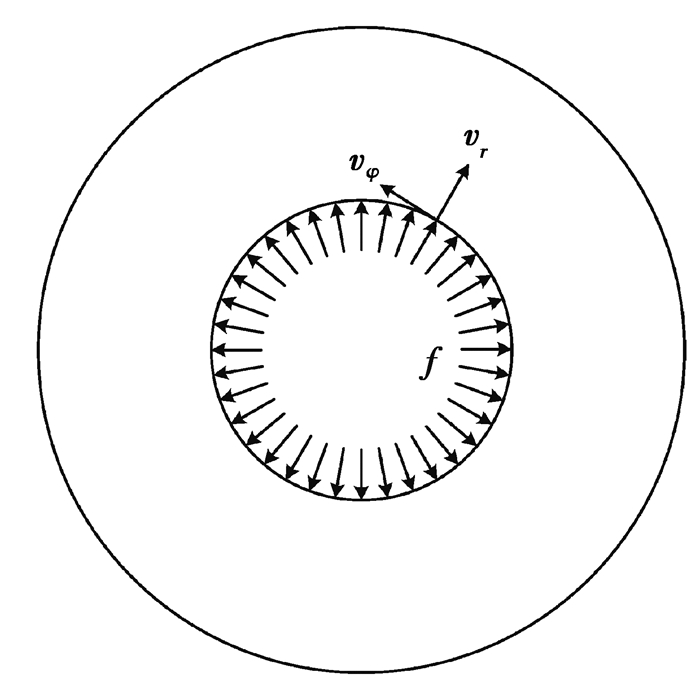
由弹性应力波求定解的边界条件式(58)可以得知,边界条件θ(0, t)、er(0, t)、eφ(0, t)和ez(0, t)(其中0位置表示加载面所在的位置)和加载面边界条件以及2019年6月25日试件材料参数相关。在数值求解过程中,试件的材料参数如表 1所示。由于偏斜应变的迹为零,所以是不相互独立的,因此速度边界条件只需要2个。加载面的边界条件如式(67)~(69)所示,其图像如图 3、4所示,加载面力和速度的加载方式如图 5所示。
| $ f(t) = \left\{ {\begin{array}{*{20}{l}} { - 5.46 \times {\rm{ \mathsf{ π} }}t \times {{10}^8}/9.466({\rm{GPa}})}&{0 \le t \le 9.466 \times {{10}^{ - 8}},}\\ 0&{t > 6.317 \times {{10}^{ - 8}}。} \end{array}} \right. $ | (67) |
| $ {v_r}(t) = \left\{ {\begin{array}{*{20}{l}} {190 \times {\rm{ \mathsf{ π} }}t \times {{10}^8}/9.466({\rm{m}}/{\rm{s}})}&{0 \le t \le 9.466 \times {{10}^{ - 8}},}\\ 0&{t > 9.466 \times {{10}^{ - 8}}。} \end{array}} \right. $ | (68) |
| $ {v_\varphi }(t) = \left\{ {\begin{array}{*{20}{l}} { - 23 \times {\rm{ \mathsf{ π} }}t \times {{10}^8}/9.466({\rm{m}}/{\rm{s}})}&{0 \le t \le 9.466 \times {{10}^{ - 8}},}\\ 0&{t > 9.466 \times {{10}^{ - 8}}。} \end{array}} \right. $ | (69) |
| 表 1 氧化铝陶瓷材料试件材料参数[28] Table 1 Alumina ceramic material test material parameters |

|
图 3 加载面速度边界条件 Fig. 3 Load face speed boundary conditions |
|
图 4 加载面力的边界条件 Fig. 4 Boundary conditions for loading face forces |
|
图 5 加载面加载方式示示意图 Fig. 5 How to load faces are loaded |
当加载面在空心圆柱内表面时,柱面波的波阵面沿半径方向向外传播,在到达自由面时,应力波发射入射、反射等界面效应。主波先到达自由面,自由面上没有应力状态,有速度所以令自由面速度为vr1(t),vφ1(t):
| $ {v_{r1}}(t) = \left\{ {\begin{array}{*{20}{l}} {137 \times {\rm{ \mathsf{ π} }}t \times {{10}^8}/9.466({\rm{m}}/{\rm{s}})}&{0 \le t \le 9.466 \times {{10}^{ - 8}},}\\ 0&{t > 9.466 \times {{10}^{ - 8}}。} \end{array}} \right. $ | (70) |
| $ {v_{\varphi 1}}(t) = \left\{ {\begin{array}{*{20}{l}} {16 \times {\rm{ \mathsf{ π} }}t \times {{10}^8}/9.466({\rm{m}}/{\rm{s}})}&{0 \le t \le 9.466 \times {{10}^{ - 8}},}\\ 0&{t > 9.466 \times {{10}^{ - 8}}。} \end{array}} \right. $ | (71) |
入射的主波在自由面发生反射之后会产生第一个主波和次波,主波仍然是体积波和形变波第一部分复合而成,并且随着波的传播,形变波分离成为两个脉冲,次波就是形变波第二部分独立形成,主波的波速为c1,次波波速为c2独立传播。入射的次波在自由面上也会发生反射产生第二个主波和次波,同样的主波是复合脉冲,即入射次波在自由面反射也有体积波和形变波产生,所以令次波在自由面反射时,自由面速度边界条件为vr2(t),vφ2(t):
| $ {v_{r2}}(t) = \left\{ {\begin{array}{*{20}{l}} {62 \times {\rm{ \mathsf{ π} }}t \times {{10}^8}/9.466({\rm{m}}/{\rm{s}})}&{0 \le t \le 9.466 \times {{10}^{ - 8}},}\\ 0&{t > 9.466 \times {{10}^{ - 8}}。} \end{array}} \right. $ | (72) |
| $ {v_{\varphi 2}}(t) = \left\{ {\begin{array}{*{20}{l}} { - 20 \times {\rm{ \mathsf{ π} }}t \times {{10}^8}/9.466({\rm{m}}/{\rm{s}})}&{0 \le t \le 9.466 \times {{10}^{ - 8}},}\\ 0&{t > 9.466 \times {{10}^{ - 8}}。} \end{array}} \right. $ | (73) |
图 6表示t=0.12 μs和t=0.96 μs复合脉冲中应变的情况,其中黑色线条表示体积波θ,体积波为压缩, 红色线条表示形变波应变在z方向的分量ez,它是拉伸脉冲。从图 6中可以发现,当t=0.12 μs的时候,形变波已经开始发生分离,经过一段时间后分成两个部分,第一部分传播的距离与体积波在相同时间传播的距离相同,说明它们的传播速度相同,都为c1,形变波第二部分传播的速度明显比复合脉冲传播速度慢,它以波速c2独立向前传播。形变波会有两部分的原因是存在2个波速,首先从波动方程出发,可以发现形变波的波动方程中含有体积应变,它是一个偏应变与体积应变复合在一起的弱耦合波动方程,而体积应变传播的波速为c1因此形变波的第一部分就从这里分离开来,当时间t=0.96 μs时,观察形变波的应变波形图,两部分的距离随着时间的推移越来越大,而形变波第一部分部分脉冲始终与体积波传播距离相同。图 7表示当时间t=0.96 μs时形变波在3个方向上分量的应变波形图,此时形变波的第一部分刚刚到达自由面。3个形变波的分量的第一部分在传播过程中始终与体积波复合在一起以相同的波速传播。从图 7中可以看出形变波在径向的分量er是压缩的,周向eφ和轴向ez则是拉伸的。在柱坐标下形变波的波动方程式(44)(45)中存在零阶项,所以图 7中er和eφ的存在残余,不过该残余的值很小对应力波的传播影响不大。而轴向ez的波动方程式(46)中没有零阶项的存在,所以其应变波形图完全分为两个部分,没有残余。由于结构中存在几何效应,在内表面加载过程中,随着半径尺度的增加,应力波应变的幅值不断变小。

|
图 6 t=0.12 μs和t=0.95 μs时θ和ez的波形图 Fig. 6 The waveform of the explosive θ and ez at t=0.12 μs and t=0.95 μs |

|
图 7 在t=0.95 μs时向外传播形变波3个分量er、eφ和ez的波形图 Fig. 7 The waveform of the explosive er, eφ and ez at t=0.95 μs |
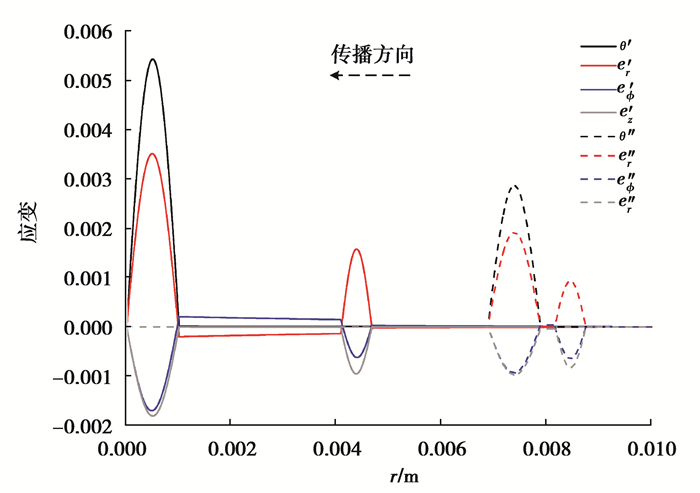
表示在t=1.9 μs时形变波第二部分形成的次波在自由面上的反射完成后产生第二个主波和次波的波形图如图 8所示。内表面加载产生的主波和次波在自由面上发生反射后,主波和次波都会产生新的主波和次波,因此如图 8所示,应力波在界面上发生一次完整的反射后,会产生4个脉冲。4个脉冲中有2个主波2个次波,2个主波都是复合脉冲,波速都为c1,2个次波都是形变波的第二部分,但是入射的脉冲不同波速都为c2。
|
图 8 完全反射后在t=1.9 μs时介质中形成4个向内传播脉冲波形图 Fig. 8 Four inward propagation pulse waveforms are formed in the medium at t=1.9 μs after full reflection |
总结了弹性应力波的发展演化,也提及了现有理论具有的一些缺陷。同时也给出了新的波动方程,并进行了求解。
通过有限差分法数值模拟了应变状态在无限长的空心圆柱体的演化过程,其中外载荷冲击到加载面时会产生两个波,分别是体积波与形变波。体积波和形变波的第一个波峰共同以波速c1前进直到与自由面接触反射形成两个波,形变波第二个波峰则以波速c2前进,并且在碰到自由面后也会产生2个反射波。
对高速冲击下材料中的动态应力应变时空演化规律进行了深入的理论探索研究。根据刘占芳课题组提出的修正的应力波理论[27],推导了柱坐标系下应力波的波动方程以及建立界面效应模型,对无限长空心圆筒内表面加载下结构中应力波的时空演化以及应力波在界面反射过程进行了数值分析,得到圆柱筒中主波与次波的时空演化关系,希望各位专家给予指正。
| [1] |
符力耘. 地震波探测地质构造复杂性的定量分析方法[J]. 中国科学(D辑:地球科学), 2009, 39(9): 1179-1190. FU Liyun. Quantitative assessment of the complexity of geological structures in terms of seismic propagators[J]. Science in China(Series D:Earth Sciences), 2009, 39(9): 1179-1190. (in Chinese) |
| [2] |
卢昌海. 时空的乐章:引力波百年漫谈(十)[J]. 现代物理知识, 2018, 30(4): 53-58. LU Changhai. The movement of time and space:the gravitational wave in the past 100 years (10)[J]. Modern Physics, 2018, 30(6): 30-36. (in Chinese) |
| [3] |
何卫忠, 樊宝珍. 声发射技术在发电设备检测中的应用[J]. 热力发电, 2006, 35(7): 73. HE Weizhong, FAN Baozhen. Application of acoustic emission technology in detection for power generation equipment[J]. Thermal Power Generation, 2006, 35(7): 73. (in Chinese) |
| [4] |
杜忠华.动能弹侵彻陶瓷复合装甲机理[D].南京: 南京理工大学, 2002. DU Zhonghua. Mechanics research on penetration of KE-projectile to ceramic composite amour[D]. Nanjing: Nanjjing University of Science and Technology, 2002. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10288-2003104675.htm |
| [5] |
朱建士, 陈裕泽. 核武器研制中的力学问题[J]. 力学与实践, 2002, 24(1): 67-71. ZHU Jianshi, CHEN Yuze. Mechanics in research and development of nuclear weapons[J]. Mechanics in Engineering, 2002, 24(1): 67-71. (in Chinese) DOI:10.3969/j.issn.1000-0879.2002.01.024 |
| [6] |
关克, 惠东. 弹药家族之四:穿甲弹:装甲的克星[J]. 现代军事, 2003(10): 59-61. GUAN Ke, HUI Dong. The ammunition family:armor-piercing projectile:armor nemesis[J]. Conmilit, 2003(10): 59-61. (in Chinese) |
| [7] |
姜鹏飞, 唐德高, 龙源. 不耦合装药爆破对硬岩应力场影响的数值分析[J]. 岩土力学, 2009, 30(1): 275-279. JIANG Pengfei, TANG Degao, LONG Yuan. Numerical analysis of influence of uncoupled explosive-charge structure on stress field in hard rocks[J]. Rock and Soil Mechanics, 2009, 30(1): 275-279. (in Chinese) DOI:10.3969/j.issn.1000-7598.2009.01.050 |
| [8] |
吴云鹏, 蔡忠军. 液体弹性波在医疗中的应用[J]. 力学学报, 1978, 10(2): 102-106, 171. WU Yunpeng, CAI Zhongjun. Application of liquid elastic wave in medical treatment[J]. Acta Mechanica Sinica, 1978, 10(2): 102-106, 171. (in Chinese) |
| [9] |
Yang C, Gao J, Wang H Y, et al. Effects of hypothalamus destruction on the level of plasma corticosterone after blast injury and its relation to interleukin-6 in rats[J]. Cytokine, 2011, 54(1): 29-35. DOI:10.1016/j.cyto.2010.12.011 |
| [10] |
Smith J E. The epidemiology of blast lung injury during recent military conflicts:a retrospective database review of cases presenting to deployed military hospitals, 2003-2009[J]. Philosophical Transactions of the Royal Society B:Biological Sciences, 2011, 366(1562): 291-294. DOI:10.1098/rstb.2010.0251 |
| [11] |
Cernak I. The importance of systemic response in the pathobiology of blast-induced neurotrauma[J]. Frontiers in Neurology, 2010, 1: 151. |
| [12] |
Adams S, Condrey J A, Tsai H W, et al. Respiratory responses following blast-induced traumatic brain injury in rats[J]. Respiratory Physiology & Neurobiology, 2014, 204: 112-119. |
| [13] |
Graff K F. Wave motion in elastic solids[M].[S.l.]: Ohio State University Press, 1975.
|
| [14] |
Meyers M A. Dynamic behavior of materials[M]. New York: A Wiley Interscience Publication, 1994.
|
| [15] |
Mindlin R D, Tiersten H F. Effects of couple-stresses in linear elasticity[J]. Archive for Rational Mechanics and Analysis, 1962, 11(1): 415-448. DOI:10.1007/BF00253946 |
| [16] |
Mindlin R D, Tiersten H F. Effects of couple-stresses in linear elasticity[J]. Archive for Rational Mechanics and Analysis, 1962, 11(1): 415-448. DOI:10.1007/BF00253946 |
| [17] |
Mindlin R D. Micro-structure in linear elasticity[J]. Archive for Rational Mechanics and Analysis, 1964, 16(1): 51-78. DOI:10.1007/BF00248490 |
| [18] |
Koiter W T. Couple-stresses in the theory of elasticity:Ⅰ and Ⅱ[J]. Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen, Series B, 1964, 67: 17-44. |
| [19] |
Fleck N A, Muller G M, Ashby M F, et al. Strain gradient plasticity:theory and experiment[J]. Acta Metallurgica et Materialia, 1994, 42(2): 475-487. DOI:10.1016/0956-7151(94)90502-9 |
| [20] |
Eringen A C. Linear theory of micropolar elasticity[J]. Journal of Mathematics and Mechanics, 1966, 15(6): 909-923. |
| [21] |
Eringen A C. Theory of micro polar elasticity[M]. New York and London: Mathematical Fundamentals, Academic Press, 1968.
|
| [22] |
Aifantis E C. Update on a class of gradient theories[J]. Mechanics of Materials, 2003, 35(3/4/5/6): 259-280. |
| [23] |
Georgiadis H G, Vardoulakis I, Lykotrafitis G. Torsional surface waves in a gradient-elastic half-space[J]. Wave Motion, 2000, 31(4): 333-348. DOI:10.1016/S0165-2125(99)00035-9 |
| [24] |
Georgiadis H G, Velgaki E G. High-frequency Rayleigh waves in materials with micro-structure and couple-stress effects[J]. International Journal of Solids and Structures, 2003, 40(10): 2501-2520. DOI:10.1016/S0020-7683(03)00054-4 |
| [25] |
Ottosen N S, Ristinmaa M, Ljung C. Rayleigh waves obtained by the indeterminate couple-stress theory[J]. European Journal of Mechanics-A, 2000, 19(6): 929-947. DOI:10.1016/S0997-7538(00)00201-1 |
| [26] |
Parfitt V R, Eringen A C. Reflection of plane waves from the flat boundary of a micropolar elastic half-space[J]. The Journal of the Acoustical Society of America, 1969, 45(5): 1258-1272. DOI:10.1121/1.1911598 |
| [27] |
刘占芳, 郭原, 唐少强, 等. 弹性应力波的双脉冲结构与平板冲击试验验证[J]. 应用数学和力学, 2018, 39(3): 249-265. LIU Zhanfang, GUO Yuan, TANG Shaoqiang, et al. Dual pulse wave structure of elastic stress waves and plate impact verification[J]. Applied Mathematics and Mechanics, 2018, 39(3): 249-265. (in Chinese) |
| [28] |
杜丘美.动态应力时空演化与结构冲击破坏模式的研究[D].重庆: 重庆大学, 2018. DU Qiumei. Study on temporal and spatial evolution of dynamic stress and corresponding failure modes[D]. Chongqing: Chongqing University, 2018. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10611-1018855506.htm |
 2020, Vol. 43
2020, Vol. 43


