2. 贵州民族大学 建筑工程学院, 贵阳 550025
2. School of Architecture and Engineering, Guizhou Minzu University, Guiyang 550025, P. R. China
湿球黑球温度WBGT(wet bulb globe temperature)起源于二十世纪五十年代,是一个考虑了代谢率的热环境评价指标。因为参数少,操作便利,它被认为是世界范围内用于热环境初步评估的友好工具之一[1]。该指数于1972年被美国国家职业安全与健康研究所(NIOSH)采用,之后又被国际标准体系ISO7243认证[2]。如今,美国政府工业卫生师协会(ACGIH)[3]、澳大利亚[4]和日本[5]等国也将WBGT作为公众的热量指标之一。在我国,《城市居住区热环境设计标准》JGJ 286—2013采用WBGT作为综合评价接触热环境时人体热负荷大小的指标[6],香港政府也采用改良的WBGT作为评估炎热环境安全性指标之一[7]。
WBGT指数是由自然湿球温度(tnw),黑球温度(tg)和空气温度(ta)三者加权组成,单位为℃。有直接太阳辐射时,加权系数为:0.7tnw +0.2tg +0.1ta;无直接太阳辐射,加权系数为:0.7tnw +0.3tg。该指数是依据人在微气候环境中感受的不同气候参数综合作用下的结果,其组成参数黑球温度(tg)是辐射热,温度和风的函数,而自然湿球温度(tnw)体现了湿度和风的冷却量,表征人体通过排汗降低身体温度的能力[8]。
WBGT在实际使用中存在局限。如在室外测试中,黑球温度和自然湿球温度测量要求较高:直径150 mm的标准黑球温度计需要放置20~30 min才能达到热平衡状态,且不同直径的黑球温度仪测量的结果也不同,有很大的偏差[2, 9]。自然湿球温度测试仪需要持续补充蒸馏水。这些测试仪器要时常维护和校准。又如在数值模拟中,直接得到WBGT结果的模拟软件很少,需要通过复杂的自定义函数才能计算出。鉴于此,现有研究中采用易于获取的气象参数建立数学模型计算WBGT的方法在实际应用中较为广泛。
笔者首先对采用气象参数计算WBGT的已有研究归类,分为热平衡法和经验法进行概述。发现简单可靠的经验法在实际应用中较为广泛,但是该方法不同地区统计的经验公式差异较大,然后使用低纬度高海拔山地城市贵阳市的实测WBGT数据对已有经验公式进行对比验证,最后通过贵阳实测的气温、相对湿度、太阳辐射、风和气压这5个常规气象参数与实测WBGT建立WBGT的简化计算公式。该公式适用于贵阳地区的城市热环境评价,我国低纬度高海拔地区使用WBGT的简化计算可参考该方法。
1 采用气象参数计算WBGT的方法概述现有的研究中,计算WBGT的数学模型主要分为两种方法:一种是基于理论的热平衡法,另一种是通过对实测数据处理分析的经验法。
1.1 热平衡法基于理论的热平衡法,把WBGT计算模型分为自然湿球温度和黑球温度2个独立的计算模型,每一个子模型都是根据传热和传质的原理迭代求解的。
ISO 7243(2017版)首次提供了从空气温度(ta)、平均辐射温度(tr)、相对湿度(RH)和空气速度(va)这4个参数预测WBGT的模型,见式(1)(2)。该标准强调了公式在空气流速低和自然对流的情况下不适用。
| $ \begin{array}{c} 4.18 v_{\mathrm{a}}^{0.444}\left(t_{\mathrm{a}}-t_{\mathrm{nw}}\right)+10^{-8}\left[\left(t_{\mathrm{r}}+273\right)^{4}-\left(t_{\mathrm{nw}}+273\right)^{4}\right]- \\ 77.1 v_{\mathrm{a}}^{0.421}\left[p_{\mathrm{as}}\left(t_{\mathrm{nw}}\right)-\mathrm{R} \mathrm{H} \cdot p_{\mathrm{as}}\left(t_{\mathrm{a}}\right)\right]=0。\end{array} $ | (1) |
平均辐射温度的计算公式为:
| $ t_{\mathrm{r}}=\left[\left(t_{\mathrm{g}}+273\right)^{4}+\frac{1.1 \times 10^{8} \times v_{\mathrm{a}}^{0.6}}{\varepsilon_{\mathrm{g}} \times d^{0.4}}\left(t_{\mathrm{g}}-t_{\mathrm{a}}\right)\right]^{1 / 4}-273, $ | (2) |
式中:tnw为自然湿球温度,℃;ta为空气温度,℃;tr为平均辐射温度,℃;va为空气速度,m/s;RH为相对湿度,%;Pas为饱和水蒸气压力,kPa;d为黑球直径,m;εg为平均发射率。
在稳态条件下,自然湿球温度(tnw)的理论计算公式(见式(1))需要进行迭代求解。该公式是以自然湿球温度计湿芯为对象建立热平衡方程。公式的第一部分代表对流换热量,第二部分代表辐射得热量,第三部分代表蒸发损失的热量。虽然ISO 7243推荐了通过理论公式预测WBGT的方法,但是该方法中平均辐射温度(tr)并不是常规的气象参数,需要通过黑球温度(tg)才能计算出(见式(2)),而黑球温度(tg)仍然需要测量。该方法依旧不能达到便捷准确的目的。在使用WBGT的60多年以来,还有很多学者致力于用常规气象参数计算WBGT的研究中。
2012年,学者Lemke等[10]对已发表的根据标准气象参数(空气温度、湿度、风速和太阳辐射4个参数)估算WBGT的方法进行实测评估,评估的方法有Dernedde和Gilbert(1991),Bernard和Pourmoghani(1999),Hunter和Minyard(2000),Tonouchi(2006),Liljegren以及Gaspar(2008年)和澳大利亚气象局ABM等学者和机构的研究,最后推荐Liljegren等[11]的方法计算室外WBGT。2013年学者Patel等[12]进一步论证了该方法的合理性,认为可以作为直接测量WBGT值的可接受替代方法。同年,Bernard等[13]通过实测也验证了该结论。但是,该方法计算复杂,需要建立自定义程序计算,除了标准的气象参数,还需要输入其他参数,如对流换热系数、净辐射通量、实际水蒸气压、反射率、发射率、太阳天顶角等,对于工科专业实用度不高。
1.2 经验法除了根据热平衡法推导的理论计算公式外,还有一类经验公式。其中,采用常规气象参数(气温、湿度、风速和太阳辐射)预测WBGT的公式,因为数据获取方便、可靠,应用广泛:
1) 澳大利亚气象局发表在官网的计算WBGT的公式[14]。该公式非常简单,只需要空气温度(ta)和水蒸气压力(ρ),但是它没有考虑太阳辐射和风速的影响。
| $ \begin{array}{c} \mathrm{WBGT}=0.567 t_{\mathrm{a}}+0.393 \rho+3.94, \end{array} $ | (3) |
| $ \rho=\mathrm{RH} / 100 \times 6.105 \exp \left(\frac{17.27 t_{\mathrm{a}}}{237.7+t_{\mathrm{a}}}\right)。$ | (4) |
2) 日本学者Ono等[15]通过统计分析日本6个地区2007—2009年的空气温度(ta),相对湿度(RH),太阳辐射(SR)和风速(v)4个气象参数,得到了WBGT估算方程,见式(5)。它可以应用于不同年份和偏差很小的不同城市。该公式估算出WBGT的偏差小于1.0 ℃,置信度为98.3%~99.8%。
| $ {\rm{ WBGT }} = 0.735{t_{\rm{a}}} + 0.0374{\rm{RH}} + 0.00292{t_{\rm{a}}}{\rm{RH}} + 7.619{\rm{SR}} - 4.557{\rm{S}}{{\rm{R}}^2} - 0.0572v - 4.064。$ | (5) |
3) 以色列学者Moran收集了以色列城市特拉维夫5—6月的数据[16],回归了WBGT的估算公式,见式(6)。
| $ \text { WBGT }=0.63 t_{\mathrm{a}}-0.03 \mathrm{RH}+0.002 \mathrm{SR}+0.0054\left(t_{\mathrm{a}} \times \mathrm{RH}\right)-0.073(0.1+\mathrm{SR})^{-1}。$ | (6) |
4)《城市居住区热环境设计标准》JGJ 286—2013规定的公式。该公式是张磊、孟庆林等学者在广州2007年7月采集的1 487组实测数据统计回归而成的。研究者认为在室外不稳定工况下,风速与自然湿球温度和黑球温度没有明显的相关性,因此WBGT的简化计算模型不包含风速参数。该公式的决定系数为R2=0.991,回归方程具有统计学意义[17]。
| $ \text { WBGT }=1.157 t_{\mathrm{a}}+17.425 \mathrm{RH}+2.407 \times 10^{-3} \mathrm{SR}-20.550。$ | (7) |
5) 中国天津学者蔡子颖、韩素芹等学者利用天津市边界层观测站2008年5—9月、2009年5—7月气象参数建立回归模型,得到了WBGT的统计方程(见式(8))。该方程的决定系数为0.757,通过显著性水平检验。研究者认为空气温度是WBGT变化的最主要原因[18]。
| $ \mathrm{WBGT}=1.0031 t_{\mathrm{a}}+0.021 \mathrm{RH}-0.083 v+0.002 \mathrm{SR}-2.822。$ | (8) |
从上述根据常规气象参数得到的WBGT经验公式可以看出,即使采用相同的气象参数,不同地区WBGT估算公式也不同。韩国学者Heo等[19]采用韩国的气象参数对澳大利亚气象局和日本学者Ono等[15]的公式进行对比验证。结果表明:与日本学者Ono等[15]的公式相比,澳大利亚气象局的公式会高估WBGT,偏差为3.076 ℃。最终采用了与韩国地理位置更接近的日本学者Ono等[15]的公式估算WBGT。可以看出,经验公式与地理位置的关系较大,因为经验公式是根据当地的测量值线性回归而成。在不同地区应用时,应该先对经验公式进行验证。
目前,已有的经验公式均属于常压地区,这些公式是否适用于低纬度高海拔地区值得探讨。低纬度高海拔地区,湿度高、气压低、云量多,太阳辐射少,而且水分蒸发量与常压地区不同,自然湿球温度中蒸发损失的热量也不同。因此,已有的室外WBGT简化公式是否适用,气压参数是否与WBGT相关以及对预测WBGT的影响度等,需要通过低纬度高海拔地区的实测数据进行验证。
2 低纬度高海拔地区WBGT测试仪器和方法选取低纬度高海拔地区典型城市贵阳市进行WBGT实测。贵阳市位于云贵高原东部,东经103°36′~109°31′,北纬24°37′~29°13′之间。全市海拔最高处为1 762 m,最低处为506 m,主城区平均海拔1 070 m。选取贵阳市3个行政区的高层居住区室外活动空间进行测点布置:点1位于花溪区,海拔1 096 m;点2位于观山湖区,海拔1 331 m;点3位于南明区,海拔1 077 m。此3点均位于贵阳市主要居住区内,对室外热环境具有代表性。实测时间为2018年8月11日—16日,测试时段为9:00—17:30,测试的内容包括:空气温度、相对湿度、风速、太阳辐射、大气压强和WBGT值。
实测仪器和采集间隔如表 1所示。仪器放置人体站立姿势的重心位置离地高度1.1 m处并按照ISO 7243(2017)的要求进行布置:天然湿球黑球温度测量仪放置在没有人工强制通风的环境中,保持仪器的湿芯暴露在空气温度、辐射、湿度和风的环境中并保证储存器中的蒸馏水水温不会因为环境辐射而升高。空气温度测量仪探头放置在直径10 cm的PVC桶中,桶外包铝箔,防止太阳辐射。同时桶内放置小风扇,保持桶内空气流通顺畅。室内黑球温度主要反映室内各个热源以及围护结构的长波辐射热作用,室外黑球温度主要反映太阳辐射、天空背景长波辐射、地面长波辐射以及周围建筑表面长波辐射等,因此,测量过程中要保证黑球温度测量仪不被其他仪器遮蔽。
| 表 1 实测仪器和数据采集时间 Table 1 Instrument and data acquisition time |
因仪器需要放置20 min以上才能达到热平衡状态,故有效数据采集的时间段为9:30—17:30。
3 实测数据分析贵阳市夏季雨热同期,雷阵雨暴雨频繁,测试中途如遇雷雨天等特殊情况下停止数据采集。为了避免其他因素对WBGT的影响,选取3个测点天气状况基本相同且同时间段(9:30—17:30)采集的有效数据进行分析。测点1有92组,测点2有95组,测点3有93组,共280组数据进行分析。
3.1 经验公式的比较验证为了验证已有的经验公式在低纬度高海拔地区的适用性,使用实测WBGT及气象数据与本文1.2节经验法所列的公式的计算结果进行逐一比较。由于WBGT为热安全指标,因此将实测数据分为2种时段进行验证,一种是白天的全部测量时段,为9:30—17:30;另一种时段采用白天WBGT数值较高的时段,为11:00—16:00。采用平均绝对误差EMAE和平均相对误差EMRE两个指标来对比各个经验公式的结果,EMAE和EMRE的计算公式如下:
| $ \begin{array}{l} {E_{{\rm{MAE}}}} = \left( {\sum\limits_{i = 1}^n {\left| {{\rm{WBG}}{{\rm{T}}_{实测}} - {\rm{WBG}}{{\rm{T}}_{计算}}} \right|} } \right)/n, \\ {E_{{\rm{MRE}}}} = \frac{1}{n}\sum\limits_{i = 1}^n {\frac{{\left. {\left| {{\rm{WBG}}{{\rm{T}}_{实测}} - {\rm{WBG}}{{\rm{T}}_{计算}}} \right|} \right)}}{{{\rm{WBG}}{{\rm{T}}_{实测}}}}} , \end{array} $ |
式中:WBGT实测为贵阳市实测WBGT值;WBGT计算为经验公式计算值;n为样本量。
从表 2中可以看到,相同的贵阳市实测气象参数参与不同地区的经验公式计算后,与实测值有一定的差距。实测WBGT最大值为32.5 ℃,只有澳大利亚和天津地区模型计算结果接近,但是天津地区模型白天11:00—16:00时段的平均相对误差大于白天9:30—17:30时段的误差。其他地区WBGT模型预测值偏小,尤其以广州的模型预测值与实际值的偏差最大,如采用此公式会严重低估室外热环境。根据白天时段平均相对误差,按从小到大排列为:澳大利亚<天津<以色列<日本<广州,可以看出预测精度与两地地理位置的接近程度无明显相关,采用澳大利亚模型预测贵阳的WBGT比广州的模型更接近。与其他地区模型相比,唯有澳大利亚模型中考虑了水蒸气压力,该参数是一个与海拔高度有关的量,其随海拔高度的增加而下降且下降比例比空气压力的比例大。因此,对于高海拔地区,考虑与海拔高度相关的参数,可以减少计算值与实测值的误差。
| 表 2 实测WBGT值与各地经验公式的比较 Table 2 Comparison of measured values with various WBGT empirical methods |
上述公式的平均相对误差仍然较高,需要根据贵阳实测的WBGT和气象参数,建立适用于该地区的WBGT简化计算公式,该方法可以应用于低纬度高海拔地区。
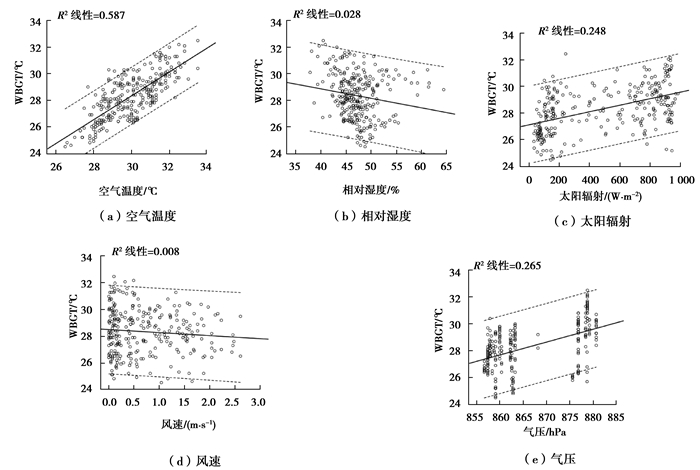
3.2 相关性分析为了得到WBGT的简化计算公式,首先需要对实测数据进行多元回归线性统计分析,回归之前,先要判断空气温度、相对湿度、太阳辐射、风速、气压与实测WBGT的相关性。通过散点图进行初步判断,如图 1所示。
|
图 1 空气温度、相对湿度、太阳辐射、风速、气压对WBGT的散点图 Fig. 1 Scatter plots between(a) air temperature, (b) relative humidity, (c) solar radiation, (d) wind speed, (e) air pressure and WBGT |
图 1中间粗实线是回归线,回归线两侧虚线是总体均数为95%的置信区间。从图中可以初步判断WBGT与空气温度、太阳辐射和气压存在正相关,与相对湿度存在负相关且相关性较弱,与风速的相关性较差。进一步采用Pearson相关系数明确相关性的存在性及其程度大小[20],见表 3。
| 表 3 空气温度、相对湿度、太阳辐射、风速、气压与WBGT的Pearson相关系数 Table 3 The Pearson correlation coefficients between air temperature, relative humidity, solar radiation, wind speed, air pressure and WBGT |
表 3中风速显著性水平p为0.134, 大于0.05,可以显著的接受相关系数为0的原假设。为了排除不同风速度大小与WBGT的相关性,根据实测数据,将风速分为小于1 m/s,1~2 m/s和2~2.61 m/s三组,分别进行Pearson相关性检验,三组的显著性水平p分别为:0.836,0.571和0.982, 均远远大于0.05,因此,可以显著的接受风速和WBGT的相关系数为0的原假设。故在后续的多元回归中不计入风速参数。这与张磊等[17]在广州地区的研究一致,同时天津气象科学研究所蔡子颖等[18]也认为风速对WBGT的影响较小,风速变化1%,WBGT值仅变化0.013%,而该研究采用的数据是气象站空旷场地10 m高的风速,如若换算为城市区域1.5 m高处的风速,风速会变低影响度将更小。在实际室外环境测试中,风速的变化十分复杂,难以测量。这也是在不稳定的室外工况下,实测的风速与自然湿球温度和黑球温度没有明显相关性的原因。
表 3中,气压与WBGT存在线性相关(p < 0.05),可以考虑纳入回归模型中。根据Pearson相关系数,4个常用气象参数相关性由高到低排序为:空气温度>气压>太阳辐射>相对湿度。
3.3 分层回归分析为了分析加入气压参数是否可以提高空气温度、太阳辐射和相对湿度对WBGT预测水平,本研究采用分层回归法,模型满足正态性、无偏性、同方差性和独立性假设,具体的回归统计信息和结果见表 4和表 5。
| 表 4 分层回归模型的统计信息 Table 4 Statistical information for hierarchical regression models |
| 表 5 回归系数及模型的假设检验 Table 5 Regression coefficient and hypothesis test |
最终模型(模型2)纳入空气温度、太阳辐射、相对湿度和气压4个变量,R2=0.797,F=268.559(p<0.001),调整R2=0.794,回归模型具有统计学意义。相比减少气压变量,只有的空气温度、太阳辐射、相对湿度3个变量的初始模型(模型1),调整R2值增加0.051,提示回归中加入气压参数后,自变量对因变量变异的解释能力增加5.1%(p < 0.001),即纳入气压变量对WBGT的预测改善有统计学意义。
采用空气温度、太阳辐射、相对湿度和气压4个参数回归WBGT的简化计算方程为:
| $ {\rm{WBGT}} = - 43.059 + 0.857{t_{\rm{a}}} + 0.064{\rm{RH}} + 0.001{\rm{SR}} + 0.048{P_{\rm{a}}}。$ | (9) |
标准化回归方程为:
| $ \mathrm{WBGT}=0.728 t_{\mathrm{a}}^{*}+0.15 \mathrm{RH}^{*}+0.262 \mathrm{SR}^{*}+0.26 P_{\mathrm{a}}^{*}。$ | (10) |
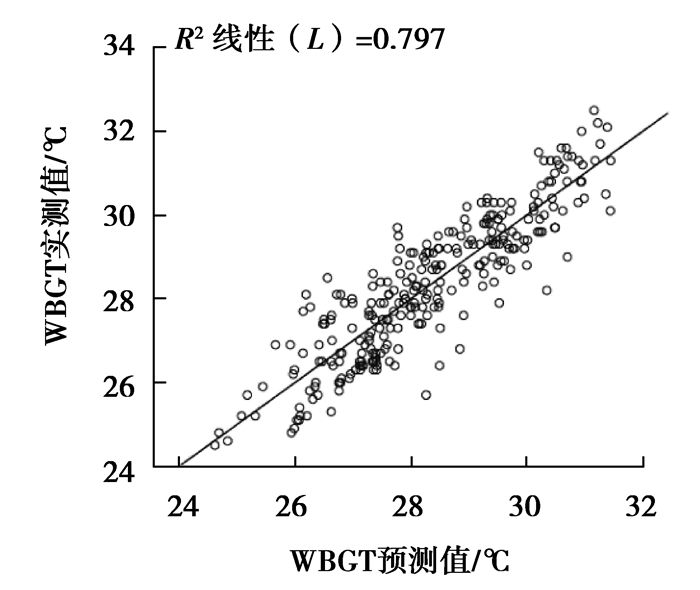
图 2为WBGT预测值和实测值的关系图,从图中可以看出所有的散点分布在对角线附近,实测WBGT与预测WBGT两条线的接近程度比较高,拟合的效果比较好,测量时段内两者残差绝对值不超过2.14 ℃,平均绝对误差为0.77 ℃,平均相对误差为2.69%,低于表 2中其他地区模型计算误差。因此,可以将WBGT的简化计算用于室外热环境预测和设计中。
|
图 2 WBGT实测值与预测值关系图 Fig. 2 Relations of WBGT measured and predicted values |
通过标准化回归系数(见表 5)可以看出,对因变量WBGT影响由大到小的自变量排序为:空气温度(0.728)>太阳辐射(0.262)>气压(0.260)>相对湿度(0.150)。
因此,气压参数不仅可以提高常规参数(空气温度、太阳辐射、相对湿度)预测WBGT的拟合度,而且对预测WBGT的影响也较大。在高海拔地区的WBGT计算模型中,气压是一个很重要的参数。
此外,就对因变量WBGT影响由大到小的自变量(除气压外)排序而言,贵阳WBGT预测模型与天津WBGT预测模型[18]相同为:空气温度>太阳辐射>相对湿度,而广州WBGT预测模型[17]影响度的排序为空气温度>相对湿度>太阳辐射,这也是表 2中天津WBGT模型平均相对误差小而广州的平均相对误差大的原因之一。
4 结论热环境评价指标WBGT已经使用了60多年,许多学者都致力于如何简便高效使用WBGT的研究中,其中以气象参数计算WBGT的研究居多,主要分为热平衡法和经验法两大类。采用热平衡法建立的数学模型,不仅计算参数多而且限制较多,如在空气流速低、高湿度和自然对流的情况下不适用等。这些条件一方面限制了实际的应用范围,一方面说明了稳态的热平衡方程难以描述动态的热平衡状态。采用经验法得到的WBGT简化计算模型是一个与地理位置有关的数学模型。通过使用在低纬度高海拔城市贵阳市实测WBGT值和气象参数对不同经验法公式进行验证,表明预测精度与两地地理位置的接近程度无明显相关,在不同地区应用经验法计算公式时,需要先对公式进行验证。
通过在低纬度高海拔城市贵阳市实测WBGT值与空气温度、相对湿度、太阳辐射、风速、气压的相关性分析和回归分析表明:风速与WBGT相关性差;气压与WBGT的相关度较高,仅次于空气温度;增加气压可以提高空气温度、相对湿度、太阳辐射对WBGT的预测水平。因此,建立了基于常规气象要素(空气温度、相对湿度、太阳辐射和气压)的WBGT简化计算方法。气压对WBGT回归模型结果影响结果较大,与太阳辐射的影响度基本相同,位于空气温度之后相对湿度之前。建议高海拔低气压地区采用常规气象参数预测WBGT时加入气压参数来提高预测的准确度。
| [1] |
Alfano F R D A, Palella B I, Riccio G. On the problems related to natural wet bulb temperature indirect evaluation for the assessment of hot thermal environments by means of WBGT[J]. Annals of occupational hygiene, 2012, 56(9): 1063-1079. |
| [2] |
Ergonomics of the thermal environment. Assessment of heat stress using the WBGT (wet bulb globe temperature) index: ISO 7243: 2017[S/OL].[2019-07-20]. https://doi.org/10.3403/30311329U.
|
| [3] |
ACGIH. TLV for heat stress and strain in threshold limit values for chemical substances and physical agents & biological exposure indices[S]. Cincinnati, USA: ACGIH, 2016.
|
| [4] |
Bureau of Meteorology of Australian Government. Heatwave Assessments[EB/OL].[2019-08-22]. http://www.bom.gov.au/australia/heatwave/index.shtml.
|
| [5] |
Japanese Ministry of the Environment. Heat illness prevention information[EB/OL].[2019-08-22]. http://www.wbgt.env.go.jp/en/.
|
| [6] |
中华人民共和国住房和城乡建设部.城市居住区热环境设计标准非书资料: JGJ 286-2013[S].北京: 中国建筑工业出版社, 2013. Ministry of Housing and Urban-Rural Construction of the People's Republic of China. Design standard for thermal environment of urban residential areas JGJ 286-2013[S]. Beijing: China Architecture & Building Press, 2013. (in Chinese) |
| [7] |
Lee K L, Chan Y H, Lee T C, et al. The development of the Hong Kong Heat Index for enhancing the heat stress information service of the Hong Kong Observatory[J]. International Journal of Biometeorology, 2016, 60(7): 1029-1039. DOI:10.1007/s00484-015-1094-7 |
| [8] |
Budd G M. Wet-bulb globe temperature (WBGT):its history and its limitations[J]. Journal of Science and Medicine in Sport, 2008, 11(1): 20-32. |
| [9] |
d'Ambrosio Alfano F R, Malchaire J, Palella B I, et al. WBGT index revisited after 60 years of use[J]. Annals of Occupational Hygiene, 2014, 58(8): 955-970. |
| [10] |
Lemke B, Kjellstrom T. Calculating workplace WBGT from meteorological data:a tool for climate change assessment[J]. Industrial Health, 2012, 50(4): 267-278. DOI:10.2486/indhealth.MS1352 |
| [11] |
Liljegren J C, Carhart R A, Lawday P, et al. Modeling the wet bulb globe temperature using standard meteorological measurements[J]. Journal of Occupational and Environmental Hygiene, 2008, 5(10): 645-655. DOI:10.1080/15459620802310770 |
| [12] |
Patel T, Mullen S P, Santee W R. Comparison of methods for estimating wet-bulb globe temperature index from standard meteorological measurements[J]. Military Medicine, 2013, 178(8): 926-933. DOI:10.7205/MILMED-D-13-00117 |
| [13] |
Bernard T E, Barrow C A. Empirical approach to outdoor WBGT from meteorological data and performance of two different instrument designs[J]. Industrial Health, 2013, 51(1): 79-85. DOI:10.2486/indhealth.2012-0160 |
| [14] |
Bureau of Meteorology of Australian Government. Thermal comfort observations[EB/OL].[2019-08-31]. http://www.bom.gov.au/info/thermal_stress/.
|
| [15] |
Ono M, Tonouchi M. Estimation of wet-bulb globe temperature using generally measured meteorological indices[J]. Japanese Journal of Biometeorology, 2014, 50: 147-157. |
| [16] |
麦金太尔D A.室内气候[M].龙惟定, 等, 译.上海: 上海科学技术出版社, 1988. McIntyre D A. Indoor climate[M]. LONG Weiding, et al. trans. Shanghai: Shanghai Scientific and Technical Publishers, 1988. (in Chinese) |
| [17] |
张磊, 孟庆林, 赵立华, 等. 室外热环境评价指标湿球黑球温度简化计算方法[J]. 重庆建筑大学学报, 2008, 30(5): 108-111, 117. ZHANG Lei, MENG Qinglin, ZHAO Lihua, et al. A simplified method to calculate the wet bulb globe temperature[J]. Journal of Chongqing Jianzhu University, 2008, 30(5): 108-111, 117. (in Chinese) |
| [18] |
蔡子颖, 韩素芹, 张长春, 等. 室外热环境指标的简化计算和应用研究[J]. 气象, 2011, 37(6): 701-706. CAI Ziying, HAN Suqin, ZHANG Changchun, et al. Simplified method to calculate outer thermal environment index and its application[J]. Meteorological Monthly, 2011, 37(6): 701-706. (in Chinese) |
| [19] |
Heo S, Bell M L, Lee J T. Comparison of health risks by heat wave definition:applicability of wet-bulb globe temperature for heat wave criteria[J]. Environmental Research, 2019, 168: 158-170. DOI:10.1016/j.envres.2018.09.032 |
| [20] |
薛薇. 统计分析与SPSS的应用[M]. 第五版. 北京: 中国人民教育出版社, 2017. XUE Wei. Statistical analysis and application of SPSS[M]. 5th edition. Beijing: People's Education Press, 2017. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43


