薄壁箱梁因其有利的受力特性而被广泛地应用于现代桥梁工程中。薄壁箱梁发生竖向挠曲变形时,由于腹板传递给翼缘板的剪力流使翼缘板在远离腹板处的纵向位移滞后于靠近腹板处的纵向位移,从而使箱梁翼缘板不满足平截面假设,这一现象被称为“剪力滞效应”[1]。
国内外对剪力滞的研究成果较为丰富,在近几年对剪力滞效应的研究主要为:①基于最小势能原理的变分法研究[2-4];②基于剪切变形规律的有限梁段法[5-6];③对剪力滞效应进行模型试验研究[7-8]。在变分法求解剪力滞问题中,翘曲位移函数的选取尤为重要。最早Reissner[9]假设翼缘板的纵向位移为二次抛物线形式,之后不同学者假设三次抛物线[10]、高次抛物线[11-13]、正余弦曲线及不同翘曲位移函数对剪力滞效应的影响[14]。但翘曲位移函数是根据翼缘板纵向实际变形假设来选取。在此之后周茂定等[15]从截面竖向剪力流方面入手,推导翘曲位移函数为2次抛物线,李夏元等[16]引入顶板悬臂板纵向翘曲位移差函数修正系数及内力平衡因子研究箱梁的应力和位移。
综上所述,目前对于剪力滞翘曲位移函数模式的理论分析主要从剪力流角度入手,分析较为复杂,对于其他方法推导剪力滞翘曲位移函数模式研究较少。笔者将翼缘板合理地简化为纵向平行的具有一定刚度的弹簧连接的弹性体,根据最小势能原理,采用能量变分原理推导出翼缘板的纵向位移函数形式,并将推导出的3种翘曲位移函数形式带入剪力滞变分方程中与实测值、实体有限元计算值进行对比分析,对剪力滞翘曲位移模式的选取做出了更合理表达与解释,且计算过程更加简便。
1 基于能量变分原理推导剪力滞翘曲位移函数 1.1 建立翼缘板弹簧模型在剪力滞效应影响下翼缘板的纵向变形由于剪力传递滞后而出现不一致,这种剪切变形不一致可视为翼缘板受到不均匀压缩或拉伸,其变形形式可以视为平行的弹簧产生不均匀的压缩或拉伸。当不考虑剪力滞效应时,在外力作用下弹簧将一致拉伸或压缩,即翼缘板发生均匀的纵向变形;而考虑剪力滞效应时,在外力作用下弹簧的拉伸或压缩不一致,导致翼缘板发生纵向不均匀变形。翼缘板等效成弹簧组成的弹性体如图 1所示。
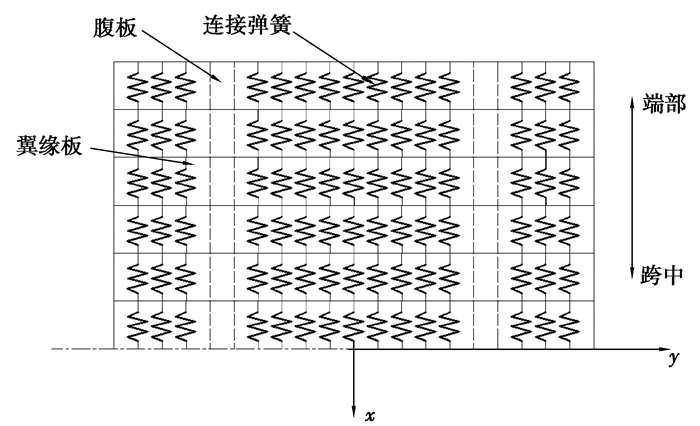
|
图 1 等效弹簧后的翼缘板 Fig. 1 Flange plate behind equivalent spring |
在竖向弯曲荷载下,腹板应力一般符合平截面假定,而箱梁各翼板剪切变形将引起纵向正应力沿翼板宽度分布不均匀,其纵向位移是由纵向剪力在传递过程中引起的,一般认为翼缘板产生的剪切转角的最大差值按照某一函数进行分布,该函数便是翘曲位移函数。在荷载作用下,由于纵向剪力在从腹板向翼缘板传递过程中发生损失,且腹板结合处刚度较大,腹板附近的翼缘板处承受了更多的变形,而远离腹板的翼板边缘承受了相对较少的变形。考虑剪力滞效应时,在顺桥向某一截面任一点的纵向位移均移动相同的距离,其纵向位移如图 2中虚线所示,仍然为一条平行于y轴的直线,明显与实际纵向变形不符。在荷载作用下腹板结合处的翼缘板向x方向的位移值大于远离腹板的翼缘板位移值,为了将翼缘板不均匀变形进行合理分配,假设翼板的翘曲位移曲线如图 2所示。
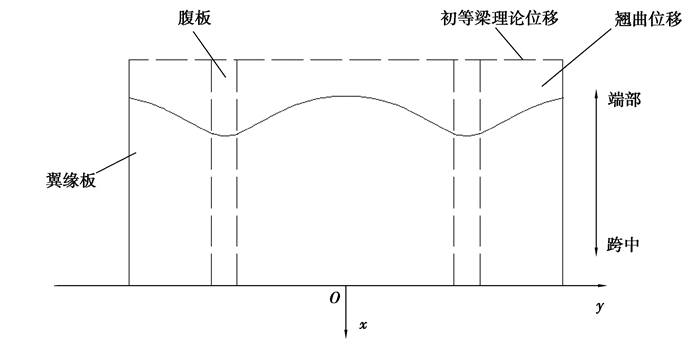
|
图 2 荷载作用下翼缘板纵向位移示意图 Fig. 2 Diagram of longitudinal displacement of flange plate under load |
为了验证翘曲位移函数的线形,以文献[17]中的有机玻璃简支试验梁为算例,建立有限元FEA(finite element analysis)模型,计算简支箱梁上翼缘板某一截面的纵向位移。取距离梁端90 mm处上翼缘板截面的纵向位移如图 3所示。

|
图 3 距离梁端90 mm处上翼缘板截面的纵向位移 Fig. 3 Longitudinal displacement of upper flange plate section at 90 mm from Beam end |
从图 3可知,远离腹板的翼缘板纵向位移明显滞后于腹板结合处的翼缘板位移,其翼缘板的整体纵向位移线形与图 2中的线形变化规律相同,说明纵向翘曲位移函数线形假设的正确性。
1.3 建立翼缘板平衡微分方程由于翼缘板简化为多根纵向平行的弹簧,其连接形式为并联,根据弹簧串并联原理,可知整个翼缘板的总弹性势能能等各个弹簧的弹性势能之和。以简化后翼缘板的一根弹簧进行分析,在整个坐标轴中积分便可得到翼缘板总弹性势能。当翼缘板截面发生纵向位移时,外力为假设弹簧的弹力。箱梁截面尺寸如图 4所示,箱形截面取单位长度范围内的翼缘板进行分析。
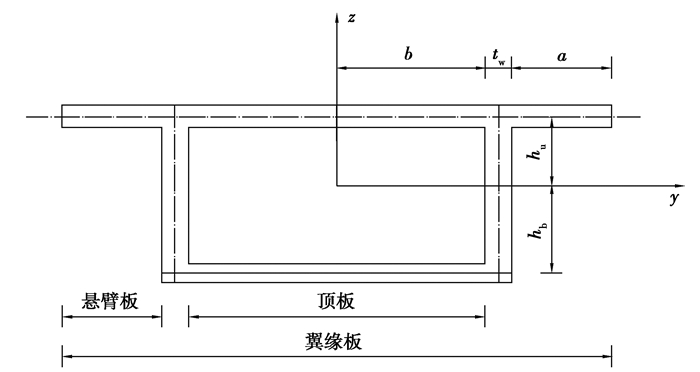
|
图 4 箱梁截面尺寸 Fig. 4 Section size of box girder |
| $ \bar W = - \frac{1}{2}\int E \alpha {(y)^2}{\rm{d}}s, $ | (1) |
式中:α(y)为翼缘板的纵向位移函数;E为混凝土弹性模量;ds为顶板或底板的微分面积,假设顶板及底板厚度为单位1,则式(1)等价于
| $ \bar W = - \frac{1}{2}\int E \alpha {(y)^2}{\rm{d}}y。$ | (2) |
| $ \bar V = \frac{1}{2}\int E {I_{\rm{d}}}{\left( {\alpha {{(y)}^{\prime \prime }}} \right)^2}{\rm{d}}y $ | (3) |
式中,Id为简化后单个翼缘板截面的惯性矩。
根据式(2)和式(3)计算翼缘板顶板的总势能
| $ \bar \Pi = \bar W + \bar V = - \frac{1}{2}\int E \alpha {(y)^2}{\rm{d}}y + \frac{1}{2}\int E {I_{\rm{d}}}{\left( {\alpha {{(y)}^{\prime \prime }}} \right)^2}{\rm{d}}y。$ | (4) |
对式(4)变分,令
| $ \left. {\begin{array}{*{20}{l}} { - E\alpha + E{I_{\rm{d}}}{\alpha ^{\prime \prime \prime \prime }} = 0}\\ {\left. {E{I_{\rm{d}}}{\alpha ^{\prime \prime }}\delta {y^\prime }} \right|_{ - b}^b = 0}\\ { - \left. {E{I_{\rm{d}}}{\alpha ^{\prime \prime \prime }}\delta y} \right|_{ - b}^b = 0} \end{array}} \right\} $ | (5) |
式中,b为箱室净宽的一半。
对式(5)进行求解,得到第一项的通解为
| $ \alpha (y) = {C_1}{{\rm{e}}^{\lambda y}} + {C_2}{{\rm{e}}^{ - \lambda y}} + {C_3}\cos \lambda y + {C_4}\sin \lambda y, $ | (6) |
式中,
因为化简后的翼缘板与腹板处可视为固定连接,不存在任意移动的δy和δy′,因此,式(5)中后2个边界条件始终满足。根据式(6)可知,翼缘板翘曲位移函数为双曲函数、三角函数的线性组合。在[0,b]范围内,翼缘板剪切转角的最大差值将按照式(6)中双曲函数、三角函数的线形组合进行分配。
在式(6)中前2项可以转化成双曲正弦函数与双曲余弦函数,其中双曲正弦函数与通常采用的三次抛物线性质较为相同,但比三次抛物线更加平缓,也更加符合翼缘板的纵向位移形式,且研究较少;双曲余弦函数与二次抛物线性质较为相同,且研究较少;余弦函数在诸多论文中被大量分析;正弦函数的一阶导数与抛物线、余弦函数及双曲函数同号,但是二阶导数与它们相反,目前诸多学者尚未进行研究。因此,研究选取双曲余弦函数、双曲正弦函数、正弦函数进行分析,其函数的线形也均符合图 2中纵向翘曲位移函数线形。
由于上述分析,在顶板中心处及腹板处翘曲位移函数的取值可以将上述3种函数进行如下假设:
① 双曲正弦函数
| $ \left\{ {\begin{array}{*{20}{l}} {\alpha (y) = 1 - \sin \mathit{h}\frac{{\ln (1 + \sqrt 2 )y}}{b},(顶板),}\\ {\alpha (y) = 1 - \sin \mathit{h}\frac{{\ln (1 + \sqrt 2 )y}}{a},(悬臂板),} \end{array}} \right. $ | (7) |
② 双曲余弦函数
| $ \left\{ {\begin{array}{*{20}{l}} {\alpha \{ y\} = 2 - \cos h \frac{{\ln (2 + \sqrt 3 )y}}{b},(顶板),}\\ {\alpha (y) = 2 - \cos h \frac{{\ln (2 + \sqrt 3 )y}}{a},\left( {悬臂板} \right),} \end{array}} \right. $ | (8) |
③ 正弦函数
| $ \left\{ {\begin{array}{*{20}{l}} {\alpha (y) = 1 - \sin \frac{{\pi y}}{{2b}},(顶板),}\\ {\alpha (y) = 1 - \sin \frac{{\pi y}}{{2a}},\left( {悬臂板} \right),} \end{array}} \right. $ | (9) |
式中:b为箱室净宽的一半;a为悬臂板的长度。
因为悬臂板与翼缘板两腹板间顶板的翘曲位移函数线形相同,则翼缘板的翘曲位移函数为
| $ u(x,y) = {h_i}\left\{ {\frac{{{\rm{d}}x}}{{{\rm{d}}x}} + [\alpha (y)]u(x)} \right\}, $ | (10) |
式中:w为梁竖向挠度;hi为上下翼缘板中心至截面形心距离。
2 箱梁剪力滞变分方程确定翼缘板翘曲位移函数后,将其代入剪力滞变分方程中,梁受到弯曲时的外力势能W为
| $ W = - \int M (x)\frac{{{{\rm{d}}^2}w}}{{{\rm{d}}{x^2}}}{\rm{d}}x, $ | (11) |
式中:w为梁纵向挠度。
腹板及上下翼板的应变能为
| $ \left. \begin{gathered} {V_{\text{w}}} = \frac{1}{2}\int E {I_{\text{w}}}{\left( {\frac{{{{\text{d}}^2}w}}{{{\text{d}}{x^2}}}} \right)^2}{\text{d}}x \hfill \\ {V_{{\text{su}}}} = \frac{1}{2}\iint {{t_{\text{u}}}}\left[ {E{{\left( {\frac{{\partial {u_u}(x,y)}}{{\partial x}}} \right)}^2} + G{{\left( {\frac{{\partial {u_u}(x,y)}}{{\partial y}}} \right)}^2}} \right]{\text{d}}x{\text{d}}y \hfill \\ {V_{{\text{sb}}}} = \frac{1}{2}\iint {{t_{\text{b}}}}\left[ {E{{\left( {\frac{{\partial {u_{\text{b}}}(x,y)}}{{\partial x}}} \right)}^2} + G{{\left( {\frac{{\partial {u_{\text{b}}}(x,y)}}{{\partial y}}} \right)}^2}} \right]{\text{d}}x{\text{d}}y \hfill \\ \end{gathered} \right\}, $ | (12) |
式中:Vw为腹板应变能;Vsu为上翼板应变能;Vsb为下翼板应变能;Iw为腹板抗弯惯性矩; tu为上翼缘板厚度;tb为下翼缘板厚度;G为剪切模量;E为弹性模量。
根据以上各部分的外力势能、应变能、计算体系总势能
| $ \begin{array}{*{20}{c}} {\Pi = - W + {V_{\rm{w}}} + {V_{{\rm{sb}}}} + {V_{{\rm{su}}}} = }\\ {\int M (x)\frac{{{{\rm{d}}^2}w}}{{{\rm{d}}{x^2}}}{\rm{d}}x + \frac{1}{2}\int E {I_{\rm{w}}}{{\left( {\frac{{{{\rm{d}}^2}w}}{{{\rm{d}}{x^2}}}} \right)}^2}{\rm{d}}x + }\\ {\frac{1}{2}{I_{\rm{s}}}\int {\left\{ {E\left[ {{{\left( {{w^{\prime \prime }}} \right)}^2} + A{w^{\prime \prime }}{u^\prime } + \frac{B}{2}{{\left( {{u^\prime }} \right)}^2}} \right] + \frac{{CG}}{{2{b^2}}}{u^2}} \right\}} {\rm{d}}x,} \end{array} $ | (13) |
式中:Is为上下翼板抗弯惯性矩之和;
① 对于双曲正弦函数:
| $ A = \frac{{2\ln (1 + \sqrt 2 ) + 2 - 2\cos \mathit{h}[\ln (1 + \sqrt 2 )]}}{{\ln (1 + \sqrt 2 )}},B = 1 + \frac{{\sin \mathit{h}[2\ln (1 + \sqrt 2 )] - 8\cos \mathit{h}[\ln (1 + \sqrt 2 )] + 8}}{{2\ln (1 + \sqrt 2 )}}, $ |
| $ C = \frac{{\ln (1 + \sqrt 2 )\{ \sin \mathit{h}2[\ln (1 + \sqrt 2 )] + 2\ln (1 + \sqrt 2 )\} }}{2}。$ |
② 对于双曲余弦函数:
| $ A = \frac{{4\ln (2 + \sqrt 3 ) - 2\sin \mathit{h}[\ln (2 + \sqrt 3 )]}}{{\ln (2 + \sqrt 3 )}},B = 9 + \frac{{\sin \mathit{h}[2\ln (2 + \sqrt 3 )] - 16\sin \mathit{h}[\ln (2 + \sqrt 3 )]}}{{2\ln (2 + \sqrt 3 )}}, $ |
| $ C = \frac{{\ln (2 + \sqrt 3 )\{ \sin \mathit{h}2[\ln (2 + \sqrt 3 )] - 2\ln (2 + \sqrt 3 )\} }}{2}。$ |
③ 对于正弦函数:
对式(13)进行变分,令
| $ \left. \begin{array}{l} EI{w^{\prime \prime }} + M(x) + \frac{1}{2}AE{I_s}{u^\prime } = 0\\ E{I_s}\left( { - \frac{B}{2}{u^{\prime \prime }} - \frac{A}{2}{w^{\prime \prime \prime }} + \frac{{CG}}{{2E{b^2}}}u} \right) = 0\\ \left. {E{I_s}\left( {\frac{A}{2}{w^{\prime \prime }} + \frac{B}{2}{u^\prime }} \right)\delta u} \right|_0^l \end{array} \right\}, $ | (14) |
式中,l为桥梁的计算跨径,并令
| $ \left. \begin{array}{l} k = \frac{1}{b}\sqrt {\frac{{GCn}}{E}} \\ n = \frac{1}{{B - \frac{{{A^2}{I_s}}}{{2I}}}} \end{array} \right\}。$ | (15) |
式(14)中3个方程组联立求解得到
| $ {u^{\prime \prime }} - {k^2}u = \frac{{AnQ(x)}}{{EI}}, $ | (16) |
式(16)的通解为
| $ u(x) = \frac{{An}}{{EI}}\left( {{C_1}{\rm{sh}}kx + {C_2}{\rm{ch}}kx + {u^*}} \right), $ | (17) |
式中:C1、C2为通解系数;u*为与方程右端相关的特解,由梁的边界条件确定。
由式(14)中的第一式可得:
| $ {w^{\prime \prime }} = - \left[ {\frac{{M(x)}}{{EI}} + \frac{{A{I_{\rm{s}}}}}{{2I}}{u^\prime }} \right]。$ | (18) |
综上可得,在考虑剪力滞效应之后的翼缘板弯曲正应力σx为
| $ {\sigma _x} = E\frac{{\partial u(x,y)}}{{\partial x}} = \pm E{h_i}\left\{ {\frac{{M(x)}}{{EI}} - \left[ {\alpha (y) - \frac{{A{I_{\rm{s}}}}}{{2I}}} \right]{u^\prime }} \right\}。$ | (19) |
式(19)中,
① 对于双曲正弦函数:
② 对于双曲余弦函数:
③ 对于正弦函数:
为了分析通过建立弹簧力学模型,并基于能量变分原理推导的翘曲位移函数形式的正确性,以文献[17]中的简支箱梁有机玻璃模型为算例,将采用研究方法计算的结果与实体有限元计算值、三次抛物线纵向位移函数计算结果和文献[17]中的实测值进行对比。材料弹性模量取E=3 000 MPa,泊松比为0.385,桥梁跨径l=0.8 m,板中面的应变取上、下测点的平均值。简支梁有机玻璃模型截面形式及荷载布置形式如图 5所示。
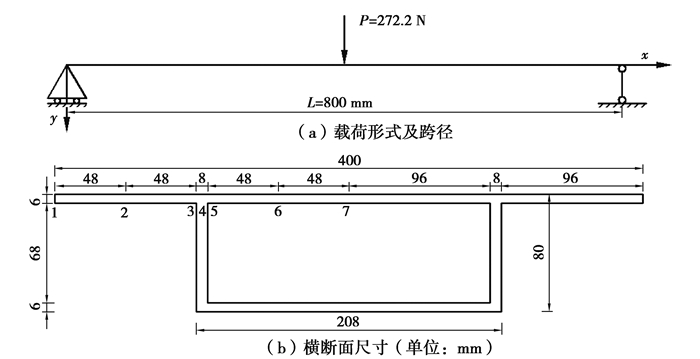
|
图 5 荷载布置、截面形式及测点 Fig. 5 Load layout, section form and measuring points |
采用实体有限元软件(FEA)建立实体模型,将上翼缘板划分为3 mm的四面体实体单元,腹板划分为边长3 mm的四面体实体单元,模型共划分153 765个单元,其简支箱梁跨中截面上翼缘正应力计算值如图 6所示。

|
图 6 实体有限元计算结果(单位:kPa) Fig. 6 Solid finite element calculation results(unit:kPa) |
将荷载作用在跨中截面,此时弯矩和剪力为分段函数,可表示为
| $ \begin{array}{l} \left. {\begin{array}{*{20}{l}} {M(x) = \frac{{Px}}{2}}\\ {Q(x) = \frac{P}{2}} \end{array}} \right\}\left( {0 \le x \le \frac{l}{2}} \right),\\ \left. {\begin{array}{*{20}{l}} {M(x) = \frac{{P(l - x)}}{2}}\\ {Q(x) = - \frac{P}{2}} \end{array}} \right\}\left( {\frac{l}{2} < x \le l} \right), \end{array} $ | (20) |
① 当
| $ {u_1} = \frac{{An}}{{EI}}P\left( {{C_1}{\rm{sh}}kx + {C_2}{\rm{ch}}kx - \frac{1}{{2{k^2}}}} \right), $ | (21) |
② 当
| $ {u_1} = \frac{{An}}{{EI}}P\left( {{C_3}{\rm{sh}}kx + {C_4}{\rm{ch}}kx + \frac{1}{{2{k^2}}}} \right), $ | (22) |
根据边界条件,
| $ \left. {\begin{array}{*{20}{l}} {{{\left. {u_1^\prime } \right|}_{x = 0}} = 0}\\ {{{\left. {u_2^\prime } \right|}_{x = l}} = 0}\\ {{u_1} = {{\left. {{u_2}} \right|}_{x = \frac{1}{2}}}}\\ {{{\left. {\left( {u_1^\prime + \frac{{AnM(x)}}{{EI}}} \right)} \right|}_{x = \frac{1}{2}}} = {{\left. {\left( {u_2^\prime + \frac{{AnM(x)}}{{EI}}} \right)} \right|}_{x = \frac{1}{2}}}} \end{array}} \right\}, $ | (23) |
由式(22)可计算出
| $ \left. {\begin{array}{*{20}{l}} {{C_1} = 0}\\ {{C_2} = \sin \mathit{h}\left( {\frac{{kl}}{2}} \right)/{k^2}\sin \mathit{h}(kl)}\\ {{C_3} = \sin \mathit{h}\left( {\frac{{kl}}{2}} \right)/{k^2}}\\ {{C_4} = - \sin \mathit{h}\left( {\frac{{kl}}{2}} \right) \cot \mathit{h}(kl)/{k^2}} \end{array}} \right\}, $ | (24) |
代入式(15)可得到
| $ \left. \begin{array}{l} {u_1} = \frac{{AnP}}{{EI{k^2}}}\left[ {\frac{{\sin h (kl/2)}}{{\sin h (kl)}}\cos h (kx) - \frac{1}{2}} \right]\\ {u_2} = \frac{{AnP}}{{EI{k^2}}}\left[ {\left( {\sin h \left( {\frac{{kl}}{2}} \right)\sin h (kx) - \sin h \left( {\frac{{kl}}{2}} \right) coth (kl)\cos h (kx) + \frac{1}{2}} \right]} \right. \end{array} \right\}, $ | (25) |
当
| $ {\sigma _x} = E\frac{{\partial u(x,y)}}{{\partial x}} = \pm \frac{{{h_i}}}{I}\left[ {M(x) - \frac{{AnP}}{k}\left( {\alpha ({\rm{y}}) - \frac{{A{I_s}}}{{2I}}} \right)\frac{{{\rm{sh}}\frac{{kl}}{2}}}{{{\rm{sh}}kl}}{\rm{sh}}kx} \right], $ | (26) |
当
| $ {\sigma _x} = E\frac{{\partial u(x,y)}}{{\partial x}} = \pm \frac{{{h_i}}}{I}\left[ {M(x) - \frac{{AnP}}{k}\left( {\alpha (y) - \frac{{A{I_s}}}{{2I}}} \right){\rm{sh}}\frac{{kl}}{2}{\rm{ch}}kx - \frac{{{\rm{sh}}\frac{{kl}}{2}}}{{{\rm{th}}kl}}{\rm{sh}}kx} \right]。$ | (27) |
式(26)和式(27)中αy、A、n、k与上述推导的不同翘曲函数有关,具体取值见式(7)和式(13)。
则简支箱梁顶板正应力值可按式(26)和式(27)计算得到。
简支箱梁有机玻璃模型的实测值、三次抛物线纵向位移函数所求出的数值引用文献[17]。
将研究采用的3种翘曲函数计算的跨中截面顶板正应力值与实体有限元计算结果、文献[17]的实测结果和三次抛物线纵向位移函数所求出的数值汇总如表 1所示。
| 表 1 简支箱梁跨中截面上翼缘板的应力(绝对值)比较 Table 1 Stress(absolute value)of flange plate on mid-span section of simply supported box girder |
将文中方法计算得到的跨中截面顶板正应力的绝对值与文献[17]的实测结果、三次抛物线纵向位移函数所求出的数值和实体有限元计算结果进行对比,如图 7所示。
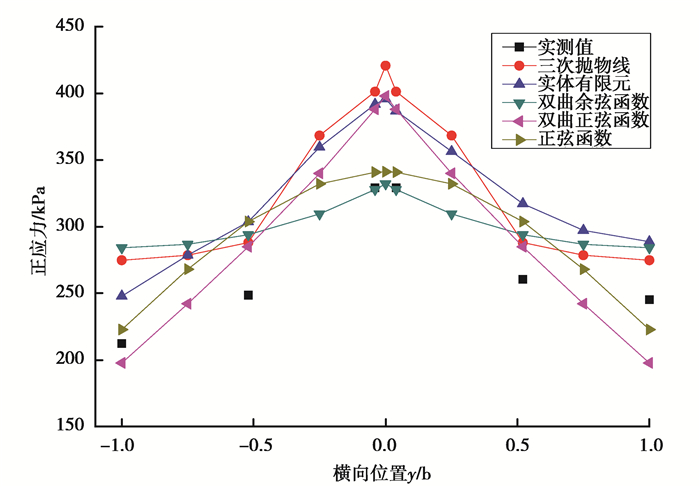
|
图 7 跨中截面顶板应力结果 Fig. 7 Top plate stress result at mid-span cross section |
根据表 1及图 7推导的翘曲位移函数形式中的3种单一函数形式进行分析,双曲余弦函数形式在远离腹板位置应力值与实测值相差较大,其值较大于实测值,在腹板结合附近翼板应力值与实测值吻合度较好,该情况与有限元计算值分布恰好相反;双曲正弦函数在悬臂板端部稍小于实测值,其他位置均较大于实测值,在腹板结合处应力值较大,与有限元计算值吻合度较好;正弦函数整体应力值与实测值吻合度较好,整体小于有限元计算值。
从函数形态角度进一步分析可知,抛物线形式二阶导数大于双曲函数、三角函数,因此其翼缘板应力计算值增幅较大,在腹板结合处存在应力突变点,远大于实测值;双曲余弦函数与二次抛物线性质相似,但增幅小于二次抛物线形式,因此应力值较小于二次抛物线形式;双曲余弦函数形式与三次抛物线性质相似,但增幅小于三次抛物线形式,因此应力值较小于三次抛物线形式;正弦函数二阶导数与抛物线、双曲函数符号相反,导致应力值从悬臂板端部向腹板结合处一定范围内增幅较大。
综上可知,推导出的翘曲位移函数采用的3种单一函数形式中,正弦函数形式计算的正应力分布与实测值吻合度较好,与有限元计算值也基本吻合,且与抛物线形式计算的应力值相比,也不会在翼板和腹板结合处出现应力突变情况。
4 结语1) 将翼缘板合理假设为由纵向平行的弹簧连接的弹性体,根据最小势能原理建立平衡微分方程。采用泛函分析方法计算推导出翼缘板的翘曲位移函数形式。
2) 将推导出的翘曲位移函数形式进行分析,并将选用的3种单一函数形式带入剪力滞变分方程中,得到以文中推导的3种函数形式作为翘曲位移函数的翼缘板应力值。将文中计算值与实测值、有限元计算值及三次抛物线作为翘曲位移函数的翼缘板正应力值进行比较分析,最终得到正弦函数作为翘曲位移函数更加合理。
3) 从函数形态角度进行分析,得到了不同函数的性质对翼缘板应力值分布规律的影响,对于翘曲位移函数的选取提供了一种更加直观、科学的思路。
4) 在推导过程中认为翼缘板简化的弹簧刚度均相同,这种假定与真实情况并不完全相符,在腹板与翼缘板结合处翼缘板刚度明显大于其他位置,若考虑此问题将使文中的研究结论更加合理。
| [1] |
张元海, 胡玉茹, 林丽霞. 基于修正翘曲位移模式的薄壁箱梁剪力滞效应分析[J]. 土木工程学报, 2015, 48(6): 44-50. ZHANG Yuanhai, HU Yuru, LIN Lixia. Analysis on shear lag effect of thin-walled box girders based on a modified warping displacement mode[J]. China Civil Engineering Journal, 2015, 48(6): 44-50. (in Chinese) |
| [2] |
Zhang Y H. Improved finite-segment method for analyzing shear lag effect in thin-walled box girders[J]. Journal of Structural Engineering, 2012, 138(10): 1279-1284. DOI:10.1061/(ASCE)ST.1943-541X.0000552 |
| [3] |
Zhou S J. Shear lag analysis in prestressed concrete box girders[J]. Journal of Bridge Engineering, 2011, 16(4): 500-512. DOI:10.1061/(ASCE)BE.1943-5592.0000179 |
| [4] |
Qin X X, Liu H B, Wang S J, et al. Symplectic analysis of the shear lag phenomenon in a T-beam[J]. Journal of Engineering Mechanics, 2015, 141(5): 04014157. DOI:10.1061/(ASCE)EM.1943-7889.0000882 |
| [5] |
周朋, 蔺鹏臻. 变截面连续箱梁剪力滞分析的有限梁段法[J]. 铁道科学与工程学报, 2018, 15(4): 948-955. ZHOU Peng, LIN Pengzhen. Finite segment method of shear lag analysis of continuous box girders with variable height[J]. Journal of Railway Science and Engineering, 2018, 15(4): 948-955. (in Chinese) DOI:10.3969/j.issn.1672-7029.2018.04.017 |
| [6] |
张元海, 李琳, 林丽霞, 等. 以附加挠度作为广义位移时薄壁箱梁剪力滞效应的梁段有限元分析[J]. 土木工程学报, 2013, 46(10): 100-107. ZHANG Yuanhai, LI Lin, LIN Lixia, et al. Beam-segment finite element analysis on shear lag effect of thin-walled box girder adopting additional deflection as generalized displacement[J]. China Civil Engineering Journal, 2013, 46(10): 100-107. (in Chinese) |
| [7] |
张玉红.薄壁箱梁剪力滞效应的理论分析与试验研究[D].兰州: 兰州交通大学, 2011. ZHANG Yuhong. The experimental study and theoretical analysis in shear lag effect on thin-walled box-girder[D]. Lanzhou: Lanzhou Jiaotong University, 2011.(in Chinese) |
| [8] |
祝明桥, 魏伏佳, 赵振中, 等. 双层均布荷载作用下混凝土伸臂箱梁剪力滞效应试验研究[J]. 公路交通科技, 2014, 31(8): 77-82. ZHU Mingqiao, WEI Fujia, ZHAO Zhenzhong, et al. Experimental research of shear lag effect of cantilever concrete box girder under double-deck uniform load[J]. Journal of Highway and Transportation Research and Development, 2014, 31(8): 77-82. (in Chinese) DOI:10.3969/j.issn.1002-0268.2014.08.014 |
| [9] |
Reissner E. On the problem of stress distribution in wide-flanged box-beams[J]. Journal of the Aeronautical Sciences, 1938, 5(8): 295-299. DOI:10.2514/8.634 |
| [10] |
Luo Q Z, Wu Y M, Li Q S, et al. A finite segment model for shear lag analysis[J]. Engineering Structures, 2004, 26(14): 2113-2124. DOI:10.1016/j.engstruct.2004.07.010 |
| [11] |
Ferradi M K, Cespedes X, Arquier M. A higher order beam finite element with warping eigenmodes[J]. Engineering Structures, 2013, 46: 748-762. DOI:10.1016/j.engstruct.2012.07.038 |
| [12] |
陈常松, 邓安. 高次位移函数时箱梁剪滞效应变分法解[J]. 重庆交通大学学报(自然科学版), 2009, 28(1): 5-7, 44. CHEN Changsong, DENG An. Variational solution of shear lag effect of box girder in high order displacement function[J]. Journal of Chongqing Jiaotong University(Natural Science), 2009, 28(1): 5-7, 44. (in Chinese) |
| [13] |
Lin Z B, Zhao J. Least-work solutions of flange normal stresses in thin-walled flexural members with high-order polynomial[J]. Engineering Structures, 2011, 33(10): 2754-2761. DOI:10.1016/j.engstruct.2011.05.022 |
| [14] |
肖军, 李小珍, 刘德军, 等. 一种剪滞翘曲位移函数的解析构造法[J]. 哈尔滨工业大学学报, 2017, 49(3): 162-167. XIAO Jun, LI Xiaozhen, LIU Dejun, et al. An analytical construction method of wraping displacement function of shear lag[J]. Journal of Harbin Institute of Technology, 2017, 49(3): 162-167. (in Chinese) |
| [15] |
周茂定, 李丽园, 张元海, 等. 薄壁箱梁的剪力滞翘曲位移函数研究[J]. 中国公路学报, 2015, 28(6): 67-73. ZHOU Maoding, LI Liyuan, ZHANG Yuanhai, et al. Research on shear-lag warping displacement function of thin-walled box girders[J]. China Journal of Highway and Transport, 2015, 28(6): 67-73. (in Chinese) DOI:10.3969/j.issn.1001-7372.2015.06.010 |
| [16] |
李夏元, 万水, 陈建兵, 等. 基于修正翘曲位移函数的薄壁箱梁剪力滞效应分析[J]. 东南大学学报(自然科学版), 2018, 48(5): 851-856. LI Xiayuan, WAN Shui, CHEN Jianbing, et al. Analysis on shear lag effect in thin-walled box girders based on modified warping displacement function[J]. Journal of Southeast University(Natural Science Edition), 2018, 48(5): 851-856. (in Chinese) |
| [17] |
康喜东.箱形梁剪力滞效应分析中的合理翘曲位移模式及其应用研究[D].兰州: 兰州交通大学, 2014. KANG Xidong. Study on reasonable warping displacement pattern and application in shear lag effect analysis of box girder[D]. Lanzhou: Lanzhou Jiaotong University, 2014.(in Chinese) |
 2020, Vol. 43
2020, Vol. 43


