2. 长江大学 "油气钻采工程"湖北省重点实验室, 武汉 430100;
3. 中石化江汉油田分公司石油工程技术研究院, 武汉 430035
2. Key Laboratory of "Oil & Gas Drilling Engineering" of Hubei, Yangtze University, Wuhan 430100, P. R. China;
3. Petroleum Engineering Technology Research Institute of Jianghan Oilfield Branch of SINOPEC Group, Wuhan 430035, P. R. China
2017年涪陵国家级页岩气示范区突破年产气量60亿方大关证明[1],水平井分段多级压裂改造工艺为实现页岩气商业开发提供了技术保障[2-3],可压性评价是选择压前“甜点”、实现有效改造的关键之一。传统的可压性评价往往采用弹性模量和泊松比计算岩石脆性[4],袁俊亮等[5]指出采用脆性表示可压性时需要考虑断裂韧性。金衍等[6-7]、Sierra等[8]以及Enderlin等[9]借助杨氏模量、泊松比等岩石常规参数回归断裂韧性表达式,但相关性不强。
Mayerhofer等[10]认为决定水力压裂是否有效的重要因素之一是缝面的剪切滑移作用。Murphy等[11]通过水力压裂过程中监测到的微震活动表面证实富含节理地层的水力压裂主要是节理面的剪切滑移。页岩储层大规模压裂时,压裂液使页岩发生滑动,页岩与压裂液会发生物理和化学反应[12],可能诱发多条具有一定导流能力的分支裂缝[13-17]。
然而在水力裂缝模拟中,文献[18-19]指出发生完全层间滑移后应将缝长剖面、缝高剖面考虑成平面应变问题,实际应用时采用平面应变假设条件的模拟效果会更好[20-22]。当裂纹尖端进入平面应变状态后,临界断裂韧性会显著降低,相同尺寸裂纹在厚度较厚时更易起裂[23]。
文献[24-25]从微观角度解释了裂缝破裂的微观机理,认为页岩宏观上的剪切破裂和滑移破裂都是由于微裂隙的剪切滑移破裂引起的。谢和平等[26]、Rawling等[27]以及Josh等[28]研究成果表明岩石微观结构特征对其破裂行为和力学性质的影响不容忽视。文献[29]结合断裂力学理论和分形理论,建立了平面应力条件和穿晶断裂模式下页岩Ⅰ型断裂韧性分形计算方法,其断裂韧性计算平均误差为3.63%,为本文的研究提供了参考。而沿晶断裂是晶体材料的一种脆性断裂形式[30],其耗能比穿晶断裂小,更容易发生[31]。
因此,考虑平面应变条件,从页岩储层裂缝微观形成机理和断裂力学理论出发,建立一种考虑平面应变和沿晶断裂条件下剪切滑移作用的页岩可压性评价方法,对指导页岩压前“甜点”选择具有重要意义。
1 平面应变下页岩微观剪切滑移裂缝断裂韧性计算方法 1.1 平面应变条件下页岩剪切滑移破坏机理由断裂力学原理可知要是裂纹扩展,需要满足裂缝扩展所需动力要大于或等于裂缝扩展阻力[32],即
| $ {G_0} \ge {R_0}, $ | (1) |
式中:G0为裂缝临界扩展力,J/m2;R0为裂缝扩展阻力,J/m2。
若忽略岩石脆性断裂时的非弹性效应,则裂缝扩展阻力为岩石单位面积的表面能,即
| $ \begin{array}{l} \\ {R_0} = 2{\gamma _{\rm{s}}}, \end{array} $ | (2) |
式中:γs为单位宏观量度的表面能,J/m2。
联立式(1)和式(2),并取临界值,则裂缝临界扩展力为,
| $ {G_0} = 2{\gamma _{\rm{s}}}。$ | (3) |
平面应变条件下裂缝扩展力与断裂韧性存在如下关系式,
| $ {G_0} = K_{{\rm{I}}{{\rm{I}}_0}}^2\left( {1 - {v^2}} \right)/E, $ | (4) |
则页岩剪切滑移型断裂韧性表达式为
| $ {K_{{\rm{II}}0}} = \sqrt {{G_0}E/\left( {1 - {v^2}} \right)} 。$ | (5) |
式中:E为岩石杨氏模量,GPa;υ为量纲一的岩石泊松比。
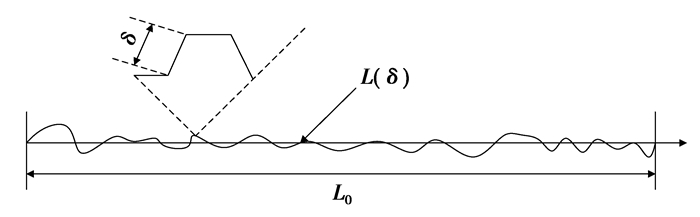
1.2 裂缝微观形态对剪切滑移破坏的影响文献[33-35]指出岩石断裂韧性受裂缝微观断裂形态影响比较大,而裂缝微观不规则壁面形态(图 1)一般具有分形特征[36-39]。
|
图 1 分形裂缝微观形态 Fig. 1 The micromorphology of fractal crack |
设裂缝线性扩展长度L0,分形裂缝扩展实际长度L(δ),则裂缝扩展时,微观角度比宏观角度所需要的裂缝扩展力增加了L(δ)/L0倍,即
| $ G = 2{\gamma _{\rm{s}}}L\left( \delta \right)/{L_0}。$ | (6) |
如图 1中分形裂缝形态所示,则有分形裂缝扩展实际长度L(δ)与裂缝线性扩展长度L0存在如下关系式,
| $ L\left( \delta \right) = {L_0}{\varepsilon ^{1 - D}}, $ | (7) |
式中:ε为量纲一的码尺;D为量纲一的分形维数。
把式(7)代入式(6)中,得到微观尺度下裂缝临界扩展力的表达式
| $ G = 2{\gamma _{\rm{s}}}{\varepsilon ^{1 - D}}. $ | (8) |
分形理论认为量纲一的码尺长度ε即为相似比γ,则式(8)可表述为
| $ G = 2{\gamma _{\rm{s}}}{\left( {\frac{1}{\gamma }} \right)^{D - 1}}, $ | (9) |
则微观视角下页岩剪切滑移型断裂韧性表达式为
| $ {K_{{\rm{II}}}} = \sqrt {GE/\left( {1 - {\nu ^2}} \right)} = \sqrt {{G_0}E/\left( {1 - {\nu ^2}} \right)} {\left( {1/\gamma } \right)^{\left( {D - 1} \right)/2}} = {K_{{\rm{I}}{{\rm{I}}_0}}}{(1/\gamma )^{(D - 1)/2}}。$ | (10) |
借助测井解释资料,采用如公式(11)(12)确定杨氏模量E、泊松比ν,
| $ \Delta {t_{\rm{s}}} = \frac{{\Delta {t_{\rm{p}}}}}{{{{[1 - 1.15\frac{{(1/{\rho _{\rm{b}}}) + {{(1/{\rho _{\rm{b}}})}^3}}}{{{{\rm{e}}^{(1/{\rho _{\rm{b}}})}}}}]}^{1.5}}}}, $ | (11) |
| $ E = \frac{{{\rho _{\rm{b}}}}}{{\Delta t_{\rm{s}}^2}} \times \frac{{3\Delta t_{\rm{s}}^2 - 4\Delta t_{\rm{p}}^2}}{{\Delta t_{\rm{s}}^2 - \Delta t_{\rm{p}}^2}},\;\;\;\nu = \frac{{0.5\Delta t_{\rm{s}}^2 - \Delta t_{\rm{p}}^2}}{{2(\Delta t_{\rm{s}}^2 - \Delta t_{\rm{p}}^2)}}, $ | (12) |
式中:Δts为横波时差,s/m;Δtp为纵波时差,s/m;ρb为岩石密度,g/cm3。
由于页岩岩石内部发育大量的天然弱结构面,基于材料破坏的最小耗能原理[40],从微观角度出发,其页岩的破坏以沿晶断裂为主,文献[41]给出图 2中穿晶断裂分形维数D=1.26。

|
图 2 穿晶断裂裂缝扩展方式示意图[10] Fig. 2 The schematic diagram of transgranular crack propagation mode |
文献[42]给出了采用晶体劈裂功法计算固体表面能的表达式,
| $ 2{\gamma _{\rm{s}}} = \frac{{{P^2}B}}{{2E}}, $ | (13) |
式中:P为单位面积岩石断裂所需的拉力,kN;B为试件厚度,cm。
页岩属于多晶材料,其内部发生剪切滑移断裂时的表面能高于单晶材料,同时剪切滑移型裂缝扩展所需能量大于张开型裂缝[30, 43-44],因此取页岩表面能计算值最大值的90%来预测断裂韧性剖面。
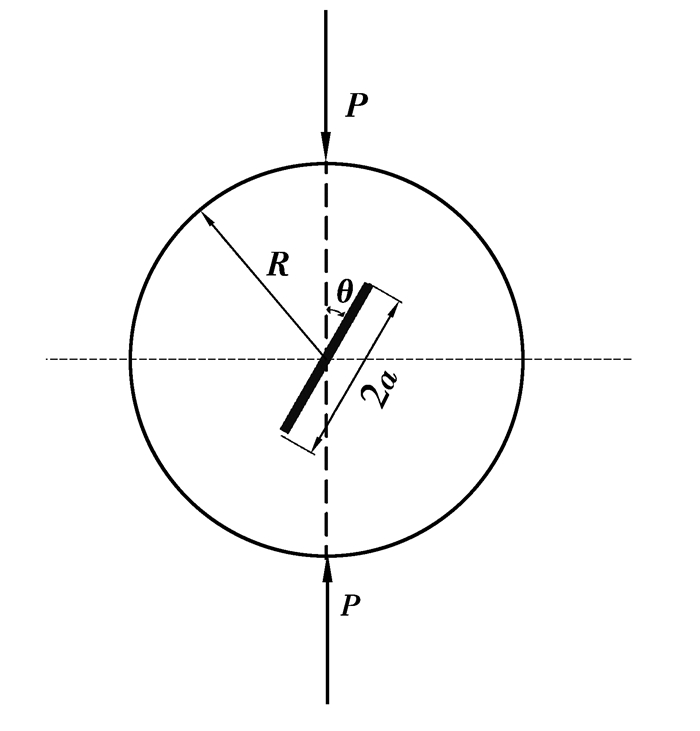
2 方法验证采用巴西圆盘实验法(cracked straight through Brazilian disc,CSTBD)测试页岩剪切滑移型岩石断裂韧性[45-46],裂缝与加载方向夹角为θ= 30°,试件尺寸如图 3所示,其断裂韧性计算公式为
| $ {{K'}_{{\rm{II}}}} = \frac{{P\sqrt a }}{{RB\sqrt {\rm{ \mathsf{ π} }} }}{N_{{\rm{II}}}}, $ | (14) |
|
图 3 巴西圆盘剪切滑移型断裂韧性试件尺寸图 Fig. 3 Specimen size of Brazilian disc for measuring the shear slip fracture toughness |
式中:P为径向加载载荷,kN;NⅡ为剪切滑移型无因次应力强度因子;K′Ⅱ为剪切滑移型断裂韧性测试值,MPa·m1/2;a为初始裂缝半长,cm;B为试件厚度,cm;R为圆盘试件半径,cm。
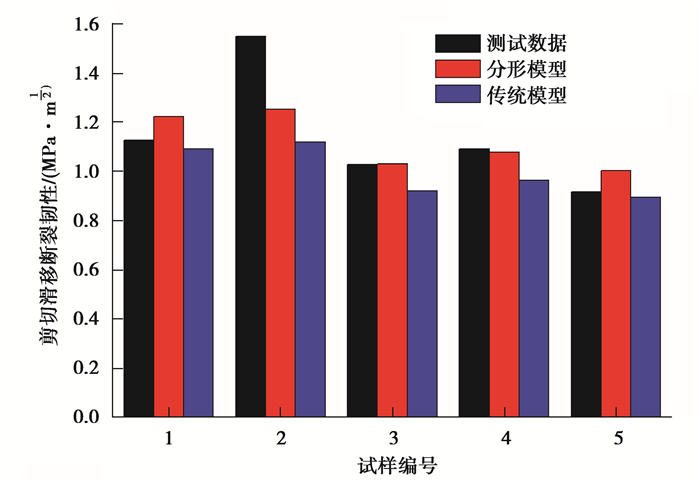
借用文献[47]中页岩剪切滑移断裂韧性实验测试结果及数据。联合式(11)~(10)计算断裂韧性KⅡ,计算结果见表 1,对比结果见图 4。从图 4中可看出,本文中所采用考虑平面应变和沿晶断裂条件下剪切滑移作用的页岩断裂韧性计算结果更接近实验测试结果,平均误差为2.93%,优于传统预测方法(-11.13%),证实了断裂韧性计算方法的准确性。
| 表 1 页岩剪切滑移型断裂韧性对比结果 Table 1 Contrast table of shale rock shear slip fracture toughness |
|
图 4 剪切滑移型断裂韧性对比结果 Fig. 4 Contrast results of shear slip fracture toughness |
为了定量评价页岩储层可压性,准确获取全井筒可压性连续剖面,选取优质的工程甜点进行压裂,可依据全井筒测井解释数据进行计算、绘制。借用文献[48]中建立的剪切滑移型断裂韧性指数计算方法,公式如下
| $ {K_{{\rm{I}}{{\rm{I}}_n}}} = \frac{{{K_{{\rm{I}}{{\rm{I}}_{max}}}} - {K_{{\rm{II}}}}}}{{{K_{{\rm{I}}{{\rm{I}}_{max}}}} - {K_{{\rm{I}}{{\rm{I}}_{\min }}}}}} \times 100, $ | (15) |
式中:KⅡn为剪切滑移型裂缝断裂韧性指数,无因次;KⅡmax为某研究对象内剪切滑移型裂缝最大断裂韧性值,MPa·m1/2;KⅡmin为某研究对象内剪切滑移型裂缝最小断裂韧性值,MPa·m1/2;KⅡ为某研究对象内剪切滑移型裂缝断裂韧性值,MPa·m1/2。
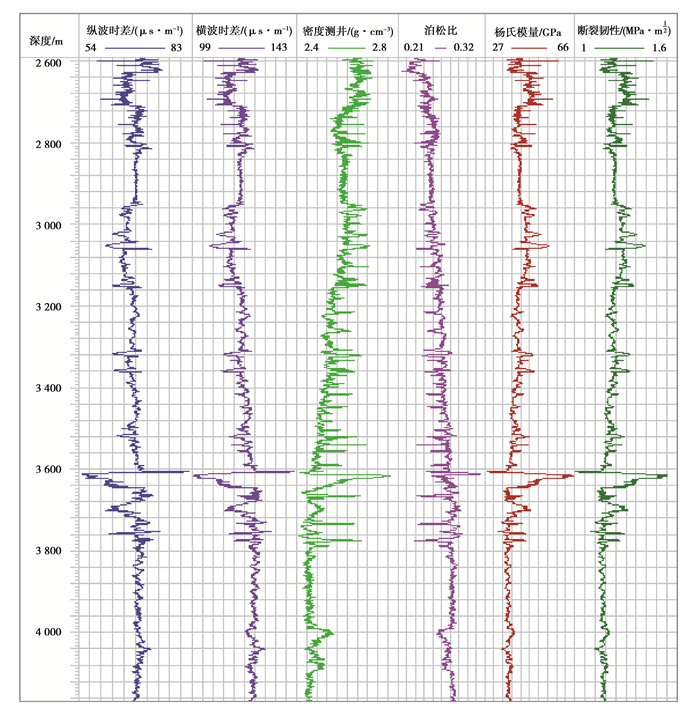
取某页岩气井测井解释成果(压裂段2 595.00~4 170.00 m),基于平面应变和沿晶断裂条件下剪切滑移作用的断裂韧性计算方法计算不同测深位置处断裂韧性大小。具体步骤为:1)取表 1中实验测试获得的页岩表面能最大值的90%作为断裂韧性剖面计算时所需单位宏观量度表面能γs;2)采用式(11)(12)计算泊松比和杨氏模量随深度的变化;3)采用式(9)计算参数G;4)采用式(15)计算断裂韧性剖面。某页岩气井各参数随深度的变化剖面见图 5,该井断裂韧性指数剖面见图 6。
|
图 5 某页岩水平井各参数剖面 Fig. 5 Horizontal well different parameters profile of shale gas reservoir |
|
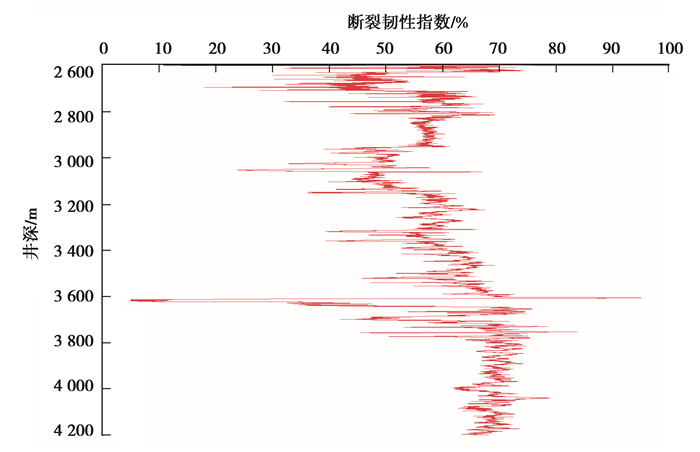
图 6 某页岩水平井断裂韧性指数剖面 Fig. 6 Horizontal well fracture toughness index profile of shale gas reservoir |
从图 6中显示曲线变化可知,该井2 595.00~4 170.00 m水平段断裂韧性指数多集中在30%~70%之间,可压性级别Ⅱ级。该井现场施工入井总液量27 483.5 m3,支撑剂总量784 m3,压后生产套压28.95 MPa,输压5.21 MPa,产量1.875×105 m3,验证了采用断裂韧性指数剖面指导页岩体积压裂的正确性。
4 结论1) 结合平面应变和沿晶断裂条件下分形描述理论,建立了一种平面应变和沿晶断裂条件下剪切滑移作用断裂韧性计算方法,计算结果与实验测试数据对比,平均误差为2.93%,验证了方法的准确性。
2) 结合密度测井、声波时差测井数据,参考某页岩水平井测井解释成果,获取了基于页岩剪切滑移型断裂韧性指数的井筒连续性剖面,为页岩工程可压性评价提供基础数据。
| [1] |
新华社.我国最大页岩气田2017年产气量突破60亿立方米[EB/OL].(2018-01-04)[2019-06-15]. http://www.gov.cn/xinwen/2018-01/04/content_5253201.htm. Xinhua Press. China's largest shale gas field in 2017 exceeded 6 billion cubic meters of gas production[EB/OL]. (2018-01-04)[2019-06-15]. http://www.gov.cn/xinwen/2018-01/04/content_5253201.htm.(in Chinese) |
| [2] |
Mayerhofer M J, Lolon E, Warpinski N R, et al. What is stimulated reservoir volume?[J]. SPE Production & Operations, 2010, 25(1): 89-98. |
| [3] |
King G E. Thirty years of gas shale fracturing: what have we learned?[C]//SPE Annual Technical Conference and Exhibition, Florence, Italy. Society of Petroleum Engineers, 2010.
|
| [4] |
唐颖, 邢云, 李乐忠, 等. 页岩储层可压裂性影响因素及评价方法[J]. 地学前缘, 2012, 19(5): 356-363. TANG Ying, XING Yun, LI Lezhong, et al. Influence factors and evaluation methods of the gas shale fracability[J]. Earth Science Frontiers, 2012, 19(5): 356-363. (in Chinese) |
| [5] |
袁俊亮, 邓金根, 张定宇, 等. 页岩气储层可压裂性评价技术[J]. 石油学报, 2013, 34(3): 523-527. YUAN Junliang, DENG Jingen, ZHANG Dingyu, et al. Fracability evaluation of shale-gas reservoirs[J]. Acta Petrolei Sinica, 2013, 34(3): 523-527. (in Chinese) |
| [6] |
金衍, 陈勉, 张旭东. 利用测井资料预测深部地层岩石断裂韧性[J]. 岩石力学与工程学报, 2001, 20(4): 454-456. JIN Yan, CHEN Mian, ZHANG Xudong. Determination of fracture toughness for deep well rock with geophysical logging data[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(4): 454-456. (in Chinese) DOI:10.3321/j.issn:1000-6915.2001.04.007 |
| [7] |
金衍, 陈勉, 王怀英, 等. 利用测井资料预测岩石Ⅱ型断裂韧性的方法研究[J]. 岩石力学与工程学报, 2008, 27(S2): 3630-3635. JIN Yan, CHEN Mian, WANG Huaiying, et al. Study on prediction method of fracture toughness of rock mode Ⅱ by logging data[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(S2): 3630-3635. (in Chinese) |
| [8] |
Sierra R, Tran M H, Abousleiman Y N, et al. Woodford shale mechanical properties and the impacts of lithofacies[C]//44th US Rock Mechanics Symposium and 5th US-Canada Rock Mechanics Symposium, June 27-30, 2010, Salt Lake City, Utah. American Rock Mechanics Association, 2010: 2033-2035, ARMA-10-461.
|
| [9] |
Enderlin M, Alsleben H, Beyer J A. Predicting fracability in shale reservoirs[C]//AAPG Annual Conference and Exhibition, April 10-13, 2011, Houston, Texas, USA. AAPG, 2011: 10-13.
|
| [10] |
Mayerhofer M J, Meehan D N. Waterfracs-results from 50 cotton valley Wells[C]//SPE Annual Technical Conference and Exhibition, New Orleans, Louisiana. Society of Petroleum Engineers, 1998.
|
| [11] |
Murphy H D, Fehler M C. Hydraulic fracturing of jointed formations[C]//International Meeting on Petroleum Engineering, Beijing, China. Society of Petroleum Engineers, 1986.
|
| [12] |
Liu X Z, Vemik L, Nur A. Effects of saturating fluids on seismic velocities in shale[C]//SEG Annual Meeting, October 23-28, Los Angeles, California. Society of Exploration Geophysicists, 1994: SEG-1994-1121.
|
| [13] |
吴建东.清水不加砂压裂机理研究[D].大庆: 大庆石油学院, 2009. WU Jiandong. Study on unproppant waterfrac mechanism[D]. Daqing: Daqing Petroleum Institute, 2009. (in Chinese) |
| [14] |
李士斌, 张立刚, 高铭泽, 等. 清水不加砂压裂增产机理及导流能力测试[J]. 石油钻采工艺, 2011, 33(6): 66-69. LI Shibin, ZHANG Ligang, GAO Mingze, et al. Study on yield increase mechanism and flow conductivity test method for water-fracturing without proppant[J]. Oil Drilling & Production Technology, 2011, 33(6): 66-69. (in Chinese) DOI:10.3969/j.issn.1000-7393.2011.06.016 |
| [15] |
邹雨时, 张士诚, 马新仿. 页岩气藏压裂支撑裂缝的有效性评价[J]. 天然气工业, 2012, 32(9): 52-55, 131-132. ZOU Yushi, ZHANG Shicheng, MA Xinfang. Assessment on the effectiveness of propped fractures in the fracturing of shale gas reservoirs[J]. Natural Gas Industry, 2012, 32(9): 52-55, 131-132. (in Chinese) DOI:10.3787/j.issn.1000-0976.2012.09.012 |
| [16] |
Zhang J J, Kamenov A, Hill A D, et al. Laboratory measurement of hydraulic-fracture conductivities in the barnett shale[J]. SPE Production & Operations, 2014, 29(3): 216-227. |
| [17] |
Ji L J, Geehan T. Shale failure around hydraulic fractures in water fracturing of shale gas[C]//SPE Unconventional Resources Conference Canada, Calgary, Alberta, Canada. Society of Petroleum Engineers, 2013.
|
| [18] |
Economides M J, Nolte K G. Reservoir stimulation[M]. Chichester: Wiley, 2000.
|
| [19] |
赵金洲, 彭瑀, 李勇明, 等. 层间滑移对缝高延伸影响的模拟分析[J]. 新疆石油地质, 2013, 34(6): 661-664. ZHAO Jinzhou, PENG Yu, LI Yongming, et al. Modeling analysis of effect of interlayer slip on fracture height growth[J]. Xinjiang Petroleum Geology, 2013, 34(6): 661-664. (in Chinese) |
| [20] |
许丹, 胡瑞林, 高玮, 等. 页岩纹层结构对水力裂缝扩展规律的影响[J]. 石油勘探与开发, 2015, 42(4): 523-528. XU Dan, HU Ruilin, GAO Wei, et al. Effects of laminated structure on hydraulic fracture propagation in shale[J]. Petroleum Exploration and Development, 2015, 42(4): 523-528. (in Chinese) |
| [21] |
Economides M J. Modern fracturing:enhancing natural gas production[M]. Houston: ET Publishing, 2007.
|
| [22] |
赵金洲, 彭瑀, 李勇明, 等. 水力裂缝平面应变假设的适用条件与解析修正[J]. 石油勘探与开发, 2017, 44(3): 423-430. ZHAO Jinzhou, PENG Yu, LI Yongming, et al. Applicable conditions and analytical corrections of plane strain assumption in the simulation of hydraulic fracturing[J]. Petroleum Exploration and Development, 2017, 44(3): 423-430. (in Chinese) |
| [23] |
张华, 张宏, 王亚龙, 等. 管线钢平面应变断裂韧性经验模型研究[J]. 焊管, 2016, 39(8): 11-15. ZHANG Hua, ZHANG Hong, WANG Yalong, et al. Study on empirical model of plane strain fracture toughness for pipeline steel[J]. Welded Pipe and Tube, 2016, 39(8): 11-15. (in Chinese) |
| [24] |
钟建华, 刘圣鑫, 马寅生, 等. 页岩宏观破裂模式与微观破裂机理[J]. 石油勘探与开发, 2015, 42(2): 242-250. ZHONG Jianhua, LIU Shengxin, MA Yinsheng, et al. Macro-fracture mode and micro-fracture mechanism of shale[J]. Petroleum Exploration and Development, 2015, 42(2): 242-250. (in Chinese) |
| [25] |
Gao Q, Tao J L, Hu J Y, et al. Laboratory study on the mechanical behaviors of an anisotropic shale rock[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2015, 7(2): 213-219. DOI:10.1016/j.jrmge.2015.03.003 |
| [26] |
谢和平, 陈至达. 岩石断裂的微观机理分析[J]. 煤炭学报, 1989, 14(2): 57-67. XIE Heping, CHEN Zhida. Analysis of rock fracture micro-mechanism[J]. Journl of China Coal Society, 1989, 14(2): 57-67. (in Chinese) DOI:10.3321/j.issn:0253-9993.1989.02.003 |
| [27] |
Rawling G C, Baud P, Wong T F. Dilatancy, brittle strength, and anisotropy of foliated rocks:experimental deformation a nd micromechanical modeling[J]. Journal of Geophysical Research:Solid Earth, 2002, 107(B10): ETG 8-1-ETG 8-14. DOI:10.1029/2001JB000472 |
| [28] |
Josh M, Esteban L, Delle Piane C, et al. Laboratory characterisation of shale properties[J]. Journal of Petroleum Science and Engineering, 2012, 88/89: 107-124. DOI:10.1016/j.petrol.2012.01.023 |
| [29] |
纪国法, 李奎东, 张公社, 等. 页岩Ⅰ型断裂韧性的分形计算方法与应用[J]. 岩土力学, 2019, 40(5): 1925-1931. JI Guofa, LI Kuidong, ZHANG Gongshe, et al. Fractal calculation method of model Ⅰ fracture toughness of shale rock and its application[J]. Rock and Soil Mechanics, 2019, 40(5): 1925-1931. (in Chinese) |
| [30] |
谢和平, 高峰, 周宏伟, 等. 岩石断裂和破碎的分形研究[J]. 防灾减灾工程学报, 2003, 23(4): 1-9. XIE Heping, GAO Feng, ZHOU Hongwei, et al. Fractal fracture and fragmentation in rocks[J]. Journal of Seismology, 2003, 23(4): 1-9. (in Chinese) |
| [31] |
谢和平. 分形岩石力学导论[M]. 北京: 科学出版社, 1996. XIE Heping. Introduction to fractal rock mechanics[M]. Beijing: Science Press, 1996. (in Chinese) |
| [32] |
李世愚, 和泰名, 尹祥础. 岩石断裂力学[M]. 北京: 科学出版社, 2016. LI Shiyu, HE Taiming, YIN Xiangchu. Rock fracture mechanics[M]. Beijing: Science Press, 2016. (in Chinese) |
| [33] |
梁亚磊.圆盘试件预制裂缝形状对其测试岩石断裂韧度值的影响性研究[D].焦作: 河南理工大学, 2011. LIANG Yalei. Research on the effect of the prefab crack shape on the rock fracture toughness tested using disc specimen[D]. Jiaozuo: Henan Polytechnic University, 2011. (in Chinese) |
| [34] |
张明明. T应力对岩石断裂韧性及裂纹起裂的影响[D].成都: 西南石油大学, 2017. ZHANG Mingming. The influence of T-stress on rock fracture toughness and crack initial angle[D]. Chengdu: Southwest Petroleum University, 2017. (in Chinese) |
| [35] |
dos Santos S F, de Anchieta Rodrigues J. Correlation between fracture toughness, work of fracture and fractal dimensions of Alumina-mullite-zirconia composites[J]. Materials Research, 2003, 6(2): 219-226. DOI:10.1590/S1516-14392003000200017 |
| [36] |
Mandelbrot B B, Passoja D E, Paullay A J. Fractal character of fracture surfaces of metals[J]. Nature, 1984, 308(5961): 721-722. DOI:10.1038/308721a0 |
| [37] |
Odling N E. Natural fracture profiles, fractal dimension and joint roughness coefficients[J]. Rock Mechanics and Rock Engineering, 1994, 27(3): 135-153. DOI:10.1007/BF01020307 |
| [38] |
Scavia C. The effect of scale on rock fracture toughness:a fractal approach[J]. Géotechnique, 1996, 46(4): 683-693. DOI:10.1680/geot.1996.46.4.683 |
| [39] |
Borodich F M. Fractals and fractal scaling in fracture mechanics[M]//Fracture Scaling. Dordrecht: Springer Netherlands, 1999: 239-259.
|
| [40] |
周筑宝. 最小耗能原理及其应用:材料的破坏理论、本构关系理论及变分原理[M]. 北京: 科学出版社, 2001. ZHOU Zhubao. The principle of minimum energy consumption and its application:material destruction theory, constitutive relationship theory and variational principle[M]. Beijing: Science Press, 2001. (in Chinese) |
| [41] |
Lung C W. Fractals and the fracture of cracked metals[M]//Pietronero L, Tosatti E. Fractals in Physics. Elsevier, 1986: 189-192.
|
| [42] |
程传煊. 表面物理化学[M]. 北京: 科学技术文献出版社, 1995. CHENG Chuanxuan. Surface physicochemical[M]. Beijing: Scientific and Technical Documents Publishing House, 1995. (in Chinese) |
| [43] |
弗杰尔, 霍尔特, 霍斯拉德, 等.石油工程岩石力学[M].邓金根, 蔚宝华, 王金凤, 等译.北京: 石油工业出版社, 2012. Fjær E, Holt R M, Horsrud P, et al. Petroleum related rock mechanics[M]. DENG Jingen, WEI Baohua, WANG Jinfeng, et al. Trans. Beijing: Petroleum Industry Press, 2012. (in Chinese) |
| [44] |
李列列, 卓莉, 邵江, 等. 岩石巴西圆盘复合型断裂力学特征及空间效应研究[J]. 工程科学与技术, 2017, 49(S1): 132-138. LI Lielie, ZHUO Li, SHAO Jiang, et al. Mechanical characteristics and spatial effect research of rocks using Brazilian disk under mixed mode loading[J]. Advanced Engineering Sciences, 2017, 49(S1): 132-138. (in Chinese) |
| [45] |
Awaji H, Sato S. Combined mode fracture toughness measurement by the disk test[J]. Journal of Engineering Materials and Technology, 1978, 100(2): 175-182. DOI:10.1115/1.3443468 |
| [46] |
Atkinson C, Smelser R E, Sanchez J. Combined mode fracture via the cracked Brazilian disk test[J]. International Journal of Fracture, 1982, 18(4): 279-291. |
| [47] |
陈建国, 邓金根, 袁俊亮, 等. 页岩储层Ⅰ型和Ⅱ型断裂韧性评价方法研究[J]. 岩石力学与工程学报, 2015, 34(6): 1101-1105. CHEN Jianguo, DENG Jingen, YUAN Junliang, et al. Determination of fracture toughness of modes Ⅰ and Ⅱ of shale formation[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(6): 1101-1105. (in Chinese) DOI:10.13722/j.cnki.jrme.2014.1187 |
| [48] |
赵金洲, 许文俊, 李勇明, 等. 页岩气储层可压性评价新方法[J]. 天然气地球科学, 2015, 26(6): 1165-1172. ZHAO Jinzhou, XU Wenjun, LI Yongming, et al. A new method for fracability evaluation of shale-gas reservoirs[J]. Natural Gas Geoscience, 2015, 26(6): 1165-1172. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43

