1b. 成都工业学院 汽车与交通学院, 成都 611730;
2. 电子科技大学 数学科学学院, 成都 611731
1b. School of Automobile and Communications, Chengdu Technological University, Chengdu 611730, P. R. China;
2. School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu 611731, P. R. China
矿产资源在推动人类社会向前发展的过程中起着举足轻重的作用, 几乎各行各业都直接或间接依赖于矿产资源[1]。然而矿产资源是不可再生资源, 随着人类对矿产资源需求量日益增大, 地球表面及浅部矿产勘查将近枯竭, 向深部地球寻求矿产已成为必然趋势[2], 这就要寻求合理的方法进行矿产预测。地球化学元素含量异常分带是进行矿产预测的一种有效的手段[3], 厘清地球化学异常分布规律, 就能圈定矿体所在区域。因此选取合理的地球化学异常提取方法至关重要。近年来, 学者们在地球化学异常识别研究工作上做了大量研究, 取得了诸多成果, 为深部盲矿预测提供了宝贵经验。如Cheng[4-5]利用多重分形奇异性理论模型来刻画地球化学异常分布;Shen[6]利用分形模型进行元素异常下限提取;Zuo[7]采用多重分形谱和接收工作特性曲线相结合的混合方式来识别空间相关的元素组合。事实上每种方法进行地球化学异常提取都需要一定的条件, 但地球化学异常形成的地质环境极为复杂, 目前难以找到合理的地球化学异常提取方法[8]。传统的均方差进行地球化学异常提取需要数据服从正态分布, 但实际地球化学数据形成的地质环境复杂, 其分布并不服从正态分布[9]。证据权法在矿产预测中有着广泛的应用, 但该方法对成矿概率临界值的确定还没有科学方法, 常采用专家经验法以及统计分布法等[10]。实际上, 地球化学异常在空间分布上与周围正常元素的分布具有一定的偏离, 其观测数据位于整个概率分布的尾部[11-12], 而极值理论中的广义帕累托分布(generalized pareto distribution, GPD)研究的是数据的后尾性分布[13]。赵鹏大院士也曾在韩国首尔举办的国际统计学会议上将地球化学异常含量分布描述为极值分布[14]。采用GPD进行原生晕地球化学元素异常提取, 有利于提取找矿标志, 进行矿产预测。目前GPD在地球化学异常下限估计方面出现了一些研究成果, 如左仁广[15]提出地质异常属于极值理论研究范畴。然而在利用GPD估计地球化学异常值的精度和确定GPD的参数方面研究较少, 并且极值理论往往只考虑元素含量的频率分布。其实可以将元素含量异常提取后, 结合元素异常对应的空间坐标, 辅以MapGis软件[16]描绘元素异常含量空间分布规律。因此, 笔者结合地球化学异常特性, 深入研究GPD模型, 对其阈值估计和参数估计进行探讨, 以此形成地球化学异常提取模型, 进行矿产预测。
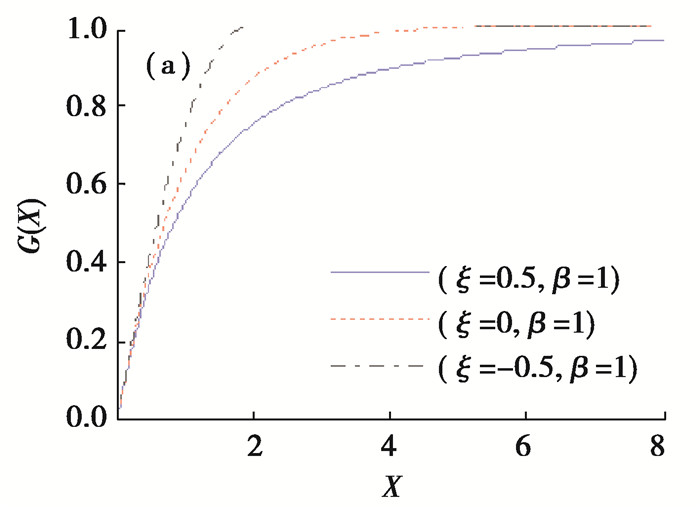
1 GPD理论基础广义帕累托分布(GPD)亦称阈值模型, 它是对样本中充分大的观测数据进行分布拟合。假设x1, x2, …, xn为一组随机变量并且属于同一分布, 如果存在一个较大的数据μ, 并且有固定常数β>0, GPD可表达为[17]
| $ G(x;\xi , \beta ) = \left\{ \begin{array}{l} 1 - {(^1} + \xi {\rm{)}} - \frac{1}{\xi }\quad \xi \ne 0, \\ \;\;\;\;1 - {e^{ - \frac{{x - \mu }}{\beta }}}\quad \xi = 0。\end{array} \right. $ | (1) |
式中:ξ为形状参数, μ为样本阈值, β为尺度参数, 当ξ≥0时, x≥μ;当ξ < 0时,
|
图 1 GPD的标准分布形式 Fig. 1 The standard distribution function of the GPD |
在式(1)中, 需要确定其尺度参数β, 形状参数ξ和阈值μ。然而阈值μ的估计至今未有明确的方法, 其中比较有效的阈值估计方法是MEF法[12, 18] (mean excess function), 假定μ0为初始阈值, 对任意阈值μ(μ>μ0), MEF定义为[18]
| $ E(\mu ) = \frac{{\beta \mu + \xi \mu }}{{1 - \xi }}, $ | (2) |
式中:E(μ)是关于阈值μ的一个线性函数。如果已知样本数据x1, x2, …, xn, xi为大于阈值μ的数据, 则E(μ)统计方法可表示为[19]
| $ E(\mu ) = \frac{{\sum\limits_{i = 1}^n {\left( {{x_i} - \mu } \right)} }}{{{N_n}}}, $ | (3) |
式中:n为样本总数;Nn为超过阈值μ的数据个数。在(μ, E(μ))的分布中选取充分大的μ0, 使得当x≥μ0时, E(μ)为近似线性函数, 该μ0定义为阈值[19]。而GPD的形状参数和尺度参数可由极大似然函数法进行估计[20]。然而, 在实际数据处理中, 通过矩法估计得出的GPD的参数较似然函数估计的结果更合理[19]。矩法估计是通过样本矩来反应总体矩, 以此对参数进行估计, 即
| $ \left\{ {\begin{array}{*{20}{l}} {\xi = \left[ {1 - {{(\bar t/\delta )}^2}} \right]/2, }\\ {\beta = \bar t \times (1 - \hat \xi )。} \end{array}} \right. $ | (4) |
式中:t, δ分别为ti(ti=xi-μ≥0)的平均值和标准差。
2 地球化学异常提取GPD模型构建地球化学数据的异常区域分布在观察数据的尾部, 这与GPD对极大值或极小值数据分布拟合吻合, 因此可以通过GPD构建地球化学异常模型, 确定地球化学找矿标志, 进行矿产预测。对一组地球化学数据X={x1, x2, …, xn}, GPD建模如下:
第1步 数据准备。
第2步 采用QQ图检验数据是否正态分布, 是否满足后尾性分布[19]。
第3步 采用式(4)估计GPD的形状参数ξ和尺度参数β。
第4步 在数据中选取不同阈值μ, 采用式(3)计算出E(μ)并绘制(μ, E(μ))散点图。当x≥μ时, E(μ)近似为线性分布, 则该处的μ即为阈值, 亦为地球化学元素异常下限。
第5步 把第3步估计出的参数ξ, β和第4步估计出的阈值μ代入式(1), 得出GPD超阈值分布函数。
第6步 利用PP图[19]进行诊断检验, 检验GPD超阈值理论分布与数据实际分布是否一致, 如果不一致, 返回第4步, 估计新的阈值, 直到理论分布与实际分布拟合程度吻合为止。
在上述构建的模型中, MEF法估计阈值比较直观, 但仍然具有一定的局限性, 因为该方法只能估计出阈值位于某个区间内, 不能估计出具体的精确值。在本文中构建了一个新的稳定性估计法。
由于样本数据的形状参数ξ与尺度参数β是固定的, 在MEF法确定的阈值区间内, 任选一个初始阈值μ0。对任意的阈值μ>μ0, 有β(μ)GPD=σGEV+ξ(μ-μ0)[18]。因此有
| $ \beta (\mu ) = \sigma + \xi \left( {{\mu _0}} \right){\rm{ 或 }}\beta (\mu ) = \beta \left( {{\mu _0}} \right) + \xi \left( {\mu - {\mu _0}} \right)。$ | (5) |
若令
| $ {\beta ^*}(\mu ) = \beta (\mu ) - \xi (\mu ), $ | (6) |
β*(μ)显然与阈值μ无关, 称β*(μ)为修正的阈值函数。因此, 如果μ0选取合理, 数据超出量xi-μ0(xi>μ0)服从GPD分布, 那么对任意的阈值μ>μ0, β*(μ)不会随着μ的变换发生改变。
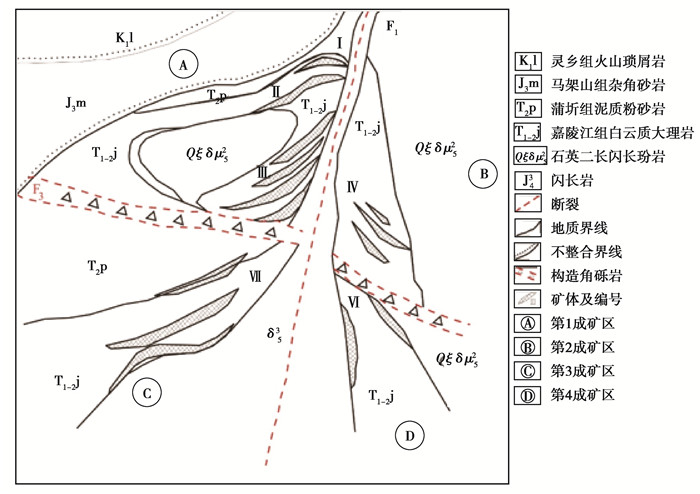
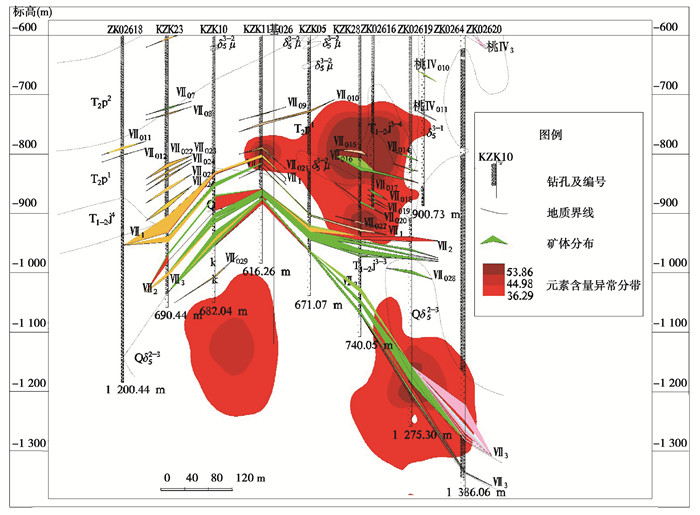
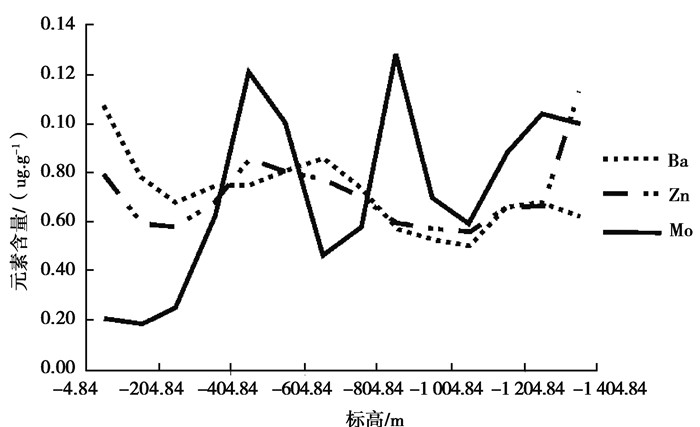
3 实际数据处理与矿产预测研究区鸡冠咀铜金矿床为中国重要的矽卡岩热液型矿床之一, 其东经为114°54′42″~114°55′45″, 北纬为30°04′45″~30°05′50″。区内地质构造复杂, 主要包括:褶皱构造、断裂构造及断裂侵入接触构造。岩浆岩主要为喷出岩和侵入岩两大类型, 侵入活动主要在燕山早期、燕山晚期及喜山早期进行。经接触交代变质作用发育为石榴子石、透辉石、金云母及绿泥石等矽卡岩矿物, 通过接触热变质作用发育为白云石大理岩。区内围岩蚀变强烈, 主要包括高岭石化、绿泥石化及矽卡岩化等。矿区有4个主矿体群和14个主矿体, 主矿体位于大理岩残留体的层间破碎带和大理岩与侵入岩的断裂接触部位。2条主断裂F1和F3把区域划分为A, B, C, D 4个部分(图 2)。区内矿产资源丰富, 尤其位于22线和34线之间的VII号矿体, 有着巨大的找矿潜力[12, 19]。笔者选取26号勘探线Ⅶ矿体Mo, Ba, Zn成矿元素的含量进行矿产预测研究。根据区域矿体前缘→矿体中部→矿体尾部走势(图 8~10), 结合3种元素面金属含量随着深度变换情况可知(图 3), Ba元素面金属含量随着深度变换呈现降低趋势, 属于前缘晕元素;Zn元素面金属含量随着深度变换呈现升高趋势, 属于尾晕元素;Mo元素面金属含量随着深度变换近似不变, 属于近矿晕元素。但实际各元素含量随着深度变换出现不同的折转(图 3), 说明矿床在不同中段表现多期次热液的叠加现象, 指示深部存在盲矿体可能, 下面将构建的模型进行盲矿体预测。
|
图 2 鸡冠咀铜金矿床模式示意图 Fig. 2 The pattern of the Jiguanzui Cu-Au mining deposit |
|
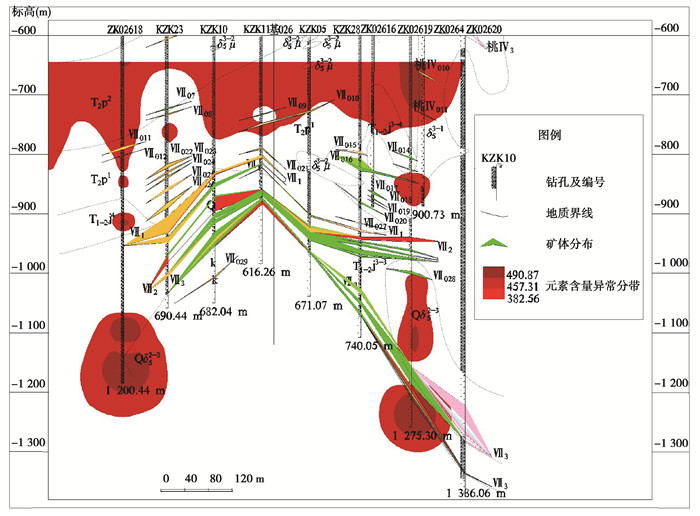
图 8 Ba元素异常空间分布 Fig. 8 The identified anomaly region of Ba |
|
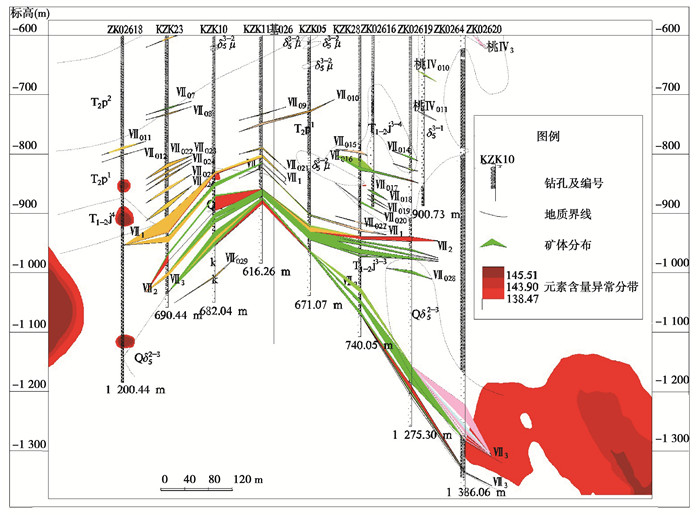
图 9 Zn元素异常空间分布 Fig. 9 The identified anomaly region of Zn |
|
图 10 Mo元素异常空间分布 Fig. 10 The identified anomaly region of Mo |
|
图 3 元素含量随深度变化曲线 Fig. 3 The variation curves of element content with depth |
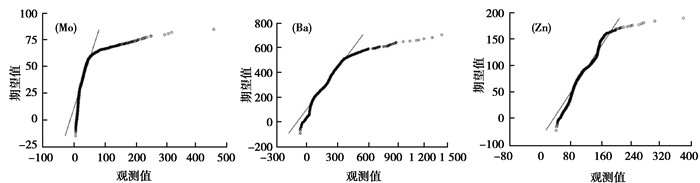
由3种元素含量统计分析(表 1)可知, 3种元素含量偏度都是正数, 不服从正态分布, 通过QQ图(图 4)进一步发现3种元素含量均为右偏, 表现后尾分布特性, 符合提出的算法模型适用条件。
| 表 1 元素统计量结果 Table 1 Element statistics |
|
图 4 Mo, Ba, Zn元素的偏态性检验 Fig. 4 The skewness test of Mo, Ba and Zn |
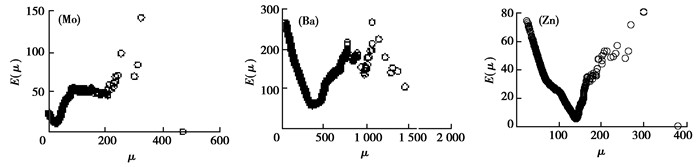
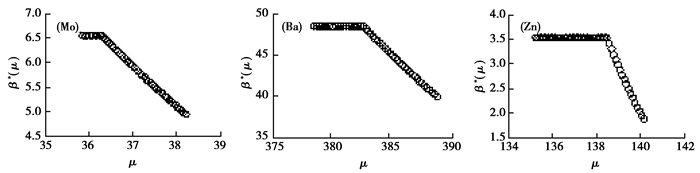
通过设计的模型分别得出Mo, Ba, Zn 3种元素含量的超额均值函数图(图 5), 由图 5可知, 3种元素含量高于区间值[35.87, 38.21], [378.42, 388.72], [135.22, 140.17]以后, 其MEF均表现线性递增, 即为阈值区间。为了选取精确的阈值, 在3个区间分别均匀插入50个点, 利用修正函数得出β*(μ)与阈值的变换情况(图 6), 由图 6知Mo, Ba, Zn元素含量分别在36.29, 382.56, 138.47后估计量β*(μ)不会随着μ变换而改变, 即为阈值, 利用式(5)得出Mo, Ba, Zn的尺度参数分别为6.94, 48.66, 3.86, 形状参数分别为0.37, 0.17, 0.30, 从而3种元素含量GPD分布为
|
图 5 Mo, Ba, Zn元素超额均值函数图 Fig. 5 The MEF diagram of Mo, Ba and Zn |
|
图 6 Mo, Ba, Zn元素的修正尺度参数β*(μ)随μ的变换关系 Fig. 6 The relations between β*(μ) and thresholds μ of Mo, Ba and Zn |
| $ \begin{array}{l} {G_{{\rm{Mo}}}}(x) = 1 - \left( {1 + \frac{{0.37}}{{6.94}}(x - 36.29)} \right) - \frac{1}{{0.37}}, {G_{{\rm{Ba}}}}(x) = 1 - \left( {1 + \frac{{0.17}}{{48.66}}(x - 382.56)} \right) - \frac{1}{{0.17}}, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{G_{{\rm{Zn}}}}(x) = 1 - \left( {1 + \frac{{0.30}}{{3.86}}(x - 138.47)} \right) - \frac{1}{{0.30}}。\end{array} $ |
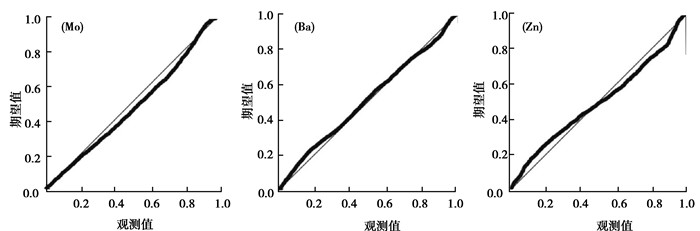
确定GPD后, 利用PP图进行诊断性检验(图 7)发现3种元素超阈值含量均依附在直线左右, 进而元素含量的GPD分布与实际地层中分布具有较高吻合性, 说明地球化学异常下限选取合理。
|
图 7 Mo, Ba, Zn元素GPD分布拟合检验 Fig. 7 The GPD fitting of Mo, Ba and Zn |
根据元素异常下限得出Mo, Ba, Zn元素含量空间分规律(图 8~10), 由图 8~10知元素含量分带能够反映矿体走势。另外, 元素Ba不仅在矿体顶部分布, 在矿体下面也存在富集, 该现象为前缘晕的反常分带(图 8);元素Zn在矿体上方与前缘晕元素出现叠加现象, 反映出元素多期次成矿特性, 并且在矿体下方与前缘同样具有共存现象, 说明深部存在找矿潜力;元素Mo分带较好地刻画了矿体分布特征, 在深部具明显的伸现象, 特别是在钻孔KZK10和KZK11以下1 100 m左右, 具有强异常分带现象, 该异常很可能是钻孔ZK2620下方1 300 m钼矿体的延伸, 说明此处可能存在盲矿体。
4 结论以实际矿区为研究对象, 通过构建地球化学异常GPD模型研究原生晕地球化学元素异常分布规律, 有利于深部矿产预测。具有如下结论:
1) 通过原生晕地区化学元素含量异常分布具有后尾性特征, 结合GPD原理构建了一套地球化学元素异常提取模型, 并对模型的参数和阈值进行了探讨和验证, 同时还设计了修正尺度函数来确定元素具体异常下限值。
2) 将所设计的GPD模型进行实际地球化学元素含量异常提取, 得出Mo, Ba, Zn元素含量异常下限分别为36.29, 382.56, 138.47, 通过诊断检验表明元素的理论分布与实际分布具有一致性, 从而设计的模型具有合理性。
3) 通过设计的模型得出Mo, Ba, Zn元素异常分带与矿体走势吻合, 根据元素异常分布规律可以确定矿体深部存在较大找矿潜力, 尤其位于钻孔KZK10和KZK11深度以下1 100 m左右具有强异常, 可能存在钼盲矿体。
| [1] |
陶建格, 沈镭. 矿产资源价值与定价调控机制研究[J]. 资源科学, 2013, 35(10): 1959-1967. TAO Jiange, SHEN Lei. The value of ore resources and pricing regulation mechanisms[J]. Resources Science, 2013, 35(10): 1959-1967. (in Chinese) |
| [2] |
姚磊, 吕志成, 陈辉, 等. 再谈矿山深部及外围找矿新发现及意义[J]. 南京大学学报(自然科学), 2018, 54(2): 296-307. YAO Lei, LU Zhicheng, CHEN Hui, et al. A reappraisal on the new discovery of deep ore exploration of mines and adjacent areas and its significances[J]. Journal of Nanjing University (Natural Science), 2018, 54(2): 296-307. (in Chinese) |
| [3] |
Xiong Y H, Zuo R G, Wang K X, et al. Identification of geochemical anomalies via local RX anomaly detector[J]. Journal of Geochemical Exploration, 2018, 189: 64-71. DOI:10.1016/j.gexplo.2017.06.021 |
| [4] |
Cheng Q M. Non-linear theory and power-law models for information integration and mineral resources quantitative assessments[M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 2008: 195-225.
|
| [5] |
Cheng Q M. Singularity analysis of magmatic flare-ups caused by India-Asia collisions[J]. Journal of Geochemical Exploration, 2018, 189: 25-31. DOI:10.1016/j.gexplo.2017.08.012 |
| [6] |
Shen W. Fractal invariable distribution and its application in large-sized and super large-sized mineral deposits[J]. Geoscience Frontiers, 2011, 2(1): 91-95. |
| [7] |
Zuo R G. Selection of an elemental association related to mineralization using spatial analysis[J]. Journal of Geochemical Exploration, 2018, 184(A): 150-157. |
| [8] |
Wang J, Zuo R G. Identification of geochemical anomalies through combined sequential Gaussian simulation and grid-based local singularity analysis[J]. Computers & Geosciences, 2018, 118: 52-64. |
| [9] |
陈健, 李正栋, 钟皓, 等. 多种地球化学异常下限确定方法的对比研究[J]. 地质调查与研究, 2014, 37(3): 187-192. CHEN Jian, LI Zhengdong, ZHONG Hao, et al. Comparison of multiple methods to determine the geochemical anomaly threshold[J]. Geological Survey and Research, 2014, 37(3): 187-192. (in Chinese) DOI:10.3969/j.issn.1672-4135.2014.03.005 |
| [10] |
严冰, 阳正熙, 周莉, 等. 证据权法成矿预测模型结合分形模型在成矿预测中的应用研究[J]. 矿业研究与开发, 2012, 32(1): 29-33, 122. YAN Bing, YANG Zhengxi, ZHOU Li, et al. Application of the combination of weights-of-evidence model and fractal model in metallogenic prediction[J]. Mining Research and Development, 2012, 32(1): 29-33, 122. (in Chinese) |
| [11] |
Tian M, Wang X Q, Nie L S, et al. Recognition ofgeochemical anomalies based on geographically weighted regression:a case study across the boundary areas of China and Mongolia[J]. Journal of Geochemical Exploration, 2018, 190: 381-389. DOI:10.1016/j.gexplo.2018.04.003 |
| [12] |
秦飞龙.原生晕地球化学和岩心高光谱粗糙集耦合建模与深部矿产预测研究[D].成都: 成都理工大学, 2017. QIN Feilong. Coupling modeling of the primary halo geochemistry and the core hyperspectral with the rough set model and its studying in the prediction of deep mineral resources[D]. Chengdu: Chengdu University of Technology, 2017. (in Chinese) |
| [13] |
Mohie El-Din M M, Sadek A, Mohie El-Din M M, et al. Characterization of the generalizedParetodistributionby general progressively Type-II right censored order statistics[J]. Journal of the Egyptian Mathematical Society, 2017, 25(4): 369-374. DOI:10.1016/j.joems.2017.05.002 |
| [14] |
Chen Y Q, Zhao P D, Chen J G, et al. Application of the geo-anomaly unit concept in quantitative delineation and assessment of gold ore targets in Western Shandong Uplift Terrain, Eastern China[J]. Natural Resources Research, 2001, 10(1): 35-49. DOI:10.1023/A:1011581414877 |
| [15] |
左仁广.基于地质异常的矿产资源定量化预测与不确定性评价[D].武汉: 中国地质大学, 2009. ZUO Renguang. Geoanomaly-based mineral resources quantitative prediction and uncertainty evaluation[D]. Wuhan: China University of Geosciences, 2009. (in Chinese) |
| [16] |
王晓华. 基于MapGIS与Grapher联合绘制地球化学剖面图[J]. 吉林地质, 2017, 36(4): 75-77. WANG Xiaohua. Geochemical profile drawing based on MapGIS and Grapher[J]. Jilin Geology, 2017, 36(4): 75-77. (in Chinese) DOI:10.3969/j.issn.1001-2427.2017.04.019 |
| [17] |
Rootzén H, Segers J, Wadsworth J L. Multivariate generalized Pareto distributions:parametrizations, representations, and properties[J]. Journal of Multivariate Analysis, 2018, 165: 117-131. DOI:10.1016/j.jmva.2017.12.003 |
| [18] |
花拥军. 极值理论究[M]. 北京: 科学出版社, 2011. HUA Yongjun. Study on extreme value theorem[M]. Beijing: Science Press, 2011. (in Chinese) |
| [19] |
Qin F L, Liu B L, Guo K, et al. Using EVT for geological anomaly design and its application in identifying anomalies in mining areas[J]. Mathematical Problems in Engineering, 2016(3): 1-11. |
| [20] |
Castillo J D, Serra I. Likelihood inference for generalized Pareto distribution[J]. Computational Statistics & Data Analysis, 2015, 83: 116-128. |
 2020, Vol. 43
2020, Vol. 43


