2. 国网浙江平阳县供电有限责任公司, 浙江 温州 325401
2. State Grid Pingyang Power Supply Company, Wenzhou 325401, Zhejiang, P. R. China
太阳能、风能等清洁可再生能源可以缓解环境污染问题和日渐严重的能源危机,从而被广泛应用[1-2]。由于自然原因的限制,可再生能源的发电具有很大的不确定性,这对电力系统的安全稳定运行有着严重的影响,而储能技术的应用将为解决这些问题提供非常有效的途径[3-5]。
大规模可再生能源的应用促进了储能技术的研究与发展,选择合适的储能配置已成为关键问题。单一类型的储能配置的性能有限,而将有互补性的储能组合配置,集合了各单一类型分布式储能系统的优势,提升了储能系统的整体性能,从而能更好地满足实际工况需求。不同类型分布式储能系统的供能特性存在差异,为充分发挥各类型分布式储能系统在电力系统中的作用,研究分布式储能系统的供能特性并对其调节能力进行量化评估显得非常重要。
目前,对分布式储能系统调节能力的相关研究中,文献[6]根据蓄电池具有能量密度大的优点和超级电容器功率密度大等优势,设计分布式储能组合系统运行控制方法,从而最大程度地实现消纳可再生能源发电。文献[7]建立了基于寿命量化的蓄电池和超级电容器混合储能模型,通过合理选择混合储能系统协调控制参数来延长蓄电池的寿命,从而提升混合储能的整体性能。文献[8]分析蓄电池和飞轮储能各自的调节特性优势,制定分布式储能组合系统的调度方案,从而提高含可再生能源的系统供电稳定性和可靠性。文献[9]建立了超导储能蓄电池简化数学模型,且充分利用蓄电池能量密度大、造价低和超导储能功率密度大、循环周期长等优点互补供电,大大改善了系统的电压性能。文献[10]结合压缩空气储能能量密度大、寿命长等优势和超级电容器储能充放电快速的特点,设计了压缩空气储能超级电容器混合储能系统无静差最优跟踪负荷控制策略,实现对电网负荷的快速寻优和跟踪。
现有文献的研究大都通过定性地配置储能系统来实现不同应用场合的需求,缺乏定量评估储能系统调节能力好坏的方法,无法定量评估不同类型储能组合模式下、不同容量配置比例下的分布式储能系统的调节能力。针对以上问题,文中提出基于模糊综合评判的储能系统调节能力评估方法,对不同类型储能组合模式下、不同容量配置比例下的分布式储能系统的调节能力进行量化分析,为在实际工况中合理配置分布式储能系统提供有效的理论支撑。
1 储能系统的供能特性分析目前常用的储能系统从放电时间尺度上归类,分为功率型储能和能量型储能。功率型储能装置主要有飞轮储能、超级电容器储能、超导储能等。能量型储能装置主要有抽水蓄能、压缩空气储能、蓄电池储能等。其中,蓄电池储能装置主要有钠硫电池、钒液流电池、铅酸电池、锂电池等。由于不同类型储能的自身机理不同,因此其供能特性也不同,其主要性能参数如表 1所示。
对储能系统主要性能参数进行分析可知,在能量型储能技术中,抽水蓄能、压缩空气储能、蓄电池储能可用于系统能量管理,进行发电调峰、平衡负载、用作系统备用电源等方面。其中,抽水蓄能和压缩空气储能容量大、寿命长,特别适用于大规模容量应用场合,但其应用场合受地形制约。蓄电池储能装置在小规模的分布式发电中应用最为广泛。其中,铅酸电池可靠性好、技术成熟,目前较多地应用于分布式发电,但其循环寿命较短,不宜深度放电,且存在有毒物质铅,严重污染周围环境。锂电池能量转换效率高、能量密度与功率密度高、无污染,但投资成本高,且在现阶段很难实现大规模应用。钒液流电池循环寿命长、安全性好,但能量转换效率较低,可适用于调峰电源和可再生能源发电等场合。钠硫电池能量密度高、能量转换效率高、安全性差,故可用于削峰填谷和电能质量调节等,但不适合在电力系统中大规模应用。能量型储能装置整体上较易实现大容量储能,然而其受响应速度、充放电次数等限制,因此不能用于实现快速的动态功率补偿、稳定电压波动、抑制动态振荡等场景。在功率型储能装置中,飞轮储能、超级电容器储能、超导储能的响应速度快、循环寿命长、能量转换效率高、安全性能好,但能量密度偏低,不适用于长时间的储能,主要适用于短时间动态功率补偿、紧急备用电源和频率调节等。另外,超级电容器储能比超导储能和飞轮储能运行维护少,可靠性高,因此在实际应用中有一定的优势。
总之,不同类型的储能系统因为其自身机理不同而有不同的供能特性,其应用也受限。单一类型的储能配置,从基本供能特性上可以实现储能的多种功能应用,但可能并不是较优的配置方案。如果能量化评估储能系统的调节能力,来充分挖掘其调节潜力,由此发挥各类储能技术的优点,从而实现储能系统的优化配置,来大大地提高储能系统的灵活性与实用性。
2 基于模糊综合评判的储能系统调节能力评估模型为量化评估储能系统的调节能力,且考虑到模糊综合评判法[13]能对同时关联着很多因素的事物做出定量性的综合评价,由此建立了基于模糊综合评判的储能系统调节能力评估模型,来定量化评估分布式储能系统的调节性能。
从第1节分析可知,储能系统的调节能力受其固有的技术特性如响应速度、能量密度、功率密度的影响,且储能系统在不同的应用场景中的性能也是有差异的。另外,由于储能系统的使用寿命、能量转化效率等也关联着储能的经济效益,所以经济性也影响着储能系统调节能力。因此,储能系统的调节能力受多方面因素影响,为量化评估其调节能力,首先要建立评估储能调节能力的因素集,即
| $ P = \{ {p_1},{p_2}, \cdots ,{p_m}\} , $ | (1) |
其中,pi是影响储能系统调节能力相关的因素。
考虑到不同因素的属性不同,运用归一化方法对各因素值进行统一量化。因素可分为效益型如功率密度、能量密度等(因素值越大越好)和成本型如响应速度、成本等(因素值越小越好),则归一化方法可表示为
| $ {e_{ij}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{e_{ij}^\prime - {\rm{min}} (e_{ij}^\prime )}}{{ {\rm{max}} (\text{e}_{ij}^\prime ) - {\rm{min}} (\text{e}_{ij}^\prime )}},}&{{\rm{ 如果 }}e_{ij}^\prime {\rm{ 为效益型因素值, }}}\\ {\frac{{ {\rm{max}} (\text{e}_{ij}^\prime ) - e_{ij}^\prime }}{{ {\rm{max}} (\text{e}_{ij}^\prime ) - {\rm{min}} (\text{e}_{ij}^\prime )}},}&{{\rm{ 如果 }}e_{ij}^\prime {\rm{ 为成本型因素值, }}} \end{array}} \right. $ | (2) |
其中, eij为第i种分布式储能系统的第j个因素的归一化值,e′ij为的原始值,
经归一化后可得因素集E的各因素值,即
| $ \mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} {{e_{11}}}& \cdots &{{e_{1j}}}\\ \vdots &{}& \vdots \\ {{e_{i1}}}& \cdots &{{e_{ij}}} \end{array}} \right]。$ | (3) |
然后,用“优”“中”“差”来评价储能系统调节能力,则建立评语集为
| $ Q = \{ {q_1},{q_2},{q_3}\} = \{ {\rm{ 优,中,差 }}\} , $ | (4) |
其中, qk(k=1, 2, 3)是对评估结果划分的等级。
其次,由于各因素值eij对不同评语的量化值是由隶属函数确定的,文中采用Gauss型函数f(x, σ, c)[14]为
| $ f(x,\sigma ,c) = {e^{ - (x - c)}}^{2/2{\sigma ^2}}, $ | (5) |
式中:x为决策因素值;σ和c为Gauss函数的2个参数,其取值可参考文献[14]。将eij带入隶属函数中,获得各因素隶属于评语集Q的评估矩阵为
| $ \mathit{\boldsymbol{O}} = \left[ {\begin{array}{*{20}{c}} {{o_{q1}}({e_{i1}})}& \cdots &{{o_{q3}}({e_{i1}})}\\ \vdots &{}& \vdots \\ {{o_{q1}}({e_{ij}})}& \cdots &{{o_{q3}}({e_{ij}})} \end{array}} \right], $ | (6) |
式中:oqk(eij)为因素值eij对评判等级qk的隶属程度大小值。
再者,在储能系统调节能力评估模型中,权重表示了各个因素对储能系统调节能力的影响程度,直接关系到最终评估的结果。目前已有很多确定权重的方法,其中属性层次分析方法(AHM, attribute hierarchical model)操作灵活简便且实用性强[15]。则文中采用AHM确定各评判因素的权重值,建立权重集为
| $ W = ({w_1},{w_2}, \cdots {w_m}), $ | (7) |
式中,wi是各因素对应的权重值。
最后,根据式(6)和式(7)确定储能系统调节能力评估结果,即
| $ \mathit{\boldsymbol{L}} = W*\mathit{\boldsymbol{O}}。$ | (8) |
文中取“优”评语等级的数值表示储能系统调节能力评估结果,且其数值越大,则储能系统调节能力就越好。
3 算例分析为验证文中所提方法的有效性,对不同储能组合模式下、不同容量配置比例下的分布式储能系统调节性能进行分析。
3.1 不同类型储能组合模式下的分布式储能系统调节能力分析目前常见的不同类型储能组合模式有蓄电池储能和超级电容器储能组合、蓄电池储能和飞轮储能组合、压缩空气储能和超级电容器储能组合,基于在技术经济上影响储能供能特性的因素,建立其调节能力评估模型,来量化分析其调节能力,并通过仿真分析来验证量化分析结果的准确性。
3.1.1 量化评估分析分布式储能的功率密度、能量密度以及响应速度能从技术性上反映其本身的供能能力,并且分布式储能的能量成本和功率成本可以体现其经济性,则选取功率密度p1、能量密度p2、响应速度p3、功率成本p4、能量成本p5这5个因素来建立因素集P,为
| $ P = \{ {p_1},{p_2},{p_3},{p_4},{p_5}\}。$ | (9) |
此外,功率密度和能量密度属于效益型因素,而响应速度和功率成本、能量成本属于成本型因素,根据表 1和公式(3)得到评判因素值矩阵。
| $ \mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} {0.36}&{0.93}&{0.98}&{0.32}&{0.99}\\ {0.28}&{0.86}&{0.98}&{0.13}&{0.04}\\ {0.24}&{0.62}&{0.39}&{0.59}&{0.03} \end{array}} \right]。$ | (10) |
每个决策者都有各自偏好,因此各评判因素在目标衡量中所占的比重会有所区别。笔者综合考虑组合储能系统的调节效果能同时保证电力系统运行的稳定性、可靠性和经济性,即组合储能系统的功率密度、能量密度、响应速度、功率成本和能量成本对综合评价其调节能力同等重要,进而利用AHM确定各因素的权重值如公式(11)所示,具体计算过程见文献[15]。
| $ W = (0.2,0.2,0.2,0.2,0.2)。$ | (11) |
由式(8)得到组合储能系统的调节能力评估结果为
| $ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {0.65}&{0.57}&{0.17}\\ {0.52}&{0.63}&{0.23}\\ {0.39}&{0.46}&{0.51} \end{array}} \right]。$ | (12) |
则不同类型储能组合模式下的分布式储能系统调节能力如图 1所示。
|
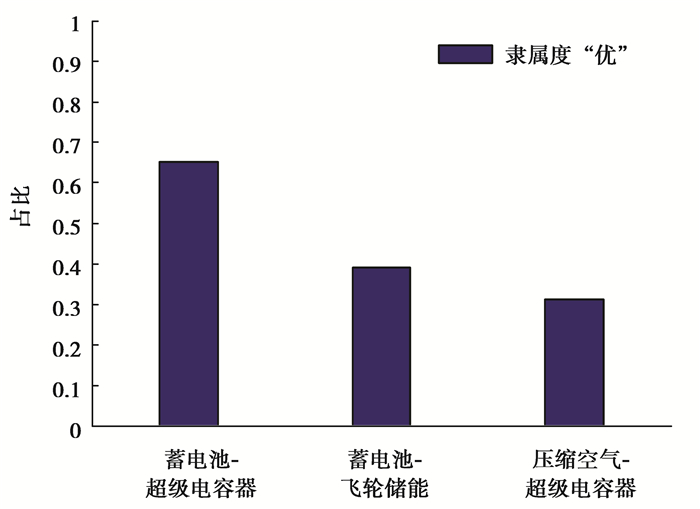
图 1 不同类型储能组合模式下的分布式储能系统调节能力 Fig. 1 Distributed energy storage system regulation capability under different types of energy storage combination modes |
由图 1知,蓄电池超级电容器储能的调节能力属于“优”的隶属度最大,蓄电池飞轮储能的次之,而压缩空气储能超级电容器储能的最小。因此,蓄电池超级电容器储能的调节能力较其他储能组合模式的调节能力好,更能保证系统稳定、可靠和经济运行。
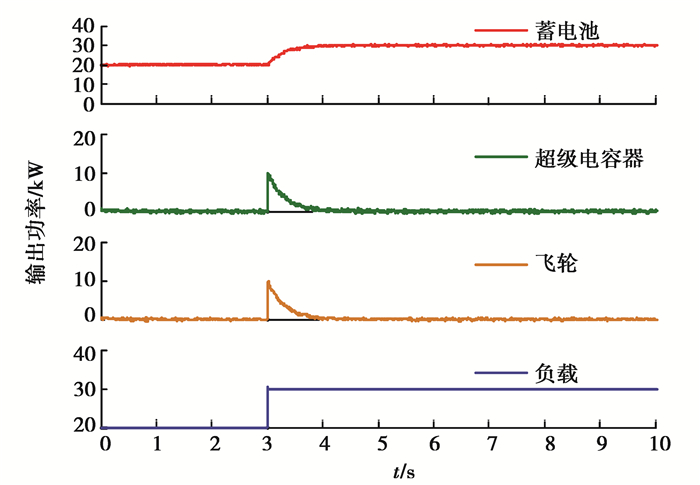
3.1.2 仿真分析通过模拟负载变化,从技术上仿真分析分布式储能组合系统的供能特性,并又结合其经济性,综合分析组合储能系统的调节能力。当负载功率在t=0~3 s内为20 kW,而当t=3 s时由负载功率从20 kW瞬时增加10 kW到30 kW后维持不变时,蓄电池储能超级电容器储能组合系统和蓄电池储能飞轮储能组合系统的功率输出结果如图 2、图 3所示。
|
图 2 单一分布式储能系统的输出特性 Fig. 2 Output characteristics of single distributed energy storage system |
|
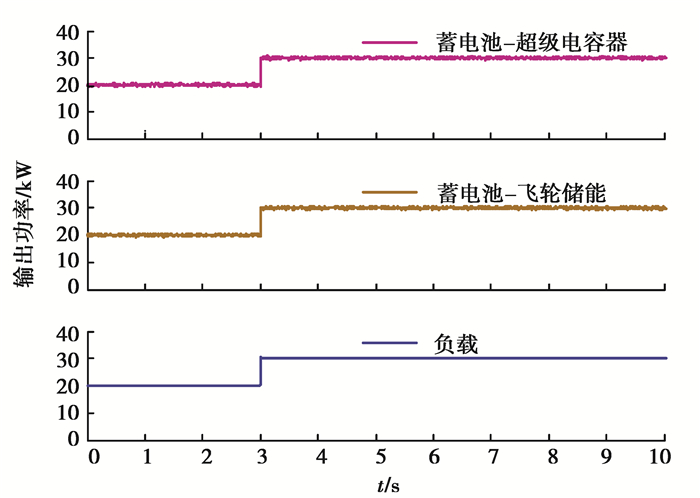
图 3 不同类型储能组合模式下的分布式储能系统的输出特性 Fig. 3 Output characteristics of distributed energy storage systems in different types of energy storage combination modes |
由图 2和图 3可知,蓄电池在t=0~10 s内持续稳定地为负载供电,而在t=3 s时不能瞬时从20 kW增加到30 kW;超级电容器和飞轮储能均由初始的0 kW,在t=3 s时瞬时补偿负载增量的10 kW后恢复到初始状态;蓄电池超级电容器储能和蓄电池飞轮储能基本都持续向负载供电且在t=3 s时瞬时响应负载变化。因此,将有蓄电池超级电容器储能和蓄电池飞轮储能都有较好的调节性能且较单一储能的调节能力好。
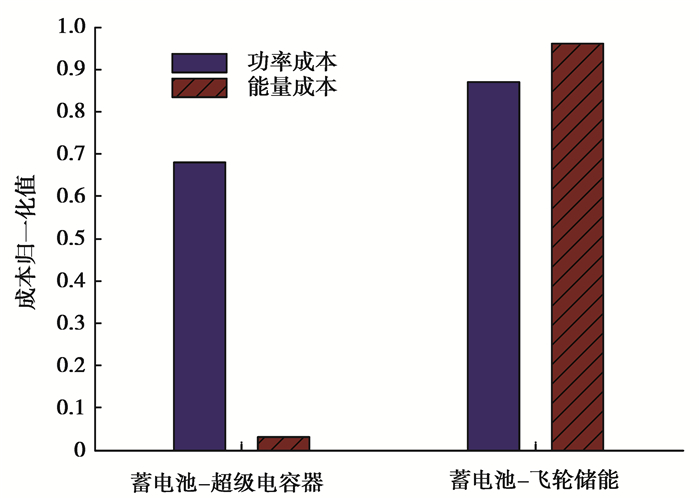
从图 3可知,蓄电池超级电容器储能和蓄电池飞轮储能有相似的调节效果。但是,如图 4所示,蓄电池超级电容器储能的功率成本和能量成本均比蓄电池飞轮储能的低。因此,从经济性上看,蓄电池超级电容器储能比蓄电池飞轮储能能更好地满足电网运行的经济性。
|
图 4 不同类型储能组合模式下的分布式储能系统的成本 Fig. 4 Cost of distributed energy storage systems under different types of energy storage combined modes |
综上所述,从技术性上看,蓄电池超级电容器储能和蓄电池飞轮储能均比单一的蓄电池、超级电容器储能、飞轮储能的供能性能好,且有相似的调节效果;从经济性上看,蓄电池超级电容器储能比蓄电池飞轮储能的成本低。总之,综合技术经济上来看,蓄电池超级电容器储能具有较好的调节能力。
3.2 不同容量配置比例下的分布式储能系统调节能力分析选取蓄电池和超级电容器储能组合系统,在削峰填谷的场景下,结合影响储能系统削峰填谷效果的主要因素,建立其不同容量配置比例下的调节能力评估模型,来量化分析其调节能力,并通过仿真分析来验证量化分析结果的准确性。
3.2.1 量化评估分析削峰率[16]表示了储能系统的调峰能力,削峰率越大则储能系统的调节能力越好;低储高发套利[17]即储能系统在电网电价低时储能、电网电价高时放电的过程中获得的经济效益,并在一定程度上反映了应用储能的收益;固定投资成本[17]能直接反映储能的初始投资成本。则从技术经济性考虑,将削峰率p1、低储高发套利p2、固定投资成本p3作为评判因素,建立模糊评判模型因素集,即
| $ P = \{ {p_1},{p_2},{p_3}\}。$ | (13) |
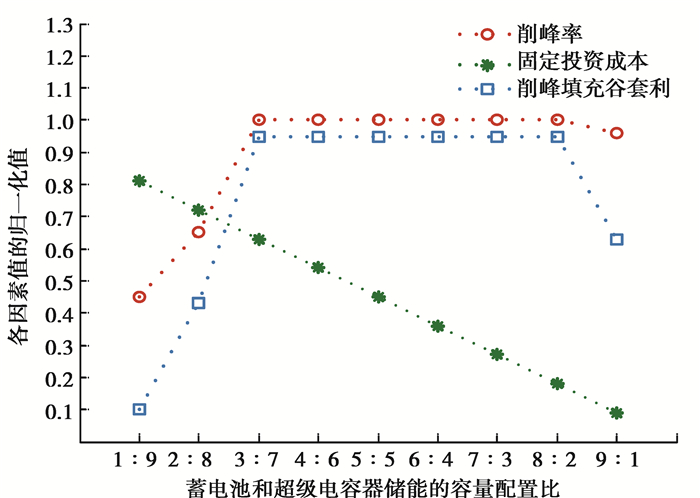
将蓄电池和超级电容器的比例分别为1:9、2:8、3:7、4:6、5:5、6:4、7:3、8:2、9:1组合成9组同等容量的储能系统进行削峰填谷仿真实验分别可获得削峰率、低储高发套利和固定投资成本。此外,削峰率和低储高发套利属于效益型因素值,而固定投资成本属于成本型因素值,根据公式(3)将数据标准化后如图 5所示,从而得到评判因素值矩阵E。
|
图 5 不同容量配置比例下的储能系统的各因素归一化值 Fig. 5 Normalized values of various factors of energy storage systems at different capacity ratios |
同理,设削峰率、低储高发套利、固定投资成本对不同容量配置比例下的蓄电池和超级电容器储能组合系统的调节能力同等重要,则利用AHM确定各因素的权重值为
| $ W = \left( {\frac{1}{3},\frac{1}{3},\frac{1}{3}} \right)。$ | (14) |
最后,由公式(8)得到不同容量配置比例下的蓄电池和超级电容器储能系统的调节能力评估结果为
| $ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {0.06}&{0.49}&{0.77}\\ {0.21}&{0.75}&{0.48}\\ {0.68}&{0.40}&{0.23}\\ {0.70}&{0.47}&{0.15}\\ {0.74}&{0.49}&{0.08}\\ {0.81}&{0.47}&{0.04}\\ {0.90}&{0.40}&{0.01}\\ {0.97}&{0.31}&{0.01}\\ {0.81}&{0.49}&{0.04} \end{array}} \right]。$ | (15) |
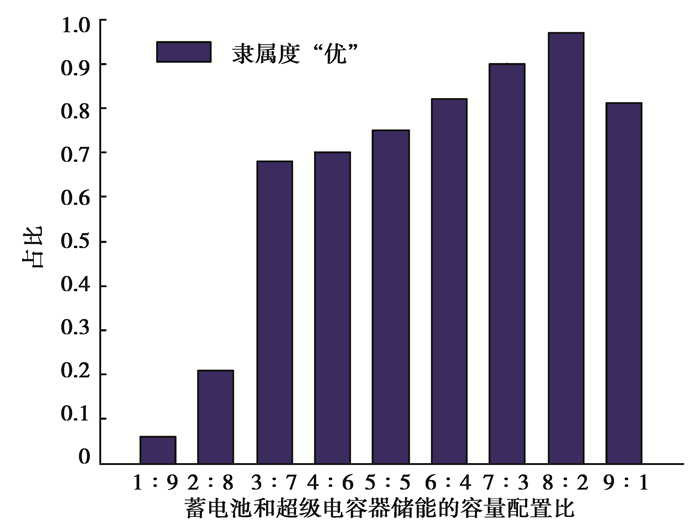
则不同容量配置比例的蓄电池和超级电容器储能系统的调节能力属于“优”的隶属度值如图 6所示。
|
图 6 不同容量配置比例下的储能系统调节能力 Fig. 6 Energy storage system regulation capacity under different capacity configuration ratios |
从图 6可知,蓄电池和超级电容器储能比例为8:2时的混合储能系统调节能力属于“优”的隶属度较其他比例的都大,这说明蓄电池和超级电容器储能比例为8:2时的储能系统调节性能较其他比例的好。
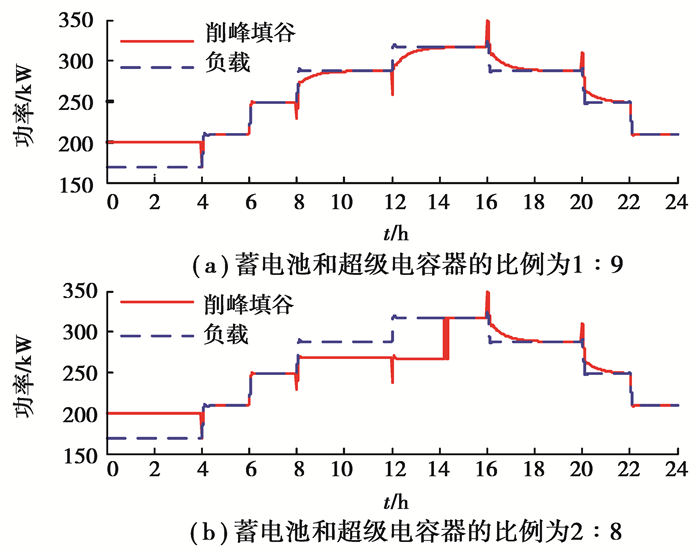
3.2.2 仿真分析以削峰填谷为蓄电池和超级电容器储能组合系统的应用场景,从技术性上来分析其调节能力。假定一天的负荷在0~4 h为低谷时段、8~20 h为高峰时段,并且设定低谷阈值为200 kW、高峰阈值为270 kW。取不同蓄电池和超级电容器的比例分别为1:9、2:8、3:7、4:6、5:5、6:4、7:3、8:2、9:1组合成9组同等容量的储能系统,在负荷出现低谷和峰值时,调节储能系统输出,达到削峰填谷的目的,仿真结果如图 7和图 8所示。
|
图 7 蓄电池和超级电容器的比例为1:9、2:8的削峰填谷效果 Fig. 7 Peak-cutting and valley-filling effect of 1:9 and 2:8 ratio of storage battery and supercapacitor |
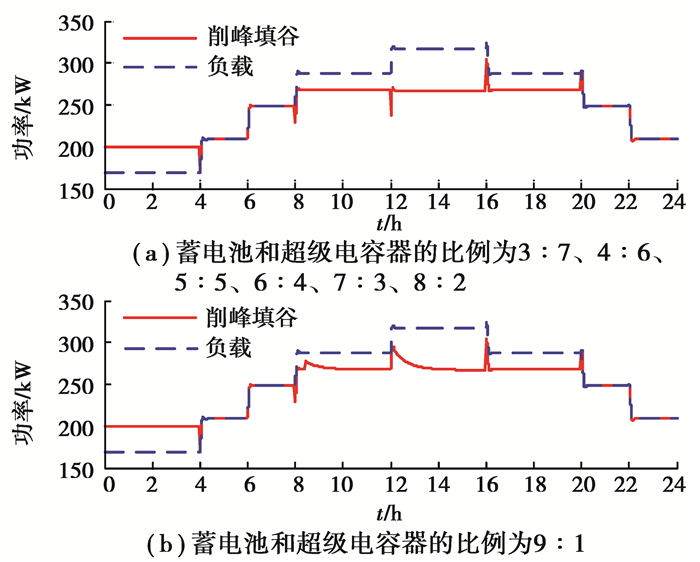
|
图 8 蓄电池和超级电容器的比例为3:7、4:6、5:5、6:4、7:3、8:2、9:1的削峰填谷效果 Fig. 8 Peak-cutting and valley-filling effect of 3:7, 4:6, 5:5, 6:4, 7:3, 8:2 and 9:1 ratio of storage battery and supercapacitor |
从图 7和图 8可知,蓄电池和超级电容器的比例为3:7、4:6、5:5、6:4、7:3、8:2有相似的调峰效果,且调峰特性较好于比例为1:9、2:8、9:1的调峰效果。然而,结合图 5可知,即使蓄电池和超级电容器的比例为3:7、4:6、5:5、6:4、7:3、8:2的削峰填谷套利值是一样的,但固定投资成本是依次减小的。因此,综合技术经济上得到蓄电池和超级电容器储能比例为8:2时的储能的调节能力较其他比例的好。
4 结论文中对各类型分布式储能系统的基本供能性能进行了比较分析,基于此又根据模糊综合评判方法,建立了储能系统的调节能力评估模型,并以评估不同组合模式下和不同容量配置比例下的储能系统调节能力为算例,定量化地评估分布式储能系统的调节能力,且又结合仿真分析检验了量化评估结果的合理性。通过理论分析和算例分析表明,文中所提出的基于模糊综合评判的储能系统调节能力评估方法具有一定的实用性,为探寻不同类型分布式储能组合系统的调节潜力及优化配置提供有效的理论指导。
| [1] |
李建林, 马会萌, 惠东, 等. 储能技术融合分布式可再生能源的现状及发展趋势[J]. 电工技术学报, 2016, 31(14): 1-10, 20. LI Jianlin, MA Huimeng, HUI Dong, et al. Present development condition and trends of energy storage technology in the integration of distributed renewable energy[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 1-10, 20. (in Chinese) DOI:10.3969/j.issn.1000-6753.2016.14.001 |
| [2] |
Luo X, Wang J H, Dooner M, et al. Overview of current development in electrical energy storage technologies and the application potential in power system operation[J]. Applied Energy, 2015, 137: 511-536. DOI:10.1016/j.apenergy.2014.09.081 |
| [3] |
Kargarian A, Hug G. Optimal sizing of energy storage systems:a combination of hourly and intra-hour time perspectives[J]. IET Generation, Transmission & Distribution, 2016, 10(3): 594-600. |
| [4] |
Feehall T, Forsyth A J, Todd R, et al. Battery energy storage systems for the electricity grid: UK research facilities[C]//IET Power Electronics, Machines and Drives 2016. IET, 2016.
|
| [5] |
Farhadi M, Mohammed O. Energy storage technologies for high-power applications[J]. IEEE Transactions on Industry Applications, 2016, 52(3): 1953-1961. DOI:10.1109/TIA.2015.2511096 |
| [6] |
于芃, 刘兴华, 孙树敏, 等. 高可再生能源渗透率海岛微电网运行控制[J]. 电网技术, 2018, 42(3): 779-788. YU Peng, LIU Xinghua, SUN Shumin, et al. Study on operation control of island microgrid with high renewable energy penetration[J]. Power System Technology, 2018, 42(3): 779-788. (in Chinese) |
| [7] |
李逢兵, 谢开贵, 张雪松, 等. 基于寿命量化的混合储能系统协调控制参数优化[J]. 电力系统自动化, 2014, 38(1): 1-5. LI Fengbing, XIE Kaigui, ZHANG Xuesong, et al. Optimization of coordinated control parameters for hybrid energy storage system based on life quantization[J]. Automation of Electric Power Systems, 2014, 38(1): 1-5. (in Chinese) |
| [8] |
李凤婷, 曾祥军, 夏令琴. 基于多变量模糊控制的直流微网混合储能策略[J]. 高电压技术, 2018, 44(1): 126-135. LI Fengting, ZENG Xiangjun, XIA Lingqin. Hybrid energy storage strategy based on multivariable fuzzy control for DC microgrid[J]. High Voltage Engineering, 2018, 44(1): 126-135. (in Chinese) |
| [9] |
杨芳华, 刘娇, 陈浩, 等. 超导-蓄电池混合储能装置接于配电网对电压稳定性的影响[J]. 电力学报, 2014, 29(3): 211-214. YANG Fanghua, LIU Jiao, CHEN Hao, et al. Influence of superconducting magnetic-battery energy storage hybrid energy storage connected to distribution on voltage stability[J]. Journal of Electric Power, 2014, 29(3): 211-214. (in Chinese) |
| [10] |
姜萍, 赵振家, 吕海建. 压缩空气与超级电容混合储能膨胀发电系统建模与最优跟踪负荷控制[J]. 电测与仪表, 2016, 53(24): 61-68. JIANG Ping, ZHAO Zhenjia, LV Haijian. The optimal tracking load control based on super capacitor for the expansion power system in compressed air energy storage[J]. Electrical Measurement & Instrumentation, 2016, 53(24): 61-68. (in Chinese) DOI:10.3969/j.issn.1001-1390.2016.24.011 |
| [11] |
Luo X, Wang J H, Dooner M, et al. Overview of current development in electrical energy storage technologies and the application potential in power system operation[J]. Applied Energy, 2015, 137: 511-536. DOI:10.1016/j.apenergy.2014.09.081 |
| [12] |
Taylor P, Bolton R, Stone D, et al. Pathways for energy storage in the UK[M/OL]. (2012-03-27)[2019-05-22]. http://oro.open.ac.uk/40087/2/Pathways_for_Energy_Storage_in_the_UK.pdf.
|
| [13] |
Yang W C, Xu K, Lian J J, et al. Multiple flood vulnerability assessment approach based on fuzzy comprehensive evaluation method and coordinated development degree model[J]. Journal of Environmental Management, 2018, 213: 440-450. |
| [14] |
彭显刚, 林利祥, 翁奕珊, 等. 基于模糊综合评判和综合赋权的抗灾型配电网骨干网架规划[J]. 电力系统自动化, 2015, 39(12): 172-178. PENG Xiangang, LIN Lixiang, WENG Yishan, et al. Decision-making method for anti-disaster distribution network backbone upgrade based on fuzzy comprehensive evaluation and comprehensive weights[J]. Automation of Electric Power Systems, 2015, 39(12): 172-178. (in Chinese) DOI:10.7500/AEPS20140910007 |
| [15] |
张晓东, 胡俊成, 杨青, 等. 基于AHM模糊综合评价法的老旧小区更新评价系统[J]. 城市发展研究, 2017, 24(12): I0020-I0022, I0027. ZHANG Xiaodong, HU Juncheng, YANG Qing, et al. Research on the evaluation system of renewal for old residential district based on AHM and comprehensive assessment method[J]. Urban Studies, 2017, 24(12): 10020-10022, 10027. (in Chinese) |
| [16] |
Oudalov A, Chartouni D, Ohler C, et al. Value analysis of battery energy storage applications in power systems[C]//2006 IEEE PES Power Systems Conference and Exposition. Atlanta, GA, USA, 2006: 2206-2211.
|
| [17] |
Kazempour S J, Moghaddam M P. Economic viability of NaS battery plant in a competitive electricity market[C]//2009 International Conference on Clean Electrical Power. Capri, Italy, 2009: 453-459.
|
 2020, Vol. 43
2020, Vol. 43


