感应耦合电能传输系统(ICPT,inductively coupled power transfer)是以电磁感应为原理[1],打破传统的物理接触,以非接触的形式实现装置与装置之间的电能传递,在水下易燃易爆、电动牙刷、人工心脏、电动汽车等领域都有着广泛的应用[2-4],该技术不仅可以一对一地充电,甚至可以实现一对多的充电方式(包括可移动充电设备)[5-8]。目前,该技术正受到国内外许多专家学者的关注与青睐。
目前,在感应耦合传输系统中常用的输出功率调节方式有调幅、调频、移相控制、能量注入控制等。文献[9]对SS和SP结构ICPT系统中不同谐振频率的功率传输特性进行了分析与优化,并未深入探究输出功率的调节方法。文献[10]提出了一种移相控制策略,通过控制全桥逆变器桥臂的直通时间来调节系统的输出功率,无需增加额外的硬件电路,但系统的谐振电压波形会随着移相角的增加而逐渐畸变,当畸变程度过大时,有可能导致系统不能正常工作。文献[11]通过移相控制逆变器的移相角调节输出功率,在此基础上提出了一种基于谐波的移相控制调节功率的方法,与文献[11]不同的是此方法用谐波代替基波传输功率。文献[12]中逆变环节采用软开关技术,并通过离散能量注入的方法调节输出功率。文献[13]提出了在次级增加DC-DC结构,调节输出功率,这种功率调节方式属于调幅方式,该方式会加大系统的可控难度,降低系统的传输效率,并带来不必要的损耗和成本。以上的功率调节方式实现的是功率的连续调节,文中提出一种基于解耦原理的拓扑结构,通过控制开关管导通的占空比,实现对电压的不连续调节,进而达到对平均输出功率动态调节的目的,通过仿真和搭建实验平台验证本方案的可行性。
1 动态解耦拓扑结构的原理分析为了保证系统输出功率实时满足负载的需求量,需要根据负载的情况对副边全桥整流电路的输出功率进行动态调节。文中提出的一种新的输出功率调节方案,即在全桥整流电路二极管D3、D4两端各并联一个全控型开关管MOSFET S1和S2,电流检测环节用电流霍尔传感器检测出输出电流的大小,驱动电路通过读取流过负载电流值的大小,与设定值进行比较,得出一个驱动信号,控制S1和S2的同时导通与关断,当S1和S2同时导通时,使全桥整流电路和负载完全脱离谐振网络,实现系统的解耦。图 1为双管功率调节方式的电路图。
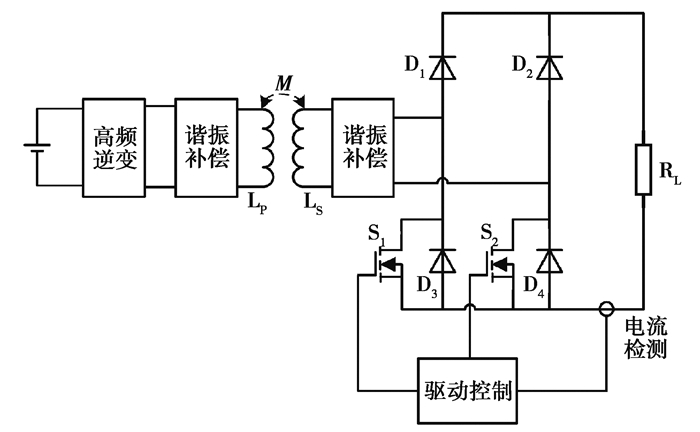
|
图 1 双管功率调节方式电路图 Fig. 1 Double tube adjustment mode circuit diagram |
图 1中在负载侧加入电流检测环节,从而获取流经负载的电流值大小,进而得到输出功率的大小,将流经负载的电流或功率输入至驱动控制模块,驱动控制模块将根据所需功率的大小来调节开关管S1和S2的占空比,实现对谐振网络输出电压的不连续调节,以此达到调节输出功率的目的。
开关管S1和S2的驱动信号为设定频率的方波信号,2个开关管采用相同的驱动信号,该驱动信号占空比在100%~0间变化时,输出功率在最大输出功率的0~100%变化。即当驱动信号占空比为100%时输出为0;占空比为0时,输出功率为最大输出功率。
2 动态解耦系统建模在系统进行动态解耦时,S1和S2 2个开关管同时导通,负载侧脱离谐振网络,谐振网络两端输出会直接短路,此时负载端的反射阻抗会发生变化,谐振网络的电流即流过2个开关管S1和S2的电流会瞬间发生变化,此时如果开关管长时间过流将导致开关管损坏,因此需要一种恒流输出的电路来保证开关管的正常使用。通过对比分析各种谐振网络结构的特点[14],LCC-LCC谐振补偿网络几乎不受负载端反射阻抗的影响,具有能够保持谐振网络输出恒定电流的特性[15],从而保证电路在解耦的过程中流过全控型开关管的电流快速稳定在一个恒定值,从而避免开关管在解耦期间因长时间过流而损坏,并且LCC-LCC谐振补偿网络具有其他结构不可比拟的输出功率稳定性[16]。图 2为基于动态解耦原理的双LCC电路拓扑。
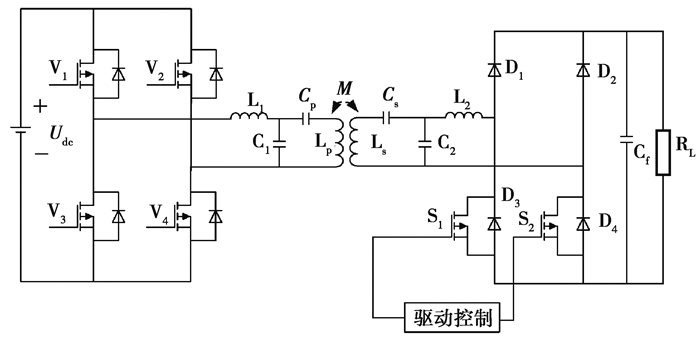
|
图 2 基于动态解耦原理的双LCC电路拓扑 Fig. 2 Dual LCC circuit topology based on dynamic decoupling principle |
图 2中Udc为电源侧输入的直流电压,Lp和Ls分别是发射线圈和接收线圈,Cp和Cs 分别是Lp和Ls的补偿电容,M是发射线圈Lp与接受线圈Ls之间的互感,开关管V1~V4构成全桥逆变器的2个桥臂,作用是将电源侧输入的直流电转变成高频的交流电加在原边电路的谐振补偿结构上,从而可以在原边的发射线圈中产生一个高频的交变电流,通过线圈Lp和Ls之间的磁场耦合,实现非物理接触供电,D1~D4构成副边全桥整流电路,使负载得到需要的直流电。双LCC谐振补偿结构还可以达到“Boost”的效果,因此可以减少电路中Boost环节的设计,降低了系统的体积和成本。
假定所有开关管和输入的直流电源都是理想的,经过全桥逆变器后的输出电压可以等效为一个脉冲电压Uin,三阶LCC原边补偿网络结构简化模型如图 3所示。

|
图 3 原边LCC补偿结构等效电路图 Fig. 3 Original circuit diagram of LCC compensation structure |
由于LCC结构是由LCL结构演变而来,在此分析电路时把Lp和Cp等效成L,可以等效成LCL结构分析,当满足L1=L时,谐振网络功率因数为1时,有功功率传输最大,Zref为副边对原边的反射阻抗。
| $ \omega = {\omega _0} = \frac{1}{{\sqrt {{L_1}{C_1}} }}, $ | (1) |
由于把Lp和Cp等效成L,它们之间关系式为
| $ j\omega L = j\omega {L_p} + \frac{1}{{j\omega {C_p}}}, $ | (2) |
原边电路总阻抗Zp为
| $ {Z_{\rm{p}}} = j\omega {L_1} + \frac{1}{{\text{j}\omega {C_1} + \frac{1}{{{Z_{ref}} + j\omega L}}}}, $ | (3) |
原边谐振网络输入电流Iin和原边线圈电流Ip为
| $ {I_{{\rm{in}}}} = \frac{{{U_{{\rm{in}}}}}}{{{Z_{\rm{p}}}}} = \frac{{{U_{{\rm{in}}}}{C_1}{Z_{{\rm{ref}}}}}}{{{L_1}}}, $ | (4) |
| $ {I_{\rm{p}}} = {I_{{\rm{in}}}}\frac{1}{{1 + \text{j}\omega {C_1}({Z_{{\rm{ref}}}} + \text{j}\omega L)}} = \frac{{{U_{{\rm{in}}}}}}{{{L_1}}}。$ | (5) |
由式(5)可以看出, 原边线圈的输出电流大小与副边对原边的反射阻抗无关,即发射端线圈输出电流的大小不受副边反射阻抗的影响,并且当发射端输入电压Uin和补偿电感L1均为定值时Ip为定值,原边电路表现为恒流输出特性。
由于原边电路的LCC补偿结构,使得原边线圈Lp可以恒流输出,根据
| $ {U_{\rm{s}}} = j{\omega _0}M{I_{\rm{P}}}, $ | (6) |
式中,Us为接收端等效电压源。由于Us为定值,因此副边线圈感应到的电压是恒定的,副边等效电路图如图 4所示。其中L3为Ls的等效电感,电压Ue为谐振网络的输出电压,Re为整流电路与负载侧的等效电阻,
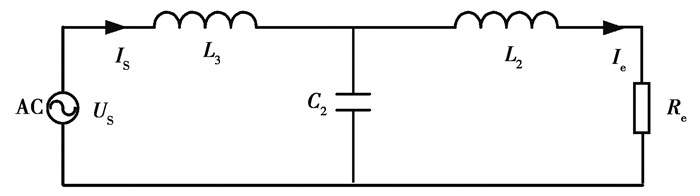
|
图 4 副边LCC补偿结构等效电路图 Fig. 4 Equivalent circuit diagram of the secondary side LCC compensation structure |
根据电路的对称性,可以直接得出谐振网络的输出电流Ie和功率P的公式。
| $ {I_{\rm{e}}} = \frac{{j\omega M{I_{\rm{p}}}}}{{{L_2}}} = \frac{{j\omega M{U_{{\rm{in}}}}}}{{{L_1}{L_2}}}, $ | (7) |
| $ P = \frac{{j\omega M{U_{{\rm{in}}}}{U_{\rm{e}}}}}{{{L_1}{L_2}}}。$ | (8) |
经过理论推导,由式(7)可以看出,谐振网络的输出电流为一恒定值,与等效负载电阻大小无关,理论上证实了双LCC电路谐振网络输出电流的恒流特性。由式(8)谐振网络的输出功率的调节可以通过改变谐振网络的输出电压来实现。
定义S1和S2开关管导通的占空比为d,则有
| $ d = \frac{t}{T}, $ | (9) |
式中:t是开关管S1和S2的导通时间;T为开关管S1和S2的导通周期。
周期内谐振网络两端输出的平均电压和平均功率为
| $ U_{\rm{e}}^\prime = (1 - d){U_{\rm{e}}}, $ | (10) |
| $ {P^\prime } = \frac{{j\omega M{U_{{\rm{in}}}}U_{\rm{e}}^\prime }}{{{L_1}{L_2}}} = \frac{{j(1 - d)\omega M{U_{{\rm{in}}}}{U_{\rm{e}}}}}{{{L_1}{L_2}}}。$ | (11) |
根据计算结果可以得出,谐振网络两端输出的平均电压和平均输出功率与占空比d存在一定的关系。当d=0时,负载侧(负载侧指的是整流电路和负载部分)与谐振网络未发生解耦,此时系统输出功率为最大输出功率的100%;当d=1时,负载侧与谐振网络解耦,谐振网络对外输出功率为0。理论上验证了当驱动信号占空比在100%~0之间变化时,输出功率在最大输出功率的0~100%变化。
3 开关管的应力分析及抑制措施当发生动态解耦时,负载侧与谐振网络脱离,造成谐振网络输出电流瞬间变大,同时开关管在导通的瞬间所承受的应力和损耗上升,因此需采取一定措施防止开关管恶化。为方便分析整流电路中2个开关管在导通与关断时的电压与电流应力问题,副边电路为图 5所示,S1和S2为整流电路下侧2个二极管旁并联的2个MOSFET,VD1和VD2分别为2个开关管的续流二极管。

|
图 5 副边电路图 Fig. 5 Secondary circuit diagram |
在开关管关断期间,开关管S1和S2承受的电压被箝位于负载两端电压值。假设开关管是理想的,当开关管迅速导通时,开关管承受的电压值为0,不存在电压尖峰,因此不需要对开关管采取尖峰抑制措施。只要在开关管选型上满足谐振网络输出电压值低于开关管所承受的电压值即可。
3.2 电流尖峰分析及抑制措施为便于讨论,一个周期内分为几个阶段对开关管S1进行分析,开关管S2的情况与S1类似,因此不做讨论。如图 6所示为控制2个开关管导通与关断的脉冲信号图。t0~t3为一个周期,设置t0~t1为开关管的导通时间,占一个周期的30%,t0~t2为半个周期。此电路每个周期的工作分3个阶段来分析。
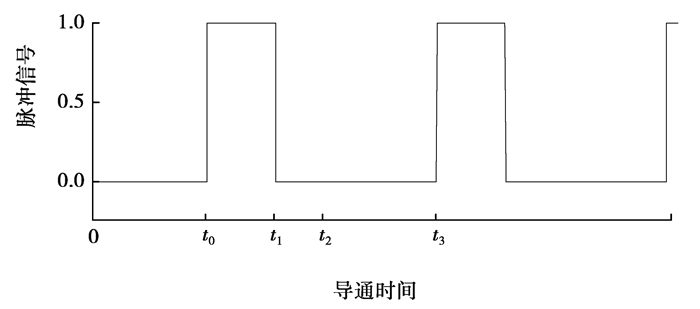
|
图 6 开关管的脉冲信号图 Fig. 6 Pulse signal diagram of the switch tube |
1) t0~t1阶段:开关管S1和S2同时导通,S1和S2形成一个回路,S1的续流二极管VD1两端承受上正下负电压。
2) t1~t2阶段:开关管S1和S2关断,电流流经整流二极管D1—负载侧—D4形成回路。S1的续流二极管VD1两端承受上正下负电压。
3) t2~t3阶段:开关管S1和S2持续关断,此时电流经过D2—负载侧—D3,S1的续流二极管VD1导通,两端承受下正上负电压。
在t0时刻开关管S1和S2同时迅速导通瞬间,负载侧迅速与谐振网络解耦,谐振网络的输出电流变大,处于反向恢复过程的续流二极管两端被施加反向电压,开始反向关断,产生的反向电流流过开关管产生很大的冲击电流,因此,开关管的电流尖峰主要是由二极管的反向恢复电流和谐振网络输出电流叠加而造成的,不仅会增加开关管损耗,影响系统的运行效率,而且极易损坏开关管。从2个方面抑制电流尖峰,一是谐振网络方面,选择恒流输出的谐振网络补偿结构,能从一定程度上减小电流尖峰;二是改善二极管的反向恢复电流。为降低反向恢复电流对开关管造成的电流尖峰,可以采取以下措施:
1) 选择反向恢复时间小的续流二极管。在开关管开通时将续流二极管反向恢复电路等效为RS与LS的串联电路。iDR为二极管的反向电流,UDR为二极管两端被施加的反向电压。
| $ {L_{\rm{S}}}\frac{{{\rm{d}}{i_{{\rm{DR}}}}}}{{{\rm{d}}t}} + {i_{{\rm{DR}}}}{R_{\rm{S}}} = {U_{{\rm{DR}}}}, $ | (12) |
| $ {i_{{\rm{DR}}}} = \frac{{{U_{{\rm{DR}}}}}}{{{R_{\rm{S}}}}}(1 - {e^{ - \frac{{R{\rm{S}}}}{{L{\rm{S}}}}t}}), $ | (13) |
式中,t为二极管的反向恢复时间,二极管的反向电流iDR越大,造成的电流尖峰越大。所以采用反向恢复时间小的二极管可以减小电流尖峰。
2) 在开关管两侧加RC吸收电路。吸收电路如图 7所示。当续流二极管被施加反向电压时,吸收电路中的电容C可以分担一部分二极管两端的电压。
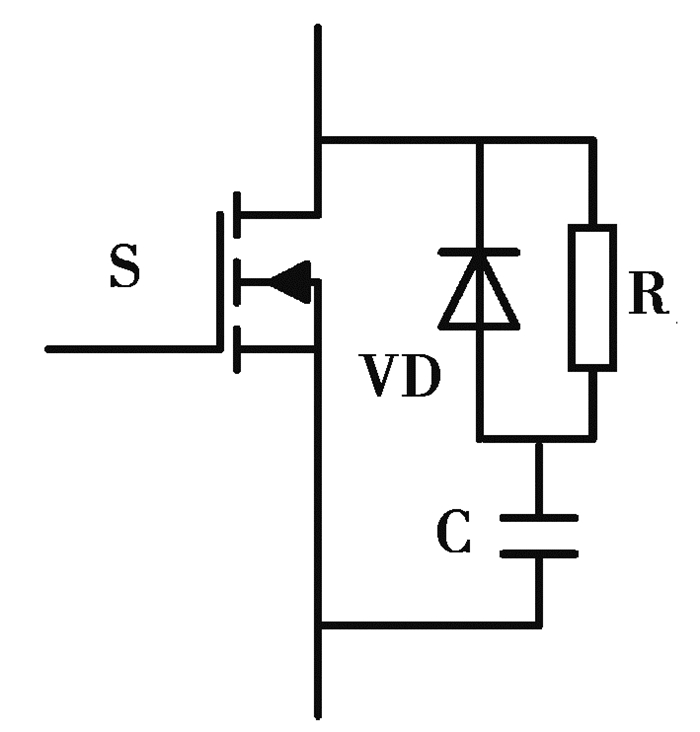
|
图 7 RC吸收电路图 Fig. 7 RC absorption circuit diagram |
图 8为未加RC吸收电路和加RC吸收电路后流过开关管的电流is1对比图。由式(13),二极管两端反向电压减小时,反向电流减小,可以降低电流尖峰,但会加长续流二极管的反向恢复时间,因此在实际应用中需恰当选取吸收电路电容值。

|
图 8 开关管电流对比图 Fig. 8 Switch tube current comparison chart |
系统在6.091 ms时同时导通开关管S1和S2, 从仿真结果来看,此时开关管占空比设置为0.8,图 8中过零的部分为S1关断的时间。未加RC吸收电路时,通过的S1电流最大值为31.44 A,最小值为-38.37 A;加入RC吸收电路后,电流的最大值和最小值分别为10.21 A与-10.45 A。因此,RC吸收电路对MOSFET电流尖峰有很好的抑制效果,减少开关管的电流应力,降低开关管损耗,保证开关管可以正常使用。
4 仿真验证与分析为了验证理论分析,基于Simulink搭建了双LCC型补偿网络ICPT系统仿真模型。具体参数如表 1所示,规定直流输入电压Uin为120 V,系统频率f为85 kΗz,S1和S2 2个开关管导通的频率为42.5 kHz进行仿真。
| 表 1 仿真系统主要参数 Table 1 Main parameters of the simulation system |
图 9(a)~ 图 9(d)展示了当占空比在不同情况下,谐振网络的输出电压U1,谐振网络输出电流I,负载两端电压值URL的系统仿真波形图。
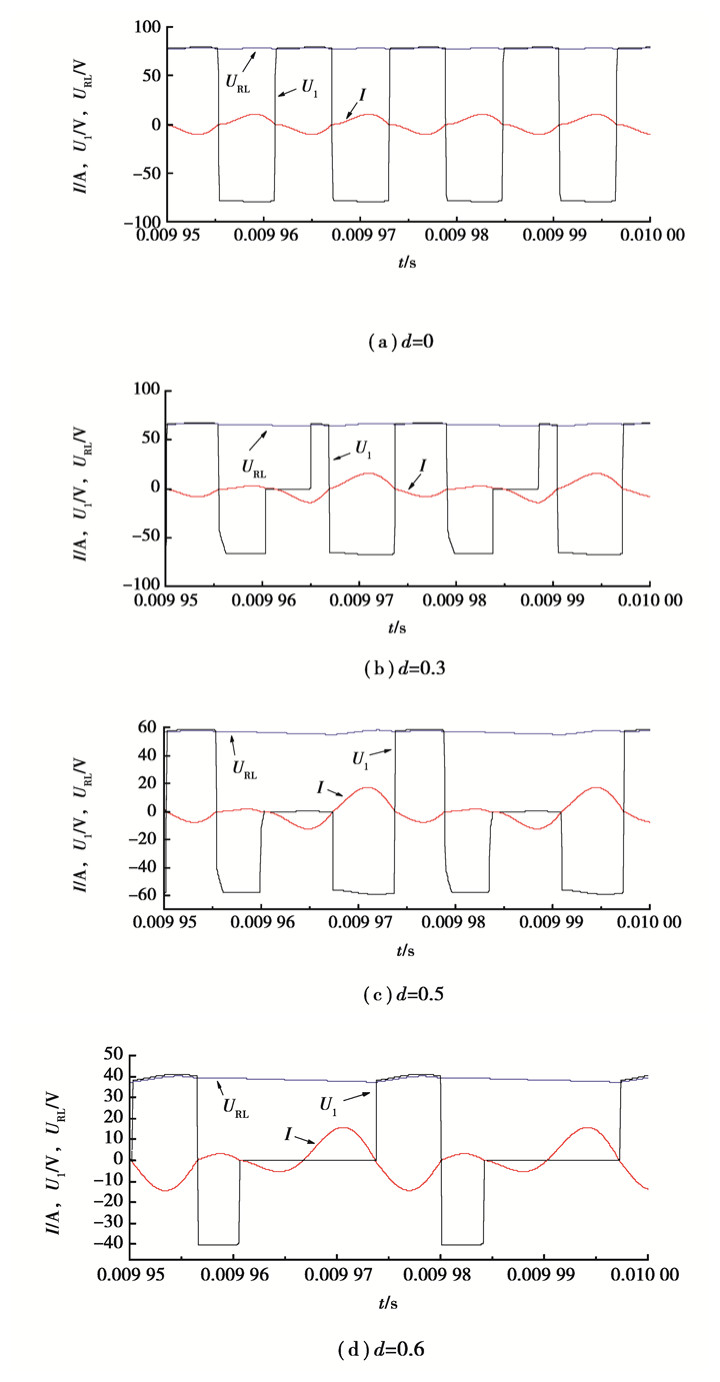
|
图 9 系统仿真波形图 Fig. 9 System simulation waveform diagram |
由于开关管的频率为系统频率的一半,开关管的周期为系统运行周期的2倍。图 9显示谐振网络输出的电流与电压同相位,系统运行在谐振状态。系统的仿真数据如表 2所示,表中的数值皆为有效值。
| 表 2 d不同时仿真数据 Table 2 d load voltage average data at different times |
当d=0时,2个开关管的驱动信号恒为0,S1和S2一直处于断开状态,此时负载的输出功率为整流电路输出最大功率530 W。
当系统由正常工作状态切换到解耦状态时,谐振网络不对外正常输出能量,即谐振网络输出电压为0,因此周期内通过这种方式改变谐振网络输出电压的平均值,进而改变输出平均功率。占空比越大,动态解耦时间越长,系统的输出功率越小。系统运行效率如表 3所示。
| 表 3 d不同时系统效率 Table 3 System efficiency when d is different |
动态解耦方式为耗能型功率调节方法,系统的效率随占空比的增加而降低。在一定范围内调节,系统效率较高,因此该调节方式适合小范围功率调节。
5 实验验证与分析为了验证对于运用动态解耦控制技术的双LCC型ICPT系统输出功率调节特性的理论分析与仿真的正确性,图 10是建立的双LCC型ICPT系统实验样机,主要由原边线圈、副边线圈、逆变箱和负载等部分组成。主要的实验参数与仿真参数一致。

|
图 10 实验装置图 Fig. 10 Experimental device diagram |
图 11(a)~图 11(d)为在占空比不同的情况下实验过程中的示波器截图,CH1为S1和S22个开关管的脉冲信号;CH2为谐振网络的输出电压;CH3为谐振网络的输出电流;CH4为负载输出电压。
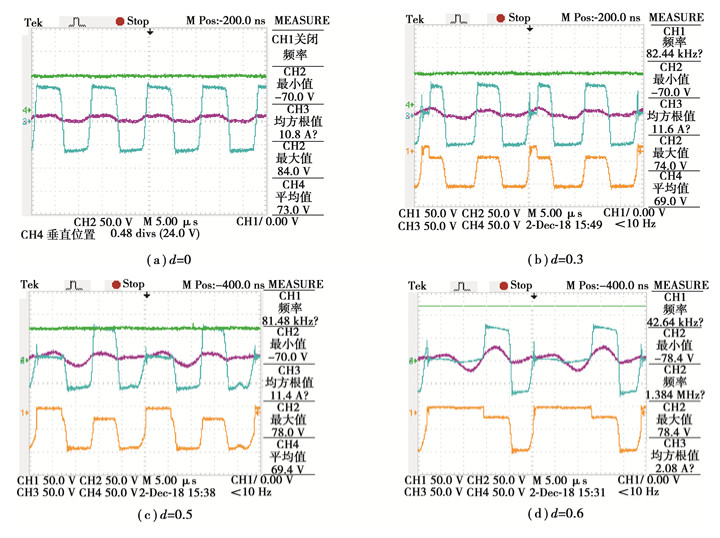
|
图 11 系统实验波形图 Fig. 11 Waveform diagram of system experiment |
当d变化时,谐振网络的输出电流波形的峰值稳定在11 V左右,验证了双LCC补偿结构的恒流输出的特性。表 4为当d变化时负载输出电压平均值的实验数据。
| 表 4 d不同时实验数据 Table 4 d load voltage average data at different times |
由于示波器存在一定误差,实验时开关管不是理想器件,当开关管触发时不会立即导通,有一定延迟,其次开关管导通时谐振网络输出电压有略微尖峰,故实验数据比仿真数据略大,但从变化趋势上看出当d变大时,负载两端输出的平均电压值变小,负载的平均输出功率也变小,验证了控制开关管S1和S2的占空比可以达到调节功率的效果。
6 结论文中提出了一种基于动态解耦控制技术的输出功率调节方法,即通过在全桥整流电路2个二极管并联2个全控型开关管实现,同时调节2个功率开关管的占空比。当占空比在0~100%变化时,系统的平均输出功率在最大输出功率的100%~0之间调整。
| [1] |
韩冲, 张波. 谐振式无线电能传输系统中高频逆变器的特性分析和参数设计[J]. 电工技术学报, 2018, 33(21): 5036-5050. HAN Chong, ZHANG Bo. Characteristics analysis and parameters design of high frequency inverters in magnetic coupling resonance wireless power transfer system[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 5036-5050. (in Chinese) |
| [2] |
Zhang Z, Pang H L, Georgiadis A, et al. Wireless power transfer:an overview[J]. IEEE Transactions on Industrial Electronics, 2019, 66(2): 1044-1058. DOI:10.1109/TIE.2018.2835378 |
| [3] |
Li S Q, Mi C C. Wireless power transfer for electric vehicle applications[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(1): 4-17. DOI:10.1109/JESTPE.2014.2319453 |
| [4] |
祝文姬, 孙跃, 高立克, 等. 电动汽车多导轨无线供电方法[J]. 电力系统自动化, 2016, 40(18): 97-101. ZHU Wenji, SUN Yue, GAO Like, et al. Wireless power supply method for multi-rail-based electric vehicles[J]. Automation of Electric Power Systems, 2016, 40(18): 97-101. (in Chinese) DOI:10.7500/AEPS20150730005 |
| [5] |
Paramesh K, Neriya R P, Kumar M V. Wireless charging system for electric vehicles[J]. International Journal of Vehicle Structures and Systems, 2017, 9(1): 23-26. |
| [6] |
Zhang W, Mi C C. Compensation topologies of high-power wireless power transfer systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(6): 4768-4778. DOI:10.1109/TVT.2015.2454292 |
| [7] |
Kim J, Kim D H, Park Y J. Analysis of capacitive impedance matching networks for simultaneous wireless power transfer to multiple devices[J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 2807-2813. DOI:10.1109/TIE.2014.2365751 |
| [8] |
Hasanzadeh S, Vaez-Zadeh S. Efficiency analysis of contactless electrical power transmission systems[J]. Energy Conversion and Management, 2013, 65: 487-496. DOI:10.1016/j.enconman.2012.07.007 |
| [9] |
孙跃, 夏晨阳, 赵志斌, 等. 电压型ICPT系统功率传输特性的分析与优化[J]. 电工电能新技术, 2011, 30(2): 9-12, 25. SUN Yue, XIA Chenyang, ZHAO Zhibin, et al. Analysis and optimization on power transmission characteristics for voltage-fed ICPT system[J]. Advanced Technology of Electrical Engineering and Energy, 2011, 30(2): 9-12, 25. (in Chinese) DOI:10.3969/j.issn.1003-3076.2011.02.003 |
| [10] |
苏玉刚, 王智慧, 孙跃, 等. 非接触供电移相控制系统建模研究[J]. 电工技术学报, 2008, 23(7): 92-97. SU Yugang, WANG Zhihui, SUN Yue, et al. Modeling of contactless power transfer systems with a phase-shifted control method[J]. Transactions of China Electrotechnical Society, 2008, 23(7): 92-97. (in Chinese) DOI:10.3321/j.issn:1000-6753.2008.07.016 |
| [11] |
蔡华, 史黎明, 李耀华, 等. 感应耦合电能传输系统输出功率调节方法[J]. 电工技术学报, 2014, 29(1): 215-220. CAI Hua, SHI Liming, LI Yaohua, et al. Output power adjustment in inductively coupled power transfer system[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 215-220. (in Chinese) DOI:10.3969/j.issn.1000-6753.2014.01.030 |
| [12] |
Li H L, Hu A P, Covic G A. A power flow control method on primary side for a CPT system[C]//Power Electronics Conference. IEEE, 2010: 1050-1055.
|
| [13] |
Seo Y S, Nguyen M Q, Hughes z, et al.Wireless power transfer by inductive coupling for implantable batteryless stimulators[C]//Microwave Symposium Digest.IEEE, 2012: 1-3.
|
| [14] |
刘闯, 郭赢, 葛树坤, 等. 基于双LCL谐振补偿的电动汽车无线充电系统特性分析与实验验证[J]. 电工技术学报, 2015, 30(15): 127-135. LIU Chuang, GUO Ying, GE Shukun, et al. Characteristics analysis and experimental verification of the double LCL resonant compensation network for electrical vehicles wireless power transfer[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 127-135. (in Chinese) DOI:10.3969/j.issn.1000-6753.2015.15.014 |
| [15] |
高键鑫, 吴旭升, 高嵬, 等. 基于LCC的磁谐振无线电能传输发射端补偿技术[J]. 电工技术学报, 2016, 31(S1): 9-15. GAO Jianxin, WU Xusheng, GAO Wei, et al. Compensation technology of magnetic resonant wireless power transfer transmitter based on LCC[J]. Transactions of China Electrotechnical Society, 2016, 31(S1): 9-15. (in Chinese) |
| [16] |
Li W H, Zhao H, Deng J J, et al. Comparison study on SS and double-sided LCC compensation topologies for EV/PHEV wireless chargers[J]. IEEE Transactions on Vehicular Technology, 2016, 65(6): 4429-4439. DOI:10.1109/TVT.2015.2479938 |
 2020, Vol. 43
2020, Vol. 43

