感应加热(induction heating)由于其拥有效率高、能精确输出功率控制和性能高等方面的优势,已成为许多工业、家庭和医疗应用的首选加热技术[1]。感应加热的主要原理是利用法拉第电磁感应定律,利用电涡流的热阻效应进行加热。因为感应加热的能量只通过磁场进行传输而不需要直接接触,所以属于非接触式加热技术。感应加热系统主要包括感应加热电源、实际工业加热线圈和负载。感应加热电源作为系统的核心,主要包括输入的交流电源、整流电路、滤波电路、逆变电路、控制与保护电路[2]。加热系统通过将一个自然频率的交流电源转换成直流电,然后再转换成频率更高的交流电,之后高频电能被输送到谐振负载。根据谐振电路振荡产生的频率,通过逆变器开关实现特定用途的加热。系统的关键目标是用有效的方式达到所需的温度,因此,功率的控制是最关键的部分。感应加热的功率调节分为直流侧调节和逆变侧调节,包括直接和间接调节等多种方式[3]。
感应加热系统中普遍在逆变侧进行功率控制,笔者则着眼于在大功率或高电压的情况下有明显优势的整流侧调功,在系统中的整流及滤波部分控制可控整流器的输出以实现加热系统负荷功率的控制。由于逆变器正常工作在谐振条件,线圈和逆变器可等效为纯阻抗,则通过控制整流器输出直流电压值就可实现系统的功率控制[4]。
IH功率控制系统中控制器的设计至关重要。尽管结构简单,设计难度低,PI控制器的应用和研究也最为普遍,但也存在基于模糊控制[5]或模型预测控制[6]等先进算法控制器的应用研究。
PI控制在IH系统的应用中暴露出了如抗干扰能力较差、容错性低等突出问题。模糊控制器和模型预测控制器虽然较PI控制器有所改善,但这些先进的控制算法隐含大量微积分环节,在实际系统中难以应用。鲁棒控制器因其结构相对简单且同时适用于标称系统和存在不确定性的系统而被考虑用来解决上述问题。
笔者设计了一种新的感应加热系统控制器,电流内环采用H∞控制模型。分析了常规的感应加热系统,并构建了基于整流侧调功的感应加热等效电路模型。为改善原系统的突出问题,基于感应加热等效模型的双闭环PI控制,结合鲁棒控制理论对其进行了改进,使其具有更好的动态特性和更高的容错率。文章结尾通过对两种控制器控制效果的仿真,进一步突出了改进的电流内环H∞控制器的优点。
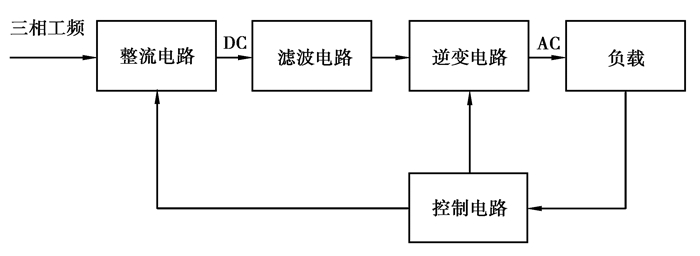
1 感应加热功率控制结构IH系统结构由各种组件组成,如图 1所示。一个常规频率的交流电经过整流和逆变两个环节之后变为特定频率的高频交流电流入感应加热线圈,被加热的金属物件以一定方式分布在感应线圈周围,能量通过电磁感应流入被加热物以实现加热。从整流侧可以看到负载所消耗的功率。因此,负载功率可以通过整流器的开关控制。
|
图 1 感应加热系统 Fig. 1 Induction heating system |
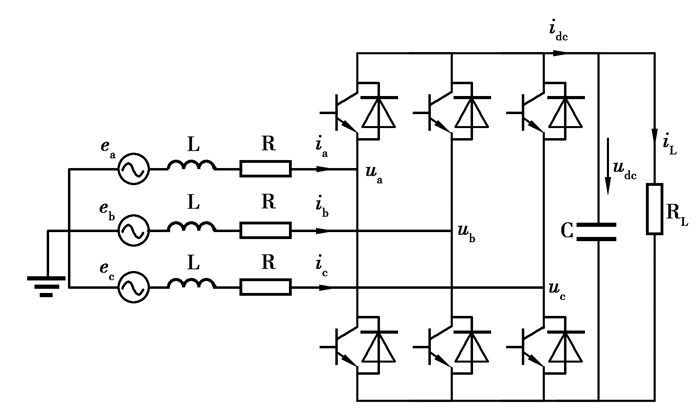
通过考虑电路参数,描述了具有等效负载的系统模型。加热线圈和电容器的电抗在电路常规工作在谐振的情况下相互抵消;输出电路的功率因数接近统一,最大功率转移到负载上。因此,电路建模时假设负载为纯阻抗电阻[7]。带热负荷的感应加热模型等效电路如图 2所示。
|
图 2 感应加热等效模型 Fig. 2 Equivalent model of induction heating |
等效感应加热系统的数学模型[8]为:
| $ \left\{ {\begin{array}{*{20}{l}} {L\frac{{{\rm{d}}{i_q}}}{{{\rm{d}}t}} + \omega L{i_d} = - R{i_q} + {e_q} - {U_{{\rm{dc}}}}{s_q},}\\ {L\frac{{{\rm{d}}{i_d}}}{{{\rm{d}}t}} - \omega L{i_q} = - R{i_d} + {e_d} - {U_{{\rm{dc}}}}{s_d},}\\ {C\frac{{{\rm{d}}{U_{{\rm{dc}}}}}}{{{\rm{d}}t}} = \frac{3}{2}({i_q}{s_q} + {i_d}{s_d}) - \frac{{{U_{{\rm{dc}}}}}}{{{R_{\rm{L}}}}},} \end{array}} \right. $ | (1) |
式中:ω为电网角频率;Udc为直流侧负载电压;(id,iq),(ed,eq),(sd,sq)分别为电网电流,电网电压和开关函数的dq轴分量。
模型包含两个变量的乘积项,属于非线性模型,对等效感应加热系统的控制带来了不便,为了方便控制对其进行线性化处理。假设开关不会产生能量的消耗,其交流侧有功功率Pac与直流侧有功功率Pdc相等,为:
| $ {P_{{\rm{ac}}}} = {P_{{\rm{dc}}}}。$ | (2) |
采用等量坐标变换则有:
| $ \begin{array}{*{20}{c}} {{P_{{\rm{ac}}}} = \frac{3}{2}{e_d}{i_d} + \frac{3}{2}{e_q}{i_q},}\\ {{P_{{\rm{dc}}}} = {U_{{\rm{dc}}}}{i_{{\rm{dc}}}} = {U_{{\rm{dc}}}}C\frac{{{\rm{d}}{U_{{\rm{dc}}}}}}{{{\rm{d}}t}} + \frac{{U_{{\rm{dc}}}^2}}{{{R_{\rm{L}}}}},}\\ {\frac{{{\rm{d}}U_{{\rm{dc}}}^2}}{{{\rm{d}}t}} = - \frac{2}{{{R_{\rm{L}}}C}}U_{{\rm{dc}}}^2 + \frac{3}{C}{e_d}{i_d} + \frac{3}{C}{e_q}{i_q}}。\end{array} $ |
交流侧的输出电压的dq轴分量分别为:
| $ {u_d} = {U_{{\rm{dc}}}}{s_d},\quad {u_q} = {U_{{\rm{dc}}}}{s_q}。$ |
Udc在系统中不会改变方向,因此可用Udc2作为状态变量替换原系统的Udc进而得到改进的数学模型为:
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}U_{{\rm{dc}}}^2}}{{{\rm{d}}t}} = - \frac{2}{{{R_L}C}}U_{{\rm{dc}}}^2 + \frac{3}{C}{e_d}{i_d} + \frac{3}{C}{e_q}{i_q},}\\ {\frac{{{\rm{d}}{i_d}}}{{{\rm{d}}t}} = - \frac{R}{L}{i_d} + \omega {i_q} + \frac{1}{L}{e_d} - \frac{1}{L}{u_d},}\\ {\frac{{{\rm{d}}{i_q}}}{{{\rm{d}}t}} = - \frac{R}{L}{i_q} - \omega {i_d} + \frac{1}{L}{e_q} - \frac{1}{L}{u_q}}。\end{array}} \right. $ | (3) |
感应加热系统中通过电磁感应流入工件的线圈电流取决于逆变器输入的直流电压[9]。因此,工件的加热功率可以通过直流环节电压调节,为
| $ P = {U_{{\rm{dc}}}}{i_{{\rm{dc}}}}。$ | (4) |
通过改变整流器直流侧电压的设定值,可使感应热功率从几千瓦提高到数百千瓦。
2 传统PI双闭环控制感应加热整流器的控制方法有很多,传统的双闭环PI控制方法由于其控制结构简单等优点,在整流器控制系统中最为常见。PI电流控制器的方程为[10]
| $ \left\{ {\begin{array}{*{20}{l}} {{u_d} = - ({K_{{\rm{iP}}}} + \frac{{{K_{{\rm{iI}}}}}}{s})(i_d^* - {i_d}) + \omega L{i_q} + {e_d},}\\ {{u_q} = - ({K_{{\rm{iP}}}} + \frac{{{K_{{\rm{iI}}}}}}{s})(i_q^* - {i_q}) - \omega L{i_d} + {e_q}}。\end{array}} \right. $ | (5) |
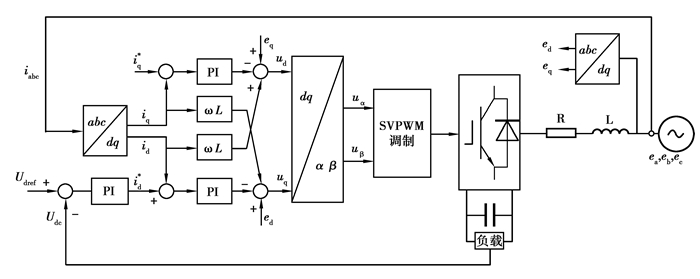
由式(5)可以看出:经过前馈解耦之后交流侧电流的有功分量和无功分量已经不再耦合,可以各自独立进行控制,得到的控制模块如图 3所示。
|
图 3 整流器双闭环控制流程 Fig. 3 Double closed loop control flow of rectifier |
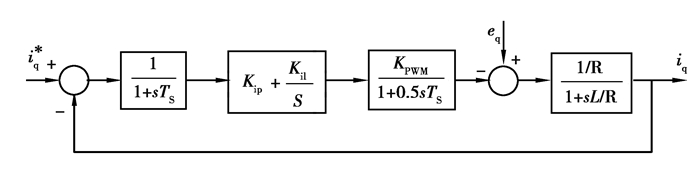
图 4为电流内环的传递函数框图。电流内环的主要控制目标为保证等效感应加热系统在单位功率因数下运行[11]。
|
图 4 电流内环传递函数结构图 Fig. 4 Structural chart of transfer function in current inner loop |
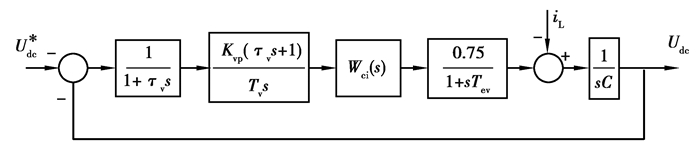
电压外环则用于控制和稳定等效感应加热系统的输出电压[12],控制框图如图 5所示。
|
图 5 电压外环传递函数结构图 Fig. 5 Structural chart of transfer function of voltage outer loop |
通过整定电压外环和电流内环的具体参数可以实现对直流侧电压和电流的控制,但是这种控制方式控制器设计中未与系统的时变状态量建立直接的联系,且都忽略了外部扰动的影响,因此可能导致控制精确度不高。并且,当系统中某一参数变化过大或者突加扰动的情况下PI控制可能会产生震荡,甚至使控制失效[13]。因此,有必要对PI双闭环控制进行进一步的改进。
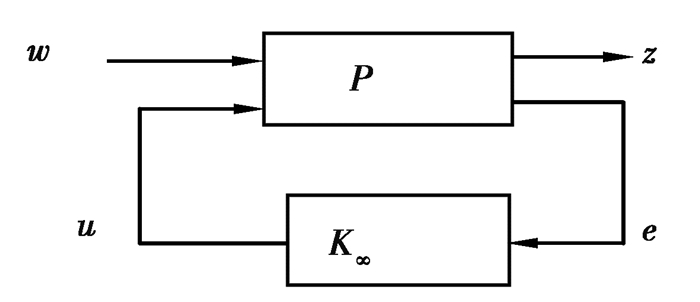
3 基于H∞的改进双闭环控制H∞控制是鲁棒控制的一种,基本原理为以系统的传递函数的无穷范数作为优化指标,设计满足稳定性以及具体的跟踪性能要求的鲁棒控制器[14]。标准控制框图如图 6所示。
|
图 6 H∞控制的标准控制框图 Fig. 6 Standard control block diagram of H∞ control |
图中w和z分别为包括构成系统所有的输入信号和输出信号,P为增广被控对象,其在控制器设计中一般会转化成标准状态方程形式为[15]:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + {\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{v}} + {\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{u,}}}\\ {\mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{C}}_1}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{C}}_{11}}\mathit{\boldsymbol{v}} + {\mathit{\boldsymbol{D}}_{12}}\mathit{\boldsymbol{u,}}}\\ {\mathit{\boldsymbol{y}} = {\mathit{\boldsymbol{C}}_2}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{D}}_{21}}\mathit{\boldsymbol{v}} + {\mathit{\boldsymbol{D}}_{22}}\mathit{\boldsymbol{u}}}。\end{array}} \right. $ | (6) |
满足特定条件的情况下控制器的设计问题可以转换为求解P的两个Riccati方程[16]:
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{X}} + \mathit{\boldsymbol{XA}} + \mathit{\boldsymbol{X}}({\gamma ^{ - 2}}{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{B}}_1^{\rm{T}} - {\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{B}}_2^{\rm{T}})\mathit{\boldsymbol{X}} + \mathit{\boldsymbol{C}}_1^{\rm{T}}{\mathit{\boldsymbol{C}}_1} = {\bf{0}},}\\ {\mathit{\boldsymbol{AY}} + \mathit{\boldsymbol{Y}}{\mathit{\boldsymbol{A}}^{\rm{T}}} + \mathit{\boldsymbol{Y}}({\gamma ^{ - 2}}\mathit{\boldsymbol{C}}_1^{\rm{T}}{\mathit{\boldsymbol{C}}_1} - \mathit{\boldsymbol{C}}_2^{\rm{T}}{\mathit{\boldsymbol{C}}_2})\mathit{\boldsymbol{Y}} + {\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{B}}_1^{\rm{T}} = {\bf{0}}}。\end{array} $ | (7) |
如果方程的解X和Y都不为负数,且满足ρ(XY) < γ2,则存在控制器:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_\infty }(s) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_\infty }}&{ - {\mathit{\boldsymbol{Z}}_\infty }{\mathit{\boldsymbol{L}}_\infty }}\\ {{\mathit{\boldsymbol{F}}_\infty }}&{\bf{0}} \end{array}} \right],}\\ {{\mathit{\boldsymbol{A}}_\infty } = \mathit{\boldsymbol{A}} + {\gamma ^{ - 2}}{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{B}}_1^{\rm{T}}{\mathit{\boldsymbol{X}}_\infty } + {\mathit{\boldsymbol{B}}_2}{\mathit{\boldsymbol{F}}_\infty } + {\mathit{\boldsymbol{Z}}_\infty }{\mathit{\boldsymbol{L}}_\infty }{\mathit{\boldsymbol{C}}_2},}\\ {{\mathit{\boldsymbol{F}}_\infty } = - \mathit{\boldsymbol{B}}_2^{\rm{T}}{\mathit{\boldsymbol{X}}_\infty },}\\ {{\mathit{\boldsymbol{L}}_\infty } = - {\mathit{\boldsymbol{Y}}_\infty }\mathit{\boldsymbol{C}}_2^{\rm{T}},}\\ {{\mathit{\boldsymbol{Z}}_\infty } = (\mathit{\boldsymbol{I}} - {\gamma ^{ - 2}}{\mathit{\boldsymbol{Y}}_\infty }{\mathit{\boldsymbol{x}}_\infty }) - 1}。\end{array} $ |
根据以上的H∞控制控制理论,对等效感应加热系统的PI双闭环控制的电流内环进行改进。根据整流器数学模型式(3)选取状态变量x=[x1 x2 x3 x4]T,其中各个变量分别取值为:
| $ \begin{array}{*{20}{l}} {{x_1} = {i_d},{x_2} = \int_0^t {(i_d^* - {i_d})} {\kern 1pt} {\kern 1pt} {\rm{d}}t,}\\ {{x_3} = {i_q},{x_4} = \int_0^t {(i_q^* - {i_q})} {\kern 1pt} {\kern 1pt} {\rm{d}}t}。\end{array} $ |
上述变量中分别对应的状态方程参数为
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} { - R/L}&0&w&0\\ { - 1}&0&0&0\\ { - w}&0&{ - R/L}&0\\ 0&0&{ - 1}&0 \end{array}} \right],}\\ {{\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} 0&0\\ 1&0\\ 0&0\\ 0&1 \end{array}} \right],{\mathit{\boldsymbol{B}}_2} = \left[ {\begin{array}{*{20}{c}} {1/L}&0\\ 0&0\\ {1/L}&0\\ 0&0 \end{array}} \right]}。\end{array} $ |
状态反馈为u=K(s) x,并且定义输出信号为:y=[y1, y2]T=[ed-ud, eq-uq]T,则有:
| $ \mathit{\boldsymbol{y}} = \left[ {\begin{array}{*{20}{c}} {Lp + R}&{ - \omega L}\\ 0&{}\\ {\omega L}&{}\\ 0&0\\ {Lp + R}&{}\\ 0&{} \end{array}} \right]\mathit{\boldsymbol{x}}。$ |
之后代入式(7)进行求解。其最优控制率为:
| $ \begin{array}{*{20}{l}} {{u_d} = {e_d} - R{i_d} + L\omega {i_q} - 1.08 \times {{10}^6}L(i_d^* - {i_d}),}\\ {{u_q} = {e_q} - R{i_q} + L\omega {i_d} - 1.08 \times {{10}^6}L(i_q^* - {i_q})}。\end{array} $ | (8) |
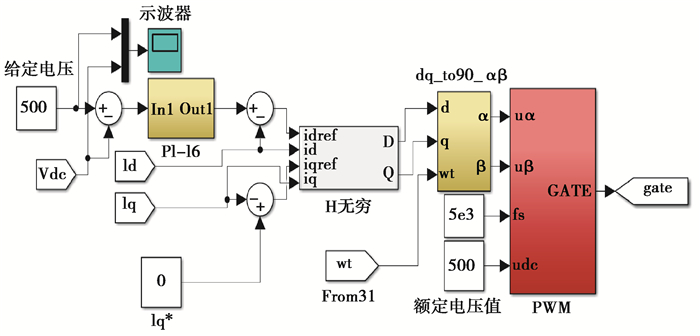
改进的电流内环如图 7所示。
|
图 7 改进的H∞电流内环控制模型 Fig. 7 Improved H∞ current inner loop control model |
等效感应加热系统的仿真的参数为:相电压有效值220 V,交流侧等效电阻与电感分别为0.1 Ω和1.2 mH,负载工作区的稳压电容为6 800 μF,系统的额定工作电压500 V,开关频率为2 000 Hz,包括逆变器和加热线圈的等效负载为50 Ω。为了更加直观地对比鲁棒控制的优越性,文中用常规的双闭环PI控制和改进的H∞电流内环控制分别对系统进行仿真,并对比仿真结果。
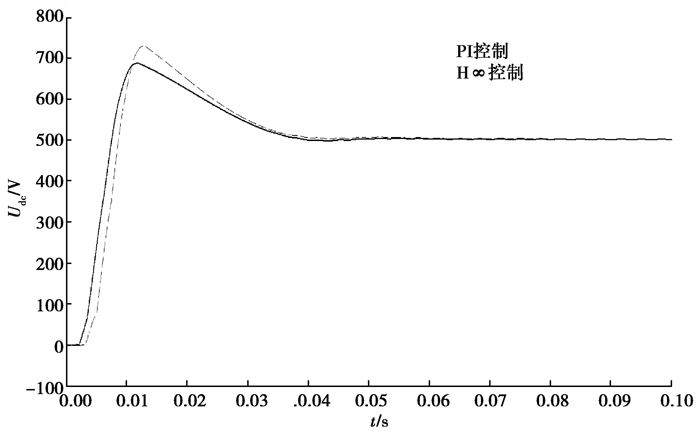
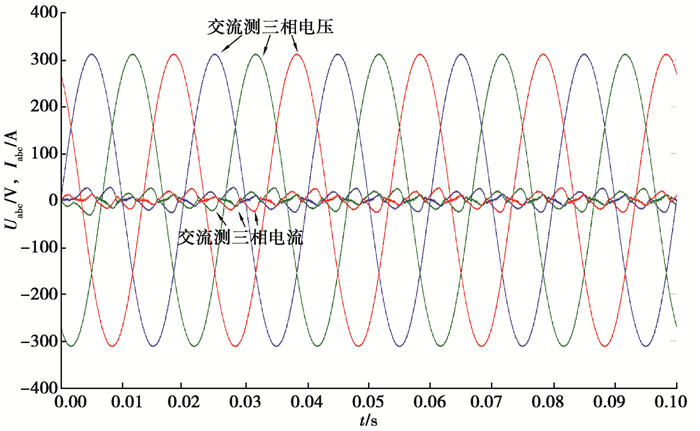
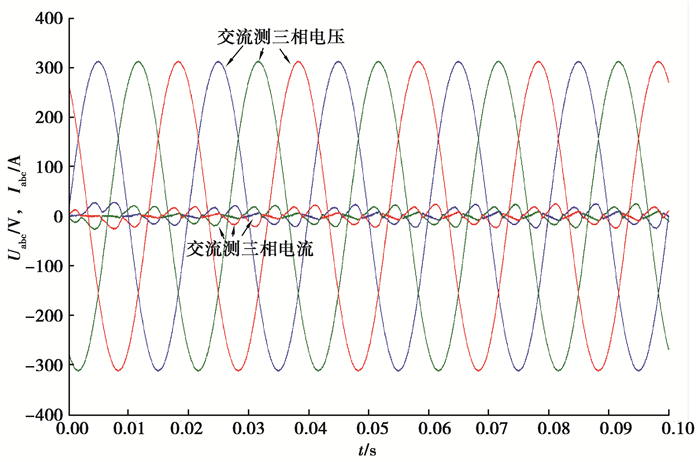
图 8为额定负载条件下等效的感应加热系统分别在常规的PI控制和改进的H∞电流内环控制的情况下的输出直流电压响应。图 9和图 10分别为两种控制器下的交流侧相电流与相电压的关系图。从图中可以清晰地看出:改进后的H∞控制系统具有更好的动态特性,并且稳定后可以实现精确的单位因数整流。
|
图 8 两种控制模式下的启动响应 Fig. 8 Start-up response in two control modes |
|
图 9 稳态下PI控制器交流侧相电压与电流关系图 Fig. 9 Relation diagram of phase voltage and current on AC side of PI controller under steady state |
|
图 10 稳态下H∞控制器交流侧相电压与电流关系图 Fig. 10 Relation diagram of phase voltage and current on AC side of H∞ controller under steady state |
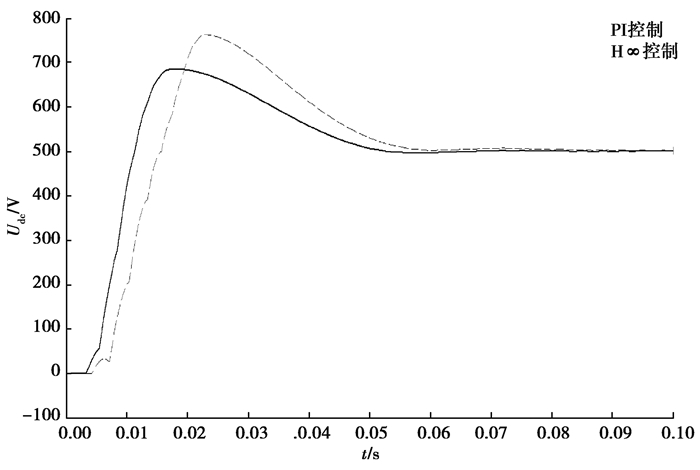
实际的系统中往往因为测量不准确或者外界干扰等因素导致系统内参数的摄动。图 11为当启动电路时交流侧等效电感由1.2 mH变为10 mH时等效的感应加热系统在两种控制条件下的直流电压响应。从图 11可以看出,在电感摄动的情况下,改进的H∞电流内环控制系统依然比PI系统具有更好的动态性能。
|
图 11 电感摄动时两种控制模式的直流电压响应 Fig. 11 DC voltage response of two control modes with inductance perturbation |
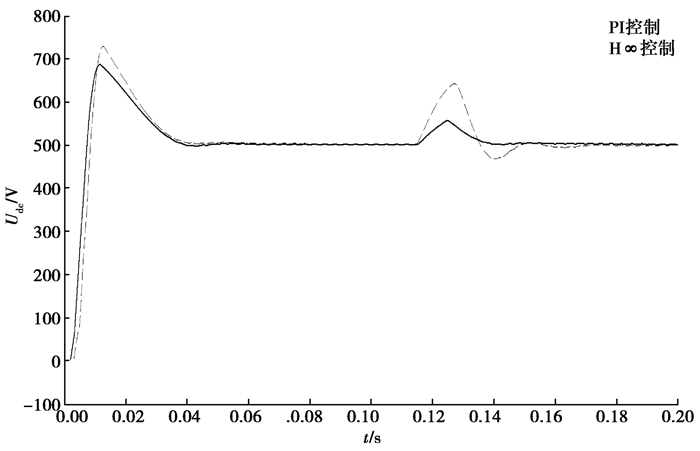
工业感应加热系统运行中难免会遇到外界环境的干扰。图 12为当启动电路至稳态过程中,对给定信号突加一个幅值为200的电压信号扰动,在此情况下PI控制和H∞控制分别对外界干扰的响应曲线。从图 12可以看出,整个过程中H∞控制器的容错率更高,对系统的冲击更小。
|
图 12 突加扰动的情况下两种控制模式下的响应 Fig. 12 Response diagrams of two control modes with sudden disturbance |
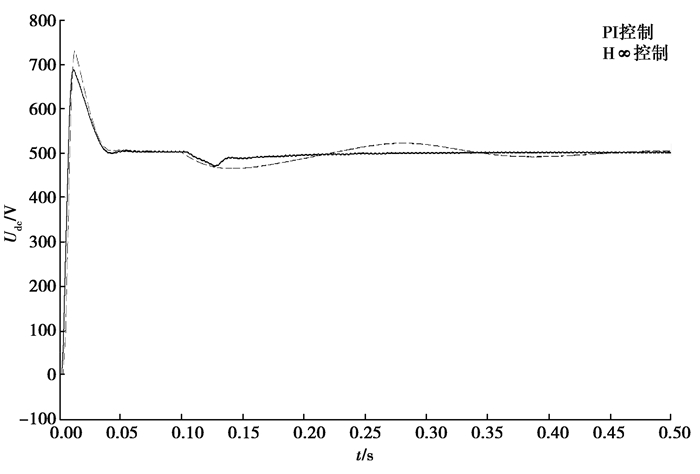
图 13为系统启动至稳态运行之后,原电路中电感参数摄动的情况下PI控制器和H∞控制器的响应曲线。显然电路本身的参数出现摄动时, 改进H∞控制器能够更好更快地恢复稳定,相比之下PI控制器不仅恢复速度慢而且出现了震荡。
|
图 13 电感摄动的情况下两种控制模式下的稳态响应 Fig. 13 Steady state response under two control modes with inductance perturbation |
1) 选择并设计在整流侧PWM整流器的控制对输出电压进行调节,以实现对IH系统的功率进行控制。
2) 对等效的感应加热系统设计了传统的双闭环PI控制器,但PI控制器在仿真过程中控制效果不理想,并且实际系统电路参数测量不准确或者存在较大干扰的情况下稳定性不佳。
3) 根据H∞鲁棒控制原理对原有控制器的电流内环部分进行了改进。对改进后的系统仿真,通过对比体现了改进H∞电流内环控制器在额定工作状态下与系统内部电路参数摄动的情况下均能较PI控制器具有更好的输出响应,证明了改进H∞控制器在感应加热系统中的优越性。
| [1] |
Héctor Sarnago, Óscar Lucía, José M. Burdío. Multi-resonant power converter for improved dual-frequency induction heating[J]. IEEE Transactions on Power Electronics, 2018, PP(99): 1. |
| [2] |
周美兰, 李艳萍, 王吉昌. 高频感应加热电源系统设计[J]. 哈尔滨理工大学学报, 2015, 20(1): 50-55. ZHOU Meilan, LI Yanping, WANG Jichang. Design of high frequency induction heating power system[J]. Journal of Harbin University of Science and Technology, 2015, 20(1): 50-55. (in Chinese) |
| [3] |
李金刚. 现代工业中感应加热技术综述(中)[J]. 变频技术应用, 2013(5): 26-32. LI Jingang. Induction heating technology in modern industry[J]. Application of frequency conversion technology, 2013(5): 26-32. (in Chinese) |
| [4] |
Pradeep V, Gunabalan R, Sridhar R. A novel power control technique for series resonant inverter-fed induction heating system with fuzzy-aided digital pulse density modulation scheme[J]. International Journal of Fuzzy Systems, 2017, 20(2): 1-15. |
| [5] |
Nawaz M, Saqib M A, Kashif S A R, et al. Constrained model predictive control for an induction heating load[J]. Transactions of the Institute of Measurement and Control, 2019, 41(1): 210-218. |
| [6] |
Héctor S, José M B, Óscar L. High-performance and cost-effective ZCS matrix resonant inverter for total active surface induction heating appliances[J]. IEEE Transactions on Power Electronics, 2019, 34(1): 117-125. |
| [7] |
周美兰, 徐泽卿, 李艳萍. 高频感应加热电源相位跟踪系统[J]. 哈尔滨理工大学学报, 2014, 19(3): 84-88. ZHOU Meilan, XU Zeqing, LI Yanping. High frequency induction heating power supply phase tracking system[J]. Journal of Harbin University of Science and Technology, 2014, 19(3): 84-88. (in Chinese) |
| [8] |
张志文, 李松, 谢小城, 等. 三相电压型PWM整流器预测功率控制研究[J]. 电源学报, 2017, 15(5): 123-130. ZHANG Zhiwen, LI Song, XIE Xiaocheng, et al. Research on predictive power control of three-phase voltage source PWM rectifier[J]. Journal of Power Supply, 2017, 15(5): 123-130. (in Chinese) |
| [9] |
Wallace I, Bendre A, Nord J P, et al. A unity-power-factor three-phase PWM SCR rectifier for high-power applications in the metal industry[J]. IEEE Transactions on Industry Applications, 2002, 38(4): 898-908. |
| [10] |
贺诗明, 熊健, 代大一, 等. 三相电压型PWM整流器建模、控制及稳定性分析[J]. 电网技术, 2019, 43(6): 2049-2057. HE Shiming, XIONG Jian, DAI Dayi, et al. Modeling, Control and stability analysis of three-phase voltage-source PWM rectifier[J]. Power System Technology, 2019, 43(6): 2049-2057. (in Chinese) |
| [11] |
许军, 周文华, 郑绍陆. 基于电网电压矢量定向的双闭环光伏并网逆变系统的研究[J]. 电子器件, 2017, 40(2): 446-450. XU Jun, ZHOU Wenhua, ZHENG Shaolu. Research of grid-connected photovoltaic inverter grid-connected system based on double closed-loop of grid voltage vector orientation[J]. Chinese Journal of Electron Devices, 2017, 40(2): 446-450. (in Chinese) |
| [12] |
付志红, 董玉玺, 朱学贵, 等. 数字锁相环与滤波技术在PWM整流器中的应用[J]. 重庆大学学报, 2010, 33(7): 35-41. FU Zhihong, DONG Yuxi, ZHU Xuegui, et al. Application of digital phase-locked loop and filtering technique in PWM rectifier[J]. Journal of Chongqing University, 2010, 33(7): 35-41. (in Chinese) |
| [13] |
Hou Y J, Tian H M, Qu X D, et al. Development of digital control system for medium frequency induction furnaces[J]. IOP Conference Series:Earth and Environmental Science, 2018, 188. |
| [14] |
Szelitzky T, Dulf E H. H∞ control of an induction heating inverter[J]. Intelligent Control System & Computer Science, 2013, 235-250. |
| [15] |
侯利民, 申鹤松, 阎馨, 等. 永磁同步电机调速系统H_∞鲁棒控制[J]. 电工技术学报, 2019, 34(7): 130-139. HOU Limin, SHEN Hesong, YAN Xin, et al. H∞ robust control of PMSM speed regulation system[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 130-139. (in Chinese) |
| [16] |
吴忠强, 肖雪飞, 汤雅超. 基于微粒群优化算法的单元机组H_∞控制[J]. 仪器仪表学报, 2013, 34(9): 2051-2057. WU Zhongqiang, XIAO Xuefei, TANG Yachao. H∞control of unit plant based on particle swarm optimization algorithm[J]. Chinese Journal of Scientific Instrument, 2013, 34(9): 2051-2057. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43


