混凝土现浇箱梁桥变形小、抗扭刚度大, 具有良好的整体性能和较大的跨越能力, 在桥梁工程中得到广泛的应用。当汽车偏心荷载作用于现浇箱梁时,偏于作用力一侧的截面由于约束扭转、畸变和翘曲等效应,引起应力增大,这种应力的增大系数称为箱梁的偏心增大系数。在使用单梁杆系进行现浇箱梁设计时,无法直接计算汽车荷载的偏载效应,通过偏心增大系数来修正平面杆系计算的应力值,包络空间分析得到的应力计算结果。研究人员通过经典力学等简化计算方法,建议设计过程中偏心增大系数直接取值为1.15。近年来,随着中国交通建设的发展和交通量的需求增大,箱梁横向宽度设计得越来越大,对于这种大宽跨比箱梁,偏心增大系数取1.15可能偏小,不能准确地体现汽车荷载作用下的箱梁截面应力,桥梁结构安全得不到有力保障。选择合理准确的偏心增大系数,对桥梁结构计算和安全影响至关重要。
《公路钢筋混凝土及预应力混凝土桥涵设计规范》[1]提出了偏心增大系数的精细化设计要求:为了对梁单元有限元计算模型进行简化设计,要对偏心增大系数进行认真分析,可以建立混凝土空间实体单元的全桥精细化有限元模型,分析整体结构全截面设计荷载偏心增大系数。对此研究人员进行了大量研究,取得了较多成果。文献[2]结合杭州某工程实例,发现实体有限元法更能真实反映结构的实际受力状态,适用性更广。宽箱梁的偏载效应明显,采用传统的经验值是偏不安全的,有必要进行详细的分析计算。文献[3]建立实体单元空间有限元模型,将全桥关键截面各个位置点的正应力增大系数计算值与已有方法所得值进行对比,探讨了该方法的可行性。文献[4]结合一座预应力变截面连续梁桥的运营期安全监测和多座新建桥梁的荷载试验,详细介绍了通过有限元法和静载试验确定偏载系数的方法,分析了箱梁在偏载作用下的偏载增大系数。文献[5]探讨了变截面连续梁偏载系数沿跨度的分布规律,提出了实用的偏载系数取值建议。文献[6-10]计算了一些非常规箱梁的偏心增大系数,在实际设计中应引起充分重视。现有研究主要针对了相关理论研究和部分实例计算,难以直接指导工程设计。文中对有限元计算软件进行二次开发,批量建立简支和连续箱梁的有限元实体单元精细化模型,计算偏心增大系数并拟合公式,指导工程设计实践。
1 简支箱梁计算 1.1 计算内容笔者前期研究成果表明[11]:对于简支箱梁偏心增大系数,宽度和跨径对其影响很大;是否设置箱梁顶底板加厚和腹板加宽,影响也较大;其余参数如约束、箱室个数、顶底板厚度、腹板宽度、梁高、截面倒角等影响较小。基于文中拟建立不同参数的箱梁有限元实体单元模型进行计算分析。
1.1.1 箱梁跨径与宽度该参数对箱梁偏心增大系数影响较大,应进行详细计算。根据《公路桥涵设计通用规范》(JTG D60—2015)[12],设计车道数大于八车道时,不再对横向车道布载系数做规定;通过计算,设计车道数小于三车道时,传统的偏心增大系数1.15基本满足要求。因此,仅对三车道至八车道内的箱梁进行计算,即箱梁宽度变化范围确定为11.6~32.4 m,步长0.1 m。计算结果表明:跨径大于42 m时,传统的偏心增大系数1.15满足要求。因此,选定跨径计算范围为16~42 m,步长为1 m。
1.1.2 箱梁其余构造尺寸是否设置箱梁顶底板加厚和腹板加宽,对偏心增大系数影响较大,计算建模时应对加厚加宽段精确建模;其余参数影响较小,根据工程设计经验取值即可。
1.1.3 荷载布置计算仅考虑汽车车道荷载,按对称和最不利偏心2种工况加载。横向加载时,第1种工况考虑文献[12]规定的车道数、车道荷载横向布置内外间距等因素,将荷载对称布置于桥面上;第2种工况在车道荷载满足距桥边的最小允许距离的情况下,将荷载尽可能靠近桥面边缘偏心布置。纵向加载时,2种工况均根据单梁模型计算截面的最大内力影响线,分别加载文献[12]规定的集中荷载和均布荷载。以六车道汽车荷载布置为例,2种工况荷载横向布置如图 1和图 2所示。

|
图 1 六车道汽车荷载对称加载时横向布置 Fig. 1 Transverse arrangement of symmetrical 6-lane vehicle load |

|
图 2 六车道汽车荷载偏心加载时横向布置 Fig. 2 Transverse arrangement of asymmetrical 6-lane vehicle load |
综上所述,文中根据宽度与跨径的选择范围,结合工程设计经验取值,对5 643座简支直线箱梁进行建模计算,并以计算结果作为数据样本,进行规律探索与公式拟合。
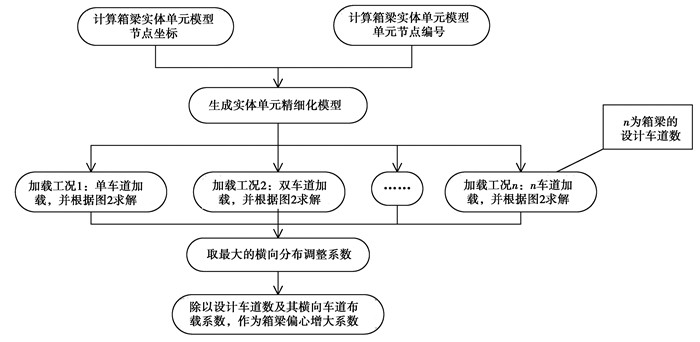
1.2 计算流程编写程序,生成批量计算简支箱梁的偏心增大系数的命令流,导入有限元软件计算。单座箱梁计算流程如图 3和图 4所示。计算过程中发现,当箱梁的计算车道数越大时,横向分布调整系数不一定越大。但设计过程中通常采用设计车道的偏心增大系数,计算其横向分布调整系数用于整体结构全截面设计,因此,在保证横向分布调整系数不变的情况下,将其转化为设计车道的偏心增大系数,以方便设计人员直接使用。
|
图 3 箱梁偏心增大系数计算流程图 Fig. 3 The calculating process about the eccentric-loaded coefficients of box girders |

|
注:图中偏心增大系数=偏载最大应力/对称加载最大应力;横向分布调整系数=偏心增大系数×车道数×横向车道布载系数。L/2截面表示跨中截面,L/4截面表示1/4跨截面。 图 4 每个加载工况下的箱梁横向分布调整系数计算流程图 Fig. 4 The calculating process about the transverse distribution adjustment coefficients of box girders under each load case |
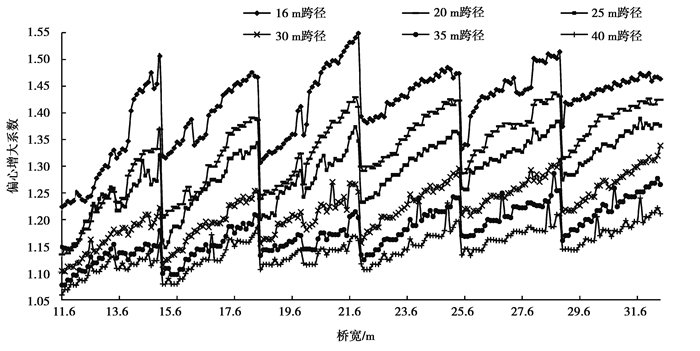
对上述5 643座简支箱梁进行计算,求解偏心增大系数,常见跨径(16 m、20 m、25 m、30 m、35 m和40 m)对应不同宽度的计算结果如图 5所示。
|
图 5 常见跨径对应不同宽度的简支箱梁偏心增大系数 Fig. 5 Eccentric-loaded coefficients of some simply supported box girders with general spans and different widths |
由图 5可知:箱梁跨径相同条件下,设计车道增大(对应箱梁宽度为15 m、18.5 m、22 m、25.5 m和29 m等)时,偏心增大系数急剧减小;车道数相同时,偏心增大系数随箱梁宽度增大而增大;箱梁宽度相同时,偏心增大系数随着跨径增大而减小;箱梁跨径较小时,偏心增大系数变化较为急剧,反之较为平缓。对5 643组计算结果进行分析,可以初步确认箱梁偏心增大系数取值在1.15~1.5之间。取计算值上浮至0.05的整数倍,作为偏心增大系数建议值。在不同跨径范围内,简支箱梁的偏心增大系数建议值,在计算样本中所占百分比如表 1所示。
| 表 1 不同跨径范围内,简支箱梁的偏心增大系数建议值所占百分比 Table 1 The Percentage of recommended eccentric-loaded coefficients of simply supported box girders within different span range % |
对5 643组原始数据进行公式拟合,建立简支箱梁的偏心增大系数μ计算公式:
| $ \mu=\alpha\left(\frac{B-18}{L}\right)^{4}+\beta\left(\frac{B-18}{L}\right)^{2}+\gamma\left(\frac{B-b_{0}}{L}\right)+\kappa,$ | (1) |
式中:μ为偏心增大系数;B为箱梁全宽;L为箱梁跨径;计算公式中各参数取值和拟合公式的相关系数R,如表 2所示。
| 表 2 简支箱梁偏心增大系数计算公式参数取值和公式相关系数 Table 2 The parameters of mathematical formula describing eccentric-loaded coefficients of simply supported box girder and its correlation coefficient |
拟合公式中相关系数R值均大于0.95,满足精度要求。
2 连续箱梁计算 2.1 连续梁偏心增大系数计算建立不同跨径和宽度的连续梁有限元实体单元精细化模型(如图 6~图 7所示),进行车道荷载加载。与简支箱梁的加载方式相同,纵向根据单梁计算的内力影响线加载,横向进行对称和偏心最不利加载,并计算全桥各计算截面的偏心增大系数。连续箱梁跨径组合分别为30 m+30 m+30 m、18 m+30 m+18 m、30 m+ 18 m+30 m、30 m+42 m+30 m、42 m+30 m+42 m,箱梁宽度分别为17.5 m、24.5 m和31.4 m,计算结果如图 8~图 10所示。

|
图 6 单箱双室三跨连续梁有限元实体单元模型 Fig. 6 The FEM models of three span continuous beam with single box double room |

|
图 7 单箱双室三跨连续梁支点和跨中处,有限元实体单元模型 Fig. 7 The FEM models in the fulcrum area and mid-span of three span continuous beam with single box double room |

|
图 8 箱梁宽度17.5 m时,不同跨径组合的1/2箱梁四车道偏心增大系数 Fig. 8 The 4-Lanes eccentric-loaded coefficients of 1/2 box girder with different span combinations while the width is 17.5 m |
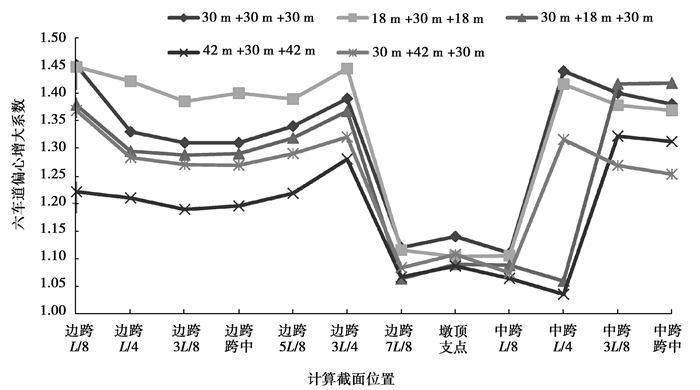
|
图 9 箱梁宽度24.5 m时,不同跨径组合的1/2箱梁六车道偏心增大系数 Fig. 9 The 6-Lanes eccentric-loaded coefficients of 1/2 box girder with different span combinations while the width is 24.5 m |
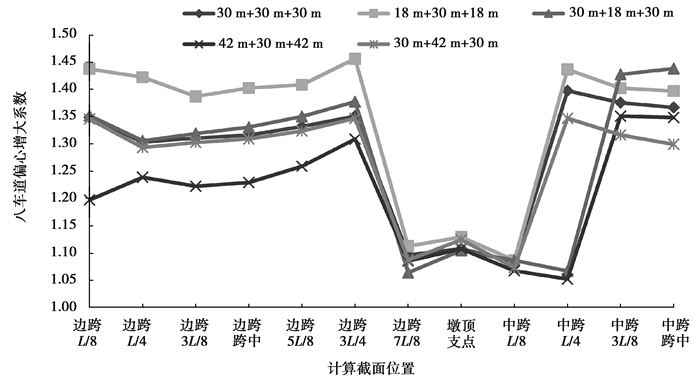
|
图 10 箱梁宽度31.4 m时,不同跨径组合的1/2箱梁八车道偏心增大系数 Fig. 10 The 8-Lanes eccentric-loaded coefficients of 1/2 box girder with different span combinations while the width is 31.4 m |
分析图 8~图 10可以发现:对于连续箱梁,边跨L/4之前、边跨3L/4处和中跨L/4处的偏心增大系数较大,但这些截面的拉应力较小,确定全桥偏心增大系数时可不参考。应选取拉应力和偏心增大系数均较大截面处的对应值,作为全桥偏心增大系数。连续梁中30 m跨的偏心增大系数如表 3所示。
| 表 3 连续梁中30m跨的偏心增大系数 Table 3 The eccentric-loaded coefficients of continuous box girder while the span is 30m |
由表 3可知:与同跨径简支梁相比,连续梁的偏心增大系数较大,修正系数(同跨径桥宽时连续梁和简支梁偏心增大系数比值)在1.03~1.12之间;箱梁宽度越大,修正系数越大;跨径组合不同,箱梁同跨径的偏心增大系数也不相同,中跨的偏心增大系数大于边跨;箱梁总跨径越小,偏心增大系数越大,反之越小。
2.2 连续梁修正系数确定建立不同跨径和宽度的连续箱梁精细化实体模型共1 112座,计算全桥偏心放大系数,修正系数在计算样本中所占百分比,如表 4所示。
| 表 4 连续梁偏心增大系数的修正系数在样本中所占百分比 Table 4 The Percentage of eccentric-loaded coefficients compensation factors of continuous box girder |
根据表 4,建议连续梁的修正系数取1.05~1.1之间。当箱梁较宽、总跨径较小、计算跨距离梁端较远时,宜选择较大的修正系数,反之选择较小值。
3 结论根据公路桥梁相关规范和有限元计算软件,对现浇箱梁的偏心增大系数进行了计算研究,得出以下结论:
1) 对于简支箱梁,车道数相同时,箱梁宽跨比越大,偏心增大系数越大,反之越小。简支箱梁的偏心增大系数初步确定在1.15~1.5之间,可通过文中公式精确求解。
2) 计算连续梁偏心增大系数时,根据各跨跨径和宽度,由文中拟合公式求出各跨的偏心增大系数,并进行修正取最大值。修正系数可根据经验在1.05~1.1之间确定,当箱梁较宽、总跨径较小、计算跨距离梁端较远时,宜选择较大的修正系数,反之选择较小值。
3) 通过对有限元软件进行二次开发,建立现浇箱梁的精细化有限元实体模型、施加荷载并进行计算和数据处理,提出了一种快速批量研究现浇箱梁受力性能的方法。这种方法可高效便捷地计算偏心增大系数,研究剪力滞和恒载作用下箱梁应力的横向分布等,实现现浇箱梁的精细化设计。
| [1] |
中华人民共和国交通运输部.JTG 3362-2018公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京: 人民交通出版社, 2018. Ministry of Transport of the People's Republic of China. JTG 3362-2018 Specifications for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts[S].Beijing: China Communications Press, 2018. (in Chinese) |
| [2] |
陈国强. 连续宽箱梁的偏载增大系数的讨论[J]. 公路交通科技, 2013, 30(7): 66-71. CHEN Guoqiang. Discussion on eccentric load enhancement coefficient of continuous wide box girder[J]. Journal of Highway and Transportation Research and Development, 2013, 30(7): 66-71. (in Chinese) DOI:10.3969/j.issn.1002-0268.2013.07.012 |
| [3] |
李旭, 林晶, 虞建成. 连续宽箱梁桥活载正应力增大系数研究[J]. 苏州科技学院学报(工程技术版), 2010, 23(4): 35-39. LI Xu, LIN Jing, YU Jiancheng. A study on amplificatory coefficient of normal stress of continuous wide-flange box girder bridge under live load[J]. Journal of Suzhou University of Science and Technology(Engineering and Technology), 2010, 23(4): 35-39. (in Chinese) |
| [4] |
陆军, 张道光. 预应力混凝土变截面连续箱梁桥偏载系数研究[J]. 现代交通技术, 2011, 8(3): 23-25. LU Jun, ZHANG Daoguang. Research on eccentric loaded coefficients of variable cross-section continuous prestressed concrete box girder bridge[J]. Modern Transportation Technology, 2011, 8(3): 23-25. (in Chinese) DOI:10.3969/j.issn.1672-9889.2011.03.007 |
| [5] |
苏俭, 刘钊, 阮静. 连续梁桥的活载正应力偏载系数研究[J]. 世界桥梁, 2009, 37(4): 34-37. SU Jian, LIU Zhao, RUAN Jing. Study of eccentric load coefficient of live load normal stress of continuous beam bridge[J]. World Bridges, 2009, 37(4): 34-37. (in Chinese) |
| [6] |
刘保东, 任红伟, 李鹏飞, 等. 波纹钢腹板组合箱梁偏心增大系数计算方法[J]. 公路交通科技, 2012, 29(3): 80-85. LIU Baodong, REN Hongwei, LI Pengfei, et al. Calculation methods of eccentric magnified factor of concrete box girder with corrugated steel webs[J]. Journal of Highway and Transportation Research and Development, 2012, 29(3): 80-85. (in Chinese) DOI:10.3969/j.issn.1002-0268.2012.03.015 |
| [7] |
袁波, 李广慧. 特大跨波形钢腹板PC组合连续梁桥偏载系数研究[J]. 管理工程师, 2014, 19(5): 11-13. YUAN Bo, LI Guanghui. Study on eccentric-loaded coefficient of large-span composite PC continuous beam bridge with corrugated steel webs[J]. Management Engineer, 2014, 19(5): 11-13. (in Chinese) DOI:10.3969/j.issn.1007-1199.2014.05.004 |
| [8] |
沈炯伟, 杨沈红. 宽幅脊骨梁矮塔斜拉桥活载偏载效应[J]. 土木工程与管理学报, 2012, 29(2): 108-112. SHEN Jiongwei, YANG Shenhong. Eccentric load effect of live load on the low pylon cable-stayed bridge with wide spine beam[J]. Journal of Civil Engineering and Management, 2012, 29(2): 108-112. (in Chinese) DOI:10.3969/j.issn.2095-0985.2012.02.021 |
| [9] |
Lei M, Zhou L Y, Li S Q, et al. Eccentric load coefficient of live load normal stress of continuous composite box-girder bridge with corrugated steel webs[J]. Procedia Earth and Planetary Science, 2012, 5: 335-340. DOI:10.1016/j.proeps.2012.01.056 |
| [10] |
Yuze N, Junliang T, Suisheng L, et al. Study of eccentric load coefficient of pre-stressed concrete partial cable-stayed bridge with corrugated steel webs[J]. Advances in Engineering Research (AER), 132: 224-230.
|
| [11] |
常诚. 现浇箱梁横向分布调整系数的实体有限元计算研究[J]. 中外公路, 2018, 38(5): 102-105. CHANG Cheng. Study on solid finite element computation of load transverse distribution adjustment coefficients of cast-in-place box girder method[J]. Journal of China & Foreign Highway, 2018, 38(5): 102-105. (in Chinese) |
| [12] |
中华人民共和国交通运输部.JTG D60-2015公路桥涵设计通用规范[S].北京: 人民交通出版社, 2015. Ministry of Transport of the People's Republic of China. JTG D60-2015 General Specifications for Design of Highway Bridges and Culverts[S].Beijing: China Communications Press, 2015. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43

