2. 重庆大学 自动化学院, 重庆 400044
2. School of Automation, Chongqing University, Chongqing 400044, P. R. China
根据定位环境不同,定位技术可以分为室外定位和室内定位。室外定位主要依靠传统卫星定位技术,其主要是通过时间测距定位、多普勒测速定位等方法获得用户的地理位置信息,比如全球定位系统(GPS, global position system)和北斗卫星导航系统(BDS, beidou navigation satellite system)[1]。目前,该技术已成熟地运用于各个领域并日趋完善,能在广阔的室外空间为人们提供精准位置服务,使得人们在室外的定位需求基本得到满足[2]。人们对室内定位精度同样有较高需求,但由于卫星信号难以穿透建筑物墙体,且易受多径效应干扰,使卫星定位系统在室内环境中精度大大下降,甚至无法进行定位[3]。面对人们在工作生活中对室内定位的急切需求,室内定位技术受到了学术界和工业界的广泛关注。
目前智能手机室内定位方法按技术类别可以分为基于无线网络、基于测量传感器以及基于视觉定位方法[4-7]。基于视觉的室内定位技术精度高、价格低,尤其当深度学习理论应用在图像处理上时,定位误差能够达到小于1 m[8]。然而,它必须频繁地使用摄像设备来获得图像信息,使用上的不便导致这种方法很难应用在现实当中[9]。无线通信技术具有安装方便、技术成熟、体积小等优点,但是其中的红外线、超声波、RFID等室内定位技术需要专有接收端设备,定位成本昂贵,并不能实现大范围的室内定位[10]。
随着智能终端和移动互联网的快速发展,越来越多的用户选择使用WIFI作为接入互联网的主要方式,因此无线接入点(AP, access points)被广泛分布在各种室内公共场所[11]。WIFI信号有着覆盖范围广、安装简单的优点,并且接收装置为人们日常使用的智能手机,不需要额外专用设备,利用WIFI实现室内定位不仅满足了人们上网的需求,同时也解决了室内位置服务的问题。因此,通过搜集WIFI信号进行指纹定位已成为目前最主流的室内定位方法之一[12]。
若室内的任一点位置都有独特的位置特征,像指纹一样一一对应,那么就可以通过位置指纹库来与待测“指纹”进行匹配,依据相应的数据处理与定位算法即可实现定位。基于WIFI位置指纹的定位技术无需额外的硬件设备支持,甚至不需要用户连接所提供的WIFI,只要用户打开自身携带移动终端的WIFI开关即可,大大降低了对WIFI热点的网络要求和技术门槛,相比较其他技术方法有着独特的成本优势与多功能性,故其也是当前室内定位领域的研究热点。近年来,传感技术、无线电与移动通信进步使得获取大量人们在特定空间中的时空位置数据成为可能;算法与理论的发展能从大量数据中寻找规律、发现知识、获取信息;云计算及人工智能的日益成熟为数据清洗、挖掘与分析提供了有力的工具,这些都使得大数据在商业分析、技术研发与分类预测等领域得到广泛运用。
室内定位技术与环境信息的结合能够为用户提供立体、实时、方便快捷的导航与生活服务。研究室内定位技术不仅有着巨大的经济效益,同时也具有一定的社会意义[13]。
1 相关模型研究基于指纹的定位匹配算法通常被分为确定性匹配算法和概率性匹配算法,其中概率性匹配算法使用的是各个参考节点(RP, reference points)的联合概率分布,需要采集大量的指纹样本,并且计算复杂度高,不适合大范围室内环境下的定位[14]。确定性匹配算法多使用距离作为训练样本和测试样本之间的相似度指标,距离越小相似度越高,典型代表为最近邻算法(NN, nearest neighbor),K近邻算法(KNN, k-nearest neighbor)、加权K近邻算法(WKNN, weighted k-nearest neighbor)等。研究将分析在WIFI指纹模型系统构建过程当中应用过的多种类型的预测方法。
1.1 最近邻算法最近邻算法(NN)是一种多分类的懒惰学习算法,它不需要通过训练得到一个分类模型,而是依靠计算待分类样本与各个已分类样本的距离来量化样本之间的相似度。在室内定位中,通常使用欧几里得距离来评估实时指纹与指纹库指纹之间的相似性
| $ D\left(R, L_{i}\right)=\sqrt{\left(R-L_{i}\right)^{2}},$ | (1) |
式中:R为待测节点所接收到的实时指纹数据;Li是指纹库中的第i个历史指纹数据;D R, Li表示两者之间的相似程度,D R, Li的值越小,2个指纹越相似[15]。将指纹库中的数据全部计算完毕后,选取最小D R, Li所属的物理位置坐标作为定位结果。
1.2 K近邻算法KNN(K-Nearest Neighbor),是机器学习领域的一种分类算法,K即为确定待分类点类型所需的最少参考点的数量,其基本思想类似于“物以类聚”,即通过分析某点周围若干点的特性来推测该点的类型。以距离特征作为判断依据为该算法常用的一种手段,包括欧式距离、马氏距离、曼哈顿距离、汉明距离和夹角余弦等等。算法的核心在于K值的选取和距离的衡量,计算效率与训练样本量将影响算法的性能和分类精度。该算法在对预存数据与实测数据之间的距离进行计算后,根据运算公式对相似度差异不大的近邻参考点进行选择后估计位置,如果距离越近,坐标估计将具有更高的精度。不足之处主要是固定的选择值对一些位置的定位精度有影响,在距离计算过程中,很多位置信息将丢掉,降低了位置定位的精度[16]。KNN与NN相似,都是用2个指纹之间的欧氏距离度量1者的相似度。但不同的是,NN只使用最相近的指纹信息,而KNN利用了前K个相似指纹的位置信息,在找出最相似的K个指纹后,用其坐标均值作为最终结果,提高了定位算法的鲁棒性[17]。坐标计算公式为
| $ \left(x_{\mathrm{est}}, y_{\mathrm{est}}\right)=\frac{1}{K} \sum\limits_{k=1}^{K}\left(x_{k}, y_{k}\right),$ | (2) |
式中:(xest, yest)为最终的定位坐标;(xk, yk)为第k位指纹所属的物理位置坐标。
1.3 加权K近邻算法在KNN算法的实际应用中,在某些场景下可能会发现,若某一类数据数量相对较多,或数据某属性(特征)对结果影响更大,那么“一视同仁”、“众点平等”的KNN算法的分类精度就可能会出现偏差。为了改善这一点,可以为每个点的距离或某属性特征赋予一个权重,距离近的点、特征区分度明显的属性权重更大,以提高分类精度。从某种程度上说,WKNN(weighted k-nearest neighbor)是对KNN算法的一种优化。WKNN和KNN相似度计算方法一样,但KNN算法的最终结果为前K个指纹坐标的均值,没有利用到前K个指纹名次之间的差异性。WKNN算法针对这个问题,改变每个名次的权重, 实现更精确的位置估算[18]。最终结果为
| $ \left(x_{\mathrm{est}}, y_{\mathrm{est}}\right)=\sum_{k=1}^{K} \omega_{k}\left(x_{k}, y_{k}\right),$ | (3) |
式中:(xest, yest)为最终的定位坐标;(xk, yk)为第k位指纹所属的物理位置坐标;ωk为第k位指纹的权值系数。
NN、KNN和WKNN算法都是基于距离的确定性定位匹配算法,有着原理简单,易于实现等优点。其中,KNN算法较之于NN算法,选用前K个相似指纹进行坐标计算,减少了由瞬时信号改变导致的定位误差过大的情况,提高了定位算法的鲁棒性。WKNN算法在KNN算法的基础上进行了改进,不仅选用前K个相似指纹进行坐标计算,还突出了前K个相似指纹排名之间的差异性,有效地提高了定位算法的精度。然而,上述方式都只利用了当前时刻的指纹信息进行定位估计,忽视了相邻时刻指纹之间的时序信息,对指纹数据的利用效率没有达到最大值。
1.4 TS-K近邻算法人的行走是一个具有强时序关联性的行为,由于人日常行走中通常保持匀速行进,很少出现跳跃的情况,因此每一步位置都和上几步的位置息息相关。利用行走时相邻时刻定位结果的时间序列趋势,提出TS-KNN(timing sequence based k-nearest neighbor)算法。该算法的基本思想是利用相近时刻的历史结果修正当前时刻的预测结果。
该算法利用KNN算法的思想,使用欧式距离计算指纹之间的相似度,找出前K个相似指纹,计算方法如公式(1)所示。找出前K个相似指纹后,需要依次计算每个指纹与上一时刻定位结果之间的距离,称为预估距离。假设当前定位时刻为t时刻,那么预估距离的计算方式为
| $ \begin{array}{*{35}{l}} {{d}_{t, k}}=\sqrt{{{\left( {{x}_{k}}-{{x}_{t-1}} \right)}^{2}}+{{\left( {{y}_{k}}-{{y}_{t-1}} \right)}^{2}}, } \\ {{d}_{t, k}}=\sqrt{{{\left( {{x}_{k}}-{{x}_{t-1}} \right)}^{2}}+{{\left( {{y}_{k}}-{{y}_{t-1}} \right)}^{2}}, } \\ \end{array} $ | (4) |
式中:(xk, yk)为当前时刻下,第k位相似指纹所属的物理位置坐标;(xt-1, yt-1)为上一时刻最终定位结果的坐标;dt, k则是第k位相似指纹的预估距离。
通常情况下,在较短时间段内,人的行走距离是非常有限的。由于人的行走速度大约是0.5 m每步,假设每个定位间隔内行走的步数为NS,那么dt, k的理论值应为0.5·NS,因此选用|dt, k-0.5·NS|作为预估距离与理论距离的偏移量。一个指纹的偏移量越大,说明该指纹的位置坐标离真实坐标的距离就越大,那么就需要在坐标计算中减弱该指纹的权值。第k个相似指纹的权值ωk计算方法为
| $ \omega_{k}=\frac{1 /\left(\left|d_{t, k}-0.5 \cdot N_{s}\right|+\varepsilon\right)}{\sum\limits_{k=1}^{K} 1 /\left(\left|d_{t, k}-0.5 ? N_{s}\right|+\varepsilon\right)}, $ | (5) |
其中,ε是一个比较小的数,防止分母为0。最终定位结果的坐标计算公式如式(6)所示
| $ \left( {{x}_{t}}, {{y}_{t}} \right)=\sum\limits_{k=1}^{K}{{{\omega }_{k}}}\left( {{x}_{k}}, {{y}_{k}} \right),$ | (6) |
式中:(xt, yt)就是当前时刻定位结果的坐标,为前K个相似指纹的位置坐标进行加权后的和。本算法的流程图如图 1所示。
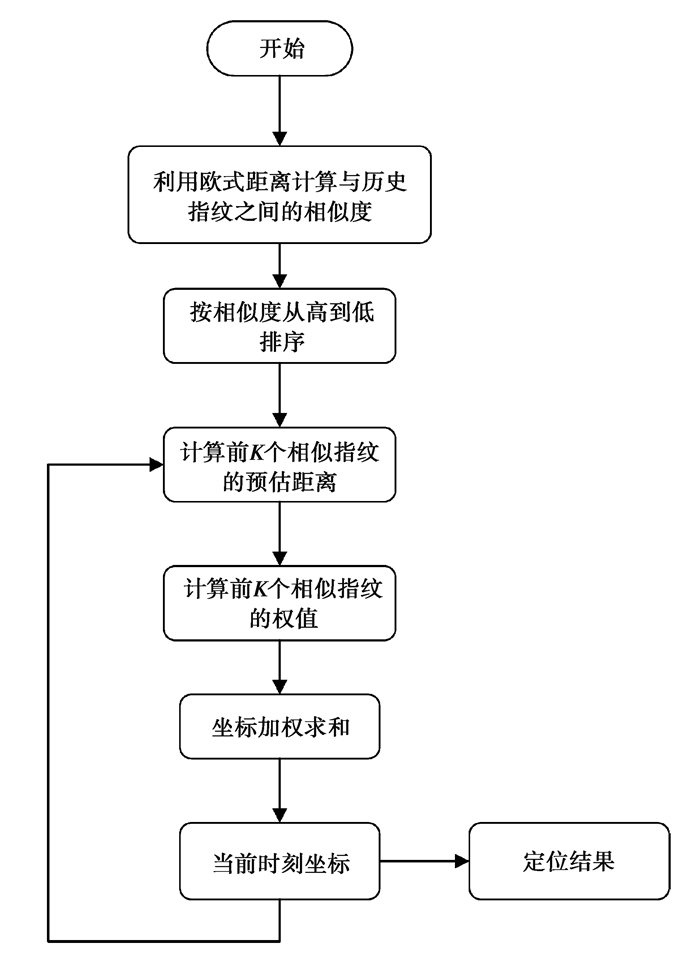
|
图 1 TS-KNN算法流程图 Fig. 1 The TS-KNN algorithm flowchart |
为验证提出的TS-KNN算法的室内定位效果,本实验选取了重庆市某广场B1层其中一段较长的过道进行实验测试,该定位区域包含10个店铺、2部扶梯和电梯,以及1间洗手间,总面积约340 m2。定位区域平面图如图 2所示。
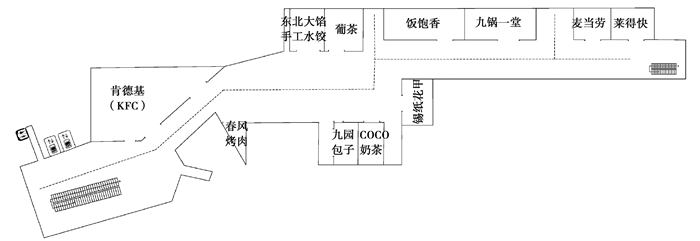
|
图 2 定位区域平面图 Fig. 2 The floor plan of the target area |
相同定位误差所造成的定位影响是有区别的。当在一条笔直的走廊中出现误差时,因为行走路线的单一,不会对人的行为判断造成太大的干扰,影响较小。当相同误差出现在T字路口等需要选择行走方向的地点时,会对人员行走判断产生较大的误导,非常影响用户体验,影响较大。因此本实验按功能的不同将AP分为覆盖型AP和引导性AP,覆盖型AP保证每个区块至少能检测到3个WIFI信号,在全局上达到一定精度的定位效果。另一种为引导性AP,该类AP部署在误差影响较大的区域,增强该区域信号分布的特异性,在局部上减少出现此类误差的概率。根据以上原则,将AP部署在定位区域相应的位置,具体部署方式如图 3所示。
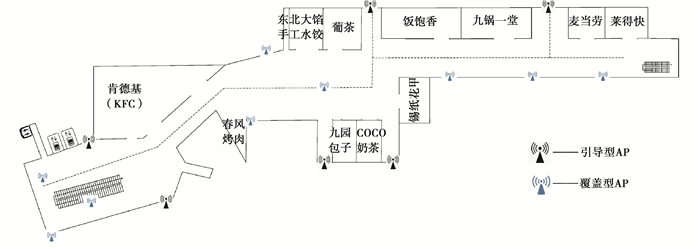
|
图 3 部署方式图 Fig. 3 The deployment method diagram |
由于WIFI信号在室内传播的复杂性,每个参考点处的信号强度观测值具有很强的波动性,并且不同的手机朝向也会导致不同的信号强度观测值[12]。因此在采集WIFI数据时,为了得到分布较为全面的数据,使用5种不同型号的手机(华为P7、小米5、荣耀6、小米3、华为P8)进行位置指纹的采集,在每一个参考节点上采集朝向正东、正南、正西和正东4个方向上的WIFI数据,每个手机在各个参考节点上采集120条WIFI数据,其中每个朝向各30条。定位区域区块划分图如图 4所示。
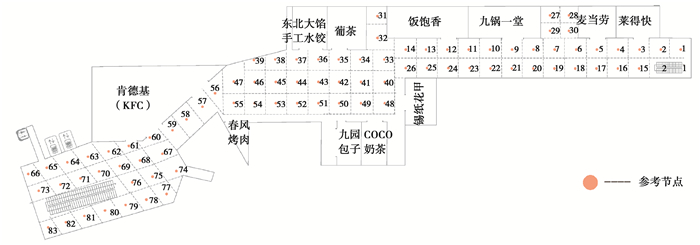
|
图 4 定位区域区块划分图 Fig. 4 The positioning area block division diagram |
每一对接收信号强度值和位置坐标确定了一个独一无二的参考点,并按照一定的数据格式存入指纹数据库中[17-19]。采集所用APP如图 5所示。
|
图 5 采集APP界面 Fig. 5 The interface of the APP used to collect information |
室内定位系统可分为指纹数据采集和实时定位2个小系统。指纹数据采集系统服务于室内定位的离线阶段,主要实现原始信号采集、信号修正与处理和指纹数据存储等功能,指纹数据采集系统结构如图 6所示。
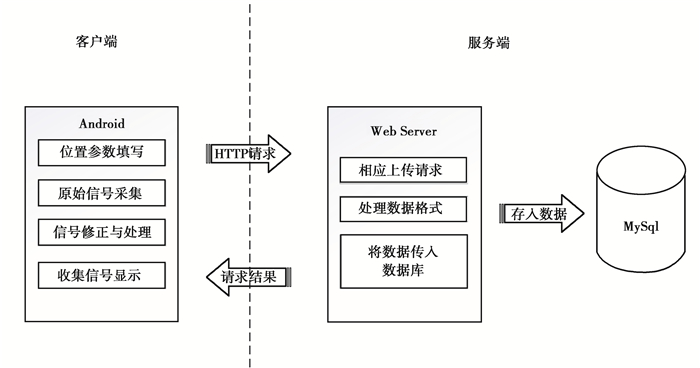
|
图 6 指纹数据采集系统结构图 Fig. 6 The structure diagram of fingerprint data collection system |
指纹数据采集系统包含一个客户端和一个服务端。客户端利用位置参数填写、原始信号采集和信号修正与处理等功能,实现了离线阶段指纹数据的采集。
实时定位系服务于室内定位的在线阶段,主要实现了实时指纹采集、位置坐标估计和定位可视化等功能,实时定位系统的整体结构如图 7所示。
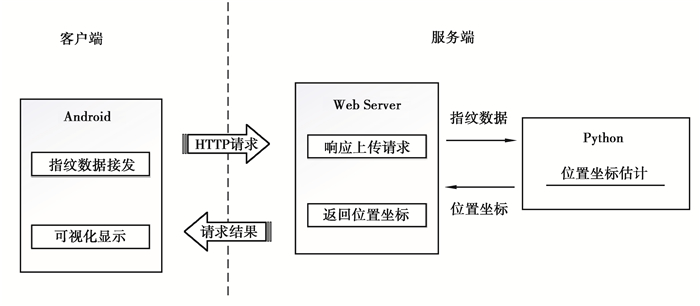
|
图 7 实时定位系统结构图 Fig. 7 The structure diagram of the real-time positioning system |
如图 7所示,客户端是一个基于Android系统的APP,利用指纹数据采集和地图可视化等功能,实现了在线阶段的位置实时估计与显示。实时定位系统客户端的主界面如图 8所示。
|
图 8 实时定位系统客户端主界面 Fig. 8 The main interface of real-time positioning system client |
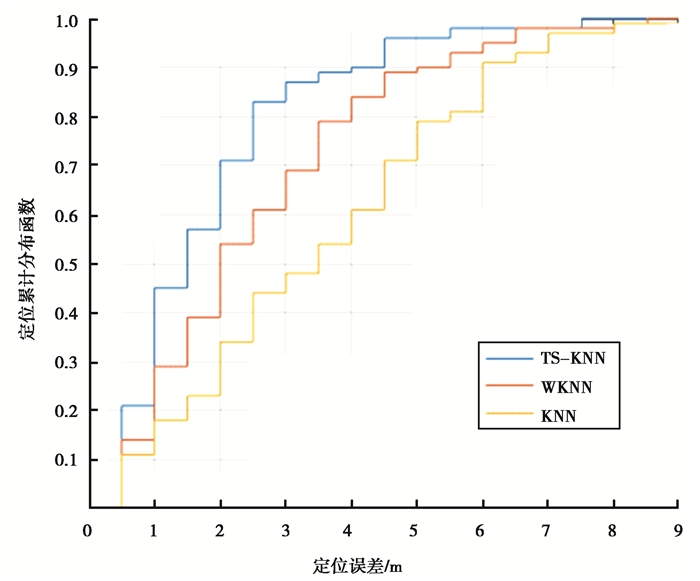
为了检验TS-KNN算法的定位效果,选择KNN,WKNN,TS-KNN 3种算法进行比较,每个算法的定位累计分布曲线如图 9所示。
|
图 9 不同算法的定位累计分布曲线 Fig. 9 The distribution curve of different algorithm positioning accumulation |
由图 9可以看出,TS-KNN算法在任何定位误差下的准确率都高于其它两者。当定位误差阈值为3 m时,其定位准确率接近90%,基本符合室内定位的要求。除此之外,当定位误差小于1 m时,三者算法的准确率差别较小,都小于25%,这是因为WIFI信号强度在1 m内变化不大,信号—空间映射关系的分辨率比较低,这是WIFI的固有属性,单纯改进算法很难分辨出差异性。虽然3种算法在极小误差下的准确率都差强人意,但当误差阈值达到3 m时,3种算法的准确率形成了极大的差别,分别为87%、69%和48%,这是因为TS-KNN算法区别于WKNN和KNN算法,利用了WIFI的时序特征,大大提高了定位的精度。同时,因为WIFI信号在较大范围内有着明显差异,所有算法在定位误差等于6 m时都达到了比较高的准确率。
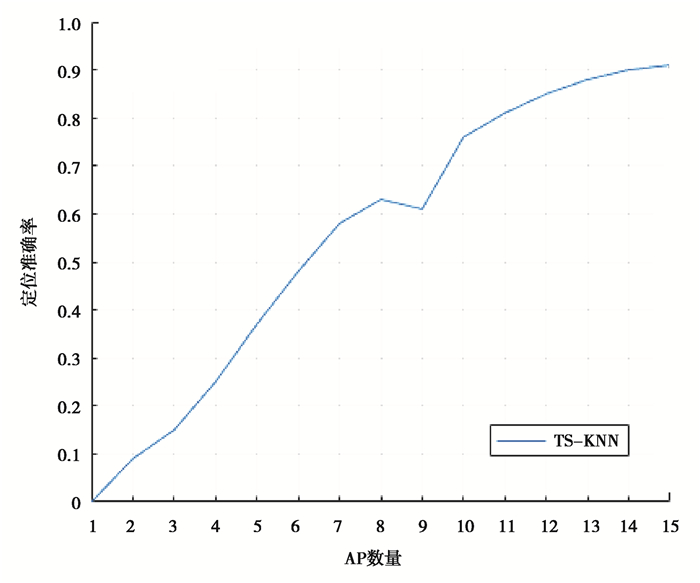
为了探究AP数量对定位效果的影响,将定位区域布置的AP的数量分别设为2、3… 15,同时利用TS-KNN算法计算各种情况下的准确率,结果如图 10所示。
|
图 10 不同AP数量下的定位准确率 Fig. 10 The positioning accuracy under different AP numbers |
图 10显示了当定位误差小于4 m时,不同AP数量下TS-KNN算法的定位准确率。可以从曲线形状上看出,在大趋势上,AP数量与定位准确率成正比,但出现了极个别AP数量增加而准确率下降的情况,这可能是因为TS-KNN是一种基于距离的定位算法,而新增加的AP虽然丰富了空间中的信号数量,但降低了信号的差异性,是一个坏特征。准确率曲线的斜率越来越低,说明当AP到达一定数量后,虽然准确率仍然会随着AP数量的增加而上升,但涨幅非常小,因此最终定位区域的AP数量的确定,需要综合考虑定位需求和定位成本。
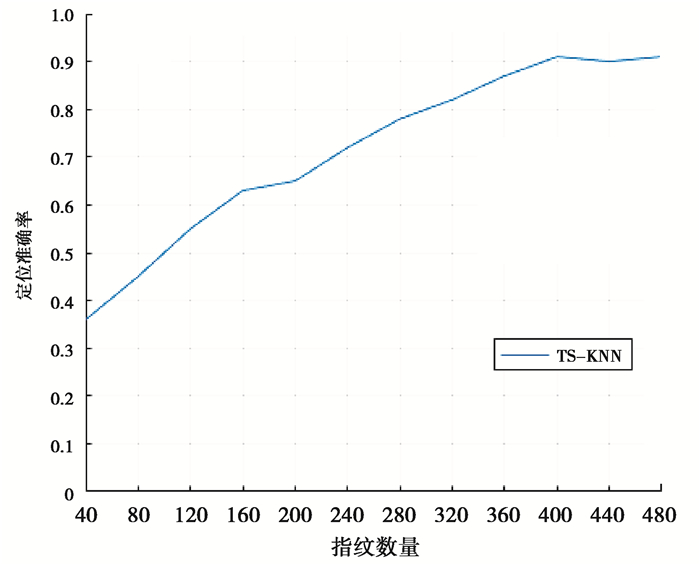
为了探究指纹数量对定位效果的影响,将每个参考节点的指纹采集数量设为40、80、120、160、200、240、280、320、360、400、440、480和520共13组指纹数量,利用TS-KNN算法计算各个数量下的准确率,结果如图 11所示。
|
图 11 不同指纹数量下的定位准确率 Fig. 11 The positioning accuracy under different fingerprint numbers |
图 11显示了当定位误差小于4 m时,不同指纹采集数量下TS-KNN算法的定位准确率。可以从曲线趋势上看出,当指纹数量小于400时,TS-KNN算法的准确率随指纹数量的增加稳步上升,并在指纹数量为400时达到最高值91%,之后趋于稳定,不再出现较大的变化。
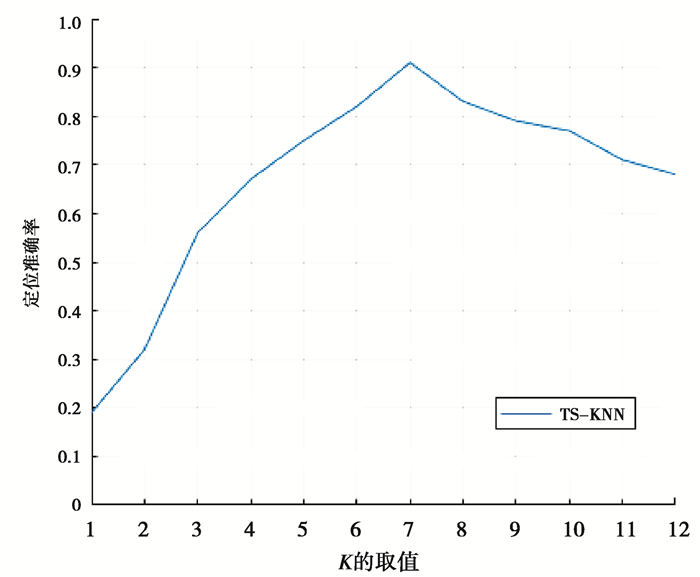
为了探究K的取值对定位效果的影响,利用TS-KNN算法计算各个K值下的定位准确率,结果如图 12所示。
|
图 12 不同K值下的定位准确率 Fig. 12 The positioning accuracy under different K values |
图 12显示了当定位误差小于4 m时,不同K值下TS-KNN算法的定位准确率。当K值等于1时的TS-KNN大致相当于NN算法,不仅丢失了指纹间的时序信息,并且大幅降低了算法的鲁棒性,定位准确率最低。当K值逐渐增加后,TS-KNN在时序信息利用上的优势体现出来,定位准确率随之升高,并在K值为7时达到最高。当K的取值大于7时,TS-KNN算法可能过多考虑了误差较大的定位结果,导致定位准确率下降。
4 结论为解决人们在工作生活中对于室内定位的急切需求,笔者对基于WIFI位置指纹大数据分析的室内定位算法进行研究,并围绕着算法实现及应用进行了设计,以人们手机接收的WIFI信号强度作为处理对象,从数据驱动出发,应用机器学习方法分析WIFI大数据的指纹特征,构建室内定位模型。
传统WIFI室内定位算法只利用了当前时刻的指纹信息进行定位估计,忽视了相邻时刻指纹间的时序信息。针对以上问题,提出一种基于指纹时序特征的KNN定位算法,该算法使用当前时刻的指纹进行基准坐标选择,然后再利用前几个时刻的定位结果对每个基准坐标进行权值修正。实验表明提出的算法优于其他几种基于近邻的定位算法,有效提高室内定位精度,降低平均定位误差。但是,本算法比较依赖于初始预测位置的准确性,初次定位误差较大可能会产生误差累计问题,其稳定性有待进一步解决。
| [1] |
Brack A. Reliable GPS+BDS RTK positioning with partial ambiguity resolution[J]. GPS Solutions, 2017, 21(3): 1083-1092. |
| [2] |
宁津生, 姚宜斌, 张小红. 全球导航卫星系统发展综述[J]. 导航定位学报, 2013, 1(1): 3-8. NING Jinsheng, YAO Yibin, ZHANG Xiaohong. Review of the development of global satellite navigation system[J]. Journal of Navigation and Positioning, 2013, 1(1): 3-8. (in Chinese) |
| [3] |
吴命.城市高密度中心区建筑导向的城市型公共空间补偿设计研究[D].大连: 大连理工大学, 2017. WU Ming. Urban high density central building-oriented urban public space compensation design research[D]. Dalian: Dalian Jiaotong University, 2017. (in Chinese) https://xueshu.baidu.com/usercenter/paper/show?paperid=17665f034a01cde1da018d00e89f2e52&site=xueshu_se |
| [4] |
Subbu K, Zhang C, Luo J, et al. Analysis and status quo of smartphone-based indoor localization systems[J]. IEEE Wireless Communications, 2014, 21(4): 106-112. |
| [5] |
Fei W, JinQiang C, Benmei C, et al. A comprehensive UAV indoor navigation system based on vision optical flow and laser fast SLAM[J]. Acta Automatica Sinica, 2013(11): 1889-1900. |
| [6] |
Davidson P, Pich'e R. A survey of selected indoor Positioning methods for smartphones[J]. IEEE Communications Surveys & Tutorials, 2017, 19(2): 1347-1370. |
| [7] |
桂振文, 吴侹, 彭欣. 一种融合多传感器信息的移动图像识别方法[J]. 自动化学报, 2015, 41(8): 1394-1404. GUI Zhenwen, WU Ting, PENG Xin. A novel recognition approach for mobile image fusing inertial sensors[J]. Acta Automatica Sinica, 2015, 41(8): 1394-1404. (in Chinese) |
| [8] |
李爽.基于视觉的室内定位算法研究[D].哈尔滨: 哈尔滨工程大学, 2017. LI Shuang. Research on the indoor location algorithm based on vision[D]. Harbin: Harbin Engineering University, 2017. (in Chinese) |
| [9] |
Cheng G, Zhou P, Han J. Learning rotation-invariant convolutional neural networks for object detection in VHR optical remote sensing images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(12): 7405-7415. |
| [10] |
Ismail A H, Tasaki R, Kitagawa H, et al. Optimum placement of wireless access point for mobile robot positioning in an indoor environment[J]. Journal of Robotics & Mechatronics, 2016, 28(2): 162. |
| [11] |
Bisio I, Lavagetto F, Marchese M, et al. Smart probabilistic fingerprinting for WiFi-based indoor positioning with mobile devices[J]. Pervasive and Mobile Computing, 2016, 31: 107-123. |
| [12] |
王博远, 刘学林, 蔚保国, 等. WiFi指纹定位中改进的加权k近邻算法[J]. 西安电子科技大学学报, 2019(5): 41-47. WANG Boyuan, LIU Xuelin, WEI Baoguo, et al. Improved weighted k-nearset neighbor algorithm for WiFi fingerprint positioning[J]. Journal of Xidian University, 2019(5): 41-47. (in Chinese) |
| [13] |
毛科禹, 陈桂兵. 室内定位技术的应用现状与发展趋势[J]. 现代测绘, 2018, 41(5): 31-34. MAO Keyu, CHEN Guibing. The application status Quo and development trend of indoor positioning technology[J]. Modern Surveying and Mapping, 2018, 41(5): 31-34. (in Chinese) |
| [14] |
Hafner P, Moder T, Wisiol K, et al. Indoor positioning based on bayes filtering using map information[J]. IFAC-PapersOnLine, 2015, 48(10): 208-214. |
| [15] |
Ge X, Qu Z. Optimization WIFI indoor positioning KNN algorithm location-based fingerprint[C/OL]. 2016 7th IEEE International Conference on Software Engineering and Service Science (ICSESS). New York, USA: IEEE, 2016(2016-03-23)[2020-01-25]. https: //doi.org/10.1109/ICSESS.2016.7883033.
|
| [16] |
吴彦波, 孟广仕. 基于Wifi网络的模糊聚类KNN位置指纹定位算法[J]. 通讯世界, 2018(6): 95-96. WU Yanbo, MENG Guangshi. KNN location fingerprint positioning algorithm based on Wifi network fuzzy clustering[J]. Telecom World, 2018(6): 95-96. (in Chinese) |
| [17] |
石欣, 印爱民, 张琦. 基于K最近邻分类的无线传感器网络定位算法[J]. 仪器仪表学报, 2014, 35(10): 2238-2247. SHI Yin, YIN Aimin, ZHANG Qi. Localization in wireless sensor networks based on K-Nearest neighbor[J]. Chinese Journal of Scientific Instrument, 2014, 35(10): 2238-2247. (in Chinese) |
| [18] |
陈空, 宋春雷, 陈家斌, 等. 基于改进WKNN的位置指纹室内定位算法[J]. 导航定位与授时, 2016, 3(4): 58-64. CHEN Kong, SONG Chunlei, CHEN Jiabin, et al. An indoor location fingerprint algorithm based on improved WKNN[J]. Navigation Positioning and Timing, 2016, 3(4): 58-64. (in Chinese) |
| [19] |
Wu C, Yang Z, Xiao C. Automatic radio map adaptation for indoor localization using smartphones[J]. IEEE Transactions on Mobile Computing, 2018, 17(3): 517-528. |
 2020, Vol. 43
2020, Vol. 43


