2. 上海航天控制技术研究所, 上海 201109
2. Shanghai Aerospace Control Technology Institute, Shanghai 201109, P. R. China
随着工业化进程加快,气体使用也变得越加普遍。由于意外气体泄漏通常是不可预测的,且气体排放没有固定通道,从而引起严重的环境污染和安全问题。解决该问题一个有效的方法就是确定气体泄漏源的位置,从源头上阻止有毒气体的扩散。如何快速和准确定位气体泄漏源成为了目前的研究热点。
当前室内气体源定位方式主要分为基于机器人的主动嗅觉和传感器网络的非主动嗅觉[1]。主动式嗅觉将气体传感器和视觉传感器安装在机器人上,尽可能地移动并接近目标,从而得到较为精确的测量值。然而这种方式对周围环境条件要求较高,对存在障碍物或者大搜索区域等复杂环境,机器人只能远离目标进行测量,导致无法完成气体源搜索和定位任务。此外,机器人因自带电源能量有限,只能在短时间内工作,严重限制了其应用范围[2]。而非主动嗅觉技术采用价格低廉的传感器节点,根据环境条件,自组织网络进行气体检测。节点的布置方式比较灵活,适用于各种环境条件(如危险区域、有障碍物区域、人员活动区域等)。另外节点能耗较低,能够长时间工作。所以基于传感器网络的气体源定位方式广泛应用于环境检测,火灾预警和工业设备安全监控等领域。
气体源定位方法主要分为三类:基于搜索行为,基于模型分析和结合视觉。由于传感器网络中节点布设位置固定,采集的图像不能有效地表达环境空间的深度信息,所以主要采用基于模型分析定位方法。此方法主要特点是利用烟羽分布模型或者流体模型,基于气体、风速等传感器测量值,估计气体源位置。Kuang使用非线性最小二乘法来对气体源定位[3-4],给出了估计误差和传感器数量、不同背景噪声之间的关系。Wang利用极大似然法定位气体源[5-6],得出估计误差和噪声服从均匀分布、高斯分布的关系。Zhang用扩展卡尔曼滤波对移动机器人定位[7],得到了很好的定位效果。Sun用无迹卡尔曼滤波对室内移动定位[8],获得比扩展卡尔曼滤波更高的精确度,且简化了计算。Zhang[9]提出一种动态分簇传感网络分布式粒子滤波定位算法,在保证参数量估计和定位精度的同时可有效降低节点能耗平衡网络生命周期。Kuang[10]基于贝叶斯原理, 提出一种粒子滤波算法用于WSN的气体污染源定位,该算法采用权重质心法确定预估定位初始点、退避定时排序法确定参与定位节点信息发送顺序及采用残差重抽样算法减少抽样方差以提高滤波性能。仿真结果表明所提出的算法定位性能优于EKF及非线性最小二乘法。
已有的文献将模型误差和测量偏差考虑为随机,从而在随机框架下讨论气体源定位问题。这类方法要求噪声必须有一定的先验知识或者满足一定的分布,而在实际情况下,噪声源是未知的。将噪声的不确定性考虑为未知且有界的集合,不仅能简化先验假设条件,提供更可靠的表达,且实际系统的噪声边界是易于确定,便于应用。鉴于此种观点,研究者提出了扩展集员滤波(ESMF, extended set-membership filter)算法。扩展集员估计算法[11]估计结果是一个可行集合而不是一个确定的值,真实值一定在可行集合中。常见的可行集合形状有椭球、区间、超平形体、全对称多胞形。由于椭球集具有仿射不变性,计算较小,自适应较强等优点,使其具有较好的应用价值。目前已广泛的应用于系统辨识、状态估计、故障诊断等领域。
将气体扩散的模型偏差和测量噪声考虑为椭球集合,提出了基于集员估计的室内气体源定位算法。设定所有的气体浓度测量值来自于气体传感器,并且是经过了数值处理。利用静态湍流模型迭代计算定位误差边界,将位置状态真实值有效地包含在估计范围内,从而能达到100%的定位可信度。同时引入最小二乘法进行初步定位,以克服ESMF的初始点选取问题。并通过基于无线电子鼻的室内定位仿真实验,证明算法的可行性和有效性。
1 室内气味源定位原理 1.1 气味源定位原理当气体泄露后,气体分子在空气中扩散运动。随着距离气味源的远近而不同,在空间中形成不同的空间浓度分布,也叫烟羽轨迹。由于无法预测空气中湍流的影响,因而在其传播过程中烟羽的结构变得复杂且分布不连续。目前常用的烟羽模型主要分为静态环境模型和动态环境模型。静态环境模型包括高斯模型(Gaussian plume puff model)、BM模型(britter and mcquaid)、FEM3模型、气体湍流扩散模型,动态环境模型包括动态室内烟羽模型、动态室外烟羽模型。
虽然在真实环境中烟羽的结构十分复杂,但是室内气体分子扩散速度通常要比风速慢,在微风的情况下,主要是空气中的湍流决定烟羽的结构。常用扩散模型包括高斯模型、基于湍流扩散理论的静态模型和动态室内烟羽模型等。这类模型是在考虑一定假设条件下得到的,但基本能表征气体在室内空间中的浓度分布特征。已有相关的定位研究中,在随机框架下,不能确定模型误差的分布,通常将模型的偏差省略。由于不需考虑干扰和噪声的概率分布,只需考虑其上下界,所以将其考虑为未知的有界系统噪声。其模型结构为
| $ {C^i}(x_m^i,y_m^i) = g(x_m^i,y_m^i,x,y) + \Delta g + {v^i}, $ | (1) |
| $ {C^i}(x_m^i,y_m^i,t) = g(x_m^i,y_m^i,x,y,t) + \Delta g + {v^i}, $ | (2) |
其中:式(1)表示静态烟羽模型包括基于湍流扩散理论的静态模型和高斯模型等;式(2)表示动态烟羽模型包括动态室内烟羽模型等。Ci,xmi,ymi分别表示第i个传感器气体浓度测量值, 横向坐标位置和纵向坐标位置;Δg表示模型偏差;vi表示第i个传感器的测量噪声,i∈(1, …, N)。将风速、扩散速率等模型的参数都考虑为定值,故在公式中忽略不计。
1.2 定位模型将公式(1)中Δg+vi合并为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{X}}_{k + 1}^i = \mathit{\boldsymbol{X}}_k^i;}\\ {Y_{k + 1}^i = g(\mathit{\boldsymbol{X}}_{k + 1}^i) + \bar v_{k + 1}^i,} \end{array}} \right. $ | (3) |
式中,下标k代表在扩散时刻,g(·)表示气体扩散模型。
1.3 定位过程在传感网络环境下,传统的定位过程分为2步:集中式预定位和分布式定位。预定位是在中心节点通讯得到各传感器节点浓度信息的情况下,进行多传感器信息融合,获得初步定位值;分布式定位是各传感器节点利用初步定位值,分布式估计定位。已有的集中式定位方法主要有极大似然法、非线性最小二乘法、粒子滤波等,但是这些方法主要基于概率模型,而且得到位置信息只是一个点,不适用于定位结果,所以需要设计能够得到集合的预定位算法,分布式定位中主要考虑ESMF方法。
2 ESMF集员滤波是一种针对未知而有界噪声的状态估计方法。而ESMF是针对非线性系统,基于拉格朗日线性化设计的集员滤波方法,可以根据噪声集合和模型线性化偏差集合,迭代分析和计算气体源的位置集合,将真实位置被限定在估计范围内,提供100%的定位可信度。主要采用椭球集合表示状态和噪声的不确定性。针对式(3),在k时刻的噪声
公式(2)中存在非线性函数项g(·),在k时刻的估计值为
| $ Y_{k + 1}^i = g(\mathit{\boldsymbol{X}}_{k + 1}^i){|_{\mathit{\boldsymbol{X}}_{k + 1}^i = \mathit{\boldsymbol{\hat X}}_{k + 1|k}^i}} + G_{k + 1}^i(\mathit{\boldsymbol{X}}_{k + 1}^i - \mathit{\boldsymbol{\hat X}}_{k + 1}^i) + O({(\mathit{\boldsymbol{X}}_{k + 1}^i)^2}) + \bar v_{k + 1}^i, $ | (4) |
| $ G_{k + 1}^i = [G_{k + 1,1}^i \cdots G_{k + 1,j}^i \cdots G_{k + 1,m}^i] = \frac{{\partial g(\mathit{\boldsymbol{X}}_{k + 1}^i)}}{{\partial \mathit{\boldsymbol{X}}}}{|_{\mathit{\boldsymbol{X}}_{k + 1}^i = \mathit{\boldsymbol{\hat X}}_{\left. {k + 1} \right|k}^i}}, $ | (5) |
将ESMF用于非线性系统分析的关键之一就在于确定Lagrange余项进行区间分析,得到其不确定性边界。故令
| $ {R^i}(\Delta \mathit{\boldsymbol{\tilde X}}_{k + 1}^i,\mathit{\boldsymbol{\hat X}}_{k + 1|k}^i) = O({(\mathit{\boldsymbol{X}}_{k + 1}^i)^2}), $ | (6) |
式中:
| $ \begin{array}{*{20}{l}} {{R^i}(\Delta \mathit{\boldsymbol{\tilde X}}_{k + 1}^i,\mathit{\boldsymbol{\hat X}}_{k + 1|k}^i) = [{R^{i,1}}(\Delta \mathit{\boldsymbol{\tilde X}}_{k + 1}^{i,1},\mathit{\boldsymbol{\bar X}}_{k + 1|k}^i), \cdots ,}\\ {{R^{i,j}}(\Delta \mathit{\boldsymbol{\tilde X}}_{k + 1}^{i,j},\mathit{\boldsymbol{\bar X}}_{k + 1|k}^i), \cdots ,{R^{i,m}}(\Delta \mathit{\boldsymbol{\tilde X}}_{k + 1}^{i,m},\mathit{\boldsymbol{\bar X}}_{k + 1|k}^i)],} \end{array} $ | (7) |
| $ {R^{i,j}}(\Delta \mathit{\boldsymbol{\tilde X}}_{k + 1}^{i,j},\mathit{\boldsymbol{\bar X}}_{k + 1|k}^i) = \frac{1}{2}{(\Delta \mathit{\boldsymbol{\tilde X}}_{k + 1}^{i,j})^{\rm{T}}}\frac{{{\partial ^2}{g^j}(\mathit{\boldsymbol{\bar X}}_{k + 1}^i)}}{{\partial \mathit{\boldsymbol{X}}}}\Delta \mathit{\boldsymbol{\tilde X}}_{k + 1}^{i,j}, $ | (8) |
| $ \mathit{\boldsymbol{\bar X}}_{k + 1}^{i,j} = [\mathit{\boldsymbol{\hat X}}_{k + 1|k}^{i,j} - \sqrt {\mathit{\boldsymbol{P}}_{k + 1|k}^{i + jj}} \mathit{\boldsymbol{\hat X}}_{k + 1|k}^{i,j} + \sqrt {\mathit{\boldsymbol{P}}_{k + 1|k}^{i,jj}} ], $ | (9) |
其中,上标j=1, …, m代表第j个状态,jj表示矩阵的(j, j)元素。
2.2 ESMF算法ESMF算法流程图如图 1所示。
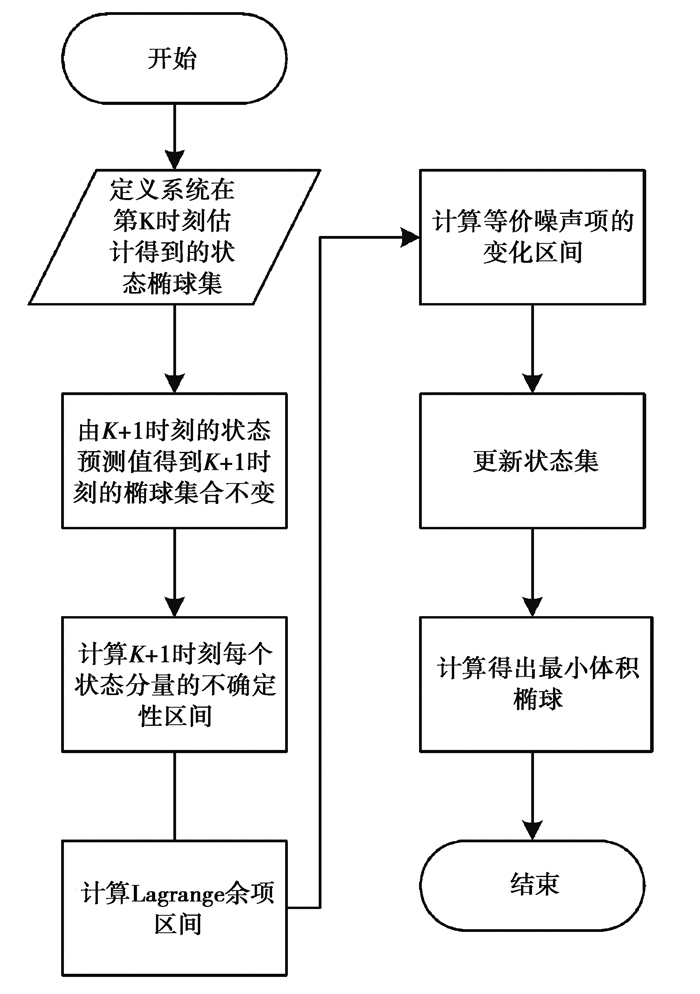
|
图 1 ESMF算法流程图 Fig. 1 ESMF Algorithm Flow-chart |
定义系统初始状态估计椭球集X0i∈E(
步骤1:状态预测值为
步骤2:根据式(9)计算k+1时刻每个状态分量的不确定性区间;
步骤3:按式(7)(8)计算Lagrange余项区间Ri(
步骤4:计算等价噪声项
| $ \tilde V_{k + 1|k}^i = \{ \bar v_{k + 1}^i:|\bar v_{k + 1}^{i,j}| \le {r_j},j = 1, \cdots ,m\} , $ | (10) |
| $ {r_j} = {\rm{rad}} ({R^{i,j}}(\Delta \mathit{\boldsymbol{\tilde X}}_{k + 1}^i,\mathit{\boldsymbol{\hat X}}_{k + 1|k}^i)) + \bar V_{k + 1}^{i,j},|\bar v_{k + 1|k}^{i,j}| \le \bar V_{k + 1}^{i,j}, $ | (11) |
步骤5:计算基于输出Yk+1i的状态集更新为
| $ S_{k + 1}^i = \cap _{j = 1}^m\{ \mathit{\boldsymbol{X}}_{k + 1}^{i,j}:Z_{k + 1}^{i,j} - {r_j} \le \mathit{\boldsymbol{G}}_{k + 1,j}^{\rm{T}}\mathit{\boldsymbol{X}}_{k + 1}^i \le Z_{k + 1}^{i,j} + {r_j}\} , $ | (12) |
| $ Z_{k + 1}^{i,j} = Y_{k + 1}^{i,j} - {g_j}(\mathit{\boldsymbol{\hat X}}_{k + 1|k}^i) + \mathit{\boldsymbol{G}}_{k + 1,j}^{\rm{T}}\mathit{\boldsymbol{\hat X}}_{k + 1|k}^{i,j}。$ | (13) |
步骤6:计算包含在交集(P k+1|ki∩Sk+1i)的最小体积椭球P k+1i;
状态值和椭球得包络矩阵初始值分别为
当j=1, …, m时,gj= Hk, iT P ki-1Hk, i,令
| $ \alpha _i^ + = \frac{{z_k^i - \mathit{\boldsymbol{H}}_{k,i}^{\rm{T}}\mathit{\boldsymbol{\hat x}}_k^{i - 1} + r_k^i}}{{\sqrt {{g_j}} }},\alpha _i^ - = \frac{{z_k^i - \mathit{\boldsymbol{H}}_{k,i}^{\rm{T}}\mathit{\boldsymbol{\hat x}}_k^{i - 1} - r_k^i}}{{\sqrt {{g_j}} }}。$ | (14) |
假如αi+>1,则令αi+=1;假如αi- < -1, 则令αi-=-1;假如
在式子
| $ \begin{array}{*{20}{c}} {(n - 1)g_i^2q_i^2 + ((2n - 1)d_i^2 - {g_i} + e_i^2){g_i}{q_i} + }\\ {(n(d_i^2 - e_i^2) - {g_i})d_i^2 = 0}。\end{array} $ | (15) |
最后得到
当传感器出现故障时,测量值不一定准确。也就是说Pk|k-1∩Sk将会是空集。这种情况下αi+ < -1或者αi->1,此算法已经处理。
3 最小二乘法预定位和初始椭球计算基于非线性模型的参数估计问题,不论是扩展卡尔曼滤波还是无迹卡尔曼滤波法,一般均需要迭代法。为了防止数值不稳定,需要确定初始搜索点。而扩展集员估计在迭代运算过程中需要确定初始椭球的大小。在传感网络环境下,通过集中非线性最小二乘法对气体源进行预定位,作为各个传感器节点进行分布式扩展集员估计的初始椭球中心点。
| $ J = \sum\limits_{ - 1}^N {({C^i} - g(} x_m^i,y_m^i,x,y){)^2},i{\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} (1, \cdots ,N), $ | (16) |
结合式(1)或者(2),利用非线性最小二乘法求解的Levenberg-Marquardt算法,大致估计出迭代估计的初值
| $ S_0^i = \cap _{j = 1}^m\{ \mathit{\boldsymbol{X}}_0^{i,j}:\tilde Z_0^{i,j} - {r_j} \le \mathit{\boldsymbol{G}}_{0,j}^{\rm{T}}X_0^i \le \bar Z_0^{i,j} + {r_j}\} , $ | (17) |
| $ \begin{array}{*{20}{l}} {\tilde Z_0^{i,j} = \mathit{\boldsymbol{\tilde Y}}_0^{i,j} - {g_j}(\mathit{\boldsymbol{\hat X}}_0^i) + \mathit{\boldsymbol{G}}_{0,j}^{\rm{T}}\mathit{\boldsymbol{\hat X}}_0^{i,j},}\\ {\bar Z_0^{i,j} = \mathit{\boldsymbol{\bar Y}}_0^{i,j} - {g_j}(\mathit{\boldsymbol{\hat X}}_0^i) + \mathit{\boldsymbol{G}}_{0,j}^{\rm{T}}\mathit{\boldsymbol{\hat X}}_0^{i,j}}。\end{array} $ | (18) |
当m大于状态的维数,此状态集合为全封闭的多面体,根据
应用Matlab仿真的方法,将基于UD分解的ESMF算法应用到气味源定位中。采用以下的湍流扩散方程来近似烟羽的分布
| $ {C_i}({x_i},{y_i}) = \frac{q}{{2\pi K}}\frac{1}{{{x_i}}} {\rm{exp}} [ - \frac{U}{{2K}}(d - \Delta x)], $ | (19) |
| $ d = \sqrt {{{({x_i} - {x_s})}^2} + {{({y_i} - {y_s})}^2}} , $ | (20) |
| $ \Delta x = ({x_i} - {x_s}) {\rm{cos}}\ \theta + ({y_i} - {y_s}) {\rm{sin}}\ \theta , $ | (21) |
式中:Ci是检测到的气体浓度(ppm);q是气体的扩散速率(m3/s);K是湍流扩散系数;U是风速(m/s);θ是风速和轴x之间的夹角;(xs, ys)是气体源的位置;(xi, yi)是当前传感器的位置。记传感器节点位置(xi, yi)=(zi1, zi2),气体湍流模型的状态空间描述如下所示
| $ \left\{ {\begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{l}} {x_{k + 1}^1}\\ {x_{k + 1}^2} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} 1&0\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {x_k^1}\\ {x_k^2} \end{array}} \right],}\\ {{y_{k + 1}} = \sqrt {{{(z_i^1 - x_{k + 1}^1)}^2} + {{(z_i^2 - x_{k + 1}^2)}^2}} - z_i^1 + x_{k + 1}^1 + {v_{k + 1}},} \end{array}} \right. $ | (22) |
在湍流扩散模型中,把气体源的位置信息作为状态变量,过程噪声设为0,则过程方程即为
| $ \left\{ {\begin{array}{*{20}{l}} {x_{k + 1}^1 = x_k^1,}\\ {x_{k + 1}^2 = x_k^2,} \end{array}} \right. $ | (23) |
对式(19)的两边同时取对数,移项可得
| $ - ( {\rm{ln}}{\kern 1pt} {\kern 1pt} {C_i}({x_i},{y_i}) - {\rm{ln}}{\kern 1pt} {\kern 1pt} q + {\rm{ln}}{\kern 1pt} {\kern 1pt} (2\pi K) + {\rm{ln}}{\kern 1pt} {\kern 1pt} {x_i})\frac{{2K}}{U} = d - \Delta x, $ | (24) |
由于q,K,U为常数,故等式左边也为常数,令
观测方程由测量浓度值和测量噪声组成
| $ {y_{k + 1}} = \sqrt {{{({x_i} - x_{k + 1}^1)}^2} + {{({y_i} - x_{k + 1}^2)}^2}} - {x_i} + x_{k + 1}^1 + {v_{k + 1}}, $ | (25) |
这里vk代表未知但有界的噪声vk ≤Vk。
Jacobian矩阵计算如下
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_k} = \frac{{\partial h(x)}}{{\partial x}}{|_x} = {{\hat x}_{k|k - 1}},}\\ {[1 - \frac{{z_i^1 - \hat x_{k|k - 1}^1}}{{\sqrt {{{(z_i^1 - \hat x_{k|k - 1}^1)}^2} + {{(z_i^2 - \hat x_{k|k - 1}^2)}^2}} }} - \frac{{z_i^2 - \hat x_{k|k - 1}^2}}{{\sqrt {{{(z_i^1 - \hat x_{k|k - 1}^1)}^2} + {{(z_i^2 - \hat x_{k|k - 1}^2)}^2}} }}],} \end{array} $ | (26) |
在式(19)中Lagrange余项为
| $ \mathit{\boldsymbol{R}}_2^1(\Delta {\tilde x_k},{\tilde X_k}) = \frac{1}{2}[\Delta \tilde x_k^1\Delta \tilde x_k^2]{\mathit{\boldsymbol{M}}_k}{[\Delta \tilde x_k^1\Delta \tilde x_k^2]^{\rm{T}}}, $ | (27) |
| $ {\mathit{\boldsymbol{M}}_k} = \left[ \begin{array}{l} \frac{{{{(z_i^2 - \tilde X_k^2)}^2}}}{{{{({{(z_i^1 - \tilde X_k^1)}^2} + {{(z_i^2 - \tilde X_k^2)}^2})}^{\frac{3}{2}}}}} - \frac{{(z_i^1 - \tilde X_k^1)(z_i^2 - \tilde X_k^2)}}{{{{({{(z_i^1 - \tilde X_k^1)}^2} + {{(z_i^2 - \tilde X_k^2)}^2})}^{\frac{3}{2}}}}}\\ - \frac{{(z_i^1 - \tilde X_k^1)(z_i^2 - \tilde X_k^2)}}{{{{({{(z_i^1 - \tilde X_k^1)}^2} + {{(z_i^2 - \tilde X_k^2)}^2})}^{\frac{3}{2}}}}}\frac{{{{(z_i^1 - \tilde X_k^1)}^2}}}{{{{(z_i^1 - \tilde X_k^1)}^2} + {{(z_i^2 - \tilde X_k^2)}^2}{)^{\frac{3}{2}}}}} \end{array} \right]。$ | (28) |
在仿真实验中,定义U=0.07, K=0.3, q=200×10-6,θ=0,测量噪声|vk|≤0.01,气体源位于(1, 1),包络矩阵P初始化为
为了验证提出算法在定位中的优越性,仿真中,首先用一个传感器的位置和检测到的浓度信息,通过单纯的ESMF算法得出最后的可行椭球集,把最后椭球集的中心作为估计值,此时初始值随机产生,结果如图 2所示。其次随机生成3个传感器位置,用Levenberg-Marquardt算法算出大致估计值后代入ESMF算法,如图 3所示。分别运行6次,单点定位和基于Levenberg-Marquardt算法的单点定位结果如表 1和表 2所示。
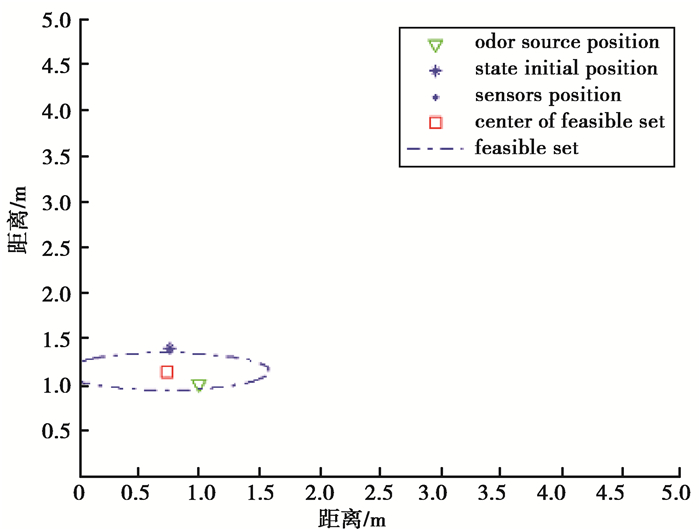
|
图 2 单点定位 Fig. 2 Single-point location |
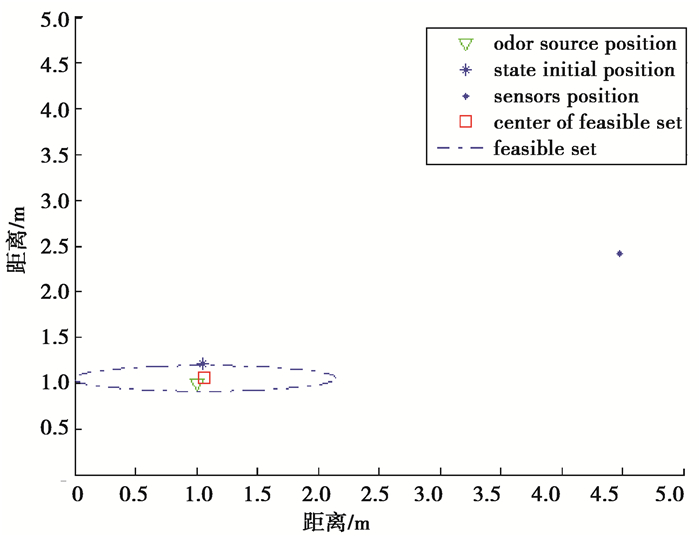
|
图 3 基于Levenberg-Marquardt算法的单点定位 Fig. 3 Levenberg-Marquardt based algorithm single-point location |
| 表 1 运行6次单点定位结果 Table 1 The result of running 6 single-point location program |
| 表 2 运行6次基于Levenberg-Marquardt算法的单点定位结果 Table 2 The result of running 6 Levenberg-Marquardt based algorithm single-point location program |
从可行椭球集面积来看,单点定位的椭球集面积从1.256 6变换到0.543 3,而基于Levenberg-Marquardt的单点定位的椭球集面积从1.256 6变换到0.473 8。从表 1和表 2的估计误差平均值来看,单点定位6次的平均误差为1.604 5,而基于Levenberg-Marquardt算法的单点定位六次的平均误差为0.509 5,显然第二种算法的精度较高。由此可知,初始值的选取对算法的影响是比较大的,合理选取初值可以减小定位误差。
4.2 基于Levenberg-Marquardt的单点定位与基于Levenberg-Marquardt的多点定位选择6个传感器进行多点定位,对获得的6个椭球集进行数据融合,计算出椭球集中心的平均值作为最后估计结果。基于Levenberg-Marquardt的多点定位如图 4所示,明显可以看出,基于Levenberg-Marquardt的多点定位的椭球集面积从1.256 6变换到0.099 3,椭球集变得比基于Levenberg-Marquardt的单点定位更小了。
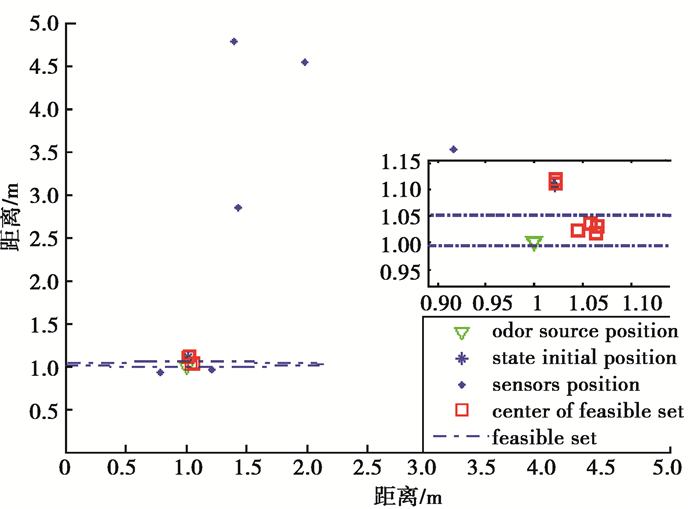
|
图 4 基于Levenberg-Marquardt的多点定位 Fig. 4 Levenberg-Marquardt based algorithm multi-point location |
表 3反映了基于Levenberg-Marquardt的多点定位算法运行6次结果。从估计误差的平均值来看,基于Levenberg-Marquardt的多点定位的误差平均值为0.088 7,明显低于单点定位的误差平均值0.509 5。因此,多个传感器协同定位的效果比单个传感器定位要好。
| 表 3 运行6次基于Levenberg-Marquardt的多点定位结果 Table 3 The result of running 6 Levenberg-Marquardt based algorithm multi-point location program |
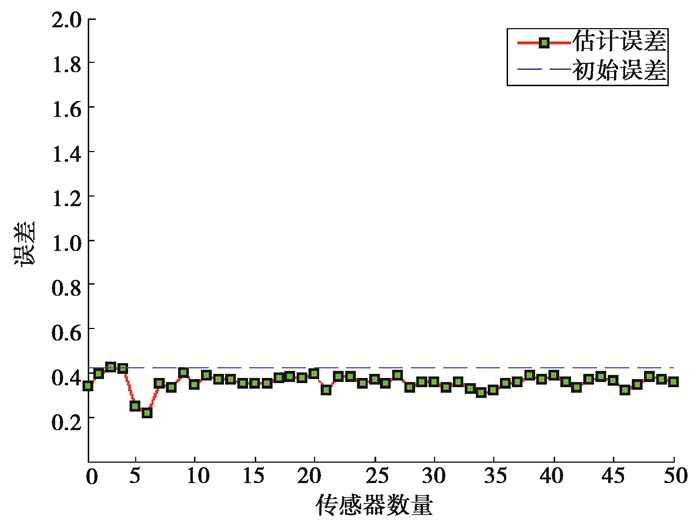
为了比较传感器个数和误差大小之间的关系,使传感器数量从1增加到50,设定迭代的初始点为一定值且均为(1.3, 1.3),得出的曲线如图 5所示。其中初始值与真实值之间的误差为0.424 3。
|
图 5 传感器个数与误差大小之间的关系 Fig. 5 The relationship between the sensor quantity and the error value |
从图 5可以看出,当初始值定位时,估计误差都小于初始误差;当传感器数量增加时,估计误差的变化并不是很明显,另外在传感器个数为6左右时,误差相对于相邻个数的传感器定位而言要小,由此可知,并不是传感器个数越多,定位效果越好,传感器个数在6左右最优。
5 结语ESMF算法被用于气味源的定位,测量噪声设为未知但有界从而能脱离随机框架的限制。利用Taylor公式展开非线性观测方程,使用区间分析计算Lagrange余项。气味源位置被限制椭球集中,椭球集越来越小。分别比较单点定位、基于Levenberg-Marquardt的单点定位和基于Levenberg-Marquardt的多点定位所得的定位结果,得出基于Levenberg-Marquardt的多点定位估计结果在椭球集大小和估计误差上均为最优。得出传感器个数和估计误差之间的关系,传感器个数在6左右误差相对较小。
| [1] |
Jatmiko W, Sekiyama K, Fukuda T. A pso-based mobile robot for odor source localization in dynamic advection-diffusion with obstacles environment:theory, simulation and measurement[J]. IEEE Computational Intelligence Magazine, 2007, 2(2): 37-51. DOI:10.1109/MCI.2007.353419 |
| [2] |
Tianlu F. Indoor odour source localisation using robot:Initial location and surge distance matter?[J]. Robotics and Autonomous Systems, 2013, 61(6): 637-647. DOI:10.1016/j.robot.2013.02.002 |
| [3] |
Kuang X H, Shao H H. Study of plume source localization based on WSN[J]. Journal of System Simulation, 2019, 19(7): 1464-1467. |
| [4] |
吴玉秀, 孟庆浩, 曾明. 基于移动传感器网络的气体源定位[J]. 天津大学学报, 2015, 48(2): 139-146. WU Yuxiu, MENG Qinghao, ZENG Ming. Gas source localization based on mobile sensor network[J]. Journal of Tianjin University, 2015, 48(2): 139-146. (in Chinese) |
| [5] |
Wang S, Yi C, Yang Z. Gas source localization based on maximum likelihood with arbitrary deployment WSN[C/OL]. Proceedings of the 33rd Chinese Control Conference. New York, USA: IEEE, 2014(2014-09-15)[2020-01-25].https: //doi.org/10.1109/ChiCC.2014.6896647
|
| [6] |
匡兴红, 邵惠鹤. 无线传感器网络在气体源预估定位中的应用[J]. 华东理工大学学报:自然科学版, 2006, 32(7): 780-783. KUANG Xinghong, SHAO Huihe. Application of sensor networks in plume source position estimation[J]. Journal of East China University of Science and Technology (Natural Science Edition), 2006, 32(7): 780-783. (in Chinese) |
| [7] |
Sun C J, Kuo H Y, Lin C E. A sensor based indoor mobile localization and navigation using Unscented Kalman Filter[C/OL]. IEEE/ION Position, Location and Navigation Symposium. New York, USA: IEEE, 2010(2010-07-08)[2020-01-25].https: //doi.org/10.1109/PLANS.2010.5507249
|
| [8] |
Zhang F, Huang L, Yuan S, et al. A novel strategy of localization based on EKF for mobile robot[C/OL]. Proceedings of the 33rd Chinese Control Conference. New York, USA: IEEE, 2014(2014-09-15)[2020-01-25]. https: //doi.org/10.1109/ChiCC.2014.6896644
|
| [9] |
张勇, 张立毅, 孟广超, 等. 分簇传感网络分布式粒子滤波气体释放源定位算法[J]. 传感技术学报, 2016, 29(8): 1239-1246. ZHANG Yong, ZHANG Liyi, MENG Guangchao, et al. Diffusive source localization algorithm based on decentralized particle filter in cluster sensor networks[J]. Chinese Journal of Sensors and Actuators, 2016, 29(8): 1239-1246. (in Chinese) DOI:10.3969/j.issn.1004-1699.2016.08.020 |
| [10] |
匡兴红, 邵惠鹤. 无线传感器网络中基于贝叶斯技术的气体源定位研究[J]. 兵工学报, 2008, 29(12): 1474-1478. KUANG Xinghong, SHAO Huihe. Plume source localization based on Bayes using wireless sensor network[J]. Acta Armamentarii, 2008, 29(12): 1474-1478. (in Chinese) DOI:10.3321/j.issn:1000-1093.2008.12.013 |
| [11] |
Scholte E, Campbell M E. A nonlinear set-membership filter for on-line applications[J]. International Journal of Robust & Nonlinear Control, 2003, 13(15): 1337-1358. |
 2020, Vol. 43
2020, Vol. 43


