现代投资组合理论由文献[1]提出并建立,创新性地使用资产价格的均值和方差来建立最优投资组合。文献[2]在Markowitz投资组合理论的基础上研究得出风险因子可以决定投资组合的收益。随着研究的深入,学者们发现仅靠均值和方差分析并不能得到稳定的收益,于是文献[3]建立了套利定价理论,指出资产的预期收益可以由多种因子来决定。这时期,文献[4]提出了有效市场理论,认为在一个有效市场中,股价完全反映了所有信息,试图击败市场的行为都是徒劳的。后来很多学者研究发现,股票市场并非有效,市场上有很多异象,可以在非有效市场获得风险溢价的超额收益。Fama等[5]建立了著名的三因子模型来解释股票市场的异象,之后,他于2015又建立了五因子模型来解释股票市场的异象。在投资组合理论发展过程中,由于行为金融学的创立与发展,文献[6]提出了前景理论,指出投资者关心的是获得财富的相对值而不是绝对财富。针对投资组合优化配置等方面的研究,如文献[7]对具有最小交易量限制的多阶段均值-半方差投资组合优化进行了研究;文献[8]对基于动态损失厌恶投资组合模型的最优资产配置进行了研究;文献[9]对含交易费用的证券组合投资模型的满意解进行求解;文献[10]研究了证券组合投资的区间数线性规划方法。另外,还有一些学者如文献[11-13]对多阶段证券组合选择进行优化模型分析,风险最小化研究以及对不同风险度量指标进行比较研究,等等。
证券投资风险与收益的数量刻画是现代投资理论与方法进入一个定量分析阶段的标志,数学分析方法的引入使得利用计算机技术与人工智能等现代方法进行证券投资管理成为可能。证券投资学现已成为国内外大部分商学院或经管学院研究生课程中的一门重要的核心课程,Zvi Bodie(波士顿大学),Alex Kane(加利福尼亚大学),Alan J.Marcus(波士顿学院)编写的教材《投资学》成为大多数高校教学的首选教材[14]。马科维茨的现代投资组合理论是这一教材以及此类教材中的核心内容[15-18],而最优风险资产组合这一概念更是资产组合理论最为关键的概念。对于经管类专业的一年级硕士研究生,要准确理解这一概念,尤其要弄清楚其中的数学原理则是一个难题。在教学过程中如果给研究生们讲清楚其中的数学原理,对提升研究生的科研能力很有帮助。
综上所述,已有研究均集中在证券投资组合理论方法的延伸及市场的应用实证上,而对基本的概念与原理的深刻阐述及其数学模型的分析推导则关注不足。文中的研究将在一定程度上弥补上述不足,即要研究证券组合选择中最优风险资产组合概念形成过程中的数学机理并进行数学推导与求解,进而确定二元证券组合中的最优风险资产组合的数学表达式,并将其推广到多元证券组合的情形。
1 数学模型构建与数学推导从数学角度来看,资产组合理论是建立在笛卡尔平面坐标第一象限的一个数学模型。横坐标是证券组合的风险(σP),纵坐标是证券组合的期望收益(E(rP))。这样,第一象限坐标中的每一点与实数对(σP,E(rP))就建立了一一对应关系,同时也对应着一个证券(也称证券组合,只包含一个证券而已,下同)或证券组合。而在经济学中的理性人假设使得投资人在面对不同的投资选择时会遵循一个原则,即期望收益率相同的证券组合,投资者会选择风险小的;风险相同的证券组合投资者会选择期望收益率高的。这样也就相当于对所有这一类的实数对(σP,E(rP))确定了一个代数中的序关系,其遵循规则如下:
在第一象限中任取2个点A、B,即2个证券组合;其对应的坐标或数对分别是(σA,E(rA))、(σB,E(rB))。则有
当E(rA)≥E(rB),且σA < σB时,则点A优于点B;
当E(rA) ≤ E(rB),且σA>σB时,则点B优于点A;
当E(rA)= E(rB),且σA=σB时,则点A等同于点B。
显然,也就有如下的推论:
当σA≤σB,且E(rA)>E(rB)时,则点A优于点B;
当σA≥σB,且E(rA) < E(rB)时,则点B优于点A;
当σA=σB,且E(rA)=E(rB)时,则点A等同于点B。
确定了上述实数对的序,则给第一象限的所有点进行优先排序成为可能。其投资学意义为在理性经济人的假设下任何两个不同的证券组合都可以比较出他们的优劣。即面对两个证券组合,当风险一定时,投资人会选择期望收益高的证券;当期望收益一定时投资人会选择风险小的证券,除非投资人是非理性的,例如精神病患者。
在证券投资学教材中,对最优证券组合的描述都归纳为两个特点:第一,风险相同时能提供最大的期望收益率;第二,期望收益率相同时能提供最小的风险。从数学角度来解释,这其中的最优、最大、最小等均要建立在有序的基础上,否则是比较不出优劣的。
可行集(也称投资机会集)代表N种证券所形成的各种可能的证券组合集,或者位于可行集的边界上,或者位于边界内。例如,对于二元证券组合(包含两种证券的组合),其可行集是第一象限平面内的一个三角形区域。这可通过数学模型推导出来。
设A、B是任意2个证券组合,其期望收益率分别是E(rA)、E(rB),风险分别是σA、σB。由它们构造一个新的证券组合P,在这个新组合中A、B所占权重分别是wA、wB,当然,wA+wB=1。根据投资学中的风险与收益率的计算规则,可以计算证券组合P的期望收益E(rP)与风险σP分别是:
| $ E({r_{\rm{P}}}) = {w_A}E({r_A}) + {w_B}E({r_B}), $ | (1) |
| $ \sigma _{\rm{P}}^2 = {({w_A}{\sigma _A})^2} + {({w_B}{\sigma _B})^2} + 2({w_A}{\sigma _A})({w_B}{\sigma _B}){\rho _{AB}}, $ | (2) |
式中,ρAB是证券组合A与B的收益率之间的相关系数,且-1≤ρAB≤1。
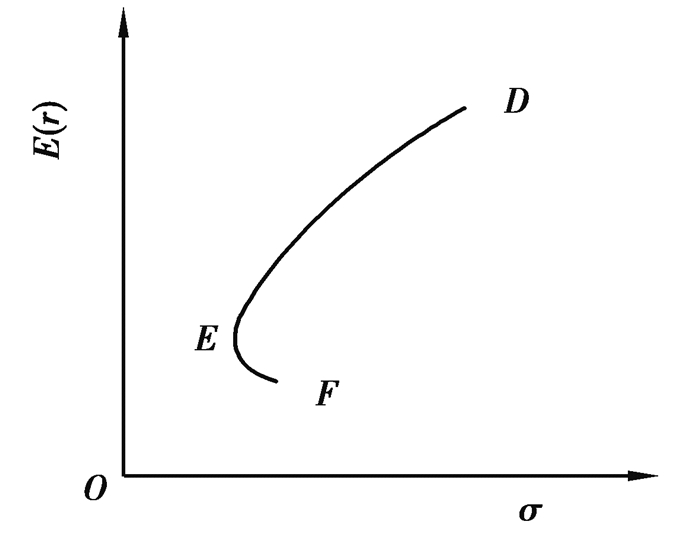
对于给定的相关系数ρAB,可在σ-E(r)平面上画出如图 1所示的抛物线DEF。
|
图 1 确定的相关系数下二元证券组合的可行集 Fig. 1 The feasible set of binary portfolio under the correlation coefficient |
特殊情况下,当ρAB=1时,可得σP=wAσA+wBσB,
当ρAB=-1时,可得σP=|wAσA-wBσB|。
下面分别讨论如下:
1) 当ρAB=1时,则有
| $ \left\{ {\begin{array}{*{20}{l}} {E({r_{\rm{P}}}) = {w_A}E({r_A}) + {w_B}E({r_B}),}\\ {{\sigma _{\rm{P}}} = {w_A}{\sigma _A} + {w_B}{\sigma _B},}\\ {{w_A} + {w_B} = 1}。\end{array}} \right. $ | (3) |
于是,可得E(rP)与σP的关系式为
| $ E({r_{\rm{P}}}) = \frac{1}{{{\sigma _A}}}{\sigma _{\rm{P}}} + (1 - {w_A})E({r_B}) - \frac{{(1 - {w_A}){\sigma _B}}}{{{\sigma _A}}}。$ | (4) |
显然,这是σ-E(r)平面上的一直线,在一象限内是一线段,是二元证券组合的一个特殊的可行集。
2) 当ρAB=-1时,又存在两种情况:σP=wAσA-wBσB,σP= wBσB - wAσA。
① 当σP=wAσA-wBσB时,可得
| $ \left\{ {\begin{array}{*{20}{l}} {E({r_{\rm{P}}}) = {w_A}E({r_A}) + {w_B}E({r_B}),}\\ {{\sigma _{\rm{P}}} = {w_A}{\sigma _A} - {w_B}{\sigma _B},}\\ {{w_A} + {w_B} = 1}。\end{array}} \right. $ | (5) |
于是有
| $ E({r_{\rm{P}}}) = \frac{{E({r_A}) - E({r_B})}}{{{\sigma _A} + {\sigma _B}}}{\sigma _{\rm{P}}} + \frac{{{\sigma _B}}}{{{\sigma _A} + {\sigma _B}}}[E({r_A}) - E({r_B})] + E({r_B})。$ | (6) |
② 当σP= wBσB - wAσA时,可得
| $ \left\{ {\begin{array}{*{20}{l}} {E({r_{\rm{P}}}) = {w_A}E({r_A}) + {w_B}E({r_B}),}\\ {{\sigma _{\rm{P}}} = {w_B}{\sigma _B} - {w_A}{\sigma _A},}\\ {{w_A} + {w_B} = 1}。\end{array}} \right. $ | (7) |
于是有
| $ E({r_{\rm{P}}}) = - \frac{{E({r_A}) - E({r_B})}}{{{\sigma _A} + {\sigma _B}}}{\sigma _{\rm{P}}} + \frac{{{\sigma _B}}}{{{\sigma _A} + {\sigma _B}}}[E({r_A}) - E({r_B})] + E({r_B})。$ | (8) |
显然,式(6)与式(8)是两条相交的直线,交点E在纵轴上,坐标为:
| $ E({r_{\rm{P}}}) = \frac{{{\sigma _B}}}{{{\sigma _A} + {\sigma _B}}}[E({r_A}) - E({r_B})] + E({r_B})。$ |
同时也可分别求出直线(4)与(6)的交点,以及直线(4)与(8)的交点。
即通过求解方程组(9)可得直线(4)与(6)的交点Q的坐标。
| $ \left\{ {\begin{array}{*{20}{l}} {E({r_{\rm{P}}}) = \frac{1}{{{\sigma _A}}}{\sigma _{\rm{P}}} + (1 - {w_A})E({r_B}) - \frac{{(1 - {w_A}){\sigma _B}}}{{{\sigma _A}}},}\\ {E({r_{\rm{P}}}) = \frac{{E({r_A}) - E({r_B})}}{{{\sigma _A} + {\sigma _B}}}{\sigma _{\rm{P}}} + \frac{{{\sigma _B}}}{{{\sigma _A} + {\sigma _B}}}[E({r_A}) - E({r_B})] + E({r_B})}。\end{array}} \right. $ | (9) |
通过求解方程组(10),可得直线(4)与(8)的交点R的坐标。
| $ \left\{ {\begin{array}{*{20}{l}} {E({r_{\rm{P}}}) = \frac{1}{{{\sigma _A}}}{\sigma _{\rm{P}}} + (1 - {w_A})E({r_B}) - \frac{{(1 - {w_A}){\sigma _B}}}{{{\sigma _A}}},}\\ {E({r_{\rm{P}}}) = - \frac{{E({r_A}) - E({r_B})}}{{{\sigma _A} + {\sigma _B}}}{\sigma _{\rm{P}}} + \frac{{{\sigma _B}}}{{{\sigma _A} + {\sigma _B}}}[E({r_A}) - E({r_B})] + E({r_B})}。\end{array}} \right. $ | (10) |
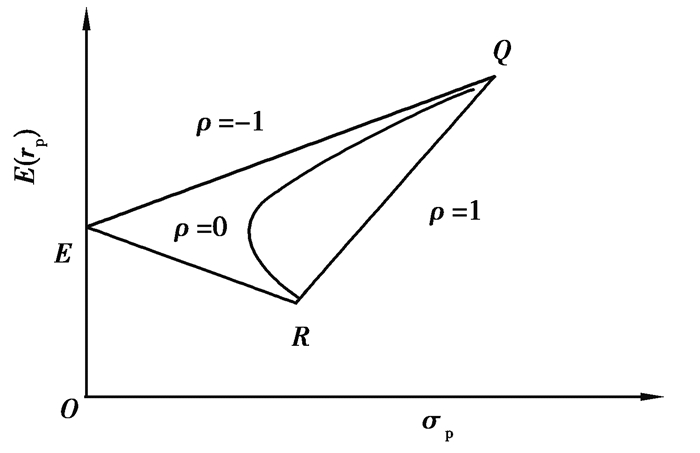
这样可以在平面上得到一个三角形EQR,如图 2所示。
|
图 2 二元证券组合中特殊情形下的投资机会集 Fig. 2 Investment opportunity set under special circumstances in binary portfolio |
当相关系数ρAB≠±1时,即-1 < ρAB < 1时,得到期望收益E(rP)与风险σP还应满足:
| $ \left\{ {\begin{array}{*{20}{l}} {E({r_{\rm{P}}}) = {w_A}E({r_A}) + {w_B}E({r_B}),}\\ {\sigma _{\rm{P}}^2 = ({w_A}{\sigma _A})2 + ({w_B}{\sigma _B})2 + 2({w_A}{\sigma _A})({w_B}{\sigma _B}){\rho _{AB}},}\\ {{w_A} + {w_B} = 1}。\end{array}} \right. $ | (11) |
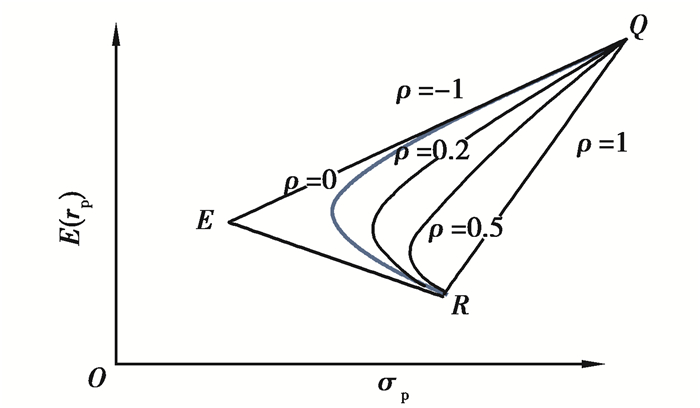
如前面所述,每给定一个ρAB的值,式(11)代表一条抛物线,如图 2中的曲线QR,即是取ρAB=0的一条较常见的抛物线。所有这些抛物线有一个共同的特点,即均经过Q、P 2点,且充满整个三角形EQR。如图 3中,画出了ρAB=0,0.2,0.5的3种情形。也就是如果在三角形EQR区域内任意取一点,则必有一条上述性质的抛物线经过这一点。所以二元证券组合的投资机会集是三角形EQR区域,如图 3所示。
|
图 3 二元证券组合的投资机会集 Fig. 3 Investment opportunity set of binary portfolio |
对于n(n>2)个证券构成的证券组合来说,可以在二元证券组合的基础上做推广,假设有S1,S2,…,Sn等n个证券构成证券组合P,他们在组合P中所占的权重分别为:w1,w2,…,wn,当然满足条件w1+w2+…+wn=1。任何两个证券Si、Sj,他们收益率之间的相关系数ρij,仍满足:-1≤ρij≤1.于是证券组合P的期望收益E(rP)与风险σP之间的关系为
| $ \left\{ {\begin{array}{*{20}{l}} {E({r_{\rm{P}}}) = {w_1}E({r_1}) + {w_2}E({r_2}) + \cdots + {w_n}E({r_n}),}\\ {\sigma _{\rm{P}}^2 = ({w_1}{\sigma _1})2 + ({w_2}{\sigma _2})2 + \cdots + ({w_n}{\sigma _n})2 + 2{\rho _{1,2}}({w_1}{\sigma _1})({w_2}{\sigma _2}) + \cdots + 2{\rho _{n - 1,n}}({w_{n - 1}}{\sigma _{n - 1}})({w_n}{\sigma _n}),}\\ {{w_1} + {w_2} + \cdots + {w_n} = 1}。\end{array}} \right. $ | (12) |
也可表达为
| $ \left\{ {\begin{array}{*{20}{l}} {E({r_{\rm{P}}}) = \sum\limits_{i = 1}^n {{w_i}} E({r_i}),}\\ {\sigma _{\rm{P}}^2 = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{w_i}} } {w_j}{\sigma _{ij}},}\\ {\sum\limits_{i = 1}^n {{w_i}} = 1}。\end{array}} \right. $ | (13) |
其中,
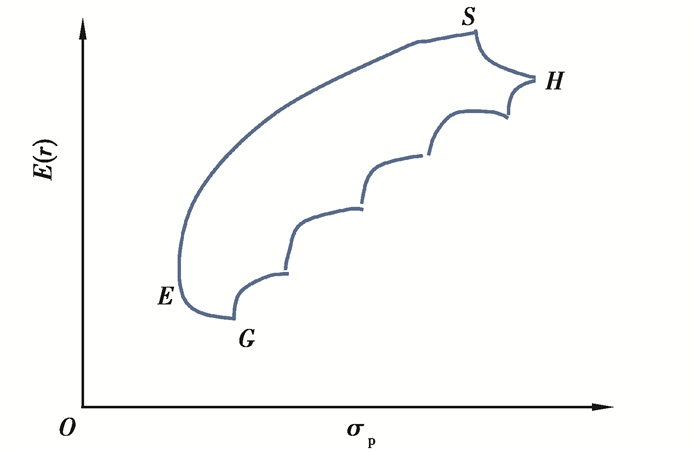
从式(12)或式(13)可知,这3个关系式代表σ-E(r)平面上一系列的抛物线,这些抛物线所围成的区域GESH,即是n-元证券组合构成的投资机会集,其中E点代表这个区域中风险最小的投资组合,如图 4所示。
|
图 4 n-元证券组合的投资机会集 Fig. 4 Investment opportunity set of n-ary portfolio |
寻找最优证券组合的问题,实际上可归结为数学上的最优解问题。通过第1节的数学建模,最优证券组合的存在性也就有了数学基础。首先从数学上看,这些区域的边界是一些具有下凹性的抛物线,所以他们围成的区域构成了平面内的一个凹集,即图 4中的GESH曲边多边形,也就是n-元证券组合的投资机会集(即可行集)。对于理性的投资者来说,他们在投资机会集中选择投资组合时,当然会根据自己的风险偏好程度在图 4中的ES边界上选择相应的点所对应的投资组合。边界ES在投资学教材中称为有效边界(有些教材译成有效前沿)。
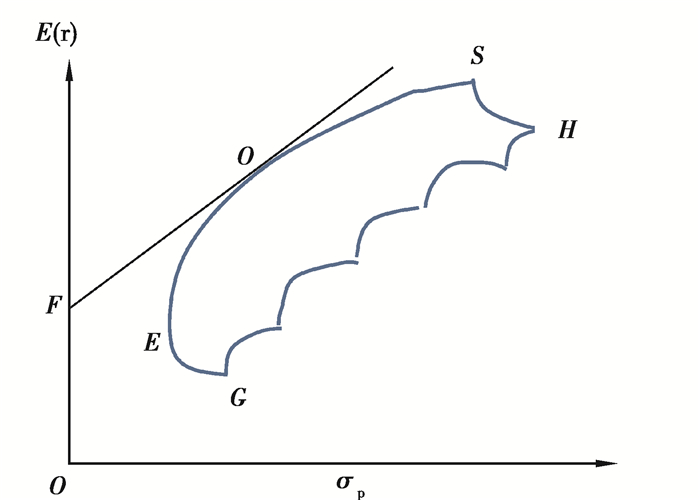
下面阐述清楚最优证券组合与最优风险(资产)组合的区别。如果证券市场上存在一个无风险收益率Rf(即无风险资产),它所对应的坐标象限的点F位于正向纵轴上,通过F点向曲线段ES作切线,切点为O点,则O点对应的证券组合是给定证券市场的最优风险(资产)组合,此组合中的资产全是风险证券,如图 5所示。
|
图 5 最优风险资产组合的确定 Fig. 5 Determination of optimal risk portfolio |
图 5中的切线FO,也是这种特殊情况下的资本分配线,针对不同风险偏好的投资者,他们将以无风险资产Rf(即对应F点)与最优风险资产组合(即对应O点)来构建最优证券组合,即对应线段FO上的点。风险厌恶型投资者将在靠F点的附近寻找投资组合,风险偏好型投资者将在靠O点的附近寻找投资组合,而风险中性型投资者将在线段FO的中点附近寻找投资组合。所以,对于给定的证券市场,所有投资者的最优风险(资产)组合是相同的,即图 4中对应的O点,而最优证券组合则是根据投资者的风险偏好程度来构建,即需权衡组合中无风险资产与最优风险组合各占多少比例而定。
3 结论与启示文章从严谨的数学模型与方法出发,对现代证券投资理论中的最优风险资产组合的数学机理与形成过程进行了分析。通过建立投资组合风险、收益与有序数对的一一对应关系,构建了形成二元证券组合的投资机会集的数学模型,求解出对应的投资机会集的边界曲线,由此推导出最优风险资产组合的数学表达式。最后将结果推广到了n-元证券组合的情形。
证券投资学是全球高校商学院中开设的一门重要的核心课程,在教学过程中如何把握这门课的核心内容的深度是值得探讨的问题。作为硕士研究生课程,对证券组合选择理论部分,既要讲清楚其中的市场应用,也要讲清楚其中的数学原理,这对提高一个研究生的数学素质及数学应用能力非常重要。本研究为解决此类问题提供了很好的借鉴。
| [1] |
Markowitz H. Portfolio selection[J]. The Journal of Finance, 1952, 7(3): 77-91. |
| [2] |
Sharpe W F. Capital asset prices:A theory of market equilibrium under conditions of risk[J]. The Journal of Finance, 1964, 19(3): 425-442. |
| [3] |
Ross S A. The arbitrage theory of capital asset pricing[J]. Journal of Economic Theory, 1976, 13(3): 341-360. DOI:10.1016/0022-0531(76)90046-6 |
| [4] |
Malkiel B G, Fama E F. Efficient capital markets:A review of theory and empirical work[J]. The Journal of Finance, 1970, 25(2): 383-417. |
| [5] |
Fama E F, French K R. A five-factor asset pricing model[J]. Journal of Financial Economics, 2015, 116(1): 1-22. DOI:10.1016/j.jfineco.2014.10.010 |
| [6] |
Daniel K, Amos T. Prospect theory:An analysis of decision under risk[J]. Econometrica, 1979, 47(2): 363-391. |
| [7] |
张鹏, 张卫国, 张逸菲. 具有最小交易量限制的多阶段均值-半方差投资组合优化[J]. 中国管理科学, 2016(7): 11-17. ZHANG Peng, ZHANG Weiguo, ZHANG Yifei. Multi stage mean semi variance portfolio optimization with minimum trading volume constraints[J]. China Management Science, 2016(7): 11-17. (in Chinese) |
| [8] |
金秀, 王佳, 高莹. 基于动态损失厌恶投资组合模型的最优资产配置与实证研究[J]. 中国管理科学, 2014(5): 16-23. JIN Xiu, WANG Jia, GAO Ying. Optimal asset allocation and empirical research based on dynamic loss aversion portfolio model[J]. China Management Science, 2014(5): 16-23. (in Chinese) |
| [9] |
赵玉梅, 鲍宏伟, 孙西超. 含交易费用的证券组合投资模型的满意解[J]. 大学数学, 2010(4): 21-25. ZHAO Yumei, BAO Hongwei, SUN Xichao. Satisfactory solution of portfolio investment model with transaction cost[J]. University Mathematics, 2010(4): 21-25. (in Chinese) DOI:10.3969/j.issn.1672-1454.2010.04.006 |
| [10] |
路应金, 唐小我, 周宗放. 证券组合投资的区间数线性规划方法[J]. 系统工程学报, 2004(1): 33-37. LU Yingjin, TANG Xiaowo, ZHOU Zongfang. Interval number linear programming method for portfolio investment[J]. Journal of systems engineering, 2004(1): 33-37. (in Chinese) DOI:10.3969/j.issn.1000-5781.2004.01.006 |
| [11] |
Liu Y J, Zhang W G, Zhang P. A multi-period portfolio selection optimization model by using interval analysis[J]. Economic Modelling, 2013(3): 113-119. |
| [12] |
Ji X D, Zhu S S. The convergence of set-valued scenario approach for downside risk minimization[J]. Journal of Systems Science and Complexity, 2016(3): 722-735. |
| [13] |
Daehwan K. Beta vs. characteristics:Comparison of risk model performances[J]. Journal of Empirical Finance, 2015, 10: 156-171. |
| [14] |
Zvi B, Alex K, Alan J.投资学[M]. 9th.汪昌云, 等译.北京: 机械工业出版社, 2013.
|
| [15] |
Zvi B, Alex K, Alan J. Investment[M]. 9th. Translated by Wang Changyun, et al. Beijing: China Machine Press, 2013. (in Chinese)
|
| [16] |
Robert C M.连续时间金融[M].郭多祚, 等译.北京: 中国人民大学出版社, 2005.
|
| [17] |
Robert C M. Continuous time finance[M]. Translated by Guo Duozuo, et al. Beijing: China Renmin University Press, 2005. (in Chinese)
|
| [18] |
James L F, Walter J R.投资组合管理理论及应用[M]. 2nd.齐寅峰, 等译.北京: 机械工业出版社, 2001.
|
| [23] |
James L F, Walter J R. Theory and application of portfolio management[M]. 2nd. Translated by Qi Yinfeng, et al. Beijing: China Machine Press, 2001. (in Chinese)
|
 2020, Vol. 43
2020, Vol. 43


