2. 中国特种飞行器研究所高速水动力航空科技重点实验室, 湖北 荆门 448035;
3. 南京航空航天大学 航空学院, 南京 210016;
4. 武汉理工大学 新材料力学理论与应用湖北省重点实验室, 武汉 430070;
5. 上海仿坤软件科技有限公司, 上海 201102
2. Key Aviation Scientific and Technological Laboratory of High-speed Hydrodynamic, China Special Vehicle Research Institute, Jingmen, Hubei 448035, P. R. China;
3. Institute of Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, P. R. China;
4. Hubei Key Laboratory of Theory and Application of Advanced Materials Mechanics, Wuhan University of Technology, Wuhan 430070, P. R. China;
5. Shanghai Fangkun Software Technology Ltd., Shanghai 201102, P. R. China
水上迫降过程中所产生的水动冲击载荷事关机乘人员的生命安全,必须被考虑在跨水域飞行的民用飞机“适坠性”结构设计中。中国民用航空规章第25部25.801条款对水上迫降、水上迫降结构和设备做出了具体的要求[1]。缩比模型试验和基于数值方法的虚拟实验是获取水动载荷的重要途径。在新构型飞机设计和适航取证中,低成本和可重复的数值方法正扮演越来越重要的角色,传统的高成本和高耗时的缩比模型试验逐步被“虚拟数值试验”和基于“相似构型模型试验”的类比外推方法所替代。无论是理论分析还是科学计算,如何描述和求解流体与结构的耦合问题都是一个非常具有挑战性的课题。
针对水上迫降这一具体问题,目前主要的流体结构耦合处理方法包括:1)传统拉格朗日接触方法[2-4];2)自适应欧拉网格(adaptive Eulerian mesh)边界方法[5-9];3)基于光滑粒子流体动力学(smooth particle hydrodynamics, SPH)的“核函数”耦合方法[10-16];4)基于拉格朗日欧拉算法(arbitrary Lagrangian-Euler algorithm,ALE)的“罚函数”耦合方法。ALE算法的网格处理方法兼具拉格朗日和欧拉方法的优点:在结构边界运动的处理上引进了拉格朗日方法的特点,能够有效地跟踪物质结构边界的运动;在内部网格的划分上,吸取了欧拉方法的长处,使内部网格单元独立于物质实体而存在;在物质域和空间域外引进了参考域,通过在参考域网格上的求解,既解决了拉格朗日描述下材料可能的严重扭曲,又解决了欧拉描述下移动边界引起的复杂性。流体与结构间的相互作用采用罚函数耦合方法进行控制[17]。从目前的水上迫降数值仿真的公开文献[18-24]来看,基于ALE的罚函数耦合方法是报道最多的方法。其优点表现为:能够兼顾拉格朗日和欧拉算法的优点,能够解决结构的非线性问题(几何非线性、材料非线性),同时又能对流体运动特性进行准确的描述,能够解决结构破口流体涌入后二次冲击作用下的结构响应问题[2, 5],通过设置流体状态方程的截断压力,可以粗略地描述尾部的空化效应。通过ALE罚函数耦合算法定义结构流体间的相互作用,可以传递流体的压缩和膨胀引起的压力变化,故可以计入水上迫降尾部的伯努利效应。其缺点表现为:ALE罚函数耦合算法通过流体渗漏和接触刚度定义流体结构之间的相互作用力,极容易引起流体渗漏;流体压力和结构压力载荷不统一,通过压力传感器单元采集到的压力信号波动较大,并且压力在相邻空间的分布连续性很差。
笔者拟采用结构化的任意拉格朗日欧拉(S-ALE)算法的流固耦合方法研究飞机水上迫降过程中的动力学问题。S-ALE流固耦合方法采用结构化网格离散流体空间,更容易实现区域的边界拟合。结构对流场的作用通过在流场控制方程中添加“源项”来实现,而流场对结构的反作用则通过结构周围的流体质点速度的插值来实现。提取飞机俯仰姿态角的变化规律和过载时间历程,与传统的ALE罚函数耦合方法预测的结果以及实验结果进行对比,并对S-ALE流固耦合方法的“渗漏现象”控制效果进行了评价。
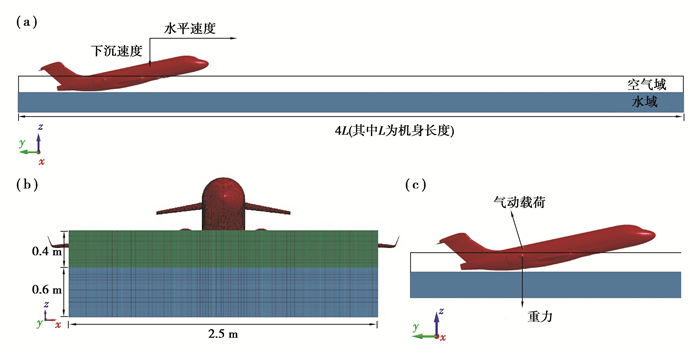
1 有限元模型和S-ALE算法 1.1 水上迫降有限元模型数值模型包含3部分:空气,水和飞机结构,其中,空气和水域采用欧拉算法进行描述,飞机结构采用拉格朗日算法进行描述。空气域和水域的几何尺寸见图 1(a)和(b)。为了减小模型规模,同时保证机身结构和流体接触处有足够的网格密度,采用渐进式网格划分,见图 1(b)。在LS-DYNA程序中传统的ALE算法需要手动进行网格划分,而S-ALE方法提供了网格自动生成的途径,需要完成*ALE_STRUCTURED_MESH_CONTROL_POINTS和*ALE_STRUCTURED_MESH这两个关键字定义,从而生成渐进网格。S-ALE算法自动生成的网格是结构化网格,更容易实现区域的边界拟合。
|
图 1 水上迫降有限元模型 Fig. 1 Finite element model for ditching |
在LS-DYNA中,空气和水的本构采用*MAT_NULL来描述,其参数见表 1。状态方程采用EOS-GRUNEISEN,其参数见表 2。
| 表 1 水和空气在*MAT_NULL材料模型中对应的参数 Table 1 Material parameters of water and air in *MAT_NULL |
| 表 2 水和空气对应的Gruneisen状态方程参数 Table 2 Material parameters of water and air in Gruneisen equation of state |
为了保证数值模型中飞机整体的惯性张量与实验一致, 本研究中采用*PART_INERTIA强制定义了飞机的质量重心、质量以及惯性张量。飞机的初始水平速度、下沉速度、初始俯仰角、质量以及转动惯量如表 3所示。
| 表 3 初始条件和飞机的惯性张量 Table 3 Initial conditions and inertia tensors of aircrafts |
在传统ALE方法中,流固耦合采用基于罚函数的耦合接触算法,其基本原理如下:
| $ f_{i}=d_{i} k_{i}。$ | (1) |
式中:i=1, 2, 3表示笛卡尔坐标系中的3个坐标轴方向;fi, di, ki分别为i方向的流固耦合力、流固耦合渗透量和流固耦合刚度。在S-ALE中流固耦合界面的处理方式参考了浸没边界法(immersed boundary method,IBM)[26]。在数学方法上,它用欧拉变量描述流体的动态,用拉格朗日变量描述结构的运动边界,用光滑delta近似函数通过分布节点力和插值速度来表示流场和结构物的交互作用。整个流场计算都使用笛卡尔网格,而不是按照物体形状生成复杂的贴体网格,无需处理从物理平面到计算平面的坐标和网格转换问题,因而可以大大提高计算效率,而且节省了网格生成所需的时间。尤其对于动态边界问题,它无需在每一时间步长上实时更新网格。
S-ALE耦合方法中流体结构耦合中结构对流场的作用通过在流场控制方程中添加“源项”来实现,而流场对结构的反作用则通过结构周围的流体质点速度的插值来实现。其基本控制方程组为:
| $ {\rho \left( {\frac{{\partial u}}{{\partial t}} + u \cdot \nabla u} \right) = - \nabla p + \mu \Delta u + F(x, t), } $ | (2) |
| $ {\nabla \cdot u = 0, } $ | (3) |
| $ {F(x, t) = \int f (s, t)\delta (x - X(s, t)){\rm{d}}s, } $ | (4) |
| $ {\frac{{\partial X}}{{\partial t}}(s, t) = u(X(s, t), t)}。$ | (5) |
方程(2)和(3)表示一般不可压N-S方程。方程(4)表示力源项的分布函数。式中:u表示流场速度;p表示流场压力;t是时间;ρ和μ分别代表流体的密度和动态粘度系数;F(x, t)表示边界传递给流场的所有体积力;x表示浸入边界的位移;f是浸入边界产生的单位力,其形式根据具体研究问题所对应的力学模型来确定;X(s,t)是Dirac delta函数;s用来描述流场和弹性体的交互作用;δ表示光滑化的Dirac函数。S-ALE耦合方法可以有效地解决罚函数方法所面临的“渗漏”,在水上迫降界面的流体结构耦合方面展现出强大的应用潜力。
2 数值结果和讨论 2.1 基于传统ALE算法预测的数值结果和讨论传统的ALE方法预测得到的飞机动力学特征(包括姿态角和过载)如图 2~3所示。图 3中V、M、D和L分别代表飞机的水平速度、气动力矩、气动阻力和气动升力;p0、g和h分别代表流体表面的大气压、重力加速度和入水深度。
|
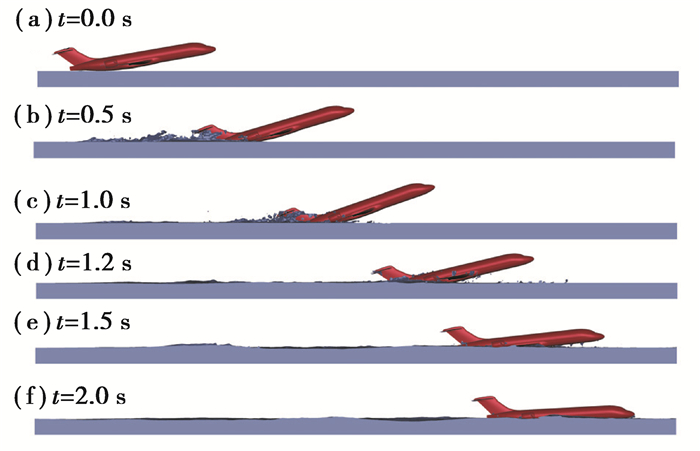
图 2 基于传统ALE方法预测得到的飞机水上迫降过程中俯仰姿态角的变化规律 Fig. 2 The pitch attitude angle-time history during the ditching of aircraft predicted by the conventional ALE method |

|
图 3 水上迫降过程中的水动和气动载荷示意图 Fig. 3 Diagram of aerodynamic and hydrodynamic loads during the ditching |
从图 2可看出飞机触水后,首先有个“抬头”的过程(0~0.5 s),然后随着水平速度减小开始“低头”,一直持续到求解结束(0.5~2.0 s)。下面从飞机受力特征,对上述动力学现象进行解释。区别于垂直入水,水上迫降过程中结构和流体的耦合作用将导致一些额外的物理现象[27],比如空气垫、通风效应、空化现象和“伯努利”效应,如图 3所示。水上迫降过程中往往伴随着明显的汽水混合现象,汽水混合现象可以改变流体的压缩力学行为,对界面处的压力作用时间和分布形式有显著的影响。飞机的俯仰姿态变化是气动载荷、重力载荷、水动载荷综合作用的结果。对于水动载荷,一个显著效应为伯努利现象。结构以较高的水平速度在水面上滑行,“迎水面”在水载荷的冲击作用下产生过压区(overpressure zone),此时该区域的流体流速较小;而在飞机尾部流体以较高的相对速度绕流,按照伯努利平衡方程(同一深度下,静水压强和动水压强之和恒定),将会产生负压区域(negative pressure zone),从而在飞机的尾部产生向下的尾部吸力作用。一般认为,“负压”会导致飞机“抬头”,而“过压”会引起飞机“低头”。重力对姿态角影响的趋势是使飞机低头,而气动载荷倾向于“抬头”。迫降前期,水平速度较大,伯努利效应占据主导地位,飞机出现“抬头”现象。但是,随着吃水深度增加以及飞机在垂直方向的投影面积增大,水动阻力越来越大,飞机的水平速度逐渐下降,伯努利效应和气动载荷影响开始减小,飞机出现“低头”现象。飞机尾部的伯努利效应与水平速度大小以及外部构型密切相关,合理利用这一特性有助于缓解机乘人员所承受的过载,提高飞机水上迫降的“适坠”性能。
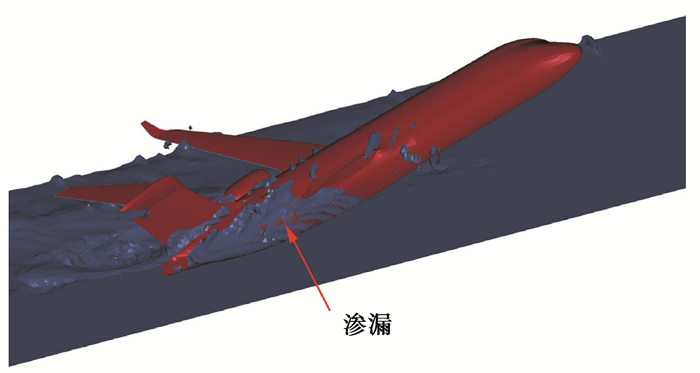
基于ALE算法预测得到的俯仰姿态角曲线与实验数据的对比见图 4。预测结果在1.0 s前和实验基本吻合,但是1.0 s后存在比较明显的差异。实验结果在1.0~1.5 s出现了二次“抬头”现象,但传统ALE算法未能预测到该现象。其主要原因是0.8 s后Lagrange壳体和Euler流体耦合过程中开始出现渗漏,在1.2 s时刻已经有大量的流体渗透入飞机内部(如图 5)。LS-DYNA中流固耦合算法规定当渗透体积超过FRCMIN+0.3,流固耦合的作用将失效。笔者曾试图调整FRCMIN和PLEAK等耦合参数来优化模型,但始终不能有效地控制渗漏现象。

|
图 4 基于ALE算法预测得到的俯仰姿态角曲线和相应的实验结果 Fig. 4 The pitch attitude angle-time history predicted by ALE method and corresponding experimental data |
|
图 5 1.2 s时刻流体的渗漏现象(1/2对称剖视图) Fig. 5 Fluid leakage phenomenon at 1.2 s (Sectional view of 1/2 model) |
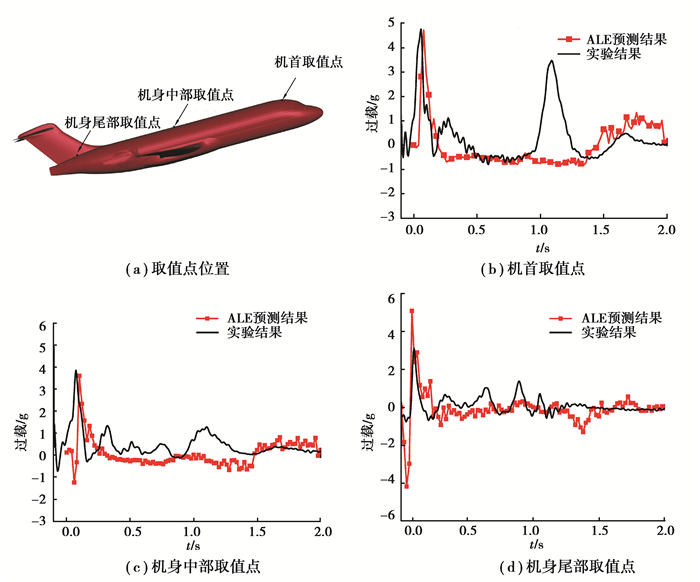
基于ALE算法预测得到的过载曲线与实验数据的对比见图 6。分别提取了机首,机中以及机尾三个关键节点(取值点参考了实验加速度传感器位置)的加速度时程曲线,并和实验的相关数据进行对比分析。由图可知,和俯仰姿态角规律相似,预测结果在1.0 s前和实验基本吻合,但是1.0 s后存在比较明显的差异。机中和机首的加速度实验在1.1 s左右有明显的二次加速度峰值,但是ALE算法却未能对此做出预测。
|
图 6 不同过载取值点基于ALE算法预测得到的过载时间历程以及实验结果 Fig. 6 Overload value points and their overload-time histories predicted by ALE method and corresponding experimental data |
综上所述,传统ALE可以对水上迫降第一次俯仰姿态角峰值和过载峰值进行预测,但却无法预测后期的二次“抬头”和二次过载峰值,原因在于流体渗漏导致的流固耦合失效。
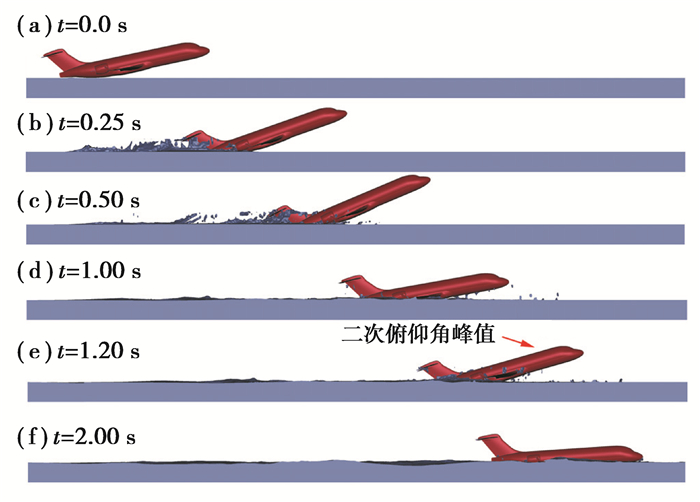
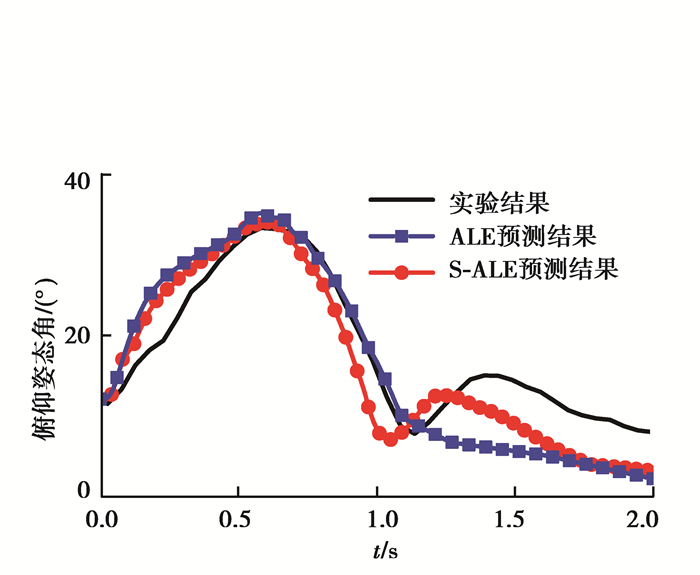
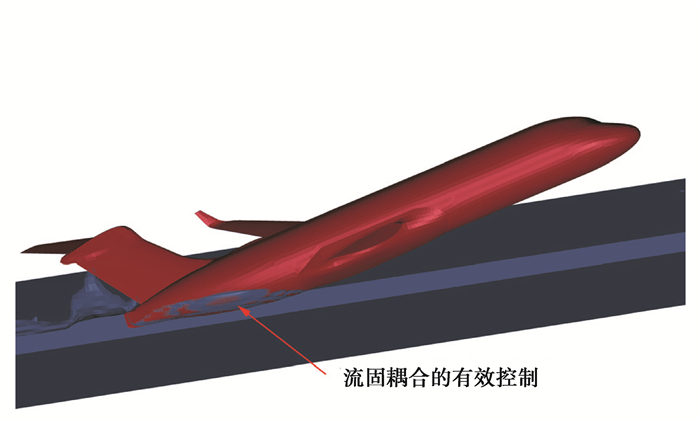
2.1 基于S-ALE耦合方法预测的数值结果和讨论图 7给出了S-ALE耦合方法预测得到的飞机水上迫降过程中俯仰姿态角的变化规律。S-ALE耦合方法预测得到的俯仰姿态角曲线与实验数据的对比见图 8。观察可知,迫降时间在0.0~1.0 s范围时,S-ALE方法预测得到俯仰姿态角的变化规律与传统的ALE方法预测结果一致;S-ALE预测到了1.0 s以后飞机的二次“抬头”现象,所得到的二次俯仰姿态角峰值比实验结果低18.7%。跟踪飞机和流体的渗漏情况,1.2 s时刻飞机/流体的界面渗漏情况如图 9所示。对比图 5中的传统ALE预测结果,S-ALE算法有效地抑制了Euler流体对Lagrange结构的渗透。
|
图 7 基于S-ALE方法预测得到的飞机水上迫降过程中俯仰姿态角的变化规律 Fig. 7 The pitch attitude angle-time history predicted by S-ALE method |
|
图 8 S-ALE算法预测姿态角变化曲线和ALE预测结果以及实验结果 Fig. 8 The pitch attitude angle-time histories predicted by S-ALE and ALE methods, and corresponding experimental data |
|
图 9 1.2 s时刻S-ALE方法对渗漏的有效控制 Fig. 9 Effective restraint to leakage in S-ALE method at 1.2 s |
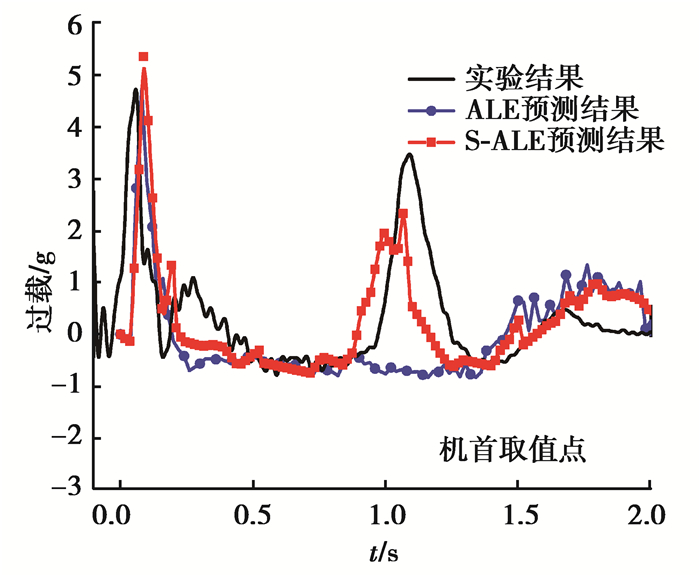
基于S-ALE算法预测得到的过载曲线与实验数据的对比见图 10。由图 6中传统ALE方法预测的过载曲线和实验数据的对比可知,ALE方法预测的加速度在机首处与实验结果差异最大,为了控制篇幅,仅选取机首处过载曲线进行对比分析。观察可知,S-ALE方法预测的过载特征与实验结果更加吻合,具备预测“二次过载”的能力。得到的二次过载峰值比实验结果低37.1%,未来我们将针对二次过载峰值过小的问题,做进一步的模型优化。
|
图 10 S-ALE算法预测得到的过载时程曲线与ALE预测结果以及实验结果的对比(加速度取值点位于机首处) Fig. 10 Comparison of overload-time histories predicted by S-ALE with the predicted results by ALE methods and corresponding experimenta data (the data point locates at the head of aircraft) |
水上迫降数值分析的核心问题是流体/固体界面相互作用的处理方式。尽管基于ALE的罚函数耦合方法已经在水上迫降的数值分析中得到应用,但是流固耦合界面的“渗漏”以及由渗漏引起的流固耦合作用失效是亟待解决的问题。基于S-ALE的耦合方法提供了优化流固耦合作用的一种途径。笔者采用基于“传统ALE的罚函数耦合方法”和“S-ALE流固耦合方法”开展了某型号飞机的水上迫降动力学分析,采集了飞机运动姿态和过载时程,并与实验测试结果对比,得到如下主要结论。
1) 基于ALE的罚函数耦合方法可以有效地预测第一次俯仰姿态角峰值和过载峰值,但不能有效地控制流体的渗漏。随着渗透量增大,流固相互耦合的作用失效,导致ALE罚函数耦合方法不能预测到二次俯仰姿态角峰值和过载峰值。
2) 基于S-ALE流固耦合算法较好地避免了流体的渗漏,预测得到的俯仰姿态角变化规律和过载变化规律和实验结果基本一致。尽管预测的二次峰值结果与实验存有一定的偏差,但依然展现较大的应用潜力。
| [1] |
中国民用航空局.中国民用航空规章第25部运输类飞机适航标准: CCAR-25-R4[S].北京: 中国民用航空局, 2011. Civil Aviation Administration of China. China civil aviation regulations Part 25: airworthiness standards of transport category aircraft: CCAR-25-R4[S]. Beijing: Civil Aviation Administration of China, 2011. (in Chinese). |
| [2] |
Nathalie T. Contribution to the modelling and simulation of aircraft structures impacting on water[D]. Stuttgart: University of Stuttgart, 2009.
|
| [3] |
Hughes K. Application of improved Lagrangian techniques for helicopter crashworthiness on water[D]. Bedfordshire, England: Granfield University, 2005.
|
| [4] |
Pentecôte N, Vigliotti A. Simulation of the impact on water ofa subfloor component and a full-scale WG30 helicopter[C/OL]//AHS International 58th Annual Forum, June 11-13, 2002, Montreal, Canada. The American Helicopter Society International Inc., 2002[2019-12-06]. https://elib.dlr.de/14972/.
|
| [5] |
Duan X P, Sun W P, Chen C, et al. Numerical investigation of the porpoising motion of a seaplane planing on water with high speeds[J]. Aerospace Science and Technology, 2019, 84: 980-994. DOI:10.1016/j.ast.2018.11.037 |
| [6] |
屈秋林, 刘沛清, 郭保东, 等. 某型客机水上迫降的着水冲击力学性能数值研究[J]. 民用飞机设计与研究, 2009(S1): 64-69. QU Qiulin, LIU Peiqing, GUO Baodong, et al. Numerical study on mechanical peoperties of civil aircrafts during the ditching[J]. Civil Aircraft Design and Research, 2009(S1): 64-69. (in Chinese) |
| [7] |
Qu Q L, Hu M X, Guo H, et al. Study of ditching characteristics of transport aircraft by global moving mesh method[J]. Journal of Aircraft, 2015, 52(5): 1550-1558. DOI:10.2514/1.C032993 |
| [8] |
Qu Q L, Liu C S, Liu P Q, et al. Numerical simulation of water-landing performance of a regional aircraft[J]. Journal of Aircraft, 2016, 53(6): 1680-1689. DOI:10.2514/1.C033686 |
| [9] |
Iranmanesh A, Passandideh-Fard M. A three-dimensional numerical approach on water entry of a horizontal circular cylinder using the volume of fluid technique[J]. Ocean Engineering, 2017, 130: 557-566. DOI:10.1016/j.oceaneng.2016.12.018 |
| [10] |
Borrelli R, Mercurio U, Alguadich S. Water impact tests and simulations of a steel structure[J]. International Journal of Structural Integrity, 2012, 3(1): 5-21. DOI:10.1108/17579861211209966 |
| [11] |
卢鸣飞, 华诚. 基于FEM-SPH耦合算法的飞机水上迫降的力学建模与分析[J]. 复旦学报(自然科学版), 2013, 52(5): 583-591. LU Mingfei, HUA Cheng. Model and numerical simulations of water ditching by FEM-SPH coupling method[J]. Journal of Fudan University (Natural Science), 2013, 52(5): 583-591. (in Chinese) |
| [12] |
Streckwall H, Lindenau O, Bensch L. Aircraft ditching:a free surface/free motion problem[J]. Archives of Civil and Mechanical Engineering, 2007, 7(3): 177-190. DOI:10.1016/S1644-9665(12)60025-9 |
| [13] |
Meringolo D D, Colagrossi A, Marrone S, et al. On the filtering of acoustic components in weakly-compressible SPH simulations[J]. Journal of Fluids and Structures, 2017, 70: 1-23. DOI:10.1016/j.jfluidstructs.2017.01.005 |
| [14] |
Xiao T H, Qin N, Lu Z Y, et al. Development of a smoothed particle hydrodynamics method and its application to aircraft ditching simulations[J]. Aerospace Science and Technology, 2017, 66: 28-43. DOI:10.1016/j.ast.2017.02.022 |
| [15] |
Woodgate M A, Barakos G N, Scrase N, et al. Simulation of helicopter ditching using smoothed particle hydrodynamics[J]. Aerospace Science and Technology, 2019, 85: 277-292. DOI:10.1016/j.ast.2018.12.016 |
| [16] |
Siemann M H, Schwinn D B, Scherer J, et al. Advances in numerical ditching simulation of flexible aircraft models[J]. International Journal of Crashworthiness, 2018, 23(2): 236-251. |
| [17] |
Derakhshanian M S, Haghdel M, Alishahi M M, et al. Experimental and numerical investigation for a reliable simulation tool for oblique water entry problems[J]. Ocean Engineering, 2018, 160: 231-243. DOI:10.1016/j.oceaneng.2018.04.080 |
| [18] |
Hua C, Fang C, Cheng J. Simulation of fluid-solid interaction on water ditching of an airplane by ALE method[J]. Journal of Hydrodynamics, 2011, 23(5): 637-642. DOI:10.1016/S1001-6058(10)60159-X |
| [19] |
Wang Y H. Numerical modeling approach of an air-launched AUV initially impacting on water[C]//Proceedings of 2012 National Conference on Information Technology and Computer Science, November 16-18, 2012. Paris: Atlantis Press, 2012: 336-340.
|
| [20] |
胡大勇, 杨嘉陵, 王赞平, 等. 某型飞机水上迫降数值化模型[J]. 北京航空航天大学学报, 2008, 34(12): 1369-1374, 1383. HU Dayong, YANG Jialing, WANG Zanping, et al. Numerical model for a commercial aircraft water landing[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(12): 1369-1374, 1383. (in Chinese) |
| [21] |
Siemann M H, Langrand B. Coupled fluid-structure computational methods for aircraft ditching simulations:comparison of ALE-FE and SPH-FE approaches[J]. Computers & Structures, 2017, 188: 95-108. |
| [22] |
Bisagni C, Pigazzini M S. Modelling strategies for numerical simulation of aircraft ditching[J]. International Journal of Crashworthiness, 2018, 23(4): 377-394. DOI:10.1080/13588265.2017.1328957 |
| [23] |
刘翔.飞机水上迫降的运动特性分析和讨论[D].武汉: 武汉理工大学, 2012. LIU Xiang. Analysis and discussion on hydrodynamic characteristics of aircraft during ditching[D]. Wuhan: Wuhan University of Technology, 2012. (in Chinese) |
| [24] |
张苏.水上迫降尾部吸能对飞机运动特性的影响[D].武汉: 武汉理工大学, 2013. ZHANG Su. Effect of energy absorption of tail structure on the kinetic behavior during aricraft ditching[D]. Wuhan: Wuhan University of Technology, 2013. (in Chinese) |
| [25] |
Anghileri M, Castelletti L M L, Francesconi E, et al. Survey of numerical approaches to analyse the behavior of a composite skin panel during a water impact[J]. International Journal of Impact Engineering, 2014, 63: 43-51. DOI:10.1016/j.ijimpeng.2013.08.008 |
| [26] |
Peskin C S. The immersed boundary method[J]. Acta Numerica, 2002, 11: 479-517. DOI:10.1017/S0962492902000077 |
| [27] |
Hughes K, Vignjevic R, Campbell J, et al. From aerospace to offshore:bridging the numerical simulation gaps - simulation advancements for fluid structure interaction problems[J]. International Journal of Impact Engineering, 2013, 61: 48-63. DOI:10.1016/j.ijimpeng.2013.05.001 |
 2020, Vol. 43
2020, Vol. 43



