反问题具有重要的研究价值和工程背景。在过去几十年里,反问题的应用已经扩展到许多领域,如热传导、电阻抗层析成像、无损检测等。弹性力学Cauchy边界条件反问题是一类经典的反问题。在这类问题中,只在解域的部分边界上可以测量或者给出边界条件,而剩余边界则不方便测量或得到任何信息。这类问题的数值反演一般是不适定的,即微小的测量误差会导致计算结果的精度严重下降。因此,提出准确有效的数值方法以克服反问题的不适定性是一项很有必要的工作。
边界元法[1]是解决工程问题的一种常用计算方法,被广泛用于求解各类力学反问题。与有限元法相比,边界元法只需离散待求区域表面,从而降低维度,减少求解问题的自由度数,节省大量时间。由于边界元法只需将区域边界离散,域内值仍可解析计算得到,因此计算精度更高。
Marin等[2]基于边界元法和共轭梯度法对弹性力学Cauchy反问题进行求解,识别了未知边界上的面力和位移。Li等[3]对有限差分法进行拓展,采用了广义有限差分法求解二维Cauchy反问题,避免了网格划分和数值求积等耗时长的工作。El Seblani等[4]提出了一种局部无网格Hermite型配点法用于求解Cauchy反问题。Marin等[5]利用基本解法和衰落正则化方法进行缺失边界数据的数值重构,并根据Morozov偏差原理确定合适的迭代步数。Grigor’ev[6]给出了一种求解弹性理论中Lame方程Cauchy反问题的解析计算方法。Yang等[7]用改进的Tikhonov正则化方法求解Cauchy反问题。Liu等[8]结合Trefftz法和基本解法,改善了Cauchy问题解的精度。Wang等[9]首次尝试用局部基本解方法求解复杂几何中的Cauchy反问题。周焕林等[10]利用截断奇异值分解法识别Cauchy边界条件,并用L-Curve法确定正则化参数,得到正则解。
近年来,元启发式算法作为一种新兴的优化类算法,广泛应用于很多领域。Mahmud等[11]将边界元法、共轭梯度法和遗传算法结合,用于Cauchy反问题的求解,识别非均匀体内的夹杂。Tian等[12]基于量子行为粒子群算法和共轭梯度法反演稳态条件下的几何形状,应用Tikhonov正则化方法处理问题的病态性。布谷鸟搜索(cuckoo search, CS)算法[13]由Yang和Deb于2009年提出,并在近年来得到广泛的关注。严俊等[14]基于CS算法反演了稳态热传导问题的导热系数。Naumann等[15]用改进的CS算法进行空气动力学的设计优化。Kaveh等[16]使用改进的CS算法对地震荷载作用下的三维钢结构框架进行尺寸优化。Walton等[17]基于改进的CS算法,讨论了非梯度算法的一些工程应用。
笔者结合CS算法和多项式近似法求解弹性力学Cauchy边界条件反问题,将待识别面力边界条件用多项式函数拟合,从而将离散结点未知边界条件求解问题转化成多项式未知系数识别问题。通过CS算法最小化已知边界上的面力计算值与给定值的最小二乘误差来反演未知面力,将反演得到的面力边界条件代入正问题求解得到未知边界位移。
1 正问题 1.1 弹性力学理论考虑一线弹性区域Ω∈Rd,R为实数集,d为所求问题的空间维数,一般d∈{1, 2, 3},并且域Ω由光滑边界
| $ G\frac{{{\partial ^2}{\kern 1pt} {u_i}(\mathit{\boldsymbol{x}})}}{{\partial {\kern 1pt} {\kern 1pt} {x_j}{x_j}}} + \frac{G}{{1 - 2\nu }}\frac{{{\partial ^2}{\kern 1pt} {u_j}(\mathit{\boldsymbol{x}})}}{{\partial {x_i}{\kern 1pt} \partial {x_j}}} = 0,\mathit{\boldsymbol{x}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varOmega ,i,j = 1,2。$ | (1) |
式中:G和ν分别为材料的剪切模量和泊松比;x为区域内一点,xi和xj为该点i和j方向上的坐标,ui和uj表示该点i和j方向上的位移。
几何方程为:
| $ {\varepsilon _{ij}}(\mathit{\boldsymbol{x}}) = \frac{1}{2}\left( {\frac{{\partial {u_i}{\kern 1pt} {\kern 1pt} (\mathit{\boldsymbol{x}})}}{{\partial {\kern 1pt} {x_j}}} + \frac{{\partial {u_j}{\kern 1pt} {\kern 1pt} (\mathit{\boldsymbol{x}})}}{{\partial {\kern 1pt} {x_i}}}} \right),\mathit{\boldsymbol{x}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varGamma ,i,j = 1,{2}。$ | (2) |
式中:εij为应变分量。由胡克定律可得应力和应变之间的关系,即:
| $ {\sigma _{ij}}(\mathit{\boldsymbol{x}}) = 2G\left( {{\varepsilon _{ij}}(\mathit{\boldsymbol{x}}) + \frac{\nu }{{1 - \nu }}{\varepsilon _{{\rm{kk}}}}(\mathit{\boldsymbol{x}})} \right),\mathit{\boldsymbol{x}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varGamma ,i,j = 1,2。$ | (3) |
式中:εkk为体积应变,σij为应力分量。
令n(x)为边界Γ上的外法线向量,且t(x)为其上一点x处的面力向量,则有:
| $ {t_i}(\mathit{\boldsymbol{x}}) = {\sigma _{ij}}(\mathit{\boldsymbol{x}}){n_j}(\mathit{\boldsymbol{x}}),\mathit{\boldsymbol{x}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varGamma ,i,j = 1,2。$ | (4) |
若在边界Γ的部分边界,即Γ2上已知所有信息,而剩余边界Γ1上边界条件全未知,则有:
| $ {u_i}(\mathit{\boldsymbol{x}}) = {{\bar u}_i}(\mathit{\boldsymbol{x}}),{t_i}(\mathit{\boldsymbol{x}}) = {{\bar t}_i}(\mathit{\boldsymbol{x}}),\mathit{\boldsymbol{x}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \in {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varGamma _2},i = 1,2。$ | (5) |
式中:
利用已知边界条件式(5)去识别剩余边界未知信息,此类问题为Cauchy型边界条件反问题,如图 1所示。
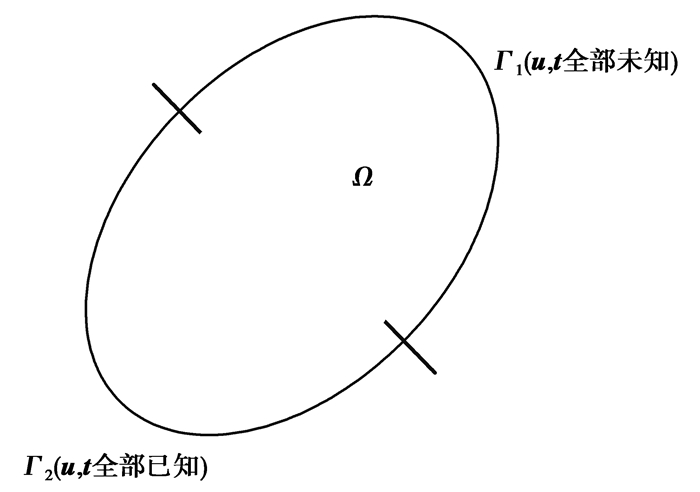
|
图 1 Cauchy边界条件反问题 Fig. 1 The inverse problem of Cauchy boundary conditions |
考虑二维弹性力学平面问题且不考虑体力项,则边界积分方程可写成:
| $ {C_{ij}}{u_j} + \int_\mathit{\Gamma} {T_{ij}^*} {u_j}{\rm{d}}\mathit{\Gamma} = \int_\varGamma {U_{ij}^*} {t_j}{\rm{d}}\mathit{\Gamma} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i,j = 1,2。$ | (6) |
对于二维各向同性线弹性体,其位移基本解和面力基本解分别为:
| $ U_{ij}^* = \frac{{ - 1}}{{8\pi G(1 - \nu )}}[(3 - 4\nu ){\rm{ln}}{\kern 1pt} {\kern 1pt} {\kern 1pt} r{\delta _{ij}} - {r_{,i}}{r_{,j}}]; $ | (7) |
| $ T_{ij}^* = \frac{1}{{4\pi (1 - \nu )r}}\{ {r_{,n}}[(1 - 2\nu ){\delta _{ij}} + 2{r_{,i}}{r_{,j}}] - (1 - 2\nu )({r_{,i}}{n_j} - {r_{,j}}{n_i})\} 。$ | (8) |
式中:Uij*和Tij*分别表示弹性体内i向作用单位集中力时引起的j向位移和面力分量;Cij为与点x位置有关的常数;δij为克罗内克函数;r为边界上源点到场点之间的距离;r, i、r, j和r, n分别表示r对xi、xj以及外法线向量n的偏导数;ni和nj分别表示外法线n在i和j方向上的方向余弦。对于平面应力问题,将ν换为
| $ \mathit{\boldsymbol{HU}} = \mathit{\boldsymbol{GT}}。$ | (9) |
式中:H和G是只与边界Γ几何有关的系数矩阵,U和T为结点的位移和面力列向量。引入已知边界条件(5)中Γ2上的位移边界条件和Γ1边界上的面力边界条件,该面力边界条件采用布谷鸟算法优化计算得到的系数进行多项式拟合后获得,式(9)可改写为:
| $ \mathit{\boldsymbol{Af}} = \mathit{\boldsymbol{s}}。$ | (10) |
式中:A为式(9)移项后形成的已知系数矩阵;s为移项后形成的已知列向量;向量f包含边界Γ1上的未知位移边界条件和Γ2上的面力边界条件计算值。
2 反问题 2.1 多项式近似假定未知面力边界条件由已知形式的m阶多项式组成,通过下式表示:
| $ {t_i}(\mathit{\boldsymbol{x}}) = {b_0} + {b_1}{x_1} + {b_2}{x_2} + {b_3}x_1^2 + {b_4}{x_1}{x_2} + {b_5}x_2^2 + \cdots + {b_{m(m + 3)/2}}x_2^m。$ | (11) |
对整个边界Γ1上未知面力进行拟合,用矩阵形式表示,则有
| $ {\mathit{\boldsymbol{t}}_i} = \mathit{\boldsymbol{bq}}(\mathit{\boldsymbol{x}})。$ | (12) |
式中:
通过多项式函数插值拟合后,未知面力边界条件识别转化为找出一组最优系数b满足收敛条件。目标函数表示如下:
| $ J(\mathit{\boldsymbol{b}}) = \sum\limits_{i = 1}^2 {\sum\limits_{l = 1}^N {{{\left\| {t_i^l - \hat t_i^l} \right\|}^2}} } 。$ | (13) |
式中:N为可测得面力和位移边界条件信息的边界上划分的结点数,til为通过边界元法计算得到的第l个结点在i方向上的面力分量计算值,
| $ {\mathit{\boldsymbol{t}}^*} = {\mathit{\boldsymbol{\hat t}}_0}(1 + \mathit{\boldsymbol{w}}p)。$ | (14) |
式中:
当目标函数J(b)满足
| $ J(\mathit{\boldsymbol{b}}) < \varepsilon 。$ | (15) |
时,迭代终止,ε为迭代终止条件。
2.3 布谷鸟搜索算法布谷鸟算法是一种新型元启发式算法。该算法通过模拟布谷鸟的繁殖寄生行为,并加入Lévy飞行机制求解最优化问题。布谷鸟搜索算法可以用如下3点理想化准则概括:
1) 每只布谷鸟单次只产1枚卵,并且随机选择宿主巢穴放入;
2) 将存有最好鸟蛋的巢穴留至下一代;
3) 用于迭代的鸟巢数量η是一定的,鸟巢中外来蛋被发现的概率是pa∈[0, 1]。
基于以上3条准则,鸟巢位置更新方式表示为:
| $ \mathit{\boldsymbol{X}}_g^{K + 1} = \mathit{\boldsymbol{X}}_g^K + \alpha \oplus L(\lambda )。$ | (16) |
式中:XgK表示第
| $ L(\lambda )\backsim z = {K^{ - \lambda }}。$ | (17) |
飞行步长λ定义为:
| $ \lambda = \frac{z}{{{{\left| v \right|}^{\frac{1}{\beta }}}}}。$ | (18) |
式中:z和v为正态分布随机变量,
| $ \sigma _z^2 = \left[ {\frac{{\mathit{\Gamma} (1 + \beta )}}{{\beta \mathit{\Gamma} (1 + \beta )/2}} \cdot \frac{{{\rm{sin}}(\pi \beta /2)}}{{{2^{(\beta - 1)/2}}}}} \right]1/\beta ,{\sigma _v} = 1; $ | (19) |
| $ {\mathit{\Gamma} _\alpha } = \int_0^\infty {{K^{\alpha - 1}}} {{\rm{e}}^{ - K}}{\rm{d}}K。$ | (20) |
式中:Γα为伽马函数;K为迭代次数。
综上所述,鸟巢位置更新公式可表示为:
| $ \mathit{\boldsymbol{X}}_g^{K + 1} = \mathit{\boldsymbol{X}}_g^K + {\alpha _0}\frac{{{\sigma _u} \times {u^{\frac{1}{\beta }}}}}{{|\nu |}}(\mathit{\boldsymbol{X}}_q^K - \mathit{\boldsymbol{X}}_{{\rm{best}}}^K)。$ | (21) |
式中:XgK+1为算法更新后得到的K+1代解,XgK和XqK是算法在K代生成的2个解,XbestK为算法在K代的最优解,α0为步长因子。
算法在根据发现概率pa抛弃部分解后,利用下式生成新解
| $ \mathit{\boldsymbol{X}}_g^{K + 1} = \mathit{\boldsymbol{X}}_g^K + \gamma (\mathit{\boldsymbol{X}}_q^K - \mathit{\boldsymbol{X}}_o^K)。$ | (22) |
式中:γ为标准正态分布随机变量;XoK是算法在第K代产生的1个随机解。
2.4 边界条件识别过程布谷鸟算法求解弹性力学边界条件反问题的步骤如下:
1) 给定所需的算法参数:未知参数个数、鸟巢数量、发现概率、最大迭代次数等。
2) 用布谷鸟算法得到η组未知参数初始值,计算每一组未知参数对应的适应度,选出当前最优的一组参数及其对应的目标函数值。
3) 验算目标函数是否满足式(15)迭代停止条件,如满足,输出最优解并转到第8步,否则转第4步。
4) 通过式(16)的Lévy游走生成新的鸟巢,并根据对应的目标函数值选出当前最优鸟巢。
5) 按概率抛弃部分鸟巢,并按照式(22)生成同样数量的新鸟巢。
6) 根据式(13)计算各鸟巢的目标函数值,找出当前最好鸟巢。
7) 更新鸟巢,返回第3步。
8) 利用得到的最优系数计算出Γ1边界上的面力边界条件,结合边界Γ2上的已知位移边界条件,代入正问题中计算得出边界Γ1上的未知位移边界条件。
3 数值算例利用2个数值算例验证布谷鸟算法联合多项式近似识别未知边界条件的有效性和准确性,选用相对误差et和eu表示反演结果的精度。
| $ {e_{\rm{t}}} = \frac{{\left\| {{t^{({\rm{num}})}} - {t^{({\rm{an}})}}} \right\|}}{{\left\| {{t^{({\rm{an}})}}} \right\|}}; $ | (23) |
| $ {e_{\rm{u}}} = \frac{{\left\| {{u^{({\rm{num}})}} - {u^{({\rm{an}})}}} \right\|}}{{\left\| {{u^{({\rm{an}})}}} \right\|}}。$ | (24) |
式中:t(num)和u(num)分别表示未知边界上反演得到的面力和位移边界条件数值解,t(an)和u(an)为精确的面力和位移边界条件。
3.1 受单向拉伸方板考虑一个[-2, 2]×[-2, 2]的受单向拉伸方板,如图 2所示。弹性模量E=5.0 N/m2,泊松比ν=0.3。边界
| $ \left\{ {\begin{array}{*{20}{l}} {u_1^{({\rm{ an }})}({x_1},{x_2}) = \frac{1}{E}{x_1},u_2^{({\rm{ an }})}({x_1},{x_2}) = - \frac{\nu }{E}{x_2};}\\ {\sigma _{11}^{({\rm{ an }})}({x_1},{x_2}) = {\sigma _0},\sigma _{12}^{({\rm{ an }})}({x_1},{x_2}) = \sigma _{22}^{({\rm{ an }})}({x_1},{x_2}) = 0;}\\ {t_i^{({\rm{ an }})}({x_1},{x_2}) = \sigma _{i1}^{({\rm{ an }})}({x_1},{x_2}){n_1}({x_1},{x_2}) + \sigma _{i2}^{({\rm{ an }})}({x_1},{x_2}){\kern 1pt} {\kern 1pt} {n_2}{\kern 1pt} {\kern 1pt} ({x_1},{x_2})}。\end{array}} \right. $ | (25) |
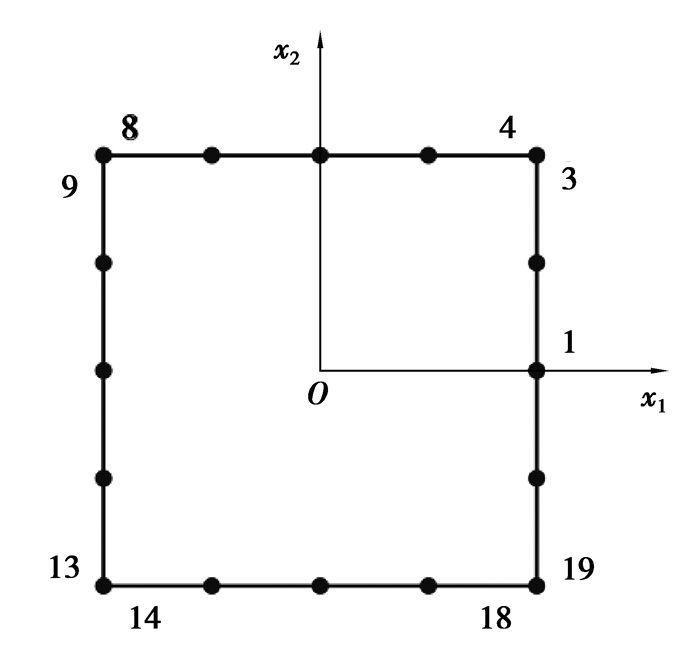
|
图 2 受单向拉伸方板 Fig. 2 Square plate under uniaxial tension |
式中:σ0=2.0 N/m2; i=1, 2。已知的边界条件为:Γ1上边界条件全未知,Γ2上边界条件全已知。收敛条件为ε=1×10-5,最大迭代次数为1 000。
3.1.1 鸟巢数量的影响不考虑测量误差,采用一阶多项式反演未知边界条件,讨论鸟巢数量分别为5,10,15,20时的计算结果。计算结果如表 1所示。
| 表 1 鸟巢数量对计算结果的影响 Table 1 Influence of nest number |
由表 1可知,随着鸟巢数量增加,反演结果精度提高,且所需迭代次数逐渐减少。鸟巢数取20时,所需迭代次数最少,获得的解精度最高。因此,为保证计算效率与精度,其余算例鸟巢数均取20。
3.1.2 多项式近似对计算结果的影响为了验证多项式近似对边界条件识别问题的有效性,考虑用布谷鸟算法直接识别未知边界条件。表 2给出了布谷鸟算法在采用多项式近似和直接反演2种情况下计算结果的对比。考虑非多项式直接反演时待识别未知量多,布谷鸟算法识别难度较大,设置算法在非多项式识别时的最大迭代次数为5 000。
| 表 2 多项式反演和直接反演的计算结果对比 Table 2 The comparison between polynomial inversion and direct inversion |
由表 2看出,算法在引入多项式函数近似未知面力边界条件后,反演结果精度提高,收敛速度也明显加快。因此对未知边界条件反演问题采用多项式近似方法,将获得更快的收敛速度和更高的计算精度。
3.1.3 多项式阶数的选取多项式的阶数取值为m=1, 2, 3,讨论不同多项式阶数对反演结果的影响。在整个待识别边界Γ1上,横坐标x1为常数,边界条件表达形式如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{t_i}({x_2}) = {b_0} + {b_2}{x_2}\quad m = 1;}\\ {{t_i}({x_2}) = {b_0} + {b_2}{x_2} + {b_5}x_2^2\quad m = 2;}\\ {{t_i}({x_2}) = {b_0} + {b_2}{x_2} + {b_5}x_2^2 + {b_9}x_2^3\quad m = 3}。\end{array}} \right. $ | (26) |
表 3给出了选用不同阶数多项式时布谷鸟算法的计算结果。
| 表 3 多项式阶数对CS计算结果的影响 Table 3 The results of CS with different polynomial degree |
结果表明,随着多项式阶数m增加,计算结果误差变大,同时需要的迭代数也大幅增加。对于本例,待识别边界上面力值为常数,多项式阶数增加不能有效提高结果精度。在多项式阶数为1的情况下获得的结果足够精确。因此,为了保证算法能快速准确收敛,多项式阶数取1。
3.1.4 测量误差的影响在1%、3%、5%三种不同测量误差下进行边界条件识别,研究测量误差对反演结果的影响。待求面力边界条件和位移边界条件的数值解与解析解之间的对比结果如图 3所示。
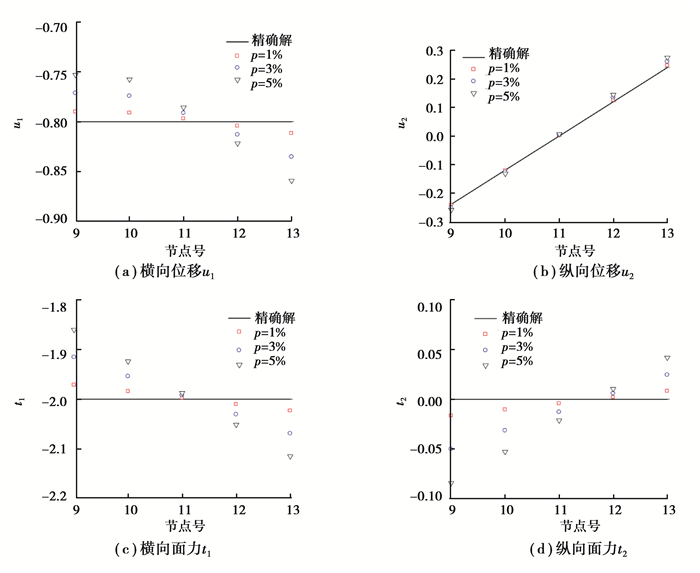
|
图 3 不同测量误差对反演结果的影响 Fig. 3 Inverse results with different measurement errors |
待求位移边界条件的相对误差分别为1.02×10-2、3.02×10-2、5.01×10-2,面力识别结果的相对误差分别为9.21×10-3、2.72×10-2、4.49×10-2。在3种测量误差水平下的迭代次数分别为300、313、352。不难看出,测量误差越大,反演精度越低,迭代次数也越多。
从图 3可以看出,测量误差对反演结果的影响较大。在误差水平为1%时,反演值与真实值相差较小,随着测量误差增加,反演值与真实值偏差逐渐增大。
3.2 受内外均匀压力作用的厚壁圆筒如图 4所示,一厚壁圆筒受内外均匀压力作用,其边界由两部分组成:
| $ \left\{ {\begin{array}{*{20}{l}} {u_i^{({\rm{an}})} = \frac{{ - (1 - \nu )}}{{2G(1 + \nu )}}{\sigma _0}{x_i};}\\ {\sigma _{ij}^{({\rm{an}})} = - {\sigma _0}{\delta _{ij}}}。\end{array}} \right. $ | (27) |
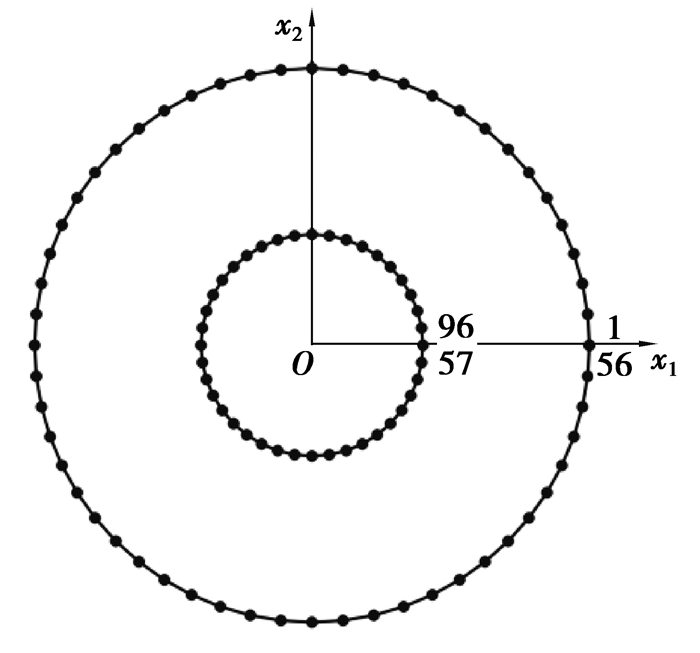
|
图 4 受均布压力作用的厚壁圆筒 Fig. 4 Thick-wall cylinder under uniform distribution pressure |
式中:σ0=100 N/m2, i=1, 2。
3.2.1 多项式近似对计算结果的影响本例待识别结点数为40,故待识别面力分量数为80,使用布谷鸟算法直接识别难度大,故考虑给出更大的容许迭代次数。在不使用多项式近似求解未知边界数值时,令最大迭代步数为10 000。不考虑测量误差,表 4给出了未采用多项式近似未知面力边界条件和采用多项式近似面力2种情况下的反演结果对比。
| 表 4 多项式反演和直接反演的计算结果对比 Table 4 The comparison between polynomial inversion and direct inversion |
使用多项式近似方法识别未知边界条件,由于待识别参数少,所以通过较少的迭代就能得到精度满足需求的结果;而直接使用布谷鸟算法进行边界条件识别时,由于未知参数过多而使得计算结果精度较差。
3.2.2 多项式阶数的选取合适的多项式阶数有利于反演过程的进行。与算例3.1不同,此例边界Γ1上的横坐标x1是变化的,所以采用如式(28)的多项式进行未知面力边界条件近似。表 5给出了采用不同阶数的多项式函数时布谷鸟算法的反演结果误差。
| $ \left\{ \begin{array}{l} {t_i}({x_1},{x_2}) = {b_0} + {b_1}{x_1} + {b_2}{x_2}\quad m = 1;\\ \begin{array}{*{20}{l}} {{t_i}({x_1},{x_2}) = {b_0} + {b_1}{x_1} + {b_2}{x_2} + {b_3}x_1^2 + {b_4}{x_1}{x_2} + {b_5}x_2^2\quad m = 2;}\\ {{t_i}({x_1},{x_2}) = {b_0} + {b_1}{x_1} + {b_2}{x_2} + {b_3}x_1^2 + {b_4}{x_1}{x_2} + {b_5}x_2^2 + {b_6}x_1^3 + {b_7}x_1^2{x_2} + {b_8}{x_1}x_2^2 + {b_9}\quad m = 3}。\end{array} \end{array} \right. $ | (28) |
| 表 5 多项式阶数对CS算法结果的影响 Table 5 The results of CS with different polynomial degree |
由表 5可以看出,在3种不同多项式阶数情况下,随着多项式阶数m增加,相对误差eu和et增大,数值结果逐渐偏离精确解。迭代次数随多项式阶数升高而增加,在多项式阶数为3时,即使迭代至最大迭代次数,计算结果仍无法令人满意。由此可知,多项式阶数的选取对反演结果有显著的影响。对于本例,由于所受荷载均匀分布在区域表面,与坐标值呈简单线性变化关系,故仅需一阶多项式即可获得足够精度的数值解。为了保证算法的准确性和计算效率,多项式阶数取1。
3.2.3 测量误差的影响考虑不同测量误差对反演结果的影响,待识别边界条件反演值与精确解之间的对比结果如图 5所示。
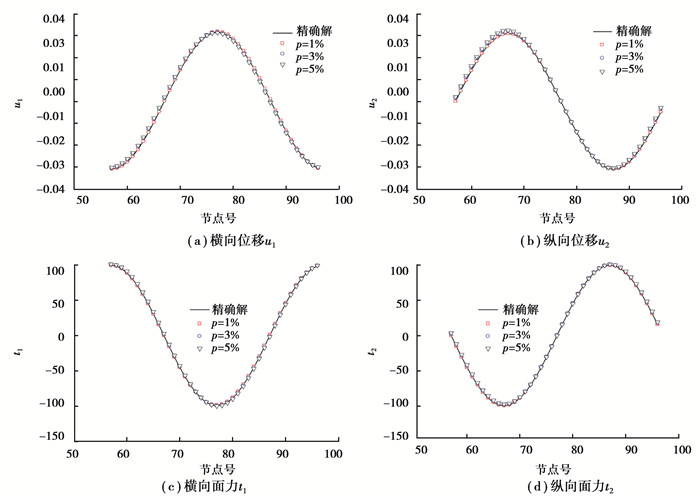
|
图 5 不同测量误差对反演结果的影响 Fig. 5 Inverse results with different measurement errors |
测量误差水平为1%、3%和5%时,位移边界条件识别结果的计算误差分别为6.20×10-3、1.61×10-2、2.63×10-2,面力反演结果的相对误差分别为3.44×10-3、8.55×10-3、1.40×10-2,迭代次数分别为320、392、500。测量误差增加会降低计算结果的精度,随着测量误差增加,迭代次数也随之增加。
4 结论笔者将布谷鸟搜索算法应用于弹性力学Cauchy边界条件反问题求解,并引入了多项式函数近似未知边界条件的方法。采用布谷鸟算法最小化已知边界上面力的计算值和给定值之间的差异,实现对未知边界上的面力边界条件的反演,并利用边界元法求解弹性力学正问题得到未知位移。通过对比未使用多项式和使用多项式近似的计算结果,验证了将未知面力边界条件进行多项式近似是一种求解Cauchy边界条件反问题的更加快速准确的方法。在布谷鸟算法识别过程中,进一步讨论了鸟巢数量、多项式阶数和测量误差对数值结果的影响。研究结果表明:鸟巢数量增加,识别精度提高;多项式阶数增加,数值结果精度下降;随着测量误差增大,反演结果误差变大并且所需迭代次数增多。因此,选择合适的鸟巢数量、多项式阶数并减少测量误差可获得更加准确的反演结果。算例验证了基于多项式近似的布谷鸟算法能准确有效地反演弹性力学边界条件。
| [1] |
姜弘道. 弹性力学问题的边界元法[M]. 北京: 中国水利水电出版社, 2008. JIANG Hongdao. Boundary element method for elasticity problems[M]. Beijing: China Water Power Press, 2008. (in Chinese) |
| [2] |
Marin L, Hào D N, Lesnic D. Conjugate gradient-boundary element method for the Cauchy problem in elasticity[J]. The Quarterly Journal of Mechanics and Applied Mathematics, 2002, 55(2): 227-247. DOI:10.1093/qjmam/55.2.227 |
| [3] |
Li P W, Fu Z J, Gu Y, et al. The generalized finite difference method for the inverse Cauchy problem in two-dimensional isotropic linear elasticity[J]. International Journal of Solids and Structures, 2019, 174. |
| [4] |
El Seblani Y, Shivanian E. Boundary value identification of inverse Cauchy problems in arbitrary plane domain through meshless radial point Hermite interpolation[J/OL]. Engineering with Computers, 2019-04-29[2019-12-05]. https://doi.org/10.1007/s00366-019-00755-8.
|
| [5] |
Marin L, Delvare F, Cimetière A. Fading regularization MFS algorithm for inverse boundary value problems in two-dimensional linear elasticity[J]. International Journal of Solids and Structures, 2016, 78/79: 9-20. DOI:10.1016/j.ijsolstr.2015.09.022 |
| [6] |
Grigor'ev Y. An analytical method for the inverse Cauchy problem of Lame equation in a rectangle[J/OL]. Journal of Physics: Conference Series, 2018, 991: 012029[2019-12-05]. https://iopscience.iop.org/article/10.1088/1742-6596/991/1/012029/pdf.DOI:10.1088/1742-6596/991/1/012029.
|
| [7] |
Yang F, Fu C L, Li X X. A modified Tikhonov regularization method for the cauchy problem of Laplace equation[J]. Acta Mathematica Scientia, 2015, 35(6): 1339-1348. DOI:10.1016/S0252-9602(15)30058-8 |
| [8] |
Liu C S, Wang F J, Gu Y. A Trefftz/MFS mixed-type method to solve the Cauchy problem of the Laplace equation[J]. Applied Mathematics Letters, 2019, 87: 87-92. DOI:10.1016/j.aml.2018.07.028 |
| [9] |
Wang F J, Fan C M, Hua Q S, et al. Localized MFS for the inverse Cauchy problems of two-dimensional Laplace and biharmonic equations[J]. Applied Mathematics and Computation, 2020, 364: 124658. DOI:10.1016/j.amc.2019.124658 |
| [10] |
周焕林, 江伟, 胡豪, 等. 二维弹性力学边界条件反识别TSVD正则化法[J]. 合肥工业大学学报(自然科学版), 2013, 36(9): 1076-1081. ZHOU Huanlin, JIANG Wei, HU Hao, et al. Inverse identification of 2-D elasticity boundary conditions by using TSVD regularization method[J]. Journal of Hefei University of Technology(Natural Science), 2013, 36(9): 1076-1081. (in Chinese) DOI:10.3969/j.issn.1003-5060.2013.09.013 |
| [11] |
Khodadad M, Ardakani M D. Inclusion identification by inverse application of boundary element method, genetic algorithm and conjugate gradient method[J]. American Journal of Applied Sciences, 2008, 5(9): 1158-1166. DOI:10.3844/ajassp.2008.1158.1166 |
| [12] |
Tian N, Zhu L C, Lai C H. Identification of boundary shape using a hybrid approach[J]. International Journal of Machine Learning and Cybernetics, 2015, 6(3): 385-397. DOI:10.1007/s13042-014-0266-9 |
| [13] |
Yang X S, Deb S. Cuckoo search via lévy flights[C]//2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), December 9-11, 2009, Coimbatore, India. IEEE, 2009: 210-214.
|
| [14] |
严俊, 周焕林, 余波, 等. 基于改进布谷鸟算法的导热系数反演[J]. 合肥工业大学学报(自然科学版), 2018, 41(12): 1667-1671, 1677. YAN Jun, ZHOU Huanlin, YU Bo, et al. Inversion of thermal conductivity based on improved cuckoo search algorithm[J]. Journal of Hefei University of Technology(Natural Science), 2018, 41(12): 1667-1671, 1677. (in Chinese) DOI:10.3969/j.issn.1003-5060.2018.12.015 |
| [15] |
Naumann D S, Evans B, Walton S, et al. A novel implementation of computational aerodynamic shape optimisation using modified cuckoo search[J]. Applied Mathematical Modelling, 2016, 40(7/8): 4543-4559. |
| [16] |
Kaveh A, Bakhshpoori T, Azimi M. Seismic optimal design of 3D steel frames using cuckoo search algorithm[J]. The Structural Design of Tall and Special Buildings, 2015, 24(3): 210-227. DOI:10.1002/tal.1162 |
| [17] |
Walton S, Hassan O, Morgan K. Selected engineering applications of gradient free optimisation using cuckoo search and proper orthogonal decomposition[J]. Archives of Computational Methods in Engineering, 2013, 20(2): 123-154. DOI:10.1007/s11831-013-9083-7 |
 2020, Vol. 43
2020, Vol. 43


