2. 湖北汽车工业学院 汽车工程系, 湖北 十堰 442002
2. Department of Automobile Engineering, Hubei University of Automotive Technology, Shiyan, Hubei 442002, P. R. China
微带天线具有体积小、重量轻、易共形等优点,特别适用于航天和移动通信领域[1-2]。但微带天线工作频带窄、增益低、损耗大等问题制约了它在诸如汽车毫米波天线等领域的应用。研究者围绕提升微带天线的性能做了大量工作,如天线阵列[3]、加载反射器[4],使用透镜[5]等,尽管如此,天线阵列需要复杂的馈电网络,同时其天线尺寸规模变大,反射器会降低天线的带宽等,上述方法尚存在一些局限性。直到本世纪初,伴随着超材料理论的发展[6-8],微带天线研究者看到了新的转机,超材料具有新颖的电磁特性,目前已被应用于高增益、小型化、多频化天线等领域[9-11]。
超材料微带天线从结构上可分为3种,即超材料基板型微带天线、超材料覆层型微带天线和复合左右手传输线型微带天线。其中超材料基板型微带天线是在微带天线辐射基板周围布置超材料基元,利用超材料的谐振特性抑制天线表面波从而提升天线性能,只是超材料基元的布置区域有较大局限性[12];复合左右手传输线型微带天线是从传输线理论角度重构电路设计微带天线,设计出的微带天线在大带宽和低损耗方面优势明显[13],只是电路理论的设计相对复杂;超材料覆层型微带天线将超材料基元放置在微带天线辐射基板上方成为天线覆层,超材料基元的布置区域存在更多的可能性[14]。
超材料微带天线的设计对超材料基元的要求比较高,往往需要设计特定性能的超材料,如近零折射率超材料、完全吸收超材料和频率选择表面等。通常基于超材料的微带天线设计首先需要凭借设计者的经验指定一个初始构型,然后对其进行必要的尺寸和形状层面的优化设计,具有一定的凑试局限性。而超材料微带天线性能设计具有主导地位的是拓扑层面的优化,基于拓扑优化的天线设计不再依赖于基元结构的初始选型,具有更大的优化空间[15-16]。
笔者提出通过拓扑优化技术来设计高增益超材料覆层微带天线,并基于遗传算法的求解策略对优化问题进行求解,最后对创新构型的超材料覆层型微带天线进行性能分析和收敛性对比研究。
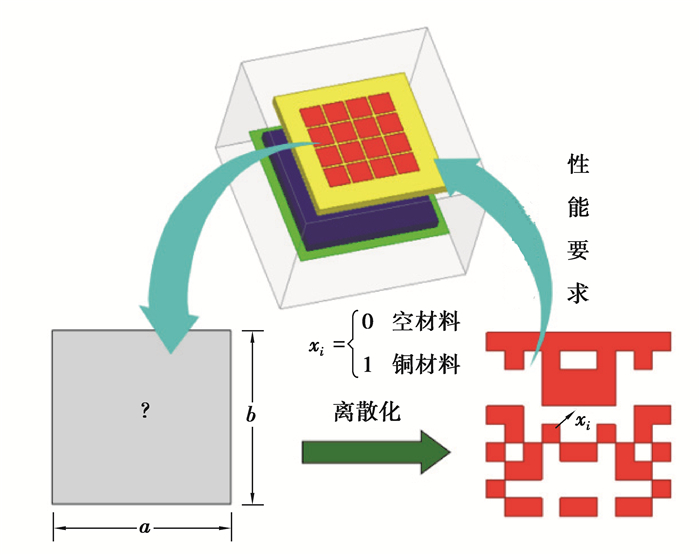
1 基于遗传算法的超材料覆层型微带天线的拓扑优化 1.1 目标函数的选取和设计变量的定义微带天线的增益是衡量天线性能的重要指标,是天线的重要设计参数之一,因此选择天线增益作为设计优化的目标函数。如图 1所示,超材料覆层型微带天线共设计16个超材料基元,每个超材料单元的尺寸规格为2.1 mm×2.1 mm,将其中每一个待设计基元离散化为一个个方格子,剩余15个超材料基元依次得到。离散后的每个方格铜贴片的存在与否取决于变量xi,设计变量采用0-1形式的二进制编码,即每个设计变量的取值为1或0,分别表示此处存在方格铜贴片或此处留空,全部方格贴片的变量xi构成了设计变量X。通过变量的0-1组合决定超材料基元微结构覆铜贴片位置的排布来获取特定性能需求的超材料覆层型微带天线。
|
图 1 超材料基元离散化示意图 Fig. 1 A schematic diagram of the metamaterial elements discretization |
分析已有的贴片型超材料基元如经典谐振环超材料、Π型超材料、树枝型超材料等结构,发现对称结构比较有利于超材料性能的发挥,同时对称的结构约束亦可以大幅降低拓扑优化设计的分析机时。对于n×n规模具有对称型微结构的超材料基元,需要满足:
| $ \left\{\begin{array}{l} x(i, n+1-j)=x(i, j), \\ \text { 其中 } i \leqslant n, j \leqslant n / 2, \end{array}\right. $ | (1) |
式中:x(i, j)为第i行第j列的方格贴片变量;i、j、n均为整数。
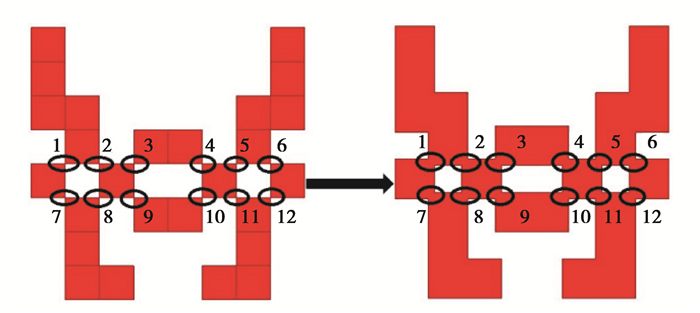
1.2 单点连接的处理方法拓扑优化设计时通常会碰到单点连接等问题[17],这类问题极不利于最终完成的设计构型样件制备,故拓扑优化中应尽量抑制单点连接的出现,可以参考消除棋盘格式的方法抑制优化结构出现单点连接,主要方法有:后处理方法、采用更稳定的有限元模型、改变目标函数的泛函、灵敏度过滤和采用拓扑描述函数等[17-21]。这里采用冗余设计消除优化中的单点连接现象[22],具体如图 2所示,不改变方格铜贴片的数量和位置,若某处需要布置方格贴片,则使用一个更大尺寸的方格贴片替换,如此以来,相邻贴片的堆叠性确保了方格贴片对角连接均为区域面接触,避免了单点接触。
|
图 2 冗余设计对单点连接的处理示意图 Fig. 2 A schematic diagram of the redundant design for point connection |
以车辆智能驾驶中常用的毫米波中短程雷达(其工作频率为24 GHz)为示例,通过优化超材料基元的拓扑结构布置来设计高增益超材料覆层型微带天线,优化问题的数学模型如下所示:
| $ \left\{\begin{array}{l} \text { find } X_{\text {cover }}=\left\{x_{1}, x_{2}, x_{3}, \cdots, x_{M}\right\} , \\ \min F(x)=-\operatorname{Gain}(f), \\ \text { s.t. } f=24 \mathrm{GHz}, \end{array}\right. $ | (2) |
式中:M为设计变量的个数,也代表覆铜贴片方格子的离散规模。由于离散规模通常较大,故优化设计的实施需要借助恰当的优化算法。拓扑优化问题中常用的算法有惩罚模型算法(SIMP)、遗传算法(GA)和水平集算法(LSM)等,考虑到电磁学领域的设计往往具有多峰性,且目标函数与设计变量间的关系比较复杂,故选择遗传算法作为本设计的求解策略。基于遗传算法的拓扑设计可以自适应地优化搜索进程,具备在尽可能获得全局最优解的同时兼具高效和强鲁棒性的优势,特别适用于天线等电磁优化设计问题[23-24]。
| $ \left\{ \begin{align} &选择算子函数:@ \text{ selectionstochu, } \\ & 交叉算子函数:@\text{ crossoverscattered, } \\ &交叉操作概率:@ \text{0}\text{.8, } \\ & 变异算子函数:@\text{ mutaxionuniform, } \\ & 变异操作因子:@\text{0}\text{.01}。\\ \end{align} \right. $ | (3) |
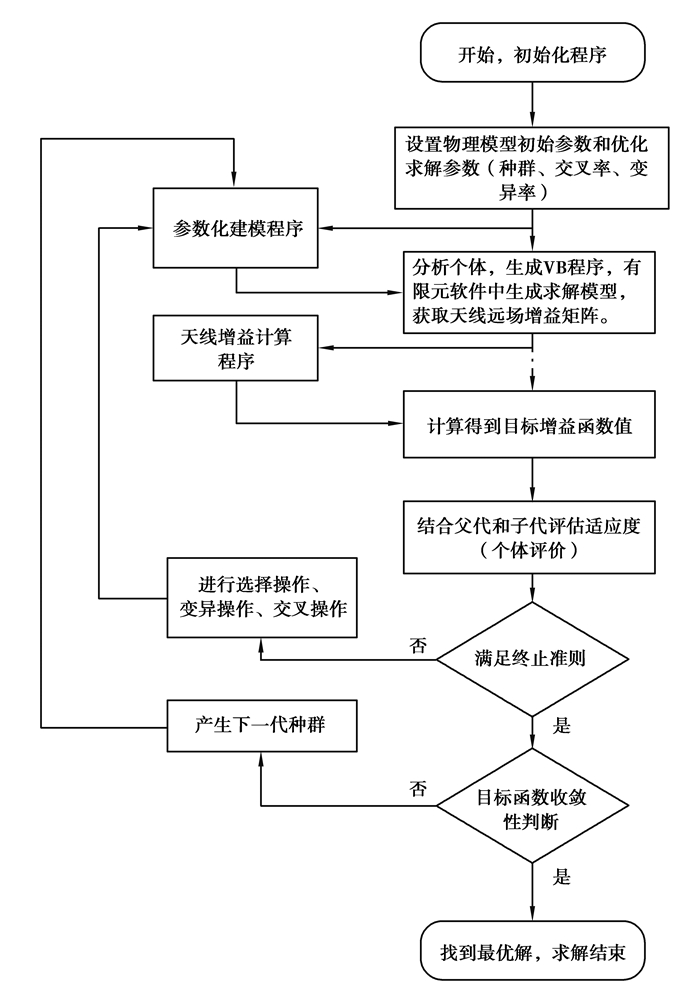
在具体的设计流程中,首先通过遗传算法随机设置一个初始种群,然后由MATLAB调用其内置函数代码对种群内的个体实施覆层型超材料微带天线3D建模,进而完成电磁仿真软件可以支持和识别的二次开发支持语言代码打包(如VB语言)等,然后基于有限元的电磁仿真软件读入打包好的参数化仿真代码,通过后续的建模分析计算获得相应的微带天线增益矩阵,最终得到目标函数值;得到目标函数后对个体进行适应度评价,如果不满足收敛性准则就对个体进行选择操作、变异操作和交叉操作,反之对目标函数进行收敛性判断,若不满足收敛条件则通过遗传算法产生下一代,直至目标函数收敛,求解结束,该优化求解流程具体如图 3所示。
|
图 3 优化设计的求解流程图 Fig. 3 A flow chart of the optimization design |
与遗传算法有关的一些相关参数如种群规模、最大遗传代数、收敛性容差等取值分别为100,50,0.01;对于选择、交叉和变异等遗传算子的操作取值如式(3)所示。
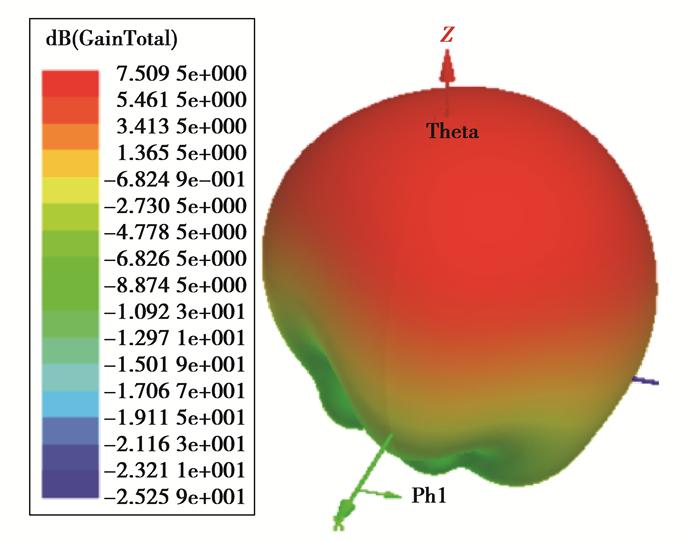
2 24 GHz高增益超材料覆层型微带天线的拓扑优化设计算例 2.1 创新构型超材料覆层型微带天线设计和结果分析这里以车用毫米波雷达的24 GHz(K波段)为例进行超材料覆层型微带天线的拓扑优化设计,天线尺寸参数如下:微带基板尺寸为14 mm×14 mm×1 mm,材料为介电常数为2.2的聚乙烯;天线采用50 Ω标准同轴线馈电,其金属辐射贴片尺寸为4.903 mm×3.471 mm,建模得到24 GHz普通微带天线的仿真模型并进行有限元计算,普通微带天线的三维远场辐射增益方向图如图 4所示,可知其最大增益为7.51 dB,接下来将通过对普通微带天线加载超材料覆层并借助拓扑优化技术设计超材料覆层的超材料基元构型来提升微带天线的增益。
|
图 4 普通微带天线三维远场辐射增益方向图 Fig. 4 The 3D far field gain and radiation pattern of common antenna |
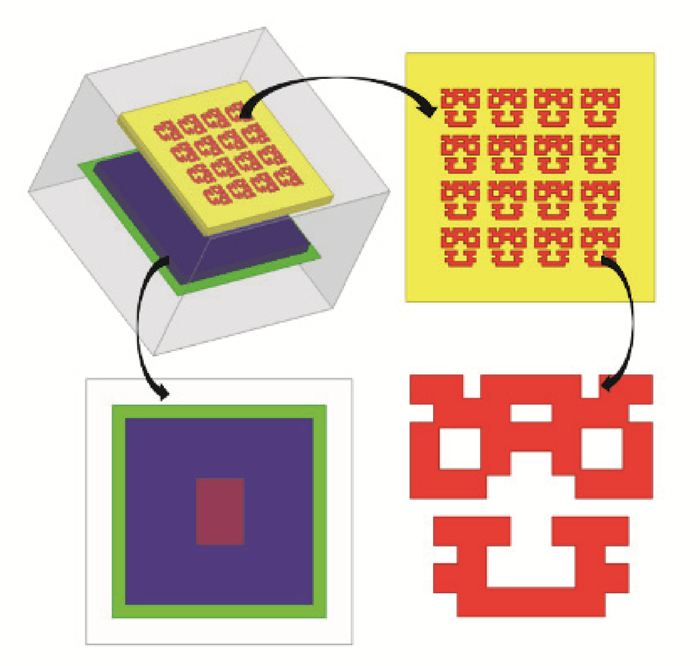
超材料覆层的基板采用环氧树脂FR4(4.4/0.02),并放置于普通微带天线(辐射基元)上方6.25 mm(半波长)处,尺寸为14 mm×14 mm×1 mm,超材料覆层均匀布置16个贴片型超材料基元,每个超材料基元尺寸为2.1 mm×2.1 mm,基元间隔为2.617 mm,覆铜厚度为0.017 mm,每个超材料基元被离散化为10×10的方形格子来进行微结构拓扑设计,每个方格子的冗余设计量均为0.05 mm,即单个方格子铜贴片的尺寸为0.26 mm×0.26 mm×0.17 mm,最终基于遗传算法迭代500次后求解收敛并结束,得到的超材料覆层型微带天线的创新构型,如图 5所示。
|
图 5 超材料覆层型微带天线设计示意图 Fig. 5 A schematic diagram of the metamaterial-clad microstrip antenna design |
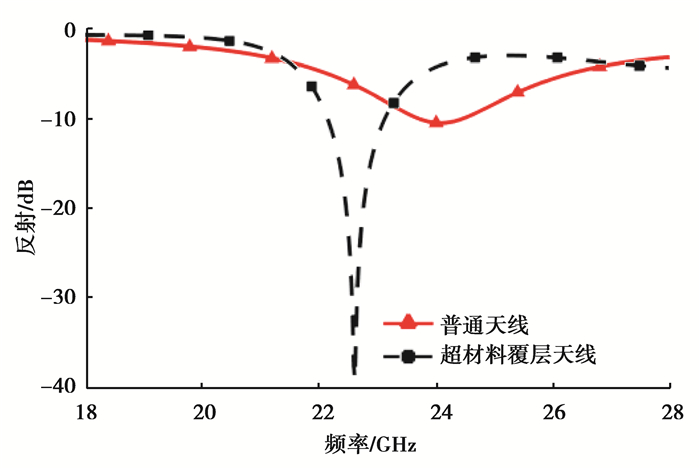
利用电磁仿真有限元软件对比分析了普通微带天线和超材料覆层型微带天线的回波损耗,如图 6所示,可以看出:普通微带天线谐振频率为24 GHz, 回波损耗峰值-10.8 dB,超材料覆层型微带天线谐振频率为22.6 GHz,回波损耗峰值为-39.3 dB。由此可知,加载超材料覆层后微带天线比较接近目标约束中的24 GHz,且与普通微带天线相比,具有更好的天线性能匹配。
|
图 6 天线回波损耗特性图对比 Fig. 6 Comparison of the antenna return loss characteristics |
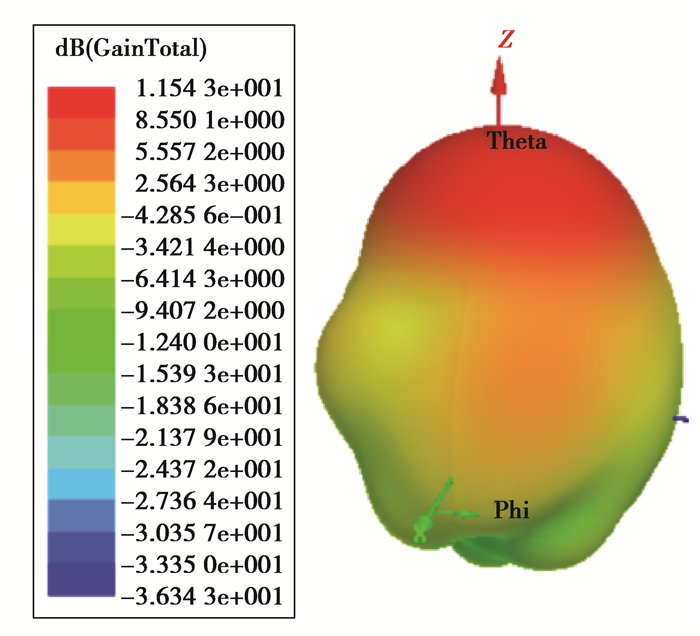
借助有限元重分析,获得了超材料覆层型微带天线在24 GHz的三维远场辐射增益方向图,如图 7所示。从图中可以看出,超材料覆层型微带天线较普通微带天线的最大增益从7.51 dB提升到11.54 dB,提升了53.66%。
|
图 7 创新构型天线的三维远场辐射增益方向图 Fig. 7 The 3D far field gain and radiation pattern of the innovative configuration antenna |
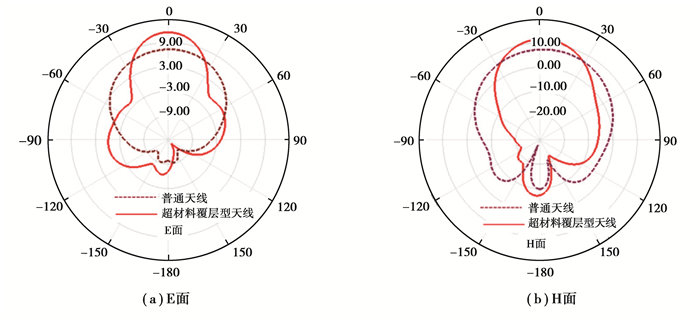
进一步分析,获得了优化前后天线E面和H面的二维远场辐射增益方向图对比,如图 8所示。从对比图中可以看出,与普通微带天线不同的是,创新构型微带天线的E面和H面二维远场辐射的主瓣辐射出现比较明显的增强,天线的增益和方向性均有很大改善;数据处理表明优化后E面方向图的半功率波束宽度从89°收缩到44°,收缩了45°,H面方向图的半功率波束宽度从94°收缩到49°,收缩了45°,侧向辐射得到了有效抑制。
|
图 8 天线E面和H面二维远场辐射增益方向图对比 Fig. 8 Comparison of 2D far field gain and radiation patterns of antenna E-plane and H-plane |
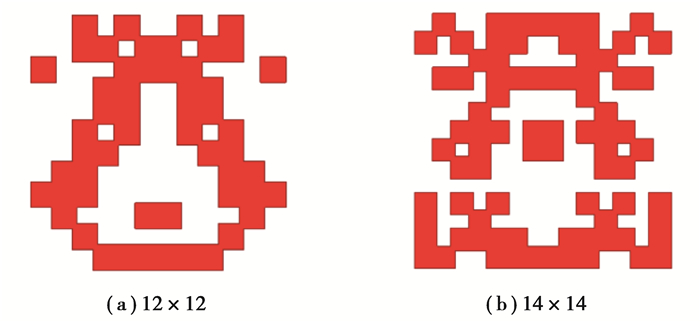
一般地,拓扑优化过程中变量的规模会直接影响计算耗时和最终的设计结果,通常优化变量的数目愈多,目标函数愈佳,但相应的计算耗时也愈长。因此,需要适当调增优化设计变量的规模(由10×10调整到12×12和14×14,即实际的设计变量数目从50调增到72和98),进而对比分析不同格子规模下微带天线的增益性能,相应的创新结构如图 9所示。
|
图 9 不同格子规模下超材料基元的创新构型 Fig. 9 Innovative configurations of metamaterial elements on different lattice sizes |
对应的仿真计算数据表明,12×12和14×14等2种不同设计变量下新型微带天线的最大增益值分别为11.60 dB和11.64 dB,由此可见,随着格子规模的增大,天线的最大增益值的确有所提升,但提升幅度很有限,且付出的计算时间成本随着格子规模的增大大幅度提高,同时亦表明3种不同格子规模下得到的创新结构的优化设计结果是收敛的。综合考量制造当中的工艺要求和计算时间成本等因素,10×10规模下的创新构型结果更优。
3 结论提出了一种超材料覆层型微带天线拓扑优化设计的系统方法,以24 GHz(K波段)高增益超材料覆层型微带天线设计为例,采用冗余设计的设计理念,基于遗传算法的求解策略对超材料覆层上阵列蚀刻的超材料基元拓扑实施了离散化的二进制编码变量设计,继而求解得到了3种不同变量规模下的创新构型优化结果,对比分析的数据表明,与普通微带天线相比较,创新构型的天线增益性能得以大幅增强,E面和H面半功率波束宽度明显收缩,侧向辐射得以有效抑制;且得到的创新构型完全消除了单点连接现象,制备性得到很好地改善,具有更佳的应用前景。
| [1] |
Liu Y H, Zhao X P. Investigation of anisotropic negative permeability medium cover for patch antenna[J]. IET Microwaves, Antennas & Propagation, 2008, 2(7): 737-744. |
| [2] |
韩庆文, 邓松, 王韬. 单点背馈圆极化微带天线的设计与实现[J]. 重庆大学学报, 2008, 31(1): 48-51. HAN Qingwen, DENG Song, WANG Tao. Design and realization of single back-feed circular polarization micro-strip antenna[J]. Journal of Chongqing University, 2008, 31(1): 48-51. (in Chinese) |
| [3] |
兰俊祥, 曹祥玉, 高军, 等. 一种新型的低散射微带天线阵设计[J]. 物理学报, 2019, 68(3): 154-163. LAN Junxiang, CAO Xiangyu, GAO Jun, et al. Novel design of microstrip antenna array with low scattering performance[J]. Acta Physica Sinica, 2019, 68(3): 154-163. (in Chinese) |
| [4] |
Garcia-Vigueras M, Gomez-Tornero J L, Goussetis G, et al. Efficient synthesis of 1-D Fabry-Perot antennas with low sidelobe levels[J]. IEEE Antennas and Wireless Propagation Letters, 2012, 11: 869-872. DOI:10.1109/LAWP.2012.2210182 |
| [5] |
Xu H X, Wang G M, Cai T, et al. Miniaturization of 3-D anistropic zero-refractive-index metamaterials with application to directive emissions[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(6): 3141-3149. DOI:10.1109/TAP.2014.2314475 |
| [6] |
Pendry J B, Holden A J, Stewart W J, et al. Extremely low frequency plasmons in metallic meso structures[J]. Physical Review Letters, 1996, 76: 4773-4776. DOI:10.1103/PhysRevLett.76.4773 |
| [7] |
Pendry J B, Holden A J, Robbins D J, et al. Magnetism from conductors and enhanced nonlinear phenomena[J]. IEEE Transactions on Microwave Theory and Techniques, 1999, 47(11): 2075-2084. DOI:10.1109/22.798002 |
| [8] |
Shelby R A, Smith D R, Schultz S. Experimental verification of a negative index of refraction[J]. Science, 2001, 292(5514): 77-79. DOI:10.1126/science.1058847 |
| [9] |
保石, 罗春荣, 赵晓鹏. S波段超材料完全吸收基板微带天线[J]. 物理学报, 2011, 60(1): 206-211. BAO Shi, LUO Chunrong, ZHAO Xiaopeng. S-wave band microstrip antenna with perfect absorbing metamaterial substrate[J]. Aata Physica Sinica, 2011, 60(1): 206-211. (in Chinese) |
| [10] |
刘敏, 张斌珍, 段俊萍. 一种基于超材料的宽频带定向性微带天线[J]. 机械工程学报, 2018, 54(9): 64-68. LIU Min, ZHANG Binzheng, DUAN Junping. Broadband and directional microstrip antenna based on metamaterials[J]. Journal of Mechanical Engineering, 2018, 54(9): 64-68. (in Chinese) |
| [11] |
刘涛, 曹祥玉, 高军, 等. 基于超材料的宽带高增益低雷达散射截面天线[J]. 电波科学学报, 2012, 27(3): 526-531. LIU Tao, CAO Xiangyu, GAO Jun, et al. Broadband high gain and low RCS metamaterial patch antenna[J]. Chinese Journal of Radio Science, 2012, 27(3): 526-531. (in Chinese) |
| [12] |
董焱章, 刘书田. 考虑超材料胞元间电磁耦合影响的五层模型[J]. 计算力学学报, 2017, 34(3): 297-302. DONG Yanzhang, LIU Shutian. Five-layer model considering the electromagnetic coupling effects of metamaterial unit cells[J]. Chinese Journal of Computational Mechanics, 2017, 34(3): 297-302. (in Chinese) |
| [13] |
赵晓鹏, 刘亚红. 微波超材料与超材料中波的行为[M]. 北京: 科学出版社, 2016: 423-464. ZHAO Xiaopeng, LIU Yahong. Microwave metamaterials and wave behavior in metamaterials[M]. Beijing: Science Press, 2016: 423-464. (in Chinese) |
| [14] |
张晨, 曹祥玉, 高军, 等. 一种基于共享孔径Fabry-Perot谐振腔结构的宽带高增益磁电偶极子微带天线[J]. 物理学报, 2016(13): 138-146. ZHANG Chen, CAO Xiangyu, GAO Jun, et al. Design of a broadband and high-gain shared-aperture Fabry-Perot resonator magneto-electric microstrip antenna[J]. Acta Physica Sinica, 2016(13): 138-146. (in Chinese) |
| [15] |
Dong Y, Liu S. Topology optimization of patch-typed left-handed metamaterial configurations for transmission performance within the radio frequency band based on the genetic algorithm[J]. Journal of Optics, 2012, 14(10): 105101. DOI:10.1088/2040-8978/14/10/105101 |
| [16] |
Shi P, Gao R, Liu S. Topology optimization based on methods and the realization programs for designing microstructures of patched metamaterials with prescribed electromagnetic properties[J]. Electronic Materials Letters, 2016, 12(5): 660-672. DOI:10.1007/s13391-016-6072-7 |
| [17] |
Jog C S, Haber R B. Stability of finite element models for distributed-parameter optimization and topology design[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 130(3/4): 203-226. |
| [18] |
Olhoff N, Bendsøe M P, Rasmussen J. On CAD-integrated structural topology and design optimization[J]. Computer Methods in Applied Mechanics and Engineering, 1991, 89: 259-279. DOI:10.1016/0045-7825(91)90044-7 |
| [19] |
Bendsoe M P, Díaz A R, Lipton R, et al. Optimal design of material properties and material distribution for multiple loading conditions[J]. International Journal for Numerical Methods in Engineering, 1995, 38(7): 1149-1170. DOI:10.1002/nme.1620380705 |
| [20] |
Sigmund O, Petersson J. Numerical instabilities in topology optimization:a survey on procedures dealing with checkerboards, mesh-dependencies and local minima[J]. Structural and Multidisciplinary Optimization, 1998, 16(1): 68-75. |
| [21] |
郭旭, 赵康. 基于拓扑描述函数的连续体结构拓扑优化方法[J]. 力学学报, 2004, 36(5): 520-526. GUO Xu, ZHAO Kang. A new topology description function based approach for stuctural topology optimization[J]. Chinese Journal of Theoretical and Applied Mechanics, 2004, 36(5): 520-526. (in Chinese) DOI:10.3321/j.issn:0459-1879.2004.05.002 |
| [22] |
史鹏飞.特定性能电磁超材料微结构及其功能器件优化设计[D].大连: 大连理工大学, 2017. SHI Pengfei. Optimization design of microctructure of electromagnetic matarials with prescribed properties and optimization of metamaterial-based functions devices[D]. Dalian: Dalian University of Technology, 2017. (in Chinese) |
| [23] |
Jafari M, Moussavian H, Chaleshtari M H B. Optimum design of perforated orthotropic and laminated composite plates under in-plane loading by genetic algorithm[J]. Structural and Multidisciplinary Optimization, 2018, 57(1): 341-357. |
| [24] |
Zandavi S M, Pourtakdoust S H. Multidisciplinary design of a guided flying vehicle using simplex nondominated sorting genetic algorithm Ⅱ[J]. Structural and Multidisciplinary Optimization, 2018, 57(2): 705-720. DOI:10.1007/s00158-017-1776-3 |
 2020, Vol. 43
2020, Vol. 43

