2. 南京理工大学 理学院, 南京 210094
2. School of Science, Nanjing University of Science and Technology, Nanjing 210094, P. R. China
随着科学技术的飞速发展,传统材料耐热性和强度等方面的劣势越来越明显,尤其是一些尖端科技,例如航天工程领域,医学领域,生物科学领域等。为了满足实际工程的需要,亟需能满足复杂工况下的新型复合材料[1]。功能梯度材料可将不同材料的优点集于一身,一经提出便引起各国学者的高度关注。它一般由金属和陶瓷按不同组分复合而成,既有金属材料强度高的特性,又有陶瓷材料耐热性好的特性,具备了传统材料不具备的优点,在航空航天领域特别是直升机旋翼、空间机械臂和太阳能帆板等复杂工况下的结构用材具有广阔的应用前景。
诸多学者们已经将假设模态法[2]、有限元法[3]、无网格法[4]、Bezier插值法[5]等运用到作大范围运动柔性体变形的离散问题中,取得了诸多的成果。吴胜宝[2]采用假设模态法进行离散均质柔性梁,建立了柔性梁作大范围运动的零次模型和一次模型,总结出零次模型和一次模型在不同转速下计算结果上的差异。张弛等[6]利用假设模态法进行离散均质楔形梁, 总结出在相同条件下梁的形状与端部有无质点对柔性梁的动力学响应产生十分明显的影响。文献[7-8]将该方法运用到离散功能梯度材料梁[9-11]中去,得到了梯度的分布规律和功能梯度指数对系统的动力学特征都会产生不同的影响。文献[12-14]使用假设模态法、有限元法、无网格法等对作定轴旋转运动的均质柔性梁进行离散,对比不同方法下的计算结果,假设模态法在计算低速旋转小变形问题的结果十分精确,在计算高速旋转大变形问题的结果不够精确,在实际工程中不适合使用。在各种情况下有限元法和无网格法的计算结果令人满意。文献[3, 12, 15]采用有限元法和Hamilton变分原理推导出刚柔耦合的一次近似模型,说明了有限元法的一次模型较零次模型的优越性。杜超凡等[16-17]利用无网格法对柔性梁进行离散,将得到的结果与假设模态法和有限元法的结果进行对比,得出有限元法、无网格法计算结果精确度更高的结论。He等[18]对作定轴旋转运动梁的固有频率进行研究,得出了不同模型固有频率的差异。
当今学者大都是对作大范围运动的均质梁进行仿真,对功能梯度梁的动力学仿真采用的是精度较低、适用范围较小的假设模态法。笔者采用有限元法描述功能梯度材料梁的变形,考虑梁的横向变形和轴向变形,以及由横向弯曲变形引起的耦合变形量,并在此基础上建立功能梯度材料梁的刚柔耦合动力学方程。采用浮动坐标系描述系统运动,运用第二类Lagrange方程推导系统动力学方程,并编制旋转功能梯度材料梁的仿真程序,将假设模态法的仿真计算结果与有限元法的仿真计算结果进行对比,表明本文方法的正确性和优越性。
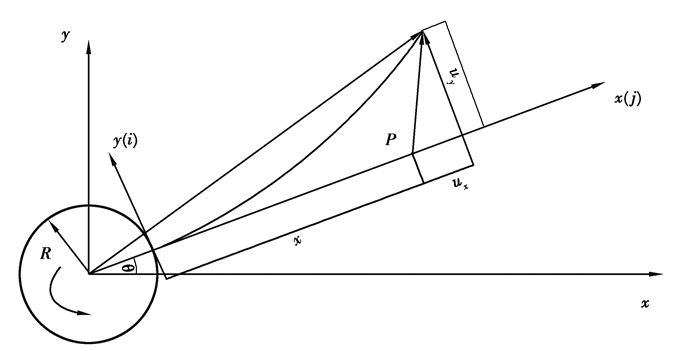
1 旋转功能梯度材料梁动力学模型 1.1 系统的物理模型图 1为水平面内作定轴旋转运动的中心刚体功能梯度材料梁系统,Oxyz为惯性坐标系,中心刚体的半径为a,外部输力矩为τ,绕z轴转动的转动惯量为Joh。功能梯度材料梁为等截面梁,功能梯度材料的物理参数为:梁的长度为L,宽度为b,厚度为h。在梁上建立浮动坐标系Oxy,梁上任意一点P的变形如图 1所示。不同于传统均质梁, 功能梯度材料梁的物理特性沿厚度方向按一定幂规律梯度分布,本文中假设梁的弹性模量E(y)和密度ρ(y)为坐标y的函数[8]。
|
图 1 功能梯度梁的变形 Fig. 1 Deformation of the FGM beam |
在惯性坐标系Oxy中,功能梯度材料梁上任意一点P变形后的矢径为
| $ {\mathit{\boldsymbol{r}} = \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}(\mathit{\boldsymbol{R}} + {\mathit{\boldsymbol{\rho }}_0} + \mathit{\boldsymbol{u}}),} $ | (1) |
式中:
| $ {\mathit{\boldsymbol{R}} = {{(a,0)}^{\rm{T}}},} $ | (2) |
| $ {{\mathit{\boldsymbol{\rho }}_0} = {{(x,y)}^{\rm{T}}},} $ | (3) |
| $ {\mathit{\boldsymbol{u}} = {{({u_x},{u_y})}^{\rm{T}}},} $ | (4) |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }} = \left( {\begin{array}{*{20}{c}} {{\rm{cos}}\theta }&{ - {\rm{sin}}\theta }\\ {{\rm{sin}}\theta }&{{\rm{cos}}\theta } \end{array}} \right)。} $ | (5) |
其中,Θ为浮动基相对于惯性坐标系的法向余弦矩阵,变形矢量u在浮动坐标系下可表示为:
| $ {{u_x}(x,y,t) = {w_1} + {w_{\rm{c}}},} $ | (6) |
| $ {{u_y}(x,t) = {w_2}}。$ | (7) |
式中:w1为柔性梁的轴向变形量,w2为柔性梁横向弯曲的挠度,wc为柔性梁横向弯曲引起的纵向变形缩短量,即非线性耦合变形量,表达式为:
| $ {w_{\rm{c}}}(x,t) = - \frac{1}{2}\int_0^x {{\kern 1pt} {\kern 1pt} {{\left( {\frac{{\partial {w_2}}}{{\partial \xi }}} \right)}^2}} {\rm{d}}\xi 。$ | (8) |
对等式(1)关于时间t求一阶导数得到柔性梁任意点P在惯性坐标系下的速度,表达式为:
| $ \mathit{\boldsymbol{\dot r}} = \mathit{\boldsymbol{ \boldsymbol{\dot \varTheta} }}(\mathit{\boldsymbol{R}} + {\mathit{\boldsymbol{\rho }}_0} + \mathit{\boldsymbol{u}}) + \mathit{\boldsymbol{ \boldsymbol{\varTheta} \dot u}}。$ | (9) |
因此系统的总动能可以表示为:
| $ T = \frac{1}{2}\int_V \rho (y){\mathit{\boldsymbol{\dot r}}^{\rm{T}}}\mathit{\boldsymbol{\dot r}}{\rm{d}}V + \frac{1}{2}{J_{{\rm{oh}}}}{\dot \theta ^2}。$ | (10) |
根据连续介质力学可以推导出柔性梁任意点P处的纵向正应变ε11,表达式为:
| $ {\varepsilon _{11}} = \frac{{\partial {w_1}}}{{\partial x}} - y\frac{{{\partial ^2}{w_2}}}{{\partial {x^2}}}。$ | (11) |
忽略梁的剪切和扭转效应,变形势能U可以表示为:
| $ U = \frac{1}{2}\int_V E (y)\varepsilon _{11}^2{\rm{d}}V。$ | (12) |
如图 2所示,采用有限单元法对作定轴旋转运动的功能梯度材料梁进行离散,将功能梯度材料梁分成N个等长的梁元,在第j个梁元内,取轴向和横向变形的位移函数对梁进行描述。
| $ \left\{ {\begin{array}{*{20}{l}} {{w_1}(\bar x,t) = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{xj}}(\bar x){\mathit{\boldsymbol{A}}_j}(t),}\\ {{w_2}(\bar x,t) = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{yj}}(\bar x){\mathit{\boldsymbol{B}}_j}(t),} \end{array}} \right. $ | (13) |

|
图 2 功能梯度梁有限元离散模型 Fig. 2 Finite element discrete model of the FGM beam |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{xj}}(\bar x) = [{\phi _{xj}}(\bar x),{\phi _{xj + 1}}(\bar x)],}\\ {{\mathit{\boldsymbol{A}}_j}(t) = {{[{u_{xj}},{u_{xj + 1}}]}^{\rm{T}}},} \end{array}} \right. $ | (14) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{yj}}(\bar x) = [{\phi _{yj}}(\bar x),{\phi _{\theta j}}(\bar x),{\phi _{yj + 1}}(\bar x),{\phi _{\theta j + 1}}(\bar x)],}\\ {{\mathit{\boldsymbol{B}}_j}(t) = {{[{u_{yj}},{u_{\theta j}},{u_{yj + 1}},{u_{{\theta _{j + 1}}}}]}^{\rm{T}}}}。\end{array}} \right. $ | (15) |
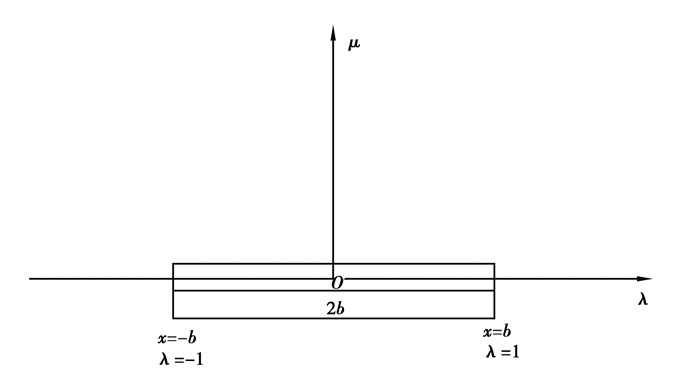
取第j个单元作为研究对象,建立梁单元自然坐标系λμ,如图 3所示,惯性系下的自然坐标系的表达式:
| $ \lambda = \frac{{\bar x}}{b}, $ | (16) |
|
图 3 梁单元的自然坐标系 Fig. 3 Natural coordinate system of the beam element |
式中
在自然坐标系下,梁单元形函数的具体表达式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\phi _{xj}}(\lambda ) = - \frac{1}{2}\lambda + \frac{1}{2},}\\ {{\phi _{xj + 1}}(\lambda ) = \frac{1}{2}\lambda + \frac{1}{2},} \end{array}} \right. $ | (17) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\phi _{yj}}(\lambda ) = \frac{1}{4}(2 - 3\lambda + {\lambda ^3}),}\\ {{\phi _{\theta j}}(\lambda ) = \frac{1}{4}b(1 - \lambda - {\lambda ^2} + {\lambda ^3}),}\\ {{\phi _{yj + 1}}(\lambda ) = \frac{1}{4}(2 + 3\lambda - {\lambda ^3}),}\\ {{\phi _{\theta j + 1}}(\lambda ) = \frac{1}{4}b( - 1 - \lambda + {\lambda ^2} + {\lambda ^3})}。\end{array}} \right. $ | (18) |
设
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{A}}_j} = \mathit{\boldsymbol{R}}_x^j\mathit{\boldsymbol{A}},}\\ {{\mathit{\boldsymbol{B}}_j} = \mathit{\boldsymbol{R}}_y^j\mathit{\boldsymbol{B}},} \end{array}} \right. $ | (19) |
其中,
| $ \mathit{\boldsymbol{R}}_x^j = \left[ {\begin{array}{*{20}{c}} 0&0& \cdots &1&0& \cdots &0\\ 0&0& \cdots &0&1& \cdots &0 \end{array}} \right], $ | (20) |
| $ \mathit{\boldsymbol{R}}_y^j = \left[ {\begin{array}{*{20}{c}} {{0_{2 \times 2}}}&{{0_{2 \times 2}}}&L&{{I_{2 \times 2}}}&{{0_{2 \times 2}}}&L&{{0_{2 \times 2}}}\\ {{0_{2 \times 2}}}&{{0_{2 \times 2}}}&L&{{0_{2 \times 2}}}&{{I_{2 \times 2}}}&L&{{0_{2 \times 2}}} \end{array}} \right]。$ | (21) |
因此,梁的轴向和横向变形位移函数可以改写为:
| $ \left\{ {\begin{array}{*{20}{l}} {{w_1}(x,t) = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_x}(x)\mathit{\boldsymbol{A}}(t),}\\ {{w_2}(x,t) = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_y}(x)\mathit{\boldsymbol{B}}(t),} \end{array}} \right. $ | (22) |
其中,
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_x}(x) = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{xj}}(\bar x)\mathit{\boldsymbol{R}}_x^j,}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_y}(x) = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{yj}}(\bar x)\mathit{\boldsymbol{R}}_y^j,} \end{array}} \right. $ | (23) |
则变形位移的二次耦合项为
| $ {w_{\rm{c}}} = - \frac{1}{2}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{B}}, $ | (24) |
式中H(x)为耦合形函数,若位于第j个单元内,则表达式为
| $ \mathit{\boldsymbol{H}}(x) = \frac{1}{b}{\kern 1pt} {\kern 1pt} \int_{ - 1}^\lambda {{\kern 1pt} {{(\mathit{\boldsymbol{R}}_y^j)}^{\rm{T}}}} \left( {\frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{yj}^{\rm{T}}(\lambda )}}{{\partial \lambda }}} \right)\left( {\frac{{\partial {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{yj}}(\lambda )}}{{\partial \lambda }}} \right)\mathit{\boldsymbol{R}}_y^j{\rm{d}}\lambda + \sum\limits_{p = 1}^{j - 1} {{\kern 1pt} \frac{1}{b}{\kern 1pt} } \int_{ - 1}^1 {{{(\mathit{\boldsymbol{R}}_y^p)}^{\rm{T}}}} \left( {\frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{yp}^{\rm{T}}(\lambda )}}{{\partial \lambda }}} \right)\left( {\frac{{\partial {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{yp}}(\lambda )}}{{\partial \lambda }}} \right)\mathit{\boldsymbol{R}}_y^b{\rm{d}}\lambda 。$ | (25) |
将功能梯度梁的轴向和横向位移函数代入系统的动能和变形势能表达式中,取广义坐标q=(θ, AT, BT)T,运用第二类Lagrange方程:
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial T}}{{\partial \mathit{\boldsymbol{\dot q}}}}} \right) - \frac{{\partial T}}{{\partial \mathit{\boldsymbol{q}}}} = - \frac{{\partial U}}{{\partial \mathit{\boldsymbol{q}}}} + \mathit{\boldsymbol{F,}} $ | (26) |
式中:F=(τ, 0, 0)T为广义力,τ为刚体上合外力关于刚体质心O的主矩。将式(10)和(12)代入式(26),经过复杂的推导可以得到动力学方程:
| $ \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{M}}_{11}}}&{{\mathit{\boldsymbol{M}}_{12}}}&{{\mathit{\boldsymbol{M}}_{13}}}\\ {{\mathit{\boldsymbol{M}}_{21}}}&{{\mathit{\boldsymbol{M}}_{22}}}&{{\mathit{\boldsymbol{M}}_{23}}}\\ {{\mathit{\boldsymbol{M}}_{31}}}&{{\mathit{\boldsymbol{M}}_{32}}}&{{\mathit{\boldsymbol{M}}_{33}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\ddot \theta }\\ {\mathit{\boldsymbol{\ddot A}}}\\ {\mathit{\boldsymbol{\ddot B}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{Q}}_\theta }}\\ {{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{A}}}}\\ {{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{B}}}} \end{array}} \right]。$ | (27) |
动力学方程(27)中的相关矩阵表达式如下:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{M}}_{11}} = {J_{{\rm{ oh }}}} + {J_{{\rm{ ob }}}} + 2{\mathit{\boldsymbol{S}}_x}\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_1}\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{B}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_2}\mathit{\boldsymbol{B}} - \underline {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{CB}}} - \\ \int_0^L \rho bh{\kern 1pt} \underline {{\kern 1pt} {\kern 1pt} [{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_x^{\rm{T}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{B}}]{\kern 1pt} } {\kern 1pt} {\kern 1pt} {\rm{d}}x + \frac{1}{4}\int_0^L \rho bh{\kern 1pt} {\kern 1pt} {\kern 1pt} \underline {[{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{B}} \cdot {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{B}}]} {\kern 1pt} {\rm{d}}x, \end{array} $ | (28) |
| $ {{\mathit{\boldsymbol{M}}_{22}} = {\mathit{\boldsymbol{M}}_1},} $ | (29) |
| $ {{\mathit{\boldsymbol{M}}_{33}} = {\mathit{\boldsymbol{M}}_2} + \int_0^L \rho bh{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \underline {[\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{H}}(x)]} {\kern 1pt} {\kern 1pt} {\rm{d}}x,} $ | (30) |
| $ {{\mathit{\boldsymbol{M}}_{21}} = \mathit{\boldsymbol{M}}_{12}^{\rm{T}} = - {\mathit{\boldsymbol{M}}_3}\mathit{\boldsymbol{B}},} $ | (31) |
| $ {\mathit{\boldsymbol{M}}_{31}} = \mathit{\boldsymbol{M}}_{13}^{\rm{T}} = \mathit{\boldsymbol{S}}_y^{\rm{T}} + \mathit{\boldsymbol{M}}_3^{\rm{T}}\mathit{\boldsymbol{A}} + \int_0^L \rho {\kern 1pt} {\kern 1pt} {\kern 1pt} \underline {bh{\kern 1pt} {\kern 1pt} {\kern 1pt} [\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_y}\mathit{\boldsymbol{B}}]} {\kern 1pt} {\kern 1pt} {\rm{d}}x - \frac{1}{2}\int_0^L \rho bh{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \underline {[\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_y^{\rm{T}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{B}}]} {\kern 1pt} {\kern 1pt} {\rm{d}}x, $ | (32) |
| $ {\mathit{\boldsymbol{M}}_{32}} = \mathit{\boldsymbol{M}}_{23}^{\rm{T}} = - \int_0^L \rho bh{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \underline {[\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_x}]{\kern 1pt} } {\kern 1pt} {\rm{d}}x, $ | (33) |
| $ \begin{array}{l} {\mathit{\boldsymbol{Q}}_\theta } = \tau - 2\dot \theta [{\mathit{\boldsymbol{S}}_x}\mathit{\boldsymbol{\dot A}} + {\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_1}\mathit{\boldsymbol{\dot A}} + {\mathit{\boldsymbol{B}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_2}\mathit{\boldsymbol{\dot B}} - {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{C\dot B}}] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_0^L \rho bh{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \underline {[\dot \theta (2{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_x^{\rm{T}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{H\dot B}} - {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{\dot B}}) - {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_y^{\rm{T}}{{\mathit{\boldsymbol{\dot B}}}^{\rm{T}}}\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{\dot B}}]} {\kern 1pt} {\kern 1pt} {\rm{d}}x + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \dot \theta \int_0^L \rho bh{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \underline {{{\mathit{\boldsymbol{\dot A}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_x^{\rm{T}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{HB}}} {\kern 1pt} {\kern 1pt} {\rm{d}}x, \end{array} $ | (34) |
| $ {\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{A}}} = {\dot \theta ^2}{\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{S}}_x^{\rm{T}} + 2\dot \theta {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{M}}_3}\mathit{\boldsymbol{\dot B}} + ({\dot \theta ^2}{\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{M}}_1} - {\mathit{\boldsymbol{K}}_1})\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{K}}_2}\mathit{\boldsymbol{B}} + \int_0^L \rho bh{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \underline {[\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_x^{\rm{T}}{{\mathit{\boldsymbol{\dot B}}}^{\rm{T}}}\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{\dot B}} - \frac{1}{2}{{\dot \theta }^2}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_x^{\rm{T}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{B}}]} {\kern 1pt} {\kern 1pt} {\rm{d}}x, $ | (35) |
| $ \begin{array}{l} {\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{B}}} = {{\dot \theta }^2}({\mathit{\boldsymbol{M}}_2} - \mathit{\boldsymbol{C}})\mathit{\boldsymbol{B}} - 2\dot \theta {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{M}}_3^{\rm{T}}\mathit{\boldsymbol{\dot A}} - {K_3}\mathit{\boldsymbol{B}} + K_2^{\rm{T}}\mathit{\boldsymbol{A}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_0^L \rho bh{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \underline {[2\dot \theta (\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_y}\mathit{\boldsymbol{\dot B}} - {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_y}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{\dot B}}) + \mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{B}}{\kern 1pt} {{\mathit{\boldsymbol{\dot B}}}^{\rm{T}}}\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{\dot B}}]} {\kern 1pt} {\kern 1pt} {\rm{d}}x + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\dot \theta }^2}\int_0^L \rho bh{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \underline {[\frac{1}{2}\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{B}}{\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{B}} - \mathit{\boldsymbol{H}}(x)\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_x}\mathit{\boldsymbol{A}}]{\kern 1pt} } {\kern 1pt} {\rm{d}}x 。\end{array} $ | (36) |
动力学方程(28)~(36)中相关矩阵系数表达式如下:
| $ {{\mathit{\boldsymbol{S}}_x} = \int_0^L \rho bh{\kern 1pt} {\kern 1pt} (R + x){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_x}(x){\rm{d}}x,} $ | (37) |
| $ {{\mathit{\boldsymbol{S}}_y} = \int_0^L \rho bh{\kern 1pt} {\kern 1pt} (a + x){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_y}(x){\rm{d}}x,} $ | (38) |
| $ {{\mathit{\boldsymbol{M}}_1} = \int_0^L \rho bh\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_x^T(x){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_x}(x){\rm{d}}x,} $ | (39) |
| $ {{\mathit{\boldsymbol{M}}_2} = \int_0^L \rho bh\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_y^T(x){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_y}(x){\rm{d}}x,} $ | (40) |
| $ {{\mathit{\boldsymbol{M}}_3} = \int_0^L \rho bh\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_x^T(x){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_y}(x){\rm{d}}x,} $ | (41) |
| $ {\mathit{\boldsymbol{C}} = \int_0^L \rho bh{\kern 1pt} {\kern 1pt} (R + x)H(x){\kern 1pt} {\rm{d}}x,} $ | (42) |
| $ {{\mathit{\boldsymbol{K}}_1} = \int_0^L {{E_1}} b\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_x^{\prime {\rm{T}}}(x)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_x^\prime (x){\kern 1pt} {\rm{d}}x,} $ | (43) |
| $ {{\mathit{\boldsymbol{K}}_2} = \int_0^L {{E_2}} b\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_x^{\prime {\rm{T}}}(x)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_y^{\prime \prime }(x){\kern 1pt} {\rm{d}}x,} $ | (44) |
| $ {{\mathit{\boldsymbol{K}}_3} = \int_0^L {{E_3}} b\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_y^{\prime \prime {\rm{T}}}(x)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_y^{\prime \prime }(x){\kern 1pt} {\rm{d}}x,} $ | (45) |
| $ {\rho = \int_{ - \frac{h}{2}}^{\frac{h}{2}} \rho (y){\rm{d}}y,} $ | (46) |
| $ {{E_1} = \int_{ - \frac{h}{2}}^{\frac{h}{2}} E (y){\rm{d}}y,} $ | (47) |
| $ {{E_2} = \int_{ - \frac{h}{2}}^{\frac{h}{2}} E (y)y{\kern 1pt} {\kern 1pt} {\rm{d}}y,} $ | (48) |
| $ {{E_3} = \int_{ - \frac{h}{2}}^{\frac{h}{2}} E (y){y^2}{\kern 1pt} {\kern 1pt} {\rm{d}}y,} $ | (49) |
式中,M1、M2、M3为弹性质量阵,K1、K2、K3为弹性刚度阵,C为一次耦合项。
本文中所研究的功能梯度材料由陶瓷和金属材料构成,材料的梯度分布为:
| $ \left. {\begin{array}{*{20}{l}} {E(y) = ({E_{\rm{h}}} - {E_{\rm{t}}}){{\left( {\frac{{2y + h}}{{2h}}} \right)}^N} + {E_{\rm{t}}}}\\ {\rho (y) = ({\rho _{\rm{h}}} - {\rho _{\rm{t}}}){{\left( {\frac{{2y + h}}{{2h}}} \right)}^N} + {\rho _{\rm{t}}}} \end{array}} \right\}, $ | (50) |
式中下标h和t分别代表陶瓷材料和金属材料。
将(50)式代入(46)~(49)式中,对密度、弹性模量的表达式进行改写,得到:
| $ {\rho = \frac{{{\rho _{\rm{h}}} + N{\rho _{\rm{t}}}}}{{N + 1}},} $ | (51) |
| $ {{E_1} = \frac{{({E_{\rm{h}}} - {E_{\rm{t}}})h}}{{N + 1}} + {E_{\rm{t}}}h,} $ | (52) |
| $ {{E_2} = \frac{{({E_{\rm{h}}} - {E_{\rm{t}}})N{h^2}}}{{2(N + 1)(N + 2)}},} $ | (53) |
| $ {{E_3} = \frac{{({N^2} + N + 2)({E_{\rm{h}}} - {E_{\rm{t}}}){h^3}}}{{4(N + 1)(N + 2)(N + 3)}} + \frac{{{E_{\rm{t}}}{h^3}}}{{12}}}。$ | (54) |
式(29)~(46)为功能梯度材料梁作大范围运动的一次模型,去掉下划线部分就得到了旋转功能梯度材料梁做大范围运动的一次近似模型。
2 动力学仿真 2.1 大范围运动规律已知的系统动力学特征式(50)的物理参数为:Eh=1.51×1011 Pa,Et=7×1010Pa,ρh=3×103 kg/m3,ρt=2.707×103 kg/m3,N为功能梯度指数,l=5 m, b=2×10-2 m, h=2×10-2m。与文献[8]中的物理参数一致。在本文中主要针对一次模型下不同的离散方法进行仿真计算。
采用假设模态法和有限元法描述柔性梁的变形场,其中假设模态法模态阶数取4,有限元法将功能梯度材料梁离散成10个单元。假定功能梯度材料梁作大范围运动的规律已知,角速度的变化规律为:
| $ \dot \theta = \left\{ {\begin{array}{*{20}{c}} {\frac{{{\Omega _1}}}{T}t - \frac{{{\Omega _1}}}{{2\pi }}{\rm{sin}}(\frac{{2\pi }}{t})}&{0 \le t \le T,}\\ {{\Omega _1}}&{t > T,} \end{array}} \right. $ | (55) |
式中T=15 s,在15 s后功能梯度材料梁以匀速Ω1旋转。Ω1分别取4,10,20 rad/s研究在功能梯度指数N=2的功能梯度材料梁在不同离散方法下的动力学特征。然后研究在转速Ω1=4 rad/s时,在不同离散方法下功能梯度指数分别取N=0,0.5,1,2,5下的动力学特征。
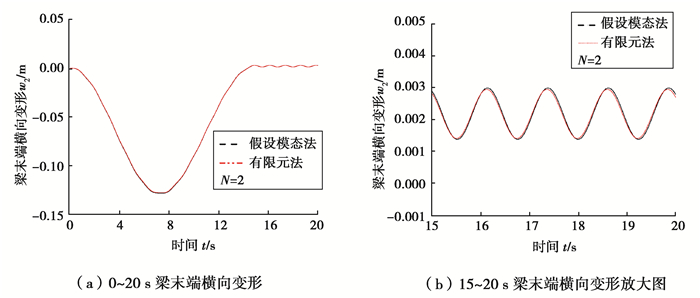
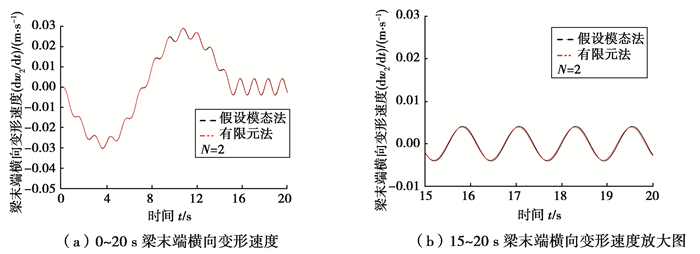
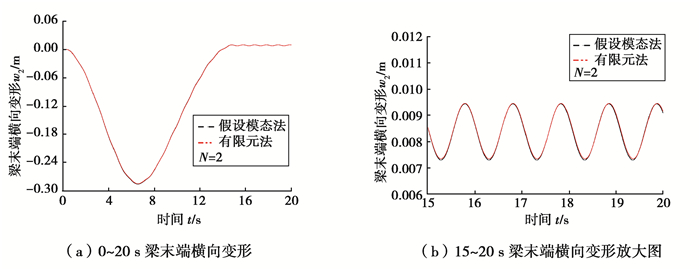
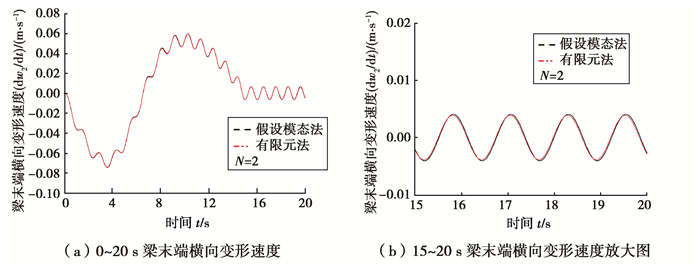
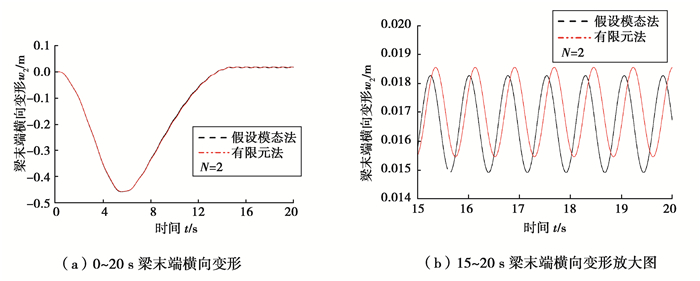
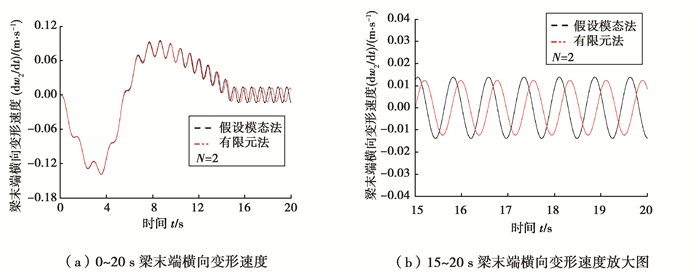
图 4~9表示在功能梯度指数N=2,Ω1分别取4,10,20 rad/s时,柔性梁末端横向变形位移和横向变形速度。从图中可以看出,在转速较低时,假设模态法和有限元法的仿真结果基本一致,说明本文有限元法所建模型的正确性。随着转速的增大,假设模态法与有限元法的偏差越来越大。这是因为假设模态法基于小变形假设,随着转速的增大变形也越来越大,假设模态法的误差也必然越来越大。从各图中的横向变形位移放大图中可以看出,振动平衡位置并不在梁轴线上,而是发生了偏移,并且转速越大偏移越明显。这是因为在N>0时,金属材料与陶瓷材料并不是均匀对称分布于梁轴线两侧,在计算变形能时产生了轴向与横向的耦合势能。
|
图 4 梯度梁末端横向变形(Ω1=4 rad/s) Fig. 4 Tip transverse deformation of the FGM beam |
|
图 5 梯度梁末端横向变形速度(Ω1=4 rad/s) Fig. 5 Tip transverse velocity of the FGM beam |
|
图 6 梯度梁末端横向变形(Ω1=10 rad/s) Fig. 6 Tip transverse deformation of the FGM beam |
|
图 7 梯度梁末端横向变形速度(Ω1=10 rad/s) Fig. 7 Tip transverse velocity of the FGM beam |
|
图 8 梯度梁末端横向变形(Ω1=20 rad/s) Fig. 8 Tip transverse deformation of the FGM beam |
|
图 9 梯度梁末端横向变形速度(Ω1=20 rad/s) Fig. 9 Tip transverse velocity of the FGM beam |
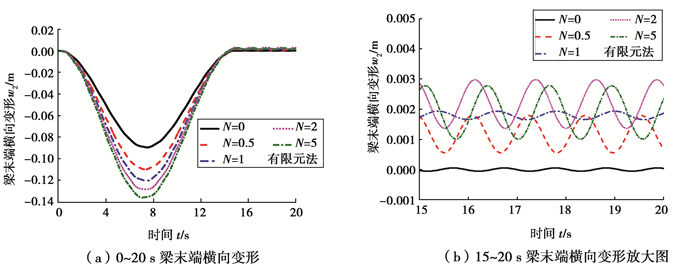
图 10为Ω1=4 rad/s,柔性梁末端横向变形随功能梯度指数N变化的情况。可明显看出在大范围运动加速展开的过程中,梁末端最大横向变形随着功能梯度指数N的增大而增大。在横向变形位移放大图中可知,当N=0时,材料退化为均质材料,振动平衡位置在梁轴线上,当N>0时,振动平衡位置发生了偏移。
|
图 10 梯度梁末端横向变形(Ω1=4 rad/s) Fig. 10 Tip transverse deformation of the FGM beam |
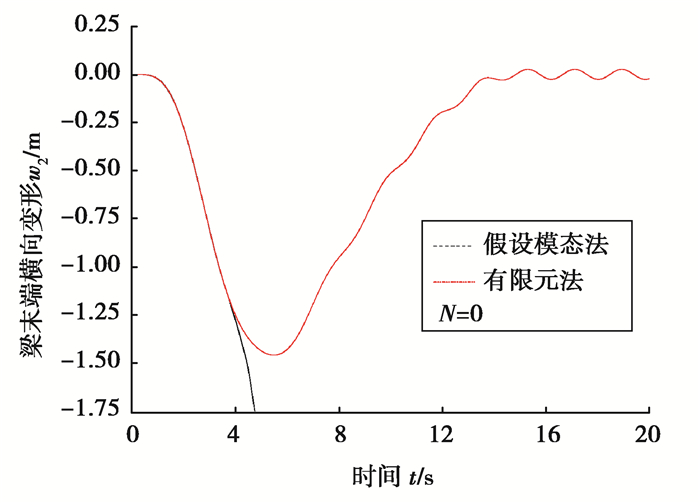
图 11表示Ω1 =10 rad/s、N=0时,将Eh缩小10倍后梁末端的横向弯曲变形。如图所示,梁的最大变形超过了1.2 m,属于大变形情况,有限元法的结果收敛而假设模态法的结果发散。进一步说明源于结构力学中固有振型的假设模态法只适用于小变形问题,并不能处理大变形问题。
|
图 11 梯度梁末端横向变形(Ω1=10 rad/s) Fig. 11 Tip transverse deformation of the FGM beam |
对作大范围运动的功能梯度梁系统的横向弯曲固有频率进行分析,不考虑横向弯曲造成的微小纵向变形, 舍去与耦合变量相关的一些高阶小量,假定大范围转动为匀速即当
| $ {\mathit{\boldsymbol{M}}_2}\mathit{\boldsymbol{\ddot B}} + [{\dot \theta ^2}(\mathit{\boldsymbol{C}} - {\mathit{\boldsymbol{M}}_2}) + {\mathit{\boldsymbol{K}}_3}]\mathit{\boldsymbol{B}} = 0, $ | (56) |
对(56)式进行无量纲化处理,引入下列无量纲化变量:
| $ {\alpha = t/T;\beta = x/L;\chi = R/L;\delta = B/L,} $ | (57) |
| $ {\gamma = \dot \theta T;\phi = {E_{\rm{h}}}/{E_{\rm{t}}};\phi = {\rho _{\rm{h}}}/{\rho _{\rm{t}}},} $ | (58) |
| $ {T = {{(12{\rho _{\rm{t}}}{L^4}/{E_{\rm{t}}}{h^2})}^{1/2}}}。$ | (59) |
式(56)可以改写成:
| $ {\mathit{\boldsymbol{\bar M}}_2}\mathit{\boldsymbol{\ddot \delta }} + [{\gamma ^2}({\mathit{\boldsymbol{\bar C}}_1} - {\mathit{\boldsymbol{\bar M}}_2}) + v{\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{\bar K}}_3}]\mathit{\boldsymbol{\delta }} = 0, $ | (60) |
| $ {{\mathit{\boldsymbol{\bar M}}}_2} = \mathop \smallint \nolimits_0^1 {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_y^{\rm{T}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_y}]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{d}}\beta {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\bar C}}}_1} = \mathop \smallint \nolimits_0^1 {\kern 1pt} {\kern 1pt} {\kern 1pt} [\beta {{\mathit{\boldsymbol{\bar H}}}_1}(\beta )]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{d}}\beta , $ | (61) |
| $ {{\mathit{\boldsymbol{\bar H}}}_1}(\beta ) = \mathop \smallint \nolimits_0^\beta {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{y,\beta }^{\rm{T}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{y,\beta }}]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{d}}\beta {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\bar K}}}_1} = \mathop \smallint \nolimits_0^1 {\kern 1pt} {\kern 1pt} {\kern 1pt} [\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{y,\beta \beta }^{\rm{T}}{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_{y,\beta \beta }}]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{d}}\beta , $ | (62) |
| $ v = (\phi - 1)\frac{{3({N^2} + N + 2)}}{{(N + \phi )(N + 2)(N + 3)}} + \frac{{N + 1}}{{N + \phi }}。$ | (63) |
表 1为中心刚体半径为0时,功能梯度指数N恒定, 采用假设模态法和有限元法得到的功能梯度材料梁横向弯曲固有频率随转速的变化情况。计算时,功能指数N=1;ϕ=151/70;φ=3 000/2 707。计算相对误差以有限元法的计算结果为计算基础。从表 1可以看出梁的横向弯曲固有频率会随着转速的增加而变大。在转速较低时,两种离散方法仿真结果基本一致,随着转速的增加,两者偏差越来越大,进一步说明在高转速下,假设模态法的结果并不可靠。这主要是因为假设模态法的模态函数是在小变形假设的前提下提出的,而有限元法的形函数并不存在小变形假设。随着转速的增加,柔性梁的变形必然增大,因而基于小变形假设的假设模态法的结果在变形较大时并不可靠。
| 表 1 功能梯度材料梁在不同转速下两种不同离散方法的固有频率比较 Table 1 Comparison of natural frequencies of FGM beams with two different discrete methods at different rotational speeds |
表 2为中心刚体半径为0,功能梯度材料梁转速恒定,采用假设模态法和有限元法得到的功能梯度材料梁横向弯曲的固有频率随功能梯度指数N的变化情况。计算时ϕ=151/70;φ=3 000/2 707,γ=3。从表 2中可以发现,当转速一定时,固有频率会随着功能梯度指数N增大而减小,说明N越大柔性梁系统的柔度越大,与图 10所示结论一致。
| 表 2 功能梯度材料梁在不同功能梯度指数下两种不同离散方法的固有频率比较 Table 2 Comparison of natural frequencies of FGM beams with two different discrete methods under different FGM indices |
1) 功能梯度梁末端最大横向变形位移随功能梯度指数N的增大而变大,当N>0时,稳态振动平衡位置会发生偏移,不在梁轴线上。
2) 假设模态法在变形较大时结果发散,不能处理大变形问题。有限元法结果收敛,可用于求解大变形问题。
3) 作大范围匀速转动的功能梯度梁的横向弯曲固有频率随着转速的增大而变大,随着功能梯度指数N的增大而减小。
因此,对比假设模态法,有限元法的计算模型更具有优越性,在工程中处理大变形问题应该优先选用有限元法。功能梯度指数N的取值对横向弯曲固有频率影响显著,工程中应该给予重视, 对构件进行设计时应选择合理的功能梯度指数材料。
| [1] |
李信, 刘海昌, 滕元成, 等. 功能梯度材料的研究现状及展望[J]. 材料导报, 2012, 26(S1): 370-373. LI Xin, LIU Haichang, TENG Yuancheng, et al. Research status and future directions on functionally gradient materials[J]. Materials Review, 2012, 26(S1): 370-373. (in Chinese) |
| [2] |
吴胜宝.作大范围运动柔性梁和柔性薄板刚柔耦合动力学建模与仿真[D].南京: 南京理工大学, 2009. WU Shengbao. Modeling and simulation of rigid-flex coupling dynamics of flexible beam and flexible thin plate[D]. Nanjing: Nanjing University of Science and Technology, 2009. (in Chinese) |
| [3] |
杨辉, 洪嘉振, 余征跃. 刚-柔耦合多体系统动力学建模与数值仿真[J]. 计算力学学报, 2003(4): 402-408. YANG Hui, HONG Jiazhen, YU Zhengyue. Dynamics modeling and numerical simulation for a rigid-flexible coupling multibody system[J]. Chinese Journal of Computational Mechanics, 2003(4): 402-408. (in Chinese) |
| [4] |
Ji Lin, Fen Chen, Yuhui Zhang, et al. An accurate meshless collocation technique for solving two-dimensional hyperbolic telegraph equations in arbitrary domains[J]. Engineering Analysis with Boundary Elements, 2019, 108: 372-384. |
| [5] |
Earl Ryan M A, Zamayla A D, Shayne Lyle M T. Decision-making system of soccer-playing robots using finite state machine based on skill hierarchy and path planning through Bezier polynomials[J]. Procedia Computer Science, 2018, 135: 230-237. |
| [6] |
张弛, 范纪华, 章定国, 等. 考虑端部质点的中心刚体-楔形梁系统动力特性研究[J]. 力学季刊, 2018, 39(2): 270-279. ZHANG Chi, FAN Jihua, ZHANG Dingguo, et al. Dynamic study of central rigid body-tapered beam system with tip mass[J]. Chinese Quarterly of Mechanics, 2018, 39(2): 270-279. (in Chinese) |
| [7] |
Rezaei V, Shafei A M. Dynamic analysis of flexible robotic manipulators constructed of functionally graded materials[J]. Iranian Journal of Science and Technology, Transactions of Mechanical Engineering, 2019, 43(1): 327-342. |
| [8] |
黎亮, 章定国, 洪嘉振. 中心刚体-功能梯度材料梁系统的动力学特性[J]. 机械工程学报, 2013, 49(13): 77-84. LI Liang, ZHANG Dingguo, HONG Jiazhen. Dynamics of hub-functionally graded material beam systems[J]. Journal of Mechanical Engineering, 2013, 49(13): 77-84. (in Chinese) |
| [9] |
Tang D, Hao L, Li Y, et al. Dual gradient direct ink writing for formation of kaolinite ceramic functionally graded materials[J]. Journal of Alloys and Compounds, 2020, 814: 152275. |
| [10] |
Zhang C, Chen F, Huang Z F, et al. Additive manufacturing of functionally graded materials:A review[J]. Materials Science & Engineering A, 2019, 764: 138209. |
| [11] |
Sun C Y, Gao H J, He W, et al. Fuzzy neural network control of a flexible robotic manipulator using assumed mode method[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(11): 5214-5227. |
| [12] |
杜超凡.基于无网格法的刚-柔耦合系统的动力学建模与仿真[D].南京: 南京理工大学, 2017. DU Chaofan. A study on the dynamic modeling and simulation for the rigid-flexible coupled system based on meshless methods[D]. Nanjing: Nanjing University of Science and Technology, 2017. (in Chinese) |
| [13] |
范纪华, 章定国. 基于变形场不同离散方法的柔性机器人动力学建模与仿真[J]. 力学学报, 2016, 48(4): 843-856. FAN Jihua, ZHANG Dingguo. Dynamic modeling and simulation of flexible robots based on different discretization method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(4): 843-856. (in Chinese) |
| [14] |
Salahshoor E, Ebrahimi S, Zhang Y. Frequency analysis of a typical planar flexible multibody system with joint clearances[J]. Mechanism and Machine Theory, 2018, 126: 429-456. |
| [15] |
蹇开林, 殷学纲. 旋转梁的固有频率计算[J]. 重庆大学学报(自然科学版), 2001, 24(6): 36-39. JIAN Kailin, YIN Xuegang. Computation of natural frequencies of a rotating beam[J]. Journal of Chongqing University (Natural Science Edition), 2001, 24(6): 36-39. (in Chinese) |
| [16] |
杜超凡, 章定国. 基于无网格点插值法的旋转悬臂梁的动力学分析[J]. 物理学报, 2015, 64(3): 406-415. DU Chaofan, ZHANG Dingguo. Dynamic analysis of rotating cantilever beam based on meshless point interpolation[J]. Acta Physica Sinica, 2015, 64(3): 406-415. (in Chinese) |
| [17] |
杜超凡, 章定国, 洪嘉振. 径向基点插值法在旋转柔性梁动力学中的应用[J]. 力学学报, 2015, 47(2): 279-288. DU Chaofan, ZHANG Dingguo, HONG Jiazhen. A meshfree method based on radial point interpolation method for the dynamic analysis of rotating flexible beams[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(2): 279-288. (in Chinese) |
| [18] |
He G L, Ding K, Wu X M, et al. Dynamics modeling and vibration modulation signal analysis of wind turbine planetary gearbox with a floating sun gear[J]. Renewable Energy, 2019, 139: 718-729. |
 2020, Vol. 43
2020, Vol. 43


