电磁学、化学、力学性能均相当优异的碳纳米管[1],在微、纳机电系统(NEMS)中已获得了广泛的应用[2],而在近几年,更是由于其颇具特点的动力学现象又在理论研究中成为了一大热点[3, 4]。基于现有的实验研究[5],可以证明碳纳米管的尺度效应明显,将非局部理论[6]适时地引入经典连续介质力学,较好地弥补了连续介质力学理论在纳米尺度下的不足,目前已作为一种纳米尺度下的分析手段获得了较为广泛的认可。Cao等[7]采用分子动力学理论研究了温度场中单壁碳纳米管的振动行为,Awrejcewicz等[8]基于欧拉伯努利梁模型及铁木辛柯梁模型研究了碳纳米管横向振动,Zhang等[9]研究了碳纳米管的超高频振动。
然而,上述研究中碳纳米管动力学特性的研究均针对的是理想约束的端部情形,在实际应用中,这类理想约束支撑可能会出现“松动”,原因基本上在于环境湿度、温度、振动或者疲劳等因素的影响,此时在“松动”的约束状态下,采用两端受扭转弹簧约束的简支梁模型来模拟则更为接近实际情形[10]。另外,近年来在对碳纳米管的进一步研究中发现[11]:碳纳米管在外界温度为-196~1 000 ℃的范围内会表现出明显的黏弹性特性,这一特性使得碳纳米管材料在振动中产生阻尼效应,因而可以将管道的黏弹性性质作为又一个研究因素加以考虑。
笔者将非局部弹性理论引入欧拉伯努利梁模型,研究中同时还引入了小尺度参数以及黏弹性参数,着重研究在扭转弹簧约束下简支单层碳纳米管前四阶振动特性。所得结论对于工程纳米机械的设计与分析将提供一定的理论支持。
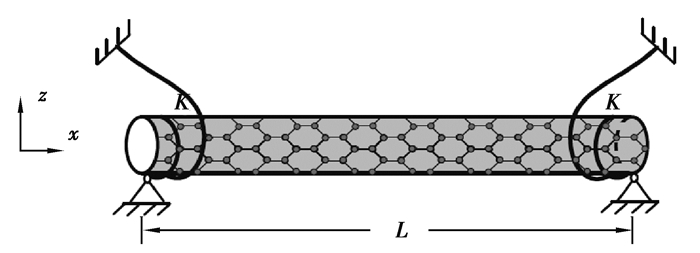
1 振动控制方程与边界条件单层碳纳米管(SWCNT)如图 1所示。端部为扭转弹簧约束下简支支撑,L、D、A、mc分别纳米管的长度、外径、横截面积以及每单位长度上的质量,EI为弯曲刚度,其中E为材料弹性模量,采用Kelvin-Voigt模型模拟材料的黏弹性特性。振动中不计重力以及管道外部拉、压力的影响,且假定管道只发生横向面内振动。
|
图 1 扭转弹簧约束下简支单层碳纳米管 Fig. 1 Schematic of simply supported elastic restrained single-walled carbon nanotube |
基于图 1所示的坐标,小变形条件下,Euler-Bernoulli梁的应变位移关系为
| $ {\varepsilon _{XX}} = - Z\frac{{{\partial ^2}W}}{{\partial {X^2}}}, $ | (1) |
式中:W(X, T)为纳米管的横向位移,εXX为X方向的应变。碳纳米管动能、应变能分别为
| $ {{E_{\rm{k}}} = \frac{1}{2}{m_{\rm{c}}}\int_0^L {{{\left( {\frac{{\partial W}}{{\partial T}}} \right)}^2}} {\rm{d}}X,} $ | (2) |
| $ {{E_{\rm{e}}} = \frac{1}{2}\int_0^L {\int_A {{\varepsilon _{XX}}} } {\sigma _{XX}}{\rm{d}}A{\kern 1pt} {\kern 1pt} {\rm{d}}X,} $ | (3) |
式中σXX为X方向的应力。
根据材料黏弹性本构关系[12]及非局部弹性理论,SWCNT应力应变关系可表示为
| $ {\sigma _{XX}} - {\eta ^2}{\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\partial ^2}{\sigma _{XX}}}}{{\partial {X^2}}} = E{\varepsilon _{XX}} + {E^*}\frac{{\partial {\varepsilon _{XX}}}}{{\partial T}}, $ | (4) |
式中:η是纳米材料中引起结构小尺度效应的参数,根据Wang[13]关于非局部参数的理论,η的数值可分别选取0~2 nm进行计算。E*为材料的黏弹性阻尼系数。
考虑到弯矩M与应力σXX的关系式
| $ \delta \int_{{T_1}}^{{T_2}} {({E_{\rm{k}}} - {E_{\rm{e}}} + {W_{{\rm{EXT}}}})} {\rm{d}}T = 0, $ | (5) |
可以得到纳米管的运动方程为:
| $ {E^*}I\frac{{{\partial ^5}W}}{{\partial {X^4}\partial T}} + EI\frac{{{\partial ^4}W}}{{\partial {X^4}}} + {m_{\rm{c}}}\frac{{{\partial ^2}W}}{{\partial {T^2}}} - {\eta ^2}{m_{\rm{c}}}\frac{{{\partial ^4}W}}{{\partial {X^2}\partial {T^2}}} = 0 $ | (6) |
对于两端扭转弹簧约束下简支纳米管,其边界条件为:
| $ \begin{array}{*{20}{c}} {X = 0:W = 0,EI\frac{{{\partial ^2}W}}{{\partial {X^2}}} = K\frac{{\partial W}}{{\partial X}};}\\ {X = L:W = 0,EI\frac{{{\partial ^2}W}}{{\partial {X^2}}} = - K\frac{{\partial W}}{{\partial X}}}。\end{array} $ | (7) |
式中K为扭转弹性系数。
2 振动控制方程求解笔者拟在对应的边界条件下,将微分变换法(DTM)推广到纳米级别管道系统的振动分析中,对上述高阶偏微分方程进行求解。较常求解高阶偏微分方程的方法有Galerkin法、微分求积法(DQM)、有限元法(FEM)等,而DTM法作为一种半解析计算方法[14],其优势除了可以简单、精确地对高阶偏微分方程进行求解,更在于其求解过程并不会随着方程阶数的增加变得繁琐。引入下列无量纲化的变量和参数便于后续的数值计算和分析:
| $ w = \frac{W}{L},x = \frac{X}{L},t = \sqrt {\frac{{EI}}{{{m_{\rm{c}}}}}} \frac{T}{{{L^2}}},\mu = \frac{{{\eta ^2}}}{{{L^2}}},\alpha = \frac{{{E^*}}}{{E{L^2}}}\sqrt {\frac{{EI}}{{{m_c}}}} $ |
其中μ为无量纲小尺度参数,α为无量纲黏弹性阻尼参数。
由此纳米管横向振动方程(6)、边界条件(7)可分别转化为下述的无量纲方程
| $ \alpha {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\partial ^5}w}}{{\partial {x^4}\partial t}} + \frac{{{\partial ^4}w}}{{\partial {x^4}}} + \frac{{{\partial ^2}w}}{{\partial {t^2}}} - \mu {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\partial ^4}w}}{{\partial {x^2}\partial {t^2}}} = 0, $ | (8) |
以及相应的无量纲边界条件:
| $ \begin{array}{*{20}{c}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x = 0:w = 0,\frac{{{\partial ^2}w}}{{\partial {x^2}}} = k{\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial w}}{{\partial x}};}\\ {x = 1:w = 0,\frac{{{\partial ^2}w}}{{\partial {x^2}}} = - k{\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial w}}{{\partial x}}}。\end{array} $ | (9) |
设方程(8)的解为
| $ \alpha {\varOmega _0}\frac{{{{\rm{d}}^4}\varphi }}{{{\rm{d}}{x^4}}} + \frac{{{{\rm{d}}^4}\varphi }}{{{\rm{d}}{x^4}}} + \varOmega _0^2\varphi - \mu \varOmega _0^2\frac{{{{\rm{d}}^2}\varphi }}{{{\rm{d}}{x^2}}} = 0, $ | (10) |
基于DTM运算法则[14],可得到方程(10)的微分变换形式:
| $ (s + 4)!{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varPhi (s + 4) + \alpha (s + 4)!{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varPhi (s + 4){\varOmega _0} + [s!{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varPhi (s) - \mu (s + 2)!{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varPhi (s + 2)]\varOmega _0^2 = 0, $ | (11) |
其相应边界条件的微分变换形式:
| $ \varPhi (0) = 0,2\varPhi (2) - k\varPhi (1) = 0, $ | (12) |
| $ \sum\limits_{s = 0}^\infty \varPhi (s) = 0,\sum\limits_{s = 0}^\infty {[s(s - 1) + k]\varPhi (s) = 0} 。$ | (13) |
令Φ(1)=C1,Φ(3)=C2,进而与式(12)一起代入式(11),迭代求得Φ(s),s=4,5,…,N。然后将Φ(s),s=1, 2, …, N代入式(13),可得到以下2个方程:
| $ \left[ {\begin{array}{*{20}{l}} {{a_{11}}}&{{a_{12}}}\\ {{a_{21}}}&{{a_{22}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{l}} {{C_1}}\\ {{C_2}} \end{array}} \right\} = 0, $ | (14) |
式中aij是关于Ω0和其他系统参数的多项式,上式有非零解的条件是其系数矩阵行列式为零,考虑
文中碳纳米管的参数为[15]:ρc=2 300 kg/m3,D=6 nm,壁厚td =0.1 nm,弹性模量E=3.4 TPa。振动中为不计剪切变形与转动惯量[16],长径比取L/D=40,其他参数在具体算例中给与说明,DTM的截断项数N=40。
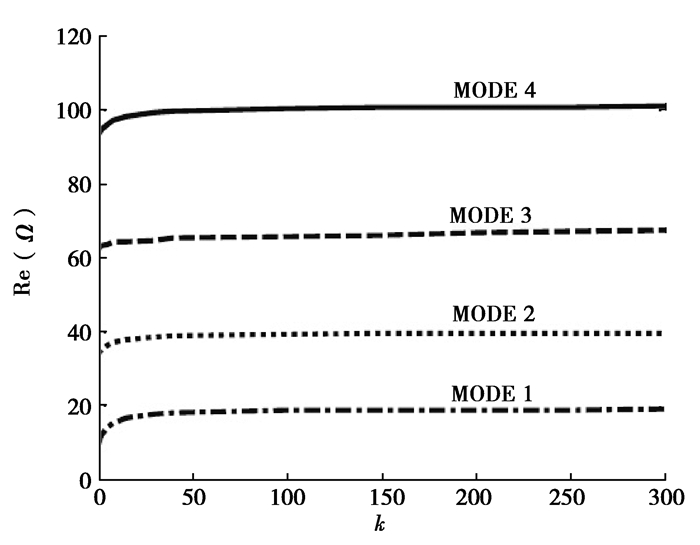
图 2为扭转弹簧约束下简支纳米管前四阶无量纲固有频率随扭转弹性刚度k的变化情况,其中无量纲小尺度参数μ以及无量纲黏弹性阻尼参数α的取值均为零。
|
图 2 无量纲固有频率随弹性系数k变化(μ=0, α=0) Fig. 2 The dimensionless frequency of the four lowest modes of the system (μ=0, α=0) as a function of the elastic coefficient, k |
从图 2中看出,纳米管前四阶固有频率随着弹性刚度的增大显现出增大趋势。这一趋势在扭转刚度处于较小数值时尤为显著,并且低阶模态的变化显著于高阶模态。说明对于纳米管的横向振动,扭转刚度对固有频率的影响很大,为了提高管道的固有频率,应该适当提高扭转弹性刚度。
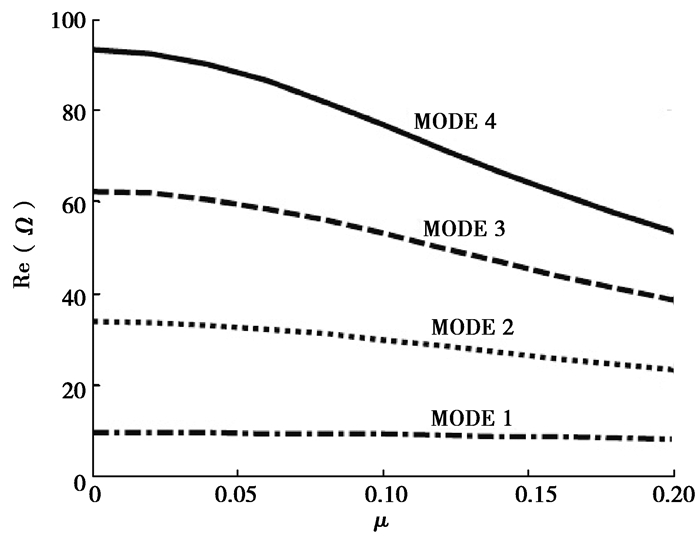
图 3为纳米管前四阶固有频率随小尺度参数μ的变化情况,扭转弹性刚度k及无量纲黏弹性阻尼参数α的取值为零。由图 3则可以看到,小尺度参数μ的增加会降低系统的固有频率,这说明小尺度效应使纳米管系统更为柔软,比较图中数据可以发现这种变化规律对高阶固有频率的影响效果更为显著。
|
图 3 无量纲固有频率随小尺度μ变化(k=0, α=0) Fig. 3 The dimensionless frequency of the four lowest modes of the system (k=0, α=0) as a function of the small-scale parameter, μ |
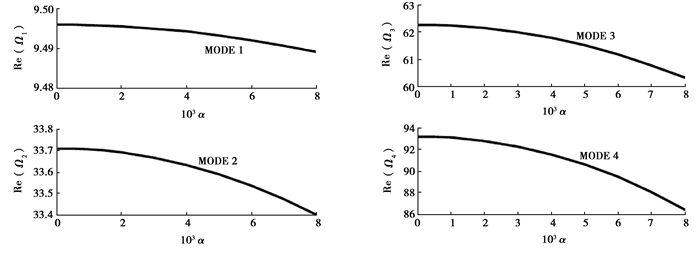
图 4(a)、(b)为纳米管前四阶固有频率随无量纲黏弹性阻尼参数α的变化情况,而小尺度参数μ, 扭转弹性刚度k的取值为零。如图 4所示,碳纳米管的黏弹性性质越显著,管道的不同阶固有振动频率的数值越小,但这种变化规律对不同模态却存在着不同的影响程度,其中第一阶固有频率受黏弹性的影响较弱,而随着固有模态阶数的提高,黏弹性的影响越就显著。
|
图 4 无量纲固有频率随黏弹性系数α变化(μ= 0, k=0) Fig. 4 The dimensionless frequency of the four lowest modes of the system (μ=0, k=0) as a function of the viscoelastic parameter, α |
讨论了扭转约束弹性刚度、管道小尺度参数和黏弹性参数对端部为扭转弹簧约束的简支碳纳米管前四阶无量纲固有频率的影响。结论表明碳纳米管小尺度参数、黏弹性阻尼参数的提高均会降低系统的各阶固有频率,且上述两类变化情况均是高阶模态的变化显著于低阶模态。不同于前面2个影响因素,扭转约束弹性刚度的增大则会提升纳米管的固有频率,但这种提升效果在扭转约束弹性刚度较小时才较为明显,并且低阶模态效果显著于高阶模态。
| [1] |
Iijima S. Helical microtubes of graphite carbon[J]. Nature, 1991, 354(6348): 56-58. DOI:10.1038/354056a0 |
| [2] |
Soltani P, Farshidianfar A. Periodic solution for nonlinear vibration of a fluid-conveying carbon nanotube, based on the nonlocal continuum theory by energy balance method[J]. Applied Mathematical Modelling, 2012, 36(8): 3712-372. DOI:10.1016/j.apm.2011.11.002 |
| [3] |
李明, 周攀峰, 郑慧明. 磁敏固支载流单壁碳纳米管在轴向磁场中的振动特性[J]. 应用力学学报, 2017, 34(4): 634-640, 811. LI Ming, ZHOU Panfeng, ZHENG Huiming. Vibration characteristics of magnetically sensitive clamped-clamped carbon nanotubes conveying fluid subjected to a longitudinal magnetic field[J]. Chinese Journal of Applied Mechanics, 2017, 34(4): 634-640, 811. (in Chinese) |
| [4] |
李明, 方康, 郑华升. 悬臂输流单层碳纳米管的颤振失稳分析[J]. 武汉科技大学学报, 2018, 41(3): 184-189. LI Ming, FANG Kang, ZHENG Huasheng. Analysis of flutter instability of cantilever single-walled carbon nanotubes conveying fluid[J]. Journal of Wuhan University of Science and Technology, 2018, 41(3): 184-189. (in Chinese) DOI:10.3969/j.issn.1674-3644.2018.03.005 |
| [5] |
Poncharal P, Wang Z L, Ugarte D, et al. Electrostatic deflections and electro-mechanical resonances of carbon nanotubes[J]. Science, 1999, 283(5407): 1513-1516. DOI:10.1126/science.283.5407.1513 |
| [6] |
Eringen A C. On differential equations of nonlocal elasticity and solution of screw dislocation and surface waves[J]. Journal of Applied Physics, 1983, 54(9): 4703-4710. DOI:10.1063/1.332803 |
| [7] |
Cao G, Chen X, Kysar J W. Thermal vibration and apparent thermal contraction of single-walled carbon nanotubes[J]. Journal of the Mechanics and Physics of Solids, 2006, 54(6): 1206-1236. DOI:10.1016/j.jmps.2005.12.003 |
| [8] |
Awrejcewicz J, Krysko A V, Zhigalov M V, et al. Chaotic vibrations in flexible multi-layered Bernoulli-Euler and Timoshenko type beams[J]. Latin American Journal of Solids and Structures, 2008, 5(4): 319-363. |
| [9] |
Zhang Y Q, Liu G R, Han X. Transvers vibrations of double walled carbon nanotubes under compressive axial load[J]. Physics Letters, 2005, 340: 258-266. DOI:10.1016/j.physleta.2005.03.064 |
| [10] |
王忠民, 冯振宇, 赵凤群, 等. 弹性地基输流管道的耦合模态颤振分析[J]. 应用数学和力学, 2000(10): 1060-1068. WANG Zhongming, FENG Zhengyu, ZHAO Fengqun. Analysis of coupled-mode flutter of pipes conveying fluid on the elastic foundation[J]. Applied Mathematics and Mechanics, 2000(10): 1060-1068. (in Chinese) DOI:10.3321/j.issn:1000-0887.2000.10.011 |
| [11] |
Xu M, Futaba D N, Yamada T, et al. Carbon nanotubes with temperature-invariant viscoelasticity from -196℃ to 1000℃[J]. Science, 2010, 330(6009): 1364-1368. DOI:10.1126/science.1194865 |
| [12] |
齐欢欢.输液管道颤振失稳的时滞控制[D].上海: 同济大学, 2009. QI Huanhuan. Delayed feedback control for flutter in the pipe conveying fluid[D]. Shanghai: Tongji University, 2009. (in Chinese) |
| [13] |
Wang Q. Wave propagation in carbon nanotubes via nonlocal continuum mechanics[J]. Journal of Applied Physics, 2005, 98(12): 124301. DOI:10.1063/1.2141648 |
| [14] |
Chen C K, Ho S H. Transverse vibration of a rotating twisted timoshenko beams under axial loading using differential transform[J]. International Journal of Mechanical Science, 1999, 41(11): 1339-1356. DOI:10.1016/S0020-7403(98)00095-2 |
| [15] |
Hosseini M, Sadeghi-Goughari M, Atashipour S A, et al. Vibration analysis of single-walled carbon nanotubes conveying nanoflow embedded in a viscoelastic medium using modified nonlocal beam model[J]. Archives of Mechanics, 2014, 66(4): 217-224. |
| [16] |
Yoon J, Ru C Q, Mioduchowski A. Flow-induced flutter instability of cantilever carbon nanotubes[J]. International Journal of Solids and Structure, 2006, 43(6): 3337-3349. |
 2020, Vol. 43
2020, Vol. 43

