2. 中国舰船研究设计中心, 武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, P. R. China
如今全球经济快速发展,在航运需求不断提高的前提下,新造船舶尺寸越来越大的同时,“绿色船舶技术”[1]已成为未来造船业和航运业发展的主旋律。减少船舶自重是现阶段国际海事组织认为实现船舶节能减排的最有效方式。由于复合材料具有重量轻、比强度高等优点,已经在船舶局部结构及中小型船舶的建造中得到应用[2]。
在船舶与海洋工程结构中有许多横向和纵向布置的舱壁,其中存在一种用于上建或舱内房间分隔的轻舱壁,一般只是起到简单的分隔作用,具有一定的刚性,不需要承担船体结构的总纵弯矩[3]。为了实现船体结构减重的目的,可考虑采用复合材料夹层结构代替传统的钢制轻舱壁结构。
复合材料夹层结构是由两个相对薄的面板和中间一层轻质的芯层粘接而成。复合材料夹层结构的面板材料通常作为主要的承力结构,因此采用具有优良力学性能的材料,如金属或纤维材料;复合材料夹层结构的芯层起到增大整体厚度,提供充足剖面模数的作用,常用材料为蜂窝材料、泡沫材料、木材等[4]。根据环境适应性、经济性、界面力学特性以及成型制备工艺性等问题的综合考虑和工程实际应用情况,目前适应于舰船结构的复合材料主要是E玻璃纤维夹层结构。
近年来,基于响应面模型的优化方法已经在复合材料及其属性设计中得到了广泛的应用[5]。文献[6-7]采用二级优化设计方法对复合材料加筋板结构进行布局优化设计;罗利龙等[8]改进遗传算法对夹层板的稳定性进行优化分析;盛涛等[9]基于响应面法优化蜂窝夹层结构件制备工艺;文献[10-12]利用人工神经网络优化复合材料加筋结构。郭占一[13]采用ANSYS建立复合材料船体上层建筑模型,使用一阶算法建立响应面,再通过筛选法逐一计算,分析复合材料上层建筑各设计变量在约束条件下对目标函数的影响。苟鹏等[14]对比分析表明Kriging方法比其他方法更加适合船舶结构的多学科设计优化。
基于响应面模型的优化方法克服了复合材料结构布局优化设计灵活且复杂等传统的数学规划法或准则法难以解决的问题,避免了直接使用有限元方法占用大量资源且无法快速实现。Kriging函数作为一种半参数化的插值技术,同时具有局部和全局的统计特性,优于传统的二次响应面拟合。同时遗传算法代替传统的筛选法,可进一步减少计算量,提高计算效率。
1 舱壁模型说明所研究的轻舱壁结构的整体几何尺寸为2 500 mm×4 000 mm。通过查阅相关资料,一般钢制轻舱壁的壁厚为3 mm,扶强材间距为0.5 m,扶强材采用6号球扁钢,计算可得钢制舱壁总重量为302.5 kg。根据相关资料,轻舱壁的设计载荷为2.94 kPa。舱壁四边采用全约束,根据计算可得在设计工况下钢制舱壁的最大变形为5.39 mm。
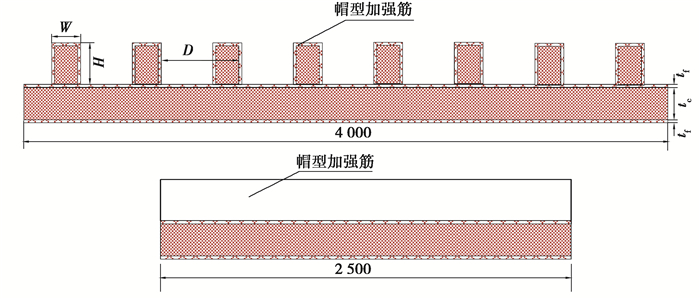
复合材料舱壁设计中将加筋高度H、加筋宽度W、芯材厚度tc、单边铺层厚度tf、加筋间距D和加筋铺层厚度ts等6个变量设为设计变量。复合材料舱壁结构以及参数对应的位置如图 1所示。
|
图 1 复合材料舱壁结构图(单位: mm) Fig. 1 Geometric configurations of composite bulkhead structure(unit: mm) |
文中复合材料舱壁为复合材料夹芯加筋板结构,其中上下面板材料玻璃钢,芯材材料为PVC泡沫。为了保证舱壁具有足够的弯曲刚度,采用一体成型技术在舱壁面板上布置帽型加强筋,其中加强筋内部填充PVC芯材,外部敷设材料为E玻璃纤维。E玻纤蒙皮可宏观视为一层各向异性的单层板,如表 1所示。PVC型号为H80,属性如表 2所示。
| 表 1 玻璃钢面板的等效材料属性 Table 1 Material properties of FRP panels |
| 表 2 PVC H80的等效材料属性 Table 2 Material properties of PVC H80 |
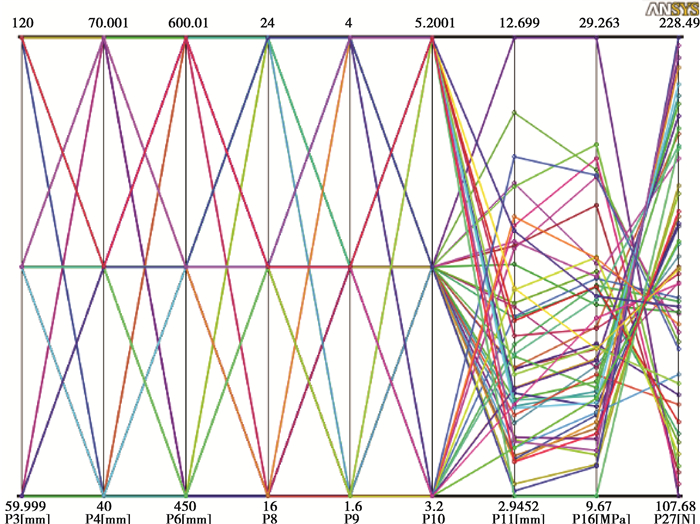
DOE实验设计作为数理统计的分支之一,其目的是在设计空间选取较少的试验点,在满足统计分析要求的前提下达到降低成本和缩短试验周期的目的。常用的试验设计有:全因子试验设计、正交实验设计、Box-Behnken设计和拉丁方试验设计等[15]。获得合适的试验点,是能够建立精确响应面模型的基础。其中Box-Behnken设计具有所有的试验点都位于等距的端点上,并不包含各变量上下水平所产生于立方体定点的试验的特点。以较少的试验次数,去估计一阶、二阶与一阶矩相交作用项之多项式模式。这里选用Box-Behnken设计(BBD)进行试验点选取,用于计算变量的最优值及考察变量间的相互作用。通过BBD法共构造出49个试验点,各个试验点参数平行图如图 2所示。
|
图 2 所有试验点参数平行图 Fig. 2 Parameters parallel chart |
响应面法(RSM)是利用函数关系拟合仿真模型,采用筛选试验来确定优化方向。以RSM为指向,按照满足约束条件和质量最轻方向寻找最优解,设定好收敛条件,就可以搜索到最佳设计。Kriging模型精度较高,而且Kriging模型可以同时提供预测位置的预测值和预测误差,这个优点十分适用于全局优化算法[16]。Kriging函数法是一种基于一般最小二乘算法的随机插值过程,其依据协方差函数对平均值为零的随机过程进行插值来模拟复杂的响应关系,其表达式为
| $ y(X)=f(X)+Z(x), $ | (1) |
式中:f(X)是关于X的多项式,Z(X)为均值为零的随机过程。
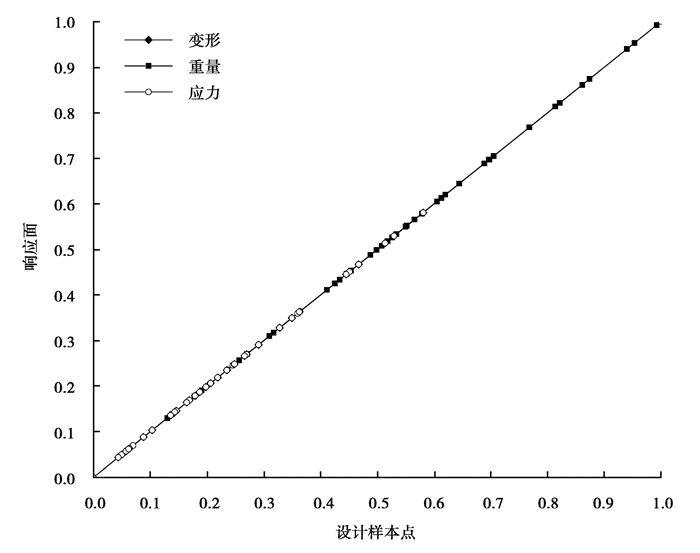
通过ANSYS Workbench中的DesignXplorer模块,在有限元参数化模型基础上,设置Kriging算法的相关参数,其中核函数设置为可变式的,最大允许改进点设置为5,最大预测允许相关误差为5%,改进点只选取最大预测相对误差的点的影响,求出Kriging响应面模型的拟合度曲线,如图 3所示。图 3中反映了舱壁总质量、最大变形和最大Mises应力3个设计参数的拟合关系,通过其可判断Kriging响应面模型的拟合计算值与BBD求得的设计值之间的对应程度。图中舱壁总质量、最大变形和最大Mises应力所对应的点,都在对角线附近,这表明BBD所得到样本点及其响应面拟合值的一致性非常好,故所得到的Kriging响应面模型与实际有限元计算的结果吻合,满足后续设计分析的需求。
|
图 3 基于Kriging函数的响应面模型拟合度曲线 Fig. 3 Response surface model fitting curve based on Kriging |
在Kriging函数法建立的舱壁响应面模型的基础上,将舱壁的质量作为目标函数,最大变形和最大Mises应力作为约束条件,加筋高度H、加筋宽度W、芯材厚度tc、单边铺层厚度tf、加筋板间距D和加强筋铺层厚度ts等6个参数作为设计变量。建立舱壁的优化数学模型如(2)所示,约束条件如(3)所示。
| $ f = \min \left( {{\mathop{\rm mass}\nolimits} \left( {H, W, D, {t_{\rm{c}}}, {t_{\rm{f}}}, {t_{\rm{s}}}} \right), {\mathop{\rm deformation}\nolimits} \left( {H, W, D, {t_{\rm{c}}}, {t_{\rm{f}}}, {t_{\rm{s}}}} \right), {\mathop{\rm stress}\nolimits} \left( {H, W, D, {t_{\rm{c}}}, {t_{\rm{f}}}, {t_{\rm{s}}}} \right)} \right), $ | (2) |
| $ \text { s.t. }\left\{\begin{array}{l} 60 \mathrm{mm} \leqslant H \leqslant 120 \mathrm{mm} , \\ 40 \mathrm{mm} \leqslant W \leqslant 70 \mathrm{mm} , \\ 450 \mathrm{mm} \leqslant D \leqslant 600 \mathrm{mm}, \\ 16 \mathrm{mm} \leqslant t_{c} \leqslant 24 \mathrm{mm}, \\ 1.6 \mathrm{mm} \leqslant t_{\mathrm{f}} \leqslant 4 \mathrm{mm} , \\ 3.2 \mathrm{mm} \leqslant t_{\mathrm{f}} \leqslant 5.2 \mathrm{mm} , \\ H+t_{\mathrm{c}}+2 t_{\mathrm{f}}+t_{\mathrm{s}} \leqslant 130 \mathrm{mm} , \\ \text { deformation } \leqslant 6 \mathrm{mm}。\end{array}\right. $ | (3) |
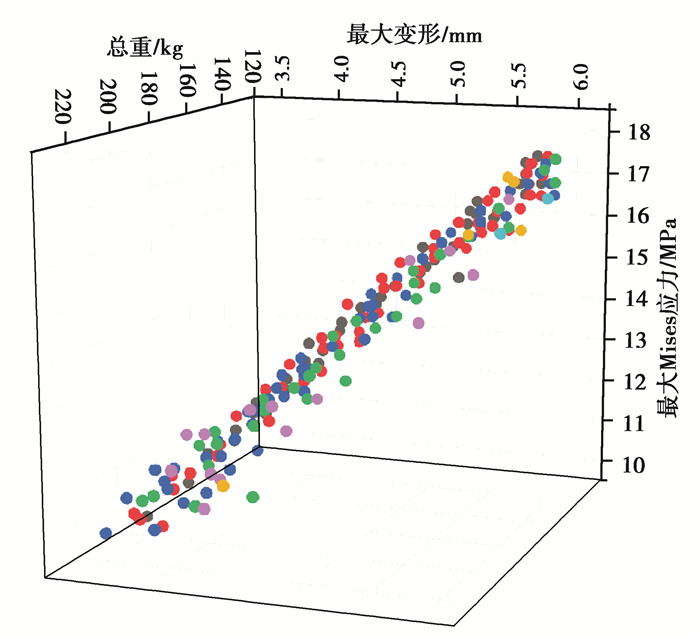
多目标遗传算法MOGA(mulit-objective genetic algorithm)适合作为全局优化的优化算法。与传统的切片法相比,该方法需要计算的样本更少,其迭代后的选择的样本更靠近通过计算分析得到Pareto可行域。考虑到已有的参数约束条件,初始样本模式设置为限制样本。初始种群数量总是设为6 000,并选取每代前1 200个为遗传算法的选择样本进行遗传迭代,权衡函数作为样本排序的计算方法,最大允许遗传代数为20代,其中变异系数为0.01,交叉系数为0.98。最大允许Pareto比例设置为60%,收敛稳定性设置为2%,如果满足上述两个条件计算结束。在DesignXplorer模块建立的响应曲面模型基础上,采用前文所述的设置进行遗传算法的求解,图 4所示为所得到的Pareto最优解。表 3所示为3组Pareto最优解,由于这里着重关注于质量的变化,故选择第3组解。
|
图 4 Pareto最优解集 Fig. 4 Solution sets of Pareto optimal |
| 表 3 Pareto最优解 Table 3 Pareto optimal solution |
灵敏度分析法是一种用于研究优化设计后研究相关参数发生是否最优的较为通用的方法。通过对比参数变化对整体系统的优化结果的影响大小,来判断哪些参数对模型有较大的影响,可为最终的优化方案提供支撑,保证其与优化目标可以最大程度的匹配。
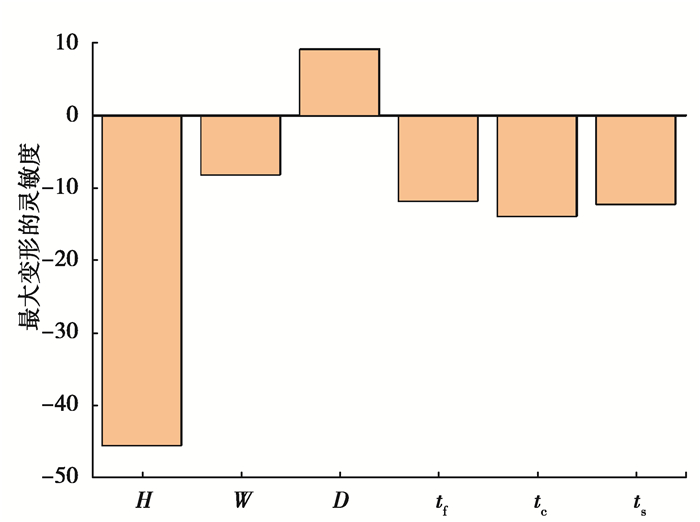
基于ANSYS Workbench的DesignXplorer模块提供的优化方案,对比各设计参数对最大变形、最大应力和最大重量的影响,获得设计参数优化的灵敏系数,如图 5~7所示。
|
图 5 各变量对最大变形的相对灵敏系数 Fig. 5 Relative sensitivity coefficients of the maximum deformation |
|
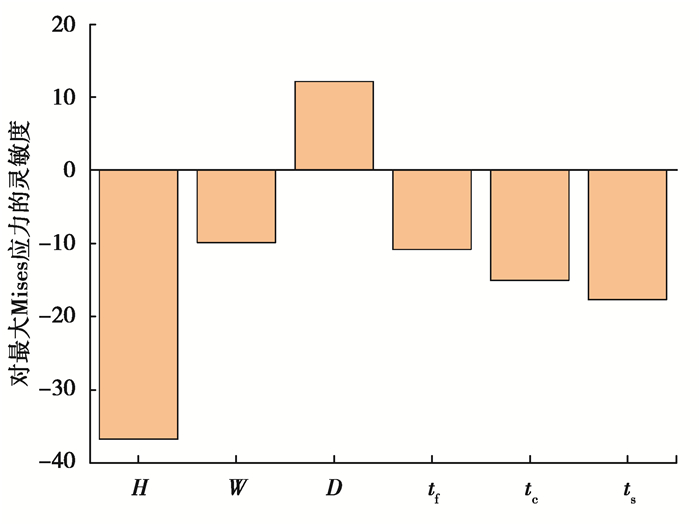
图 6 各变量对最大Mises应力的相对灵敏系数 Fig. 6 Relative sensitivity coefficients of maximum Mises stress |
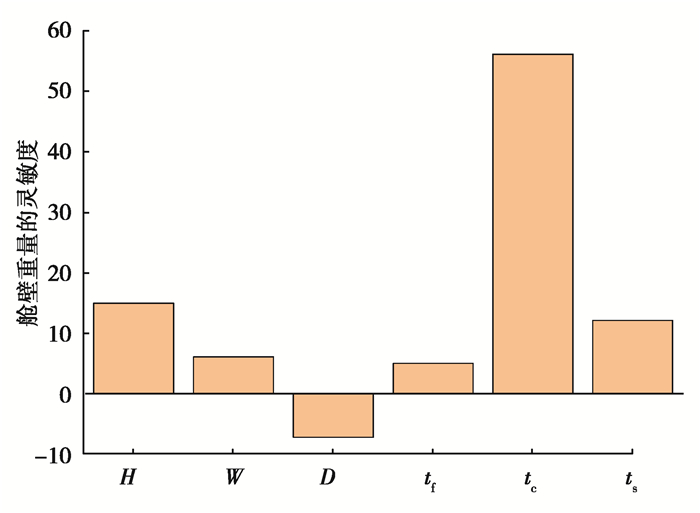
|
图 7 各变量对结构重量的相对灵敏系数 Fig. 7 Relative sensitivity coefficients of the weight |
设计灵敏度反映了设计变量的改变对目标函数变化的影响程度,其本质为因变量对于各自变量的偏导数,因此其只能反映出各自变量和因变量之前的相对关系。在各设计变量中,加强筋高度对变形的影响最大,加筋宽度和加筋间距对变形的影响相对较小。单边铺层的厚度对结构重量的影响最大,芯材厚度和加筋宽度对结构质量的影响较小。
由材料力学可知,对于承受面外载荷的结构,结构的惯性矩决定其自身的刚度。帽型加强筋的高度、铺层的厚度以及芯层的厚度等垂向构件的尺寸对整体变形起到主要作用。对于平板结构,受力最大的位置在上下表面,因此对于夹层结构,面板一般采用具有优良力学性能的玻璃钢,而芯层一般采用轻质材料。一般芯层的厚度约为玻璃钢上下面板厚度之和的5倍,这种设计方式可以有效的降低舱壁结构的重量。
目标是在满足刚度、强度的前提下,在优化中追求结构整体质量最小。因此通过图中的比例系数,可知对于各设计变量的优化优先级,依次是:单边铺层厚度、加强筋铺层厚度、加筋宽度、加筋间距、芯材厚度、加筋高度。
2.4 结果优化验证采用ANSYS Workbench对优化后的复合材料舱壁模型参数建模进行有限元计算分析,得到舱壁质量、最大变形和最大Mises应力直接计算解。直接计算结果与响应面优化算法的计算结果对比如表 4所示。从表 4中可以看出,通过优化算法得到的变形比直接计算得到的变形大3.02%,应力增大了4.81%,总质量基本一致。分析可知通过基于响应面的优化算法得到解的误差都在在5%以内,这充分表明所提出的设计方法是有效和可行的。
| 表 4 结构可靠性对比 Table 4 The comparison of structural reliability |
考虑到舱壁和钢制船体的连接问题,需要在复合材料端部用钢板过渡。根据初步估算按照5 mm的钢板以及配套螺栓连接结构,舱壁的总重量将增加约90 kg,因此最优结果的复合材料舱壁总重应为232.5 kg。与常规的钢制舱壁相比其重量减少了约23%,舱壁的重量得到了较大幅度的优化,满足工程上的要求。
3 结论利用响应面模型及遗传算法对某复合材料舱壁结构进行优化,具体包括建立复合材料舱壁的数学模型、BBD实验设计计算、基于Kriging函数法建立响应面模型,最后利用遗传算法进行优化,确定最优设计参数。优化结果和直接计算的结果对比表明所提出优化方法有效可行,对复合材料舱壁的改进设计具有一定的指导意义。同时对船体其他局部结构或类似复杂机械结构的优化问题也可采用本文中所提出的优化方法。
| [1] |
张信学, 赵峰, 王传荣, 等. 绿色船舶技术发展战略研究[J]. 中国工程科学, 2016, 18(2): 66-71. ZHANG Xinxue, ZHAO Feng, WANG Chuanrong, et al. Research on the development strategy of green ship technology[J]. Engineering Sciences, 2016, 18(2): 66-71. (in Chinese) |
| [2] |
Mouritz A P, Gellert E, Burchill P, et al. Review of advanced composite structures for naval ships and submarines[J]. Composite Structures, 2001, 53(1): 21-42. |
| [3] |
李鹏.舱室轻量化壁板结构仿真分析方法研究[D].青岛: 中国海洋大学, 2014. LI Peng. A study on simulation analysis method of lightweight bulkhead[D]. Qindao: Ocean University of China, 2014. (in Chinese) |
| [4] |
Eirc Greence Associates.舰船复合材料(第二版)[M].赵成壁, 唐友宏译.上海: 上海交通大学出版社, 2013. Eirc Greence Associates. Ship Composites (Second Edition)[M]. Translated by ZHAO Chengbi, TANG Youhong. Shanghai: Shanghai Jiao Tong University Press, 2013. (in Chinese) |
| [5] |
Wang G G, Shan S. Review of metamodeling techniques in support of engineering design optimization[J]. Journal of Mechanical Design, 2007, 129(4): 370-380. |
| [6] |
吴莉莉, 姚卫星. 复合材料加筋板结构的二级协同优化设计方法[J]. 南京航空航天大学学报, 2011, 43(5): 645-649. WU Lili, YAO Weixing. Two-level collaborative optimum design method for composite stiffened panel[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2011, 43(5): 645-649. (in Chinese) |
| [7] |
Rikards R, Abramovich H, Auzins J, et al. Surrogate models for optimum design of stiffened composite shells[J]. Composite structures, 2004, 63(2): 243-251. |
| [8] |
罗利龙, 赵美英, 穆朋刚. 一种改进的自适应遗传算法及其在层合板优化中的应用研究[J]. 机械科学与技术, 2012, 31(5): 694-697. LUO Lilong, ZHAO Meiying, MU Penggang. An ameliorative self-adaptive GA method and application to optimization of the laminate composite[J]. Mechanical Science and Technology, 2012, 31(5): 694-697. (in Chinese) |
| [9] |
盛涛, 王旭, 王晓蕾, 等. 基于响应面法优化蜂窝夹层结构件制备工艺[J]. 高科技纤维与应用, 2019(1): 43-52. SHENG Tao, WANG Xu, WANG Xiaolei, et al. Response surface methodology to optimize the honeycomb sandwich fabrication process[J]. Hi-Tech Fiber and Application, 2019(1): 43-52. (in Chinese) |
| [10] |
李烁, 徐元铭, 张俊. 复合材料加筋结构的神经网络响应面优化设计[J]. 机械工程学报, 2006, 42(11): 115-119. LI Shuo, XU Yuanming, ZHANG Jun. Neural network response surface optimization design for composite stiffened structures[J]. Journal of Mechanical Engineering, 2006, 42(11): 115-119. (in Chinese) |
| [11] |
Xu Y M, Li S, Rong X M. Composite structural optimization by genetic algorithm and neural network response surface modeling[J]. Chinese Journal of Aeronautics, 2005, 18(4): 310-316. |
| [12] |
Bisagni C, Lanzi L. Post-buckling optimisation of composite stiffened panels using neural networks[J]. Composite Structures, 2002, 58(2): 237-247. |
| [13] |
郭占一.一体化复合材料上层建筑力学性能及其连接结构设计研究[D].哈尔滨: 哈尔滨工程大学, 2016. GUO Zhanyi. Mechanical analysis and joints design of integrated composite superstructure[D]. Harbin: Harbin Engineering University, 2016. (in Chinese) |
| [14] |
苟鹏, 刘蔚, 崔维成. 船舶结构多学科设计优化近似方法的比较[J]. 船舶力学, 2007, 11(6): 913-923. GOU Peng, LIU Wei, CUI Weicheng. A comparison of approximation methods for multidisciplinary design optimization of ship structures[J]. Journal of Ship Mechanics, 2007, 11(6): 913-923. (in Chinese) |
| [15] |
Montgomery D C. Design and analysis of experiments[M]. New York, USA: John Wiley & Sons, 2004.
|
| [16] |
张崎.基于Kriging方法的结构可靠性分析及优化设计[D].大连: 大连理工大学, 2005. ZHANG Qi. Structural reliability analysis and optimal design based on kriging method[D]. Dalian: Dalian University of Technology, 2005. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43

