泄洪雾化是一种非自然的危害性气象事件,它常常带来强风和强降雨,给水电工程的安全运行带来危害。近年来,随着中国水电事业逐步向西南部发展,一批高坝或超高坝相继建设运行,坝址所在地区多处于高山峡谷地带[1-2]。泄洪水头越来越高、泄流量不断增大,坝址所在地区的高边坡窄峡谷地形环境越来越复杂,使得泄洪雾化问题越来越凸显,从而成为高坝泄洪安全的挑战性难题之一[3-4]。
泄洪雾化是一种复杂的水气相互掺混运动,受到包括下泄流量、消能方式、下游水深、河谷形态、气象条件等多种因素的影响[5-8]。人们对泄洪雾化产生的机理以及对雾化风场、雨场的预测仍然有待进一步提高[9-11]。目前主要采用原型观测、模型试验以及数学模型对泄洪雾化展开研究,在泄洪雾化的定性描述分析以及定量评价方面取得了重要进展[12-13]。梁在潮[14]、吴修锋等[15]、刘宣烈等[7]对泄洪雾化展开了大量的原型观测,取得了泄洪雾化过程中风速、雾化雨强、雨滴谱等一手资料。陈瑞等[16-17]、吴时强等[18]、Falvey[19]和Zhou等[20]进行了大比尺模型试验,在模型与原型之间的模型律、雨强缩尺效应等方面取得了重要进展,增强了采用模型试验预测泄洪雾化的可行性。在采用数学模型预测泄洪雾化方面,随机喷溅模型、BP神经网络模型、模糊预测等数学模型也得到了广泛的应用[21-26]。
近年来,有学者在泄洪雾化的数值模拟方面展开了研究,谭立新等[27]提出了掺气水流的双流体及单流体模型,并对水垫塘的掺气水流进行了数值模拟;许唯临等[28]建立了水气两相紊流的数学模型,对水垫塘掺气射流进行了数值模拟,计算结果与试验结果吻合较好;沙海飞等[29]基于VOF方法采用水气两相流二维紊流数值模型,对坝身泄洪水气两相流进行了数值模拟,并与1:50比尺的模型试验结果进行了对比;柳海涛等[30]基于水雾对流扩散方程的求解,通过雾雨强度与水雾浓度转换公式对泄洪雾化降雨强度进行了预测。受限于流体力学的求解难度,现有的数值研究仅能对简单的或部分的水力现象进行求解,且往往基于简化模型展开。例如,VOF模型认为水气之间有分界面,而在泄洪过程中,尤其在水气剧烈掺混区域不存在严格意义上的水气分界面[31]。实际上,泄洪雾化过程本质上仍然是水气两相的相互掺混运动,采用基于质量守恒、动量守恒以及能量守恒的三大偏微分方程能够对其进行较为完备的数学描述。基于守恒定律的方程组能够求出泄洪雾化过程中的水气运动速度、压力以及浓度等参数,进而实现对泄洪雾化风速场及降雨场的预测。
笔者基于水气两相流理论,忽略泄洪雾化过程中的温度变化,采用质量守恒及动量守恒方程对泄洪雾化过程进行数学描述,进而确定求解过程中所需的本构关系,采用有限元法,解决或改善求解中出现的高度非线性、数值稳定性、收敛性等难题,以水布垭面板堆石坝为例,模拟了其泄洪过程,对其风场、雨场分布进行了预测,并与2016年的泄洪实测数据进行了对比。
1 基于水气两相流的泄洪雾化数学模型洪水下泄过程实际上是水体势能转变为水、气的动能及热能的过程,由于温度变化不是本研究的重点,因此忽略三大守恒定律中的能量守恒定律,采用质量守恒及动量守恒方程对泄洪雾化过程中的水、气运动进行描述。在对水气两相流进行研究时,通常采用单流体模型、VOF模型以及双流体模型[27, 32-33]。其中,单流体模型将水气混合流体视为一种特殊的单质流体,忽略了水气之间的相互作用,其求解与常规的单流体流动并无本质区别,能够从宏观上对水气混合流体的流动进行描述;而双流体模型分别对水、气的运动进行描述,建立两者之间的相互作用力模型,由于水气之间作用机理复杂,往往难以有完备的模型对其相间力进行准确描述,模型的引入导致求解难度增大以及计算结果不准确[33-36]。
本研究中首先采用单流体模型对泄洪雾化的宏观运动趋势进行描述,然后采用双流体模型对水、气各自的运动进行描述,最后对其进行联立求解。一方面能够从宏观上对水气混合流体的总体运动趋势进行描述,另一方面在双流体模型中引入单流体模型计算得到的部分结果能够显著降低求解的难度。
1.1 质量守恒方程将水气混合流体视为密度为ρM,运动速度为(uM, vM, wM)的单质流体,其质量守恒方程可表述为[37]:
| $ \frac{{\partial {\rho _{\rm{M}}}}}{{\partial t}} + {u_{\rm{M}}}\frac{{\partial {\rho _{\rm{M}}}}}{{\partial x}} + {v_{\rm{M}}}\frac{{\partial {\rho _{\rm{M}}}}}{{\partial y}} + {w_{\rm{M}}}\frac{{\partial {\rho _{\rm{M}}}}}{{\partial z}} + {\rho _{\rm{M}}}\left( {\frac{{\partial {u_{\rm{M}}}}}{{\partial x}} + \frac{{\partial {v_{\rm{M}}}}}{{\partial y}} + \frac{{\partial {w_{\rm{M}}}}}{{\partial z}}} \right) = 0。$ | (1) |
式中:t为时间;x, y, z分别为直角坐标系的坐标轴。式(1)描述了混合流体的密度随时间和空间的变化特性,建立的是混合流体密度与速度的关系。对混合流体而言,其密度和压力关系可表示为:
| $ {\rho _{\rm{M}}} = \frac{{{\rho _{{\rm{M0}}}}}}{{1 - \frac{{p - {p_0}}}{{{K_{\rm{M}}}}}}} = \frac{{{K_{\rm{M}}}{\rho _{{\rm{M0}}}}}}{{{K_{\rm{M}}} - p + {p_0}}}。$ | (2) |
式中:KM为混合流体的压缩模量,ρM0为混合流体在标准大气压条件下的密度,p为混合流体所受到的压力,p0为标准大气压,通常取101.325 kPa。
将式(2)代入到式(1)中,考虑到混合流体压缩模量KM远大于压力增量Δp=p0-p,故在分母中忽略掉压力增量部分,可得到由水气混合流体压力表示的质量守恒方程:
| $ \frac{1}{{{K_{\rm{M}}}}}\frac{{\partial p}}{{\partial t}} + \frac{1}{{{K_{\rm{M}}}}}\left( {{u_{\rm{M}}}\frac{{\partial p}}{{\partial x}} + {v_{\rm{M}}}\frac{{\partial p}}{{\partial y}} + {w_{\rm{M}}}\frac{{\partial p}}{{\partial z}}} \right) + \frac{{\partial {u_{\rm{M}}}}}{{\partial x}} + \frac{{\partial {v_{\rm{M}}}}}{{\partial y}} + \frac{{\partial {w_{\rm{M}}}}}{{\partial z}} = 0。$ | (3) |
在泄洪雾化过程中,水的运动也遵循质量守恒定律,在任一给定空间点上水的质量可用其浓度表示出来。基于质量守恒定律,水的传输方程可表示为:
| $ \frac{{\partial {C_1}}}{{\partial t}} + {u_1}\frac{{\partial {C_1}}}{{\partial x}} + {v_1}\frac{{\partial {C_1}}}{{\partial y}} + {w_1}\frac{{\partial {C_1}}}{{\partial z}} + {C_1}\left( {\frac{{\partial {u_1}}}{{\partial x}} + \frac{{\partial {v_1}}}{{\partial y}} + \frac{{\partial {w_1}}}{{\partial z}}} \right) = 0。$ | (4) |
式中:Cl为水的体积浓度,ul,vl,wl分别为水在x, y, z方向的速度。
鉴于空间内水、气的体积浓度存在互补关系(即Cl+Cg=1),故实际计算时,空间点气的浓度可通过水的浓度显式求解。
1.2 动量守恒方程水气混合流体在流动过程中同样遵循动量守恒定律。根据动量守恒,混合流体在某方向的动量变化等于外界传输量加上内、外力产生的量,在坐标轴3个方向上的动量变化可用关于水气混合流体速度的时空变化方程描述。
x方向:
| $ \begin{array}{l} \frac{{\partial {u_{\rm{M}}}}}{{\partial t}} + {u_{\rm{M}}}\frac{{\partial {u_{\rm{M}}}}}{{\partial x}} + {v_{\rm{M}}}\frac{{\partial {u_{\rm{M}}}}}{{\partial y}} + {w_{\rm{M}}}\frac{{\partial {u_{\rm{M}}}}}{{\partial z}} - \frac{{{\mu _{\rm{M}}}}}{{{\rho _{\rm{M}}}}}\left( {\frac{{{\partial ^2}{u_{\rm{M}}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{u_{\rm{M}}}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{u_{\rm{M}}}}}{{\partial {z^2}}}} \right) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\mu _{\rm{M}}}}}{{3{\rho _{\rm{M}}}}}\left( {\frac{{{\partial ^2}{u_{\rm{M}}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{v_{\rm{M}}}}}{{\partial xy}} + \frac{{{\partial ^2}{w_{\rm{M}}}}}{{\partial xz}}} \right) + \frac{1}{{{\rho _{\rm{M}}}}}\frac{{\partial p}}{{\partial x}} - {f_x} = 0。\end{array} $ | (5-1) |
y方向:
| $ \begin{array}{l} \frac{{\partial {v_{\rm{M}}}}}{{\partial t}} + {u_{\rm{M}}}\frac{{\partial {v_{\rm{M}}}}}{{\partial x}} + {v_{\rm{M}}}\frac{{\partial {v_{\rm{M}}}}}{{\partial y}} + {w_{\rm{M}}}\frac{{\partial {v_{\rm{M}}}}}{{\partial z}} - \frac{{{\mu _{\rm{M}}}}}{{{\rho _{\rm{M}}}}}\left( {\frac{{{\partial ^2}{v_{\rm{M}}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{v_{\rm{M}}}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{v_{\rm{M}}}}}{{\partial {z^2}}}} \right) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\mu _{\rm{M}}}}}{{3{\rho _{\rm{M}}}}}\left( {\frac{{{\partial ^2}{u_{\rm{M}}}}}{{\partial xy}} + \frac{{{\partial ^2}{v_{\rm{M}}}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{w_{\rm{M}}}}}{{\partial yz}}} \right) + \frac{1}{{{\rho _{\rm{M}}}}}\frac{{\partial p}}{{\partial y}} - {f_y} = 0。\end{array} $ | (5-2) |
z方向:
| $ \begin{array}{l} \frac{{\partial {w_{\rm{M}}}}}{{\partial t}} + {u_{\rm{M}}}\frac{{\partial {w_{\rm{M}}}}}{{\partial x}} + {v_{\rm{M}}}\frac{{\partial {w_{\rm{M}}}}}{{\partial y}} + {w_{\rm{M}}}\frac{{\partial {w_{\rm{M}}}}}{{\partial z}} - \frac{{{\mu _{\rm{M}}}}}{{{\rho _{\rm{M}}}}}\left( {\frac{{{\partial ^2}{w_{\rm{M}}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{w_{\rm{M}}}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{w_{\rm{M}}}}}{{\partial {z^2}}}} \right) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\mu _{\rm{M}}}}}{{3{\rho _{\rm{M}}}}}\left( {\frac{{{\partial ^2}{u_{\rm{M}}}}}{{\partial xz}} + \frac{{{\partial ^2}{v_{\rm{M}}}}}{{\partial yz}} + \frac{{{\partial ^2}{w_{\rm{M}}}}}{{\partial {z^2}}}} \right) + \frac{1}{{{\rho _{\rm{M}}}}}\frac{{\partial p}}{{\partial z}} - {f_z} = 0。\end{array} $ | (5-3) |
式中:μM为混合流体的粘滞系数,fx、fy、fz分别是重力加速度在x、y、z方向上的分量。
同样,对水气混合流体中的水单独使用动量守恒定律,可得到描述水相速度随时空演化的关系方程。
x方向:
| $ \begin{array}{*{20}{c}} {\frac{{\partial {u_1}}}{{\partial t}} + {u_1}\frac{{\partial {u_1}}}{{\partial x}} + {v_1}\frac{{\partial {u_1}}}{{\partial y}} + {w_1}\frac{{\partial {u_1}}}{{\partial z}} - \frac{{{\mu _1}}}{{{\rho _1}}}\left( {\frac{{{\partial ^2}{u_1}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{u_1}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{u_1}}}{{\partial {z^2}}}} \right) - }\\ {\frac{{{\mu _1}}}{{3{\rho _1}}}\left( {\frac{{{\partial ^2}{u_1}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{v_1}}}{{\partial xy}} + \frac{{{\partial ^2}{w_1}}}{{\partial xz}}} \right) + \frac{1}{{{\rho _1}}}\frac{{\partial P}}{{\partial x}} - {f_x} + \frac{{{\omega _x}}}{{{\rho _1}}} = 0}。\end{array} $ | (6-1) |
y方向:
| $ \begin{array}{*{20}{c}} {\frac{{\partial {v_1}}}{{\partial t}} + {u_1}\frac{{\partial {v_1}}}{{\partial x}} + {v_1}\frac{{\partial {v_1}}}{{\partial y}} + {w_1}\frac{{\partial {v_1}}}{{\partial z}} - \frac{{{\mu _1}}}{{{\rho _1}}}\left( {\frac{{{\partial ^2}{v_1}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{v_1}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{v_1}}}{{\partial {z^2}}}} \right) - }\\ {\frac{{{\mu _1}}}{{3{\rho _1}}}\left( {\frac{{{\partial ^2}{u_1}}}{{\partial xy}} + \frac{{{\partial ^2}{v_1}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{w_1}}}{{\partial yz}}} \right) + \frac{1}{{{\rho _1}}}\frac{{\partial p}}{{\partial y}} - {f_y} + \frac{{{\omega _y}}}{{{\rho _1}}} = 0}。\end{array} $ | (6-2) |
z方向:
| $ \begin{array}{*{20}{l}} \begin{array}{l} \frac{{\partial {w_1}}}{{\partial t}} + {u_1}\frac{{\partial {w_1}}}{{\partial x}} + {v_1}\frac{{\partial {w_1}}}{{\partial y}} + {w_1}\frac{{\partial {w_1}}}{{\partial z}} - \frac{{{\mu _1}}}{{{\rho _1}}}\left( {\frac{{{\partial ^2}{w_1}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{w_1}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{w_1}}}{{\partial {z^2}}}} \right) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\mu _1}}}{{3{\rho _1}}}\left( {\frac{{{\partial ^2}{u_1}}}{{\partial xz}} + \frac{{{\partial ^2}{v_1}}}{{\partial yz}} + \frac{{{\partial ^2}{w_1}}}{{\partial {z^2}}}} \right) + \frac{1}{{{\rho _1}}}\frac{{\partial p}}{{\partial z}} - {f_z} + \frac{{{\omega _z}}}{{{\rho _1}}} = 0。\end{array} \end{array} $ | (6-3) |
式中:ωz、ωy、ωz分别表示水气之间x、y、z方向的相间力;μl为水的粘滞系数。由于各方向水气混合流体动量等于该方向水的动量加上气的动量(如在x方向上:ρMuM=(Clρlul+Cgρgug),故气体的动量守恒方程不再单独列出。
1.3 本构方程求解中,需要确定混合流体的密度、粘滞性、压缩模量、水气相间力等参数的表达式。水气混合流体的密度主要取决于水、气各自的体积含量及其单相密度的大小,可表示为水、气密度对各自体积含量加权之和:
| $ {\rho _{\rm{M}}} = (1 - {C_1}){\rho _{{\rm{ g }}}} + {C_1}{\rho _{{\rm{ 1 }}}}。$ | (7) |
式中:ρg为气体密度,ρl为水的密度。因空气的密度相对较小,水气混合流体的密度主要取决于水的密度。
水气混合流体的压缩模量可表示为水、气相各自压缩模量及其体积含量的函数:
| $ {K_{\rm{M}}} = \frac{{{K_{\rm{g}}} \times {K_1}}}{{(1 - {C_1}) \times {K_1} + {C_1} \times {K_{\rm{g}}}}}。$ | (8) |
式中:Kg为气体的压缩模量,其数值大小通常等于气压力;Kl为水的压缩模量。
水气混合流体的粘滞性模型较多[38-41],本研究采用Beattie和Whalley模型[39]:
| $ {\mu _{\rm{M}}} = {\mu _1}(1 - {C_{\rm{g}}})(1 + 2.5{C_{\rm{g}}}) + {\mu _{\rm{g}}}{C_{\rm{g}}}。$ | (9) |
式中:μM为混合流体粘滞系数;μg为空气的粘滞系数。
水气之间的相间作用力种类繁多,形成的机理各不相同,大致可分为两类:一类是与相间相对运动无关的力,例如惯性力、压差力、表面张力等;另一类是与相间相对运动有关的力,例如形状升力、Magnas力、Suffman升力、附加质量力、Basset力、相间阻力等[33, 42-44]。目前描述这些相间力的公式都是经验性的,对不同的流动,参数的取值也各异。本研究将相间力表示为浓度和水气相对速度的函数,阻力系数采用Hench-Johnston阻力关系式[45],相对加速度采用Drew模型[46]:
| $ {\omega _i} = f({C_1},{u_{i1}} - {u_{i{\rm{g}}}}) = - 41.2{\rho _1}{C_1}{(1 - {C_1})^3}|{u_{i1}} - {u_{i{\rm{g}}}}|({u_{i1}} - {u_{i{\rm{g}}}}) - {C_{{\rm{vm}}}}{\rho _1}{C_1}(1 - {C_1})\left( {\frac{{d{u_{i1}}}}{{{\rm{d}}t}} - \frac{{d{u_{i{\rm{g}}}}}}{{{\rm{d}}t}}} \right)。$ | (10) |
式中:ωi为坐标轴i方向(x、y、z)的水气相间力;uil为水在i方向的速度;uig为空气在i方向的速度;Cvm为附加质量系数,一般依赖于气泡尺寸、掺气浓度等,利用Bataille等[47]的试验结果,水工高速掺气水流中Cvm的取值范围为1~10。
2 模型求解 2.1 求解策略水、气运动控制方程包含空间坐标的一阶和二阶导数项,需基于数值网格进行空间离散才能进行方程求解。考虑到有限元法在二阶导数离散较传统差分方法而言有较高的精度,故采用有限元法计算空间离散[48],采用迎风取权的有限元法离散传输项,采用非交叉取权的有限元方法离散一阶项[49]。以上离散方法可以兼顾传统有限元和有限体积法的优点,也可有效避免求解过程的数值震荡,提高了数值求解过程的稳定性和收敛性。
对于方程中涉及的一阶时间导数项,通常采用差分方法离散。差分法又可分为向前差分、中心差分、向后差分,可用公式表示为
| $ \frac{{\partial X}}{{\partial t}} = \frac{{{X^{n + 1}} - {X^n}}}{{\Delta t}},X = \eta {X^{n + 1}} + (1 - \eta ){X^n}。$ | (11) |
式中:n为时间步;Δt为时间步长;η为参数,当η=0时,为向前差分,η=1时,为向后差分,η=0.5时,为中心差分,η=2/3时,为伽辽金差分方案。在本研究中,采用中心差分法对时间项进行离散。
控制方程经时间和空间离散后,形成了关于基本未知量的非线性方程组。对于非线性方程组的求解,主要涉及求解过程中的数值稳定性和收敛性两个关键问题。数值稳定性和收敛性不仅与主元系数是否病态有关,也与求解方法及求解路径相关。为避免总方程组的严重病态,在计算中将压力场和速度场分开求解,然后通过两者间相互迭代计算来实现压力场与速度场间的相互关联。非线性迭代采用牛顿拉夫逊方法(Newton-Raphson method),最底层线性方程组求解采用BCGSTAB(the bi-conjugate gradient stabilized method)法。迭代求解过程中计算的收敛标准设定如下:
| $ {\rm{max}}\left( {\left| {\frac{{{P_{n + 1}} - {P_n}}}{{{P_n}}}} \right|} \right) \le {\varepsilon _P}, $ |
以及
| $ {\rm{max}}\left( {\left| {\frac{{{U_{n + 1}} - {U_n}}}{n}} \right|} \right) \le {\varepsilon _U}。$ |
式中:Pn+1为第n+1次迭代计算的压力;Pn为第n次迭代计算的压力;εP为压力迭代收敛标准,本计算设为10-3;Un+1为第n+1次迭代计算的速度;Un为第n次迭代计算的速度;εU为速度迭代收敛标准,本计算设为10-4。
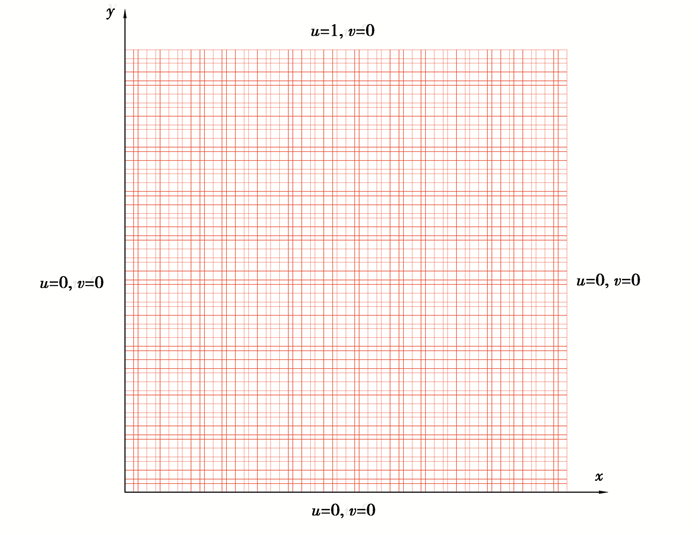
2.2 模型验证为验证模型的正确性,采用方腔驱动流对程序进行了考证[50-52]。计算网格及边界条件如图 1所示,网格数量为60×60;模型中设置初始浓度为0,顶部流速给定为1,计算了雷诺数为1 000时稳定的流场分布。
|
图 1 方腔驱动流动计算网格及边界条件 Fig. 1 Computational grid and boundary conditions of square cavity driven flow |
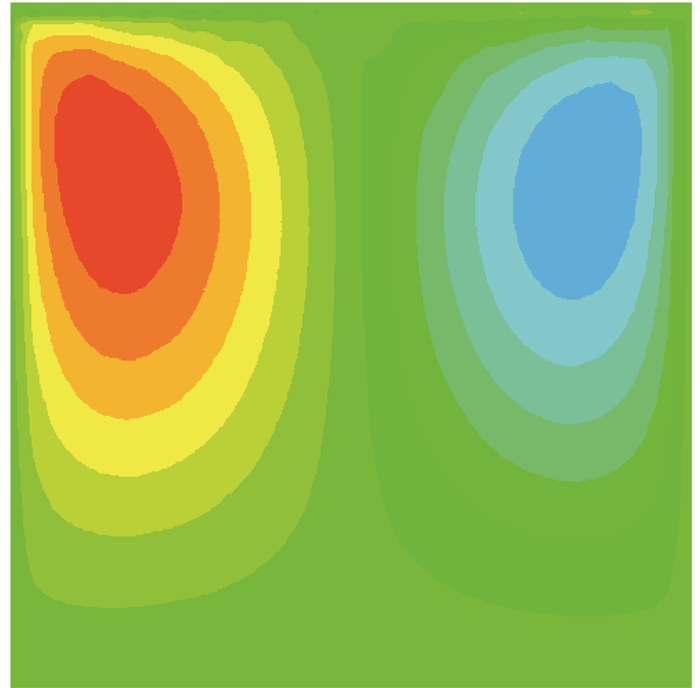
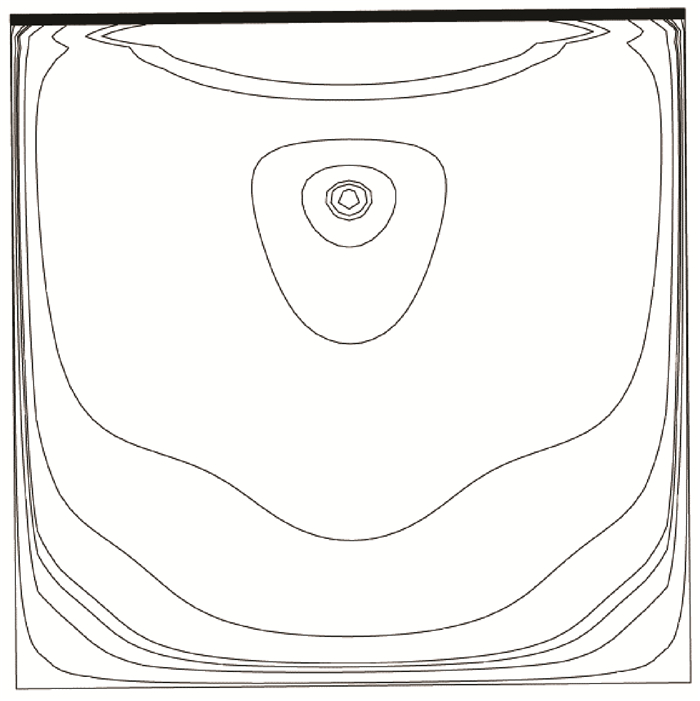
流场稳定时,方腔内x、y向速度分布如图 2所示,流线图如图 3所示,与文献[51]中的计算结果对比表明该模型对方腔驱动流动具有较好的模拟能力。
|
图 2 方腔驱动流动y方向速度分布云图 Fig. 2 Cloud diagram of y-direction velocity distribution of square cavity driving flow |
|
图 3 方腔驱动流动流线图 Fig. 3 Streamline diagram of square cavity driven flow |
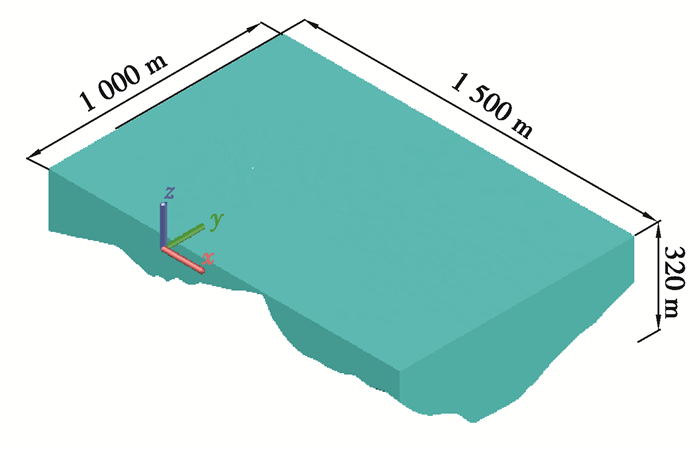
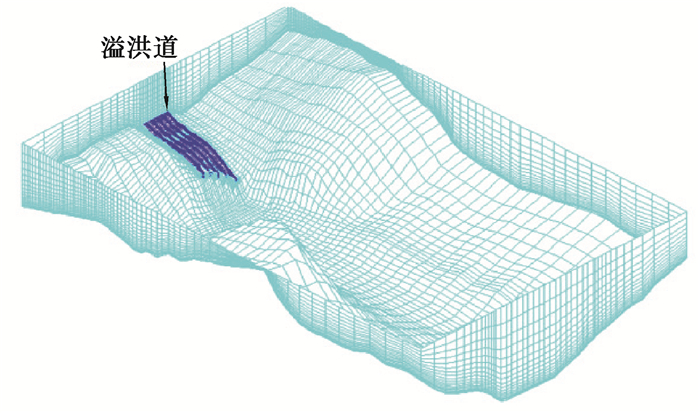
水布垭面板堆石坝采用岸边溢洪道宣泄洪水,溢洪道泄洪水头落差171 m,最大泄量18 320 m3/s。在进行三维数值建模时,以3号泄洪槽入口中心为起点,向下游延伸1 500 m,垂直河流方向向左右两岸各延伸500 m,高度方向从下游河床底部(海拔约180 m)起至海拔高程500 m,模型高度约320 m。模型范围覆盖水布垭电站溢洪道、马崖高边坡、大岩淌滑坡、电厂及其附属设施、大坝等关键部位。三维计算网格如图 4~5所示,共计64 216个节点,58 840个单元。
|
图 4 水布垭电站泄洪雾化数值计算模型范围 Fig. 4 Range of numerical calculation model for flood discharge atomization of Shuibuya Hydropower Station |
|
图 5 水布垭电站泄洪雾化计算网格 Fig. 5 Calculation grid of flood discharge atomization of Shuibuya Hydropower Station |
计算中所给定的边界条件如下:1)上游边界上除溢洪道进口外的节点采用三向速度约束,不考虑顺河向风的因素,x、y、z方向上速度设为0;2)下游面边界仅约束y向和z向速度,允许有顺河向速度。下游面边界给压力边界条件,其数值等于据尾水位和大气压算得的静水(气)压;3)左右面边界上的节点仅约束y向速度;4)地表面三向速度均约束,模型顶部的点约束水平向速度(x向和y向),允许有法向速度。模型顶部边界给压力边界条件,其数值为据所在的海拔高程算得的大气压力;5)溢洪道进口处边界节点给x向流速边界条件,速度的大小根据闸门开启情况、组合方式及下泄总流量计算得到,进口处节点水的体积分数(浓度)设为1。初始条件为:1)考虑到初始速度相对较小且难以准确获得,本计算中初始时刻空间内各节点水、气速度均设为0;2)水位以下的节点初始水相浓度设为1,水位以上设为0;3)各节点初始压力设为根据水气浓度分布算得的静水压力和静气压力。
涉及到的模型参数如表 1所示。
| 表 1 水布垭电站泄洪雾化计算模型参数 Table 1 Parameters of calculation model for flood discharge atomization of Shuibuya Hydropower Station |
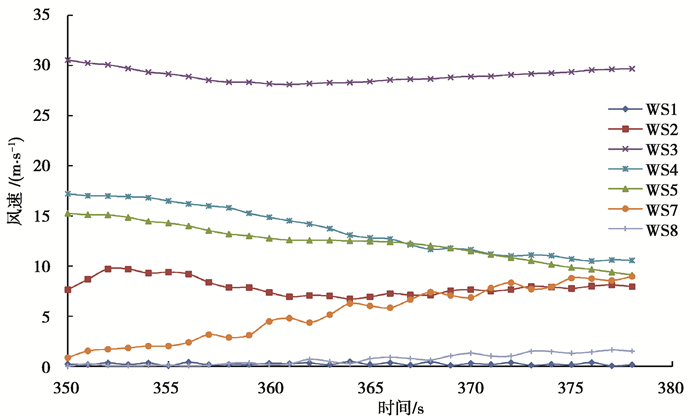
实际泄洪中所监测到的雾化风里既包含水也包含空气,因此,在数值计算中雾化风速对应水气混合流体的合速度。在计算中选定特定位置点(WS1~WS8)的风速与实测风速进行对比,计算结果表明,各部位的风速是不断变化的,随着时间变化而不断波动,但总体较为稳定(图 6)。
|
图 6 不同风速测点的计算风速随时间变化曲线 Fig. 6 Calculated wind speed changing with time at different wind-speed monitoring points |
将8个观测点在一段时间内的最大值、平均值与实测值对比(表 2)发现,测点的计算风速与实测风速的大小分布规律吻合度较好,例如,计算和实测平均风速、瞬时风速的最大值均为WS3测点位置,同样,较小风速分别出现在WS1和WS8测点位置。总体上计算得到的泄洪雾化风速比实测值小,总体偏差在±15%以内。造成这种偏差的主要原因有:1)受计算能力的限制,计算网格尺度较大,大的网格单元对实际风场分布有一定均化作用,使计算结果偏小;2)由于泄洪过程中外来风(如河谷风)具体情况未知,计算中忽略了外来风场的影响可能是导致计算风速整体小于实测风速的原因。
| 表 2 各测点计算风速与实测风速比较一览表 Table 2 Comparison of calculated wind speed and measured wind speed of each measuring point |
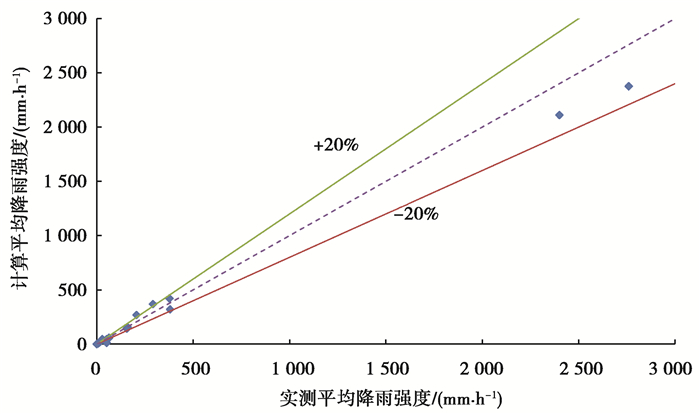
雾化降雨是由雾化风裹挟的水雾形成的,在泄洪雾化数值计算中,通常通过建立雾化降雨强度与雾化风速、水雾浓度之间的相关关系来求得雾雨强度[30, 53-54]。本研究中采用文献[53]所提出的雾雨转化公式,公式中的雾化风速以及水雾浓度均可通过模型直接求出。在水布垭电站2016年实际泄洪过程中,对水电站范围内不同位置处的降雨强度进行了监测,在计算中选取同样位置地表附近点的降雨强度进行对比。以实测平均降雨强度为横轴,计算平均降雨强度为纵轴,将实测结果与计算结果进行对比(图 7)。
|
图 7 计算平均降雨强度与实测平均降雨强度对比 Fig. 7 Comparison between the calculated average rainfall intensity and the measured average rainfall intensity |
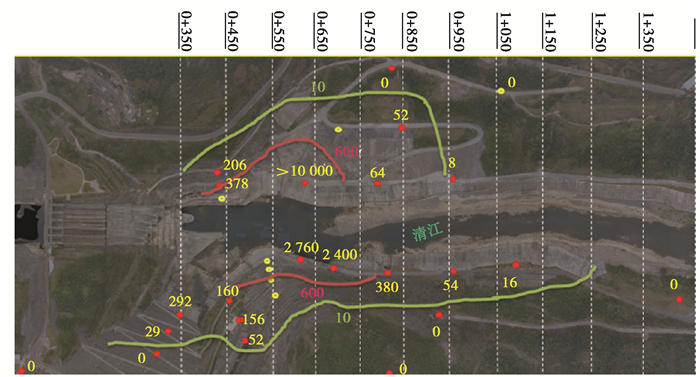
通过图 7可知,计算平均降雨强度与实测值的偏差约在±20%以内,综合考虑初始及外来风场的影响以及有限元网格均化等因素,认为计算结果与实测值较为吻合。在泄洪实测过程中,部分监测点的雾化降雨强度超过10 000 mm/h;在数值模拟中,泄洪中心区域的降雨强度也能达到这一量级(图 9),其出现的位置和量级与实际情况较为吻合,可见该数值方法对雾化降雨强度的预测范围较广。在雾化降雨的形成过程中,雾化风是输运雾滴的主要介质,模型预测得到的降雨强度较大的地方,往往与该处的风速值较为匹配,即雾化风速大的地方,其对应的雾化降雨强度也较大。为了进一步验证模型的预测能力,将实测的降雨强度分布与计算得到的降雨分布进行对比(图 8~9)。
|
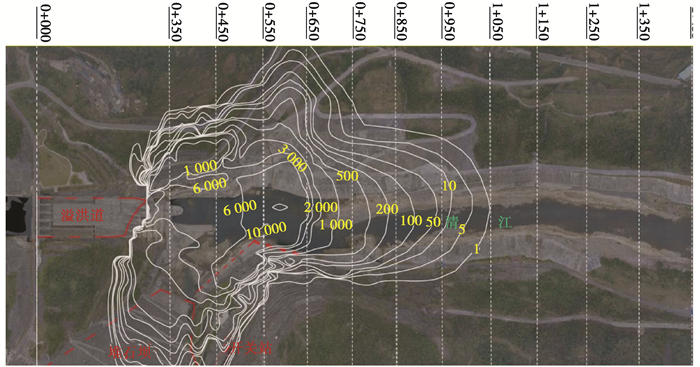
图 8 水布垭电站实测雾化降雨强度(单位:mm/h)分布(顶部0+350, …, 1+350是距溢洪道入口处的桩号),数据由湖北清江水电开发有限公司提供 Fig. 8 Distribution of measured atomization rainfall intensity in Shuibuya Hydropower Station, data provided by Hubei Qingjiang Hydroelectric Development Co., Ltd. |
|
图 9 计算得到的水布垭电站雾化降雨强度(单位:mm/h)分布 Fig. 9 Distribution of calculated atomization rainfall intensity of Shuibuya Hydropower Station |
对比图 8~9可知,模型计算得到的雾化降雨影响范围与实测基本一致,雾化降雨可影响到坝体下游1 km左右,实际泄洪过程中雾化降雨的影响范围比计算得到的影响范围大,这种差异性主要集中在降雨强度较小的区间。与实测值类似,计算得到的雾化降雨分布具有局部强度大、雨强分布变化快的特征,在较短的距离内,降雨强度从500 mm/h降为10 mm/h左右,尤其是在下游右岸马崖高边坡附近,雾化降雨强度变化最为剧烈。根据图 9可知,河谷地形会影响水雾的传输扩散,雾雨强度在水电站下游左右岸呈不对称分布,电站下游左岸坡体较缓,雾化降雨扩散的范围相对较广;而右岸坡体较陡,阻挡了雾化降雨的传输扩散,导致右岸的雾化影响区域小于左岸。数值模拟中考虑了河谷三维地形的影响,因此,数值模拟得到雾化降雨的规律与实测得到的类似。
4 结论目前已有的泄洪雾化研究大多以模型试验以及半经验半理论的数学模型为主,对高坝泄洪过程中的降雨强度及风速预测往往不够准确。笔者基于水气两相流原理从描述物质运动的质量及动量守恒定律的角度,对水气混合流体及水相运动进行了数学描述,采用有限元法对泄洪过程进行了数值求解,进而预测了泄洪雾化过程中的风场和雨场。通过与实测结果对比发现,数值模拟得到的预测结果具有一定的可靠性。
采用数值模拟方法对泄洪雾化进行研究,能够综合考虑河谷地形、水气间相互作用等因素的影响,不受相似比尺的限制,从而克服了传统模型试验及经验性模型的不足,是对泄洪雾化研究的有效补充。尽管如此,该数值方法仍需要进一步验证和完善,从而对雾化产生的机理进行进一步分析,提高预测精度,为保障中国西南地区高坝、特高坝的泄洪安全提供理论和技术支撑,从而保证中国水电资源开发的和谐持续健康发展。
致谢
湖北清江水电开发有限公司为本研究提供了2016年水布垭面板堆石坝的泄洪实测数据,在此表示感谢。
| [1] |
练继建, 刘丹, 刘昉. 中国高坝枢纽泄洪雾化研究进展与前沿[J]. 水利水电快报, 2019, 40(5): 5. LIAN Jijian, LIU Dan, LIU Fang. Research progress and frontiers on flood discharge atomization of Chinese high dam projects[J]. Express Water Resources & Hydropower Information, 2019, 40(5): 5. (in Chinese) |
| [2] |
Lian J J, Li C Y, Liu F, et al. A prediction method of flood discharge atomization for high dams[J]. Journal of Hydraulic Research, 2014, 52(2): 274-282. |
| [3] |
Liu S H, Sun X F, Luo J. Unified model for splash droplets and suspended mist of atomized flow[J]. Journal of Hydrodynamics, 2008, 20(1): 125-130. |
| [4] |
庞博慧, 马洪琪. 高海拔地区气压环境对高速水流水舌挑距的影响[J]. 水力发电学报, 2018, 37(2): 88-95. PANG Bohui, MA Hongqi. Influence of low atmospheric pressure on trajectory distance of high velocity jet nappes at high altitude[J]. Journal of Hydroelectric Engineering, 2018, 37(2): 88-95. (in Chinese) |
| [5] |
Lu S Q, Xu M. Stability analysis of engineering slope under flood discharging atomization rain[C]//2010 International Symposium on Multi-Field Coupling Theory of Rock and Soil Media and Its Applications. Sydney: Orient Academic Forum, 2010: 640-645.
|
| [6] |
张华.水电站泄洪雾化理论及其数学模型的研究[D].天津: 天津大学, 2003. ZHANG Hua. Study on the theory of flood discharging atomization and it's mathematic model in hydropower station[D]. Tianjin: Tianjin University, 2003.(in Chinese) |
| [7] |
刘宣烈, 安刚, 姚仲达. 泄洪雾化机理和影响范围的探讨[J]. 天津大学学报, 1991, 24(S1): 30-36. LIU Xuanlie, AN Gang, YAO Zhongda. The investination on the mechanism and sphere of influence of atomization by discharge flow[J]. Journal of Tianjin University, 1991, 24(S1): 30-36. (in Chinese) |
| [8] |
陈惠玲, 李定方, 黄颖蕾.泄洪雾化的雨和雾研究[C]//第十六届全国水动力学研讨会.上海: 《水动力学研究与进展》杂志社, 2002: 209-220. CHEN Huiling, LI Dingfang. Study on the rainfall and fog in the flood discharge atomization[C]//The 16th National Symposium on Hydrodynamics. Shanghai: Editorial Office of Chinese Journal of Hydrodynamics, 2002: 209-220. (in Chinese) |
| [9] |
Liu S. Study of the atomized flow in hydraulic engineering[J]. Journal of Hydrodynamics (Serial B), 1999, 11(2): 77-83. |
| [10] |
秦蕊, 朱燕梅, 田健秋, 等. 高坝泄洪雾化研究进展及雾化雨对边坡的稳定影响分析[J]. 中国农村水利水电, 2015(9): 153-156. QIN Rui, ZHU Yanmei, TIAN Jianqiu, et al. Research progress of high dam flood discharge atomization and analysis of influence of atomization rain on slope stability[J]. China Rural Water and Hydropower, 2015(9): 153-156. (in Chinese) |
| [11] |
姚克烨, 曲景学. 挑流泄洪雾化机理与分区研究综述[J]. 东北水利水电, 2007, 25(4): 7-9, 71. YAO Keye, QU Jingxue. Summarization of trajectory flood discharging atomization mechanism and subzone study[J]. Water Resources & Hydropower of Northeast China, 2007, 25(4): 7-9, 71. (in Chinese) |
| [12] |
Liu H T, Liu Z P, Xia Q F, et al. Computational model of flood discharge splash in large hydropower stations[J]. Journal of Hydraulic Research, 2015, 53(5): 576-587. |
| [13] |
Duan H D, Liu S H, Luo Q S, et al. Rain intensity distribution in the splash region of atomized flow[J]. Journal of Hydrodynamics, 2006, 18(3): 362-366. |
| [14] |
梁在潮. 雾化水流计算模式[J]. 水动力学研究与进展(A辑), 1992, 7(3): 247-255. LIANG Zaichao. A computation model for atomization flow[J]. Journal of Hydrodynamics (Serial A), 1992, 7(3): 247-255. (in Chinese) |
| [15] |
吴修锋, 吴时强, 周辉, 等. 湾塘水电站泄洪雾化原型观测[J]. 水利水运工程学报, 2001(4): 71-74. WU Xiufeng, WU Shiqiang, ZHOU Hui, et al. Atomization measurement for Wantang Hydroplant[J]. Hydro-Science and Engineering, 2001(4): 71-74. (in Chinese) |
| [16] |
陈端, 金峰, 李静. 高坝泄洪雾化降雨强度模型律研究[J]. 水利水电技术, 2005, 36(10): 47-49. CHEN Duan, JIN Feng, LI Jing. Study on model law for intensity of rainfall from atomization of flood-discharging flow for high dam[J]. Water Resources and Hydropower Engineering, 2005, 36(10): 47-49. (in Chinese) |
| [17] |
陈端, 金峰, 张鹤. 构皮滩工程大坝泄洪雾化物理模型试验研究[J]. 湖北水力发电, 2007(3): 48-51. CHEN Duan, JIN Feng, ZHANG He. Physical model test for flood discharge atomization of Goupitan Hydropower Project[J]. Hubei Water Power, 2007(3): 48-51. (in Chinese) |
| [18] |
吴时强, 吴修锋, 周辉, 等. 底流消能方式水电站泄洪雾化模型试验研究[J]. 水科学进展, 2008, 19(1): 84-88. WU Shiqiang, WU Xiufeng, ZHOU Hui, et al. Model experiment study of effect of discharge atomization for energy dissipation by hydraulic jump[J]. Advances in Water Science, 2008, 19(1): 84-88. (in Chinese) |
| [19] |
Falvey H T. Air-water flow in hydraulic structures: engineering monograph No. 41[R]. Denver: Water and Power Resources Service, 1980.
|
| [20] |
Zhou H, Wu S, Chen H, et al. Similarity criterion of flood discharge atomization[J]. Water Science and Engineering, 2008, 1(2): 59-65. |
| [21] |
张华, 练继建. 应用水滴随机喷溅数学模型预测挑流泄洪雾化的雨强分布[J]. 三峡大学学报(自然科学版), 2004, 26(3): 210-213. ZHANG Hua, LIAN Jijian. Application of mathematic model of water drops random spattering to prediction ofrainfall intensity distribution in deflecting flood release and atomization[J]. Journal of China Three Gorges University(Natural Sciences), 2004, 26(3): 210-213. (in Chinese) |
| [22] |
曾理, 路前平, 魏艳婷, 等. 加纳布维水电站泄洪雾化降雨强度模糊综合评判预报[J]. 西北水电, 2014(3): 75-78. ZENG Li, LU Qianping, WEI Yanting, et al. Fuzzing comprehensive judgment and predication of flood-discharge atomized rainfall intensity[J]. Northwest Hydropower, 2014(3): 75-78. (in Chinese) |
| [23] |
戴丽荣, 张云芳, 张华, 等. 挑流泄洪雾化影响范围的人工神经网络模型预测[J]. 水利水电技术, 2003, 34(5): 7-9, 63. DAI Lirong, ZHANG Yunfang, ZHANG Hua, et al. An artificial neural network model of flood discharge atomization prediction of hydropower station[J]. Water Resources and Hydropower Engineering, 2003, 34(5): 7-9, 63. (in Chinese) |
| [24] |
柳海涛, 刘之平, 孙双科. 水舌入水喷溅的随机数学模型[J]. 水利水电科技进展, 2009, 29(6): 1-4. LIU Haitao, LIU Zhiping, SUN Shuangke. Stochastic mathematical model of splashing from water jets[J]. Advances in Science and Technology of Water Resources, 2009, 29(6): 1-4. (in Chinese) |
| [25] |
张华, 练继建, 李会平. 挑流水舌的水滴随机喷溅数学模型[J]. 水利学报, 2003, 34(8): 21-25. ZHANG Hua, LIAN Jijian, LI Huiping. Mathematical model of droplet randomly formed by splash of nappe[J]. Journal of Hydraulic Engineering, 2003, 34(8): 21-25. (in Chinese) |
| [26] |
周辉, 陈慧玲. 挑流泄洪雾化降雨的模糊综合评判方法[J]. 水利水运科学研究, 1994(1): 165-170. ZHOU Hui, CHEN Huiling. Method of fuzzy synthetic evaluation for atomization-rain of jet overflow[J]. Hydro-Science and Engineering, 1994(1): 165-170. (in Chinese) |
| [27] |
谭立新, 许唯临, 杨永全, 等. 水气二相流特点及其单流体模型[J]. 西安理工大学学报, 2000, 16(3): 280-283. TAN Lixin, XU Weilin, YANG Yongquan, et al. Behaviors of air-water two-phase flow and its homogeneous model[J]. Journal of Xi'an University of Technology, 2000, 16(3): 280-283. (in Chinese) |
| [28] |
许唯临, 王韦, 谭立新, 等. 水工水气两相流的数值模拟[J]. 水动力学研究与进展(A辑), 2001, 16(2): 225-229. XU Weilin, WANG Wei, TAN Lixin, et al. Numerical simulation of air-water two-phase flows in hydraulic engineering[J]. Journal of Hydrodynamics (Serial A), 2001, 16(2): 225-229. (in Chinese) |
| [29] |
沙海飞, 周辉, 吴时强, 等. 坝身泄洪水气两相流二维数值模拟[J]. 水动力学研究与进展(A辑), 2007, 22(3): 311-316. SHA Haifei, ZHOU Hui, WU Shiqiang, et al. 2-D Numerical simulation of two-phase flow from surface outlet into plunge pool[J]. Journal of Hydrodynamics (Serial A), 2007, 22(3): 311-316. (in Chinese) |
| [30] |
柳海涛, 孙双科, 刘之平. 泄洪雨雾输运模型及其计算验证[J]. 水利水电科技进展, 2011, 31(4): 45-48, 94. LIU Haitao, SUN Shuangke, LIU Zhiping. Mathematical model for rain-fog transportation during flood discharge and its verification[J]. Advances in Science and Technology of Water Resources, 2011, 31(4): 45-48, 94. (in Chinese) |
| [31] |
Hirt C, Nichols B. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201-225. |
| [32] |
刘大有. 关于二相流、多相流、多流体模型和非牛顿流等概念的探讨[J]. 力学进展, 1994, 24(1): 66-74. LIU Dayou. Discussion on the concepts of two-phase flow, multiphase flow, multifluid model and non-Newtonian flow[J]. Advances in Mechanics, 1994, 24(1): 66-74. (in Chinese) |
| [33] |
谭立新.水气二相流数值模拟研究[D].成都: 四川大学, 1999. TAN Lixin. Mathematical modelling of air-water two-phase flows[D]. Chengdu: Sichuan University, 1999.(in Chinese) |
| [34] |
刘大有. 论气体混合物和两相流中的压强和热流[J]. 力学学报, 1986, 18(6): 492-501. LIU Dayou. On pressure and thermal flux in gas-mixture flow and in two-phase flow[J]. Acta Mechanica Sinica, 1986, 18(6): 492-501. (in Chinese) |
| [35] |
Sokolichin A, Eigenberger G, Lapin A. Simulation of buoyancy driven bubbly flow:Established simplifications and open questions[J]. AIChE Journal, 2004, 50(1): 24-45. |
| [36] |
Drew D A. Mathematical modeling of two-phase flow[J]. Annual Review of Fluid Mechanics, 1983, 15(1): 261-291. |
| [37] |
Wallis G B. One-dimensional two-phase flow[M]. New York: McGraw-Hill Book Company, 1969.
|
| [38] |
Einstein A. A new determination of molecular dimensions[J]. Annalen der Physik, 1906, 19: 289-306. |
| [39] |
Beattie D R H, Whalley P B. A simple two-phase frictional pressure drop calculation method[J]. International Journal of Multiphase Flow, 1982, 8(1): 83-87. |
| [40] |
Dukler A E, Wicks M, Cleveland R G. Frictional pressure drop in two-phase flow:B. an approach through similarity analysis[J]. AIChE Journal, 1964, 10(1): 44-51. |
| [41] |
刘刚, 童富果, 刘创, 等. 考虑掺混程度的水气混合流体动力黏滞性模型[J]. 水动力学研究与进展(A辑), 2019, 34(5): 645-654. LIU Gang, TONG Fuguo, LIU Chuang, et al. Dynamic viscosity model of water-air two-phase mixture fluid considering mixing degree[J]. Chinese Journal of Hydrodynamics (Serial A), 2019, 34(5): 645-654. (in Chinese) |
| [42] |
张宏伟, 刘之平, 张东, 等. 掺气水流声速的研究[J]. 水利学报, 2013, 44(9): 1015-1022. ZHANG Hongwei, LIU Zhiping, ZHANG Dong, et al. Study on the sound velocity in an aerated flow[J]. Journal of Hydraulic Engineering, 2013, 44(9): 1015-1022. (in Chinese) |
| [43] |
张宏伟.掺气水流双流体模型数值模拟研究[D].西安: 西安理工大学, 2002. ZHANG Hongwei. Study on numerical simulation of aerated water flow with a two-fluid model[D]. Xi'an: Xi'an University of Technology, 2002.(in Chinese) |
| [44] |
赵建福, 李炜. 可压缩掺气水流的一维特征分析[J]. 水动力学研究与进展(A辑), 1999, 14(1): 1-7. ZHAO Jianfu, LI Wei. The characteristic analysis of one dimensional compressible aerated flows[J]. Journal of Hydrodynamics (Serial A), 1999, 14(1): 1-7. (in Chinese) |
| [45] |
Hench J E, Johnston J P. Two-dimensional diffuser performance with subsonic, two-phase, air-water flow[J]. Journal of Basic Engineering, 1972, 94(1): 105-119. |
| [46] |
Sharma S L, Ishii M, Hibiki T, et al. Beyond bubbly two-phase flow investigation using a CFD three-field two-fluid model[J]. International Journal of Multiphase Flow, 2019, 113: 1-15. |
| [47] |
Kim J H, Rohatgi U S, Hashemi A, et al. Advances in gas-liquid flows, 1990: presented at the Winter Annual Meeting of the American Society of Mechanical Engineers, Dallas, Texas, November 25-30, 1990[M]. New York: ASME, 1990.
|
| [48] |
Zienkiewicz O C, Taylor R L. The finite element method: basic formulation and linear problems[M]. New York: McGraw-Hill, 2000.
|
| [49] |
刘卫东, 王振国, 周进. 采用二阶迎风格式的PISO算法研究[J]. 航空动力学报, 1998, 13(1): 81-84. LIU Weidong, WANG Zhenguo, ZHOU Jin. Application of a second-order upwind scheme to PISO algorithm[J]. Journal of Aerospace Power, 1998, 13(1): 81-84. (in Chinese) |
| [50] |
赵博渊, 李江飞, 王雅菲, 等. SIMPLE算法方腔流动数值仿真[J]. 辽宁化工, 2016, 45(6): 760-763. ZHAO Boyuan, LI Jiangfei, WANG Yafei, et al. Calculation of driven square cavity flow based on SIMPLE method[J]. Liaoning Chemical Industry, 2016, 45(6): 760-763. (in Chinese) |
| [51] |
杨晶. 基于Simple算法的方腔驱动流问题数值模拟[J]. 电力学报, 2010, 25(1): 88-90. YANG Jing. Numerical simulation of the driven cavity flow based on simple method[J]. Journal of Electric Power, 2010, 25(1): 88-90. (in Chinese) |
| [52] |
马龙, 刘侃, 任卫武, 等. 应用LAMPS求解方腔驱动流问题[J]. 价值工程, 2016, 35(25): 207-209. MA Long, LIU Kan, REN Weiwu, et al. LAMPS used to solve cavity driven flow problem[J]. Value Engineering, 2016, 35(25): 207-209. (in Chinese) |
| [53] |
李建会, 冉从勇, 何兰. 猴子岩水电站泄洪雾化区堆积体治理设计[J]. 人民长江, 2014, 45(8): 51-54. LI Jianhui, RAN Congyong, HE Lan. Control design for deposit body in flood-discharge atomization zone of Houziyan Hydropower Station[J]. Yangtze River, 2014, 45(8): 51-54. (in Chinese) |
| [54] |
陈辉, 姜伯乐, 陈端. 某电站泄洪雾流降雨数值计算研究[J]. 长江科学院院报, 2013, 30(8): 58-62. CHEN Hui, JIANG Bole, CHEN Duan. Study on the flood discharging atomization in hydropower station by mathematical model[J]. Journal of Yangtze River Scientific Research Institute, 2013, 30(8): 58-62. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43


