云计算集成了分布在不同设备上的硬件和软件资源,以便协同工作,其中软件、硬件和平台资源以服务的形式打包和交付。亚马逊、谷歌和IBM等公司面向市场提供云数据库、云服务器,这些服务以基础设施即服务(IaaS, infrastructure as a service)、平台即服务(PaaS, platform as a service)和软件即服务(SaaS, software as a service)等形式提供[1]。同时,用户可将数据和程序以服务的形式部署到云上,以低成本获得极大的灵活性。当单个服务不能满足用户提出的复杂需求时,自动化选择多个已有服务并将其组合在一起解决的复杂任务[2]。云上存在大量服务,如何选择合适的服务组合并满足功能性与非功能性的要求是一个NP难问题[3]。当前,服务质量(QoS, quality of service)感知的Web服务组合已进行了广泛的研究,从服务组合的场所看,分为基于内存的服务组合[4]和基于数据库的服务组合[3]。在内存中进行服务组合比较灵活,但受限于内存大小,且会重复组合。基于数据库实现的可将经常使用的组合存储起来,提升搜索速度。从优化的程度看,分为全局性优化和局部优化。布谷鸟搜索算法[5]是一种全局优化算法,可解决服务组合问题,通过在地理分布式云环境中应用此方法来评估,该方法可以找到接近最优的解。文献[4]提出一种基于综合QoS与规划图的服务组合方法,这是一种局部优化算法,使用模糊层次分析法(FAHP, fuzzy analytic hierarchy process)与熵权法合成综合QoS,然后在规划图的后向搜索过程中选择当前最优的服务。为解决服务定价问题,文献[6]制定了一个非合作服务定价博弈,为多个提供商战略性地投标如何提供和定价他们的基本服务,并建立纳什均衡作为最终服务组合方案。服务在物理空间上分布在云端和边缘端,文献[7]对服务组合在云边缘下进行优化,提出了一种优化的服务缓存策略,以提高服务提供系统的性能。此外,服务生态系统演化问题也受到了学术界的关注[8]。
为了继续探索解决方法,笔者在有向二分图的基础上提出服务组合图,利用Neo4j图数据库的大存储空间与顶点边关联的图形结构,使用最少服务数组合查询和Dijkstra搜索算法来寻找服务数量最少或QoS优化的解决方案。研究的主要贡献如下:
其一,在带索引的图数据库中,基于有向二分图构建服务组合图,解决服务组合问题。
其二,根据服务的可用性,对图数据库中构建的服务组合图进行更新,以保证服务组合图的有效性。
其三,经实验验证,基于图数据库的服务组合,可以减少服务组合过程中内存占用量,且速度快。
1 相关工作物联网和云服务成功推动了边缘计算的发展[8]。移动边缘计算技术解决服务请求的响应时间、电池寿命限制、带宽的消耗,以及数据的安全及隐私等问题。文献[9]在边缘计算模型下提出基于物联网(IoT, internet of things)服务驱动的组合方法,网络延时可以被有效降低。首先,介绍了移动边缘计算模型。然后,基于边缘计算模型提出一种消耗导向的搜索算法来决定缓存的策略。利用缓存策略,合适的服务被存储到边缘服务器上,为用户提供更好的服务。为了解决边缘计算服务器放置问题,文献[10]把问题抽象成多目标约束的优化问题,即在移动用户和边缘服务器之间平衡工作负载和最小化延迟,并使用混合整数规划算法找到优化的解决方案。文献[11]不仅专注于服务的有效组合,而且从能源消耗角度去考虑,并把问题抽象成多目标优化问题,使用0~1线性规划找到优化的解决方案。
由于动态关联数据的增长,越来越多的数据库以图的形式存储数据。以语义网为例,其关联数据要求采用资源描述框架(RDF, resource description framework)三元组模型,这种模型更适合采用图而不是关系型数据库模式[12]。当前,图数据库已经应用到各个领域[13],如知识图谱、生物工程、社交分析、地理信息处理等。文献[14]提出了基于Neo4j图数据库的领域本体过程。其专注于油田本体的数据存储和信息检索,并设计了来自本体文件的映射规则来规范Neo4j数据库,这可以大大减少所需的存储空间并提高检索效率。在服务组合领域,文献[15]提出一种基于遗传算法和图数据库的服务组合方法,首先根据存储在图数据库中的信息生成新的组合,然后使用遗传算法优化其质量。然而,它是针对特定目标进行优化的。笔者提出一种不针对预设目标的预连接的服务组合图,其预处理服务组合并将其作为路径存储在图数据库的有向二分图中,使用Dijkstra算法获取服务组合解决方案,并对图数据库中构建的服务组合图进行更新,以保证服务组合图的有效性。
2 背景知识 2.1 QoS感知的服务组合定义1 服务w可以用三元组(win, wout, Q)来表示。其中,win是w的一组输入参数,只有当服务的所有输入参数都满足时,服务才会被唤醒;wout是w的一组输出参数;Q是w的一组非功能属性。
通常,服务的描述有2个部分:功能属性和非功能属性。非功能属性QoS标准决定了服务的可用性和实用性。文中将响应时间、吞吐量、花费作为服务的QoS标准。
响应时间(R):开始收到查询消息到发送响应消息的时间间隔(单位:ms)。
吞吐量(T):经由通信信道成功传递消息的平均速率,例如每秒10次成功调用(单位:requests /s)。
花费(C):用户为使用Web服务资源所付出的代价(单位:元)。
由于不同的QoS标准具有不同的量纲和单位,因此需要归一化QoS标准,使其具有可比性。使用最小最大归一化技术,QoS标准之间的差异可以忽略不计,并且可以保留QoS值的原始分布。文中利用方程(1)对吞吐量进行归一化,利用方程(2)对响应时间进行归一化,利用方程(3)对花费进行归一化。
| $ T({w_j}) = \left\{ \begin{array}{l} \frac{{{T^{{\rm{max}}}} - T({w_j})}}{{{T^{\max }} - {T^{\min }}}},{\rm{if}}\;{T^{\max }} - {T^{\min }} \ne 0,\\ \begin{array}{*{20}{c}} {}&{1,}&{} \end{array}\;\;\;\;\;\;\;\;\;{\rm{if}}\;{T^{\max }} - {T^{\min }} = 0, \end{array} \right. $ | (1) |
| $ R({w_j}) = \left\{ \begin{array}{l} \frac{{R({w_j}) - {R^{\min }}}}{{{R^{\max }} - {R^{\min }}}},{\rm{if}}\;{R^{\max }} - {R^{\min }} \ne 0,\\ \begin{array}{*{20}{c}} {}&{1,}&{} \end{array}\;\;\;\;\;\;\;\;\;{\rm{if}}\;{R^{\max }} - {R^{\min }} = 0, \end{array} \right. $ | (2) |
| $ C({w_j}) = \left\{ \begin{array}{l} \frac{{C({w_j}) - {C^{{\rm{min}}}}}}{{{C^{\max }} - {C^{\min }}}},{\rm{if}}\;{C^{\max }} - {C^{\min }} \ne 0,\\ \begin{array}{*{20}{c}} {}&{1,}&{} \end{array}\;\;\;\;\;\;\;\;\;{\rm{if}}\;{C^{\max }} - {C^{\min }} = 0, \end{array} \right. $ | (3) |
式中:T代表吞吐量,requests/s;R代表响应时间,ms;C代表花费,元;wj代表Web服务。归一化的QoS值越小表示质量越高。
定义2 Web服务组合问题可以用四元组(S, Cin, Cout, Q)来表示。其中:S是服务的有限集;Cin是输入参数有限集;Cout是输出参数有限集;Q是服务质量的有限集。
Web服务可以按照顺序的方式连接,也可以按照并行的方式连接。顺序连接的服务是一个接一个被唤醒的(w1; w2; …; wn), 并行连接的服务是并行着被唤醒的(w1||w2||…||wn)。可以使用单一QoS维度来表示一个组合的性能,并通过任一标准比较不同组合的QoS值。
| $ R({w_1};{w_2}; \ldots ;{w_n}) = \sum {R({w_i}),} $ | (4) |
| $ R({w_1}||{w_2}||{w_3}|| \ldots ||{w_n}) = \max R({w_i}), $ | (5) |
| $ T({w_1};{w_2}; \ldots ;{w_n}) = \min T({w_i}), $ | (6) |
| $ T({w_1}||{w_2}||{w_3}|| \ldots ||{w_n}) = \min T({w_i}), $ | (7) |
| $ C({w_1};{w_2}; \ldots ;{w_n}) = \sum {C({w_i}),} $ | (8) |
| $ C({w_1}||{w_2}||{w_3}|| \ldots ||{w_n}) = \sum {C({w_i}).} $ | (9) |
Web本体语言(OWL, Web ontology language)[16]通过使用本体将服务的前提条件和效果表示为“概念”,并定义概念之间的关系。在文中,Web服务的输入和输出参数也是“概念”的实例,“概念”是服务的前提和效果。通常,服务的匹配度定义为精确匹配度(exact)、插件匹配度(plug-in)、子类匹配度(subsume)和失败匹配度(fail)[17]。文中利用精确匹配度和子类匹配度对服务进行匹配。
精确匹配:如果w的输出参数wout与w′的输入参数w′in是等价的概念;则形式上为Τ|=wout≡w′in。
子类匹配:如果wout是w′in的一个超概念;则形式上为T|=w′inwout。
2.2 Web服务组合定义3 有向二分图是用G = (V, E)表示的二分图。图的顶点分为两个不相交的独立集合V1和V2;图的有向边表示为集合E,其中{∀(i, j)∈E|(i∈V2∧j∈V1)∨(i∈V1∧j∈V2)}。
定义4服务组合图是有向二分图,表示为SC=(V, E),其中V=C∪S。C是所有服务的一组输入或输出参数,其中{∀c∈C|c是一个服务的所有输入参数集∨c是一个服务的所有输出参数集};S是所有服务的一组集合,其中,{∀w∈S|win∈C∧wout∈C};E是一组有向边的集合,其中,{∀w1∈S, ∃(c, w1)∈E(c=w1.in)∨{∀w1∈S, ∃(w1, c)∈E(c=w1.out)∨∀w1∈S, ∃(w1, w2.in)∈E(∃w2∈S, ∀p∈w2.in, ∃q∈w1.out, p⊑q)}∨{∀w1∈S, ∃(w1, w2.out)∈E(∃w2∈S, ∀p∈w2.out, ∃q∈w1.in, p⊑q)。
定义5服务组合图SCG=(V, E)的路径可以用一个四元组(S, Cin, Cout, Q)来表示。其中,S={w1, …, wk, …, wn|1≤k≤n∧wk∈S}是一个服务序列,并且{∀wk∈S|wk.in⊆wk-1.out∧1<k≤n};Cin=
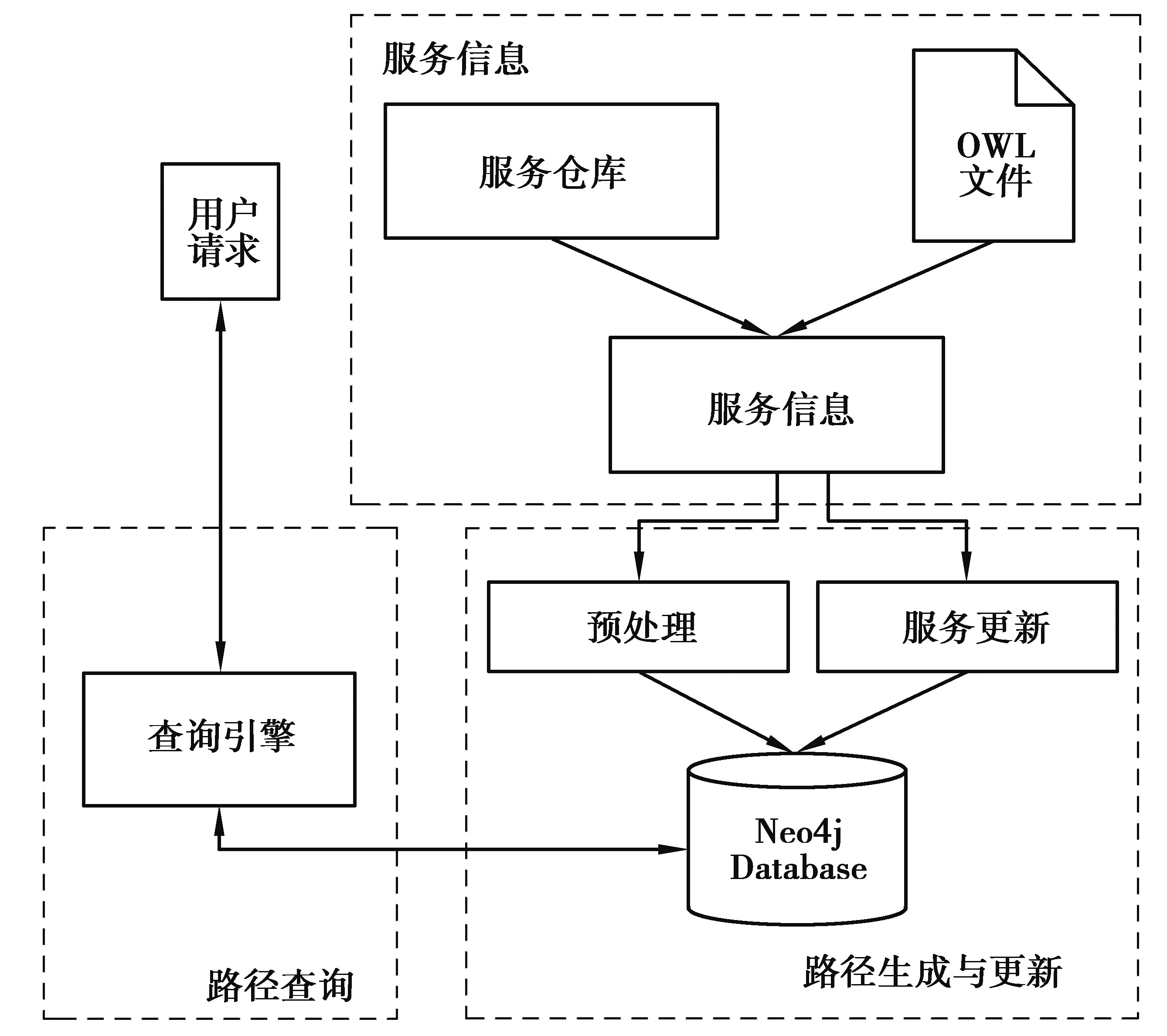
文中提出的系统架构由3个模块组成:服务信息模块、路径生成与更新模块和路径查询模块,如图 1所示。
|
图 1 系统架构 Fig. 1 System architecture |
服务信息模块:该模块用于解析Web服务信息和本体。其中,Web服务被加载到“服务仓库”中,服务的本体描述定义在“OWL文件”中,服务的名称、输入、输出和QoS值等服务信息存储在“服务信息”中。
路径生成模块:该模块计算服务组合的所有路径,连同QoS信息存储在图数据库中。此外,根据服务的可用性,更新数据库中存储的服务与服务组合路径。其中,“预处理”用于构建初始服务组合图,并将其存储在图数据库中。“服务更新”用于更新图数据库中存储的服务与服务组合。关键算法将在3.1节与3.2节作进一步描述。
路径查询模块:该模块搜索符合用户请求和目标的最优服务组合路径。所有路径存储在图数据库中后,“查询引擎”组件接收查询问题,并将相应的信息转换为Cypher查询语言。通过对图数据库的查询,将满足用户功能需求且QoS值最优的(如最小响应时间或最大吞吐量或最小花费)路径将返回给用户,关键算法将在3.2节中作进一步描述。
3.1 路径生成关键算法在“预处理”中,使用了2种算法来生成图数据库中服务组合的路径。
算法1 服务信息创建
输入:服务仓库SR
1. FOR each srv in SR DO
2. service ← CreateService (srv)
3. Cin, Cout← GetConceptOfService (w1)
4. response, throughput, cost ← GetQosOfService(srv)
5. inputConcept ← SearchConcept (Cin)
6. outputConcept ← SearchConcept (Cout)
7. IF intputConcept =ØTHEN
8. inputConcept ←CreateConcept (Cin)
9. END IF
10. IF outputConcept←ØTHEN
11. outputConcept ←CreateConcept(Cout)
12. END IF
13. link ← CreateLink(from inputConcept to service)
14. WriteWeight(link, response, throughput, cost)
15. link ← CreateLink(from service to outputConcept)
16. WriteWeight(link, 0, 0, 0)
17. END FOR
算法2 路径生成
输入:服务存储库SR
1. FOR each service w1 in SR DO
2. FOR each service w2 in SR and w2≠w1 DO
3. C1in, C1out← getConceptOfService (w1)
4. C2in, C2out← getConceptOfService (w2)
5. IF C1in subsume or exact match to C2out THEN
6. link ← CreateLink(from w2 to C1in)
7. WriteWeight(link, 0, 0, 0)
8. END IF
9. IF C1out subsume or exact match to C2out THEN
10. link ← CreateLink(from w2 to C1out)
11. WriteWeight(link, 0, 0, 0)
12. END IF
13. END FOR
14. END FOR
算法1服务信息创建了服务与其输入/输出参数集在服务组合图中的表示。首先,该算法为服务仓库SR中的每个服务srv在数据库中创建一个顶点Service(第2行)。其次,如果输入/输出参数集不存在于数据库中(第3~12行),则分别创建服务的输入参数集和输出参数集顶点。然后,分别创建一个从输入参数集顶点到服务顶点的有向边,和一个从服务顶点到输出参数集顶点的有向边,并基于式(1)~式(3)标准化响应时间、吞吐量及花费值与有向边的属性关联(第13~16行)。具体来说,从输入参数集顶点到服务顶点的有向边的属性是吞吐量、响应时间及花费的标准化值(第14行),从服务顶点到输出参数集顶点的有向边的属性设置为零(第16行)。
算法2路径生成构建服务间的组合路径。将SR中的所有服务相互比较。如果w1.in中的每个元素与w2.out中某一个元素存在精确匹配或子类匹配关系,将创建从服务w2到w1.in的边,并将属性设置为零(第5~8行)。如果w1.out中的每个元素与w2.out中某一个元素存在精确匹配或子类匹配关系,将创建从服务w2到w1.out的边,并将属性设置为零(第9~12行)。
3.2 数据库更新在“服务更新”中,使用了2种算法在数据库中添加和删除服务,对服务组合图进行更新。
算法3 服务删除
输入:srv
1. service←SearchService(srv)
2. links←LinksOfAService(service)
3. removeFromDB(links)
4. removeFromDB (service)
5. removeConceptsWithoutLinksFromDB()
算法4 服务添加
输入:新服务ns,服务仓库SR,图数据库DB
1. service ← CreateService (ns)
2. Cin, Cout← getConceptOfService (ns)
3. response, throughput, cost←GetQosOfService(ns)
4. inputConcept ← SearchConcept (Cin)
5. outputConcept ← SearchConcept (Cout)
6. IF intputConcept =Ø THEN
7. inputConcept ←CreateConcept (Cin)
8. END IF
9. IF outputConcept=Ø THEN
10. outputConcept ←CreateConcept (Cout)
11.END IF
12.link ← CreateLink(from Cin to ns)
13.WriteWeight(link, responseTime, throughput, cost)
14.link ← CreateLink(from ns to Cout)
15.WriteWeight(link, 0, 0, 0)
16.CreatePath(ns, SR)
算法3服务删除用于查找消失的服务,并将其相关信息删除。首先,找到要删除的服务(第1行),及其关联的有向边(第2行)。其次,删除服务和有向边(第3行)。然后,删除服务(第4行)。最后,删除数据库中没有任何有向边关联的输入/输出参数集。
算法4服务添加用于将新服务添加到图数据库中。首先,在数据库中创建一个新的服务ns顶点(第1行)。其次,创建输入/输出参数集顶点(第2~11行),并创建相关有向边并关联到输入/输出参数集顶点(第13~15行)。然后,为服务ns创建与其他服务的组合路径(第16行),与算法2(第5~16行)类似。
将算法3与算法4顺序执行,即构成服务更新。
3.3 路径查询关键算法在“路径查询”中,利用两种查询算法,根据用户的需求,在图数据库中找到最优的服务组合路径,并用Cypher查询语言进行描述。
算法5 Dijkstra组合查询
输入:Cin, Cout, qos:输入、输出参数集和指定的QoS
输出:path, total
1. from←SearchConcept(Cin)
2. to←SearchConcept (Cout)
3. path←Dijkstra (from, to, qos)
4. IF qos equals response THEN
5. totalresponse←calculateResponse(path)
6. RETURN path, totalresponse
7. ELSE IF qos equals throughput THEN
8. totalthroughput←calculateThroughput(path)
9. RETURN path, totalthroughput
10. ELSE IF qos equals cost THEN
11. totalcost←calculateCost(path)
12. RETURN path, totalcost
13. END IF
算法6 最少服务数组合查询
输入:Cin, Cout;输入、输出参数集
输出:path, totalresponse, totalthroughput, totalcost
1. from←SearchConcept (Cin)
2. to←SearchConcept (Cout)
3. path←Fewest(from, to)
4. totalresponse←CalculateResponse(path)
5. totalthroughput←CalculateThroughput(path)
6. totalcost←CalculateCost(path)
7. RETURN path, totalresponse, totalthroughput, totalcost
算法5 Dijkstra组合查询使用Dijkstra方法寻找响应时间最短或吞吐量最大或花费最少的服务组合路径。它以用户的功能需求和QoS为输入。如果用户需要具有最小响应时间的解决方案路径,那么它会找到具有最小归一化响应时间总和的路径(第3~6行)。如果用户需要具有最大吞吐量的解决方案路径,则执行第7~9行。如果用户需要具有花费最少的解决方案路径,则执行第10~13行。
算法6最少服务数组合查询采用最短双向广度优先的方法去找到服务数量最少的服务组合路径。它将用户的功能需求作为输入,然后搜索服务数量最少的路径(第3行),并根据式(4)~式(9)计算总响应时间、吞吐量及花费(第4~6行)。
4 实验结果 4.1 实验环境在具有以下配置的计算机上运行实验:①CPU:Intel(R)Core(TM)i5-7200U 2.50GHz2.71GHz; ②RAM:8.00GB DDR4-2400;③硬盘:LITEON T11 256GB,TOSHIBA MQ01ACF050 500GB; ④操作系统:Windows 10专业版64位; ⑤数据库:Neo4j Desktop版本1.1.13。算法用Java实现。
4.2 数据集使用文献[3]中的TestsetGenerator生成5个数据集。其中,数据集1具有572个服务,1 578个概念。数据集2具有4 129个服务,12 388个概念。数据集3具有8 138个服务,18 573个概念。数据集4拥有8 301个服务,18 673个概念。数据集5拥有15 211个服务,31 044个概念。
表 1~表 3分别提供了精确匹配、子类匹配、规划图算法[4]的实验结果。执行测试以评估提出的方法,该方法随机选择数据集中的一个路径用于比较。从表 1、表 2中可以看出,精确匹配无法找到解决方案,而在相同条件下子类匹配可以。对于最少服务数组合查询算法和规划图算法,表中每个单元格中的数据(用斜杠分割)分别表示服务组合数量、响应时间、吞吐量及花费。Dijkstra只列出服务数量及相应QoS。其中,Dijkstra响应时间、Dijkstra吞吐量、Dijkstra花费分别表示通过Dijkstra算法以响应时间、吞吐量、花费为边权值搜索出的服务组合。对于搜索算法的比较,可以看到Dijkstra算法和最少服务数组合查询及规划图算法在组合中具有相同数量的服务,但是Dijkstra算法获得的QoS值较最少服务数组合查询及规划图算法获得的QoS值相同或更好。
| 表 1 精确匹配的实验结果 Table 1 Experimental results of precise matching |
| 表 2 子类匹配的实验结果 Table 2 Experimental results of subsumption matching |
| 表 3 规划图算法的实验结果 Table 3 Experimental results of planning graph |
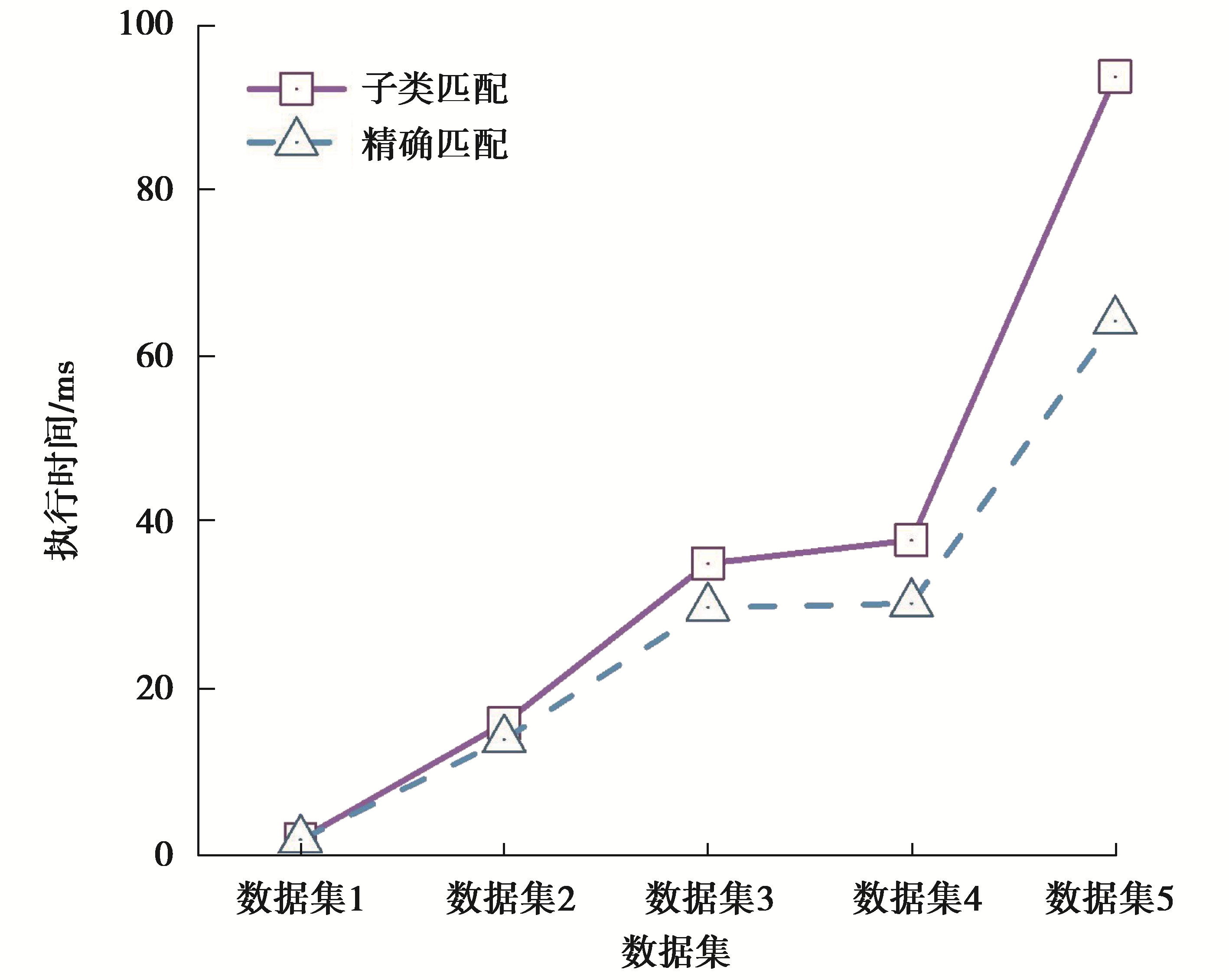
在预处理方面,如图 2所示,可以看到精确匹配和子类匹配具有非常相似的执行时间。随着服务数量的增加,预处理时间变得更长。当服务数量达到15 000时,需要1 h以上的时间才能完成。表 1显示,子类匹配具有更多路径来满足用户需求,而从子类匹配方法中选择的路径可能无法用精确匹配的方法找到(Number为0)。尽管预处理非常耗时,但可以在查询过程中快速找到解决方案。
|
图 2 预处理时间 Fig. 2 Pre-processing time |
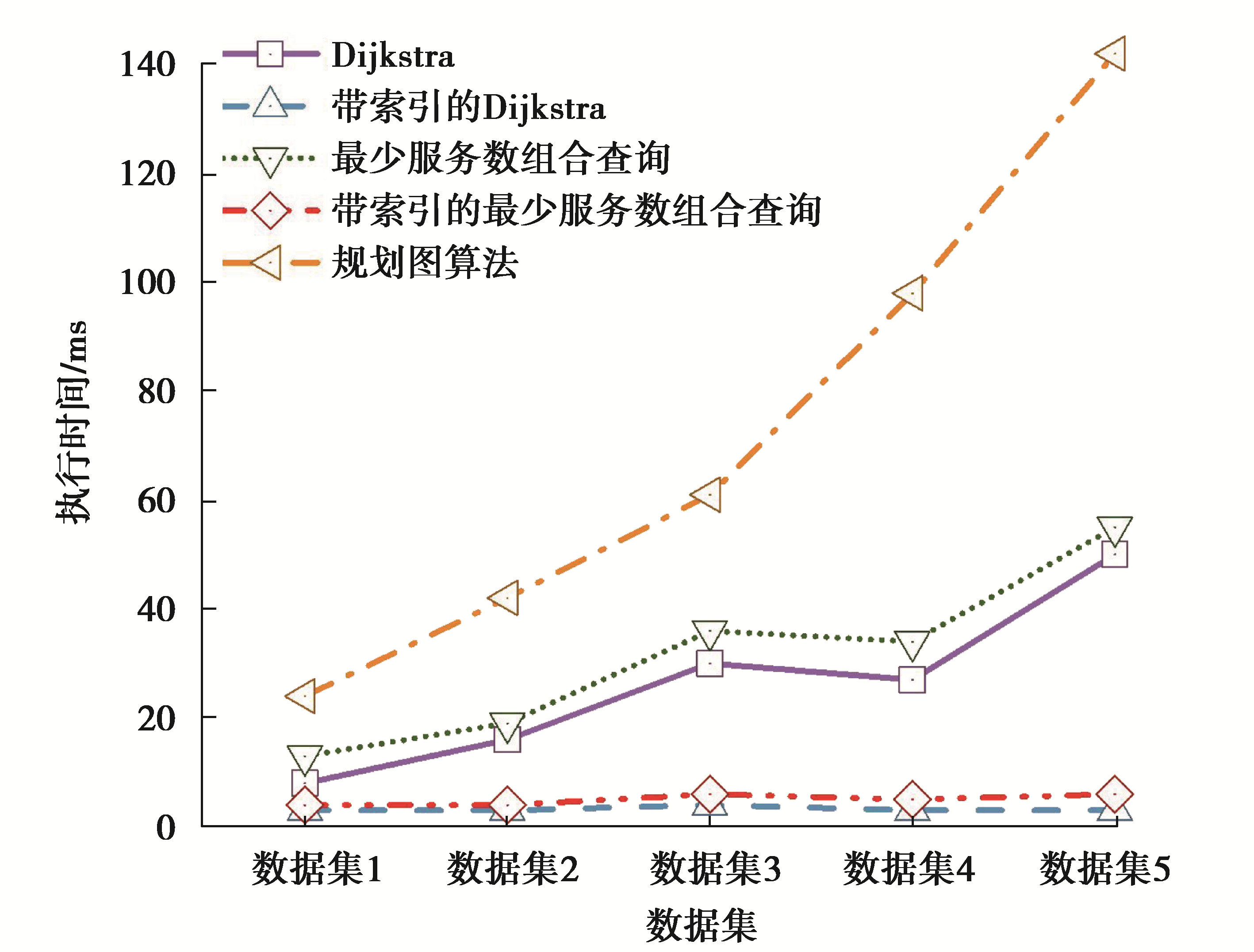
在搜索时间方面,Dijkstra算法比最少服务数组合查询的执行时间要短,如图 3所示。前者可以找到具有更好QoS值的路径,而后者可以找到服务较少的组合,但不能保证满足QoS要求。
|
图 3 查询时间 Fig. 3 Query time |
就索引而言,如图 3所示,可以看到随着服务数量的增加,索引方法会显著减少执行时间。例如,当服务数量超过15 000时,非索引方法的执行时间是索引方法的执行时间的近30倍。
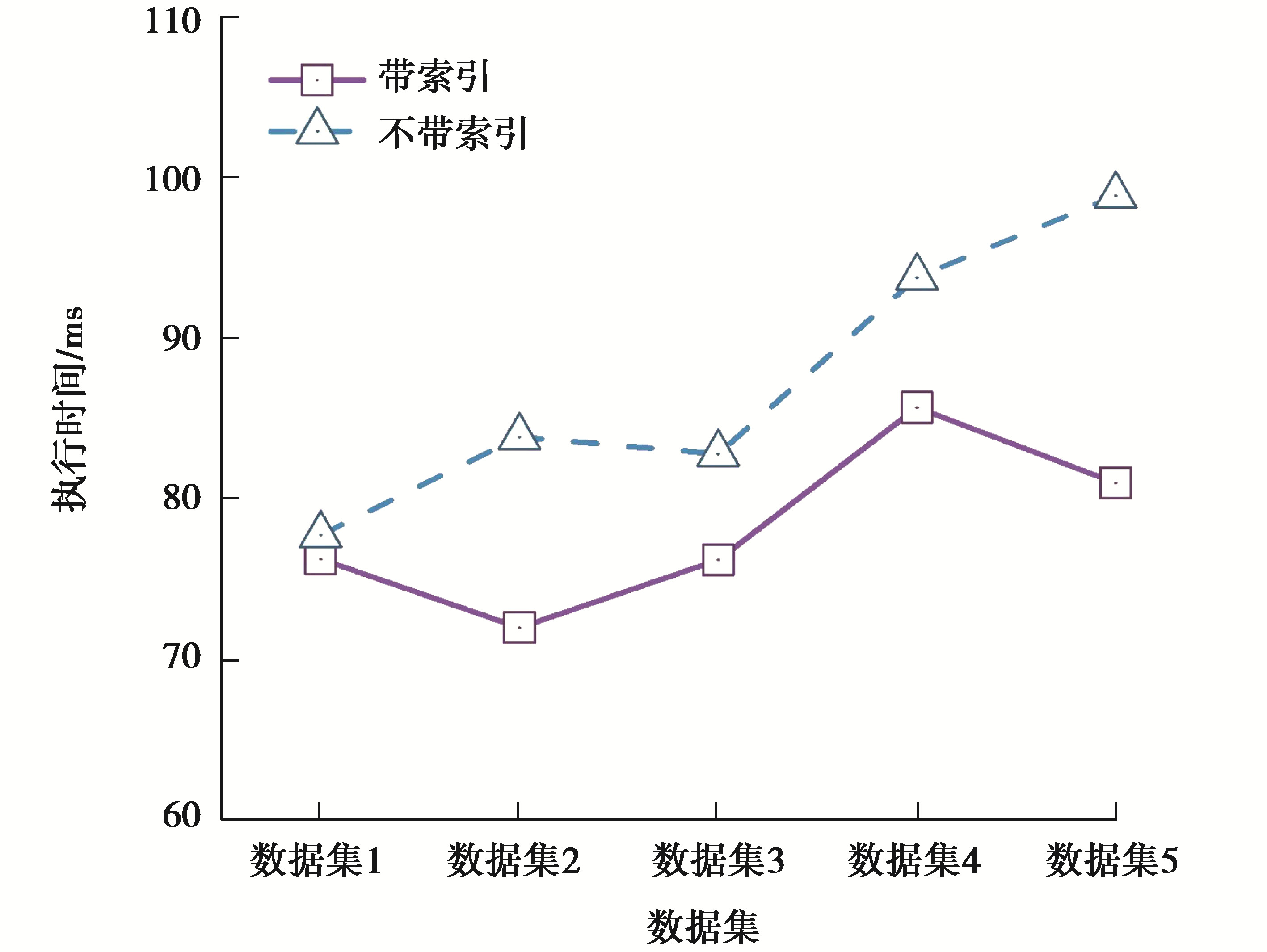
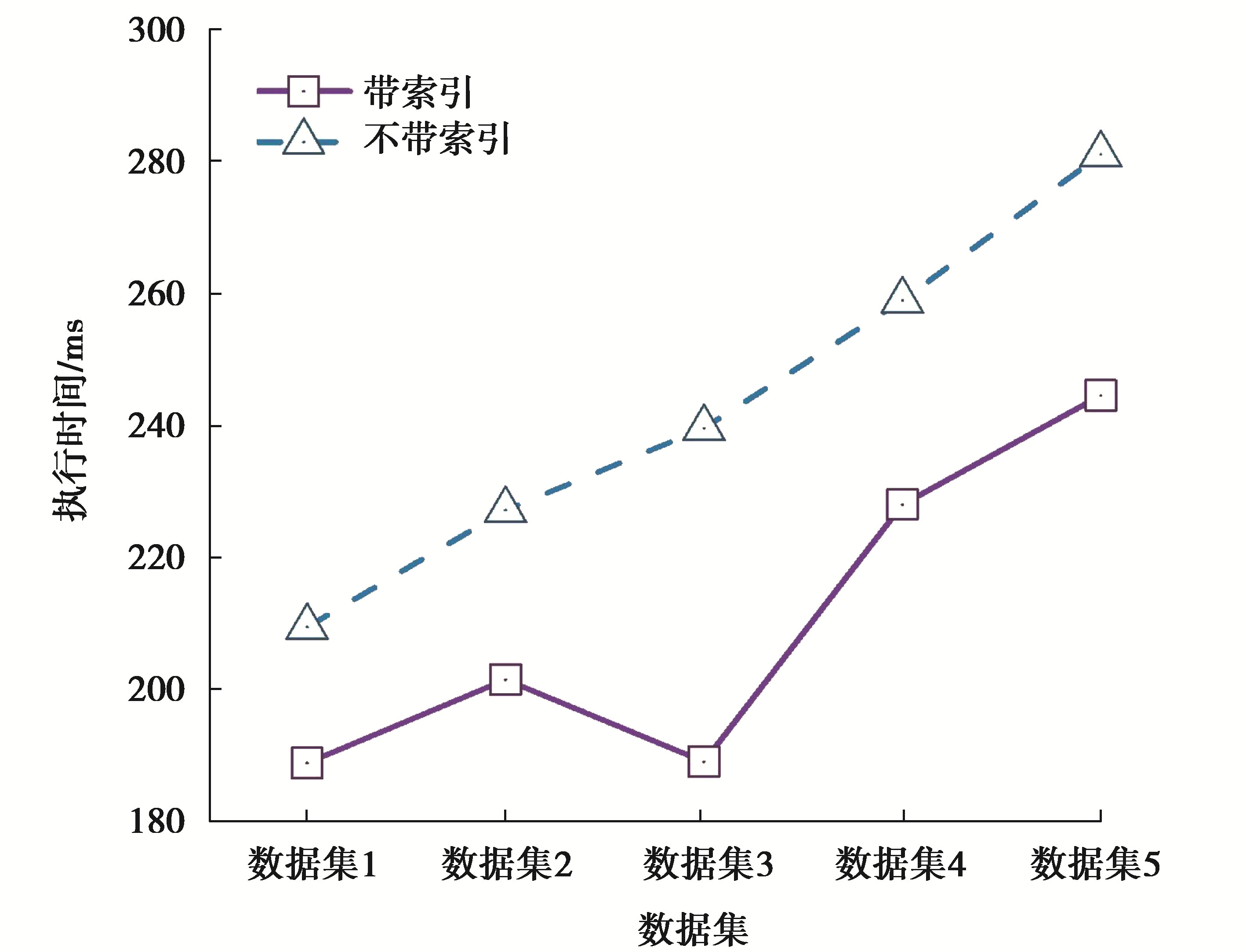
在服务删除中,随机删除一个服务及与该服务相关的记录。在服务名称上构建索引,并在执行时间方面比较有和没有索引的性能。如图 4所示,如预期的那样,当服务名称上没有索引时,查找和删除记录需要更多时间。
|
图 4 服务删除时间 Fig. 4 Service deletion time |
在添加服务实验中,数据库中添加一个新服务,然后获取生成新路径的时间。从图 5中可以看出,随着数据库中原始服务数量的增加,执行时间也相应增加。这是因为随着服务的数量增加,新生成的路径的数量线性增加。
|
图 5 服务添加时间 Fig. 5 Service addition time |
在搜索空间方面,基于服务组合图的图数据库中,随着服务与概念的规模扩大,在搜索过程所需的内存空间大小基本保持稳定,仅有小幅增量。但在规划图算法中,为了应对更大规模的服务与概念,则需要增加更多的内存空间以构造更大的规划图。如图 6所示,Neo4j基础内存占用表示数据库开启但尚未执行查询的内存占用情况。Neo4j搜索占用内存表示执行查询命令时,数据库的内存增加量。图数据库方法中测试集合1与测试集合5的内存差异很小,而规划图方法中测试集合1与测试集合5的内存差异为600 M。
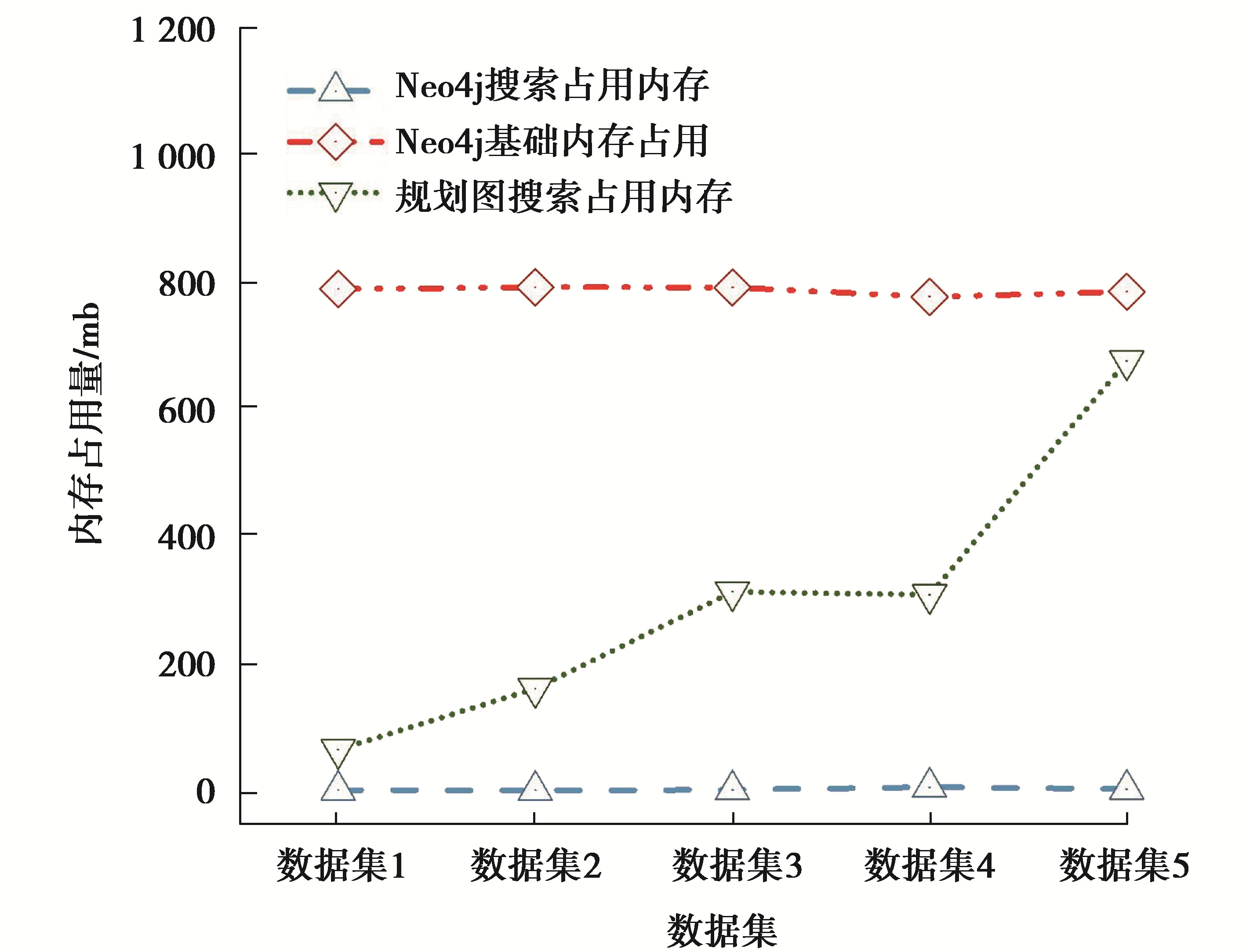
|
图 6 内存占用 Fig. 6 Memory usage |
文章研究和探索了图数据库中的服务组合问题,提出一种基于有向二分图与图数据库的QoS感知服务组合方法。该方法预处理服务组合,在Neo4j图数据库中生成和存储路径,并对图数据库中构建的服务组合图进行更新,以保证服务组合图的有效性。在用户查询过程中,使用最少服务数组合查询和Dijkstra搜索算法来寻找解决方案。实验结果表明,该方法能够在短时间内找到有效的解决方案。但也存在一些限制,例如,暂不支持插件匹配度去处理服务组合。将来计划使用插件匹配度来匹配服务并解决组合问题,并将其应用到真实的服务环境中。
| [1] |
Jula A, Sundararajan E, Othman Z. Cloud computing service composition:A systematic literature review[J]. Expert Systems With Applications, 2014, 41(8): 3809-3824. |
| [2] |
Ye Z, Mistry S, Bouguettaya A, et al. Long-term QoS-aware cloud service composition using multivariate time series analysis[J]. IEEE Transactions on Services Computing, 2016, 9(3): 382-393. |
| [3] |
Li J, Yan Y H, Lemire D. Full solution indexing for top-K web service composition[J]. IEEE Transactions on Services Computing, 2018, 11(3): 521-533. |
| [4] |
Zhu M, Fan G D, Li J, et al. An approach for QoS-aware service composition with GraphPlan and fuzzy logic[J]. Procedia Computer Science, 2018, 141: 56-63. |
| [5] |
Ghobaei-Arani M, Rahmanian A A, Aslanpour M S, et al. CSA-WSC:cuckoo search algorithm for web service composition in cloud environments[J]. Soft Computing, 2018, 22(24): 8353-8378. |
| [6] |
Pan L, An B, Liu S, et al. Nash equilibrium and decentralized pricing for QoS aware service composition in cloud computing environments[C]//2017 IEEE International Conference on Web Services (ICWS). New York, USA: IEEE, 2017: 154-163.
|
| [7] |
Deng S G, Xiang Z Z, Yin J W, et al. Composition-driven IoT service provisioning in distributed edges[J]. IEEE Access, 2018, 6: 54258-54269. |
| [8] |
Wang X H, Feng Z Y, Chen S Z, et al. DKEM: A Distributed Knowledge Based Evolution Model for Service Ecosystem[C]//2018 IEEE International Conference on Web Services (ICWS). New York, USA: IEEE, 2018: 1-8.
|
| [9] |
Shi W S, Cao J, Zhang Q, et al. Edge computing:vision and challenges[J]. IEEE Internet of Things Journal, 2016, 3(5): 637-646. |
| [10] |
Wang S G, Zhao Y L, Xu J, et al. Edge server placement in mobile edge computing[J]. Journal of Parallel and Distributed Computing, 2019, 127: 160-168. |
| [11] |
Wang S G, Zhou A, Bao R, et al. Towards green service composition approach in the cloud[J]. IEEE Transactions on Services Computing, 2018, 1. |
| [12] |
Vicknair C, Macias M, Zhao Z, et al. A comparison of a graph database and a relational database: a data provenance perspective[C]//Proceedings of the 48th annual Southeast regional conference. Oxford, Mississippi. New York, USA: ACM Press, 2010: 42.
|
| [13] |
Angles R, Arenas M, Barceló P, et al. Foundations of modern query languages for graph databases[J]. ACM Computing Surveys (CSUR), 2017, 50(5): 68. |
| [14] |
Gong F, Ma Y, Gong W, et al. Neo4j graph database realizes efficient storage performance of oilfield ontology[J]. PloS one, 2018, 13(11): e0207595. |
| [15] |
Silva A S D, Moshi E, Ma H, et al. A QoS-aware web service composition approach based on genetic programming and graph databases[C]//International Conference on Database and Expert Systems Applications.Cham: Springer International Publishing, 2017: 37-44.
|
| [16] |
W3C OWL Working Group. (2012) Owl 2 web ontology language document overview (Second Edition).[J/OL].[2019-12-16]. http://www.w3.org/TR/owl2-overview/.
|
| [17] |
Oh S, Yoo J, Kil H, et al. Semantic web-service discovery and composition using flexible parameter matching[C]//The 9th IEEE International Conference on E-Commerce Technology and The 4th IEEE International Conference on Enterprise Computing, E-Commerce and E-Services. Tokyo, Japan. New York, USA: IEEE, 2007: 533-542.
|
 2020, Vol. 43
2020, Vol. 43


