1b. 东莞理工学院 经济与管理学院, 广东 东莞 523808;
2. 思克莱德大学 设计制造工程管理学院, 格拉斯哥 G1 1XJ
1b. School of Economics and Management, Dongguan University of Technology, Dongguan, Guangdong 523808, P. R. China;
2. Department of Design, Manufacturing and Engineering Management, University of Strathclyde, Glasgow, G1 1XJ, UK
业务流程优化是提高企业生产、管理等业务效益的关键。随着信息技术的发展,云制造优势日渐显现,逐渐成为企业追逐的趋势,基于业务流程的云制造服务的执行效率亦显重要。充分发挥流程各执行节点的执行效率,并注重各节点的协同效益,是流程优化的核心。
虽然业务流程优化已经不是新鲜的概念了,各行各业都不同程度地注重并开展各自的业务流程优化,追求流程效益,但目前大多是从流程节点、流程路径上考虑,将不必要的流程节点予以合并或删除,从而缩短流程路径[1-3],或从流程业绩上考虑[4-6],将业绩差的节点加以改善优化,如改进其设备、人力等,以提高生产能力或管理能力。上述方法,尽管兼顾了流程节点的效率,以及流程节点的配合,也能起到流程优化的作用,但当前存在的普遍问题是:一方面,很多在流程结构上表现出不协调,尤其是在选择分支结构之间,以及并行结构分支之间,导致这些分支之间差距明显,配合不齐,在执行时间上出现过长的时间等待,从而影响流程的高效推进。另一方面,由于流程分支之间的服务质量参差不齐,如若一味加快某分支的执行时间容易导致该分支的服务质量下降,而一味注重服务质量则容易导致分支执行时间加长。再者,一定的投入会改进分支的服务质量、执行时间,但这是建立在牺牲一定投入的基础之上的。因此,改进业务流程分支结构的时间差异是一个优化问题,而且非常有必要,对流程的整体执行效率以及服务质量有着重要的影响,也正因为如此,随着云服务在制造业中的广泛、深入应用,这对基于业务流程的制造服务流程的优化更显必要。
工业界和学术界对业务流程结构优化已经进行了许多较有成效的研究与实践。对业务流程从量的角度进行分析,郭哲等[7]基于过程代数对电子商务定价业务流程进行了优化重组,重组后的定价业务流程,能减少工作量和工作失误,加强定价系统对电子商务企业的快速响应能力;王云鹏等[8]利用Petri网技术构建了现有环境下的生产物流流程模型,对其进行了数学特性分析,并使用Exspect软件模拟分析了原流程及优化后流程的优劣。从智能算法角度对业务流程进行优化,Huang等[9]提出了一种任务操作模型为业务流程管理中的资源配置优化方法;Vergidis等[10]研究了在进化框架下(EMOOA和NSGA2)业务过程设计与属性配置优化。从业务流程控制结构的冗余角度进行优化,Olkhovich[11]研究了基于冗余控制流探测的半自动化业务流程性能优化。从业务流程平台建设的角度,Grzech等[12]研究了为业务流程优化的方法和平台;Soti等[13]研究了业务流程优化用于医疗系统RHIOs。
上述研究,虽然从不同角度研究了业务流程优化的方法及其工程应用,但都没有从业务流程的分支结构的不平衡性进行时间优化的考虑。然而,业务流程的控制结构直接影响到业务任务执行的路径,进而影响到任务执行的时间、质量、价格等。笔者考虑到业务流程控制结构对流程工作效率的影响,尤其是分支结构不平衡性导致的不均衡、不同步导致的时间拖延,进而影响业务流程的执行效率,对基于业务流程的制造服务流程的各种分支结构进行分析,进而构建了差异化分支结构的制造服务流程优化模型,弥补了借鉴现有的业务流程重构的传统方法不能解决由于分支结构差异化导致的工作效率拖延的这一不足。
1 制造服务流程相关概念与计算方法 1.1 制造服务流程优化的相关概念定义1 制造服务流程执行节点(manufacturing service process node, MSPN)是指具有一定业务功能的流程活动节点,其形式化可表示为MSPN=(name, id, func, attributes), 分别表示为节点的名称、标识号、功能、属性。
云制造环境下,往往这些节点由制造服务组成。因此,文中不做特殊说明,MSPN指的是制造服务。
定义2 制造服务流程执行节点的服务能力(abbility of manufacturing service process node, AoMSPN)是指流程执行节点完成任务的能力,其形式化可表示为AoMSPN=(t, c, q),t, c, q为服务能力三要素,其中t表示其完成任务的执行时间,c是指其完成任务所花费的价格,q则是表示其执行任务的服务质量(QoS, quality of service),即完成情况的好坏程度,一般由用户评价。
它们各自的度量方法:t, c采用实际耗费来计算,而q是表示品质的量,难以准确度量其值,一般是通过用户评价而获得,是个连续变量,其取值范围q∈(0, 1]。
定义3 制造服务流程路径是指由制造服务流程各执行节点按一定的逻辑控制结构组成的路径。制造服务流程基本控制结构一般有4种:顺序、选择、循环、并行。其中选择结构和并行结构具有分支结构。
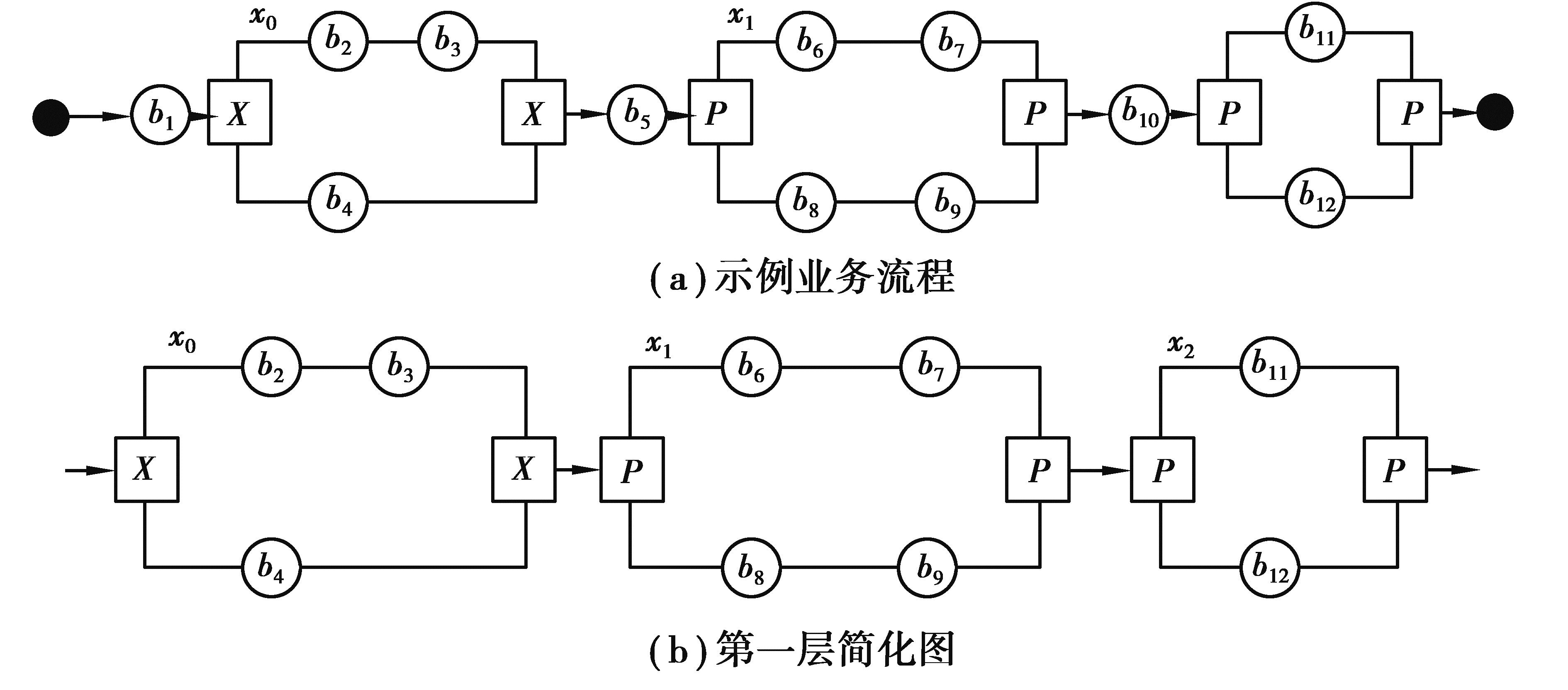
制造服务流程路径表示方法可有多种,这里参考文献[14]提供的业务流程串来表示。图 1的路径可表示为:b1.X(b2, b3).b4.P(b5, b6).b7.P((b8, P(b10, b11), b14), (b9, P(b12, b13), b15))。
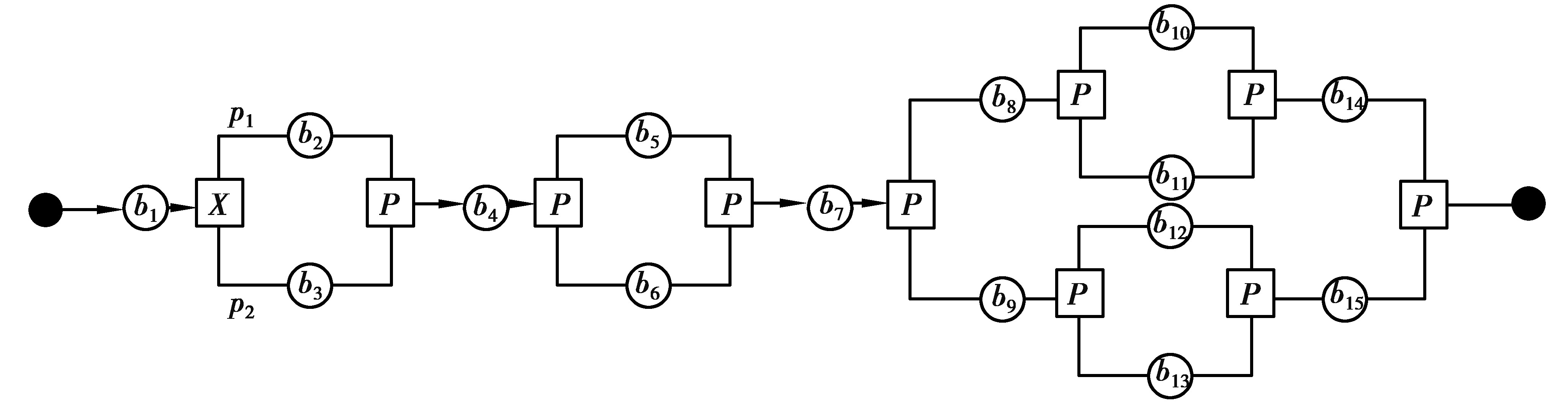
|
图 1 带分支的制造服务流程示例 Fig. 1 Example of manufacturing service process with branches |
选择结构分支的含义是指基于概率选择执行不同路线,在任何时刻都只存在一条分支路径。而并行结构则是多个分支同时执行。它们的共同点是:各分支都有自己的分任务目标。
定义4 制造服务流程主题任务是指流程的主要目标任务,流程上各执行节点都围绕着目标任务发挥作用,并且各节点协同完成该任务。形式化描述为:∀MSPNi∈bp∪∀MSPNi.task∈Task,bp为制造服务流程,Task为bp的目标任务,MSPNi.task表示节点的任务属性。
定义5 制造服务流程路径任务相关性是指制造服务流程路径上各节点与主题任务的相互关系。关系越强则相关程度越大,反之越小。
任务相关性可采用主题相关距离度量的方法(可参照文献[15]的方法)。有些制造服务流程,不同分支上的流程任务关联性不大,导致时间相关性不强。这类制造服务流程的任务不单纯,可对该流程进行处理,使流程的任务变得单一,各节点的协同紧密关联,时间相关性就会越强。
定义6 制造服务流程路径规范化是指能将制造服务流程路径转化为流程路径任务相关性更为集中且程度更强的制造服务流程路径。
规范化措施是将2个不相关的流程路径进行拆分,得到2条新的执行路径,直到流程路径上的各分支在任务上、时间上紧密相关,共同完成一件目标任务。规范化路径后得到的制造服务流程为规范制造服务流程。
规范制造服务流程的主题任务相关性集中,但由于存在分支结构执行能力的差异,如何合理配置分支结构的任务量或改进其服务能力,对整个流程的执行效率有至关重要的影响。
性质1:规范制造服务流程的选择结构分支、并行结构分支对整个制造服务流程执行时间来说各自均具有时间相关性。
本文为了突出研究分支结构的服务能力差异影响下的优化配置,忽略顺序结构对前后节点的执行时间的影响,于是有下列业务流程路径简化定义。
定义7 制造服务流程路径简化是指对任一规范制造服务流程,将其路径简化为只包含2种影响路径时间的分支结构:选择结构和并行结构的组合路径,并且分层、分结构块对其进行简化。经制造服务流程路径简化了的制造服务流程图称为制造服务流程简化图,层次和分块可用于结构的定位标识。
简化原则:分层次、由外向内、由大到小地进行流程路径简化,以突显流程路径时间相关性,为路径时间优化提供基础。
例如,对图 1的业务流程,不妨称之为bp1,其第一层简化后的路径如图 2(a),根据简化原则,可进一步对内层的图进行简化,结果如图 2(b)。第1层简化后变为3个分块,分别为X(b2, b3)、P(b5, b6)、P(b8.P(b10, b11),b9.P(b12, b13));第2层简化是对第1层的复合结构进一步简化,即对P(b8.P(b10, b11),b9.P(b12, b13))简化为P(b10, b11)、P(b12, b13)。
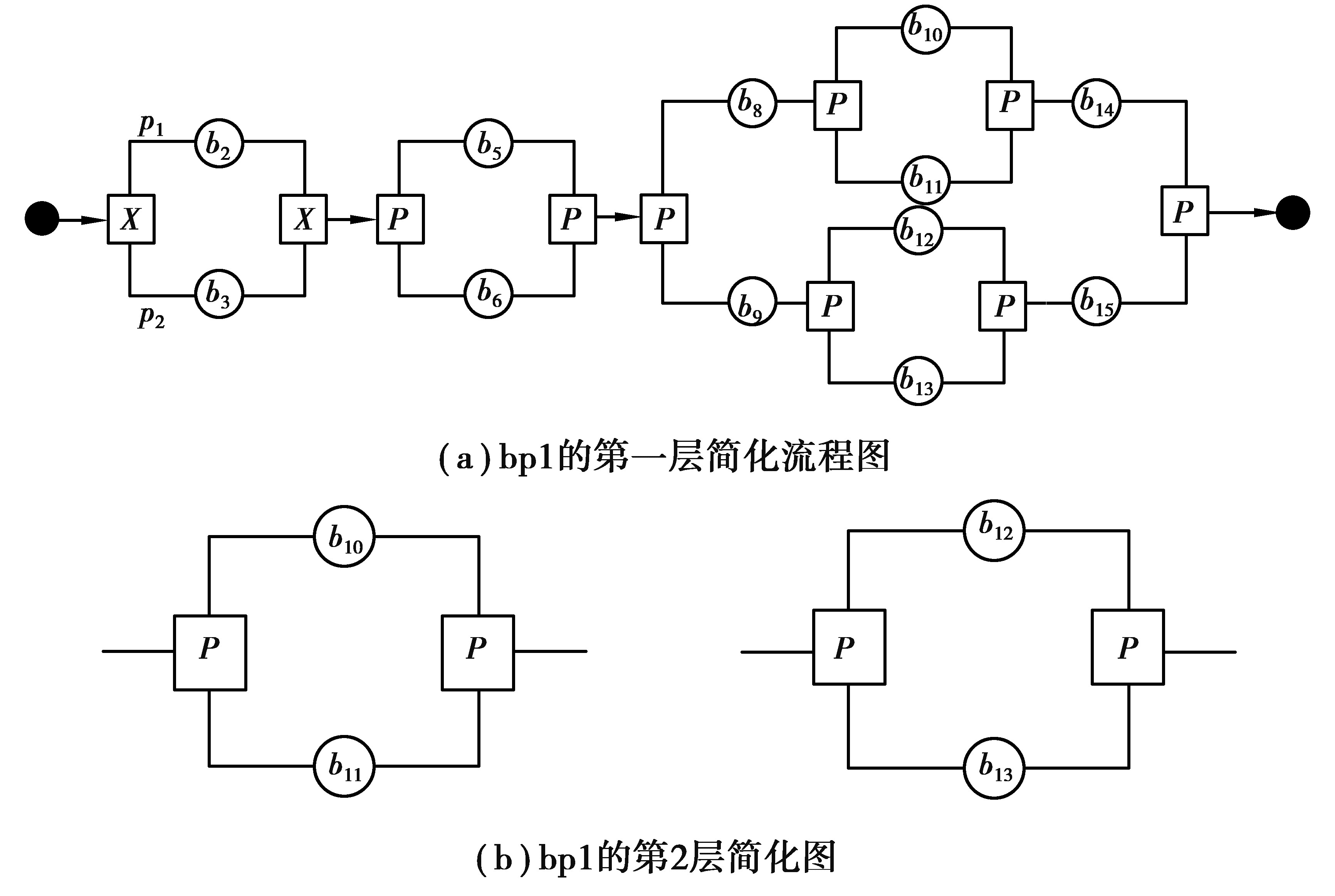
|
图 2 业务流程图的简化示例 Fig. 2 Example of simplization of business process |
定义8 制造服务流程结构时间优化是对规范制造服务流程的选择结构和并行结构的分支进行时间优化,使该制造服务流程路径总体时间变得更短。
如对图 2(a)简化的规范制造服务流程图,其第一个为选择结构,包含2条分支,第2个控制结构为并行结构,也包含2条分支,第3个也为并行结构,它又包含了子控制结构。对它的第一层,如果这些控制结构的上下分支效率不均衡,势必影响总体执行效率,故需要优化。
1.2 制造服务流程结构的属性计算方法下面对流程控制结构的执行时间、价格、服务质量特性进行分析。
对顺序结构,t、c为各节点值的累加,而q作为服务质量,各节点的q各不相同,要通过它们的平均值才能体现整体的q。
对选择结构,根据其分支的概率,其t、c为各分支的概率贡献值相加而成,而q由于只有在分支执行时才能贡献其服务质量,因此也是按概率贡献服务质量的。
对并行结构,分为并行分流分支类型和并行子任务结构,对分流类型,由于各分支同时进行,因此,t表现为分支大的作为其结构的t,而对c,根据其分流大小计算累加值,而对q,其服务质量贡献大小也是根据其分流量来进行相加而成;而对并行子任务结构,其q和s都是在增量基础上进行的计算,而t仍然是以分支大的为其度量。
对循环结构,q取其单节点的值,而t、c则取其累加值。
基于上述分析,各控制结构的t,c,q的计算如表 1所示。
| 表 1 制造服务流程控制结构的属性计算公式 Table 1 Attribute calculation formula for control structure of manufacturing service process |
表 1中,parrelle Ⅰ、parrelle Ⅱ分别表示分流并行结构、子任务并行结构。对并行结构的parrelle Ⅰ,Si表示各分支分流的比例,
| $ q_i^\Delta = \frac{{c_i^{{\rm{add}}}}}{{c_i^0}} \cdot q_i^0, $ | (1) |
式中:ciadd表示该分支的增加投入;ci0表示该分支单位质量qi0所需要的投入量。
| $ t_i^\Delta = \frac{{c_i^{{\rm{add}}}}}{{ct_i^0}} \cdot t_i^0, $ | (2) |
式中,cti0表示该分支单位时间ti0改善所需要的投入量。
对parrelle Ⅰ的t,分流比率为Si,不妨将分支分为2条(大于2条分支的余下部分为嵌套分支),设原分支的时间分别为ti1、ti2,则分流后分支的时间分别为(任务量为1):Si·ti1、(1-Si)·ti2,于是有
| $ {\rm{max}}({t_i}) = ({s_i} \cdot {t_{i1}},(1 - {s_i}) \cdot {t_{i2}})。$ | (3) |
对parrelleⅡ,同理将分支分为2条,结合改进的时间量,则分支的时间分别为(任务量为1),
| $ {\rm{max}}({t_i}) = ({t_{i1}},{t_{i2}} - \frac{{c_{i2}^{{\rm{ add }}}}}{{ct_{i2}^0}} \cdot t_{i2}^0)。$ | (4) |
由于复合结构可以看作是顺序结构的一个节点,流程的t、c、q都可看作由顺序结构的各个节点的t、c、q分别相加而成。文中为了重点研究分支结构的执行能力差异对整个流程执行的影响,可暂不考虑前后节点不协调性的影响,即忽略前后节点衔接的影响。由于选择结构、并行结构具有分支,各分支的执行时间差异将会因时间不协调而影响流程的执行效率。研究中,只对分支结构,即对流程的选择结构和并行结构进行分析,其余结构的节点都可不用考虑和改变。
2 基于分支结构时间差异化改进的制造服务流程优化方法 2.1 制造服务流程执行时间优化策略下面对流程执行时间优化进行分析。
对制造服务流程的4种控制结构的时间、价格等属性的计算可参照表 1,其中,对选择结构,各分支的总执行时间为
对制造服务流程的并行结构,根据表 1,各分支的总执行时间为max(ti),即并行结构的执行时间以分支中花费执行时间最大的为其度量。要想对并行结构进行时间优化,较之选择结构要复杂一些。对并行结构需要分以下情况进行考虑。
1) 同一任务而多任务并行:这种情况是针对同一任务的批量情况。由于各个并行分支的服务质量(q)、执行价格可能不同,它们的执行时间也不同。要想对这种并行结构进行时间优化,有2种方法:分流处理;投入成本改进分支的服务能力。
2) 对同一任务而多并行子任务:这种情况是针对具有并行子任务的情况。由于各个并行分支的功能、作用对象不同,并具有不同的服务质量、执行价格等,其执行时间也可能不同。这种情况的并行结构的执行时间优化,由于不能分流,因此,只能投入成本改进执行时间长的分支的执行时间。
通过对上述选择结构、并行结构这些分支结构的时间优化分析,可归纳出一般的时间优化方法。于是,综合得到一般制造服务流程的执行时间的优化方法如下:
1) 同一任务而多任务并行:对选择结构进行概率调节,对并行结构进行分流处理;对选择结构进行概率调节,对并行结构投入成本以改善分支服务能力。
2) 对同一任务而多并行子任务:对选择结构进行概率调节,对并行结构投入成本以改善分支服务能力。
对任意一制造服务流程实例,可进行规范化处理,得到任务单一的制造服务流程。而对同一任务的制造服务流程所包含的分支控制结构,即选择结构、并行结构,可以统一处理。即:选择结构作为一类分支结构,按其概率进行调节,且按两个分支进行处理(如多个选择分支,则可分解为这样的2条:1条分支与另外多条组合的复合分支),当求得复合分支的概率后,再对其复合分支进一步按相同方法求解;对并行结构,又可按不同类型进行分类,即分子任务的为一类,而分流的为一类,它们可以并存,不会影响优化结果。同样,对多个并行分支,也可先按2个分支处理(其中1条为复合分支),而复合分支也在求得其概率后再进一步按相同方法求解所包含的各分支的概率分配。
2.2 优化分析与建模下面再分析时间优化方法与其他因素:q、c等的影响关系。
2.2.1 单个结构的分析1) 选择结构
对图 1的选择结构部分,设分支分配概率为x0,则另一分支的概率为1-x0,设t1、c1、q1表示上分支的属性,而t2、c2、q2则表示为下分支的属性(后续的也如此,不再赘述)。结合表 1的各结构的属性计算方法,上下分支的各个属性值分别为:x0·t1,x0·c1,x0·q1;(1-x0)·t2,(1-x0)·c2,(1-x0)·q2,则该选择结构的各属性值为:x0·t1+(1-x0)t2,x0·c1+(1-x0)c2,x0·q1+(1-x0)q2。
根据上面计算的属性结果可知,时间花费大的选择分支,其执行的q优于另一时间小的分支,调节概率使得时间大的分支的概率变低,在总的任务执行中,势必会降低选择结构的服务质量。因此,在改善执行时间的同时,需考虑q的情况,使q满足用户的要求。另外,在价格上,同样也是如此,如果时间大的分支的概率变低,其总的价格会增加。因此,需考虑价格的变化不能超过用户的要求。
2) 并行结构
对并行结构,根据并行结构的特性分情况分析如下:
① parrelleⅠ
仍以图 1为例,假设图 1的并行结构部分为并行任务分流类型的,不妨设x1为上分支的分流量,根据表 1的计算方法,则该并行结构的t、c、q各属性值为:max(x1·t1, (1-x1)·t2),x1·c1+(1-x1)·c2,x1·q1+(1-x1)·q2。
从上面计算结果可知,若时间长的分支其q却较强,则分流不能太多。于是最大时间t不变,但分流后,对多分支的并行结构,其执行总时间为
② parrelleⅡ
假设图 1示例中的第二层简化图中,b10、b11两节点组成的并行结构属于parrelleⅡ。不妨设x2为上分支的q改进量,则该并行结构的各属性值计算为:
从上述计算结果可知,改善分支耗费时间大的分支的服务能力,这需要投入一定的成本。从而降低其执行时间。同时,不能一味投入,使整体c过高。
2.2.2 更一般结构的业务流程分析基于上述的分析,对更一般结构的制造服务流程(可包含嵌套结构)(见图 3,包含n个带分支的嵌套结构,这些嵌套结构包含选择、两类并行结构若干)得到下面的时间执行优化模型。这里,由于简化后不影响分支结构的优化结果,可将流程的非选择结构和非并行结构上的节点过滤,只对这两类结构进行计算。对流程上的并行结构进行分类,如分流任务并行或子任务并行,然后根据各自的优化方法进行计算,于是得到:
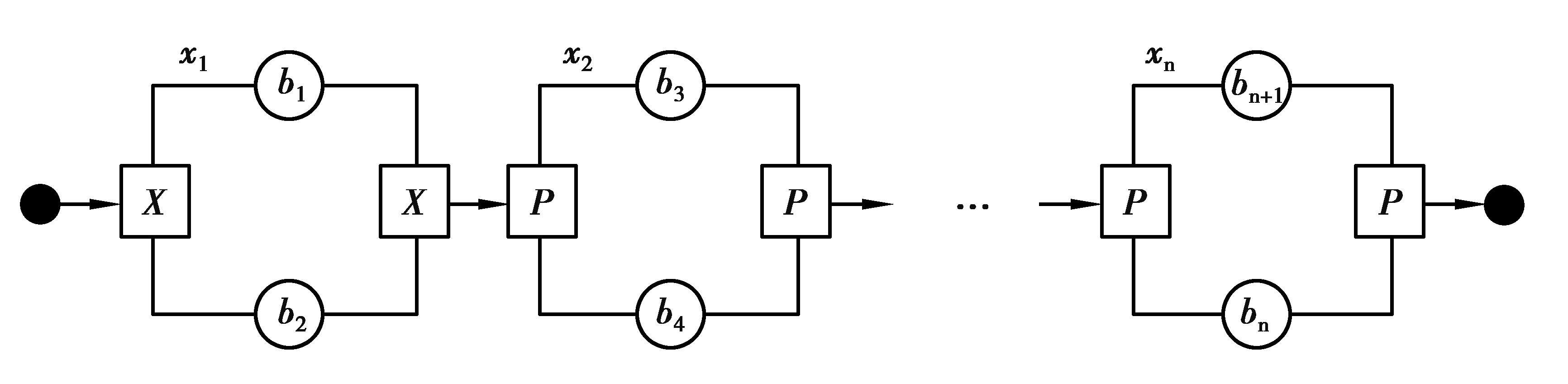
|
图 3 一般结构的制造服务流程执行路径图 Fig. 3 Diagram of executing path of manufacturing service process with general structure |
| $ {\rm{Min}} T = \sum\limits_{i = 1}^{m0} {({x_i} \cdot {t_{i1}} + (1 - {x_i}) \cdot {t_{i2}})} + \sum\limits_{j = 1}^{m1} {{\rm{max}}} ({x_j} \cdot {t_{j1}},(1 - {x_j}) \cdot {t_{j2}}) + \sum\limits_{k = 1}^{m2} {{\rm{max}}} ({t_{k1}},{t_{k2}} - \frac{{c_{kt}^{{\rm{add}}}}}{{ct_{k2}^0}} \cdot t_{k2}^0), $ | (5) |
| $ \begin{array}{l} {\rm{s}}{\rm{.t}}{\rm{.}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^{m0 + m1} {({x_i} \cdot q_i^1 + (1 - {x_i}) \cdot q_i^2)} + \sum\limits_{j = 1}^{m2} {((} q_{\rm{j}}^1 + \frac{{c_{\rm{j}}^{{\rm{ add }}}}}{{c_{\rm{j}}^0}} \cdot q_{\rm{j}}^0) + q_{\rm{j}}^2)/2 \ge (m0 + m1 + m2)\delta , \end{array} $ | (6) |
| $ \sum\limits_{i = 1}^{m0 + m1} {({x_i} \cdot c_i^1 + (1 - {x_i}) \cdot c_i^2)} + \sum\limits_{j = 1}^{m2} {(c_{\rm{j}}^1 + c_{\rm{j}}^2 + c_{\rm{j}}^{{\rm{add}}})} \le \xi , $ | (7) |
| $ {{x_i} \ge 0,} $ | (8) |
| $ {c_{\rm{j}}^{{\rm{ add }}} \ge 0,} $ | (9) |
式中:xi表示为流程上第i个选择/并行结构中的概率或分流;m0,m1,m2分别表示选择结构、分流并行结构,以及并行子任务类型的结构的数量。式(5)代表优化目标函数,式(6)~式(9)为约束函数,分别代表流程的服务质量约束、流程的价格约束、配置量约束以及价格增量约束。这是一个线性规划的优化问题,可利用线性规划方法求解。
2.3 基于线性规划的制造服务流程优化算法对上述所建线性规划模型进行优化求解。总体思想是:先计算出第一层的优化结果后,如果还有嵌套结构,再在所得的优化配置结果下进行第二层优化。由于第二层简化图是分块的,因此对不同的块需要进行分开优化。每层优化的结果将作为其接下来的内层优化参数,这样就能逐步求得各层的优化配置量。从而完成对整个业务流程路径的优化配置。
其算法流程如图 4所示。算法首先对流程分支结构加以提取,然后进行分层分块优化计算,优化方法具体是对每层的分支结构进行线性规划求解。值得注意的是,对复合嵌套结构,采取先求外层的方法,确定外层的变量值后,然后以这些变量值为基础,对每个复合结构再进行上述同样的线性规划求解,可获得次层的各控制结构的优化配置变量值,以此类推,就可算出混合结构不同层次不同控制结构块的配置变量值。
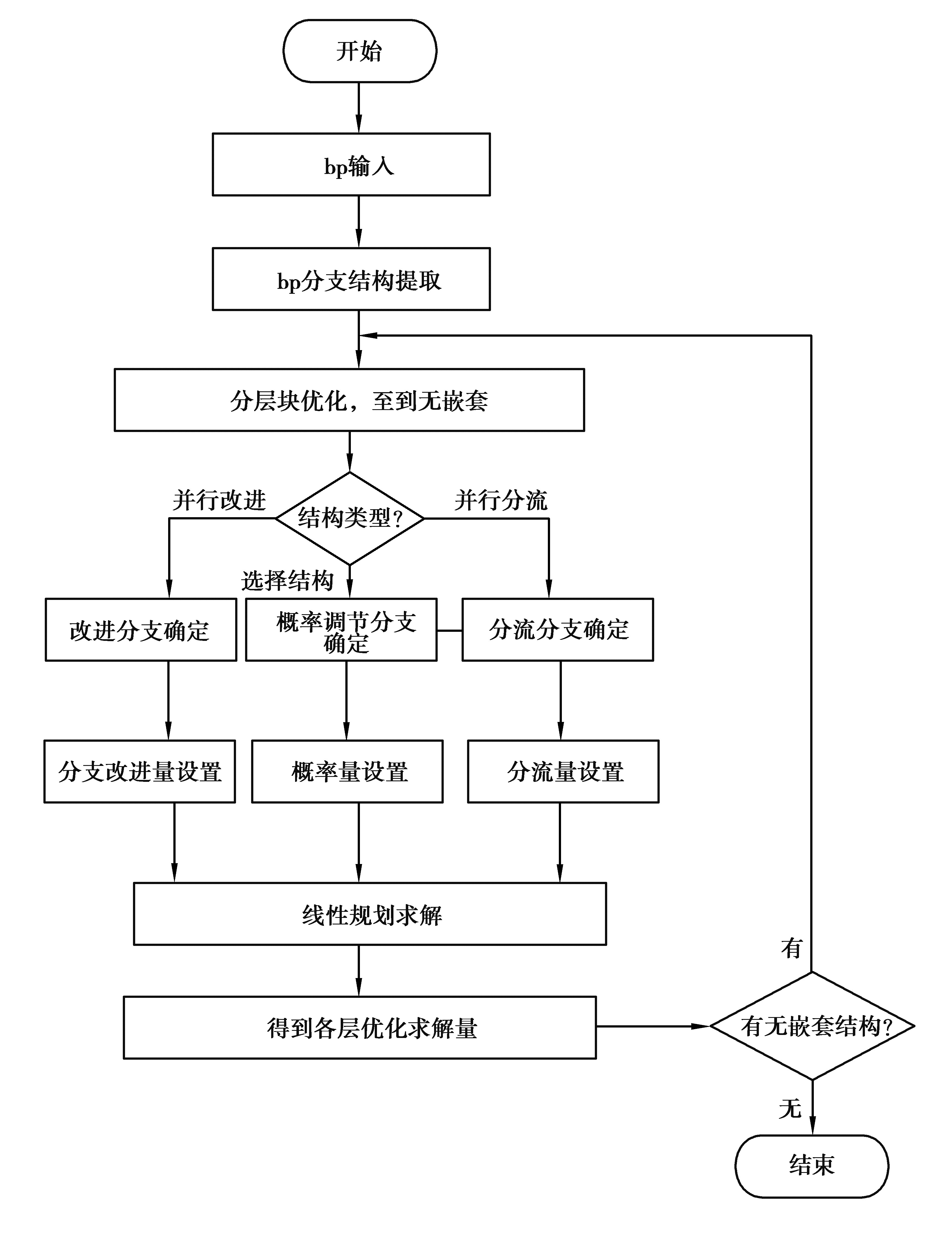
|
图 4 制造服务流程分支结构分层分块优化算法流程图 Fig. 4 Flow chart of hierarchical and block optimization algorithm of branches structure of manufacturing servce process |
某企业有一业务流程如图 5所示,包含3个分支结构,节点上分别为不同功能的制造服务,并且该流程上的分支控制结构依次分别为选择结构、parrelle Ⅰ、parrelle Ⅱ,原有流程参数如下:x0=0.5、x1=0.5、x2=0.5。实验环境是:AMD A10-8700P Radeon R6, 10 Computer Cores 4C+6G 1.80GHZ, 4G RAM, Windows 7,开发工具选用Matlab r2017a。不失一般性,文中实验只求解第一层优化配置量。表 2是该实例流程简化图的各节点的属性数据。
|
图 5 制造服务流程图及其简化图 Fig. 5 Flow diagram and its reduced graph of manufacturing service process |
| 表 2 制造服务流程简化图的各节点属性实验数据 Table 2 Attributes data of all nodes of reduced graph of manufacturing service process |
图 5(a)经过预处理得到图 5(b)的结构优化简化图。其优化模型为:
| $ {\rm{Min}} T = ({x_0} \cdot {t_{11}} + (1 - {x_0}){t_{12}}) + {\rm{max}}({x_1} \cdot {t_{21}},(1 - {x_1}){t_{22}}) + {\rm{max}}({x_2} \cdot {t_{31}},(1 - {x_2}){t_{32}}), $ | (10) |
| $ \begin{array}{l} {\rm{s}}{\rm{.t}}{\rm{.}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({x_0} \cdot {q_{11}} + (1 - {x_0}){q_{12}}) + ({x_1} \cdot {q_{21}} + (1 - {x_1}){q_{22}}) + ({x_2} \cdot {q_{31}} + (1 - {x_2}){q_{32}}) \ge 3{q_{{\rm{request}}}}, \end{array} $ | (11) |
| $ ({x_0} \cdot {c_{11}} + (1 - {x_0}){c_{12}}) + ({x_1} \cdot {c_{21}} + (1 - {x_1}){c_{22}}) + ({x_2} \cdot {c_{31}} + (1 - {x_2}){c_{32}}) \le {c_{{\rm{request}}}}, $ | (12) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_i} \ge 0,i = 0,1,2\\ [x,{\rm{faval}}] = {\rm{linprog}} (c,\mathit{\boldsymbol{A}},{\mathit{\boldsymbol{A}}_{{\rm{eq}}}},{\mathit{\boldsymbol{v}}_{{\rm{lb}}}},{\mathit{\boldsymbol{v}}_{{\rm{ub}}}})。\end{array} $ | (13) |
向时间大的分支靠齐,这里两个并行结构的各自分支中,有
| $ {\rm{max}}({x_1} \cdot {t_{21}},(1 - {x_1}){t_{22}}) = (1 - {x_1}){t_{22}},{\rm{max}}({x_2} \cdot {t_{31}},(1 - {x_2}){t_{32}}) = (1 - {x_2}){t_{32}}。$ |
于是,目标函数化简为
| $ {\rm{Min}} T = ({x_0} \cdot {t_{11}} + (1 - {x_0}){t_{12}}) + (1 - {x_1}){t_{22}} + (1 - {x_2}) \cdot {t_{32}}{f_{{\rm{val}}}}, $ |
然后对上述式子进行转化为下列标准化形式:
| $ {\rm{Min}} {T^\prime } = ({t_{11}} - {t_{12}}){x_0} - {t_{22}}{x_1} - {t_{32}}{x_2}, $ | (14) |
| $ \begin{array}{l} {\rm{s}}{\rm{.t}}{\rm{.}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({q_{12}} - {q_{11}}){x_0} + ({q_{22}} - {q_{21}}){x_1} + ({q_{32}} - {q_{31}}){x_2} \le - 3{q_{{\rm{ request }}}} + {q_{12}} + {q_{22}} + {q_{32}}, \end{array} $ | (15) |
| $ {({c_{11}} - {c_{12}}){x_0} + ({c_{21}} - {c_{22}}){x_1} + ({c_{31}} - {c_{32}}){x_2} \le {c_{{\rm{ request }}}} - {c_{12}} - {c_{22}} - {c_{32}},} $ | (16) |
| $ {{x_0} \ge 0,} $ | (17) |
| $ {{x_1} \le {t_{22}}/({t_{21}} + {t_{22}}),} $ | (18) |
| $ {{x_2} \le {t_{32}}/({t_{31}} + {t_{32}}),} $ | (19) |
这里,T′=T-t12-t22-t32。
在具体计算时,对该实验流程,不失合理性,可考虑parrelle Ⅰ、parrelle Ⅱ不同时出现,这里,都作为parrelle Ⅰ类型处理;另外,考虑到分支的任务量分配是时间耗费大的少分配,均衡方向是确定的,因此在并行分支的最大值选择上就是选择时间耗费大的分支。上述转化模型可利用Matlab线性规划函数[x, faval]=linproc(c, A, b, Aeq, beq, vlb, vub)求解。这里的参数经计算得到的值分别为:c=[0.05-0.65-0.7],A=[-0.025 0.01 0.02;-0.5-0.3-0.5],b=[?; ?],Aeq=[],beq=[],vlb=[0;0;0], vub=[1;0.52;0.5385],其中b随用户的服务能力需求和价格需求变化,分别设为qrequest、crequest。为了更好地观察测试结果,对它们取多组数值进行实验(这里为了简化,不影响结果的正确性,除去第一层次简化掉的节点的值),于是计算得到各分支结构的优化分配量x0, x1,x2和优化时间见表 3所示。
| 表 3 不同需求下的时间优化结果 Table 3 Time optimization results under different demands |
在没有采用文中方法优化情况下,其执行时间为1.2 h,而采用文中优化方法后,其结果从表 3可看出,大部分都在1.2 h之下,并且表 3中优化结果提高了5.4%,这个结果与用户的服务能力和价格需求有关,好的情况下能提高更多。反过来也说明,通过文中方法得到优化时间情况,能指导用户对流程在服务能力和价格上提出更为精确的需求,从而使流程效率得到提高。另外,优化的效果与各分支结构的实际情况相关,如果选择分支结构本身概率分配比较恰当、并行分支服务能力比较均衡,优化提高幅度也就会相应变小,而如果各分支结构本身配置较差,则优化改进的幅度将增大。某些需求下,优化后的时间反而不如优化前,如表 3所示的1.9 h,这是由于要求变高,尤其价格需求和服务能力需求同时变高时,不利于时间的优化。
4 结语业务流程优化一直是学术界和工业界研究的热点,尽管已有许多的研究成果和实际应用,但已有的传统方法未能从流程分支结构的特性上考虑业务流程执行时间的性能优化。文章正是考虑到这种流程分支结构的时间差异化,以及与其他属性因子的关系,用于对制造服务流程优化的研究,构建了制造服务流程优化模型及其算法,文中创新点主要为以下几点:
1) 提出了流程路径规范化等概念,并构建了制造服务流程控制结构的属性计算方法;
2) 构建了基于业务流程分支结构时间差异化改进的制造服务流程时间优化模型;
3) 设计了基于线性规划的分层分块的制造服务流程执行时间优化算法。
文中研究的应用场景适合顺序结构上前后节点衔接较好,而分支结构需要优化的制造服务流程。实际上,顺序结构上前后节点的衔接对执行时间也具有重要的影响,今后将进一步结合顺序结构进行研究,即考虑节点前后时间衔接的影响,使其更具通用性,并在云制造应用中发挥其更大的实际应用价值。
| [1] |
肖宗水, 孟令童, 孔兰菊, 等. 基于数据库日志关联规则挖掘的业务流程优化[J]. 计算机集成制造系统, 2017, 23(5): 993-999. XIAO Zongshui, MENG Lingtong, KONG Lanju, et al. Business process optimization approach based on association rules mining of database logs[J]. Computer Integrated Manufacturing Systems, 2017, 23(5): 993-999. (in Chinese) |
| [2] |
高雅楠, 方贤文, 王丽丽. 基于Petri网行为紧密度的业务流程配置优化分析[J]. 计算机科学, 2017, 44(S1): 539-542. GAO Yanan, FANG Xianwen, WANG Lili. Optimized analysis of business process configuration based on petri net behavior closeness[J]. Computer Science, 2017, 44(S1): 539-542. (in Chinese) |
| [3] |
刘红, 刘祥伟, 王丽丽. 基于配置变迁的业务流程模型优化分析方法[J]. 计算机科学, 2016, 43(S2): 509-512. LIU Hong, LIU Xiangwei, WANG Lili. Business process model optimized analysis method based on configuration change[J]. Computer Science, 2016, 43(S2): 509-512. (in Chinese) |
| [4] |
陈霞, 丁静之. 汽车零配件进口物流业务流程优化:以A企业为例[J]. 物流工程与管理, 2017, 39(5): 74-77, 37. CHEN Xia, DING Jingzhi. Business process optimization from the auto parts imports logistics perspective:take A enterprise as an example[J]. Logistics Engineering and Management, 2017, 39(5): 74-77, 37. (in Chinese) DOI:10.3969/j.issn.1674-4993.2017.05.027 |
| [5] |
赵思萌, 李宗平. 基于Petri网的铁路物流中心卸车业务流程优化[J]. 交通运输工程与信息学报, 2018, 16(3): 109-113. ZHAO Simeng, LI Zongping. Optimizing business processes of railway logistics center based on petri net[J]. Journal of Transportation Engineering and Information, 2018, 16(3): 109-113. (in Chinese) DOI:10.3969/j.issn.1672-4747.2018.03.016 |
| [6] |
尤建新, 蔡文珺, 尤筱玥. 基于质量改善视角的业务流程优化研究[J]. 工业工程与管理, 2017, 22(6): 161-168. YOU Jianxin, CAI Wenjun, YOU Xiaoyue. Empirical research on process optimization based on quality improvement[J]. Industrial Engineering and Management, 2017, 22(6): 161-168. (in Chinese) |
| [7] |
郭哲, 吴俊新, 唐加福, 等. 基于过程代数的电子商务定价业务流程的重组与优化[J]. 东北大学学报(自然科学版), 2009, 30(6): 777-781. GUO Zhe, WU Junxin, TANG Jiafu, et al. Pricing business process reengineering and optimization based on process algebra in electronic commerce[J]. Journal of Northeastern University(Natural Science), 2009, 30(6): 777-781. (in Chinese) |
| [8] |
王云鹏, 李善兴, 王占中, 等. 基于Petri网的汽车制造业生产物流流程优化[J]. 吉林大学学报(工学版), 2008, 38(S1): 59-62. WANG Yunpeng, LI Shanxing, WANG Zhanzhong, et al. Optimization of production logistics process of automobile manufacture enterprise based on petri Net[J]. Journal of Jilin University(Engineering and Technology Edition), 2008, 38(S1): 59-62. (in Chinese) |
| [9] |
Huang Z X, Lu X D, Duan H L. A task operation model for resource allocation optimization in business process management[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part A:Systems and Humans, 2012, 42(5): 1256-1270. DOI:10.1109/TSMCA.2012.2187889 |
| [10] |
Vergidis K, Tiwari A. Business process design and attribute optimization within an evolutionary framework[C/OL]. 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence). New York, USA: IEEE, 2008(2008-09-23)[2019-09-25]. https: //ieeexplore.ieee.org/document/4630867.
|
| [11] |
Olkhovich L. Semi-automatic business process performance optimization based on redundant control flow detection[C/OL]//Advanced Int'l Conference on Telecommunications and Int'l Conference on Internet and Web Applications and Services (AICT-ICIW'06). New York, USA: IEEE, 2006(2006-04-03)[2019-09-25]. https: //ieeexplore.ieee.org/document/1602279.
|
| [12] |
Grzech A, Juszczyszyn K, S'wiątek P. Methodology and platform for business process optimization[M]. .
|
| [13] |
Soti P, Pandey S. Business process optimization for RHIOs[J]. Journal of healthcare information management:JHIM, 2007, 21(1): 40-47. |
| [14] |
谭伟, 刘璇, 徐钦桂. 服务环境下多粒度制造资源自适应组织与发现[J]. 计算机集成制造系统, 2014, 20(9): 2283-2296. TAN Wei, LIU Xuan, XU Qingui. Adaptive organization and discovery of multi-granularity manufacturing resource in service environment[J]. Computer Integrated Manufacturing Systems, 2014, 20(9): 2283-2296. (in Chinese) |
| [15] |
彭志平, 李晓明, 柯文德. 基于本体概念群组划分的语义距离计算方法[J]. 模式识别与人工智能, 2011, 24(2): 194-200. PENG Zhiping, LI Xiaoming, KE Wende. An ontology concept-based cluster partition approach for computing the semantic distance between concepts[J]. Pattern Recognition and Artificial Intelligence, 2011, 24(2): 194-200. (in Chinese) DOI:10.3969/j.issn.1003-6059.2011.02.006 |
 2020, Vol. 43
2020, Vol. 43

