1b. 昆明理工大学云南省计算机技术应用重点实验室, 昆明650500;
2. 云南大学 信息学院, 昆明 650091
1b. Yunnan Provincial Key Laboratory of Computer Technology Application, Kunming University of Science and Technology, Kunming 650500, P. R. China;
2. School of Information Science and Engineering, Yunnan University, Kunming 650091, P. R. China
在线服务作为一种利用互联网技术,向用户提供线上服务的方式,近年来在电子商务、电子政务等领域扮演着越来越重要的角色[1]。伴随着互联网的不断发展,用户在选择自己需要的服务时也涌现出了多方面的问题。一是,在线服务的数量越来越庞大,用户需要耗费大量的时间和精力来挑选自己想要的服务[2];二是,由于网络环境的虚拟性,用户难以对服务产生直观的印象并做出有效的判断;三是,在市场竞争中,服务提供商为了自身利益可能提供不真实的信息[3-5]。上述问题使得用户需要借助以第三方观点为基础形成的在线服务信誉来辅助用户对服务进行选择。信誉是对服务已有质量或特性的综合度量,反映服务履行其承诺服务的水平和用户对它的总体信任程度[6]。有效的在线服务信誉度量方法有利于用户了解服务的信用状况,从而使其更有效地选择服务, 也能约束服务提供者的欺诈行为并且指导其提高服务质量。
近年来,国内外研究人员致力于研究更合理有效的在线服务信誉度量方法。基于用户对服务的评分计算在线服务信誉的方法应用十分广泛,常用的有累加法(SUM)和平均法(AVG)[7]。淘宝(Taobao)和eBay采用累加法,通过将所有用户对同一个服务的评分进行累加得到该服务的信誉,计算出所有服务的信誉,最终得到这些服务的信誉排序。亚马逊(Amazon)网站采用平均法,首先将所有用户对同一个服务的评分进行累加后除以该服务的被评分次数得到该服务的信誉,然后计算出所有服务的信誉,最终得到这些服务的信誉排序。文献[8]提出一种基于低阶矩阵分解通过用户评分进行商品项目信誉度量的方法。文献[9]根据统计学理论为基础提出了一种灵活简单的Beta信誉计算方法,使用β概率密度函数和用户反馈数据最终计算出信誉排序。上述方法均假设所有的用户按照同一评价准则[10]对服务进行客观的评价,然而用户在与服务交互时,有的用户看重服务的结果,有的用户看重与服务交互时的体验;有的用户更宽容,习惯给服务偏高的评分,有的用户更严格,习惯给服务偏低的评分[11]。用户不同的评价准则使得同一服务可能得到不同的评分,致使用户对同一服务的评分不具有公正的可比性,使得最终得到的信誉结果难以反映在线服务真实的性能[12]。另外,如果有用户试图操纵服务的信誉,通过用户对服务的评分计算得到在线服务信誉度量结果能被轻易地改变。
基于序数偏好的信誉度量方法可有效解决用户评价准则不一致时的信誉度量问题。该方法以用户对服务的偏好排序为基础而不是用户对服务的评分为基础计算服务信誉,避免了具有不同评价准则的用户评分之间的比较。文献[13]提出了一种利用Kendall tau距离找到与所有用户服务排序距离最小的信誉排序,满足了多数准则性质。文献[14]提出了一种根据成对服务之间的占优关系建立有向无环图来计算最终的信誉排序,满足了单调性以及多数准则等性质。这些方法满足了一些社会选择理论中的常见性质,比如孔多塞性[15],单调性[16],多数准则[17],反转对称性[18]等。将用户对服务的个人排序聚集成最终的集体排序。对于服务而言,某个服务从客观上会比另一个服务好,即可以通过其自身真实的质量被客观地比较,因此服务之间存在客观的优劣关系,即事实上存在唯一潜在的真实服务排序(即真相)[19]。每一个用户对服务的偏好排序受主观因素影响,可以被看作对这个真相服务排序的带噪估计[20]。进而在线服务信誉度量可被视作找出一个与真相最接近的服务排序的过程。现有基于序数偏好的信誉度量方法通常以是否满足社会选择中的单调性、多数准则等性质对最终的服务排序质量进行评价[13-14, 21],但不能证明满足这些性质有利于得到或者接近真相。
为了解决上述问题,文中以社会选择理论为基础,提出一种面向误差最小化的在线服务信誉度量方法EMR(error minimization rule), 以用户对服务的偏好排序为基础,无须假设所有用户具有一致的评价准则。根据距离尺度来衡量服务排序与真相之间的误差。找出可能为真相的服务排序集合,找出与这个集合之间平均误差最小的在线服务信誉向量作为最终的服务信誉,从而保证了最终返回的结果与真相之间的误差最小。文中方法考虑了用户对不同服务的排名关系,提高了方法的抗操纵性。另外,由于任何一个服务排序都有可能是潜在的真相,导致信誉计算时间复杂度较高,因此采用分支切割法寻找最优信誉向量,保证了信誉度量的效率。
1 问题描述文中着眼于解决在用户评价准则不一致情况下找到与潜在的真相服务排序最接近的服务信誉度量结果的问题。为方便阐述,对在线服务信誉度量相关概念定义如下:
定义1. U表示所有用户的集合,U={u1, u2, …, un},其中,|U|=n。设S表示所有在线服务的集合,S={s1, s2, …, sm},其中,|S|=m。
定义2. σx表示用户ux对所有在线服务的偏好排序,σx=(sx1, sx2, …, sxm),其中,x1, …, xm∈[1, m],x1≠x2≠…≠xm。sx1为用户ux偏爱程度最高的服务。令σx(si)表示服务si在σx中的位次。σx(si)的值越小说明服务si在σx中越靠前。如果在σx中σx(si) < σx(sj),表示用户ux认为服务si优于服务sj,记为sixsj。
定义3. π表示U中n个用户对服务的偏好排序集合,π={σ1, σ2, …, σn},其中,|π|=n。
定义4. L(S)表示S中服务所有可能的完整服务偏好排序,即:
| $ L(S) = \{ \sigma |\sigma = ({s_{i1}} \in S,{s_{i2}} \in S/{s_{i1}}, \cdots ,{s_{im}} \in S/\{ {s_{i1}}, \cdots {s_{im - 1}}\} )\} , $ | (1) |
对于服务集合S={s1, s2, …, sm},可能的服务偏好排序有m!种,
定义5. L(S)中每一个服务偏好排序都有可能是真相服务排序,但真相服务排序是唯一的。令σ*表示在线服务集合S上的真相服务排序,σ*∈L(S)。
定义6.令ε代表 2个排序之间误差的衡量尺度,ε(σ, σ*)表示一个服务排序σ和真相σ*之间的误差。ε(σ, σ*)越大,表示这个服务排序与真相之间的一致性越小,ε(σ, σ*)越小,表示这个服务排序与真相之间的一致性越大。
目前在线服务信誉度量方法忽略了用户评价准则不一致和寻找真相的问题。例如,平均法默认不同用户对在线服务的评价标准一致,通过计算在线服务获得的所有用户评分的平均值作为该服务的信誉,假设最终在线服务信誉排序中,服务sx的信誉高于服务sy,通过信誉对在线服务进行选择时,用户应该选择sx,但在真实在线服务场景中,不同用户对服务的偏好不同,不同表现的服务可能得到相同的评分,相同表现的服务可能得到不同的评分,致使最终的信誉结果不一致,所以事实上服务sx、sy的信誉是不可比较的。
基于序数偏好的在线服务信誉度量方法将用户的服务偏好排序聚集成一个最终的服务偏好排序作为信誉向量,最终的服务偏好排序与用户偏好排序的集合一致性最大并且尽可能多地满足社会选择理论中的一些常见性质。每个用户的服务偏好排序与真相之间存在不同程度的误差,也就是说找到与本身就和真相之间存在误差的用户偏好排序集合一致性最大的服务排序时引入了二次误差,无法保证与真相之间误差最小。
文中以用户对服务的偏好关系为基础计算最终的服务信誉向量,避免了用户评价准则不一致导致的问题,利用距离尺度衡量最终结果与真相之间的误差,找出与真相排序误差最小的在线服务信誉排序σz。
2 面向误差最小化的服务信誉度量在社会选择理论中,社会选择方法是一种将个人偏好聚集成集体偏好的函数,该理论表明基于序数偏好进行偏好聚集可以避免用户评价准则不一致的问题[22]。考虑到在线服务信誉度量领域中的用户评价准则不一致的问题,文中方法结合社会选择理论的思想以用户对服务的偏好排序为基础来度量服务信誉。
根据社会选择理论,将个人偏好聚集为集体偏好有两大主流方向,一种是力求得到与所有用户偏好最一致的结果,这种方向适用于民主选举等场景;另一种是力求得到真相,这一方向适用于候选项能通过质量等因素被客观地比较的场景[23]。而在线服务可以通过真实质量被客观地比较,文中将用户对服务的偏好排序集合π中的n个用户偏好排序视作对真相排序σ*的带噪估计。根据这些对σ*的带噪估计,力求得到一个与σ*误差最小的服务信誉排序。
2.1 基于Kendall tau的服务排序误差度量基于以上分析,提出一种面向误差最小化的在线服务信誉度量方法。排序之间的误差通过距离尺度来衡量。常见的用来衡量2个排序之间的距离尺度[24]主要有以下几种:
1) Kendall tau距离:根据2个排序中顺序不一致的成对服务的数量衡量距离。
2) Footrule距离:根据2个排序中相同元素的位置之差的绝对值总和衡量距离。
3) Maximum Displacement距离:根据2个排序中所有相同元素之间最大的位置之差衡量距离。
4) Cayley距离:根据一个排序中的元素交换位置使其与另一个排序相同的最少的次数衡量距离。
Kendall tau距离考虑到了排序中每个元素与其他所有元素之间的关系,而Footrule和Maximum Displacement 2个距离只考虑了2个排列中相同元素的位置差异,Cayley与Kendall tau 2个距离都可以看作是将一个排序恢复成另一个排序需要的最少次数,但是Cayley直接交换元素位置的方式忽略了被交换元素与其他元素之间的关系。Kendall tau距离是目前衡量2个排序之间距离最重要的衡量尺度[10]。文中选用Kendall tau距离来衡量2个排序之间的误差,排序σi和σj之间的Kendall tau距离KT(σi, σj)的计算方法为:
| $ KT({\sigma _i},{\sigma _j}) = (a,b):a < b,({\sigma _i}(a) < {\sigma _j}(b) \wedge {\sigma _i}(a) > {\sigma _j}(b)) \vee ({\sigma _i}(a) > {\sigma _j}(b) \wedge {\sigma _i}(a) < {\sigma _j}(b)), $ | (2) |
式中,σi(a)和σj(b)分别表示元素a和元素b在排序σi和σj中的位置。从式(2)可以看出,KT(σi, σj)说明2个排序的Kendall tau距离为排列顺序不一致的2个元素的成对数量,体现了2个排序之间的一致性。KT(σi, σj)越小,表明这2个排序之间的一致性越大;KT(σi, σj)越大,表明这2个排序之间的一致性越小;KT(σi, σj)=0,表明这2个排序完全相同。
将Kendall tau距离应用于服务排序之间的误差衡量中,通过计算2个服务偏好排序中服务对的顺序不一致的数量来衡量这2个排序之间的误差。计算2个排序之间的误差ε(σx, σy),首先统计2个不同的服务在σ中的优先关系,令kx(i, j)=1表示σx(si) < σx(sj),kx(i, j)=0表示σx(si)>σx(sj)。对于2个不同的服务si和sj,它们在σx和σy之间的距离ki, j(σx, σy),可以通过这对服务之间的优先关系来计算:
| $ {k_{i,j}}({\sigma _x},{\sigma _y}) = \left\{ {\begin{array}{*{20}{l}} {0,{k_{x(i,j)}} = {k_{y(i,j)}},}\\ {1,{k_{x(i,j)}} \ne {k_{y(i,j)}},} \end{array}} \right. $ | (3) |
式中,ki, j(σx, σy)=0表示用户ux和uy对于服务si和sj的偏好是一致的;ki, j(σx, σy)=1表示用户ux和用户uy对于服务si和服务sj的偏好是相反的。
对于服务集合服务S,服务排序σx与服务排序σy之间的误差可以通过成对服务的距离之和计算得到,即:
| $ \varepsilon ({\sigma _x},{\sigma _y}) = \sum\nolimits_{{s_i},{s_j} \in S} {{k_{i,j}}} ({\sigma _x},{\sigma _y})。$ | (4) |
对于服务数量为m的排序,成对服务数量为Cm2。从式(4)可以看出,使用Kendall tau距离衡量2个服务排序之间误差的时间复杂度为O(m2),在实验中,利用冒泡排序思想将时间复杂度改进为O(mlogm)。
2.2 真相未知时的信誉度量每个用户的服务偏好排序被看作对真相排序的带噪估计,在缺少其他信息来判断的情况下,任意一个服务偏好排序都有可能是潜在的真相排序。而本质上,所有的用户都是根据个人对服务的使用体验给出主观的服务偏好排序,每个用户的服务偏好排序都与真相之间存在一定的误差。用户对服务的偏好排序集合π与真相之间的总误差用
| $ \varepsilon (A,B) = \frac{1}{{|A||B|}}\sum\limits_{\sigma \in A} {\sum\limits_{{\sigma ^\prime } \in B} \varepsilon } (\sigma ,{\sigma ^\prime })。$ | (5) |
在现实场景中,真相是客观存在的,由于无法辨认真相是哪一个,导致衡量结果的误差没有比较对象,无法判断是否与真相误差最小。文中的做法是首先找到一些可能是真相的服务排序,然后根据可能的真相集合来判断结果的误差。而用户对服务的偏好排序都可以被视作对真相的带噪估计,每个用户的偏好排序与真相之间存在一个误差值,可以利用这些排序寻找可能的真相。假设用户的偏好排序与真相排序σ*之间的平均误差不超过t。则所有与用户偏好排序集合π的平均误差不超过t的服务排序都是可能的真相排序。即假设ε(π, σ*)≤t,可能的真相集合βt(π)则为
| $ {\beta _t}(\pi ) = \{ \sigma \in L(S)|\varepsilon (\pi ,\sigma ) \le t\} 。$ | (6) |
根据上述假设,当真相与集合π之间的平均误差不超过t时,真相排序σ*∈βt(π)。这样就可以通过衡量最终的结果与βt(π)之间的误差来判断与真相排序之间的误差是否最小。显然,误差上限t的取值会影响集合βt(π)中的元素,进而对最终的信誉度量结果产生影响。误差上限t在合适的范围内取值非常重要,在实验中将进一步验证。另外文中方法对于误差上限有如下证明。
定理1.对于有n个用户服务排序的集合π,当π与真相之间的平均误差不超过t时,至少存在1个与可能的真相集合βt(π)误差不超过t的服务排序。
证明:
| $ \varepsilon (\pi ,{\beta _t}(\pi )) = \frac{1}{{n|{\beta _t}(\pi )|}}\sum\limits_{\sigma \in \pi } {\sum\limits_{{\sigma ^\prime } \in {\beta _t}(\pi )} \varepsilon } (\sigma ,{\sigma ^\prime }) = \frac{1}{{|{\beta _t}(\pi )|}}\sum\limits_{{\sigma ^\prime } \in {\beta _t}(\pi )} {\frac{1}{n}} \sum\limits_{\sigma \in \pi } \varepsilon (\sigma ,{\sigma ^\prime }) = \frac{1}{{|{\beta _t}(\pi )|}}\sum\limits_{{\sigma ^\prime } \in {\beta _t}(\pi )} \varepsilon ({\sigma ^\prime },\pi ) \le t。$ | (7) |
根据式(7)得知,如果π和βt(π)之间的平均误差不超过t,那么至少存在1个服务偏好排序σ″∈π,使得ε(σ″, βt(π))≤t。说明无论误差上限t的取值如何,总能找到1个与可能的真相集合之间误差不超过t的服务排序。
2.3 面向误差最小化的信誉度量根据2.2节可以通过衡量最终结果与可能的真相集合之间的误差,判断最终的服务排序能否作为误差最小的在线服务信誉。在计算服务排序与集合之间的误差时,对于m个在线服务,有m!种可能的服务排序,当在线服务的数量较大时,如果计算每个可能的服务排序与用户对服务的偏好排序集合π之间的距离,会导致计算量巨大。为了提高计算服务排序与π之间距离的效率,提前统计用户对服务偏好排序集合π中每个用户偏好排序形成占优关系的服务对数量。对于用户对服务偏好排序集合中的所有服务偏好排序σ,用Pij表示σ(si) < σ(sj),用Pji表示σ(sj) < σ(si),则集合π中
计算ε(π, σ)要计算对于每两个不同的服务在σ与π之间的距离,对于两个不同的服务si, sj∈S(i≠j),它们在服务偏好排序σr与用户的服务偏好排序集合π之间的距离为
| $ \sum\limits_{{\sigma _x} \in \pi } {{k_{i,j}}} ({\sigma _r},{\sigma _x}) = \left\{ {\begin{array}{*{20}{l}} {|{P_{ij}}|,{\sigma _r}(i) > {\sigma _r}(j),}\\ {|{P_{ji}}|,{\sigma _r}(i) < {\sigma _r}(j)}。\end{array}} \right. $ | (8) |
服务集合S、服务排序σr与用户的服务偏好排序集合π之间的平均距离,通过计算S中所有成对服务与用户的服务偏好排序集合π距离之和得到:
| $ \varepsilon (\pi ,{\sigma _r}) = \frac{1}{{|U|}}\sum\limits_{{\sigma _i} \in \pi } {\sum\limits_{{s_i},{s_j} \in S} {{k_{i,j}}} } ({\sigma _r},{\sigma _i})。$ | (9) |
由于没有其他的信息判断哪个排序更可能是真相,βt(π)中所有服务排序都有着相等的可能性是真相服务排序。文中目标是找到与可能的真相集合βt(π)平均距离最小的服务排序。令EMR(t, π)表示与βt(π)平均距离最小的服务排序,即
假设| βt(π)| =k,对于m个在线服务,L(S)=m!,从式(6)分析可知,此时计算βt(π)需要从L(S)中找到所有不超过平均误差上限的服务排序,时间复杂度为O(nm!mlogm),计算EMR(t, π)的时间复杂度为O((n+k)m!mlogm),在经过提前统计π中每个用户偏好排序形成占优关系的服务对数量之后,可以避免每次重复计算π中服务排序的服务对的占优关系,只需要计算所求服务排序中Cm2个服务对的占优关系。根据式(8),计算βt(π)的时间复杂度为O(m! m2), 在现实中,用户数量n通常远远大于服务数量m,经过优化,计算EMR(t, π)的时间复杂度为O((m2m! +km! mlogm))。
对于服务集合S,用户对服务的偏好序列集合π,可以将信誉度量最优化问题转化为0~1整数规划问题,目标函数为
| $ f({\sigma _z}) = \mathop {{\rm{min}}}\limits_{{\sigma _z} \in L(S)} \frac{1}{{|U|}}\sum\limits_{{\sigma _x} \in {\beta _t}(\pi )} {\sum\limits_{{s_i},{s_j} \in S} {{k_{i,j}}({\sigma _z},{\sigma _x})} } , $ | (10) |
式中,σz为目标函数f(σz)的一个可能解,其中σz∈L(S)。
例1 .令服务集合为S={a, b, c},用户集合为U={u1, u2, u3, u4, u5}, 用户对服务的偏好排序集合为
| $ {\varepsilon (\pi ,a \succ b \succ c) = 0.8\varepsilon (\pi ,a \succ c \succ b) = 1.0\varepsilon (\pi ,b \succ a \succ c) = 1.4,} $ |
| $ {\varepsilon (\pi ,c \succ a \succ b) = 1.6\varepsilon (\pi ,c \succ b \succ a) = 2.2\varepsilon (\pi ,b \succ c \succ a) = 2.0}。$ |
通过判断服务排序与π之间的平均误差是否超过t=1.5,可以得到可能的真相集合为
对于不同的误差上限t,会产生不同的可能的真相集合,从而导致不同的误差最小排序。在实验中,将会验证在不同的误差上限t取值对ε(EMR(t, π), σ*)的影响。
2.4 基于分支切割法寻找最优信誉向量寻找最优信誉向量是一个NP难问题[21],随着在线服务s数量的增加,解空间L(S)的规模呈指数级增长。如果使用传统的枚举算法寻找最优信誉向量需要计算每一种可能的在线服务排序与用户对服务的偏好排序集合π之间的平均误差,筛选出所有与π之间的平均误差不超过误差上限t的在线服务排序作为可能的真相集合βt(π),计算每一种可能的在线服务排序与βt(π)之间的平均误差,将误差最小的在线服务排序作为服务信誉,计算量随着在线服务的数量增加而变得巨大且需要消耗大量的存储空间。
分支切割法(Branch-and-Cut)[25]是一种可以解决各种整数规划问题的精确算法,结合了分支定界法和割平面法2种算法,通过求解整数规划问题的松弛问题运行。分支定界法每次将问题分为2个子问题来求解,将求解范围不断缩小;割平面法通过添加约束条件,提高问题的松弛度,加快了分支定界算法的速度。该算法可以提供最优性的保证,在多个应用领域中的大量问题已经都用分支切割法成功的解决[25]。
对于σz中的任意服务,若服务si优于服务sj,即若kz(i, j)=1,则必有kz(j, i)=0,可得到约束条件kz(i, j)+ kz(j, i)=1;若服务sj优于服务si,服务sl优于服务sj,则必有
利用分支切割法作为寻找最优信誉向量的算法,算法的初始输入为π和t,βt(π)是未知的,将式(10)中的βt(π)用π代替当作初始的整数规划问题,用来寻找βt(π),即初始整数规划问题
步骤1.将初始的整数规划问题用ILP0表示。将目标函数f(σz)的函数值ε(π, σz)的上界设为+∞,记为ε (π, σz)=+∞,函数值下界设为-∞,记为
步骤2.使用单纯形法计算整数规划问题的松弛问题LP的最优解,记为x0。
步骤3.如果x0为整数解,则将x0对应的服务排序σx0=(sx0, sx1, …, sxm)添加到可能的真相集合βt(π)中。
步骤4.如果x0不是整数解,在最优解x0中选择一个值不符合整数约束条件的决策变量x0i,该决策变量代表在线服务s0i,根据x0i的值ai构造2个整数约束条件:
步骤5.继续对各个子问题的松弛问题通过单纯形法进行求解,找出令目标函数值最小的解,将函数值记为z′,更新
步骤6.若z*≤t,将整数解x1对应的服务偏好排序σ继续添加到βt(π)中,同时添加约束条件f(σz)> z*。
步骤7.对子问题的约束条件添加松弛变量来得到新的约束条件,将约束条件继续添加到对应的子问题中,利用步骤5对子问题进行求解。
步骤8.重复步骤2~7,直至
步骤9.重复步骤2求解新的整数规划问题ILP1,如果此时x0为整数解,那么x0对应的服务排序就是最终的在线服务信誉排序σz,否则继续重复步骤4、5、7,直至
步骤10.将得到的最优解作为服务偏好排序σz的最优服务信誉。
基于上述步骤,假设|βt(π) |=k,算法会在k+1次后得到最优信誉向量。对于用户数为n,服务数为m的目标函数中决策变量的数量为m(m-1),约束条件的数量为m(m-1)(m-2)。在本算法利用单纯形法中求解一次松弛问题时,时间复杂度为O(m5),需要进行O(logm3)次,综合上述部分,文中方法经过分支切割法优化后的时间复杂度为O(nkm5logm)。
3 实验结果及分析根据第2节提到的面向误差最小化的在线服务信誉度量方法,设计实现了在线服务信誉度量方法。实验环境为PC机,Windows10操作系统,Core i5 CPU,8GB RAM,开发环境为PyCharm 2017.2.3,开发语言为Python3.6。为了验证方法的有效性,笔者使用包含并标出真相排序σ*的真实数据集dots[26](实验选择1号dots数据集)。该数据集包含795个用户,每个用户根据4张图上黑点的数量从少到多得到这4张图排序。在考虑用户评价准则不一致的情况下,聚合序数偏好的社会选择函数都可以获得服务群体排序。近年来,社会选择方法已经被用来作为在线服务信誉度量的方法,例如文献[13]使用模拟退火实现Kemeny方法进行在线服务的信誉度量。文中方法与Plurality、Borda、Kemeny、Copeland 4种社会选择方法[23]进行对比。实验将方法输出的最终服务排序(这一过程可看作恢复真相的过程)与真相之间的误差作为方法误差的衡量标准。通过生成一个排序作为真相,然后在真相排序中随机选择两个服务交换它们的位置,并且随机选择数次。最后将新的服务排序作为一个用户对服务的偏好排序,以这种方式模拟200~800个用户和10~50个在线服务的不同样本规模数据集,实验在这些模拟数据集下验证了该方法的有效性和运行效率。
3.1 噪音对恢复真相的影响为了验证不同程度的噪音对方法结果与真相之间的误差大小的影响,实验通过随机将dots数据集中的用户偏好排序重新排列的方式来得到不同程度的加噪数据集。设置用户偏好集合对于真相的平均误差上限为t*=ε(π, σ*),其中,σ*为数据集中存在的真相排序。
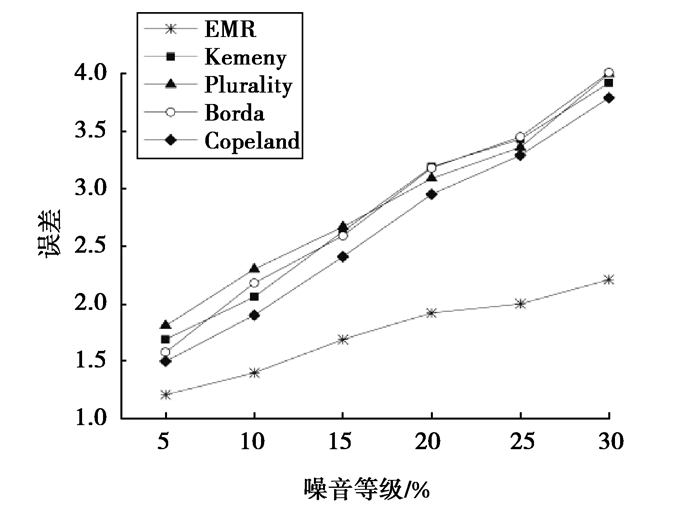
实验中,抽取5%~30%的用户对服务的偏好排序进行随机重排列得到不同带噪程度的数据集,在不同的噪音程度下,记录在200次实验下根据文中方法EMR得到的最优服务排序σz与真相排序σ*之间的误差ε(σz, σ*)、以及Kemeny、Plurality、Borda,Copeland 4种对比方法得到的服务排序与真相之间的误差ε(σK, σ*)、ε(σP, σ*)、ε(σB, σ*),ε(σC, σ*)的平均值,如图 1所示。
|
图 1 噪音与真相相关性实验 Fig. 1 Correlation of truth with noise levels |
由图 1可知,随着用户服务偏好集合的带噪程度即与真相之间的平均误差增大,ε(σz, σ*)、ε(σK, σ*)、ε(σP, σ*)、ε(σB, σ*)、ε(σC, σ*)都会出现增长。用户服务排序集合的带噪程度也就是π与σ*之间的平均误差与最终结果与真相之间的误差呈正相关,表明用户对服务的偏好排序的带噪程度会对方法结果与真相之间的误差值产生正相关的影响。
可以看出,在误差上限t取值为t*时,EMR方法的结果误差明显低于其他方法,这是因为对比方法没有考虑潜在的真相,例如,Kemeny方法得到与所有用户偏好排序一致性最大的服务排序,当用户的服务偏好排序集合与真相之间的误差越大,这些方法的结果与真相之间的误差可能也会越大。另外,注意t*不一定是实现误差最小的t的最优值。
3.2 误差上限取值对恢复真相的影响在现实情况中,真相是未知的,无法计算用户偏好排序集合对真相的真实平均误差,需测试估计误差上限
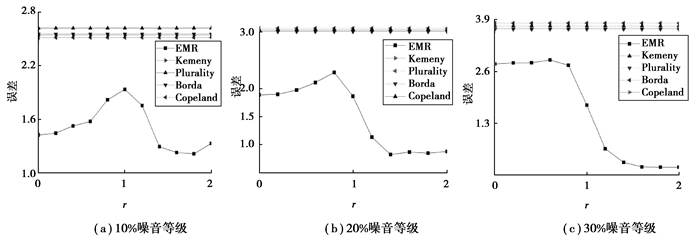
实验中,分别在>10%、20%、30% 3种不同带噪程度的数据集中对文中方法和上述4种对比方法进行测试,记录在200次实验下得到的最终服务排序与真相之间的误差的平均值在不同的r取值下的表现。实验中,取r∈[0, 2];当r∈(1, 2]时,
|
图 2 不同r取值的误差 Fig. 2 Error under different values of r |
图 2表示在10%、20%、30%的带噪数据集下的实验结果。实验中Kemeny、Plurality、Borda,Copeland 4种对比方法的结果并不会随着误差上限t的取值不同而变化,图中结果与真相之间的误差是一条没有波动的横线。可以看出,在不同的噪音等级下,EMR方法的结果随着误差上限t取值的变化而变化。
当r∈[0, 1),即对误差上限t的取值为用户对服务的偏好集合与真相之间的正确误差t*的过低估计时,EMR方法的结果与真相之间的误差呈上升趋势,在r=1附近时,EMR方法的结果与真相之间的误差达到了最大,但也比Kemeny、Plurality、Borda,Copeland这4种常见方法得到的结果与真相之间的误差小。当r∈(1, 2]的范围内,即对误差上限t的取值适当高估时,EMR方法结果与真相之间的误差可以达到最小。
在实际中,t的取值必须通过估计,为了寻找合适的误差上限参考值(该参考值可以通过已知数据计算)。选择样本规模为20个在线服务,200~800个用户数量的4个数据集。记录4个不同数据集下用户偏好排序集合与真相之间的真实误差t*、L(S)中偏好排序与用户偏好排序集合π之间的最小平均距离值tmad以及π中偏好排序与π之间的最小平均距离值tπ,tπ=minσ∈πε(σ, π)。如表 1所示。
| 表 1 误差上限的参考值 Table 1 Upper bound of error references |
由表 1可知,当
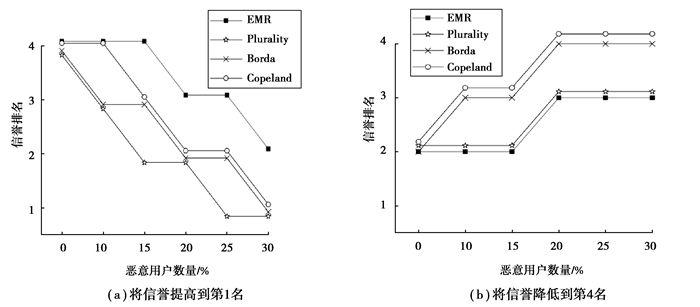
随机选取某个服务,增加对其高排名和低排名的用户数量来操纵该服务的信誉。若该方法得到的服务信誉排名无明显变化,则具有较强的抗操纵性。为了验证文中方法的操纵复杂性,随机选取dots数据集中的2个服务,分别增加10%、15%、20%、25%、30%数量的操纵服务排名的恶意用户。采用文中方法、Plurality方法、Borda方法、Copeland方法分别计算在增加不同数量的恶意用户提升和降低在线服务的信誉排名时,该服务的信誉排名,结果如图 3所示。
|
图 3 操纵复杂性验证 Fig. 3 Verification of manipulation resistence performance |
根据图 3(a)所示,随着恶意提高服务信誉的用户数量的增加,文中方法比Plurality、Borda、Copeland 3种对比方法得到的服务信誉排名提升得更慢。根据图 3(b)所示,随着恶意降低服务信誉的用户数量的增加,文中方法与Plurality方法得到的服务信誉排名一致,比Borda方法和Copeland方法得到的服务信誉排名降低得更慢,因此文中方法具有更好的抗操纵性。
3.4 较大规模数据集上的可行性为了验证文中方法效率,在200~800个用户和10~50个在线服务不同样本规模的数据集中进行测试,设定用户对服务的偏好排序与真相之间的平均误差上限t的取值,使得
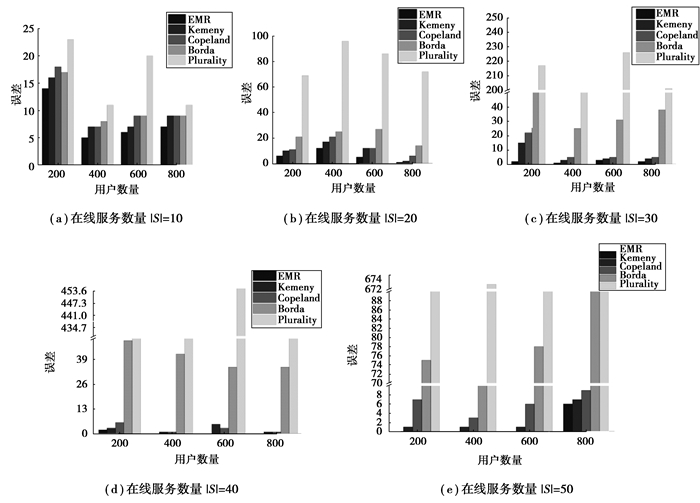
图 4的5张图分别记录了文中方法EMR和对比方法在不同样本规模中结果与真相之间的误差,同时记录了EMR方法每次进行在线服务信誉度量的运行时间,如图 5所示;最后在用户数为800,在线服务数为10~50的情况下,对比文中方法和不使用分支切割法时,进行信誉度量即穷举法的运行时间,如图 6所示。
|
图 4 不同样本下的误差 Fig. 4 Error of different users numbers and services numbers |
|
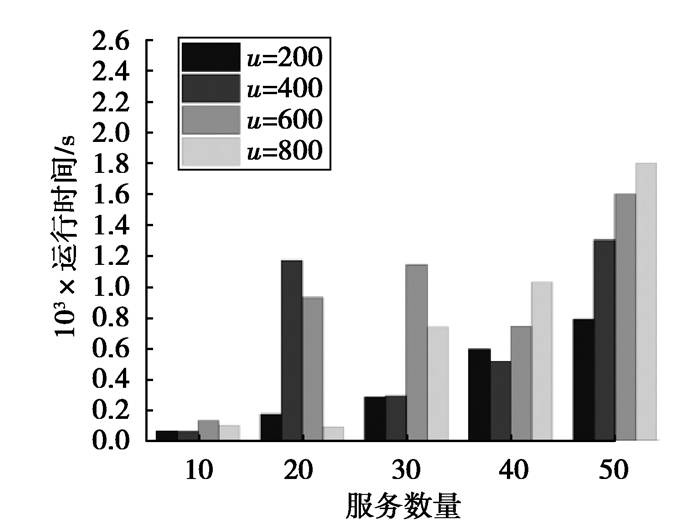
图 5 运行时间 Fig. 5 Runtime of different users numbers and services numbers |
|
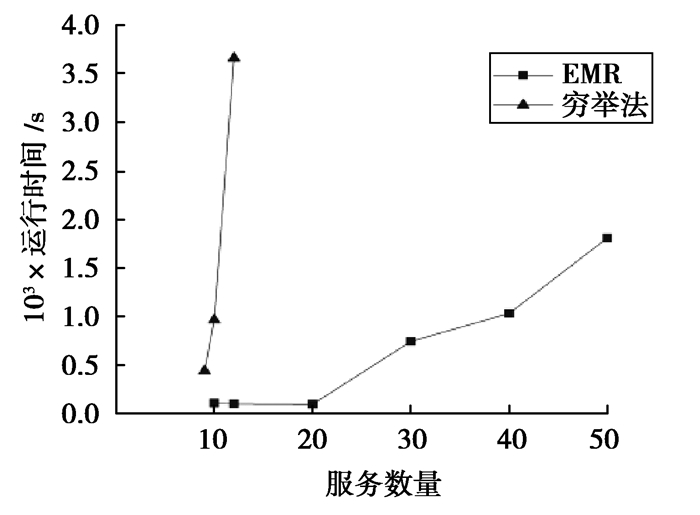
图 6 EMR和穷举法的运行时间对比 Fig. 6 Runtime comparison between EMR and Enumeration method |
由图 4可以看出,EMR方法在不同规模的较大数据集中得出的在线服务信誉结果与真相之间的误差均比其他4种方法小,可以得到与真相更为接近的服务排序。其中,Plurality方法的结果与真相之间的误差在各种样本规模的数据集中均显著高于其他方法。Plurality方法完全遵循社会选择理论中的多数准则性质,可以看出这一性质对于恢复真相没有作用。另外,在线服务数量为40时,如图 3(d)所示,EMR方法在用户数为400、600及800的样本规模中得到的最终结果与真相之间的误差为0;在线服务数量为50时,如图 3(e)所示,EMR方法在用户数为200、400及600的样本规模中得到的最终结果与真相之间的误差为0,得到的最终结果即为真相。由图 5可以看出,文中方法在不同规模的较大数据集上的运行时间都在可接受范围内。随着服务数量的增加,EMR方法的运行时间整体呈增长趋势。当服务数量为20,用户数为400和600时,方法运行时间偏长,这是因为满足与用户的偏好排序集合π之间的平均误差不超过设置的误差上限的服务排序较多,使得可能的真相集合βt(π)中元素较多,寻找βt(π)时消耗的时间偏长,导致总体运行时间偏长,但总体依旧在可接受范围内。
由图 6可以看出,在直接使用穷举法而不使用分支切割法进行在线服务信誉度量时,当服务数量超过11后开始呈指数级增长,导致无法计算大规模数据集,而使用分支切割法进行优化求解之后,方法的运行时间随着服务数量的增加呈线性增长,并且保持在可接受的范围内。因此,当用户数和服务数较大时,利用分支切割法大大提高了文中方法的效率。
4 结束语提出一种面向误差最小化的在线服务信誉度量方法,以解决因为用户评价准则不一致导致在线服务的信誉不具有可比性,以及如何寻找与真相排序误差最小的服务排序的问题。根据用户对服务的偏好排序可被视作真相排序的带噪估计,使用Kendall tau距离衡量服务排序与真相之间的误差,将信誉度量问题建模为最优化问题,最后使用分支切割法寻找在线服务的最优信誉排序,对在线服务信誉度量的思路进行了新的扩展。通过理论和实验证明了该方法的有效性和高效性。当可能的真相集合元素较多时,该方法进行信誉度量的运行时间偏长,未来的工作将着重针对这一点,研究更高效并且保持低误差的在线服务信誉度量方法。
| [1] |
Krause A, Horvitz E. A utility-theoretic approach to privacy in online services[J]. Journal of Artificial Intelligence Research, 2010, 39: 633-662. |
| [2] |
Jøsang A, Ismail R, Boyd C. A survey of trust and reputation systems for online service provision[J]. Decision Support Systems, 2007, 43(2): 618-644. DOI:10.1016/j.dss.2005.05.019 |
| [3] |
Chen M, Singh J P. Computing and using reputations for Internet ratings[C]. Proceedings of the 3rd ACM conference on Electronic Commerce-EC'01. New York, USA: ACM Press, 2001: 154-162.
|
| [4] |
Dellarocas C. Immunizing online reputation reporting systems against unfair ratings and discriminatory behavior[C]. Proceedings of the 2nd ACM conference on Electronic commerce-EC'00. New York, USA: ACM Press, 2000: 150-157.
|
| [5] |
Jiang Z Y, Han J H, Wang Z. An optimization model for dynamic QoS-aware web services selection and composition[J]. Chinese Journal of Computers, 2009, 32(5): 1014-1025. DOI:10.3724/SP.J.1016.2009.01014 |
| [6] |
Huang A F M, Lan C W, Yang S J H. An optimal QoS-based Web service selection scheme[J]. Information Sciences, 2009, 179(19): 3309-3322. DOI:10.1016/j.ins.2009.05.018 |
| [7] |
Zhang X Z, Cui L S, Wang Y. CommTrust:computing multi-dimensional trust by mining E-commerce feedback comments[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(7): 1631-1643. DOI:10.1109/TKDE.2013.177 |
| [8] |
Ling G, King I, Lyu M R. Proceedings of the twenty-third international joint conference on artificial intelligence a unified framework for reputation estimation in online rating systems[J]. Science of Surveying & Mapping, 2014, 27(4): 896-896. |
| [9] |
Jøsang A, Ismail R. The beta reputation system[C]. Proceeding of the 15th Bled Electronic Commerce Conference. Bled, Slovenia: The Pennsylvania State University. 2002: 2502-2511.
|
| [10] |
Fu X D, Yue K, Liu L, et al. Aggregating ordinal user preferences for effective reputation computation of online services[C/OL]. 2016 IEEE International Conference on Web Services (ICWS). San Francisco, CA, USA. New York, USA: IEEE, 2016(2016-09-01)[2019-09-25]. https://ieeexplore.ieee.org/document/7558047.
|
| [11] |
Limam N, Boutaba R. Assessing software service quality and trustworthiness at selection time[J]. IEEE Transactions on Software Engineering, 2010, 36(4): 559-574. DOI:10.1109/TSE.2010.2 |
| [12] |
Jøsang A, Guo G B, Pini M S, et al. Combining recommender and reputation systems to produce better online advice[M]. Modeling Decisions for Artificial Intelligence. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013: 126-138.
|
| [13] |
郑苏苏, 付晓东, 岳昆, 等. 基于Kendall tau距离的在线服务信誉度量方法[J]. 计算机研究与发展, 2019, 56(4): 884-894. ZHENG Susu, FU Xiaodong, YUE Kun, et al. Online service reputation measurement method based on Kendall tau distance[J]. Journal of Computer Research and Development, 2019, 56(4): 884-894. (in Chinese) |
| [14] |
Fu X D, Yue K, Liu L, et al. Reputation measurement for online services based on dominance relationships[J]. IEEE Transactions on Services Computing, 2019: 1.https://doi.org/10.1109/tsc.2018.2854873.
|
| [15] |
de Condorcet N. Essai Sur l'application de l'analyse À la probabilitÉ des dÉcisions rendues à la pluralité des voix[M]. Essai sur l'application de l'analyse à la probabilité des décisions rendues à la pluralité des voix. Cambridge: Cambridge University Press, 2014: 1-2.
|
| [16] |
Bisquert P, Croitoru M, Kaklamanis C, et al. A decision-making approach where argumentation added value tackles social choice deficiencies[J]. Progress in Artificial Intelligence, 2019, 8(2): 229-239. DOI:10.1007/s13748-019-00173-3 |
| [17] |
Bubboloni D, Gori M. Anonymous and neutral majority rules[J]. Social Choice and Welfare, 2014, 43(2): 377-401. DOI:10.1007/s00355-013-0787-2 |
| [18] |
Brandl F, Peters D. An axiomatic characterization of the borda mean rule[J]. Social Choice and Welfare, 2019, 52(4): 685-707. DOI:10.1007/s00355-018-1167-8 |
| [19] |
Benade G, Kahng A, Procaccia A D. Making right decisions based on wrong opinions[C]. Proceedings of the 2017 ACM Conference on Economics and Computation-EC'17. New York, USA: ACM Press, 2017: 267-284.
|
| [20] |
Procaccia A D, Shah N, Zick Y. Voting rules as error-correcting codes[J]. Artificial Intelligence, 2016, 231: 1-16. DOI:10.1016/j.artint.2015.10.003 |
| [21] |
付晓东, 李俊, 刘骊, 等. 基于排序对社会选择函数的在线服务评价[J]. 清华大学学报(自然科学版), 2018, 58(8): 715-724. FU Xiaodong, LI Jun, LIU Li, et al. Evaluating online services based on a ranked pairs social choice function[J]. Journal of Tsinghua University(Science and Technology), 2018, 58(8): 715-724. (in Chinese) |
| [22] |
Arrow Kennethj. Social choice and individual values[M]. New Haven, USA: Yale university press, 2012[2019-09-25]. https://www.jstor.org/stable/j.ctt1nqb90.
|
| [23] |
Brandt F, Conitzer V, Endriss U, et al. Introduction to computational social choice[M]. Handbook of Computational Social Choice. Cambridge: Cambridge University Press, 2016: 1-20.
|
| [24] |
Procaccia A, Shah N. Is approval voting optimal given approval votes[C]. NIPS'15 Proceedings of the 28th International Conference on Neural Information Processing Systems. Cambridge, MA, USA: MIT Press. 2015: 1801-1809.
|
| [25] |
Mitchell J. Branch-and-cut algorithms for combinatorial optimization problems 1[J]. Handbook of applied optimization, 2002, 1: 65-77. |
| [26] |
Mao A, Procaccia A, Chen Y. Better human computation through principled voting[C]. Proceeding of the 27th AAAI Conference on Artificial Intelligence. Bellevue, Washington, USA: AAAI Press, 2013: 1142-1148.
|
 2020, Vol. 43
2020, Vol. 43


