2a. 桂林电子科技大学信息与通信学院, 广西桂林541004;
2b. 桂林电子科技大学广西精密导航技术与应用重点实验室, 广西桂林541004
2a. College of Information and Communication, Guang Xi University of Electronic Technology, Guilin, Guang Xi 541004, P. R. China;
2b. Guangxi Key Laboratory of Precision Navigation Technology and Application, Guang Xi University of Electronic Technology, Guilin, Guang Xi 541004, P. R. China
随着位置服务(LBS, location based services)的发展,人们对于位置服务中定位精度的要求越来越高。超宽带(UWB, ultra wide band)通过纳秒至微秒级的非正弦波窄脉冲传输数据,UWB的显著特点之一是数据传输速率高。此外,UWB还具有较强的防干扰能力,传输速率快,系统内存大,穿透性能好,发送功率小等特点,在许多无线定位技术中脱颖而出[1], UWB技术可以实现高精度的室内定位, 为位置服务提供精确的定位导航。
到达时间(TOA, time of arrival)主要基于节点间信号传输到达的时间测量,所以TOA在各节点时间同步方面的要求是较为严格的。此外TOA定位算法进行距离测量时至少需要基站与移动台之间进行3次双向通讯,这也是基站和移动台的功率损耗大幅度增加的主要原因。到达时间差(TDOA, time difference of arrival)定位技术仅需要接收器中精确的时间同步,而不是接收器和发送器之间的绝对时间同步,时钟精度比TOA定位方法更容易实现[2]。因此,TDOA应用更加广泛。传统的TDOA定位算法有Chan算法、Fang算法、Taylor算法等。Chan算法[3]在视距(LOS, line of sight)情况或者TDOA测量误差小的情况下定位精度高;在非视距(NLOS, not line of sight)情况或者信道性能比较差的时候,定位的准确度会大幅下降,影响定位精度的重要因素之一就是非视距误差。Taylor级数展开法[4]是递归算法的一种,这种方法需要对初始位置进行估计, 计算复杂度比较大,初始位置的估计值对定位精度影响较大。Fang算法[5]只能利用3个基站进行定位,对于其他基站给出的TDOA测量值并不充分利用。文献[6-7]仿真结果表明,在实际的UWB定位中,Chan算法,Taylor算法是定位精度比较高的2种算法。
支持向量机常用于话音识别[8]、生物医学[9]、噪音处理[10]等方面。支持向量机可以解决高维问题,解决小样本下机器学习问题、能够处理非线性特征的相互作用、无局部极小值问题、无须依赖整个数据、泛化能力比较强。文中提出了一种利用支持向量机来对UWB的定位坐标解算的方法,并给出了支持向量机进行TDOA定位的位置解算方法和算法过程,通过仿真实验表明,与Chan、Taylor等传统定位算法相比较,文中方法在定位精度和实时性上均优于以上算法,能够满足定位精度高且复杂度小的定位要求。
1 TDOA定位原理TDOA,即到达时间差,是指无线射频信号同时抵达2个基站的时间的差值。TDOA是一种无线定位技术,它是依据无线射频信号抵达2个基站之间的距离的差值来进行定位的一种表达[11]。通过测量移动台到达不同基站的到达时间差就可以得到TDOA[12], 这种方法不需要移动台和基站之间进行严格的时间同步,但必须确保各个基站之间的同步以及同时传输到每个基站的射频信号之间的时间差是定值,而时间差与光速之积即为距离差。根据双曲线算法,移动台的位置确认至少需要2条相交双曲线,信号源的位置是其交点,至少需要3个不同的基站来定位移动台。
实验定位系统定位的主要依据是通过携带标签的可移动物体或人员到达不同天线的时间差来定位。上文提到过同一时刻所发射的标签信号源传输到不同天线间的时间差是一个定值,接下来将到达2个天线间的时间差与光速相乘得到距离差并由此得出1条双曲线,如果对2个基站的时间差估计的信号源位置不能十分确定,那么可以通过3个或者3个以上不同的无线基对时间差进行测量,根据测量的结果以及算法能够得出2条或多条双曲线,双曲线相交的位置便是可移动物体发射信号源的估测位置。一般使用以下2种方式对信号源的位置进行估测,一是通过2个不同基站的信号到达时间的TOA差来进行,或者使用互相关技术把2个不同基站所接收到的信号做出相关处理得出估计值。图 1所示的便是双曲线模型。实验主要根据标签到达的距离差建立双曲线模型并进行求解,其交点即为信号源估计位置[13]。
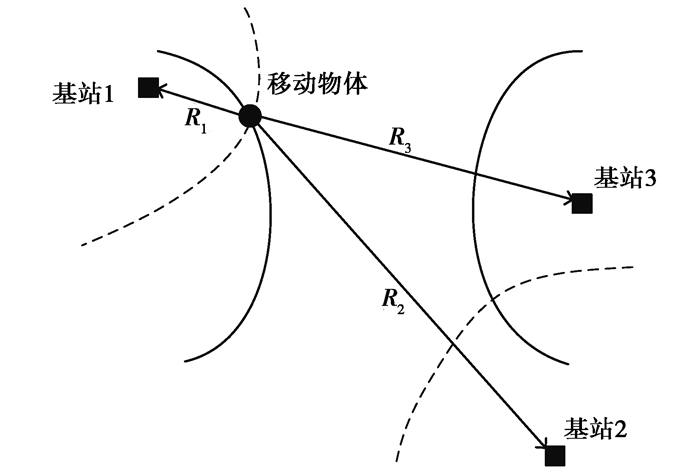
|
图 1 TDOA双曲线模型 Fig. 1 TDOA hyperbolic model |
文中利用支持向量机来实现超宽带的室内定位,将定位问题转化为分类回归问题。其定位过程如图 2所示。
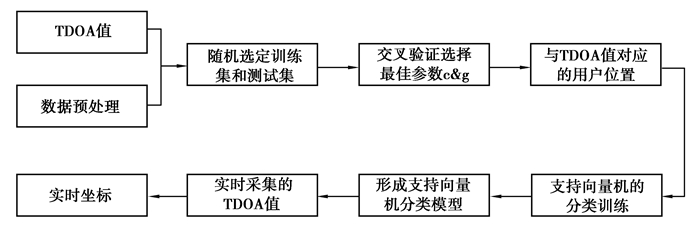
|
图 2 定位流程 Fig. 2 Positioning process |
首先采集定位区域的TDOA值,将采集到的TDOA值和坐标值划分为测试集和训练集。接下来将训练集输入支持向量机中对支持向量机进行分类训练。假设TDOA向量集为{D}m*n, 其中,m=1, 2, 3…i, n=1, 2, 3…j, m为采集的样本点的个数,n为TDOA差值的数量。{D}m*n∈Rn×K。由于样本数据在低维空间不可分, 所以需要通过非线性映射将向量机从空间Rn映射到高维线性可分的空间。利用核函数可将高维特征空间中的点积运算转换为低维输入空间的核函数进行运算。不同核函数训练的SVM模型不同。选择合适的核函数可以改善分类和回归的精度,提高位置精度[14]。常用的核函数为线性核函数、多项式核函数[15]、RBF核函数和Logistic核函数等。在使用不同核函数的训练后,RBF核均方根误差最小。RBF核函数均方根误差为1.001 461 51。分别计算了其他3个的均方根误差为1.201 94、1.327 519 5、3.416 845,选择RBF核函数,式(1)为高斯核函数的表达式:
| $ k\left(x_{i}, x_{j}\right)=\exp \left(-\frac{\left\|x_{i}-x_{j}\right\|^{2}}{2 \sigma^{2}}\right), $ | (1) |
式中,σ为高斯核的带宽。
2.2 分类问题的求解支持向量机常用于分类问题,常用的分类方法有一对一法和一对多法。
一对一法就是在所有样本中任意挑选2个样本设计支持向量机,k个样本就需要k×(k-1)/2个支持向量机,最后采用投票选择法,票数多的即为输出。这样k个样本的多分类问题就转化成了多个二分类问题的求解。一对一法由于只涉及2个样本的分类,可以较大地减少训练时间,由于多个分类器样本数目均衡,分类的准确率高。文中选择一对一法对数据集进行分类,利用一对一分类模型实现了坐标值的解算,提高了坐标解算速度分类过程如图 3所示。
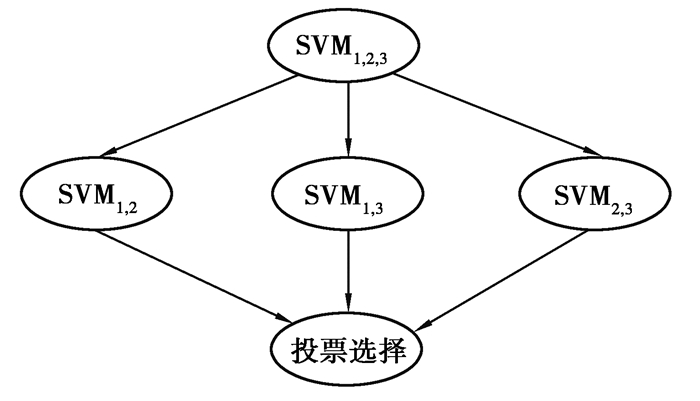
|
图 3 一对一分类 Fig. 3 One-to-one classification |
一对多法如图 4所示。对于k个样本的分类问题则需要构造k个二分类器,在分类时,属于该样本的即为+1,剩余样本记为-1,全部样本都要参与训练,而且还会使得样本重复训练,训练时间变长,每一个二分类器中+1样本远远小于-1样本,导致分类器不均衡,分类准确度较低。最后决策输出时,k个二分类器中决策函数最大值所对应的一类作为输出。
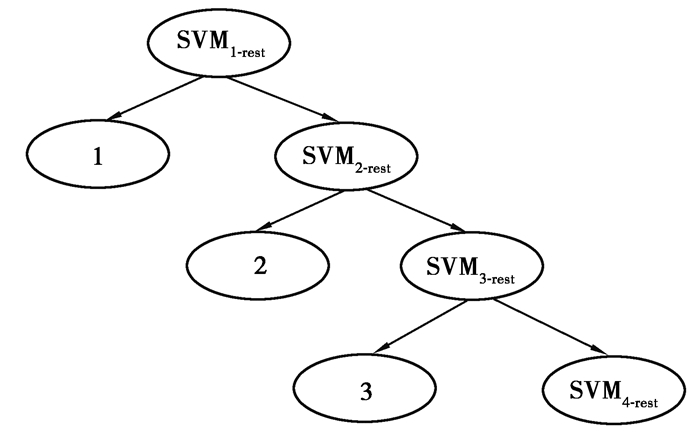
|
图 4 一对多分类 Fig. 4 One-to-multi classification |
在数据集的一对一分类中,TDOA值为属性值,输出坐标为标签值。确定了属性矩阵和标签就可以建立分类模型。每次任意取2组TDOA值判断其属于哪一种标签,最后选出获得票数最多的坐标值即为输出。利用训练好的分类模型可以进行回归预测,定位问题就转化为了一个分类问题的求解。具体过程包含以下5个步骤:
Step 1:使用TDOA值,通过训练测试将必要的信息输入网络,通常样本数据越多,训练结果越接近目标结果,但这样就会加大数据收集和数据分析的困难程度。为了使用最小的样本得到最好的效果,文中在第3节对样本数量与训练效果的关系做了对比。在仿真过程中,最终在选取4 500个样本数据进行训练。
Step 2:用函数
| $ f: x \rightarrow y-\frac{x-x_{\min }}{x_{\max }-x_{\min }}。$ | (2) |
对于输入的训练集样本进行归一化处理,减小大属性值对小属性值的影响。
Step 3:通过网格搜索法遍历所有的c和g参数,计算所有参数的结果,用交叉验证把训练的平均正确率进行排序。在遍历所有可能的结果之后得出一个合适的分类器。
Step 4:将测试集输入训练好的模型中,得出的结果进行反归一化,最后可以得到决定系数和均方根误差来验证模型回归的好坏。
Step 5:输入实际采集到的TDOA值,就可以得出实时的坐标。
3 仿真对比实验 3.1 支持向量机的训练和仿真为了使支持向量机的性能达到最佳。文中对于不同数量样本下均方根误差和决定系数做了对比。在数量样本为4 500的时候,均方根误差最低,决定系数接近最大。选择训练数据样本为4 500来训练支持向量机。
文中支持向量机算法的输入为3个TDOA值,与TDOA值相对应的坐标值为输出。分别从X, Y, Z 3个方向上分析了本算法的定位精度。数据点的采集在三维空间25 m×25 m×2 m, 采样间隔为0.5 m,总共采样10 000个点。在10 000个采样点中随机选取4 500个作为训练样本,测试集和训练集的比例一般为1 :4。
为了对比文中算法和传统算法的定位精度,在不同TDOA差值的情况下对比了Chan算法、Taylor算法和文中算法,如图 6所示。可以看出,Taylor算法的均方根误差要远大于Chan算法,由于Taylor算法需要根据初始位置不断地递归求解,初始估计位置对最后的求解结果影响很大,所以会造成均方根误差比较大的情况;而Chan算法实际上是一种非递归双曲线方程组的求解,其复杂度比Taylor算法小很多,两次迭代就能解算出位置坐标,所以Chan算法的均方根误差要小于Taylor算法。文中算法在输出坐标前已经将模型训练好,所以在不同TDOA差值的情况下也可以达到很小的均方根误差。
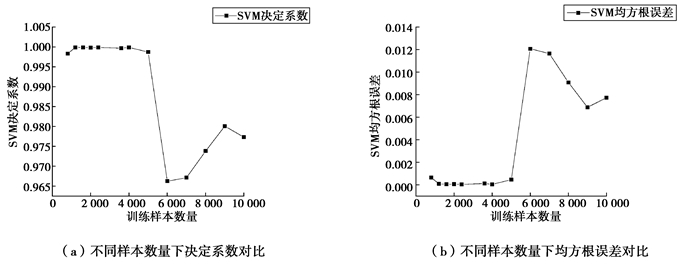
|
图 5 不同样本数量SVM决定系数、均方根误差对比 Fig. 5 Comparison of SVM determination coefficient and root mean square error for different sample sizes |
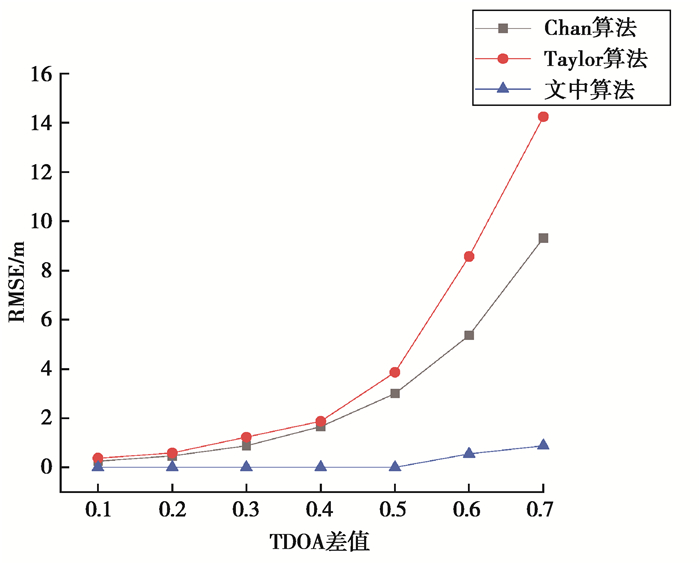
|
图 6 3种算法在不同TDOA差值下均方根误差对比 Fig. 6 Comparison of root mean square error of three algorithms under different TDOA differences |
随着定位点数量的增多,Chan算法和Taylor算法定位所用的时间也越来越多,对比了不同定位数量点下3种算法所用的时间,如图 7所示。可以看出,Taylor算法和Chan算法解算坐标的复杂度相对于文中算法来说比较高,Taylor算法和Chan算法定位所用的时间要远大于文中的算法。将支持向量机用于UWB的TDOA的解算,在训练模型时需要花费一定的时间,而在模型训练好之后定位样本点所用的时间随着样本点数量的增多定位时间也在增加,定位时间的变化如图 7所示。在定位点数量达到7 000的时候定位时间为1.025 s。在定位精度相当的情况下,文中算法实时性要远好于传统定位算法。
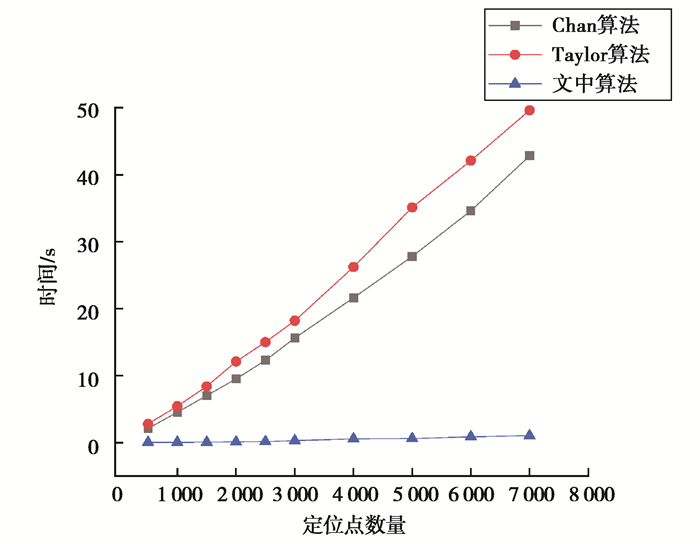
|
图 7 3种算法在不同数量定位点下定位时间对比 Fig. 7 Comparison of positioning time of three algorithms with different number of positioning points |
当支持向量机网络训练好之后,文中算法的3D定位结果如图 8所示,标签的预估位置与实际位置误差为10.15 cm,更好地验证了3.1节中仿真结果的正确。
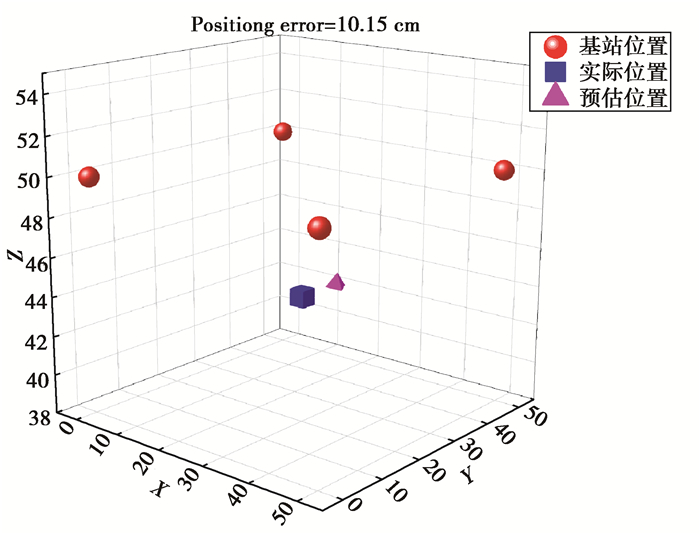
|
图 8 3D定位仿真结果 Fig. 8 positioning simulation results |
针对室内高密度环境下UWB定位误差大、刷新率低、功耗大的问题,提出基于支持向量机的UWB室内定位方法,将定位问题转化为多分类问题的求解,采用了仿真对比实验对该算法进行了性能测试。结果表明,支持向量机算法对解决超宽带在室内定位时误差大、刷新率低、功耗大的问题有显著的成效,在定位精度和定位时间上均优于传统算法,因此支持向量机算法在定位精度为厘米级实时定位中,要求高密度、低功耗的应用条件下具有十分广泛的应用前景。
| [1] |
Zhong Y, Liu T X, Li B F, et al. Integration of UWB and IMU for precise and continuous indoor positioning[C]. 2018 Ubiquitous Positioning, Indoor Navigation and Location-Based Services (UPINLBS). New York, USA: IEEE, 2018.
|
| [2] |
Zhao G, Niu H. Research and application of indoor positioning based on UWB[C]//Third International Conference on Cyberspace Technology (CCT 2015). New York, USA: IEEE, 2015.
|
| [3] |
Chan Y T, Ho K C. A simple and efficient estimator for hyperbolic location[J]. IEEE Transactions on Signal Processing, 1994, 42(8): 1905-1915. DOI:10.1109/78.301830 |
| [4] |
Foy W. Position-location solutions by Taylor-series estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1976. |
| [5] |
Fang B T. Simple solutions for hyperbolic and related position fixes[J]. IEEE Transactions on Aerospace and Electronic Systems, 1990, 26(5): 748-753. DOI:10.1109/7.102710 |
| [6] |
蒋康荣.蜂窝网络中基于TDOA的定位算法研究[D].南京: 南京邮电大学, 2017. JIANG Kangrong. Study on positioning algorithms based on TDOA in cellular networks[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2017. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10542-2007174480.htm |
| [7] |
杨凡凡.基于UWB的无线定位算法的研究与实现[D].沈阳: 东北大学, 2014. YANG Fanfan. Research and implementation of wireless location algorithm based on UWB[D]. Shenyang: Northeastern University, 2014. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10145-1016010167.htm |
| [8] |
Campbell W M. A SVM/HMM system for speaker recognition[C]//2003 IEEE International Conference on Acoustics, Speech, and Signal Processing, 2003. Proceedings. (ICASSP'03). New York, USA: IEEE, 2003.
|
| [9] |
Cuingnet R, Rosso C, Chupin M, et al. Spatial regularization of SVM for the detection of diffusion alterations associated with stroke outcome[J]. Medical Image Analysis, 2011, 15(5): 729-737. DOI:10.1016/j.media.2011.05.007 |
| [10] |
Kumar R, Kulkarni A, Jayaraman V, et al. Symbolization assisted SVM classifier for noisy data[J]. Pattern Recognition Letters, 2004, 25(4): 495-504. DOI:10.1016/j.patrec.2003.12.012 |
| [11] |
孙胜, 李辉, 韩崇昭. 基于TDOA定位技术的仿真研究[J]. 无线通信技术, 2002, 11(4): 40-43. SUN Sheng, LI Hui, HAN Chongzhao. Simulation research based on TDOA positioning Technology[J]. Wireless Communications Techology, 2002, 11(4): 40-43. (in Chinese) DOI:10.3969/j.issn.1003-8329.2002.04.011 |
| [12] |
马灵芝.基于TDOA无线传感定位算法的研究及应用[D].济南: 山东大学, 2012. MA Lingzhi. Research and application of the algorithm based on TDOA for wireless sensor locationing[D]. Jinan: Shandong University, 2012. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10422-1012466679.htm |
| [13] |
胡中玉, 杨泳, 李小文. 基于双曲型TDOA的无线定位方法研究[J]. 信息通信, 2006, 19(1): 18-20. HU Zhongyu, YANG Yong, LI Xiaowen. Research of wireless location based on hyperbolic TDOA[J]. Information & Communications, 2006, 19(1): 18-20. (in Chinese) DOI:10.3969/j.issn.1673-1131.2006.01.006 |
| [14] |
赵银龙, 安胜彪. 基于核化K-means和SVM分类回归的Wi-Fi室内定位算法[J]. 信息技术, 2018, 42(1): 113-117. ZHAO Yinlong, AN Shengbiao. Wi-Fi indoor localization algorithm based on kernel K-means and SVM classification regression[J]. Information Technology, 2018, 42(1): 113-117. (in Chinese) |
| [15] |
Selamat M H, Md Rais H. Image face recognition using Hybrid Multiclass SVM (HM-SVM)[C]//2015 International Conference on Computer, Control, Informatics and its Applications (IC3INA). New York, USA: IEEE, 2015: 159-164.
|
 2020, Vol. 43
2020, Vol. 43


