2. 华东师范大学 计算机科学与技术学院, 上海 200062
2. School of Computer Science and Technology, East China Normal University, Shanghai 200062, P. R. China
与内燃车相比,充电汽车因其不依赖于化石燃料和对环境友好的特点[1-3]受到大量关注,各大城市都大量新建充电站,以解决充电汽车里程短和充电难问题[4-6]。然而,由于大规模充电汽车的无序充电行为容易导致电网中断或者不必要的用电高峰[7-10],急需在充电服务调度系统的全局控制器(GC, global controller)中部署灵活的有序充电策略,以达到稳定电网和推移用电高峰的目的。当前已有研究主要关注如何提高车主便捷性和降低充电花费[11-15]。在文献[11-13]中,作者期望最大化车主的便捷性和最小化充电站的成本,没有对如何减少充电过程中的电池寿命损耗进行研究。另外,当前的充电控制通常采用集中式控制策略[16-18]。充电服务调度系统控制器(GC, global controller)接收充电请求、车辆状态、计划的停留时间、以及实时电价等信息而控制充电汽车什么时候充电和充多少电。随着充电汽车数量增长,问题的计算复杂度和数据通信开销相应加大,并且,集中式控制GC需要知道充电汽车的停留时间和车辆相关信息,容易引起车主对隐私泄露的担忧。与集中式相比,分布式控制方式更具优势[16-18],不仅可以降低充电调度问题的计算复杂度,还可以保护车主隐私。
本研究重点关注如何在提高用户便捷性同时减少电池充电损耗这一优化目标,并针对该目标下充电过程信息直接交互带来的隐私泄露和高充电汽车数目带来的高计算复杂度问题,提出了基于交替方向多乘子ADMM(alternating direction method of multipliers)[19-21]的分布式有序充电服务调度算法。研究的主要贡献如下所示:
1) 建模并形式化一个新的充电汽车有序充电服务调度问题,该问题旨在如何最大化用户便捷性同时降低充电汽车充电电池的充电损耗。
2) 针对上述有序充电服务调度问题,提出一种基于ADMM的分布式有序充电调度算法,降低了计算复杂度,同时保护用户隐私。
3) 大量仿真实验结果表明研究算法相较其他算法有很大提升,能减少33.0%的电池寿命损耗和18.3%的电费支出。
1 相关工作充电汽车的大规模无序充电行为对已有电网设备运行的安全性和稳定性也造成极大挑战[22-24]。由于充电汽车在充电站或其他个人充电场所的停留时间远大于它所需要的充电时间,这使得采用一定的调度策略,实现有序充电而不影响车主的正常用车成为可能。
在文献[11]中,作者提出一种集中式充电管理方式。文献[12]关注了充电汽车车主的利益,定义与车辆状态和电价相关的优先级因子,当车辆剩余充电时间越少,未充电量越高,电价越低时,充电优先级越高,提出在满足充电需求前提下,根据充电因子高低来调度集中式充电管理方式。在文献[13]中,作者提出一种新的充电站管理策略,通过同时管理控制充电汽车入站策略和定价机制来达到最大化充电站利润的目的。文献[25]提出了LLLP(less laxity and longer remaining processing time)原则,在充电过程中最小化总的充电代价。在文献[26]中,作者针对开放式停车场充电问题,研究了两类车的充电习惯,包括周期性到达充电和随机到达充电,以最大化停车场收益和最大化满足充电需求为目标,提出集中式的充电管理策略。与上述研究相比,研究的是一个新的不同的优化问题,即关注如何在提高用户便捷性的同时减少电池充电损耗。
在充电服务的优化调度研究中,分布式算法得到了更多关注。在文献[16]中,基于ADMM算法提出了一种具有计算伸缩性的优化框架,但是使用这个框架需要变量之间耦合度较低,不适用于目标和约束较多的复杂场景。在文献[17]中,作者把数据中心员工汽车充电管理问题和数据中心用电管理问题结合起来,提出了一种用电成本最小化的分布式管理策略。但由于是数据中心场景,缺乏在充电站场景中对充电汽车车主便捷性的考虑。文献[18]基于充电汽车的当前状态定义了用户的便捷性,提出了一种最大化用户便捷性的分布式控制策略。在文献[27]中,作者基于车主驾驶习惯的不确定性和难以预测性,建模了多个驾驶场景,基于ADMM算法提出了一种分布式的管理策略。与上述研究相比,笔者主要使用ADMM算法来进行同时提升用户便捷性和减少电池充电损耗的有序充电服务的调度优化,使用的模型、系统架构、优化目标均与上述研究不同。
2 系统定义随着充电汽车数量的增加,越来越多的充电站趋向于安装更多的充电桩来为更多充电汽车提供服务。但由于充电站可以提供的最大总功率通常是有限的,同时不同种类的充电汽车的最大充电功率也不相同,导致所有的充电汽车无法同时充电或以最大功率充电。由于充电汽车在充电站的停留时间一般会超过它所需要的充电时间,一般情况下,充电汽车不需要以最大功率充电,并且也不需要一直充电,因此,在充电控制及充电服务调度中,可以实行灵活的充电服务调度策略,来协调所有充电汽车的充电行为,以满足充电站最大总功率限制和车主停留时间的约束。
研究定义了离散的等间隔时间槽
| $ 0 \le {Q_{it}} \le {P_i}{\kern 1pt} {\kern 1pt} {\rm{max}}。$ | (1) |
该约束表明充电槽在任意时刻的充电功率均不会超过充电汽车的最大充电功率Pi max。设定充电站最大总功率为Pmax,有以下约束
| $ \sum\limits_1^N {{Q_{it}}} \le {P^{{\rm{max}}}}, $ | (2) |
该约束表明所有充电槽的总功率不应超过充电站的最大可使用功率。设定充电汽车总电容量为Capi,当前电池有电状态为SOCi。充满还需充电量
| $ {E_{it}} = Ca{p_i} * (1 - {\rm{SO}}{{\rm{C}}_i})。$ | (3) |
设定充电汽车开始充电时间为Tib,离开时间为Tie,有以下约束
| $ \sum\limits_{T_i^b}^{T_i^e} {{Q_{it}}\hat t} \ge {E_{it}}。$ | (4) |
该约束表明充电结束时,充电汽车的充电量应大于等于充满所需要的充电量。
3 问题构建研究需要找到最优的充电配置,即分配每个时间槽每台充电汽车的充电功率,简单来说就是确定最优的Qit。
首先考虑为不同的车赋予充电优先级λit。认为剩余充电时间越短、剩余充电量越高的车有越高的充电优先级。笔者以充电优先级来表征充电车主获得的便捷性大小,充电优先级越高,表明该用户获得的便捷性越高。另外,所有车主都希望在电价低时充更多的电,设定剩余充电时间为lit
| $ {l_{it}} = T_i^e - {T^{{\rm{cur}}}}, $ | (5) |
剩余充电量为Eit,预估一天当中最低电价为rmin,最高电价为rmax。
设定价格因子为
| $ r = \frac{{{r_{it}} - {r_{{\rm{min}}}}}}{{{r_{{\rm{max}}}} - {r_{{\rm{min}}}}}}。$ | (6) |
设定充电优先级
| $ {\lambda _{it}} = \frac{{{l_{it}}}}{{{E_{it}}}}\frac{{{r_{it}} - {r_{{\rm{min}}}}}}{{{r_{{\rm{max}}}} - {r_{{\rm{min}}}}}}。$ | (7) |
建模充电优先级(用户便捷性)损失函数为
| $ {\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {C_1} = \sum\limits_{i = 1}^N {\sum\limits_{t = 1}^T {{\lambda _{it}}} } {Q_{it}}。$ | (8) |
由于充电功率对充电汽车电池寿命有很大影响,建模电池折旧损失为关于充电功率的二次损失函数
| $ {\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {C_2} = \sum\limits_{i = 1}^N {\sum\limits_{t = 1}^T {\frac{\sigma }{2}} } {Q_{it}}^2。$ | (9) |
σ作为折损率。
最后总的损失函数为
| $ {\rm{min}}C = {C_1} + {C_2} = \sum\limits_{i = 1}^N {\sum\limits_{t = 1}^T {{\lambda _{it}}} } {Q_{it}} + \sum\limits_{i = 1}^N {\sum\limits_{t = 1}^T {\frac{\sigma }{2}} } {Q_{it}}^2。$ | (10) |
| $ {\rm{s}}{\rm{.t}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{(1)(2)(4)}}。$ | (11) |
ADMM适用于解决在统计学、机器学习和其他相关领域的大规模分布式凸优化问题。这个框架能被应用于具有下列形式的问题中。
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{min}}f(x) + g(z),}\\ {{\rm{s}}{\rm{. t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} Ax + Bz = c,}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x \in {C_1},z \in {C_2},} \end{array} $ | (12) |
其中:
| $ \begin{array}{*{20}{c}} {{L_p}(x,z,\mathit{\boldsymbol{\lambda }}) = f(x) + g(z) + }\\ {{\mathit{\boldsymbol{\lambda }}^{\rm{T}}}(Ax + Bz - c) + \frac{p}{2}\left\| {Ax + Bz - c} \right\|_2^2,} \end{array} $ | (13) |
其中λ∈Rp是拉格朗日乘子。ρ>0二次惩罚项的惩罚因子。
ADMM能够在多个循环内解决上述问题,在第k+1轮循环有下述操作
| $ {{x^{k + 1}} = {\rm{arg}}\mathop {{\rm{min}}}\limits_{x \in {C_1}} {L_p}(x,{z_k},{\lambda _k}),} $ | (14) |
| $ {{z^{k + 1}} = {\rm{arg}}\mathop {{\rm{min}}}\limits_{z \in {C_2}} {L_p}({x_k},z,{\lambda _k}),} $ | (15) |
| $ {{\lambda ^{k + 1}} = \lambda + \rho (Ax + By - c)}。$ | (16) |
当前优化问题无法直接使用ADMM框架,因为约束式(2)和式(4)造成所有变量耦合在一起,而ADMM框架解决形如式(13)的优化问题。为了解决ADMM框架不适用问题,引入了新的辅助变量Zit, Rt,使得
| $ {{\rm{min}}C = \sum\limits_{i = 1}^N {\sum\limits_{t = 1}^T {\frac{\sigma }{2}} } {Q_{it}}^2 + \sum\limits_{i = 1}^N {\sum\limits_{t = 1}^T {{\lambda _{it}}} } {Z_{it}},} $ | (17) |
| $ {{\rm{ s}}{\rm{.t}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{.}}\sum\limits_{i = 1}^N {{Q_{it}}} + {R_t} = {P_{{\rm{ total }}}},} $ | (18) |
| $ {\sum\limits_{T_i^b}^{T_i^e} {{Z_{it}}} \ge {k_i}{E_i},} $ | (19) |
| $ {0 \le {Z_{it}} \le {P^{{\rm{max}}}},} $ | (20) |
| $ {{Q_{it}} = {Z_{it}}}。$ | (21) |
可以观察到式(17)已经满足ADMM形式(12),并且完全等价于原式(10)。现在优化函数可以分解为分别与变量集Qit,Zit和Rt相关的3个函数。变量集Qit控制电池折损的最小化。而变量集Zit控制优先级损失的最小化。而变量集Qit和变量集Zit由约束式(20)联系在一起。辅助变量的引入使得总功率约束式(17)和用户充电汽车充电量约束式(19)的分离成为可能。
函数式(17)转化为对应的拉格朗日函数为
| $ \begin{array}{*{20}{l}} {f = \sum\limits_{i = 1}^N {\sum\limits_{t = 1}^T {\frac{\sigma }{2}} } Q_{it}^2 + \sum\limits_{i = 1}^N {\sum\limits_{t = 1}^T {{\lambda _{it}}} } {Z_{it}} + \sum\limits_{t = 1}^T {{\omega _t}} (\sum\limits_{i = 1}^N {{Q_{it}}} + {R_t} - {P_{{\rm{ total }}}}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^N {\sum\limits_{t = 1}^T {{\theta _{it}}} } ({Q_{it}} - {Z_{it}}) + \frac{\rho }{2}\sum\limits_{t = 1}^T {{{(\sum\limits_{i = 1}^N {{Q_{it}}} + {R_t} - {P_{{\rm{ total }}}})}^2}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\rho }{2}\sum\limits_{i = 1}^N {\sum\limits_{t = 1}^T {{{({Q_{it}} - {Z_{it}})}^2}} ,} } \end{array} $ | (22) |
| $ {{\rm{ s}}{\rm{.t}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{T_i^b}^{T_i^e} {{Z_{it}}} \ge {k_i}{E_i},} $ | (23) |
| $ {0 \le {Z_{it}} \le {P^{{\rm{max}}}}}。$ | (24) |
在第k+1轮循环,根据式(14),Q-min问题涉及解决以下问题
| $ \begin{array}{*{20}{c}} {{\rm{min}}\sum\limits_{i = 1}^N {\sum\limits_{t = 1}^T {(\frac{\sigma }{2}Q_{it}^2 + {\theta _{it}})} } + \sum\limits_{t = 1}^T {{\omega _t}} (\sum\limits_{i = 1}^N {{Q_{it}}} ) + }\\ {\frac{\rho }{2}\sum\limits_{t = 1}^T {{{(\sum\limits_{i = 1}^N {{Q_{it}}} + {R_t} - {P_{{\rm{ total }}}})}^2}} + }\\ {\frac{\rho }{2}\sum\limits_{i = 1}^N {\sum\limits_{t = 1}^T {{{({Q_{it}} - {Z_{it}})}^2}} } }。\end{array} $ | (25) |
根据不同的Qit,目标函数和约束能被分解为N*T个独立的小问题。每辆充电汽车负责独立地解决与其相关的T个问题。把式(25)分解为如下子问题(P1)
| $ \left( {{P_{\rm{1}}}} \right){\rm{min}}\left( {\frac{\sigma }{2}Q_{it}^2 + {\theta _{it}}} \right) + \sum\limits_{t = 1}^T {{\omega _t}} (\sum\limits_{i = 1}^N {{Q_{it}}} ) + \frac{\rho }{2}{(\sum\limits_{i = 1}^N {{Q_{it}}} + {R_t} - {P_{{\rm{ total }}}})^2} + \frac{\rho }{2}{({Q_{it}} - {Z_{it}})^2}。$ | (26) |
根据Karush-Kuhn-Tucker(KKT)最优条件,有
| $ \sigma {Q_{it}} + {\omega _t} + {\theta _{it}} + \rho (\sum\limits_{i = 1}^N {{Q_{it}}} + {R_t} - {P_{{\rm{ total }}}}) + \rho ({Q_{it}} - {Z_{it}}) = 0。$ | (27) |
为了得到
| $ \sum\limits_{i = 1}^N {{Q_{it}}} = \frac{{N{P_{{\rm{ total }}}} - N{R_t}}}{{\frac{\sigma }{\rho } + N + 1}} + \frac{{\sum\nolimits_{i = 1}^N {{Z_{it}}} - \frac{1}{\rho }(N{\omega _t} + \sum\nolimits_{i = 1}^N {{\theta _{it}}} )}}{{\frac{\sigma }{\rho } + N + 1}}。$ | (28) |
最后将式(28)带回式(27),得到最终结果。
| $ {Q_{it}} = \frac{{\rho {Z_{it}} - \rho (\sum\nolimits_{i = 1}^N {{Q_{it}}} + {R_t} - {P_{{\rm{ total }}}}) - {\omega _t} - {\theta _{it}}}}{{\sigma + \rho }}。$ | (29) |
求解第k+1轮式(25)的解Qitk+1的算法如算法1所示。算法以充电桩数量N,常数ρ,电池折损率常数σ,充电站最大供电功率Ptotal,第k轮式(37)的解Rtk,第k轮式(29)的解Zitk,第k轮对偶变量θitk和ωtk的值作为输入;以第k+1轮式(24)的解Qitk+1作为输出。程序遍历当前时间槽至时间槽T。根据式(28),计算得到
算法1.求解第k+1轮式(24)的解Qitk+1.
输入:充电桩数量N,常数ρ,电池折损率常数σ,充电站最大供电功率Ptotal,第k轮式(37)的解Rtk,第k轮式(29)的解Zitk,第k轮对偶变量θitk和ωtk的值。
输出:第k+1轮式(25)的解Qitk+1
1.FOR t=Tcur, Tcur+1, …, T DO
2. GC根据问题(28),获得
3.FOR i=1, 2, …, N DO
4.所有充电汽车同时根据问题(27)计算得到Qitk+1
在第k+1轮循环,根据式(15),Z-min问题涉及解决以下问题
| $ \begin{array}{*{20}{l}} {{\rm{min}}\sum\limits_{i = 1}^N {\sum\limits_{t = 1}^T {({\lambda _{it}} - {\sigma _{it}})} } {Z_{it}} + \frac{\rho }{2}\sum\limits_{i = 1}^N {\sum\limits_{t = 1}^T {{{({Q_{it}} - {Z_{it}})}^2}} ,} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{ s}}{\rm{.t}}{\rm{. (23),(24)}}} \end{array} $ | (30) |
根据不同的Zit,目标函数和约束能被分解为N*T个独立的小问题。每辆充电汽车负责解决与其相关的T个问题,把式(30)分解为如下子问题(P2)
| $ \begin{array}{*{20}{c}} {({P_2}){\rm{min}}({\lambda _{it}} - {\theta _{it}}){Z_{it}} + \frac{\rho }{2}\sum\limits_{i = 1}^N {\sum\limits_{t = 1}^T {{{({Q_{it}} - {Z_{it}})}^2}} ,} }\\ {s.t.(23),(24)} \end{array} $ | (31) |
根据KKT最优条件,有
| $ {{\lambda _{it}} - {\theta _{it}} + \rho ({Z_{it}} - {Q_{it}}) + \eta = 0,} $ | (32) |
| $ {\eta \ge 0,{\theta _{it}} \ge 0,} $ | (33) |
| $ {\eta (\sum\limits_{t = T_i^b}^{T_i^e} {{Z_{it}}} - {k_i}{E_i}) = 0}。$ | (34) |
最后有
| $ {{Z_{it}} = {\rm{min}}(P_i^{{\rm{max}}},{\rm{max}}(0,\frac{{{\theta _{it}} - {\lambda _{it}} - \eta }}{\rho }))}。$ | (35) |
求解第k+1轮式(31)的解Zitk+1的算法如算法2所示。算法以常数ρ,优先级常数λit,充电汽车最大充电功率Pimax,第k+1轮式(25)的解Qitk+1,第k轮对偶变量θitk的值作为输入;把第k+1轮式(30)的解Zitk+1作为输出。从等式(32),观察到只有η未知,通过折半查找来找到合适的η值,由式(32)和式(33)可以得到最小值式(36)和最大值式(37)。
| $ {{\eta _{{\rm{min}}}} = 0 - {\rm{max}}(\lambda ) + \rho * (0 - {\rm{max}}(Z)),} $ | (36) |
| $ {{\eta _{{\rm{max}}}} = {\rm{max}}(\theta ) - {\rm{min}}(\lambda ) + \rho * ({\rm{max}}(Q) - 0),} $ | (37) |
程序遍历当前时间槽至时间槽T,在每个时间槽进行下列任务。GC根据式(36)和式(37)计算得到ηmin, ηmax。然后GC和充电汽车配合进行下列任务,直到满足精度要求。更新η,把更新结果传回所有充电汽车,而所有充电汽车同时根据式(35), 更新Z, 然后把Z传回给GC。根据一定二分查找法准测更新ηmax或者ηmin。
算法2.第k+1轮式(30)的解Zitk+1
输入:常数ρ,优先级常数λit,充电汽车最大充电功率Pimax,第k+1轮式(25)的解Qitk+1,第k轮对偶变量θitk。
输出:第k+1轮式(30)的解Zitk+1
1) FOR i=1, 2, …, N DO;
2) GC根据式(35)和式(36)计算得到ηmin, ηmax;
3) WHILE ηmax-ηmin≥10-5 DO;
4) GC计算
5) FOR t=Tcur, Tcur+1, …, T DO;
6) 所有充电汽车同时根据式(34)获得Zitk+1;
7) IF
8) GC更新ηmax=ηmin;
9) ELSE IF
10) GC更新ηmin =η;
11) ELSE;
12) GC更新ηmax =η;
在第k+1轮循环,根据式(15)R-min问题涉及解决以下问题
| $ {\rm{min}}\sum\limits_{t = 1}^T {{\omega _t}} {R_t} + \frac{\rho }{2}\sum\limits_{t = 1}^T {{{(\sum\limits_{i = 1}^N {{Q_{it}}} + {R_t} - {P_{{\rm{ total }}}})}^2}} 。$ | (38) |
根据之前的论述,有
| $ {\omega _t} + \rho (\sum\limits_{i = 1}^N {{Q_{it}}} + {R_t} - {P_{{\rm{ total }}}}) = 0, $ | (39) |
最后给出
| $ {R_t} = {\rm{max}}(0, - \frac{{{\omega _t}}}{\rho } - (\sum\limits_{i = 1}^N {{Q_{it}}} - {P_{{\rm{ total }}}}))。$ | (40) |
根据式(15),在获得最优的Q,Z和R之后,更新对偶变量ω和θ
| $ {\omega _t^{k + 1} = \omega _t^k + \rho * (\sum\limits_{i = 1}^N {Q_{it}^{k + 1}} - {P_{{\rm{ total }}}}),} $ | (41) |
| $ {\theta _{it}^{k + 1} = \theta _{it}^k + \rho * (Q_{it}^{k + 1} - Z_{it}^{k + 1})}。$ | (42) |
设定实验周期H为24 h,按照时间槽长度
考虑到不同充电汽车种类的差异性会对实验造成影响,定义了4种不同类型的充电汽车。以(容量, 在辆充电汽车中所占比例, 最大充电功率)的形式,它们分别是EV1(8kWh,20%,1.6kW),EV2(17kWh,30%,3.4kW),EV3(18kWh, 30%, 3.6kW), EV4(48kWh, 20%, 9.6kW)。
本实验环境在Matlab 2019a上搭建,电脑配置为Intel(R) Core(TM) i5-7200 CPU@2.7GHZ处理器和8G内存。
4.2 对比方法及评价指标实验中,所提方法(BPCS, battery protection and cost saving)和其他经典的先到先服务方法(FCFS, first come first serrice)和最短截止日期优先方法(EDF, early deadline first)进行了对比。FCFS总是给予先到达的用户更高的优先级,把充电资源优先供应给先到达车辆,保证先到达车辆以最佳功率充电,而对于后到达车辆不作保证。而EDF会优先分配有更短截止日期的充电汽车,优先保证充电时间剩余少的充电汽车有足够的充电资源。
对比指标如下:
·充电花费:在整个模拟周期内,所有车完成充电任务的总花费。
·电池折损:在式(9)中定义了电池损失为关于充电功率的二次损失函数C2。此处通过所有电池折损之和来描述总的电池损失情况,总电池损耗之和为
·时间槽平均使用数目:完成充电任务所消耗的时间。
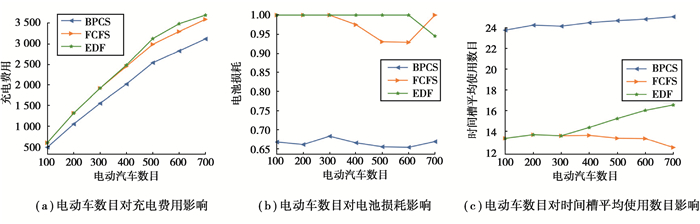
4.3 实验结果首先研究不同电动汽车数目在不同方法调度下的实验结果。以电动汽车数目M∈{100, 200, …, 700}分别进行实验。其中充电槽数目N=800, 该值较大,这样设置可以避免因为拥塞导致数据不准确的情况。图 1(a)描述了电动汽车数目对充电费用的影响,可以观察到随着充电汽车数量的增加,所有方法的充电费用均增加;但是相比其他方法,方法BPCS一直能帮助节省电费。方法BPCS相比其他方法在最好的情况下能够节省18.3%的电费支出。图 1(b)描述了电动汽车数目对电池损耗的影响,为了方便比较,图中已经做了归一化处理,可以观察到研究的方法相比其他方法能够提升33.0%的电池保护。图 1(c)描述了电动汽车数目对时间槽平均使用数目的影响。在Fig 1(c)中,可以观察到方法相比其他方法延长了42.8%的充电时间,充分利用了电动汽车停留时间远大于其充电时间的优点;而FCFS方法能最大力度的节省充电时间,这个特点能很好地应付充电站拥塞的情况,但是缺乏灵活性,不能帮助节省电费和保护电池。
|
图 1 不同电动汽车数目下的算法性能比较 Fig. 1 Comparison of algorithm performance under different number of EVs |
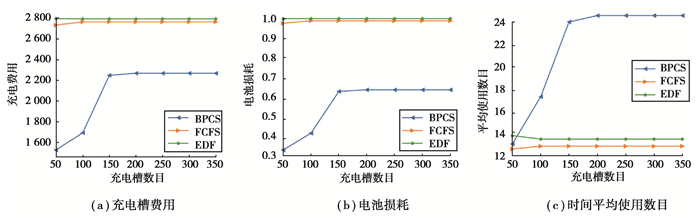
通过上述观察可以发现方法在利用电动汽车停留时间远大于其充电时间的优点的情况下,发挥出了极大作用,能帮助用户节省了至多18.3%的电费支出,同时又能够提升33.0%的电池保护。接着,研究不同调度方法在不同充电槽数目下的实验结果。设置充电槽数目N∈{50, 100, …, 350}进行实验,其中充电汽车数目为450。图 2(a)描述了充电槽数目对充电费用的影响,方法FCFS和EDT对费用的影响几乎不受充电槽数目的影响;但是方法BPCS受充电槽数目的制约。在图 2(a)中,当充电槽数目N>150时,可以观察到,方法BPCS相比其他方法能够节省18.0%的电费支出;但是,当N < 150时,数据异常。方法BPCS通过有序调控延长了充电汽车的充电时间,导致后续车辆的等待充电时间变长,后续车辆的可用充电时间变少。当资源充裕时不存在问题,但是当资源短缺,充电站拥塞时,充电汽车无法得到足够的充电时间,造成数据异常。图 2(b)描述了充电槽数目对电池折损的影响。在图 2(b)中充电槽数目N>150,可以观察到方法相比其他方法有32.9%的电池保护的提升;但是,当N < 150,因为拥塞导致数据异常。图 2(c)描述了充电槽数目对充电槽平均使用数目的影响。在图 1(c)中充电槽数目N>150,可以观察到方法相比其他方法延长了充电时间;但是,当N < 150, 因为拥塞导致数据异常。
|
图 2 不同充电桩数目下的算法性能比较 Fig. 2 Comparison of algorithm performance under different number of charging slots |
通过上述观察可以发现当充电槽充足时方法保持优势;但是当充电槽数量不充足时,会因为拥塞导致车辆等待时间过长,在离开时间确定的情况下,导致充电时间减小,引发异常。但是这种情况只针对充电槽短缺的情况,而实际生活中如果充电槽短缺,车辆会离开去其他充电站充电,或者提高最后的离开时间,给充电任务留下足够的时间。
5 结语随着电动汽车的大规模普及,大量电动车的无序充电行为容易造成电网过载和电池寿命的损耗。主要研究如何在有序充电过程中实现最大化车主便捷性的同时减少电池损耗这一重要问题,对这个问题进行了系统地建模和形式化,并提出了一个有序充电策略来协调充电行为,以实现最大化车主便捷性的同时降低电池损耗。为了阻止充电过程中信息直接交换造成不必要的隐私泄露和降低计算复杂度,还提出了一个基于交替方向多乘子ADMM的分布式有序充电服务调度算法。大量实验表明所提算法较已有算法有显著提升,能减少33.0%的电池寿命损耗和减少18.3%的电费支出。未来将对大规模充电汽车场景下如何减小充电费用和电池寿命损耗,以及新能源发电场景下有序充电服务的优化调度进行深入研究。
| [1] |
Axsen J, Bailey J, Castro M A. Preference and lifestyle heterogeneity among potential plug-in electric vehicle buyers[J]. Energy Economics, 2015, 50: 190-201. DOI:10.1016/j.eneco.2015.05.003 |
| [2] |
Knez M, Jereb B, Obrecht M. Factors influencing the purchasing decisions of low emission cars:a study of slovenia[J]. Transportation Research, 2014, 30D: 53-61. |
| [3] |
Turcksin L, Mairesse O, Macharis C. Private household demand for vehicles on alternative fuels and drive trains:a review[J]. European Transport Research Review, 2013, 5(3): 149-164. DOI:10.1007/s12544-013-0095-z |
| [4] |
Csiszár Csaba. Urban public charging station locating method for electric vehicles based on land use approach[J]. Journal of Transport Geography, 2019(74): 173-180. |
| [5] |
Luo C, Huang Y F, Gupta V. Placement of EV charging stations-balancing benefits among multiple entities[J]. IEEE Transactions on Smart Grid, 2015, 8(2): 759-768. |
| [6] |
Feng Y, Wang X, Dai W, et al. Congestion-aware deployment of electric vehicle charging stations[C]//ACM TURC'19: Proceedings of the ACM Turing Celebration Conference. New York, USA: ACM, 2019: 1-5.
|
| [7] |
Hadley, Stanton W, Alexandra A. Potential impacts of plug-in hybrid electric vehicles on regional power generation[J]. The Electricity Journal, 2009, 22(10): 56-68. DOI:10.1016/j.tej.2009.10.011 |
| [8] |
Muratori, Matteo. Impact of uncoordinated plug-in electric vehicle charging on residential power demand[J]. Nature Energy, 2018, 3: 193-201. DOI:10.1038/s41560-017-0074-z |
| [9] |
Zheng Yanchong. Integrating plug-in electric vehicles into power grids:A comprehensive review on power interaction mode, scheduling methodology and mathematical foundation[J]. Renewable and Sustainable Energy Reviews, 2019(112): 424-439. |
| [10] |
Faddel S, Elsayed A, Youssef T A, et al. Experimental verification of the effect of uncoordinated charging of electric vehicles on power grids[C/OL]. 2019 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT). Piscataway, NJ: IEEE, 2019(2019-08-08)[2020-04-05]. https://doi.org/10.1109/ISGT.2019.8791580
|
| [11] |
Chung H M, Li W T, Yuen C, et al. Electric vehicle charge scheduling mechanism to maximize cost efficiency and user convenience[J]. IEEE Transactions on Smart Grid, 2019, 10(3): 3020-3030. |
| [12] |
Leehter Y, Hong Lim W, Shih Tsai T. A real-time charging scheme for demand response in electric vehicle parking station[J]. IEEE Transactions on Smart Grid, 2016, 8(1): 52-62. |
| [13] |
Wang S, Bi S, Zhang Y J, et al. Electrical vehicle charging station profit maximization:admission, pricing, and online scheduling[J]. IEEE Transactions on Sustainable Energy, 2018, 9(4): 1722-1731. DOI:10.1109/TSTE.2018.2810274 |
| [14] |
Chenrui J, Jian T, Ghosh P. Optimizing electric vehicle charging with energy storage in the electricity market[J]. IEEE Transactions on Smart Grid, 2013, 4(1): 311-320. |
| [15] |
J in, Chenrui, Jian T, et al. Optimizing electric vehicle charging:a customer's perspective[J]. IEEE Transactions on Vehicular Technology, 2013, 62(7): 2919-2927. DOI:10.1109/TVT.2013.2251023 |
| [16] |
Rivera, Jo se, Christoph Goebel, et al. Distributed convex optimization for electric vehicle aggregators[J]. IEEE Transactions on Smart Grid, 2016, 8(4): 1852-1863. |
| [17] |
Yu L, Jiang T, Zou Y, et al. Joint energy management strategy for geo-distributed data centers and electric vehicles in smart grid environment[J]. IEEE Transactions on Smart Grid, 2016, 7(5): 2378-2392. DOI:10.1109/TSG.2016.2542261 |
| [18] |
Malhotra A, Binetti G, Davoudi A, et al. Distributed power profile tracking for heterogeneous charging of electric vehicles[J]. IEEE Transactions on Smart Grid, 2017, 8(5): 2090-2099. DOI:10.1109/TSG.2016.2515616 |
| [19] |
Rivera J, Wolfrum P, Hirche S, et al. Alternating direction method of multipliers for decentralized electric vehicle charging control[C/OL]. Conference on Decision & Control. Piscataway, NJ: IEEE, 2014(2014-05-10)[2020-04-05]. https://doi.org/10.1109/CDC.2013.6760992.
|
| [20] |
Bertsekas, Dimitri P, Tsitsiklis, et al. Parallel and distributed computation: numerical methods[J/OL]. Optimization & Neural Computation, 1989[2020-04-05]. http://hdl.handle.net/1721.1/3719.
|
| [21] |
Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine Learning, 2010, 3(1): 1-122. |
| [22] |
Yuan H, Junyong L, Xiaodong S, et al. The interaction between the large-scale EVs and the power grid[J]. Smart Grid and Renewable Energy, 2013, 4(2): 137. |
| [23] |
Zhang P, Qian K, Zhou C, et al. A methodology for optimization of power systems demand due to electric vehicle charging load[J]. IEEE Transactions on Power Systems, 2012, 27(3): 1628-1636. |
| [24] |
Sortomme E, Hindi M M, Macpherson S D J, et al. Coordinated charging of plug-in hybrid electric vehicles to minimize distribution system losses[J]. IEEE Transactions on Smart Grid, 2011, 2(1): 198-205. |
| [25] |
Xu Y, Pan F, Tong L. Dynamic scheduling for charging electric vehicles:A priority rule[J]. IEEE Transactions on Automatic Control, 2016, 61(12): 4094-4099. DOI:10.1109/TAC.2016.2541305 |
| [26] |
Kuran M S, Carneiro Viana A, Iannone L, et al. A smart parking lot management system for scheduling the recharging of electric vehicles[J]. IEEE Transactions on Smart Grid, 2015, 6(6): 2942-2953. DOI:10.1109/TSG.2015.2403287 |
| [27] |
Vaya M G, Göran A, Boyd S. Decentralized control of plug-in electric vehicles under driving uncertainty[C/OL]. Innovative Smart Grid Technologies Conference Europe. Piscataway, NJ: IEEE, 2015(2015-04-02)[2020-04-05]. https://doi.org/10.1109/ISGTEurope.2014.7028989
|
 2020, Vol. 43
2020, Vol. 43



