b. 北方工业大学 数据工程研究院, 北京 100144
b. Institute of Data Engineering, North China University of Technology, Beijing 100144, P. R. China
物联网和各类监控系统产生了海量时序数据,用户往往并不关心原始数据,更关注不同维度数据聚合后的结果信息。时序数据的多维聚合查询服务期望能够根据用户的动态需求,交互产生查询统计结果,这种多维度的交互式聚合查询被认为是批计算和实时计算之外的另一种数据计算模式[1-2],在各行业中存在普遍需求。以国家电网谐波监测系统需求为例,其数万个监测终端每天采集TB级的电能质量监测数据,业务管理人员需要即时了解各种指标维度上(如时间、空间及电压、电流等)的聚合统计结果(如平均值、百分位数、最值等),以便随时对全网谐波状况进行评判。
以电能质量监测数据为代表的物联网监测时序数据具有规模大、维度多等特点,直接进行聚合查询性能不佳,如何实现可交互式的时序数据聚合查询服务成为挑战性问题。
当前研究主要包括:1)使用采样方法约减数据规模,通过近似计算得到结果,提升查询效率,但采样结果严格来讲是不准确的。2)利用并行计算框架提升计算能力。已有的MapReduce、Spark[3]等框架适用于离线计算和实时计算,通过多设备并行处理提升计算效率,但离线计算框架无法返回近实时结果,实时处理框架无法实现交互式的使用效果。3)使用物化视图等预计算方法对聚合结果进行缓存。物化视图的优点在于不需要去访问大量的基表数据,但物化视图仍然存储在磁盘上,磁盘IO开销大,查询性能仍然不理想[4]。可以考虑将物化视图放在缓存中,但基于预计算的聚合查询存在“维度爆炸”问题,由于缓存空间的限制,不能像磁盘一样存储大量的物化视图。因此,需要评估物化视图的构建策略。
借鉴并行计算及物化视图思想,实现了一种时序数据多维聚合查询服务,通过预聚合将历史数据的多维聚合结果保存在内存中,利用实时计算对内存中的实时数据进行聚合,并根据需要归并和整合实时及历史数据聚合的结果。重点研究该服务实现的内存结构设计以及预聚合“维度爆炸”的任务选择问题。
1 相关工作时序数据[5-6]为以时间序列索引的连续数据,聚合查询包括简单的聚合查询和迭代式聚合查询[4]。聚合查询目的是帮助人们理解一段时间内数据集的变化[7]。
在近似计算方面,使用了采样技术[2],提出了增量式样本扩容与误差估计方法, 这种方法在快速获得近似结果同时又能保障近似结果的准确性,但对于稀疏数据可能产生不准确的结果;文献[8]描述了如何基于分位数概要结构进行近似化查询,提出了基于分位数概要的多值对象K近邻算法,关键方法是使用2个多值对象距离分布的-ϕ分位数来衡量它们的接近性;研究优化了在线聚集[9],提出一种基于内容的数据划分算法及数据块索引、放置策略, 通过提高在线聚集的采样效率和样本质量、保证计算与存储负载均衡, 实现在线聚集执行性能的大幅提升。
在并行计算框架方面,MapReduce分布式计算框架和聚合管道的方式被一些数据库用来处理聚合操作,但查询过程中产生了大量的磁盘和计算开销,低效耗时,无法满足即席查询的需求[6]。
在预计算方面,描述了概要表, 概要表在写入数据的同时,计算并保存相应的概要信息,从而发生查询时,直接从概要表中查询并返回结果。此类方法提高了查询效率。笔者首先描述了物化视图的选择,其次描述了物化视图的查询重写,但存在可派生物化视图的过滤方法效率低、查询重写自身占用时间长的问题,当存储空间、系统吞吐率等资源条件受到限制时,无法判定出哪些是最具保存价值的物化视图。
综上所述,基于抽样近似计算方法一定程度上可以提升聚合查询性能,但其存在准确性问题;现有的并行计算框架并不能满足交互式聚合查询需求,但并行处理的思路是可借鉴的;预计算方法具有较好的查询性能,但物化视图由于需要持久化,对物化视图的查询可能存在性能问题,将预计算结果(中观数据[5])放入内存是优化方向,但内存空间的限制,特别是聚合查询的维度爆炸必然要求设计一种有效的预计算任务的选择方法。
2 时序数据的聚合查询服务 2.1 基本实现思路时序数据的聚合查询包括:实时查询和历史查询。当数据到来时,采用混合处理框架Lambda[10],分别将其送入批处理层和实时处理层。批处理层可以进行数据分析和处理,如进行预聚合运算,其分析的结果可用于实时数据处理层中[1],历史查询主要是在批处理层进行计算,而实时查询主要是在实时处理层进行计算。
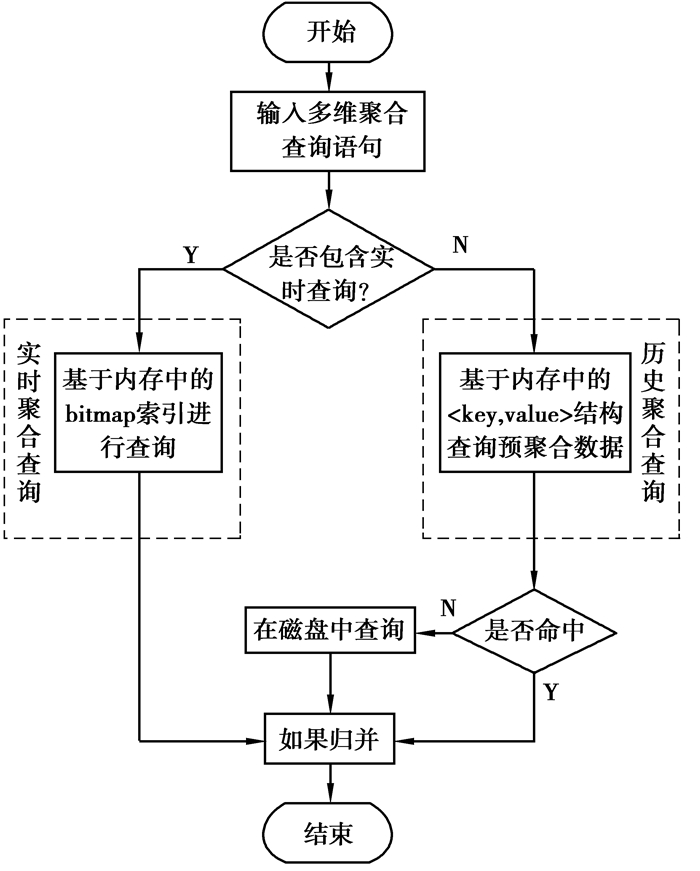
交互式查询流程图如图 1所示, 历史数据具有数据量过大的特点,考虑对历史数据进行预聚合,只将预聚合的结果放入内存,在进行预聚合任务时,为避免聚合任务过多而内存空间有限导致的“维度爆炸”问题,需要在有限的内存空间与允许预聚合的时间基础上选择一组尽量多的任务来执行。
|
图 1 交互式查询流程图 Fig. 1 Interactive query flow chart |
基于相应内存存储结构,对内存中构建好位图索引[11]的实时数据与历史数据的预聚合数据,用户在输入一个查询语句之后,按照如下过程1所示的查询步骤进行查询。
过程1.交互式查询步骤
1) 接收查询语句,将查询语句作为一个任务。
2) 对于实时数据,获取条件表达式中的对应维度列的对应值,在维度列对应的维度字典哈希表中查询到对应值的Id,在每个维度存储位图索引的哈希表中找到对应Id的相应位图索引,将获取的几个bitmap索引哈希表的value值进行逻辑与运算,返回与运算结果为1的行号,在内存的堆结构缓存区中对实时数据的SkipList,根据已知的行号,进行从上层到下层逐步推进的查询,获得最终结果。
3) 对预聚合数据,基于map < key, value>的哈希结构,获取到该任务的聚合结果。若没有查询到任务结果,则需要到磁盘进行查询。
4) 将实时查询与历史查询按照以上步骤查询的结果进行并行聚合运算,然后将结果进行归并,返回给用户。
常用的聚合函数包括count,sum,avg,min,max等,在归并时公式如下:
avg(s)=sum(sum(s1), sum(s2), …, sum(sn))/sum(count(s1), count(s2), …, count(sn))
min(s)=min(min(s1), min(s2), …, min(sn))
max(s)=max(max(s1), max(s2), …, max(sn))
count(s)=sum(count(s1), count(s2), …, count(sn))
sum(s)=sum(sum(s1), sum(s2), …, sum(sn))
……
可发现这些聚合函数便于并行计算,可以由多线程并行计算s1, s2, …, sn对应的聚合函数值,对于每一个s,先汇总s1的查询结果与s2的查询结果,将其作为中间结果,如果还有其他查询任务,则再进行归并,如此迭代,最终返回结果给展示部分累加多维查询,依次对各任务结果进行汇总[12]。
2.2 内存存储结构为满足交互式查询,考虑尽量将数据存储在内存中,合理的内存存储结构是提升查询效率的关键。对于实时数据来说,采用SkipList结构来存放,进入内存后以列式存储,并为每列数据建立位图索引[11],同时使用不同的压缩算法对索引数据进行压缩;对于历史数据的预聚合数据,为每一个查询任务建立 < key, value>的哈希表结构,key为一个查询任务,value为查询结果。
key::= < target> <table>[ <condition>][<
column>]
target::=count( <column >)|max( <column >)|min(< column >)|sum( <column >)|avg([distinct|all] <column >)
condition= < conditional_exp>[< and|or> <conditional_exp>]|*
conditional_exp ::= < column> < comparison operator> <value>
comparison operator ::=’>’|’=’|’ < ’|’>=’|’ < =’
|’ < >’|’!=’|’!>’|’! < ’
根据 < key, value>结构获取到该任务的聚合结果, 从而能根据用户的查询语句,在预聚合数据中快速判断是否命中。
2.3 预聚合任务选择算法预聚合是提升聚合查询性能的有效方法。但在面对大量聚合查询及其带来的维度爆炸问题时,需要在有限的内存和允许预聚合时间的基础上进行一组查询任务的选择,来保证执行尽量多的查询任务并将查询结果放入内存中,作为历史数据的预聚合数据,加速数据查询。在查询任务中存在时间、空间等内部任务互相依赖的维度,如空间聚合粒度为省的任务在粒度为市的任务基础上聚合时间比在原始数据上聚合的时间短,所以空间之间是相互依赖的,称这些相互依赖的任务为分级任务。
以这个问题为背景,可抽象出如下问题:在总时间为T,总内存为M的约束条件下,共有N个可选聚合条件,按照维度不同分成K组,其中聚合任务i属于第k组(i=1, …, N),聚合任务i占用内存mi,耗时ti,分级任务因为组内任务间有依赖关系所以需要重新计算权重;非分级的任务组内每个任务权值相同,求出满足约束条件的一组聚合任务数最多的结果。
分析:这个问题可以用经典的动态规划方法解决,如经典的背包问题与本问题十分相似,在不考虑分级任务之间联系的情况下,通过分组背包与二维背包结合的方式来进行聚合任务选择,主要步骤如下:1)将任务分组,多个分级任务作为一组,每个非分级任务为一组。2)视每个任务的权重都相同,对于每组任务,在时间与内存花费允许的情况下,选择一个任务或不选。
但是由于本问题中分级任务的存在,分级任务的完成时间之间互相影响,分级任务的权重也不相同,因而需要将分级任务与非分级任务分情况解决,非分级任务用0—1背包解决方式来解决,分级任务用依赖背包与分组背包、泛化背包结合的解决方式来解决,具体过程如下算法1所示。
算法1.最优预聚合任务选择算法
输入:N个可选聚合任务
输出:满足约束条件的一组最优聚合任务
1) 将N个可选聚合任务按照维度进行分组,组数为k;
2) 接收第k组,判断其中是否为分级任务;
3) 第k组为分级任务,进行组内等级排序,并根据等级排序重新计算任务权值,具体计算方法为:(n-S+1)*wi*n/Q,其中n为这个组的任务数,S为某个任务在组内的排序,wi为这个任务的权重,Q为从1到n的累加和,Q=1+2+…+n;
4) 根据步骤3中获得的等级排序,将每个等级作为主件,依赖于这个等级的其他任务作为该等级的附件;
5) 根据步骤4中获得的主件,对每一个主件,将其附件进行组合处理,将每个组合作为一个新的附件,根据时间花费的依赖关系重新计算每个新附件的时间花费,内存花费及权重则进行简单的相加即可,将最终得出的主件的多个新附件进行0—1背包处理,状态转移方程为:
6) 将步骤5中获得的所有任务作为一组,从组中所有任务中选择一个任务或不选,状态转移方程如下:
7) 第k组为非分级任务,直接对每一个任务进行0-1背包运算;
8) 返回一组聚合任务。
在本实验中,权值设定相差不大,但实际上用户进行交互式查询时会出现一些任务是总不被查询的情况,权重的应该比被查询频率较高的任务小,由于实验方法也是考虑到权重的,因此同样适用于冷热数据权重不一致的情况。
3 实验结果及评价 3.1 实验目的最优预聚合任务选择算法能在限定的时间花费与空间花费下选择出尽量多的一组预聚合任务。为了验证该结果,通过实验详细描述了验证过程。实验数据来源于电网谐波监测系统的实际采集数据。实验环境为在可用时间花费与内存花费分别为(120 min, 4 G)、(240 min, 8 G)、(360 min, 16 G)、(480 min, 32 G)的情况下进行任务选择计算,对任务选择的结果进行比较分析。
实验数据包含多个维度的聚合任务,例如空间维度(省、市、县)、时间维度(年、月、日)、指标维度(电压220 kV、500 kV、1 000 kV等)。
将这些任务分组,每个任务的初始权重都设定为1,为每个任务预估时间花费与内存花费,这些任务组有分级任务,也有非分级任务(同一组包含几个任务的为分级任务,一组只有一个任务的为非分级任务)。
对于非分级任务,时间、内存花费及权重与给定的花费相同,不会发生变化;而对于分级任务,由于组内关系存在相互依赖,因此时间、内存花费及权重需要在给定的花费基础上根据重要性重新计算。对于分级任务,在组内的位置越靠前说明重要性越小,需要按照最优预聚合任务选择算法的步骤3重新计算组内每个任务的权重,同时按照步骤4与步骤5,为分级任务的每一个任务选择出一组最优附件,与该任务组合成一个新的任务,重新计算每个任务的时间与内存花费,替换该任务,这样对于分级任务来说,一个任务也同时包含了几个任务,并且任务的时间花费、内存花费以及权重都经过了重新计算。经过重新计算,这100个任务的时间花费、内存花费以及权重的指标如下表 1所示。
| 表 1 初始任务指标表 Table 1 Table of indicators for initial tasks |
研究进行了2个不同的测试:1)在相同时间与内存花费的情况下,使用不同可选聚合任务数进行测试;2)在相同可选聚合任务数量的条件下,对不同的时间与内存花费进行测试。
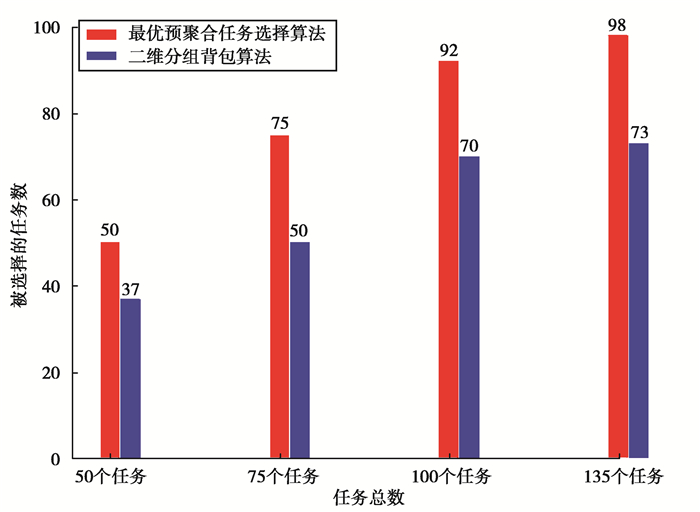
在时间花费与内存花费为(480 min, 32 G)的情况下,将考虑分级任务带来影响的结果与不考虑分级任务带来影响的结果进行比较,经过最优预聚合任务选择算法及二维分组背包算法分别对50个、75个、100个、200个测试任务进行计算,得到最终任务选择结果如图 2所示。
|
图 2 相同花费不同任务数结果对比图 Fig. 2 Comparisons of the results of different tasks with the same expenditure |
在可选任务相同均为100个任务的前提下,令时间花费与内存花费分别为(120 min, 4 G)、(240 min, 8 G)、(360 min, 16 G)、(480 min, 32 G),将考虑分级任务带来影响的结果与不考虑分级任务带来影响的结果进行比较,经过最优预聚合任务选择算法及二维分组背包算法对100个测试任务的计算,得到最终任务选择结果。
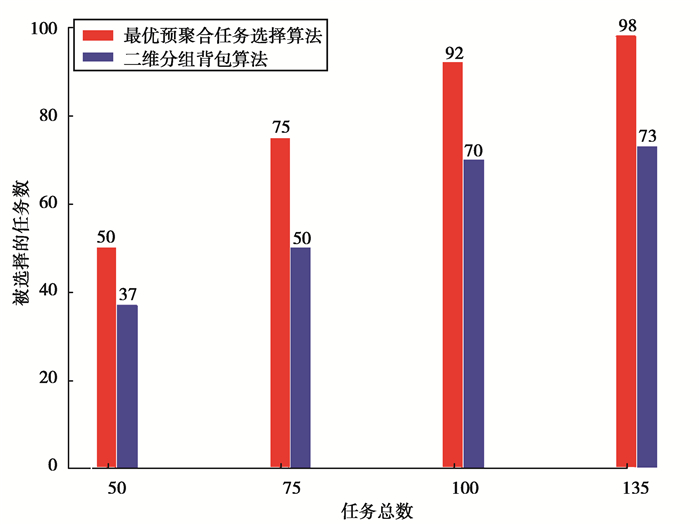
3.2 实验结果分析图 3中红色柱状图为使用最优预聚合任务选择算法得到的任务数,蓝色柱状图为使用二维分组背包算法得到的任务数,通过图 3可以看到,在相同(480 min, 32 G)花费的条件下,分别对50个、75个、100个、135个任务进行选择,任务选择算法都能够选择出比二维分组背包算法更多的任务。
|
图 3 基于花费的任务选择对比图 Fig. 3 Comparisons chart of the task selection based on the same cost |
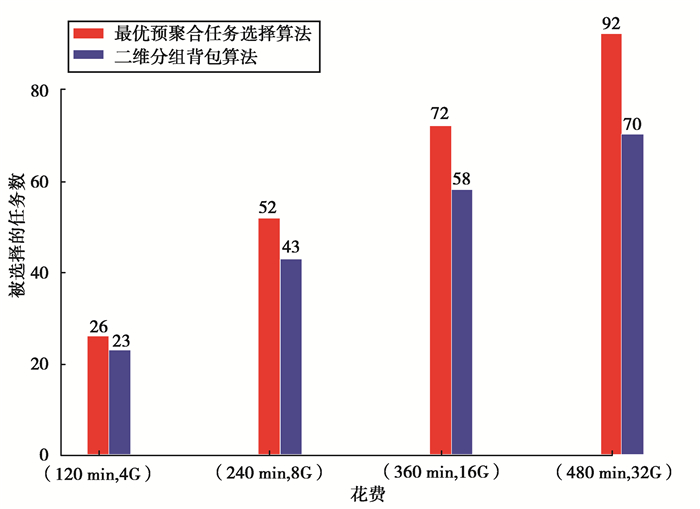
通过图 4可以看到,在可选任务相同均为100个任务的条件下,分别对时间花费及内存花费为(120 min, 4 G)、(240 min, 8 G)、(360 min, 16 G)、(480 min, 32 G)的情况下进行选择,通过柱状图可以看出,在任务数相同、花费变化的情况下任务选择算法都能够选择出更多的任务。
|
图 4 不同花费相同任务数结果对比图 Fig. 4 Comparisons of the results of the same number of tasks with different expenditures |
基于上述分析,提出的预聚合任务选择算法利用对分级任务时间、内存花费及权重的重新计算,选择出了尽量多的预聚合任务。
4 结论笔者提出了时序数据的聚合查询服务,主要解决了交互式多维聚合查询问题,将实时数据及历史数据的预聚合数据存储在内存中,设计了一种内存存储结构,对内存中的实时数据建立位图索引,使用SkipList结构存储数据;对历史数据的预聚合数据建立哈希存储结构,当接收到查询请求时,对实时查询进行基于内存中的位图索引进行查询,对历史查询基于内存中的哈希结构查询预聚合数据。为弥补现有时序数据库在预聚合时只能由用户随机指定聚合任务不足,解决可能导致的“维度爆炸”问题,使用最优预聚合任务选择算法在有限内存空间以及允许的预聚合时间条件下,使尽量多的任务可被执行。通过实验证明最优预聚合任务选择算法与二维分组背包算法相比,可在内存与时间花费有限的情况下选择出一组尽量多的任务,进而提升交互式聚合查询的命中率。
| [1] |
陈军成, 丁治明, 高需. 大数据热点技术综述[J]. 北京工业大学学报, 2017, 43(3): 358-367. CHEN Juncheng, DING Zhiming, GAO Xu. Survey of big data hot techniques[J]. Journal of Beijing University of Technology, 2017, 43(3): 358-367. (in Chinese) |
| [2] |
Li J, Li D S, Zhang Y M. Efficient distributed data clustering on spark[C/OL]. 2015 IEEE International Conference on Cluster Computing. Piscataway, NJ: IEEE, 2015(2015-10-29)[2020-04-05]. https://doi.org/10.1109/CLUSTER.2015.84
|
| [3] |
高彦杰, 陈冠诚. Spark SQL:基于内存的大数据处理引擎[J]. 程序员, 2014(8): 104-107. GAO Yanjie, CHEN Guancheng. Spark SQL:Big data processing engine based on memory[J]. Programmer, 2014(8): 104-107. (in Chinese) |
| [4] |
张茜.基于聚合函数的物化视图关键技术的研究[D].南京: 南京理工大学, 2010. ZHANG qian. Research on key technology of materialized view based on aggregation function[D]. Nanjing: Nanjing University of Science and Technology, 2010. (in Chinese) http://cdmd.cnki.com.cn/article/cdmd-10288-2010097025.htm |
| [5] |
丁治明, 蔺春华, 郭黎敏, 等.一种物联网感知大数据的缓存设计和查询方法[P].中国: CN201810314923.2. 2018-09-14. DING Zhiming, LIN Chunhua, GUO Limin, et al. IoT-aware big data cache design and query method[P]. China: CN201810314923.2. 2018-09-14. (in Chinese) |
| [6] |
冯诗淳, 曹斌, 晁德文, 等. 结合HBase的散列概要森林索引方案[J]. 小型微型计算机系统, 2018, 39(1): 100-104. FENG Shichun, CAO Bin, CHAO Dewen, et al. Hash synopsis forest index schema based on HBase[J]. Journal of Chinese Computer Systems, 2018, 39(1): 100-104. (in Chinese) DOI:10.3969/j.issn.1000-1220.2018.01.021 |
| [7] |
钟丽娟.时间序列数据相似性与聚合top-k查询算法研究与应用[D].杭州: 浙江大学, 2016. ZHONG Lijuan. Time series similarity, aggregate top-k query algorithms and applications[D]. Hangzhou: Zhejiang University, 2016. (in Chinese) |
| [8] |
王丹.基于数据库的Summary查询研究[D].沈阳: 东北大学, 2013. WANG Dan. Research on summary query based on database[D]. Shenyang: Northeastern University, 2013. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10145-1015701956.htm |
| [9] |
Wand Y X, Luo J Z, Song A B, et al. Partition-based online aggregation with shared sampling in the cloud[J]. Journal of Computer Science and Technology, 2013, 28(6): 989-1011. DOI:10.1007/s11390-013-1393-6 |
| [10] |
欧阳辰, 刘麒赟, 张海雷, 等. Druid实时大数据分析原理与实践[M]. 北京: 电子工业出版社, 2017. OUYANG Chen, LIU Qiyun, ZHANG Hailei, et al. Principles and practice of druid real-time big data analysis[M]. Beijing: Electronic Industry Press, 2017. (in Chinese) |
| [11] |
范欣欣.时序数据库技术体系-Druid多维查询之Bitmap索引[DB/OL]. http://hbasefly.com/2018/06/19/timeseries-database-8/. (2018-06-19)[2020-04-15]. FAN Xinxin. Time series database technology system-Druid multidi-mensional query bitmap index[DB/OL]. http://hbasefly.com/2018/06/19/timeseries-database-8/. (2018-06-19)[2020-04-15]. |
| [12] |
王璐华, 肖敏, 周伟强, 等.一种多维数据立方体增量聚合及查询优化方法[P].中国: CN102360379 A. 2013-04-10. WANG Luhua, XIAO Min, ZHOU Weiqiang, et al. An incremental aggregation and query optimization method for multidimensional data cubes[P]. China: CN102360379 A. 2013-04-10. |
 2020, Vol. 43
2020, Vol. 43


