随着风能的广泛应用, 电力系统中风电的比例越来越高, 风电机组的高运维成本、长时间停机已成为风电行业发展的障碍, 根据现有的统计数据, 海上风机的运维成本每年大概是10 ~30万英镑, 陆上风机是4.5万英镑, 因此降低风机的运维成本越来越受到关注[1]。目前开展的研究主要致力于降低运维成本和停机时间, 重点是基于预测状态的维修[2]。
齿轮箱作为风机的关重零部件, 其故障导致的风机停机时间最长[3], 当前关于风力发电机的故障诊断主要集中在齿轮箱上, 基于风机齿轮箱的研究有2个发展方向, 一是在诊断方法上的创新, 采取更为精确的混合故障诊断模型, 如模糊逻辑和神经网络相结合, 深度学习(DL)和支持向量机(SVM)相结合等; 其次是关于诊断对象的变化, 对象的变化也有2个方向, 一是由小变大, 即由齿轮箱扩展到整个传动链甚至是整机, 二是由大变小, 即由齿轮箱具体到齿轮箱内部关重零部件, 如轴承、齿轮箱轴承引起的。国家可再生能源实验室一篇论文表明齿轮箱70%的故障是由轴承故障引起的, 26%的故障是由齿轮故障引起的[4]。所以轴承的运行状态至关重要, 它关系到风机经济效益。
过去关于轴承的故障诊断大多针对单一传感器获得的信息进行分析, 如诊断分析[5]、声发射分析[6]、热成像解释[7]等, 但风机运行环境恶劣, 传感器的可靠性无法保证, 且单一传感器的故障信息具有局限性, 会出现误诊情况, 诊断精度有时也难以达到要求。为了得到准确的识别结果, 需多个传感器获取故障信息。多信息融合就是充分利用不同时空的数据, 通过一定的准则将传感器观测数据进行分析, 获得对观测对象的一致性描述与解释, 做出综合决策, 获得比单信息更准确与充分的信息[8]。信息融合应用于很多领域, 常用的方法有人工神经网络(ANN)、深度学习(DL)、支持向量机(SVM)、遗传算法(GA)和D-S证据理论等。文献[9]融合加速度和重力传感器的数据, 能够检测出有缺陷的轴承和故障位置, 文献[10]将神经网络和D-S证据理论用于风机振动故障诊断, 可以避免误诊, 提高准确率, 文献[11]将基于集合深度卷积神经网络和改进D-S证据理论融合方法用于轴承故障诊断, 但文献[9-11]使用的信号维度较少, 诊断准确率也不太高, 缺乏将多信息融合应用于风电齿轮箱轴承故障诊断。
目前的风电场中基本都安装有SCADA (supervisory control and data acquisition)系统和CMS(condition monitoringsystems)系统, 利用大数据挖掘其中蕴含的信息及人工智能融合多源信息已成为优化风机运维策略的有效措施和研究热点。笔者以风电齿轮箱轴承为研究对象, 基于信息融合将神经网络和DS证据理论相结合, 使两者优势互补, 挖掘SCADA系统中的信息, 提出一种行之有效的风机齿轮箱轴承故障诊断模型, 从而提高风机运行的可靠性, 降低风机运维成本。
1 多信息融合的故障诊断算法 1.1 BP神经网络BP神经网络的特点是信号的正向传输和误差的反向传播, 它可以实现输入信号和输出信号之间的非线性映射, 根据Kolrnogorov定理, 一个3层BP神经网络能够实现对任意非线性函数的逼近[12]。它广泛应用于故障诊断领域, 文献[13]采用随机森林、支持向量机、隐马尔可夫模型和BP网络作为比较, 用于滚动轴承故障诊断, 文献[14]提出将卷积神经网络算法结合softmax分类器并将其用于滚动轴承故障识别, 文献[15]采用紧凑型自适应卷积神经网络(CNN)应用于轴承故障检测和诊断等。
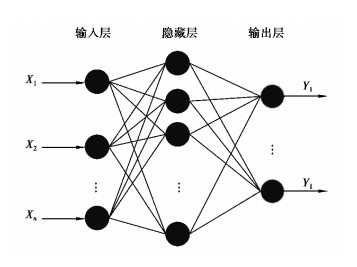
一个3层的神经网络拓扑结构如图 1所示, 网络中的每一个节点都是一个神经元, 输入节点数与训练数据的组数一致, 输出节点数与输出状态等级一致, 隐藏层节点数对输出结果的准确性和泛化能力有很大的影响, 隐藏层节点数太少将影响网络的存储能力, 太多会增加训练的时间, 误差也不一定最佳, 所以确定隐藏层神经元个数至关重要, 文献[16]对隐含层节点数的确定给出了相关经验公式:
| $ m = \sqrt {n + l} + \beta , $ | (1) |
| $ m =2n +1 $ | (2) |
|
图 1 BP神经网络拓扑结构图 Fig. 1 BP neural networktopology diagram |
式中:m为隐含层节点数; n为输入层节点数; l为输出层节点数; β为1~10的常数。
给出的公式是基于经验总结所得, 只是给出了隐含层节点数量一个大致的范围, 确定最优的节点数需根据实际的仿真实验。各神经网络的隐藏层节点数均由多次实验所确定, 确定的原则就是训练时间最短、误差最小、网络性能最好[17]。
神经网络用于设备故障诊断是近年来迅速发展起来的新研究领域, 神经网络作为一种新的模式识别技术, 在设备故障诊断领域显示了极大的潜力。目前, 神经网络在设备故障诊断领域的应用研究主要集中在3个方面:1)模式识别, 神经网络作为分类器进行故障分类; 2)故障预测, 神经网络作为动态预测模型进行故障预测; 3)知识处理, 建立基于神经网络的故障诊断专家系统。随着人工智能和计算机技术的迅速发展, 神经网络故障诊断技术具有广阔的发展前景。
1.2 D-S证据理论D-S证据理论是Dempster和Shafer于1976年开发的一种新的理论[18], 它将来自多源的证据进行融合, 并提供了事件将要发生的概率度量(BPA, basic probability assignment)。D-S证据理论在信息融合领域有着广泛的应用, 文献[19]将D-S证据理论和AHP相结合应用于故障诊断, 文献[20]在传统灰色关联分析的基础上, 将D-S证据理论应用于减速机壳体故障诊断, 文献[21]利用D-S证据理论融合RBF神经网络结果, 用于旋转机械的故障诊断, 文献[22]将证据理论和堆栈降噪自编码(SDAE)应用于齿轮故障诊断。
作为一种有效信息融合技术, 证据理论具有扎实的理论基础和严格的组合规则, 依靠多条证据的融合, 不断缩小假设集, 建立了量化函数即基本概率分配函数BPA, 其值决定了命题为真的程度。
1.2.1 相关概念1) 辨识框架Θ。辨识框架是一个包含所有故障类型的集合, 表示为:Θ = {F1, F2, …, Fn }, 每一个元素分别代表一种故障模式。
2) 基本概率分配函数m (A)。映射m :2Θ[0, 1], 若满足:对空集ø, 有m (Θ) =0, 对∀A ∈2Θ , 有
利用D-S证据理论进行融合, n条证据的融合公式如下:
| $ \begin{array}{*{20}{l}} {m(A) = ({m_1} \oplus {m_2} \oplus ... \oplus {m_n})(A) = \frac{{\sum\limits_{{A_1} \cap {A_2} \cap ... \cap {A_n} = A} {{m_1}({A_1})\begin{array}{*{20}{l}} \cdot \end{array}{m_2}({A_2})...{m_n}({A_n})} }}{{1 - \sum\limits_{{A_1} \cap {A_2} \cap ... \cap {A_n} = \emptyset } {{m_1}({A_1})\begin{array}{*{20}{l}} \cdot \end{array}{m_2}({A_2})...{m_n}({A_n})} }},}\\ {} \end{array} $ | (3) |
| $ \sum\limits_{{A_1} \cap {A_2} \cap ... \cap {A_n} = \emptyset } {{m_1}({A_1})\begin{array}{*{20}{l}} \cdot \end{array}{m_2}({A_2})...{m_n}({A_n})} ,\forall {A_i} \subseteq {\rm{ }}\Theta $ | (4) |
式中:m (A)为故障A融合后的BPA值; k为冲突因子, 其值的大小反映了各证据之间的冲突性大小, 且0≤k ≤1, k越大各证据之间冲突性越大, 反之, 则越小。mn为各个证据的BPA值; An为各证据中包含故障A的故障集合
1.2.3 诊断决策准则设ƎA1, A2 ⊂Θ满足[24] :
| $ m({A_1}) = \max \left\{ {m({A_i}), \subset \Theta } \right\}, $ | (5) |
| $ m({A_2}) = \max \left\{ {m({A_i}),{A_i} \subset \Theta {\rm{且 }}{A_i} \ne {A_1}} \right\}. $ | (6) |
若有:
| $ m({A_1}) - m({A_2}) > {\varepsilon _1} $ | (7) |
| $ m(\Theta ){\rm{ < }}{\varepsilon _2} $ | (8) |
| $ m({A_1}) > m(\Theta ), $ | (9) |
式中:ε1, ε2为预先设定的阈值, 则A1为判决的结果, 根据经验要求, 取ε1 =0.7, ε2 =0.1。
1.3 改进D-S证据理论D-S证据理论有许多优点, 但D-S证据理论也存在一个缺陷, 即当各证据之间发生高度冲突时, 融合规则就会失效, 产生与事实相悖的结论[25]。鉴于此, 笔者采取2种方法减小证据间的冲突, 首先采用BP神经网络和D-S证据理论相结合, 将神经网络的输出结果作为D-S证据理论的BPA值, 神经网络的输出可以近似认为是相互独立的, 但并不是完全独立的, 其次, 在此基础上提出一种改进的D-S证据理论, 将各证据基于加权的思想进行改进, 具体步骤如下[26] :
1) 2个证据E1和E2之间的相似系数d12可以表示为
| $ {d_{12}} = \frac{{\sum\nolimits_{B \cap C \ne \emptyset } {{m_1}(B){m_2}(C)} }}{{\sum {m_1^2(B) + \sum {m_2^2(A)} } }}, $ | (10) |
其中:d12 ∈ [0, 1], 相似系数描述证据间的相似程度, 值越大说明两证据相似度越高, 值越小说明两证据独立性越高, 且dij =dji。
2) 其他证据对证据Ei的支持度S(mi)为
| $ S\left( {{m_i}} \right) = \sum {{d_{ij}}} ,i,j = 1,2...,n, $ | (11) |
其中:n表示证据的数量, 如果一个证据和其他证据比较相似, 则它们相互支持的程度也高。
3) 将支持度归一化后得到证据Ei的可信度为
| $ C\left( {{m_i}} \right) = \frac{{S\left( {{m_i}} \right)}}{{\sum\limits_{i = 1}^n {S\left( {{m_i}} \right)} }}, $ | (12) |
可信度C(mi)反映了证据Ei的可信程度。
最后再利用融合规则将改进的证据进行融合。
2 基于BP神经网络和改进D-S证据理论风机齿轮箱轴承故障诊断模型信息融合按照数据抽象的程度分为3种:数据层融合、特征层融合和决策层融合。分析各层次融合方法的优劣, 选择采用特征层、决策层相互结合的信息融合模型。根据神经网络的特点, 神经网络用于对风机齿轮箱轴承的特征层诊断, 这样既保留了一定数量的原始信息, 又实现了一定的数据压缩[27], 根据D-S证据理论的特点, 决策层融合采取D-S证据理论。
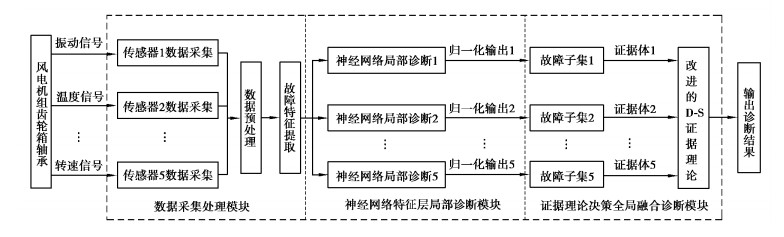
该模型具体步骤是, 首先挖掘蕴含在SCADA系统中有关风机齿轮箱轴承多种信号的故障特征, 然后将各信号的故障特征量作为神经网络输入, 将神经网络的输出进行归一化作为D-S证据理论的BPA值, 基于加权思想改进各证据, 最后利用组合规则将各条证据进行融合, 得出最终诊断结果。该诊断模型是将两种方法进行串联, 利用两种方法优势互补, 各子BP神经网络可以根据实际情况灵活处理参数, 大大增强了诊断模型的适应性, 同时该模型还具有一定的通用性。该研究的技术路线图如图 2所示。
|
图 2 基于BP神经网络和改进D-S证据理论故障诊断技术路线图 Fig. 2 Fault diagnosis technical scheme based on BP neural network andimproved D-Sevidence theory |
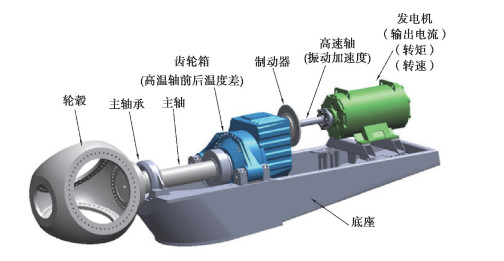
笔者以某风场2 MW风机运行的真实数据为例, 数据是风场SCADA系统采集的2017年3月7号~3月14号的数据。SCADA系统中有多种类型的数据, 其中振动信号、温度信号、电流信号、转矩信号和转速信号很具代表性, 能够很好地反映齿轮箱轴承的运行状态。振动信号是采用齿轮箱高速轴振动加速度(m/s2); 温度信号采用齿轮箱进出口油温差(℃), 由于温度为缓变信号, 输入数据取5 min的平均值; 电流信号采用发电机输出电流(A); 转矩信号采用发电机转矩(N· m); 转速信号采用发电机转速(r/min)。信号采集的具体情况如图 3所示。
|
图 3 信号采集具体情况 Fig. 3 Detail drawing of signal collection |
将采集到的原始数据输入模型之前, 需要进行数据预处理以保证模型的收敛速度, 主要采用以下2种方法:
1) 归一化处理。由于原始数据幅值大小不一, 有时相差较为悬殊, 如果直接输入神经网络, 数据大的波动就会抑制神经网络的学习, 使其不能反映小监测值的变化。要神经网络能对各种状态进行分类识别, 需要剔除各特征参数物理单位的干扰, 而且Sigmoid函数的输出也在0~1之间, 网络的输出也是如此, 所以需要对输入样本进行归一化处理。数据归一化处理公式为
| $ x_j^* = {\rm{ }}\frac{{{x_j} - {x_{{\rm{max}}}}}}{{{x_{{\rm{max}}}} - {x_{{\rm{min}}}}}}, $ | (13) |
式中:xj*为数据归一化后的值;xj为输入的第j个数据;xmax和xmin为样本数据的最大值和最小值。
2) 剔除奇异点。数据信号的奇异点是指突然出现比其他时刻相差很多的信号, 由于风机运行环境恶劣, 极有可能出现奇异值, 其次, 数据信号奇异点的存在还会增加网络的训练时间, 导致网络不收敛, 所以必须将这种错误的数据剔除。剔除奇异点的原则:一般是通过计算各组采样值的标准偏差σ, 再按照“3σ ”原则剔除数据。
将预处理后的数据作为神经网络输入样本, 然后将神经网络的输出值进行归一化作为每种故障模式的BPA值送入决策融合模块, 归一化公式为
| $ m\left( {{A_k}} \right) = \frac{{y\left( {{A_k}} \right)}}{{\sum\limits_{k = 1}^4 {y\left( {{A_k}} \right) + {E_s}} }} $ | (14) |
式中:m (Ak)为Ak故障模式的BPA值; y (Ak)为神经网络的实际输出; Es为网络输出误差, 其计算式为
| $ {E_s} = \frac{1}{2}{\sum\limits_{k = 1}^4 {\left( {t_k^s - y_k^s} \right)} ^2},s = 1,2...,5, $ | (15) |
式中tks, yks分别为第s个神经网络的第k个输出神经元的理想输出和实际输出。
将上述各证据按照改进规则进行改进得到独立的证据, 最后运用D-S证据理论进行融合, 得出综合的诊断结果。
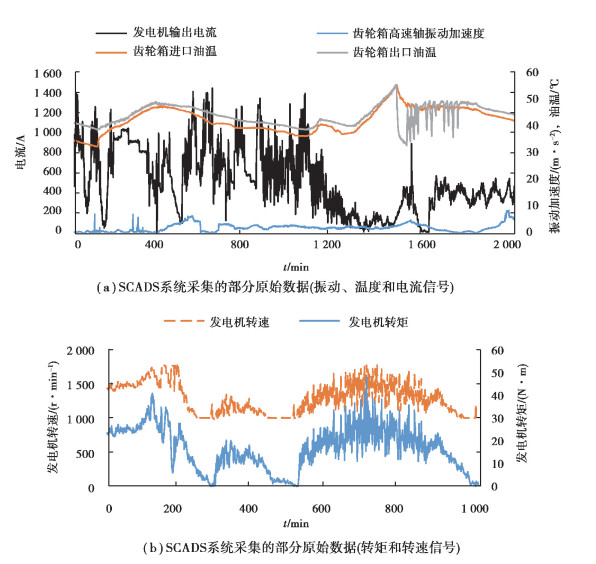
3 实例分析 3.1 BP神经网络特征层诊断发电机组齿轮箱轴承常见的故障有:轴承外圈故障、轴承内圈故障、滚动体故障、正常状态和不确定状态5种故障域, 构建证据理论的辨识框架:Θ = {F1, F2, F3, F4, F5 }, F5表示不确定状态。因此, 神经网络的输出层有4个神经元, 每个神经元代表一种故障状态, 输出误差对应不确定状态。SCADA系统在2017年3月7号~3月14号期间采集的部分数据指标如图 4所示, 风电机组齿轮箱轴承故障诊断模型理想输出如表 1所示。
|
图 4 风电场SCADS系统采集的部分原始数据 Fig. 4 Part ofthe original datacollected bythe windfarm SCADSsystem |
| 表 1 风电机组齿轮箱轴承故障诊断模型理想输出 Table 1 Ideal output of windturbinesgearbox bearingsfault diagnosis model |
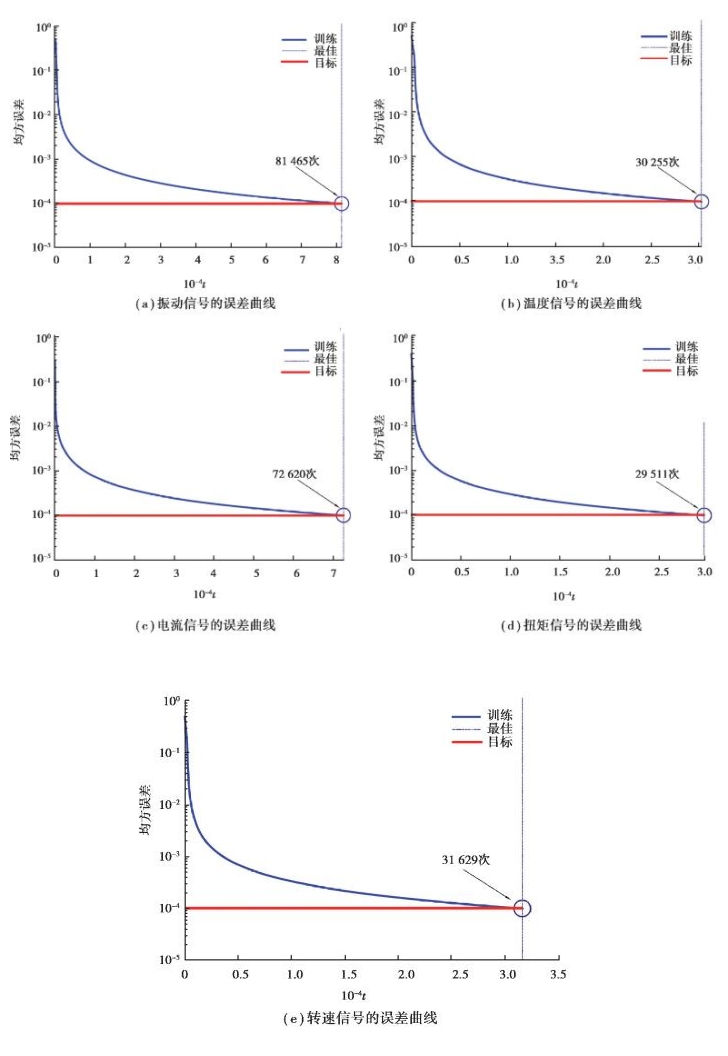
基于信息融合, 即将其中任意种类信号依据融合规则进行融合, 得到综合诊断结果。由于神经网络的输出是作为D-S证据理论的BPA值, 网络的输出在[0, 1]之间, 因此输出层选用‘logsig’函数, 隐含层激励函数选取‘tansig’函数。为获得良好的诊断效果, 所选取的样本需要包含齿轮箱轴承的各种状态。采用不同的参数经过多次训练, 对比训练效果, 最终神经网络的参数选取如下:训练算法采用traingdm(有动量的梯度下降法), 性能函数选取mse, 学习率0.02, 动量因子0.9, 网络训练的目标误差为10-4。将训练组的样本数据输入神经网络来训练网络中的训练参数, 利用Matlab编程训练神经网络, Matlab训练5个子神经网络的结果如图 5所示(训练次数用t表示)。
|
图 5 5个神经网络训练误差曲线 Fig. 5 Curves of the training erroro f5 neural networks |
从图 5中可以看出, 振动信号、温度信号、电流信号、转矩信号和转速信号对应的神经网络分别经过81 465, 30 255, 72 620, 29 511和31 629次的训练才满足误差要求。
将测试组的样本数据输入到上述已经训练好的神经网络进行网络测试, 测试组的样本数据是轴承发生内圈故障时的数据, 即神经网络的理想输出为(0, 1, 0, 0), 5个网络的输出结果如表 2所示。
| 表 2 5个神经网络的输出结果 Table 2 Outputs of 5 neural networks |
利用式(14) (15)归一化表 2的结果得到各条证据的BPA值如表 3所示。
| 表 3 各条证据的基本概率分配值(改进前) Table 3 Basic probability assignment ofeachevidence (beforeimprovement) |
1) 计算各证据之间的相似系数dij。d12 =0.575 1, d13 =0.538 5, d14 =0.550 2, d15 =0.551 7, d23 =0.677 6, d24 =0.666 2, d25 =0.659 7, d34 =0.540 9, d35 =0.625 5, d45 =0.647 5。
2) 计算支持度S(mi)。
3) 得到各证据的可信度C (mi)。
| 表 4 各条证据的基本概率分配值(改进后) Table 4 Basic probability assignment ofeachevidence (afterimprovement) |
最后利用证据理论组合规则将5条证据进行融合, 将其中任意2条证据融合得到结果如表 5所示。
| 表 5 各故障模式的BPA值(融合任意2条证据) Table 5 BPA value for each failure mode (fusingany two pieces of evidence) |
将其中任意3条证据融合得到结果如表 6所示。
| 表 6 各故障模式的BPA值(融合任意3条证据) Table 6 BPA value for each failure mode (fusinganythree pieces ofevidence) |
将其中任意4条和5条证据融合得到结果如表 7所示。
| 表 7 各故障模式的BPA值(融合任意4条和5条证据) Table 7 BPA value for each failure mode (fusinganyfour pieces andfive pieces ofevidence) |
由表 3~7结果可以看出:1)仅仅用BP神经网络一种方法诊断发生轴承内圈故障的概率振动信号是61.08%, 温度信号是65.88%, 电流信号是64.41%, 转矩信号是62.92%, 转速信号是63.78%, 由于它们诊断准确率均小于70%, 不满足阈值要求, 据此所得诊断结果不具有参考性。此外, 其他状态的概率也较大, 如振动信号诊断结果认为正常状态的概率达到了24.24%, 外圈故障达到了13.90 %等, 温度信号诊断不确定状态的概率达到了12.41%。2)将其中任意2种信号采用D-S证据理论进行融合时的准确率振动 & 温度是88.63%, 振动 & 电流是86.29 %, 振动 & 转矩是87.39 %, 振动 & 转速是87.79 %, 温度 & 电流是92.87%, 温度 & 转矩是92.49 %, 温度 & 转速是92.42 %, 电流 & 转矩是90.51 %, 电流 & 转速是90.46 %, 转矩 & 转速是89.04 %, 2种信号融合准确率比任意一种信号的准确率有明显的提高, 准确率最高的是温度和电流信号的融合结果, 达到了92.87 %, 此外, 其他状态的概率明显降低, 尤其是不确定状态的概率降为0。3)将其中任意3种信号进行融合, 其结果如表 6所示, 诊断的准确率较融合2种信号进一步提高, 其他状态的概率进一步降低, 准确率最高的是温度、电流和转矩的融合, 结果达到了98.23%。4)将其中任意4种信号进行融合, 其结果如表 7所示, 诊断的准确率较融合3种信号进一步提高, 其他状态的概率进一步降低, 准确率最高的是温度、电流、转矩和转速的融合, 结果达到了99.55%。最后, 将5种信号进行融合, 诊断准确率达到了99.83%, 其他状态的概率几乎为0。
由于上述实例数据是在大量数据中随机抽取的, 且随后用1 000组测试数据输入到该诊断模型中得到的结果都有相同的趋势, 所以能够说明该风电机组齿轮箱轴承故障诊断模型的正确性。
4 结论笔者基于大数据技术, 挖掘风场SCADA系统中蕴含的信息, 将BP神经网络和改进的D-S证据理论相结合应用于风电机组齿轮箱轴承故障诊断, 两种方法串联, 优势互补, 将BP神经网络的输出作为证据理论的输入, 解决了证据理论构造基本概率赋值函数难的问题, 通过改进各条证据, 解决了各证据之间的冲突问题, 最后通过对某风场2 MW风电机组实际运行数据的实例分析, 得出以下几个结论:
1) 基于单一信号即只采用BP神经网络局部诊断结果不具有很强的参考性, 该研究所得准确率分别为:振动信号61.08%, 温度信号65.88%, 电流信号64.41%, 转矩信号62.92%, 转速信号63.78%。而且依据相关诊断决策准则无法得出诊断结果, 因此单独采用BP神经网络诊断出的效果不够理想。
2) 通过将其中2种、3种、4种和5种信号每进行一次融合, 实际故障的BPA值就进一步提高, 其他故障的BPA值就进一步降低, 使诊断结果更加准确, 最终实现了发电机组齿轮箱轴承故障的准确诊断, 融合多种信号的诊断准确率明显高于单一信号诊断的结果, 并且具有较强的诊断能力和可靠性。
3) 融合2种信号准确率最高的组合是温度和电流信号, 达到了92.87%, 融合3种信号准确率最高的组合是温度、电流和转矩, 达到了98.23%, 融合4种信号准确率最高的组合是温度、电流、转矩和转速, 达到了99.55%, 将5种信号全部融合的准确率达到了99.83%.
| [1] |
ChenJ L, Pa nJ, Li Z P. Generator bearingfault diagnosisfor windturbine via empirical wavelettransform using measured vibrationsignals[J]. Renewable Energy, 2016, 89: 80-92. DOI:10.1016/j.renene.2015.12.010 |
| [2] |
Tian Z G, Jin T D, Wu B R, et al. Condition based maintenance optimizationfor wind power generation systems under continuous monitoring[J]. Renewable Energy, 2011, 36(5): 1502-1509. DOI:10.1016/j.renene.2010.10.028 |
| [3] |
雷亚国, 何正嘉, 林京, 等. 行星齿轮箱故障诊断技术的研究进展[J]. 机械工程学报, 2011, 47(19): 59-67. LEI Yaguo, HE Zhengjia, LIN Jing, et al. Research advances of fault diagnosis technique for planetary gearboxes[J]. Journal of Mechanical Engineering, 2011, 47(19): 59-67. (in Chinese) |
| [4] |
Bangalore P, Tjernberg L B. Anartificial neural net work approach for earlyfault detectionof gear box bearings[J]. IEEE Transactions on Smart Grid, 2015, 6(2): 980-987. DOI:10.1109/TSG.2014.2386305 |
| [5] |
Gelman L, Murray B, Patel T H. Vibration diagnos tics of rolling bearings by no velnon linearnon-stationary wavelet bicohe rencetechnology[J]. Engineering Structures, 2014, 80: 514-520. DOI:10.1016/j.engstruct.2014.08.030 |
| [6] |
Jena D P, Panigrahi S N. Automatic gear and bearing fault localization using vibration and acoustic signals[J]. Applied Acoustics, 2015, 98: 20-33. DOI:10.1016/j.apacoust.2015.04.016 |
| [7] |
Janssens O, Schulz R, Slavkovikj V, et al. Thermal image based fault diagnosis for rotating machinery[J]. Infrared Physics & Technology, 2015, 73: 78-87. DOI:10.1016/j.infrared.2015.09.004 |
| [8] |
潘泉, 王增福, 梁彦, 等. 信息融合理论的基本方法与进展(Ⅱ)[J]. 控制理论与应用, 2012, 29(10): 1233-1244. PAN Quan, WANG Zengfu, LIANG Yan, et al. Basic methods and progress ofinformation fusion (Ⅱ)[J]. Control Theory & Applications, 2012, 29(10): 1233-1244. (in Chinese) |
| [9] |
Safizadeh M S, Latifi S K. Using multi-sensor data fusion for vibration fault diagnosis of rolling element bearings by accele rometerand loadcell[J]. Information Fusion, 2014, 18: 1-8. DOI:10.1016/j.inffus.2013.10.002 |
| [10] |
Xu C M, Zhang H, Peng D G. Study off ault diagnosis of integrate of D-S evidence theory base donneural network for turbine[J]. Energy Procedia, 2012, 16: 2027-2032. DOI:10.1016/j.egypro.2012.01.308 |
| [11] |
Li S B, Liu G K, Tang X H, et al. An ensemble deep convolutional neural network model withimproved D-S evidence fusionfor bearingfault diagnosis[J]. Sensors, 2017, 17(8): 1729. DOI:10.3390/s17081729 |
| [12] |
王致杰, 徐余法, 刘三明, 等. 大型风力发电机组状态监测与智能故障诊断[M]. 上海: 上海交通大学出版社, 2013. WANG Zhijie, XU Yufa, LIU Sanming, et al. State monitoring and intelligent fault diagnosis of large wind turbine[M]. Shanghai: ShanghaiJiao Tong University Press, 2013. (in Chinese) |
| [13] |
Xiang Z, Zhang X N, Zhang W W. Fault diagnosis of rolling bearing under fluctuating speed and variable loadbased on TCO Spectrum and Stacking Auto-encoder[J]. Measurement, 2019, 138: 162-174. DOI:10.1016/j.measurement.2019.01.063 |
| [14] |
冯新扬, 张巧荣, 李庆勇. 基于改进型深度网络数据融合的滚动轴承故障识别[J]. 重庆大学学报, 2019, 42(2): 52-62. FENG Xinyang, ZHANG Qiaorong, LI Qingyong. Faul trecognition of rolling bearing based on improved deep networks with data fusion in unbalanced data sets[J]. Journal of Chongqing University, 2019, 42(2): 52-62. (in Chinese) |
| [15] |
Eren L, Ince T, Kiranyaz S. A generic intelligent bearing fault diagnosis system using compact adaptive 1D CNN classifier[J]. Journal of Signal Processing Systems, 2019, 91(2): 179-189. DOI:10.1007/s11265-018-1378-3 |
| [16] |
Ren C, An N, WangJ Z. Optimal parameters selection for BP neural network based on particle swarm optimization: acase study of wind speed for ecasting[J]. Knowledge-Based Systems, 2014, 56: 226-239. DOI:10.1016/j.knosys.2013.11.015 |
| [17] |
柯炎, 樊波, 谢一静, 等. 基于小波包分析和Elman神经网络的军用电源智能故障诊断[J]. 重庆大学学报, 2019, 42(9): 67-73. KE Yan, FAN Bo, XIE Yijing. Fault diagnosis of military power based on wavelet packet analysis and Elmanneural network[J]. Journal of Chongqing University, 2019, 42(9): 67-73. (in Chinese) |
| [18] |
Quan H W, LiJ H, Peng D L. Multisensorfault diagnosis based on datafusion using D-Stheory[C/OL].Proceedings of the33rd Chinese Control Conference. Piscataway, NJ: IEEE, 2014(2014-09-15)[2020-03-02].https:∥doi.org/10.1109/ChiCC.2014.6896234.
|
| [19] |
Ye Q, Wu X P, Song Y X. Fault diagnosis method based on D-Stheory of evidence and AHP[C/OL]. 2006 6th World Congress on Intelligent Control and Automation. Piscataway, NJ: IEEE, 2006 (2006-10-23)[2020-04-25 ]. https:∥doi.org/10.1109/WCICA.2006.1714147.
|
| [20] |
Han XJ, Zhang X L, Chen F, etal. Faultdiagnosis methodcombining multi-relationindexes with D-Sevidencetheory[C/ OL]. 2011 IEEEInternational Conferenceon Automationand Logistics (ICAL). Piscataway, NJ: IEEE, 2011(2011-09- 23)[2020-03-02].https:∥doi.org/10.1109/ICAL.2011.6024690.
|
| [21] |
Jiang F, Li W, Wang Z Q, et al. Fault diagnosis of rotating machinery based on MFES and D-S evidence theory[C/ OL]. 2012 24th Chinese Controland Decision Conference (CCDC). Piscataway, NJ: IEEE, 2012(2012-07-19)[2020-03-02].https:∥doi.org/10.1109/CCDC.2012.6243014.
|
| [22] |
李松柏, 康子剑, 陶洁. 基于信息融合及堆栈降噪自编码的齿轮故障诊断[J]. 振动与冲击, 2019, 38(5): 216-221. LI Songbai, KANG Zijian, TAO Jie. Gear fault diagnosis based on information fusion and stacked de-noising autoencoder[J]. Journal of Vibrationand Shock, 2019, 38(5): 216-221. (in Chinese) |
| [23] |
Huang J P, Liu W Y, Sun X M. A pavement crack detection method combining 2D with 3D information based on dempster-shafertheory[J]. Computer-Aided Civil and Infrastructure Engineering, 2014, 29(4): 299-313. DOI:10.1111/mice.12041 |
| [24] |
Liu B. Three-dimensional aircraft recognition based on neural network and the D-S evidence theory[C/OL]. 2011 International Conference on Electrical and Control Engineering. Piscataway, NJ: IEEE, 2011 (2011-10-24)[2020-03- 02].https:∥doi.org/10.1109/ICECENG.2011.6058107.
|
| [25] |
向阳辉, 张干清, 庞佑霞. 结合SVM和改进证据理论的多信息融合故障诊断[J]. 振动与冲击, 2015, 34(13): 71-77. XIANG Yanghui, ZHANG Ganqing, PANG Youxia. Multi-information fusion fault diagnosis using SVM & improved evidencetheory[J]. Journal of Vibrationand Shock, 2015, 34(13): 71-77. (in Chinese) |
| [26] |
杨风暴, 王肖霞. D-S证据理论的冲突证据合成方法[M]. 北京: 国防工业出版社, 2010. YANG FengBao, WANG Xiaoxia. Combination method of conflictive evidences in D-S evidence theory[M]. Beijing: National DefenseIndustry Press, 2010. (in Chinese) |
| [27] |
李伟, 梁玉英, 朱赛. 基于神经网络和证据理论的信息融合在故障诊断中的应用[J]. 计算机测量与控制, 2012, 20(11): 2888-2890, 2893. LI Wei, LIANG Yuying, ZHU Sai. Fault diagnosis based on neural network and evidence theory information fusion[J]. Computer Measurement & Control, 2012, 20(11): 2888-2890, 2893. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43


