石灰石作为一种重要的工业原料, 在冶金、建筑、供电等行业都得到广泛的使用。特别在冶金行业石灰石分解产生CaO可较好地脱硫脱碳, 是转炉炼钢不可或缺的造渣材料。对于石灰石分解动力学研究不同的专家学者给出了不同的看法, 石灰石种类、粒度、反应环境以及研究方法的不同导致得到的反应机理完全不同[1-3]。一般认为石灰石为大颗粒时反应主要受热传递控制, 粒径为微米级时CO2传递逐渐占据主要控制地位, 当颗粒小至纳米级别时则化学反应速率变成主导因素[4]。
石灰石分解动力学研究方法很多, 如热重分析、等温和非等温结合分析, 从厘米至纳米级别, 从静态至动态至悬浮态和完全离散态。其中郑瑛等[5-6]认为石灰石(13.4 μm)分解机理可用收缩核解释, 机理为n =2/3形核生长过程。李辉[7]等发现, CO2浓度越高石灰石(44 μm)热分解活化能越高, 反应级数越大。Ar等[8]研究了10种不同的石灰石, 发现均符合收缩核模型, 且反应后气孔率变化很大。张丽娜等[9]提出900 μm石灰石热分解属于三维相边界反应模型。陈鸿伟等[10]认为温度是影响石灰石煅烧的关键因素, 温度越高, 反应越快; CO2分压和粒径增大对石灰石分解反应有一定抑制作用。
已报道的石灰石分解研究很多, 涉及的分解温度一般不超过1 200 ℃, 粒径小于10 mm, 且多采用动态法分析石灰石分解动力学, 但有关高温静态法(恒温)大颗粒石灰石分解的分析却较少[11-12]。在此背景下, 笔者对不同温度、不同时间以及不同物质传热下的高温大粒径石灰石分解动力学机理进行了研究, 探寻高温大粒径石灰石的分解机理及其影响因素之间的关系。
1 实验研究方法 1.1 实验原料实验选用石灰石来自湖北武汉江夏乌龙泉矿区, 化学成分见表 1。石灰石的主要成分为CaCO3, 其中含极少量的SiO2和MgO。荷兰Philips公司生产Nova400 Nano SEM型场发射扫描电镜BSED模式下石灰石晶粒排列情况见图 1。图中石灰石晶粒呈规则块状结构排列, 晶粒大小在1~4 μm, 晶粒之间紧密结合, 孔隙度接近0。

|
图 1 石灰石微观晶粒形貌(×10 000倍) Fig. 1 Micrograin morphology oflimestone |
| 表 1 乌龙泉矿区石灰石化学成分 Table 1 Chemical composition of limestone in Wulongquan mining area |
实验中石灰石加热使用上海全硕电炉有限公司QSH-CTF型高温立式加热碳管炉, 功率25 kW, 其加热温度上限可达1 700 ℃, 一般从下部连接热电偶测温, 并通入氮气做保护气体。
图 2(a)所示为模拟溅渣护炉时加入石灰石的分解反应。选取等量大颗粒石灰石(粒径4~8 mm、8~12 mm、12~15 mm、15~20 mm、20~25 mm), 装入与钼杆连接的钼丝网中, 在碳管炉内进行等温加热反应(1 200~1 500 ℃, 步长50 ℃)。钼杆上端连接电子天平和电脑, 记录存储实时质量。石灰石分解转率α可通过下式进行计算:
| $ a = \frac{{{w_0} - {w_1}}}{{{w_0} - {w_a}}} \times 100\% , $ | (1) |
式中:w0为石灰石试样的初始质量, wt为反应时间为t时石灰石试样的质量, wa表示完全反应后试样的剩余质量。天平记录质量为石灰石、钼杆与钼丝吊篮的总质量。
图 2(b)所示为模拟开吹时加入石灰石的分解反应。选取圆柱状石灰石(直径15 mm)与钼杆连接在高温(1 500 ℃和1 550 ℃)转炉渣中动态旋转不同时间进行试验。钼杆上接旋转电机, 可调节钼杆转数大小。反应后取出剩余试样, 截取横断面, 根据横断面生成氧化钙的半径来计算反应转化率α。
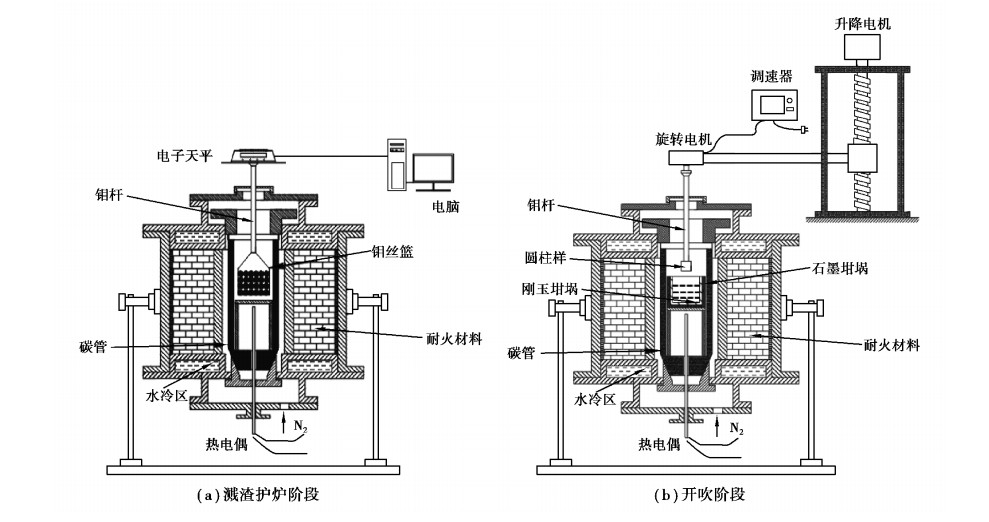
|
图 2 模拟炼钢不同阶段石灰石分解反应实验装置 Fig. 2 Experimental device for simulating limestone decomposition reactionin differentstages of BOF (basic oxygenfurnace) |
许多专家学者对CaCO3分解过程进行了研究分类[13-16], 一般分为5个步骤(图 3) :
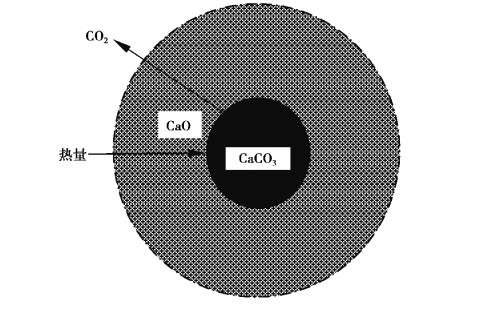
|
图 3 CaCO3分解过程 Fig. 3 CaCO3 decomposition process |
1) 热量由外部环境传递到CaO表面, 并继续向内传递;
2) 热量由CaO层向内传递, 至未反应CaCO3表面;
3) CaCO3吸收足够热量产生分解反应;
4) 分解反应产生的CO2穿过CaO层;
5) CO2在CaO外的扩散。
2.2 CaCO3分解速度影响因子 2.2.1 传质限速环节石灰石模型建立假设石灰石均为球状颗粒, 且反应过程中石灰石的大小不变, 但反应界面逐渐向内推进, 则可列出以下关系式:
CO2生成速率:
| $ {N_1} = 4{\rm{\pi }}r_{\rm{c}}^2{k_{\rm{r}}}\left( {{C^*} - {C_{\rm{c}}}} \right)。$ | (2) |
CO2产物层扩散速率:
| $ {N_2} = - 4{\rm{\pi }}{r^2}\frac{{{\rm{d}}C}}{{{\rm{d}}r}}{D_{\rm{e}}}。$ | (3) |
CO2向外扩散速率:
| $ {N_3} = 4{\rm{\pi }}r_0^2{k_{\rm{g}}}\left( {{C_{\rm{s}}} - {C_{\rm{b}}}} \right)。$ | (4) |
假设准稳态:
| $ N = {N_1} = {N_2} = {N_3}。$ | (5) |
球状石灰石转化率α :
| $ a = 1 - {\left( {\frac{{{r_{\rm{c}}}}}{{{r_0}}}} \right)^3}。$ | (6) |
式中:rc为球形石灰石未反应核半径, m; kr为反应速率常数, m/s; C *为CO2平衡浓度, mol/m3; Cc为反应界面CO2浓度, mol/m3; r为产物层半径, m; C为产物层半径r处的CO2的浓度, mol/m3; De为CO2在产物层内的有效扩散系数, m2/s; r0为CaCO3初始颗粒半径, m; kg为CO2的传质系数, m/s; Cs为颗粒表面CO2浓度, mol/m3; Cb为环境中CO2浓度, mol/m3。
合并式(2) ~(6)并计算可得石灰石转化率α和时间t之间的关系:
| $ t = \frac{{{r_0}\rho {\rm{CaC}}{{\rm{O}}_3}}}{{{k_{\rm{r}}}\left( {{C^*} - {C_{\rm{b}}}} \right)}}\left\{ {\left[ {1 - {{\left( {1 - a} \right)}^{1/3}}} \right] + \frac{{{k_{\rm{r}}}{r_0}}}{{6{D_{\rm{e}}}}}\left[ {1 - 3{{\left( {1 - a} \right)}^{2/3}} + 2\left( {1 - a} \right)} \right] + \frac{{{k_{\rm{r}}}}}{{3{k_{\rm{g}}}}}a} \right\}。$ | (7) |
式中ρCaCO3为体积为1 m3的CaCO3的摩尔数, mol/m3。
界面反应限速时:
| $ t = \frac{{{r_0}\rho {\rm{CaC}}{{\rm{O}}_3}}}{{{k_{\rm{r}}}\left( {{C^*} - {C_{\rm{b}}}} \right)}}\left[ {1 - {{\left( {1 - a} \right)}^{1/3}}} \right]。$ | (8) |
CO2扩散限速时:
| $ t = \frac{{r_0^2\rho {\rm{CaC}}{{\rm{O}}_3}}}{{6{D_{\rm{e}}}\left( {{C^*} - {C_{\rm{b}}}} \right)}}\left[ {1 - 3{{\left( {1 - a} \right)}^{2/3}} + 2\left( {1 - a} \right)} \right]。$ | (9) |
当考虑球状石灰石分解传热为限制环节时, 传热速度之间存在以下关系:
表面传热速度:
| $ {Q_{\rm{c}}} = 4{\rm{\pi }}r_0^2h\left( {{T_{\rm{b}}} - {T_{\rm{s}}}} \right), $ | (10) |
产物层内导热速度:
| $ {Q_{\rm{d}}} = 4{\rm{\pi }}{r^2}{\lambda _{\rm{e}}}\frac{{{\rm{d}}T}}{{{\rm{d}}r}}, $ | (11) |
界面吸热速度:
| $ {Q_{\rm{r}}} = \left( { - 4{\rm{\pi }}r_{\rm{c}}^2\rho {\rm{CaC}}{{\rm{O}}_3}\frac{{{\rm{d}}{r_{\rm{c}}}}}{{{\rm{d}}t}}} \right)\Delta H, $ | (12) |
准稳态:
| $ {\rm{ }}{{\rm{Q}}_{\rm{c}}}{\rm{ = }}{{\rm{Q}}_{\rm{d}}}{\rm{ = }}{{\rm{Q}}_{\rm{r}}}{\rm{ = Q,}} $ | (13) |
式中:T为温度, K; h为传热系数, W/(m2 · K); Tb为气相主体温度, K; Ts为CaCO3表面温度, K; λe为固体产物层有效导热系数, W/(m· K); Tc为反应界面温度, K; rc为球形石灰石未反应核半径, m; ΔH为生成1 mol CO2所吸收的热量, J/mol。
合并式(6)和式(10) ~(13)并计算可得石灰石转化率和时间之间的关系:
| $ t = \frac{{\Delta H\rho {\rm{CaC}}{{\rm{O}}_3}{r_0}}}{{6h\left( {{T_{\rm{b}}} - {T_{\rm{c}}}} \right)}}\left\{ {\left[ {2a + \frac{{h{r_0}}}{{{\lambda _{\rm{e}}}}}3{{\left( {1 - a} \right)}^{2/3}} + 2\left( {1 - a} \right)} \right]} \right\}。$ | (14) |
表面传热限速:
| $ t = \frac{{\Delta H\rho {\rm{CaC}}{{\rm{O}}_3}{r_0}}}{{3h\left( {{T_{\rm{b}}} - {T_{\rm{c}}}} \right)}}a, $ | (15) |
产物层导热限速:
| $ t = \frac{{\Delta H\rho {\rm{CaC}}{{\rm{O}}_3}r_0^2}}{{6{\lambda _{\rm{e}}}\left( {{T_{\rm{b}}} - {T_{\rm{c}}}} \right)}}\left[ {1 - 3{{\left( {1 - a} \right)}^{2/3}} + 2\left( {1 - a} \right)} \right]。$ | (16) |
模拟开吹后分批次将石灰石投入转炉的分解动力学模型见图 4, 此时转炉中石灰石与熔融态的炉渣接触, 高温迅速分解, 释放出大量的CO2向外逸出[17-18]。
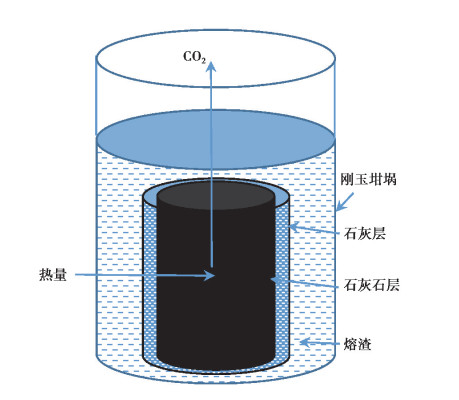
|
图 4 石灰石在转炉渣中分解模型 Fig. 4 Model oflimestone decompositionin BOFslag |
同理参考2.2.1得传质限速时转化率和时间的关系:
| $ t = \frac{{{r_0}\rho {\rm{CaC}}{{\rm{O}}_3}}}{{{k_{\rm{r}}}\left( {{C^*} - {C_{\rm{b}}}} \right)}}\left\{ {\left[ {1 - {{\left( {1 - a} \right)}^{1/2}} + \frac{{{k_{\rm{r}}}{r_0}}}{{4{D_{\rm{e}}}}}\left[ {a + \left( {1 - a} \right)\ln \left( {1 - a} \right)} \right] + \frac{{{k_{\rm{r}}}{r_0}a}}{{2{k_{\rm{g}}}}}} \right]} \right\}。$ | (17) |
界面化学反应限速:
| $ t = \frac{{{r_0}\rho {\rm{CaC}}{{\rm{O}}_3}}}{{{k_{\rm{r}}}\left( {{C^*} - {C_{\rm{b}}}} \right)}}\left[ {1 - {{\left( {1 - a} \right)}^{1/2}}} \right]。$ | (18) |
CO2扩散限速:
| $ t = \frac{{r_0^2\rho {\rm{CaC}}{{\rm{O}}_3}}}{{4{D_{\rm{e}}}\left( {{C^*} - {C_{\rm{b}}}} \right)}}\left[ {a + \left( {1 - a} \right)\ln \left( {1 - a} \right)} \right]。$ | (19) |
CO2传质限速:
| $ t = \frac{{2r_0^2\rho {\rm{CaC}}{{\rm{O}}_3}}}{{{k_{\rm{g}}}\left( {{C^*} - {C_{\rm{b}}}} \right)}}a。$ | (20) |
采用2.2.2节的方法可计算出转炉渣中圆柱石灰石在传热限速时转化率与时间的关系:
| $ t = \frac{{\Delta H\rho {\rm{CaC}}{{\rm{O}}_3}}}{{\left( {{T_{\rm{b}}} - {T_{\rm{c}}}} \right)}}\left\{ {\frac{{{r_0}a}}{{2h}} + \frac{{r_0^2\left[ {\left( {1 - a} \right)\ln \left( {1 - a} \right) + a} \right]}}{{4{\lambda _{\rm{e}}}}}} \right\}。$ | (21) |
石灰石与熔渣传热限速:
| $ t = \frac{{\Delta H\rho {\rm{CaC}}{{\rm{O}}_3}{r_0}}}{{2h\left( {{T_{\rm{b}}} - {T_{\rm{c}}}} \right)}}a。$ | (22) |
产物层导热限速:
| $ t = \frac{{\Delta H\rho {\rm{CaC}}{{\rm{O}}_3}r_0^2}}{{4{\lambda _{\rm{e}}}\left( {{T_{\rm{b}}} - {T_{\rm{c}}}} \right)}}\left[ {\left( {1 - a} \right)\ln \left( {1 - a} \right) + a} \right]。$ | (23) |
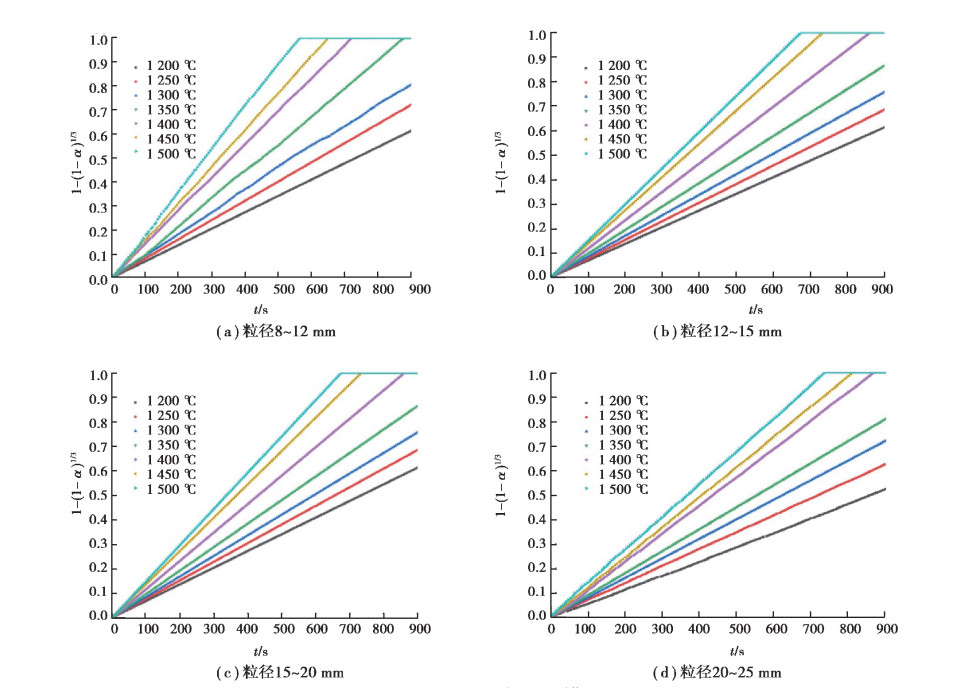
以4~8 mm粒径石灰石为例, 分别在CO2扩散、表面传热、产物层传热和界面化学反应控速4种情况下对其高温分解数据进行处理, 通过观察图 5曲线形状知界面化学反应控速情况下其影响因子1- (1-α )1/3和时间t具有较好的线性关系。进一步分析了8~25 mm粒径界面化学反应控速曲线(见图 6)发现均具有很好的线性关系。所以在此情况下, 界面化学反应为控速环节, 故可使用与界面反应相关的活化能来表征此种动力学模型。
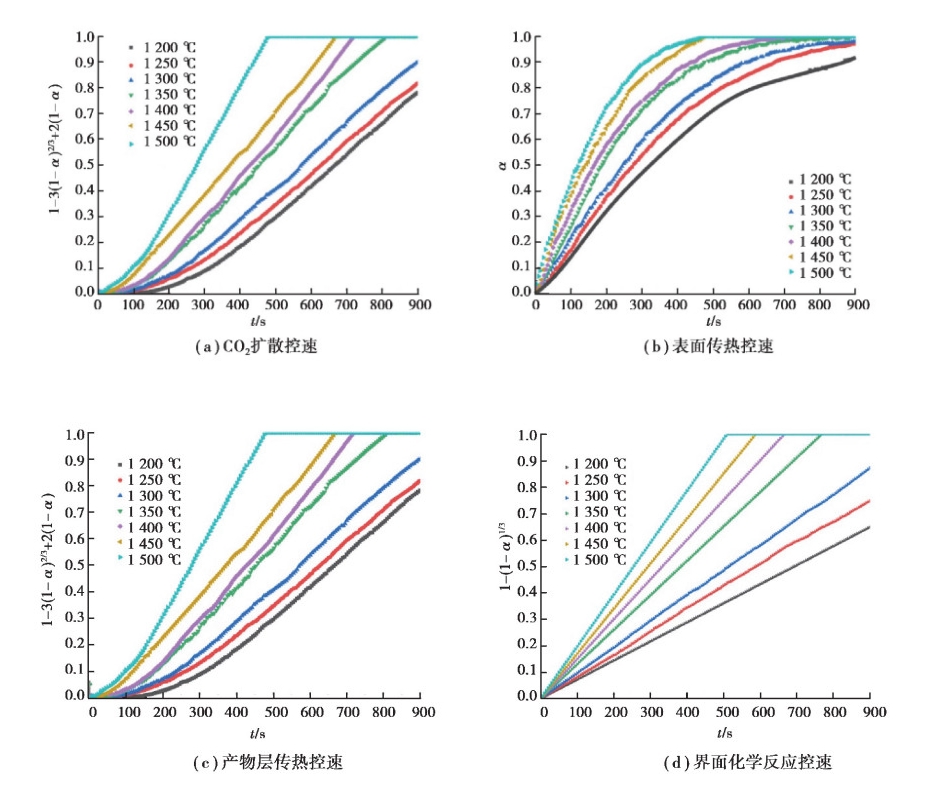
|
图 5 粒径4~8 mm石灰石分解不同环节控速曲线 Fig. 5 Curve of 4~8 mm size limestone decomposition by differentrate-determining step |
|
图 6 粒径8~25 mm石灰石界面化学反应控速曲线 Fig. 6 Interfacial chemical-reaction-speedcontrol curves of8~25 mmsizelimestone |
由阿伦尼乌斯方程
| $ \frac{{{\rm{d}}a}}{{{\mathop{\rm d}\nolimits} t}} = A\exp \left( { - \frac{E}{{RT}}} \right)f\left( a \right), $ | (24) |
| $ G\left( a \right) = \int_0^a {\frac{{{\rm{d}}a}}{{f\left( a \right)}}} 。$ | (25) |
式中:k为速率常数; A为指前因子; E 为活化能; R 为摩尔气体常量, 取8.314 J/(mol· K); f (α)为微分机理函数; G (α)为积分机理函数。
将积分方程式(25)转化为
| $ G\left( a \right) = \int_0^t {A\exp \left( { - \frac{E}{{RT}}{\rm{d}}t} \right)} = kt。$ | (26) |
当CaCO3恒温分解时, 速率常数k为定值, 其f (α)和G (α)是可分离的, 采用模式配合法(modelfittingmethod) [19]可分别求出动力学三因子G (α)、E、A :
1) 根据CaCO3反应机理在常用的动力学机理函数表(见表 2)中选择可能的机理函数G (α)若干组。
| 表 2 常见的动力学机理函数列表 Table 2 Common kinetic mechanism functions |
2) 在一条等温的α-t曲线上选取一组α, t值代入选取的G (α)中, G (α) -t为一条直线, 其斜率为k, 选取线性最佳的G (α)作为最概然机理函数。
3) 在不同温度下使用同一方法可得一组k值, 根据公式lnk = -mE/(RT) +ln A, 由其斜率和截距可分别求得E和A 值。其中m为校正经验参数, 保证活化能在一定范围内适用。
根据已知常用动力学机理函数[20], 选取较适合CaCO3 分解的几种动力学函数作为可能的最概然机理函数进行分析。
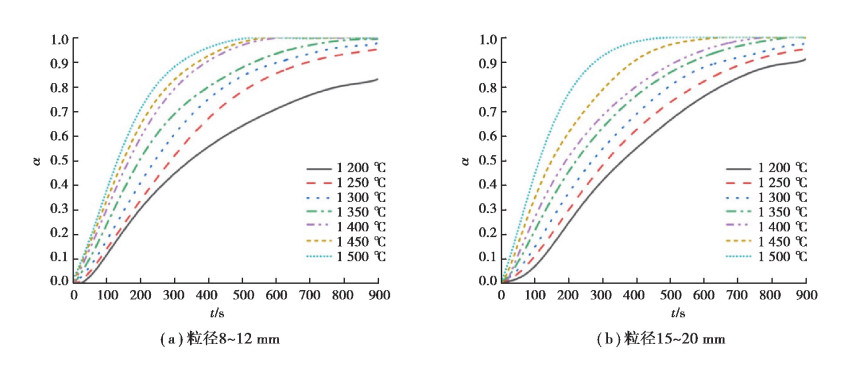
图 7为粒径8~12 mm与15~20 mm石灰石分解转化率与时间的关系图。由图 7知随时间推进, 石灰石的转化率α不断变大, 直至最大值1。其增幅先增后减, 最小值为0。温度越高, 相同反应时间石灰石转化率α越大。粒径越大, 相同反应时间石灰石转化率α越小, 反应完全用时越长。使用origin2017对表 2中共计20种机理函数G (α)分别做不同粒径的G (α) -t曲线, 对比研究得出不同粒径相关系数值较高的3种模式为Avrami-Erofeev(A E)成核(n =2/3)、A E成核(n =3/4)与收缩球体。需在3种模式中继续甄选出最概然函数。其中8~12 mm和15~20 mm粒径相关机理函数列表见表 3和表 4。
|
图 7 大粒径石灰石分解转化率α与时间t的关系 Fig. 7 Dependence of decomposition conversion ratioo flimestone with large particlesize ontime |
| 表 3 粒径8~12 mm石灰石拟合度较高3种机理函数相关系数与k值 Table 3 Correlation coefficient and k ofthree mechanism functions with higher fitgoodness for 8 mmto12 mmlimestone |
| 表 4 粒径15~20 mm石灰石拟合度较高3种机理函数相关系数与k值 Table 4 Correlation coefficient and k ofthree mechanismfunctions with higher fitgoodness for 15 mm to 20 mm limestone |
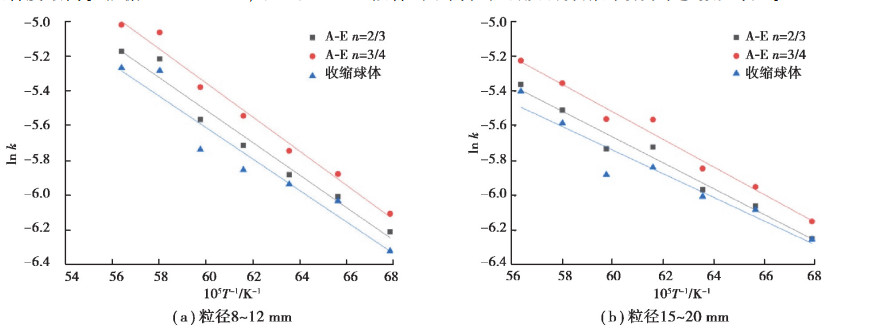
根据表 3、表 4分别作出不同粒径3种积分函数情况下lnk和1/T的关系图, 见图 8。选取线性条件最好的积分函数做最概然函数, 确定活化能E的大小及指前因子A 的值。图 8(a)与图 8(b)中可见A En =3/4的lnk和1/T线性拟合相关度最好。说明这种情况下石灰石分解反应符合随机成核和随后生长模型。经过统计分析4~25 mm性拟合度最高。根据lnk = -mE/(RT ) +ln A拟合出不同粒径石灰石分解的动力学参数见表 5。
|
图 8 不同粒径石灰石3种机理模式拟合结果 Fig. 8 Fittingresults ofthree mechanism modelforlimestone ofdifferentsizes |
| 表 5 不同粒径石灰石动力学参数表 Table 5 The dynamics parameters oflimestone with different sizes |
根据lnk = -mE/(RT) +ln A, 当k与A值恒定, 可求得在此情况下不同温度的活化能值。
相比粉末状、微米及纳米级别, 粒状石灰石随粒径增加, 传质、传热将受到很大阻碍。所以大颗粒石灰石分解符合随机成核逐层分解模型, 颗粒越大, 反应阻力越大。
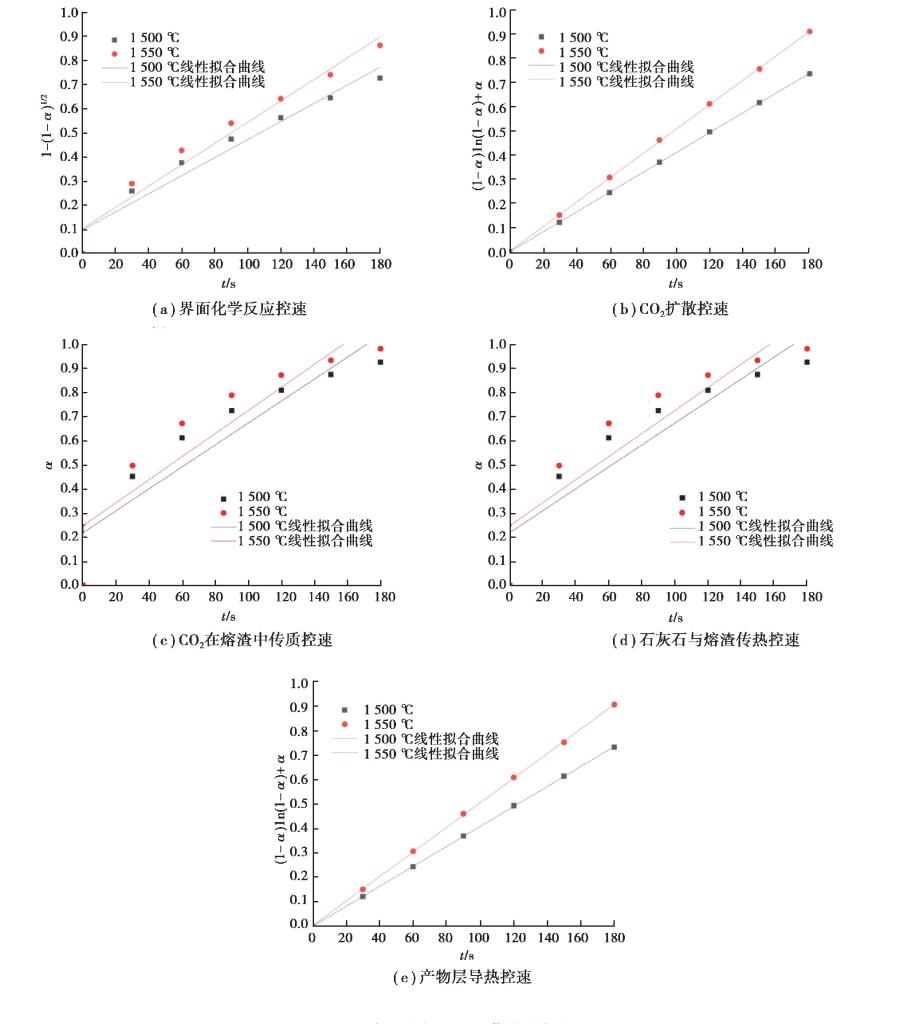
3.2 模拟炼钢开吹阶段石灰石分解反应 3.2.1 开吹阶段石灰石分解限速环节确定统计分析实验结果, 使用2.3中的方法分别对石灰石传热与传质中5种不同控速环节进行拟合分析(见图 9和表 6), 结果表明产物层导热控速和CO2扩散控速时线性拟合度较高, 其相关系数值均达到0.999, 说明此种情况下石灰石在转炉渣中分解受产物层传热与CO2扩散共同控制。
| 表 6 不同环节控速线性拟合相关系数与k值 Table 6 Correlation coefficient and k of linear fitting for different speed control steps |
|
图 9 石灰石分解不同环节控速曲线 Fig. 9 Curves of limest one decomposition for different speed control steps |
在产物层传热与CO2扩散共同控速条件下, 开吹阶段圆柱状石灰石分解时间和转化率之间的关系与产物层传热控速相同, 用式(23)表示。
气相主体温度为Tb=25 ℃, 界面反应温度Tc =1 500 ℃或1 550 ℃, ρCaCO3 =29 300 mol/m3, 生成1 molCO2吸收热量176 000 J/mol, r0 =7.5 mm, 可通过当前温度下的斜率求得此温度下石灰石的导热系数。
转化率与时间的关系在1 500 ℃时为
| $ \left( {1 - a} \right)\ln \left( {1 - a} \right) + a = 4.07 \times {10^{ - 3}}t, $ | (27) |
在1 550 ℃时为
| $ \left( {1 - a} \right)\ln \left( {1 - a} \right) + a = 5.01 \times {10^{ - 3}}t。$ | (28) |
柱状石灰石在转炉渣中分解时, 首先在外部随机成核, 表面部分石灰石先反应, 形成具有一定气孔的石灰层, 产物层由于气孔率较大, 很容易将热量带入石灰石内部, 故初期石灰石反应剧烈, 反应速度较快。但随着反应进行, 反应界面会聚集越来越多的CO2, 较多的CO2 会抑制分解反应正向进行。随着CO2浓度增加, 其分压也不断变大, 所以会逐渐向外扩散, 温度越高, 其扩散速率也越大, 直至分解完成。
3.3 微观形貌分析图 10为模拟炼钢开吹阶段和溅渣护炉阶段石灰石分解的微观形貌剖面图。图 10(a)中反应后石灰石晶粒间存在大量的孔洞, 是因为高温时石灰石急速分解, 瞬间产生大量的CO2气体, CO2 需向内外扩散, 导致石灰石内部压力增大, 气体冲击形成孔洞。图 10(b)石灰石整体浸入转炉渣中反应, 故石灰石表面存在大量的转炉渣。炉渣从石灰石表面晶界渗入, 外层包裹CaCO3并从CaCO3晶间向内推进反应, 所以图中石灰石晶粒较光滑圆润。开吹阶段和溅渣护炉阶段石灰石高温分解过程中的“团聚”[21]现象表现不同。在开吹阶段气体氛围传热均匀, 效果较好, 晶粒尺寸相差不大, “团聚”效果不明显。石灰石在转炉渣中分解时, 表面随机成核, 出现不规则孔洞, 渣沿孔洞渗入, 与CaO反应生成致密硅酸钙层, 阻碍反应进行, 导致不同位置传热效果偏差较大, 出现尺寸相差较大的晶粒, “团聚”效果明显。

|
图 10 模拟炼钢不同阶段石灰石分解微观形貌 Fig. 10 Microstructure oflimestone decomposition in simulated different steel-making stage |
对大粒径石灰石高温分解反应的动力学进行了研究, 发现了以下规律:
1) 大粒径石灰石转化率随粒径增加减小, 随温度升高变大。
2) 模拟溅渣护炉阶段大粒径石灰石高温分解的限速环节为界面化学反应, 满足随机成核与随后生长模式(A - E), 最概然函数积分式为G (α) = [-ln(1-α)]n (n =3/4)。
3) 模拟开吹阶段大粒径石灰石高温分解的限速环节为产物层传热与CO2扩散, 可用下式表示时间和转化率之间的关系:
| $ \left( {1 - a} \right)\ln \left( {1 - a} \right) + a = \frac{k}{{r_0^2}}t。$ |
4) 石灰石分解过程中存在“团聚”现象, 影响石灰石分解速率; 由于界面CO2聚集及致密硅酸钙层阻碍其扩散, 转炉渣中石灰石分解“团聚”现象更严重。
| [1] |
王俊杰, 颜碧兰, 汪澜, 等. 高温悬浮态下碳酸钙分解反应动力学的研究[J]. 武汉理工大学学报, 2013, 35(5): 41-44. WANG Junjie, YAN Bilan, WANG Lan, et al. Research on the decomposing kinetics of calcium carbonate under high temperature and suspension state[J]. Journal of Wuhan Universityof Technology, 2013, 35(5): 41-44. (in Chinese) |
| [2] |
张保生, 刘建忠, 周俊虎, 等. 基于无模式法推断石灰石分解机理新方法[J]. 化工学报, 2007, 58(5): 1204-1209. ZHANG Baosheng, LIU Jianzhong, ZHOU Junhu, et al. New model-free method based approach to mechanism of limestone decomposition[J]. Journal of Chemical Industry and Engineering (China), 2007, 58(5): 1204-1209. (in Chinese) |
| [3] |
王世杰, 陆继东, 周琥, 等. 石灰石颗粒分解的动力学模型研究[J]. 工程热物理学报, 2003, 24(4): 699-702. WANG Shijie, LU Jidong, ZHOU Hu, et al. Kinetic model study on thermal decomposition of limestone particles[J]. Journal of Engineering Thermophysics, 2003, 24(4): 699-702. (in Chinese) |
| [4] |
冯云, 陈延信. 碳酸钙的分解动力学研究进展[J]. 硅酸盐通报, 2006, 25(3): 140-145,154. FENG Yun, CHEN Yanxin. Development of research on calcium carbonate for decomposed kinetics[J]. Bulletin of the Chinese Ceramic Society, 2006, 25(3): 140-145, 154. (in Chinese) |
| [5] |
郑瑛, 陈小华, 周英彪, 等. CaCO3分解机理和动力学参数的研究[J]. 华中科技大学学报(自然科学版), 2002, 30(12): 86-88. ZHENG Ying, CHEN Xiaohua, ZHOU Yingbiao, et al. The decomposition mechanism of CaCO3 and its kinetics parameters[J]. Journal of Huazhong Universityof Scienceand Technology, 2002, 30(12): 86-88. (in Chinese) |
| [6] |
郑瑛, 陈小华, 郑楚光. CaCO3分解机理的研究[J]. 动力工程, 2004, 24(2): 280-284. ZHENG Ying, CHEN Xiaohua, ZHENG Chuguang. Research on the decomposition mechanism of CaCO3[J]. Power Engineering, 2004, 24(2): 280-284. (in Chinese) |
| [7] |
李辉, 张乐乐, 段永华, 等. 高二氧化碳浓度下石灰石的热分解反应动力学[J]. 硅酸盐学报, 2013, 41(5): 637-643. LI Hui, ZHANG Lele, DUAN Yonghua, et al. Kinetics of thermal decomposition reaction of limestone at high carbon dioxide concentration[J]. Journal of the Chinese Ceramic Society, 2013, 41(5): 637-643. (in Chinese) |
| [8] |
A rī, Do gu G. Calcination kinetics of high purity limestones[J]. [Chemical Engineering Journal, 2001, 83(2): 131-137. |
| [9] |
张利娜, 袁章福, 李林山, 等. 石灰石热分解动力学研究[J]. 有色金属科学与工程, 2016, 7(6): 13-18. ZHANG LIna, YUAN zhangfu, LI linshan, et al. Model research of thermal decomposition kinetics of limestone[J]. Nonferrous Metals Scienceand Engineering, 2016, 7(6): 13-18. (in Chinese) |
| [10] |
陈鸿伟, 陈江涛, 危日光, 等. 石灰石分解特性及微观结构迁移规律研究[J]. 热能动力工程, 2013, 28(1): 73-77. CHEN Hongwei, CHEN Jiangtao, WEI Riguang, et al. Study on decomposition characteristics and microstructure migration of limestone[J]. Journal of Engineeringfor Thermal Energyand Power, 2013, 28(1): 73-77. (in Chinese) |
| [11] |
张廷安, 豆志河. 宏观动力学研究方法[M]. 北京: 化学工业出版社, 2014: 66-97. ZHANG Ting'an, DOU Zhihe. Research methods for macrokinetics[M]. Beijing: Chemical Industry Press, 2014: 66-97. (in Chinese) |
| [12] |
唐彪.石灰石用于转炉炼钢的基础研究[D].沈阳: 东北大学, 2015: 57-99. TANG Biao. Fundamental studyon application of limestonein BOF steelmaking[D]. Shenyang: Northeastern University, 2015: 57-99. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10145-1018079446.htm |
| [13] |
王雨, 郭戌, 谢兵, 等. 转炉脱磷炉渣中石灰溶解的动力学[J]. 钢铁研究学报, 2011, 23(5): 8-10,33. WANG Yu, GUO Xu, XIE Bing. WANG Yu, GUO Xu, XIE Bing, etal. Dissolution kinetics of limein the slag of converter dephosphorization[J]. Journal of Ironand Steel Research, 2011, 23(5): 8-10,13. (in Chinese) |
| [14] |
郑瑛, 陈小华, 周英彪, 等. CaCO3分解动力学的热重研究[J]. 华中科技大学学报(自然科学版), 2002, 30(8): 71-72. ZHENG Ying, CHEN Xiaohua, ZHOU Yingbiao, et al. The thermogravimetric study on kinetics of decomposition of calciumcarbonate[J]. Journal of Huazhong Universityof Scienceand Technology, 2002, 30(8): 71-72. (in Chinese) |
| [15] |
Deng T F, Nortier P, Ek M, et al. Limestone dissolutionin converter slag at 1873 K (1600 ℃)[J]. [Metallurgical and Materials Transactions B, 2013, 44(1): 98-105. DOI:10.1007/s11663-012-9761-0 |
| [16] |
陈凯锋, 薛正良, 李建立. 高温煅烧下快速加热石灰石的热分解反应动力学[J]. 硅酸盐学报, 2016, 44(5): 754-762. CHEN Kaifeng, XUE Zhengliang, LI Jianli. Kinetics of thermal decomposition reaction of limestone for flash heating of limestone at high temperature[J]. Journal ofthe Chinese Ceramic Society, 2016, 44(5): 754-762. (in Chinese) |
| [17] |
Wang N, Zhang GZ, Chen M, et al. Decomposition behavior of limestone inearly converter slag[J]. Powder Technology, 2017, 320: 73-79. DOI:10.1016/j.powtec.2017.07.037 |
| [18] |
Lu H, Li C X, Mao W W, et al. Laboratory study of CaCO3 decomposition, influence of BOF converter slag[J]. Metallurgical Research & Technology, 2017, 114(1): 15-18. |
| [19] |
Vyazovkin S, Wight C A. Isothermal and non-isothermal kinetics of thermally stimulated reactions of solids[J]. International Reviewsin Physical Chemistry, 1998, 17(3): 407-433. DOI:10.1080/014423598230108 |
| [20] |
胡荣祖, 高胜利, 赵凤起. 热分析动力学[M]. 北京: 科学出版社, 2008: 148-155. HU Rongzu, GAO Shengli, ZHAO Fengqi. Thermal analysis kinetics[M]. Beijing: Science Press, 2008: 148-155. (in Chinese) |
| [21] |
尚建宇, 王松岭, 王春波, 等. 煅烧石灰石过程中团聚体颗粒内的晶粒融合现象分析[J]. 中国电机工程学报, 2010, 30(14): 44-49. SHANG Jianyu, WANG Songling, WANG Chunbo. The grain amalgamation phenomenon and itsinfluence within calcination limestone aggregate particle[J]. Proceedings ofthe CSEE, 2010, 30(14): 44-49. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43


