Büttiker等[1]在1983年预言了静态磁场在孤立的介观金属环中会产生持续的电流。随后Chandrasekhar等[2]在1991年首次在实验中观测到了周期为Ф0的磁通中孤立环里的持续电流。该持续电流不仅仅存在于介观金属环内, 还广泛存在于其他环形[3-4]和圆柱形[5]体系中, 比如石墨烯纳米环[6-7]、环状碳纳米管[8]、碳纳米管[9]和多壁碳纳米管[10]等量子体系。准一维纳米材料碳纳米卷[11-12]在理论上也可以弯曲后首尾相接, 成封闭的环状碳纳米卷(toroidal carbon nanoscrolls, TCNS), 该环状体系中的持续电流目前很少有相关理论研究及报道。
笔者在TCNS紧束缚模型基础上, 采用数值计算的方法系统地研究了扶手椅(armchair)型和锯齿(zigzag)型2种TCNS(即TACNS和TZCNS)的持续电流, 并详细地讨论了TCNS的几何结构、分离能级、温度及塞曼效应对持续电流的影响, 得到了一些有意义的结论, 为TCNS的实验研究提供理论基础。
1 前言TCNS横截面内卷环结构可以用阿基米德螺线ρ =raφ +r[13]描述, 式中:ρ为极径; ra为阿基米德螺旋线系数; φ为极角; r为卷的最内圈半径。当TCNS的尺寸比较大时, 可以忽略卷曲效应, 只考虑成键π轨道和反成键π *轨道。根据二维石墨烯能量色散关系[13], 考虑卷口及磁场中卷环的圆周方向上的周期性边界条件[13-15] :k · Ch=2πj -θ, k · Ct=2π(l +Φ/Φ0) (其中卷口圆周矢量Ch =ma1 +na2, 卷环圆周矢量Ct = pa1 +qa2, 这里m, n, p, q均为整数, 常用来表征TCNS; a1, a2为石墨烯蜂窝点阵单位矢量; θ为结构参数; Φ为磁通量; k为波矢)可推导出磁场中高对称的锯齿型TZCNS(m, 0, p, -2p)和扶手椅型TACNS(m, m, p, -p)的能量色散关系[16]分别为:
| $ E(j,l,\Phi ,\theta ) = \pm {\gamma _0}{\left\{ {1 \pm 4{\rm{cos}}\left[ {\frac{{\pi (l + \frac{\Phi }{{{\Phi _0}}})}}{p}} \right] \cdot {\rm{cos}}\left[ {\frac{{\pi (j - \frac{\theta }{{2\pi }})}}{m}} \right] + 4{\rm{co}}{{\rm{s}}^2}\left[ {\frac{{\pi (j - \frac{\theta }{{2\pi }})}}{m}} \right]} \right\}^{\frac{1}{2}}}, $ | (1) |
| $ E(j,l,\Phi ,\theta ) = \pm {\gamma _0}{\left\{ {1 \pm 4{\rm{cos}}\left[ {\frac{{\pi (l + \frac{\Phi }{{{\Phi _0}}})}}{p}} \right] \cdot {\rm{cos}}\left[ {\frac{{\pi (j - \frac{\theta }{{2\pi }})}}{m}} \right] + 4{\rm{co}}{{\rm{s}}^2}\left[ {\frac{{\pi (l + \frac{\Phi }{{{\Phi _0}}})}}{p}} \right]} \right\}^{\frac{1}{2}}}, $ | (2) |
式中:γ0约等于3.033 eV, 表示最近邻的跃迁积分; Ф0 = h/e, 这里h为普朗克常数, e为电子电荷; (j, l)为电子状态指数, j =1, 2, …, 2m, l =1, 2, …, 2p。显然, E (j, l, Ф/Ф0, θ) =E (j, l -1, Ф/Ф0 +1, θ), 即E (j, l, Ф, θ)是以Ф0为周期随Ф变化的周期性函数, 所以后面关于持续电流的讨论就可以限定在一个周期内。
|
图 1 均匀磁场B中的环状碳纳米卷 Fig. 1 Troidal carbon nanoscrolls in the uniform magnetic field B |
根据式(1)和(2)可以直接计算TZCNS和TACNS内总的持续电流[8, 17] :
| $ I(\Phi , T) = - \sum\limits_{j, l} {f\left[ {E\left( {j, l, \Phi , \theta } \right)} \right]} \cdot{i_{j, l}}, $ | (3) |
T为温度;
| $ {i_{j, l}}\begin{array}{*{20}{l}} { = - } \end{array}\frac{{\partial E\left( {j, l, \begin{array}{*{20}{l}} \Phi \end{array}, \theta } \right)}}{{\partial \Phi }}。$ | (4) |
将式(1)和(2)带入式(4)可得:
| $ \frac{{\begin{array}{*{20}{l}} {\partial E{{(j,l,\Phi ,\theta )}_{TZCNS}}} \end{array}}}{{\partial \Phi }} = \frac{{\begin{array}{*{20}{l}} { \mp 2{\rm{ \mathsf{ π} }}{\gamma _0}{\rm{sin}}\left[ {{\rm{ \mathsf{ π} }}(l + \begin{array}{*{20}{l}} {\Phi /{\Phi _0})/p} \end{array}} \right]\left\{ { \pm \cos \left[ {{\rm{ \mathsf{ π} }}\left( {j - \theta /2{\rm{ \mathsf{ π} }}} \right)/m} \right]} \right\}} \end{array}}}{{p{\Phi _0}{{\left\{ {1 \pm 4\cos \left[ {\frac{{{\rm{ \mathsf{ π} }}\left( {l + \Phi /{\Phi _0}} \right)}}{p}} \right]\begin{array}{*{20}{l}} { \bullet {\rm{cos}}} \end{array}\left[ {\frac{{{\rm{ \mathsf{ π} }}\left( {j - \theta /2{\rm{ \mathsf{ π} }}} \right)}}{m}} \right] + 4{{\cos }^2}\left[ {\frac{{{\rm{ \mathsf{ π} }}\left( {j - \theta /2{\rm{ \mathsf{ π} }}} \right)}}{m}} \right]} \right\}}^{\frac{1}{2}}}}}, $ | (5) |
| $ \frac{{\begin{array}{*{20}{l}} {\partial E{{(j,l,\Phi ,\theta )}_{TZCNS}}} \end{array}}}{{\partial \Phi }} = \frac{{\begin{array}{*{20}{l}} { \mp 2{\rm{ \mathsf{ π} }}{\gamma _0}{\rm{sin}}\left[ {{\rm{ \mathsf{ π} }}(l + \begin{array}{*{20}{l}} {\Phi /{\Phi _0})/p} \end{array}} \right]\left\{ { \pm \cos \left[ {{\rm{ \mathsf{ π} }}\left( {j - \theta /2{\rm{ \mathsf{ π} }}} \right)/m} \right]} \right\} + 2\cos \left[ {{\rm{ \mathsf{ π} }}(l + \begin{array}{*{20}{l}} {\Phi /{\Phi _0})/p} \end{array}} \right]} \end{array}}}{{p{\Phi _0}{{\left\{ {1 \pm 4\cos \left[ {\frac{{{\rm{ \mathsf{ π} }}\left( {l + \Phi /{\Phi _0}} \right)}}{p}} \right]\begin{array}{*{20}{l}} { \cdot {\rm{cos}}} \end{array}\left[ {\frac{{{\rm{ \mathsf{ π} }}\left( {j - \theta /2{\rm{ \mathsf{ π} }}} \right)}}{m}} \right] + 4{{\cos }^2}\left[ {\frac{{{\rm{ \mathsf{ π} }}(l + \begin{array}{*{20}{l}} {\Phi /{\Phi _0})} \end{array}}}{p}} \right]} \right\}}^{\frac{1}{2}}}}}。$ | (6) |
结合式(3), 从式(5)和(6)分母的二次根式可知, 持续电流和E (j, l, Φ, θ) /γ0成反比, 这说明费米能附近的能级对持续电流贡献较大, 其他能级贡献较小。因此, 能隙Eg较大的TCNS几乎观察不到持续电流, 比如TZCNS(18, 0, 2887, -5 774)在θ =2π/3时Eg=0.495 eV, 当Ф变化一个周期, Eg仅变化了7 μeV[16], 对应持续电流I约为10-18 A。所以为了方便研究, 本研究中将主要讨论金属型及能隙较小的半导体型TCNS。
另外, 在磁场中讨论能量色散关系时, 一般来说还应考虑塞曼效应, 即π电子的自旋—磁场相互作用的能量[17, 21] :
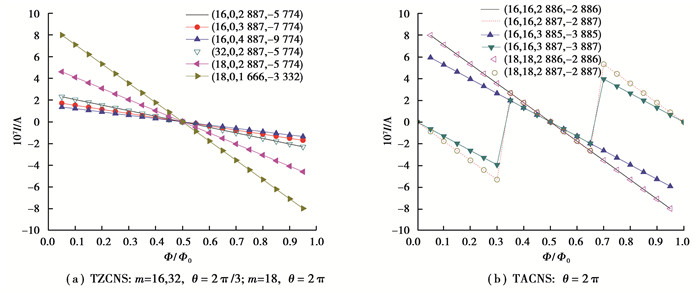
图 2显示了TZCNS及TACNS内持续电流随磁通变化的情况。通过对比很容易发现, 不管是TZCNS还是TACNS, 其内部的持续电流I数量级仅为10-7A, 其主要原因是TCNS有些能态承载的持续电流相互抵消了, 比如TACNS, 仅有(j =m+θ/2π, l<p/3)及(j =m +θ/2π, l ≥2p/3)能级对持续电流有较大贡献, 而其他能级(j =m, p/3≤l<2p/3)及(j ≠m, l)因为承载的持续电流相互抵消或远离费米能级而贡献很小。
|
图 2 随磁通变化的持续电流 Fig. 2 Persistent currents varying with magnetic flux |
TZCNS与TACNS内持续电流随磁通变化的规律并不完全相同。首先是持续电流方向不完全相同, 比如在一个周期内, 当Ф比较小时, TZCNS及p =3i (i为整数)TACNS的持续电流为正, 但p ≠3i TACNS的持续电流为负, 如图 2所示, 这说明前者具有顺磁性, 后者具有抗磁性。另外, TZCNS的持续电流变化都呈线性关系, 而TACNS则出现了曲线, 这主要是由它们的能隙在磁场中不同的变化规律引起, 比如TZCNS的Eg=0 eV都出现在Ф =iФ0处, 而TACNS则有2种可能, 如果是p =3i的金属型, 则Eg =0 eV出现在Ф =iФ0处, 如果是p ≠3i的半导体型, 则最小能隙出现在Ф =(i ±1/3)Ф0处。由于费米能附近的能级对持续电流的贡献最大, 也最容易受到磁场的影响, 因此半导体型TACNS在(i ±1/3)Ф0处发生越变从而形成了曲线。这种在Ф =iФ0和Ф =(i ±1/3)Ф0处容易受影响的表现, 在考虑温度或塞曼效应影响时还会再次出现。
卷环周长对持续电流有重要的影响, 随着卷环周长增大, TZCNS及TACNS内的持续电流都逐渐减小, 如图 2(a)中m =16的TZCNS, 随着p =2 887, 3 887, 4 887取值增大, 持续电流明显减小, 图 2(b)中m =16的TACNS随着p取值增大也有类似的现象。另外, 当卷环周长相同时, 持续电流大小相等, 比如图 2(a)中p =2 887的TZCNS在m =16, 32时, 持续电流曲线重合, 其大小完全相同; 图 2 (b)中m =16, 18的TZCNS在p =2 886时持续电流曲线也完全重合。这些现象说明持续电流大小与卷环周长密切相关, 而与卷口大小无关。
另外值得注意的是, 除了卷环周长, 结构参数θ对持续电流也有很大的影响。对比图 2(a)m =18, p =1 666的TZCNS与图 2(b)中m =16, p =2 886的TACNS, 可以发现, 尽管TCNS类型不同, 可当两者卷环周长相等, 结构参数θ都取值2π时, 持续电流曲线完全相同; 而图 2(a)中m =16, 18的TZCNS虽然TCNS类型相同, 也具有完全相同的卷环周长(p =2 887), 但持续电流却完全不同, 其主要原因是它们的结构参数θ不同, 分别取值2π/3和2π。
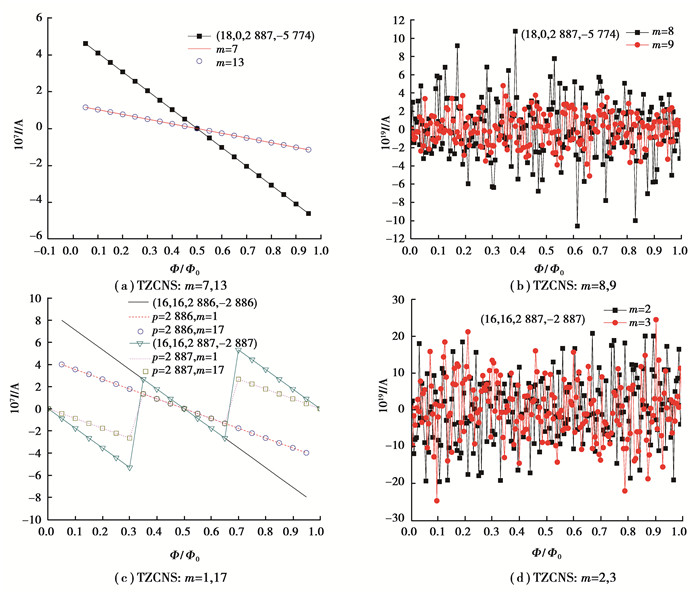
2.2 前言图 3显示了TZCNS及TACNS各分离能级对持续电流的贡献。对于TZCNS, 其持续电流几乎都是由j =m/3+θ/2π及2m/3+θ/2π能级贡献的, 比如图 3(a)中的m =7, 13能级, 其上承载的持续电流大小相等, 相加后几乎和总持续电流重合, 而远离费米能级的m =8, 9能级, 其上持续电流I约为10-19A, 大约只占总电流的千亿分之一, 如图 3 (b)所示。TACNS也有类似的规律, 有主要贡献的能级是j =θ/2π及m +θ/2π, 如图 3(c)和(d)。以上现象说明各分离能级中, 靠近费米能级的能级对持续电流有主要贡献, 其他能级贡献非常小, 其变化规律与式(5)和(6)的结论完全相同。
|
图 3 能级对持续电流的贡献 Fig. 3 Contribution of energy level to persistent currents |
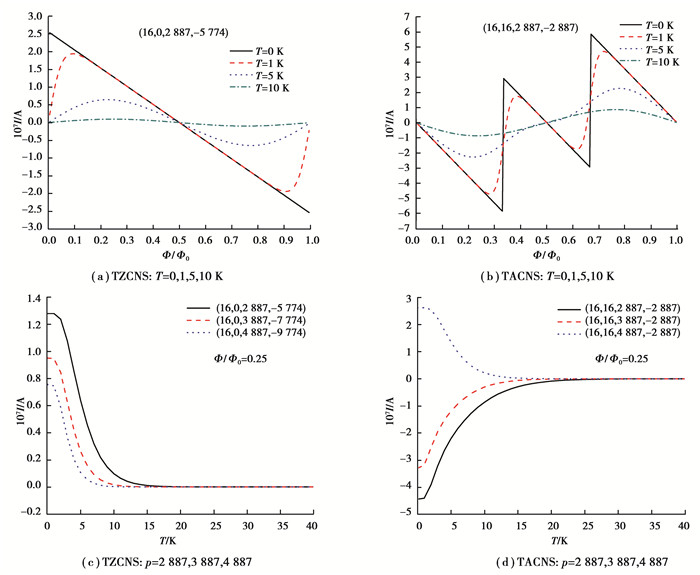
温度没有改变持续电流的周期性和对称性, 如图 4(a)和(b)所示, 这点还可以从式(1)和(2)看出, 温度没有影响TCNS的电子结构。当T ≠0 K, 电子受热激发影响, 将占据E (j, l, Φ, θ) >0的能级, 其上产生的持续电流和E (j, l, Φ, θ)<0能级承载的持续电流方向相反, 从而会出现相互抵消的现象。随着温度逐渐升高, 抵消越显著, 总的持续电流下降幅度越大, 如图 4所示。卷环越大受温度影响越明显, 电流消失得越快。对于p =2 887的TACNS, 当T =30 K时I约为10-10A, 而p =2887的TZCNS在T =17 K时就已经降到此数量级, 此时的持续电流太小, 几乎消失, 如图 4(c)和(d)所示。另外, 随着温度升高, 持续电流变化最显著的位置出现在Ф =iФ0和Ф = (i ±1/3)Ф0处, 该现象和几何结构影响分析结果一致。
|
图 4 温度对持续电流的影响 Fig. 4 Effect of temperature on persistent currents |
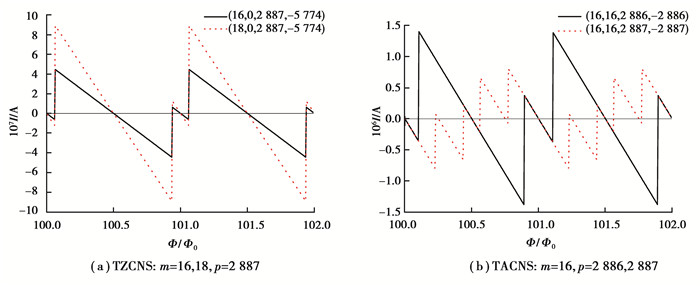
在Φ比较大的情况下, 还必须考虑塞曼效应的影响。图 5显示的是T=0K、Ф =100Ф0 ~102Ф0时, 考虑塞曼分裂后的持续电流变化情况。由于自旋-磁场相互作用, 自旋向下的能态能量降低, 变为占据态, 而自旋向上能态的能量升高, 变为非占据态, 使TCNS能级出现了新的越变, 该越变跨过了费米能级, 产生了新的金属→半导体转变, 从而导致对应能级的持续电流也出现了新的越变。通过比较图 4, 可以发现在Ф = iФ0和Ф =(i ±1/3)Ф0附近持续电流出现了新的越变, 新越变的具体位置可由E (j, l, Φ, θ) =E (σ, Φ)给出。另外还发现, 考虑塞曼效应后, 在每个周期内Φ取值较小时, TZCNS及p =3i TACNS从顺磁性都变为抗磁性。
|
图 5 塞曼分裂对持续电流的影响 Fig. 5 Theeffect of Zeeman sppitting on persistent currents |
在紧束缚模型的基础上, 导出了相应的持续电流表达式, 并系统地研究了TCNS几何结构、分离能级、温度及塞曼效应对持续电流的影响。结果表明, 在每个周期内Φ取值较小时, TZCNS及p =3i TACNS具有顺磁性, p ≠3i TACNS具有抗磁性; 卷环周长及结构参数θ对持续电流有重要影响, 随着卷环周长增大, TCNS内的持续电流逐渐减小; TZCNS的j =m/3+θ/2π及2m/3+θ/2π能级, TACNS的j =θ/2π及m +θ/2π能级都靠近费米能级, 它们几乎承载了所有持续电流, 而远离的其他能级贡献非常小; 随着温度升高, 持续电流急剧减小, 卷环越大, 持续电流下降得越快, 当T ≥30 K时, p =2 887 TACNS的持续电流几乎消失; 对于较大的Φ, 考虑塞曼效应后, TCNS能级出现了新的越变, 并跨过了费米能级, 从而导致持续电流在Ф =iФ0和Ф =(i ±1/3)0Ф附近出现了新的越变。
| [1] |
Büttiker M, Imry Y, Landauer R, et al. Josephson behavior in small normal one-dimensional rings[J]. Physics Letters A, 1983, 96(7): 365-367. DOI:10.1016/0375-9601(83)90011-7 |
| [2] |
Chandrasekhar V, Webb R A, Brady M J, et al. Magnetic response of a single, isolated goldloop[J]. Physical Review Letters, 1991, 67(25): 3578. DOI:10.1103/PhysRevLett.67.3578 |
| [3] |
Liu J, Dai H J, HafnerJ H, et al. Fullerene 'cropcircles'[J]. Nature, 1997, 385(6619): 780-781. |
| [4] |
Haddon R C, et al. Electronic properties of carbon toroids[J]. Nature, 1997, 388(6637): 31-32. |
| [5] |
Louis E, Vergés J A, Chiappe G, et al. Dimensional and band-structure effects on persistent currents in mesoscopic metallic rings[J]. Physical Review B, 1998, 58(11): 6912. DOI:10.1103/PhysRevB.58.6912 |
| [6] |
Bolívar N, Medina E, Berche B, et al. Persistent charge and spin currents in the long-wavelength regime for graphene rings[J]. Physical Review B, 2014, 89(12): 125413. DOI:10.1103/PhysRevB.89.125413 |
| [7] |
缪晶晶, 张潇元, 史友进, 等. 石墨烯纳米环的电子结构和持续电流[J]. 应用物理, 2017, 7(3): 71-76. MIU Jingjing, ZHANG Xiaoyuan, SHI Youjing, et al. Electronic structure and persistent current in graphene rings[J]. Applied Physics, 2017, 7(3): 71-76. (in Chinese) |
| [8] |
Lin M F, Chuu D S, et al. Persistent currents in toroidal carbon nanotubes[J]. Physical Review B, 1998, 57(11): 6731-6737. DOI:10.1103/PhysRevB.57.6731 |
| [9] |
Dutta P, Maiti S K, KarmakarS N, et al. Magnetic response in a zigzag carbon nanotube[J]. The European Physical Journal B, 2012, 85(4): 126. DOI:10.1140/epjb/e2012-20434-7 |
| [10] |
Szopa M, Margańska M, Zipper E, et al. Coherence of persistent currents in multiwall carbon nanotubes[J]. Physical Review B, 2004, 70(7): 075406. DOI:10.1103/PhysRevB.70.075406 |
| [11] |
Bacon R, et al. Growth, structure, and properties of graphite whiskers[J]. Journal of Applied Physics, 1960, 31(2): 283-290. DOI:10.1063/1.1735559 |
| [12] |
Viculis L M, MackJ J, Kaner R B, et al. A chemical route to carbon nanoscrolls[J]. Science, 2003, 299(5611): 1361. DOI:10.1126/science.1078842 |
| [13] |
Hamzah M A N, Johari Z, Hamid F K A, et al. Geometry effect on grapheme nanoscrolls band gap[J]. Journal of Computational and Theoretical Nanoscience, 2013, 10(3): 581-586. DOI:10.1166/jctn.2013.2737 |
| [14] |
Chen Y, L uJ, Gao Z X, et al. Structural and electronic study of nanoscrolls rolled up by a single graphene sheet[J]. The Journal of Physical Chemistry C, 2007, 111(4): 1625-1630. DOI:10.1021/jp066030r |
| [15] |
Bovin S A, Chibotaru L F, Ceulemans A, et al. The quantum structure of carbontori[J]. Journal of Molecular Catalysis A: Chemical, 2001, 166(1): 47-52. DOI:10.1016/S1381-1169(00)00458-1 |
| [16] |
王昭, 等. 磁场中环状碳纳米卷电子结构的紧束缚法研究[J]. 四川大学学报(自然科学版), 2019, 56(1): 119-124. WANG Zhao, et al. Tight binding studies on the electronic structure of toroidal carbon nanoscrolls in a magnetic field[J]. Journal of Sichuan University(Natural Science Edition), 2019, 56(1): 119-124. (in Chinese) DOI:10.3969/j.issn.0490-6756.2019.01.022 |
| [17] |
Chen R B, Lu B J, Tsai C C, et al. Persistent currents in finite zigzag carbon nanotubes[J]. Carbon, 2004, 42(14): 2873-2878. DOI:10.1016/j.carbon.2004.06.033 |
| [18] |
Cheung H F, Gefen Y, Riedel E K, et al. Persistent currents in small one-dimensional metal rings[J]. Physical Review B, 1988, 37(11): 6050-6062. DOI:10.1103/PhysRevB.37.6050 |
| [19] |
KokurinI A, et al. Electronic states and persistent currents in nanowire quantum ring[J]. Semiconductors, 2018, 52(4): 535-538. DOI:10.1134/S1063782618040188 |
| [20] |
Filippone M, Bardyn C E, Giamarchi T, et al. Controlled parity switch of persistent currents in quantum ladders[J]. Physical Review B, 2018, 97(20): 201408. DOI:10.1103/PhysRevB.97.201408 |
| [21] |
Xu N, Ding J W, Ma M M, et al. Curvature and Zeeman effects on persistent currents in a multi-walled carbon nanotorus[J]. Chinese Physics B, 2010, 19(1): 016101. DOI:10.1088/1674-1056/19/1/016101 |
 2019, Vol. 43
2019, Vol. 43

